Diffraction Impact onto Regularized Plasma Channel Formation by Femtosecond Laser Filamentation
Abstract
:1. Introduction
2. Experimental Setup
3. Results
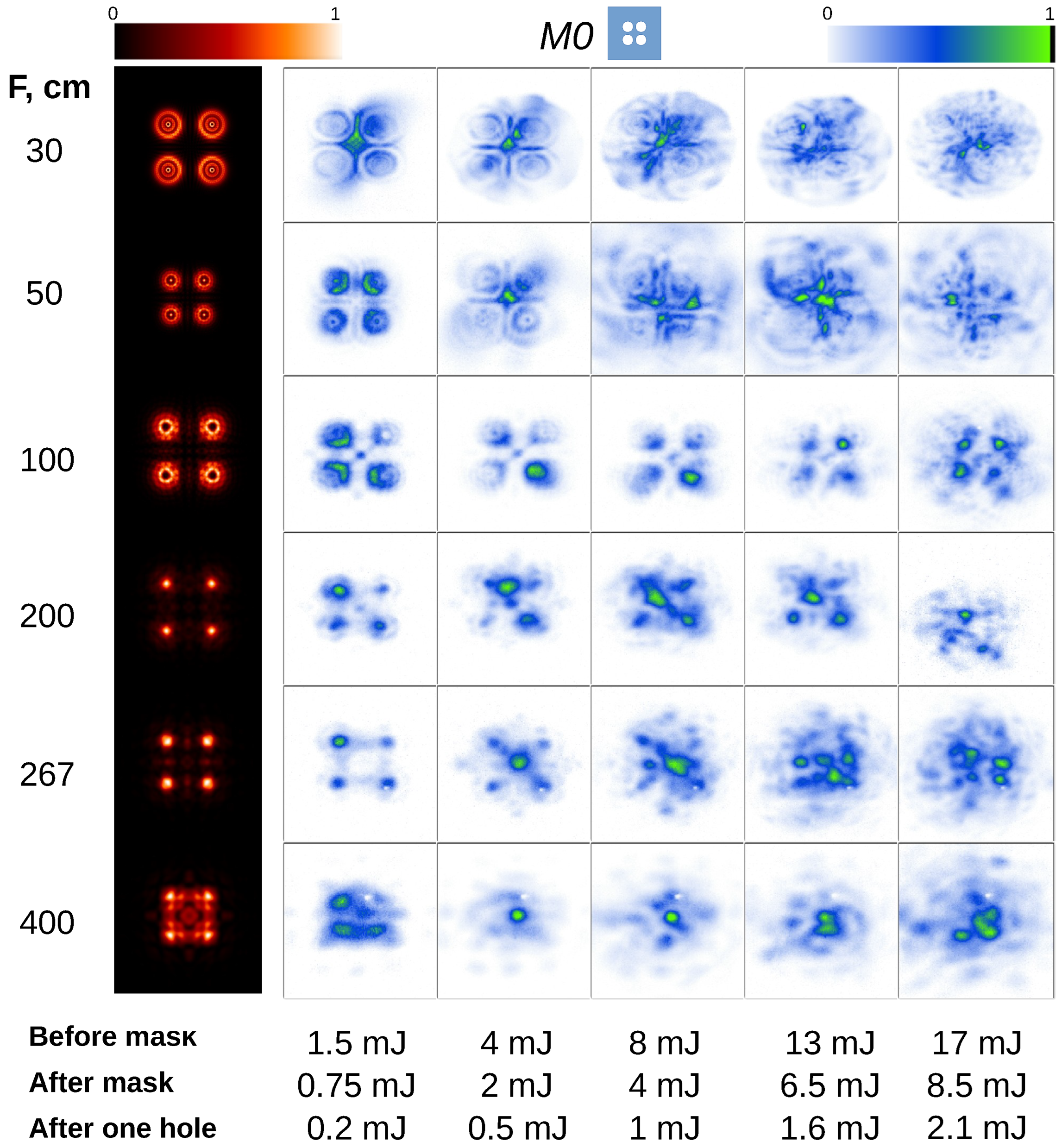
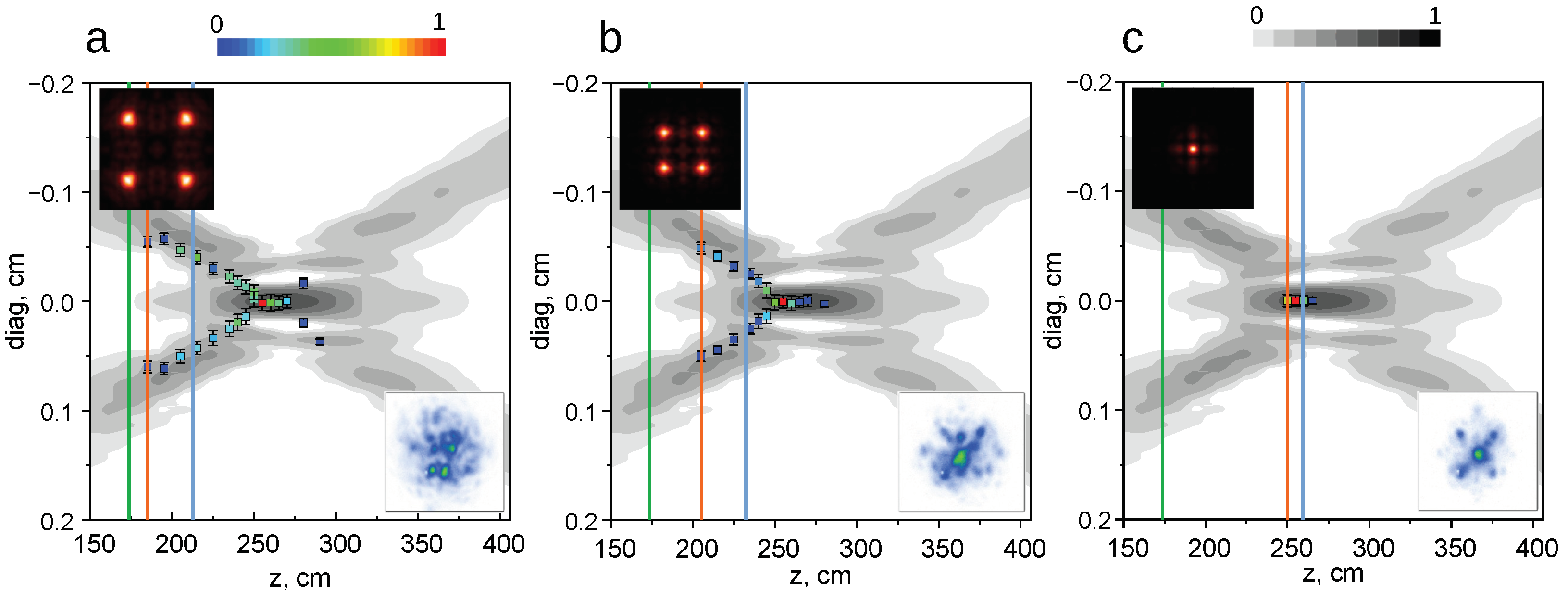
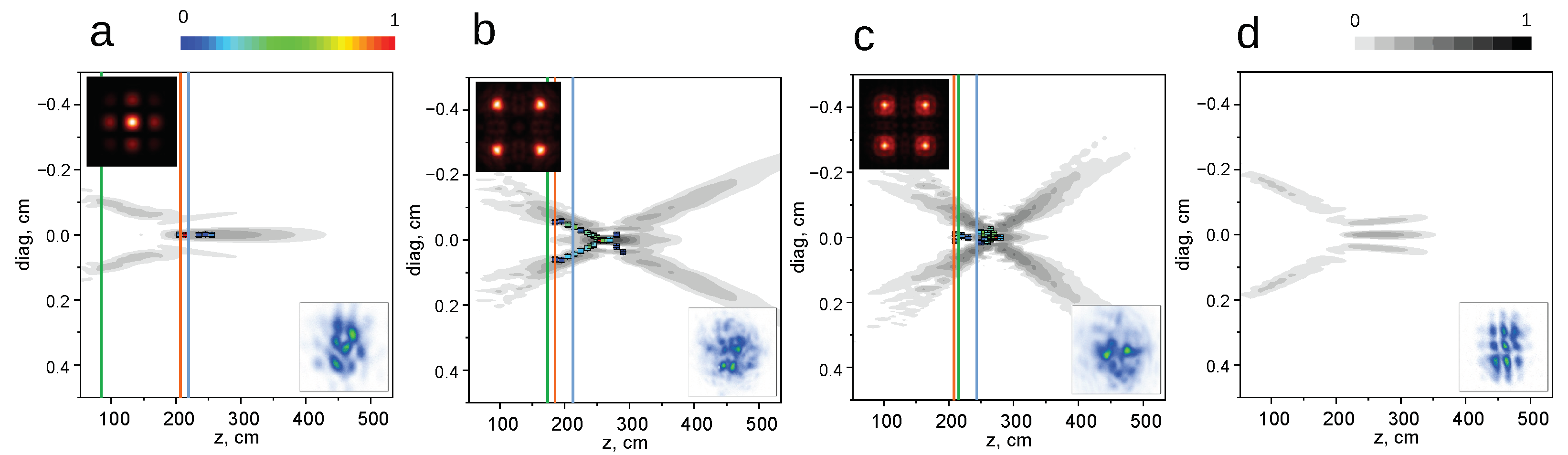
3.1. Experimental Results with M0 Mask versus Linear Diffraction Theory
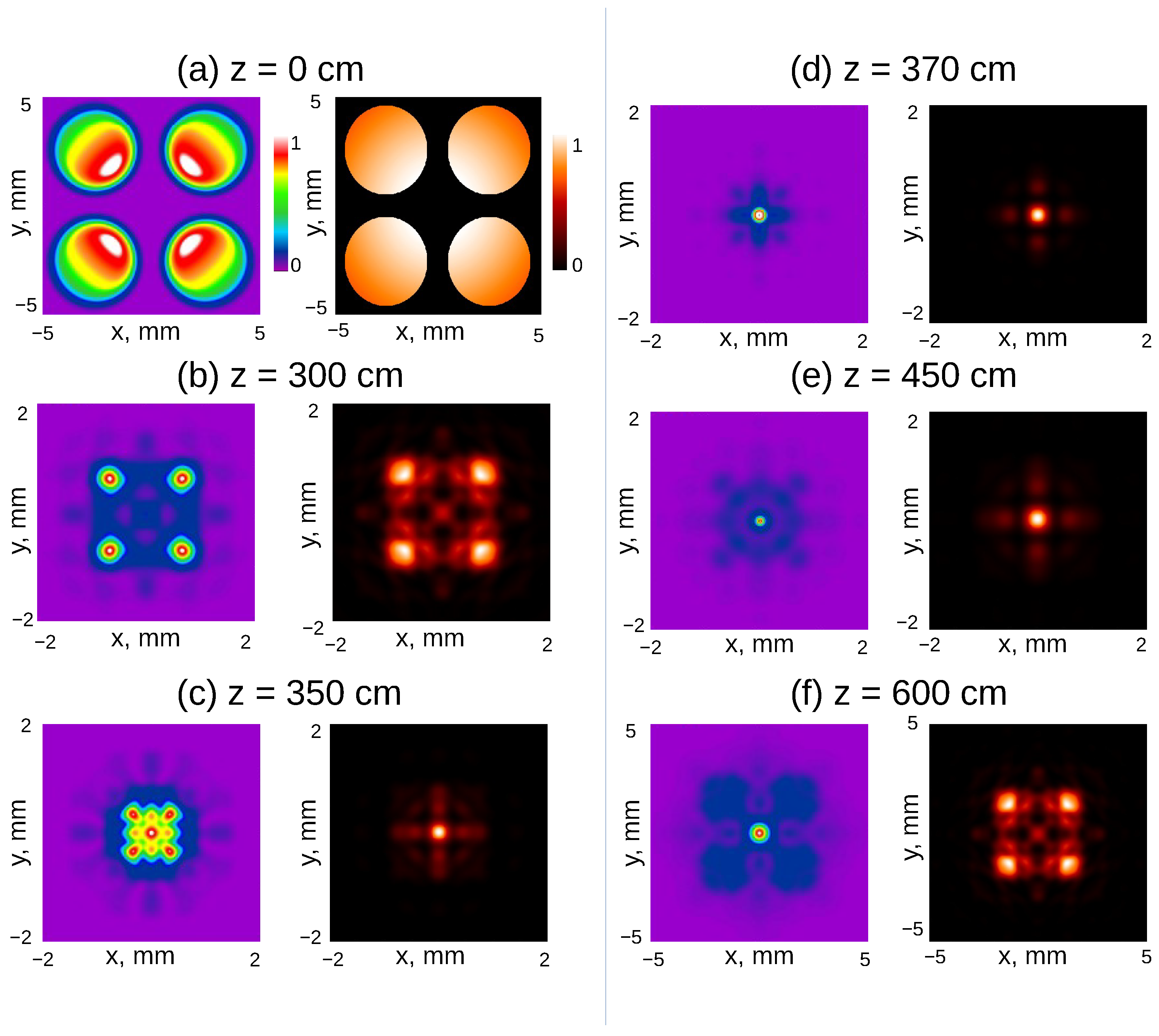
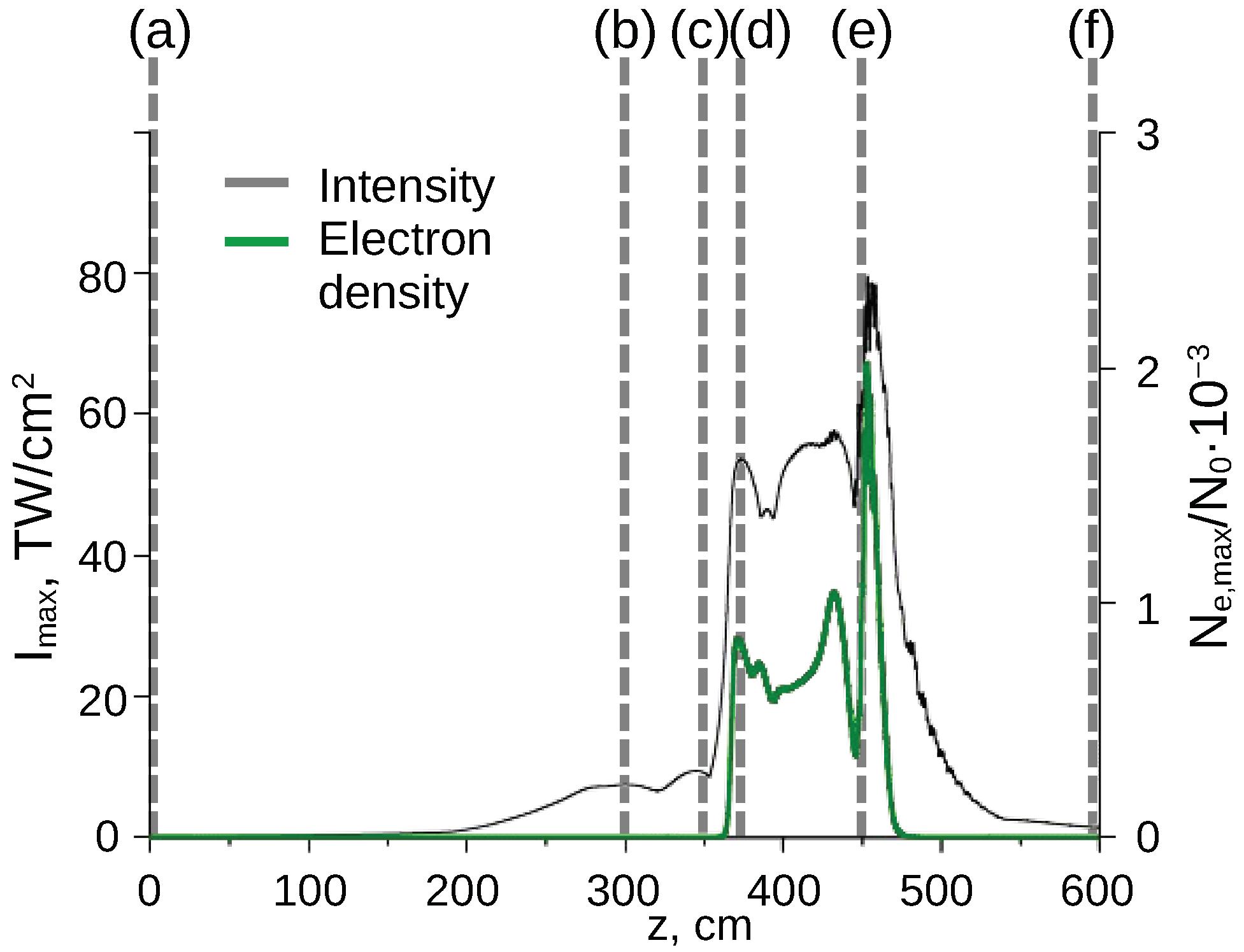
3.2. Non-Linear Simulations of Filamentation with Amplitude Mask
3.3. Effect of Mask Parameters
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Couairon, A.; Mysyrowicz, A. Femtosecond filamentation in transparent media. Phys. Rep. 2007, 441, 47–189. [Google Scholar] [CrossRef]
- Kandidov, V.P.; Shlenov, S.A.; Kosareva, O.G. Filamentation of high-power femtosecond laser radiation. Quantum Electron. 2009, 39, 205. [Google Scholar] [CrossRef]
- Chin, S.L. Femtosecond Laser Filamentation; Springer: Berlin/Heidelberg, Germany, 2010; Volume 55. [Google Scholar]
- Liu, X.; Umstadter, D. Self-focusing of intense subpicosecond laser pulses in a low pressure gas. In Shortwavelength V: Physics with Intense Laser Pulses; Optica Publishing Group: Washington, DC, USA, 1993; p. PUIP45. [Google Scholar]
- Braun, A.; Korn, G.; Liu, X.; Du, D.; Squier, J.; Mourou, G. Self-channeling of high-peak-power femtosecond laser pulses in air. Opt. Lett. 1995, 20, 73–75. [Google Scholar] [CrossRef] [PubMed]
- Brodeur, A.; Chien, C.; Ilkov, F.; Chin, S.; Kosareva, O.; Kandidov, V. Moving focus in the propagation of ultrashort laser pulses in air. Opt. Lett. 1997, 22, 304–306. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Zhang, J.; Li, Y.; Zhang, J.; Li, Y.; Chen, Z.; Teng, H.; Wei, Z.; Sheng, Z. Characteristics of self-guided laser plasma channels generated by femtosecond laser pulses in air. Phys. Rev. E 2002, 66, 016406. [Google Scholar] [CrossRef] [Green Version]
- Durand, M.; Houard, A.; Prade, B.; Mysyrowicz, A.; Durécu, A.; Moreau, B.; Fleury, D.; Vasseur, O.; Borchert, H.; Diener, K.; et al. Kilometer range filamentation. Opt. Express 2013, 21, 26836–26845. [Google Scholar] [CrossRef] [Green Version]
- Théberge, F.; Liu, W.; Simard, P.T.; Becker, A.; Chin, S.L. Plasma density inside a femtosecond laser filament in air: Strong dependence on external focusing. Phys. Rev. E 2006, 74, 036406. [Google Scholar] [CrossRef] [Green Version]
- Hamster, H.; Sullivan, A.; Gordon, S.; White, W.; Falcone, R. Subpicosecond, electromagnetic pulses from intense laser-plasma interaction. Phys. Rev. Lett. 1993, 71, 2725. [Google Scholar] [CrossRef]
- Liu, Y.; Houard, A.; Prade, B.; Akturk, S.; Mysyrowicz, A.; Tikhonchuk, V. Terahertz radiation source in air based on bifilamentation of femtosecond laser pulses. Phys. Rev. Lett. 2007, 99, 135002. [Google Scholar] [CrossRef] [Green Version]
- Mitryukovskiy, S.I.; Liu, Y.; Prade, B.; Houard, A.; Mysyrowicz, A. Coherent synthesis of terahertz radiation from femtosecond laser filaments in air. Appl. Phys. Lett. 2013, 102, 221107. [Google Scholar] [CrossRef] [Green Version]
- Panov, N.; Andreeva, V.; Kosareva, O.; Shkurinov, A.; Makarov, V.; Bergé, L.; Chin, S. Directionality of terahertz radiation emitted from an array of femtosecond filaments in gases. Laser Phys. Lett. 2014, 11, 125401. [Google Scholar] [CrossRef]
- Wahlstrand, J.; Jhajj, N.; Rosenthal, E.; Zahedpour, S.; Milchberg, H. Direct imaging of the acoustic waves generated by femtosecond filaments in air. Opt. Lett. 2014, 39, 1290–1293. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vidal, F.; Comtois, D.; Chien, C.Y.; Desparois, A.; La Fontaine, B.; Johnston, T.W.; Kieffer, J.C.; Mercure, H.P.; Pépin, H.; Rizk, F.A. Modeling the triggering of streamers in air by ultrashort laser pulses. IEEE Trans. Plasma Sci. 2000, 28, 418–433. [Google Scholar] [CrossRef]
- Goffin, A.; Larkin, I.; Tartaro, A.; Schweinsberg, A.; Valenzuela, A.; Rosenthal, E.; Milchberg, H. Optical guiding in 50-meter-scale air waveguides. Phys. Rev. X 2023, 13, 011006. [Google Scholar] [CrossRef]
- Jhajj, N.; Rosenthal, E.; Birnbaum, R.; Wahlstrand, J.; Milchberg, H. Demonstration of long-lived high-power optical waveguides in air. Phys. Rev. X 2014, 4, 011027. [Google Scholar]
- Bespalov, V.; Talanov, V. Filamentary structure of light beams in nonlinear liquids. Sov. J. Exp. Theor. Phys. Lett. 1966, 3, 307. [Google Scholar]
- Mlejnek, M.; Kolesik, M.; Moloney, J.; Wright, E. Optically turbulent femtosecond light guide in air. Phys. Rev. Lett. 1999, 83, 2938. [Google Scholar] [CrossRef]
- Hosseini, S.; Luo, Q.; Ferland, B.; Liu, W.; Chin, S.; Kosareva, O.; Panov, N.; Aközbek, N.; Kandidov, V. Competition of multiple filaments during the propagation of intense femtosecond laser pulses. Phys. Rev. A 2004, 70, 033802. [Google Scholar] [CrossRef]
- Liu, W.; Chin, S. Direct measurement of the critical power of femtosecond Ti: Sapphire laser pulse in air. Opt. Express 2005, 13, 5750–5755. [Google Scholar] [CrossRef]
- Kandidov, V.P.; Akozbek, N.; Scalora, M.; Kosareva, O.G.; Nyakk, A.V.; Luo, Q.; Hosseini, S.; Chin, S. A method for spatial regularisation of a bunch of filaments in a femtosecond laser pulse. Quantum Electron. 2004, 34, 879. [Google Scholar] [CrossRef]
- Méchain, G.; Couairon, A.; Franco, M.; Prade, B.; Mysyrowicz, A. Organizing multiple femtosecond filaments in air. Phys. Rev. Lett. 2004, 93, 035003. [Google Scholar] [CrossRef] [PubMed]
- Roskey, D.; Kolesik, M.; Moloney, J.; Wright, E. The role of linear power partitioning in beam filamentation. Appl. Phys. B 2007, 86, 249–258. [Google Scholar] [CrossRef]
- Dubietis, A.; Tamosauskas, G.; Fibich, G.; Ilan, B. Multiple filamentation induced by input-beam ellipticity. Opt. Lett. 2004, 29, 1126–1128. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fibich, G.; Eisenmann, S.; Ilan, B.; Zigler, A. Control of multiple filamentation in air. Opt. Lett. 2004, 29, 1772–1774. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, H.; Chu, W.; Yu, G.; Zeng, B.; Zhao, J.; Wang, Z.; Liu, W.; Cheng, Y.; Xu, Z. Femtosecond laser filament array generated with step phase plate in air. Opt. Express 2013, 21, 4612–4622. [Google Scholar] [CrossRef]
- Shipilo, D.; Panov, N.; Sunchugasheva, E.; Mokrousova, D.; Shutov, A.; Zvorykin, V.; Ustinovskii, N.; Seleznev, L.; Savel’ev, A.; Kosareva, O.; et al. Fifteen meter long uninterrupted filaments from sub-terawatt ultraviolet pulse in air. Opt. Express 2017, 25, 25386–25391. [Google Scholar] [CrossRef]
- Chu, C.; Shipilo, D.E.; Lu, D.; Zhang, Z.; Chuchupal, S.V.; Panov, N.A.; Kosareva, O.G.; Liu, W. Femtosecond filament emergence between π-shifted beamlets in air. Opt. Express 2020, 28, 1002–1013. [Google Scholar] [CrossRef]
- Mitina, E.; Uryupina, D.; Zhidovtsev, N.; Volkov, R.; Kosareva, O.; Savel’ev, A. Long-range robust multifilament arrays from terawatt femtosecond beam. Laser Phys. Lett. 2021, 19, 015201. [Google Scholar] [CrossRef]
- Pushkarev, D.; Lar’kin, A.; Mitina, E.; Zhidovtsev, N.; Uryupina, D.; Volkov, R.; Karpeev, S.; Khonina, S.; Karabutov, A.; Geints, Y.E.; et al. Robust multifilament arrays in air by Dammann grating. Opt. Express 2021, 29, 34189–34204. [Google Scholar] [CrossRef]
- Kandidov, V.; Akozbek, N.; Scalora, M.; Kosareva, O.; Nyakk, A.; Luo, Q.; Hosseini, S.; Chin, S. Towards a control of multiple filamentation by spatial regularization of a high-power femtosecond laser pulse. Appl. Phys. B 2005, 80, 267–275. [Google Scholar] [CrossRef]
- Cook, K.; Kar, A.; Lamb, R. White-light filaments induced by diffraction effects. Opt. Express 2005, 13, 2025–2031. [Google Scholar] [CrossRef] [PubMed]
- Uryupina, D.; Bychkov, A.; Pushkarev, D.; Mitina, E.; Savel’ev, A.; Kosareva, O.; Panov, N.; Karabutov, A.; Cherepetskaya, E. Laser optoacoustic diagnostics of femtosecond filaments in air using wideband piezoelectric transducers. Laser Phys. Lett. 2016, 13, 095401. [Google Scholar] [CrossRef]
- Pushkarev, D.; Mitina, E.; Shipilo, D.; Panov, N.; Uryupina, D.; Ushakov, A.; Volkov, R.; Karabutov, A.; Babushkin, I.; Demircan, A.; et al. Transverse structure and energy deposition by a subTW femtosecond laser in air: From single filament to superfilament. New J. Phys. 2019, 21, 033027. [Google Scholar] [CrossRef]
- Brea, L.S. Diffractio, Python Module for Diffraction and Interference Optics. 2019. Available online: https://pypi.org/project/diffractio/ (accessed on 9 February 2019).
- Shen, F.; Wang, A. Fast-Fourier-transform based numerical integration method for the Rayleigh-Sommerfeld diffraction formula. Appl. Opt. 2006, 45, 1102–1110. [Google Scholar] [CrossRef] [PubMed]
- Daigle, J.F.; Kosareva, O.; Panov, N.; Wang, T.J.; Hosseini, S.; Yuan, S.; Roy, G.; Chin, S. Formation and evolution of intense, post-filamentation, ionization-free low divergence beams. Opt. Commun. 2011, 284, 3601–3606. [Google Scholar] [CrossRef]
- Dawes, E.L.; Marburger, J. Computer studies in self-focusing. Phys. Rev. 1969, 179, 862. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2004; Volume 85. [Google Scholar]
- Boyd, R.W. Nonlinear Optics, 2nd ed.; Academic Press: London, UK, 1992. [Google Scholar]
- Oleinikov, P.A.; Platonenko, V.T. Raman transitions between rotational levels and self-phase modulation of subpicosecond light pulses in air. Laser Phys. 1993, 3, 618. [Google Scholar]
- Perelomov, A.M.; Popov, V.S.; Terent’ev, M.V. Ionization of atoms in a varying electric field. Sov. Phys. JETP 1966, 23, 924. [Google Scholar]
- Rae, S.; Burnett, K. Detailed simulations of plasma-induced spectral blueshifting. Phys. Rev. A 1992, 46, 1084. [Google Scholar] [CrossRef]
- Brunel, F. Harmonic generation due to plasma effects in a gas undergoing multiphoton ionization in the high-intensity limit. JOSA 1990, 7, 521–526. [Google Scholar] [CrossRef]
- Liu, W.; Théberge, F.; Arévalo, E.; Gravel, J.F.; Becker, A.; Chin, S. Experiment and simulations on the energy reservoir effect in femtosecond light filaments. Opt. Lett. 2005, 30, 2602–2604. [Google Scholar] [CrossRef] [PubMed]



| Identifier | M0 | M1 | M2 | M3 |
|---|---|---|---|---|
| Mask type | 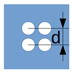 |  | 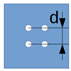 |  |
| d, mm | 5 | 3 | 5 | 8 |
| D, mm | 4 | 2 | 2 | 6 |
| , m | 5 | 1.25 | 1.25 | 11.25 |
| Transmittance, % | 50 | 16 | 10 | 41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitina, E.; Uryupina, D.; Shipilo, D.; Nikolaeva, I.; Panov, N.; Volkov, R.; Kosareva, O.; Savel’ev, A. Diffraction Impact onto Regularized Plasma Channel Formation by Femtosecond Laser Filamentation. Photonics 2023, 10, 928. https://doi.org/10.3390/photonics10080928
Mitina E, Uryupina D, Shipilo D, Nikolaeva I, Panov N, Volkov R, Kosareva O, Savel’ev A. Diffraction Impact onto Regularized Plasma Channel Formation by Femtosecond Laser Filamentation. Photonics. 2023; 10(8):928. https://doi.org/10.3390/photonics10080928
Chicago/Turabian StyleMitina, Ekaterina, Daria Uryupina, Daniil Shipilo, Irina Nikolaeva, Nikolay Panov, Roman Volkov, Olga Kosareva, and Andrei Savel’ev. 2023. "Diffraction Impact onto Regularized Plasma Channel Formation by Femtosecond Laser Filamentation" Photonics 10, no. 8: 928. https://doi.org/10.3390/photonics10080928
APA StyleMitina, E., Uryupina, D., Shipilo, D., Nikolaeva, I., Panov, N., Volkov, R., Kosareva, O., & Savel’ev, A. (2023). Diffraction Impact onto Regularized Plasma Channel Formation by Femtosecond Laser Filamentation. Photonics, 10(8), 928. https://doi.org/10.3390/photonics10080928






