Analysis and Prediction of Image Quality Degradation Caused by Diffraction of Infrared Optical System Turning Marks
Abstract
:1. Introduction
2. Methods
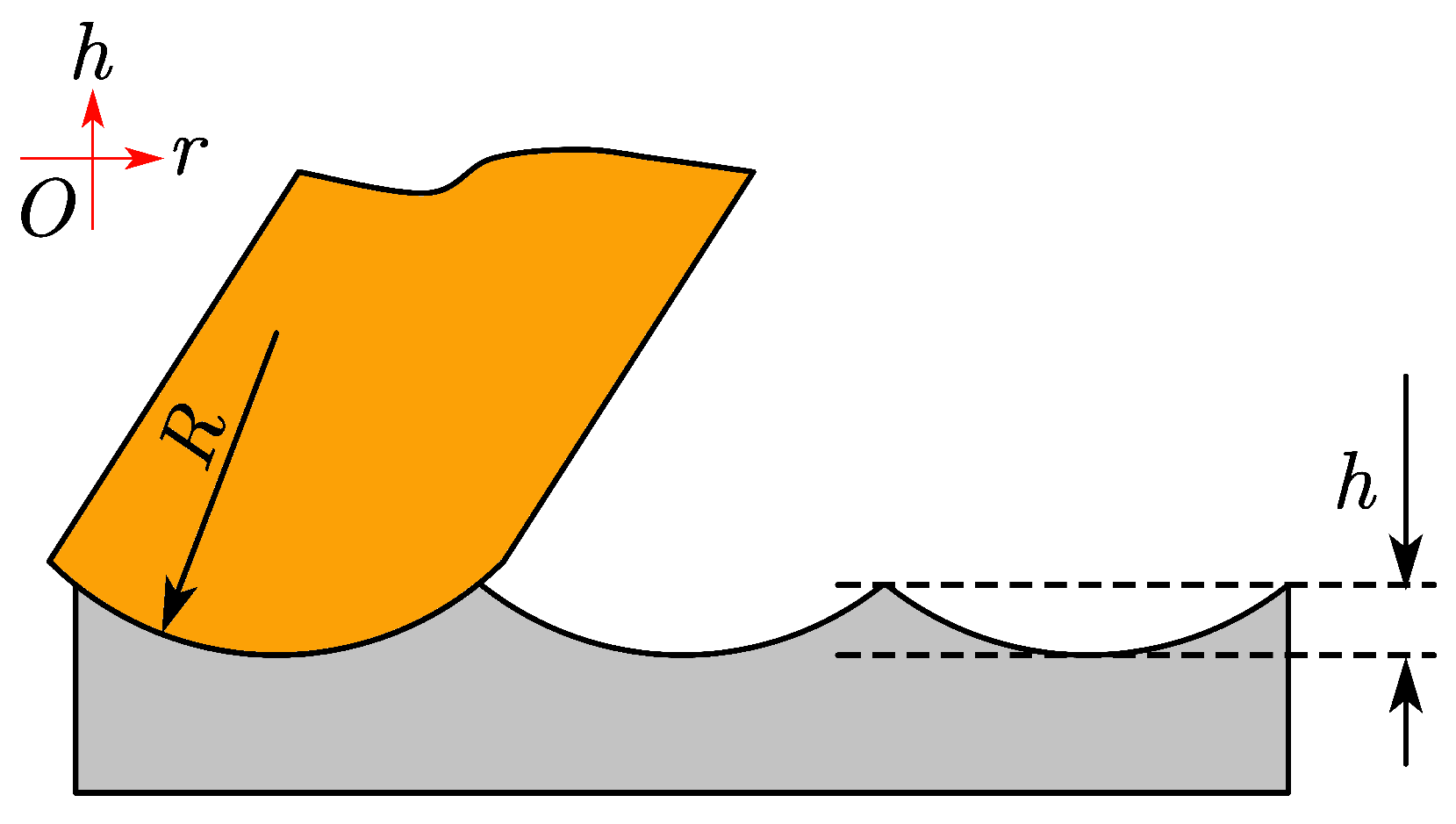
2.1. Modeling of Turning Marks Diffraction
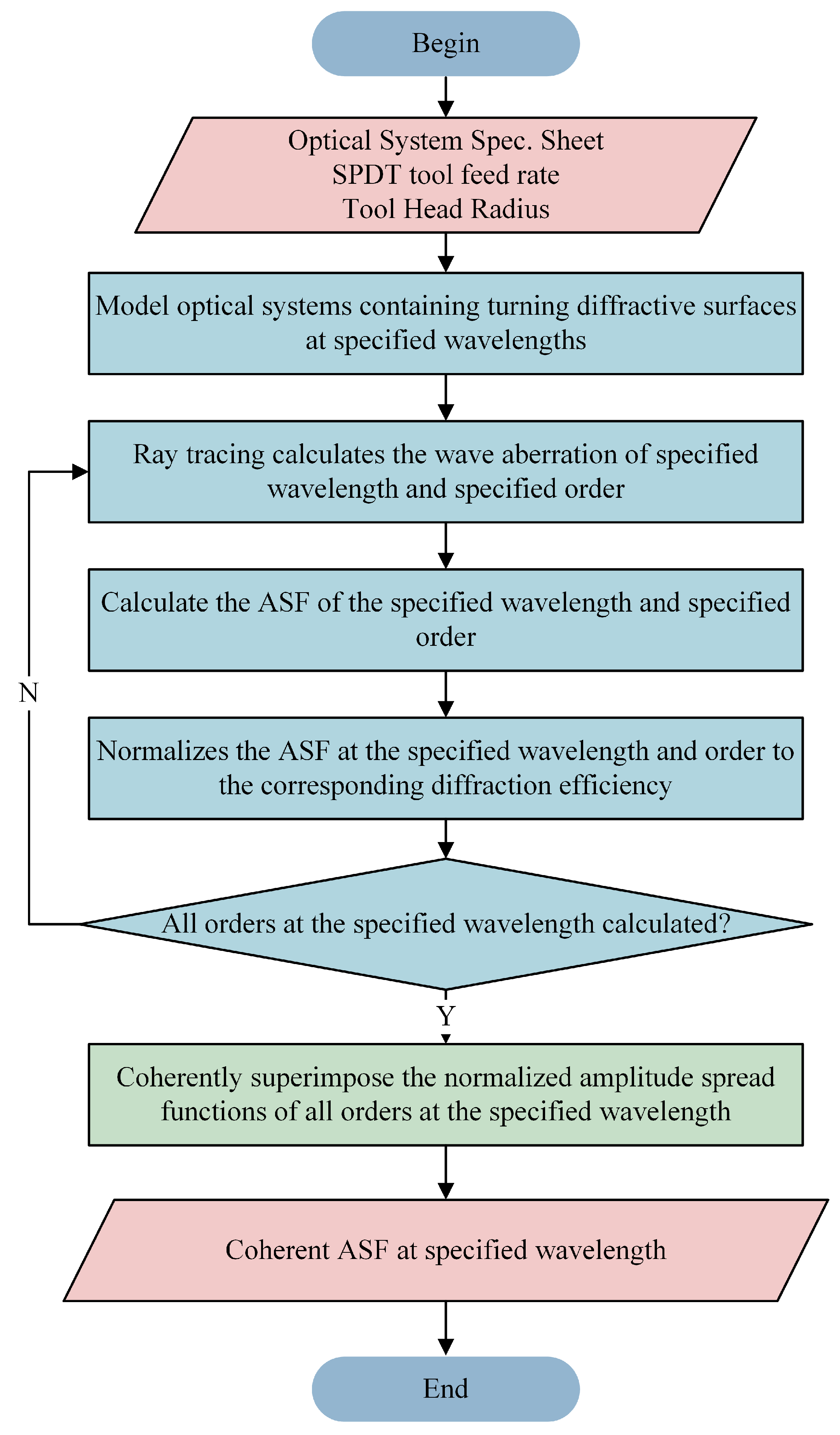
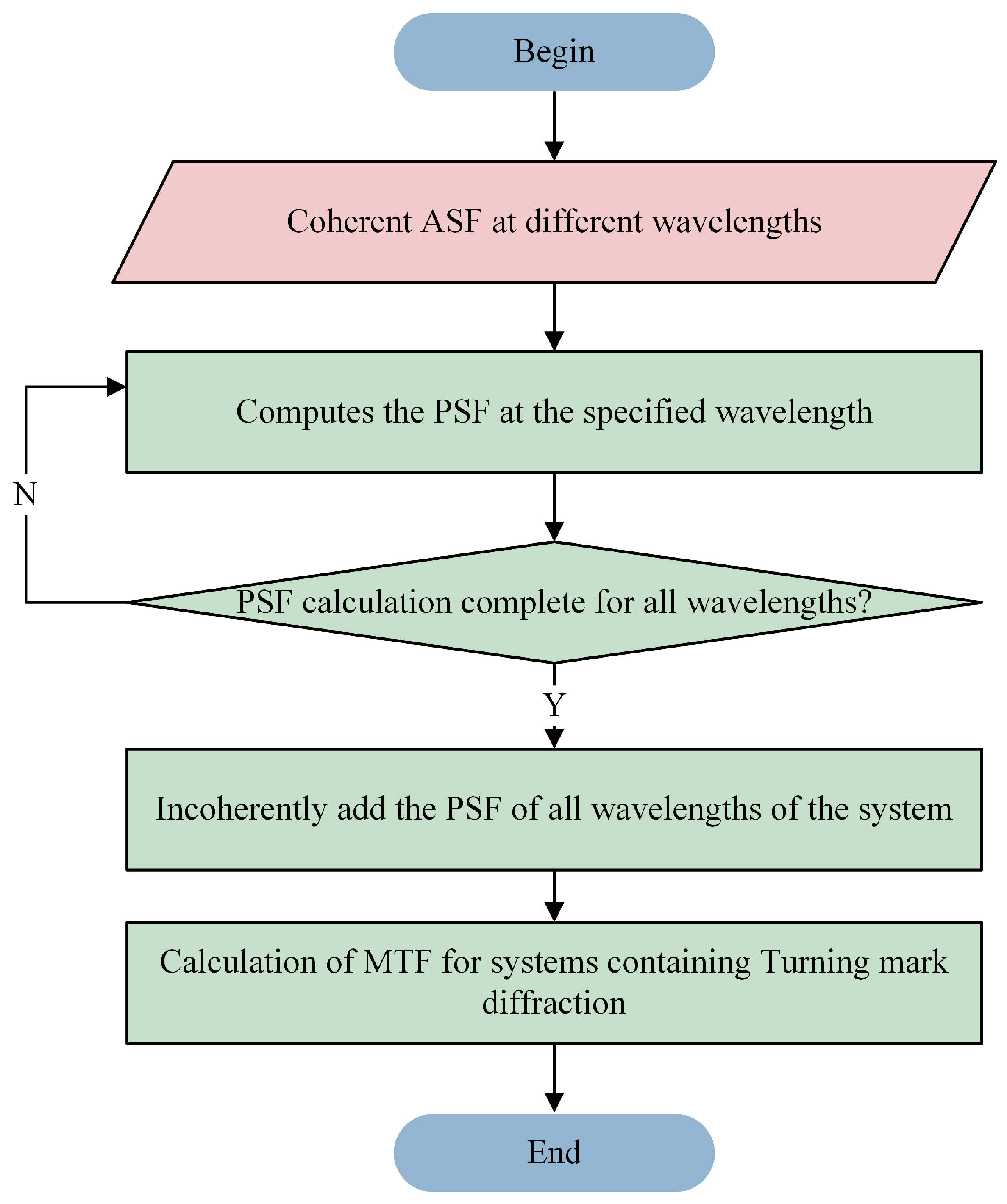
2.2. Proposed MTF Calculation Method for Turning Marks Diffraction
3. Experiments and Results
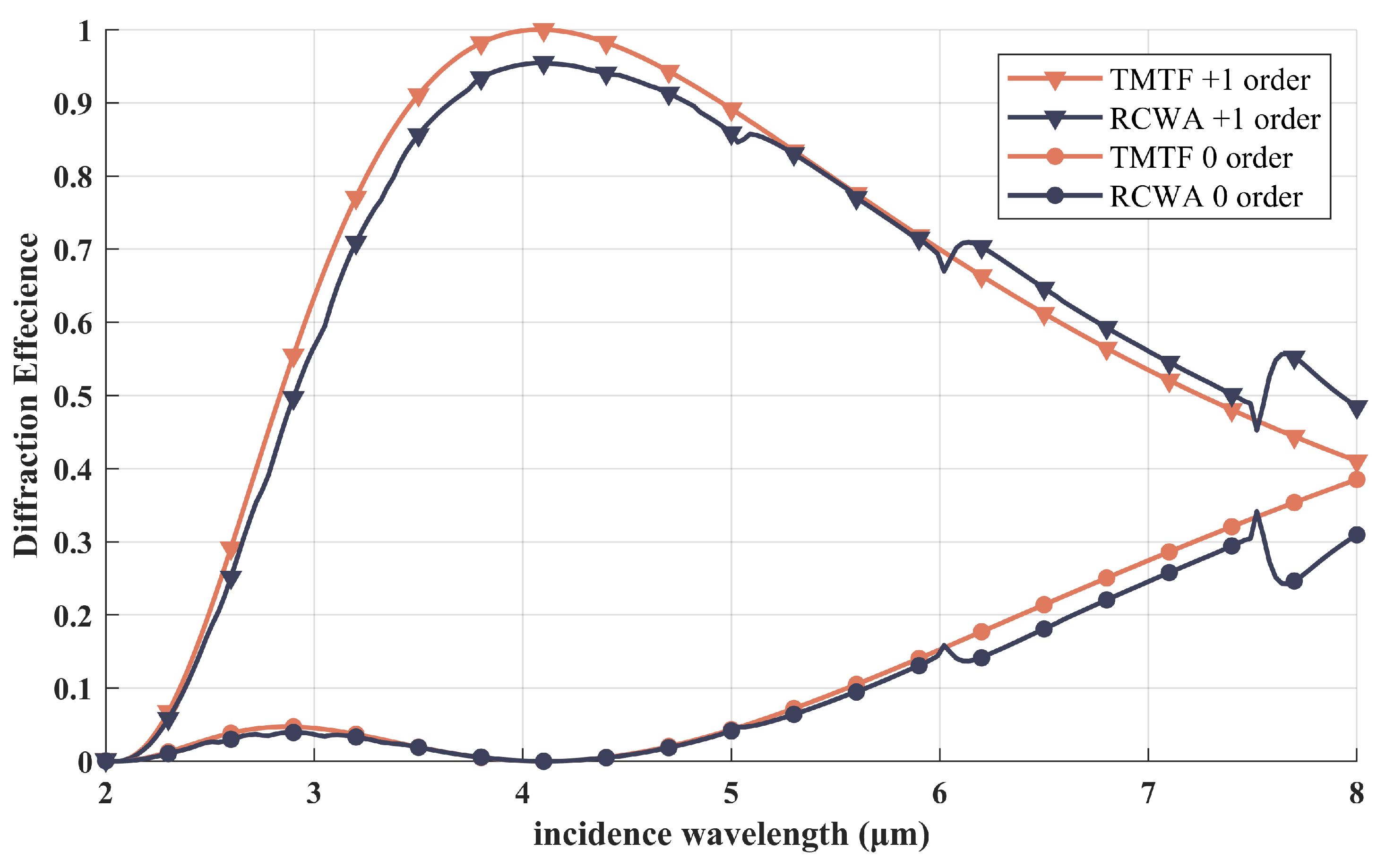
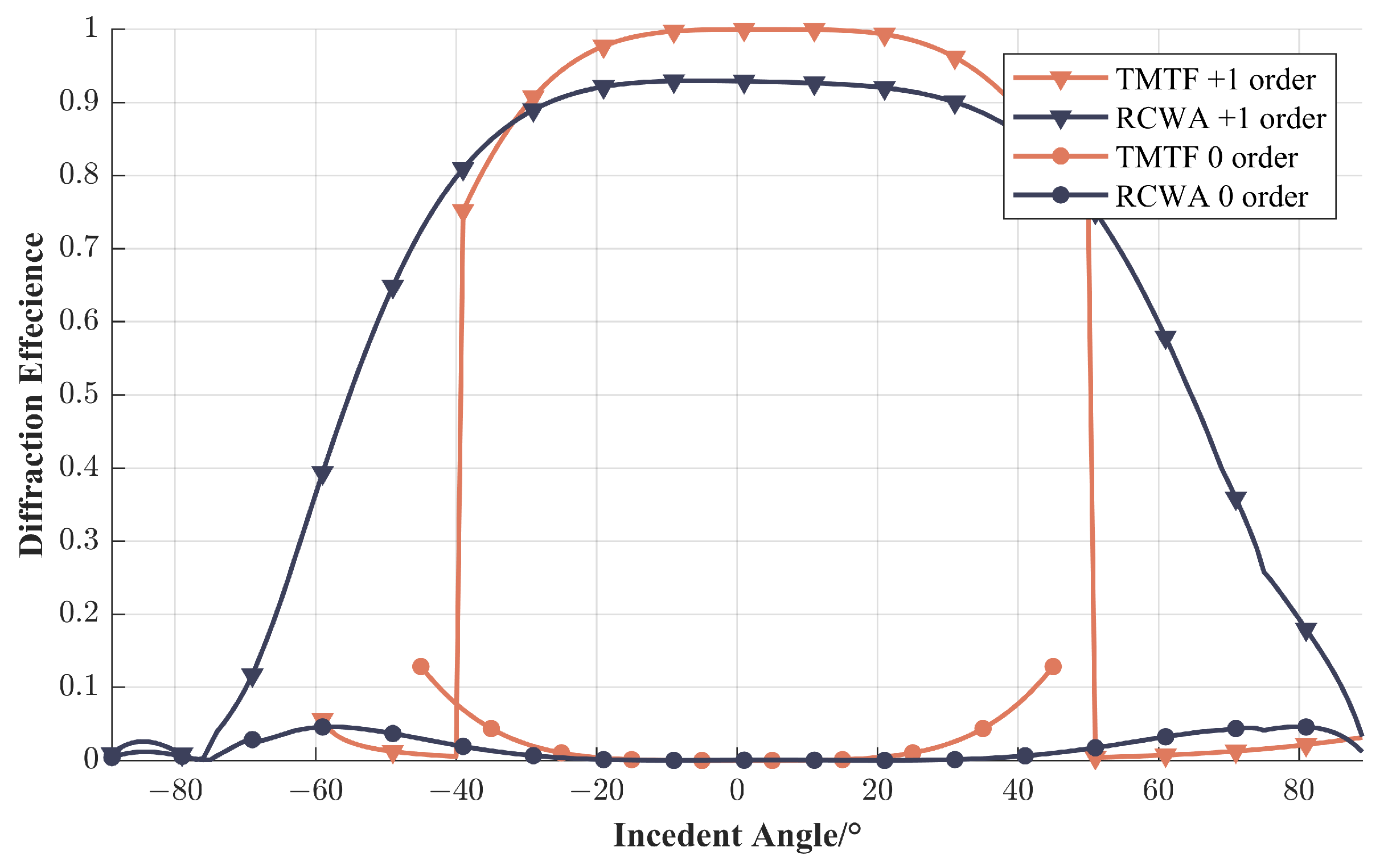
3.1. Simulation of Diffraction Efficiency Calculation by TMTF Algorithm and RCWA Algorithm
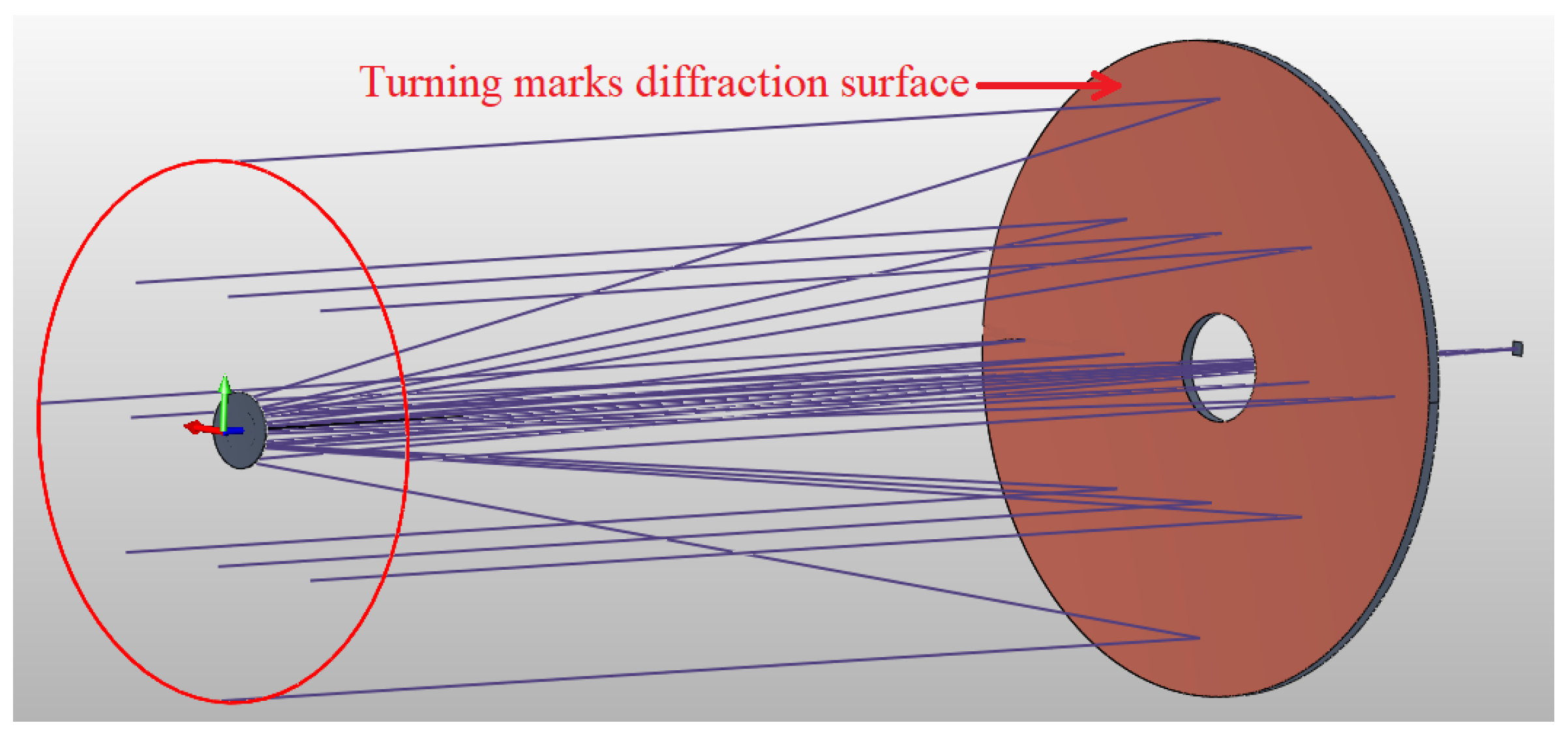
3.2. Simulation Experiment and Results of Metal-Based Mirror System
3.2.1. Diffraction Efficiency Calculation
3.2.2. Calculation of MTF for Metal-Based Reflective Optical Systems
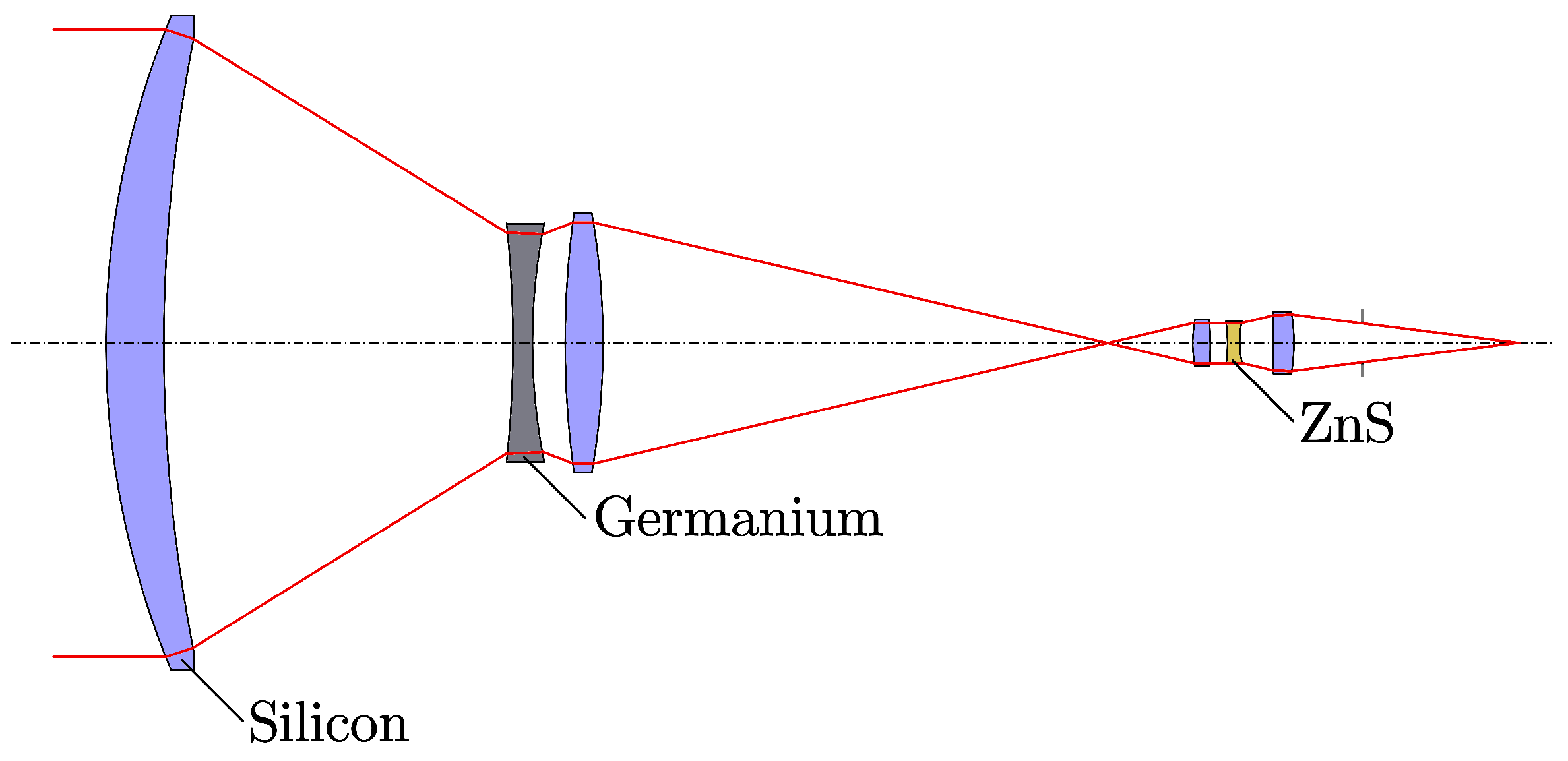
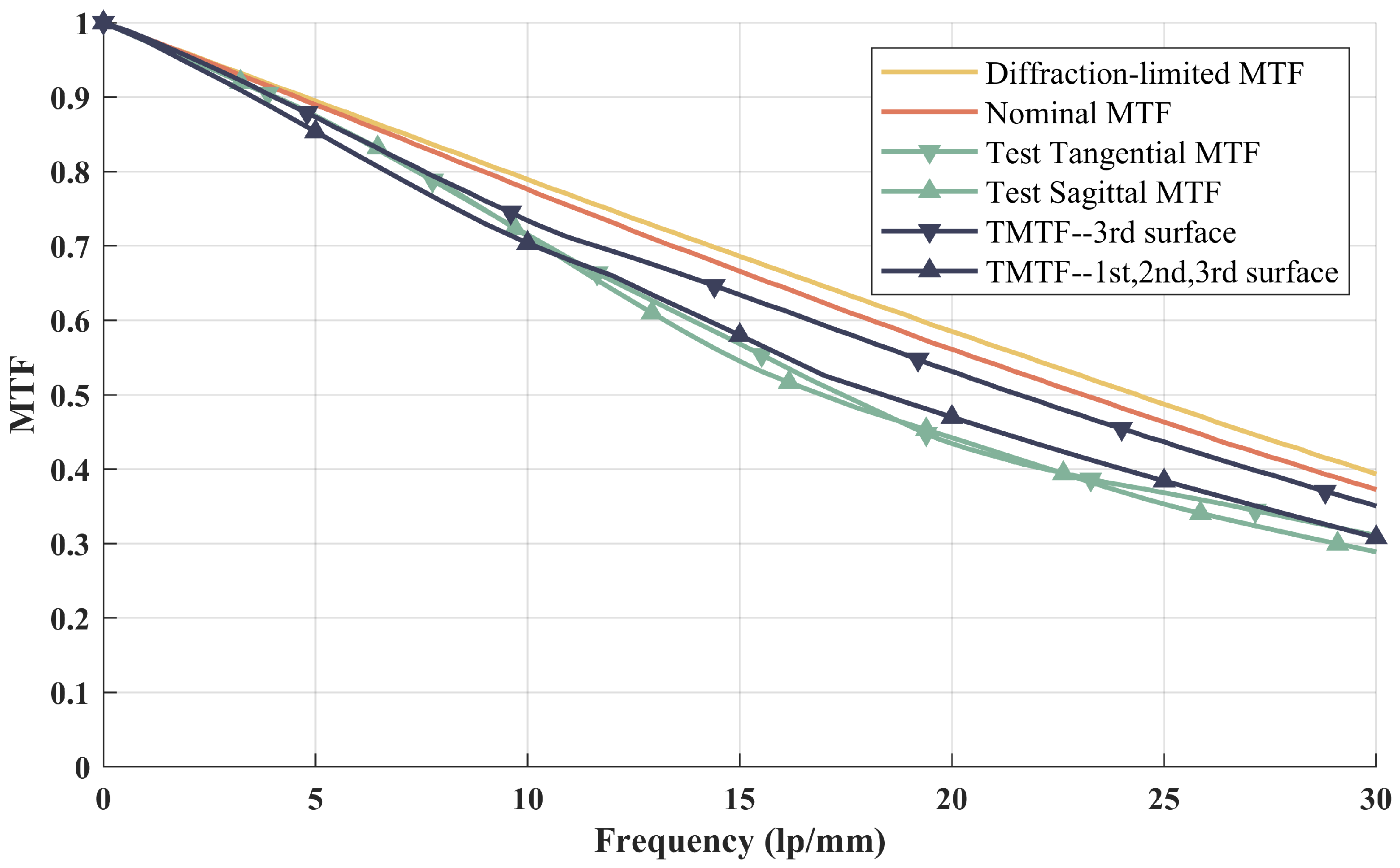
3.3. Experimental Results of Mid-Wave Infrared Optical System
4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Z.; Fang, F.; Zhang, X.; Liu, X.; Gao, H. Highly efficient machining of non-circular freeform optics using fast tool servo assisted ultra-precision turning. Opt. Express 2017, 25, 25243–25256. [Google Scholar] [CrossRef]
- Gong, H.; Ao, S.; Huang, K.; Wang, Y.; Yan, C. Tool path generation of ultra-precision diamond turning: A state-of-the-art review. Nanotechnol. Precis. Eng. 2019, 2, 118–124. [Google Scholar] [CrossRef]
- Tan, S.; Zhang, X.; Wang, L.; Wu, H.; Fu, Q.; Yan, L.; Hu, M. Equivalent Modeling and Verification of a High-Steepness and Lightweight Elliptical Aluminum Mirror. Appl. Sci. 2022, 12, 9091. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.; Qu, H.; Guan, H.; Wang, H.; Zhang, X.; Xie, X.; Wang, H.; Zhang, K.; Li, L. Design and Fabrication of an Additively Manufactured Aluminum Mirror with Compound Surfaces. Materials 2022, 15, 7050. [Google Scholar] [CrossRef]
- Church, E.L.; Zavada, J.M. Residual Surface Roughness of Diamond-Turned Optics. Appl. Opt. 1975, 14, 1788–1795. [Google Scholar] [CrossRef]
- Wu, D.; Kang, C.; Liang, F.; Yan, G.; Fang, F. Diffractive Optical Characteristics of Nanometric Surface Topography Generated by Diamond Turning. J. Manuf. Process. 2021, 67, 23–34. [Google Scholar] [CrossRef]
- Harvey, J.E.; Pfisterer, R.N. Understanding Diffraction Grating Behavior: Including Conical Diffraction and Rayleigh Anomalies from Transmission Gratings. Opt. Eng. 2019, 58, 087105. [Google Scholar] [CrossRef]
- Zhou, T.; Zhou, J.; Chen, H.; Wang, Z.; Ruan, B.; Zhao, W.; Wang, X. Study of diffractive fringes caused by tool marks for fast axis collimators fabricated by precision glass molding. Opt. Express 2022, 30, 26581–26596. [Google Scholar] [CrossRef]
- Zhou, P.; Xue, C.; Yang, C.; Liu, C.; Liu, X. Diffraction Efficiency Evaluation for Diamond Turning of Harmonic Diffractive Optical Elements. Appl. Opt. 2020, 59, 1537–1544. [Google Scholar] [CrossRef]
- Youngworth, R.N.; Stone, B.D. Simple Estimates for the Effects of Mid-Spatial-Frequency Surface Errors on Image Quality. Appl. Opt. 2000, 39, 2198–2209. [Google Scholar] [CrossRef]
- Liang, K.; Forbes, G.W.; Alonso, M.A. Validity of the Perturbation Model for the Propagation of MSF Structure in 2D. Opt. Express 2019, 27, 3390–3408. [Google Scholar] [CrossRef]
- Liang, K.; Forbes, G.W.; Alonso, M.A. Validity of the Perturbation Model for the Propagation of MSF Structures in 3D. Opt. Express 2020, 28, 20277–20295. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Collins, S.A., Jr.; Yi, A.Y. Optical Effects of Surface Finish by Ultraprecision Single Point Diamond Machining. J. Manuf. Sci. Eng. 2010, 132. [Google Scholar] [CrossRef]
- Fang, F.Z.; Huang, K.T.; Gong, H.; Li, Z.J. Study on the Optical Reflection Characteristics of Surface Micro-Morphology Generated by Ultra-Precision Diamond Turning. Opt. Lasers Eng. 2014, 62, 46–56. [Google Scholar] [CrossRef]
- Yin, Z.; Yi, Z. Direct polishing of aluminum mirrors with higher quality and accuracy. Appl. Opt. 2015, 54, 7835–7841. [Google Scholar] [CrossRef]
- Peng, W.; Hao, Z.; Yapeng, J.; Kun, Y.; Weihao, L. Removal of the single point diamond turning marks by spiral sine trace bonnet polishing process. Infrared Laser Eng. 2020, 49, 20200212-1–20200212-6. [Google Scholar] [CrossRef]
- Du, C.; Dai, Y.; Hu, H.; Guan, C. Surface roughness evolution mechanism of the optical aluminum 6061 alloy during low energy Ar+ ion beam sputtering. Opt. Express 2020, 28, 34054–34068. [Google Scholar] [CrossRef] [PubMed]
- Du, C.; Dai, Y.; Guan, C.; Hu, H. High efficiency removal of single point diamond turning marks on aluminum surface by combination of ion beam sputtering and smoothing polishing. Opt. Express 2021, 29, 3738–3753. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, Q. A Model for Predicting Surface Roughness in Single-Point Diamond Turning. Measurement 2015, 69, 20–30. [Google Scholar] [CrossRef]
- He, C.L.; Zong, W.J.; Xue, C.X.; Sun, T. An Accurate 3D Surface Topography Model for Single-Point Diamond Turning. Int. J. Mach. Tools Manuf. 2018, 134, 42–68. [Google Scholar] [CrossRef]
- He, C.L.; Wang, S.J.; Zong, W.J.; Zhang, S.T. Influence of tool edge waviness on the diffraction effect of diamond-turned optics: Theoretical simulation and experimental validation. Appl. Opt. 2019, 58, 1596–1605. [Google Scholar] [CrossRef] [PubMed]
- He, C.L.; Zong, W.J. Diffraction Effect and Its Elimination Method for Diamond-Turned Optics. Optics Express 2019, 27, 1326–1344. [Google Scholar] [CrossRef]
- He, C.; Zong, W. Influencing Factors and Theoretical Models for the Surface Topography in Diamond Turning Process: A Review. Micromachines 2019, 10, 288. [Google Scholar] [CrossRef] [PubMed]
- Sheng, P.; Shen, Z.; Jiang, L.; Fang, S.; Wang, Z. Turning Parameters Optimization for Diffraction Effect Suppression of Diamond-Turned Surface Combining Surface Micro-Topography Model and Scattering Theory. J. Manuf. Sci. Eng. 2021, 143, 111011. [Google Scholar] [CrossRef]
- Gaskill, J.D. Linear Systems, Fourier Transforms, and Optics, 1st ed.; Wiley-Interscience: New York, NY, USA, 1978. [Google Scholar]
- Harvey, J.E. Integrating optical fabrication and metrology into the optical design process. Appl. Opt. 2015, 54, 2224–2233. [Google Scholar] [CrossRef]
- Andrews, L.C. Special Functions of Mathematics for Engineers, 2nd ed.; SPIE–The International Society for Optical Engineering: Bellingham, WA, USA, 1997. [Google Scholar]
- Gross, H. (Ed.) Handbook of Optical Systems, Volume 1: Fundamentals of Technical Optics, 1st ed.; Wiley-VCH: Weinheim, Germany, 2005. [Google Scholar]
- Riley, K.F.; Hobson, M.P.; Bence, S.J. Mathematical Methods for Physics and Engineering: A Comprehensive Guide, 3rd ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2006. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics: 60th Anniversary Edition, 7th ed.; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Wolf, E. Introduction to the Theory of Coherence and Polarization of Light; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]





| Design Parameters | Design Value |
|---|---|
| Blaze wavelength | = 4.1 m |
| Design period | g = 30 m |
| Blaze order | |
| Incident wavelength | 2 m∼8 m |
| Incident angle | −89∼89 |
| Substrate material | Aluminum |
| System Parameter | Value |
|---|---|
| Pupil Diameter | 4 mm |
| Central Wavelength | 1550 nm |
| Focal Length | 288 mm |
| Mirror Substrate Material | Aluminum |
| Tool Head Radius | 1 mm |
| Feed Rate | 2 m/r |
| Algorithm | Order | Waste Time | ||
|---|---|---|---|---|
| 0 | +1 | −1 | ||
| TMTF | 94.67% | 1.23% | 2.06% | <1 min |
| VirtualLab Fusion (RCWA algorithm) | 97.468% | 0.00021379% | 0.00021379% | ∼4 h |
| Parameter | Value |
|---|---|
| Entrance pupil diameter | 76.6 mm |
| Effective focal length | 305 mm |
| Wavelength | 3.7 m, 4.1 m, 4.8 m |
| Tool radius | 1 mm |
| Feed rate | 1 m/r |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, H.; Zhang, J.; Zhao, S.; Liu, M.; Zhang, X. Analysis and Prediction of Image Quality Degradation Caused by Diffraction of Infrared Optical System Turning Marks. Photonics 2023, 10, 937. https://doi.org/10.3390/photonics10080937
Ye H, Zhang J, Zhao S, Liu M, Zhang X. Analysis and Prediction of Image Quality Degradation Caused by Diffraction of Infrared Optical System Turning Marks. Photonics. 2023; 10(8):937. https://doi.org/10.3390/photonics10080937
Chicago/Turabian StyleYe, Haokun, Jianping Zhang, Shangnan Zhao, Mingxin Liu, and Xin Zhang. 2023. "Analysis and Prediction of Image Quality Degradation Caused by Diffraction of Infrared Optical System Turning Marks" Photonics 10, no. 8: 937. https://doi.org/10.3390/photonics10080937
APA StyleYe, H., Zhang, J., Zhao, S., Liu, M., & Zhang, X. (2023). Analysis and Prediction of Image Quality Degradation Caused by Diffraction of Infrared Optical System Turning Marks. Photonics, 10(8), 937. https://doi.org/10.3390/photonics10080937




