Generation of Narrow Beams of Ultrarelativistic Positrons (Electrons) in the Breit–Wheeler Resonant Process Modified by the Field of a Strong Electromagnetic Wave
Abstract
:1. Introduction
2. Amplitude of the Process
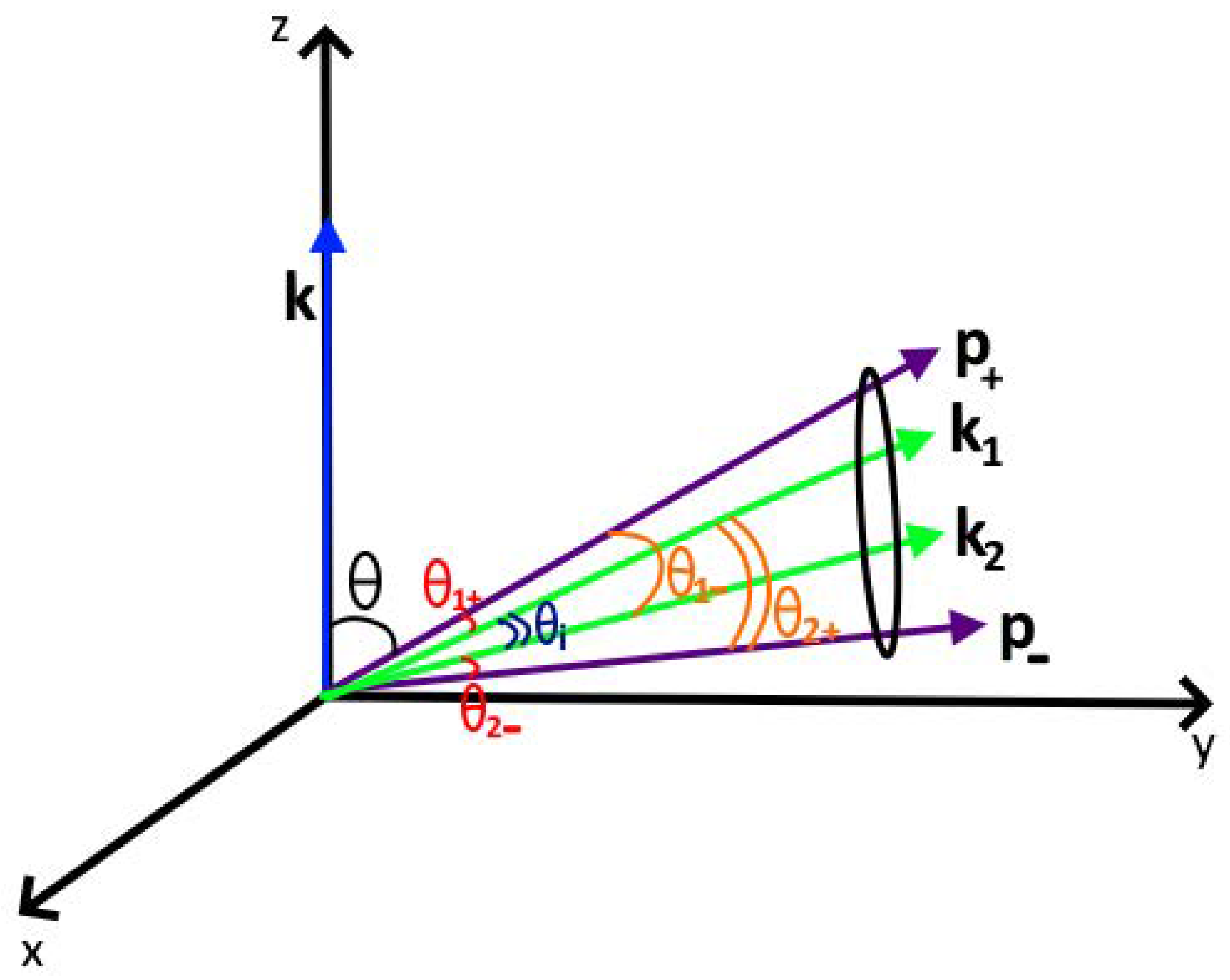
3. The Resonant Kinematics
4. The Resonant Differential Cross Section
5. Conclusions
- (1)
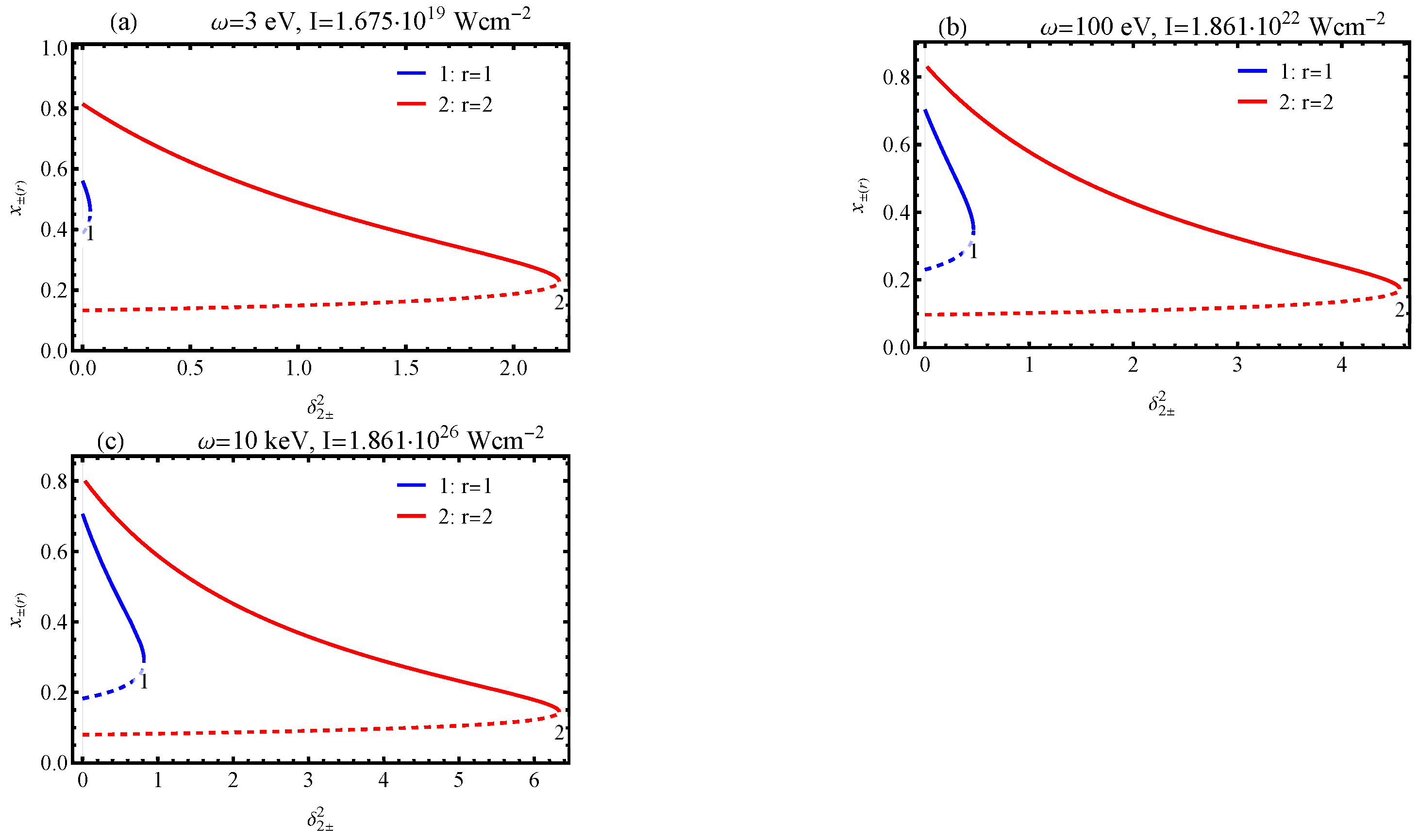
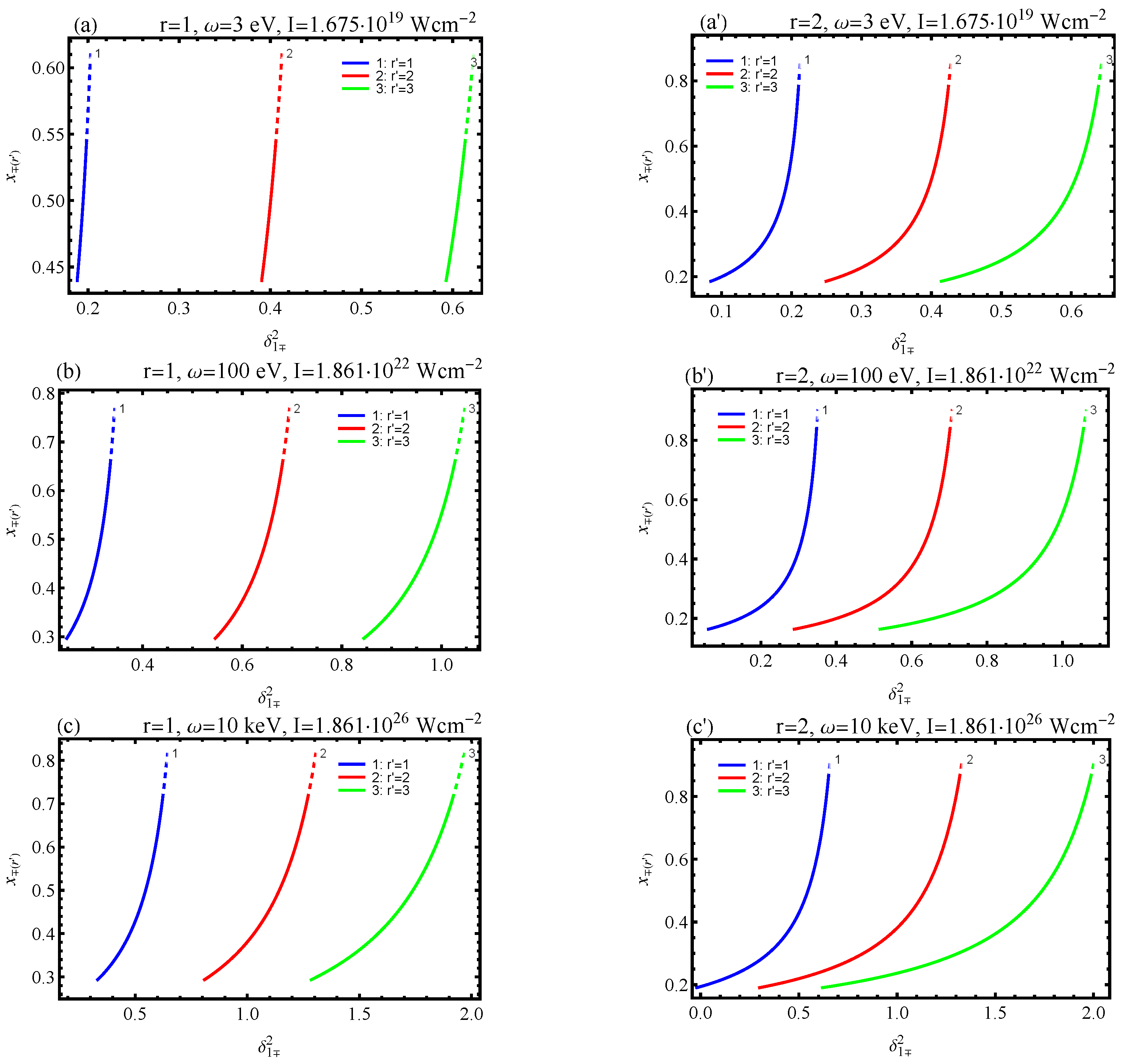
- The resonant kinematics of the process were studied in detail. It was demonstrated that the problem involves two characteristic energies: the Breit–Wheeler energy (31) and the Compton effect energy (36). These energies differed from each other by a factor of four. The ratios of the initial gamma quanta energies to these characteristic energies significantly affected the number of absorbed or emitted wave photons and, ultimately, the probability of the process.
- (2)
- (3)
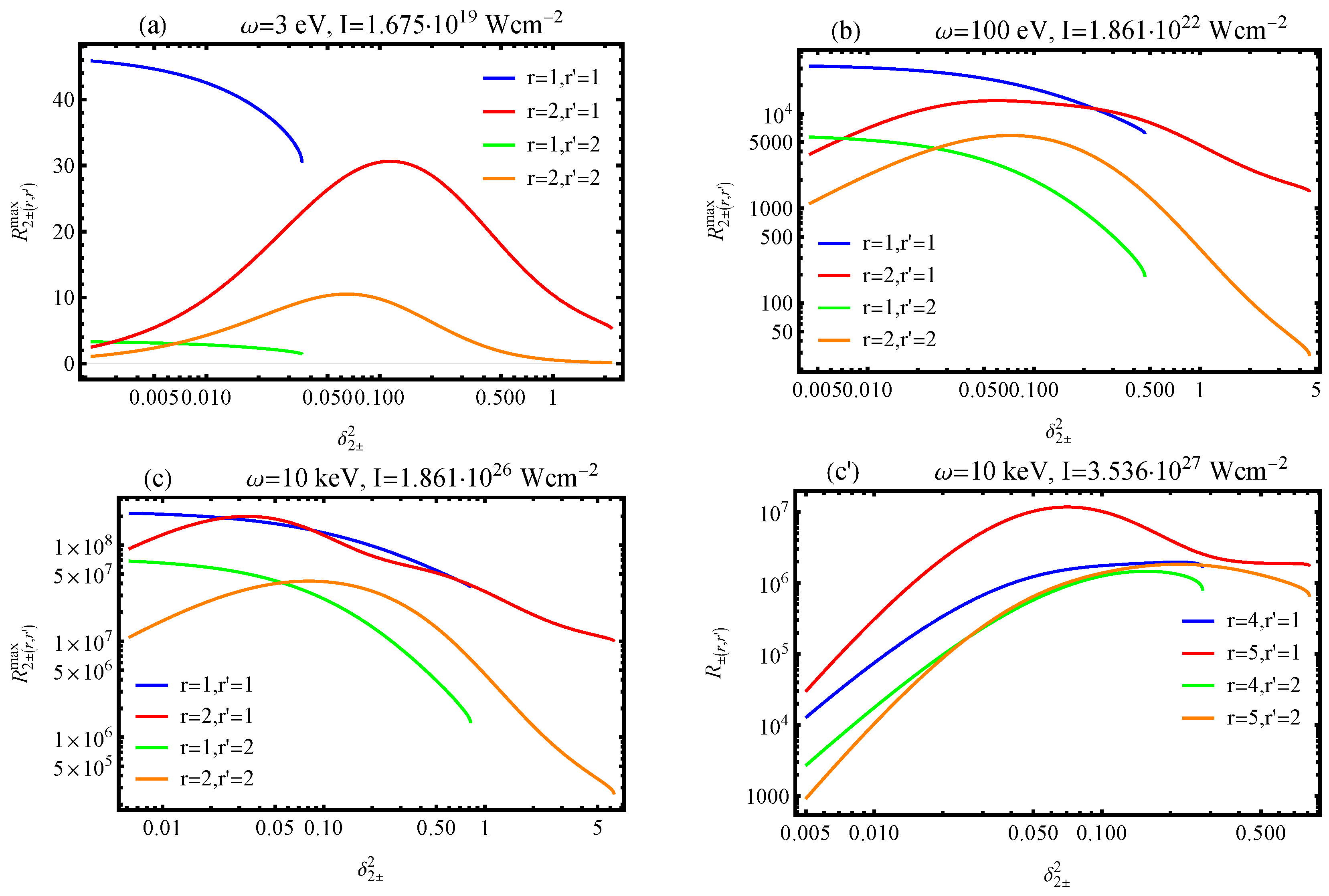
- The maximum resonant differential cross section was achieved when the energy of one of the initial gamma quantum slightly exceeded the characteristic Breit–Wheeler energy. In this case, for the optical frequency range and , the maximum resonant cross section was , whereas, for the X-ray frequency range, it was .
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ritus, V.I.; Nikishov, A.I. Quantum electrodynamics phenomena in the intense field. In Trudy FIAN; Nauka: Moscow, Russia, 1979; Volume 111, pp. 1–276. [Google Scholar]
- Roshchupkin, S.P. Resonant effects in collisions of relativistic electrons in the field of a light wave. Laser Phys. 1996, 6, 837–858. [Google Scholar]
- Roshchupkin, S.P.; Tsybul’nik, V.A.; Chmirev, A.N. The Probability of Multiphoton Processes in Quantum-Electrodynamic Phenomena in a Strong Light Field. Laser Phys. 2000, 10, 1256–1272. [Google Scholar]
- Roshchupkin, S.P.; Lebed’, A.A.; Padusenko, E.A.; Voroshilo, A.I. Quantum electrodynamics resonances in a pulsed laser field. Laser Phys. 2012, 22, 1113–1144. [Google Scholar] [CrossRef]
- Di Piazza, A.; Müller, C.; Hatsagortsyan, K.Z.; Keitel, C.H. Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 2012, 84, 1117–1228. [Google Scholar] [CrossRef]
- Mironov, A.A.; Meuren, S.; Fedotov, A.M. Resummation of QED radiative corrections in a strong constant crossed field. Phys. Rev. D 2020, 102, 053005. [Google Scholar] [CrossRef]
- Gonoskov, A.; Blackburn, T.G.; Marklund, M.; Bulanov, S.S. Charged particle motion and radiation in strong electromagnetic fields. Rev. Mod. Phys. 2022, 94, 045001. [Google Scholar] [CrossRef]
- Roshchupkin, S.P.; Voroshilo, A.I. Resonant and Coherent Effects of Quantum Electrodynamics in the Light Field; Naukova Dumka: Kiev, Ukraine, 2008. [Google Scholar]
- Roshchupkin, S.P.; Lebed’, A.A.; Padusenko, E.A.; Voroshilo, A.I. Resonant effects of quantum electrodynamics in the pulsed light field. In Quantum Optics and Laser Experiments; Lyagushyn, S., Ed.; Intech: Croatia, Rijeka, 2012; Chapter 6; pp. 107–156. [Google Scholar]
- Roshchupkin, S.P.; Lebed’, A.A. Effects of Quantum Electrodynamics in the Strong Pulsed Laser Fields; Naukova Dumka: Kiev, Ukraine, 2013. [Google Scholar]
- Bula, C.; McDonald, K.T.; Prebys, E.J.; Bamber, C.; Boege, S.; Kotseroglou, T.; Melissinos, A.C.; Meyerhofer, D.D.; Ragg, W.; Burke, D.L.; et al. Observation of Nonlinear Effects in Compton Scattering. Phys. Rev. Lett. 1996, 76, 3116–3119. [Google Scholar] [CrossRef]
- Mourou, G.A.; Tajima, T.; Bulanov, S.V. Optics in the relativistic regime. Rev. Mod. Phys. 2006, 78, 309–371. [Google Scholar] [CrossRef]
- Bagnoud, V.; Aurand, B.; Blazevic, A.; Borneis, S.; Bruske, C.; Ecker, B.; Eisenbarth, U.; Fils, J.; Frank, A.; Gaul, E.; et al. Commissioning and early experiments of the PHELIX facility. Appl. Phys. B 2010, 100, 137–150. [Google Scholar] [CrossRef]
- Burke, D.L.; Field, R.C.; Horton-Smith, G.; Spencer, J.E.; Walz, D.; Berridge, S.C.; Bugg, W.M.; Shmakov, K.; Weidemann, A.W.; Bula, C.; et al. Positron Production in Multiphoton Light-by-Light Scattering. Phys. Rev. Lett. 1997, 79, 1626–1629. [Google Scholar] [CrossRef]
- Bamber, C.; Boege, S.J.; Koffas, T.; Kotseroglou, T.; Melissinos, A.C.; Meyerhofer, D.D.; Reis, D.A.; Ragg, W.; Bula, C.; McDonald, K.T.; et al. Studies of nonlinear QED in collisions of 46.6 GeV electrons with intense laser pulses. Phys. Rev. D 1999, 60, 092004. [Google Scholar] [CrossRef]
- Kanya, R.; Morimoto, Y.; Yamanouchi, K. Observation of Laser-Assisted Electron-Atom Scattering in Femtosecond Intense Laser Fields. Phys. Rev. Lett. 2010, 105, 123202. [Google Scholar] [CrossRef] [PubMed]
- Hartin, A. Strong field QED in lepton colliders and electron/laser interactions. Int. J. Mod. Phys. A 2018, 33, 1830011. [Google Scholar] [CrossRef]
- Magnusson, J.; Gonoskov, A.; Marklund, M.; Esirkepov, T.Z.; Koga, J.K.; Kondo, K.; Kando, M.; Bulanov, S.V.; Korn, G.; Bulanov, S.S. Laser-Particle Collider for Multi-GeV Photon Production. Phys. Rev. Lett. 2019, 122, 254801. [Google Scholar] [CrossRef] [PubMed]
- Oleinik, V.P. Resonance effects in the field of an intense laser beam. Sov. Phys. JETP 1967, 25, 697–708. [Google Scholar]
- Oleinik, V.P. Resonance effects in the field of an intense laser ray ii. Sov. Phys. JETP 1968, 26, 1132–1138. [Google Scholar]
- Florescu, A.; Florescu, V. Laser-modified electron bremsstrahlung in a Coulomb field. Phys. Rev. A 2000, 61, 033406. [Google Scholar] [CrossRef]
- Flegel, A.V.; Frolov, M.V.; Manakov, N.L.; Starace, A.F.; Zheltukhin, A.N. Analytic description of elastic electron-atom scattering in an elliptically polarized laser field. Phys. Rev. A 2013, 87, 013404. [Google Scholar] [CrossRef]
- Zheltukhin, A.N.; Flegel, A.V.; Frolov, M.V.; Manakov, N.L.; Starace, A.F. Resonant electron-atom bremsstrahlung in an intense laser field. Phys. Rev. A 2014, 89, 023407. [Google Scholar] [CrossRef]
- Zheltukhin, A.N.; Flegel, A.V.; Frolov, M.V.; Manakov, N.L.; Starace, A.F. Rescattering effects in laser-assisted electron–atom bremsstrahlung. J. Phys. B 2015, 48, 075202. [Google Scholar] [CrossRef]
- Li, A.; Wang, J.; Ren, N.; Wang, W.; Zhu, W.; Li, X.; Hoehn, R.; Kais, S. The interference effect of laser-assisted bremsstrahlung emission in Coulomb fields of two nuclei. J. Appl. Phys. 2013, 114, 124904. [Google Scholar] [CrossRef]
- Heinzl, T.; Ilderton, A. Exact Classical and Quantum Dynamics in Background Electromagnetic Fields. Phys. Rev. Lett. 2017, 118, 113202. [Google Scholar] [CrossRef] [PubMed]
- Nedoreshta, V.N.; Voroshilo, A.I.; Roshchupkin, S.P. Resonant scattering of a photon by an electron in the moderately-strong-pulsed laser field. Phys. Rev. A 2013, 88, 052109. [Google Scholar] [CrossRef]
- Krachkov, P.A.; Di Piazza, A.; Milstein, A.I. High-energy bremsstrahlung on atoms in a laser field. Phys. Lett. B 2019, 797, 134814. [Google Scholar] [CrossRef]
- Roshchupkin, S.P.; Larin, N.R.; Dubov, V.V. Resonant photoproduction of ultrarelativistic electron-positron pairs on a nucleus in moderate and strong monochromatic light fields. Phys. Rev. D 2021, 104, 116011. [Google Scholar] [CrossRef]
- Roshchupkin, S.P.; Starodub, S.S. The effect of generation of narrow ultrarelativistic beams of positrons (electrons) in the process of resonant photoproduction of pairs on nuclei in a strong electromagnetic field. Laser Phys. Lett. 2022, 19, 115301. [Google Scholar] [CrossRef]
- Roshchupkin, S.P.; Dubov, A.V.; Dubov, V.V.; Starodub, S.S. Fundamental physical features of resonant spontaneous bremsstrahlung radiation of ultrarelativistic electrons on nuclei in strong laser fields. New J. Phys. 2022, 24, 013020. [Google Scholar] [CrossRef]
- Breit, G.; Wheeler, J.A. Collision of two light quanta. Phys. Rev. 1934, 46, 1087–1091. [Google Scholar] [CrossRef]
- Zhao, Q.; Wu, Y.X.; Ababekri, M.; Li, Z.P.; Tang, L.; Li, J.X. Angle-dependent pair production in the polarized two-photon Breit-Wheeler process. Phys. Rev. D 2023, 107, 096013. [Google Scholar] [CrossRef]
- He, Y.; Yeh, I.L.; Blackburn, T.G.; Arefiev, A. A single-laser scheme for observation of linear Breit–Wheeler electron–positron pair creation. New J. Phys. 2021, 23, 115005. [Google Scholar] [CrossRef]
- Ivanov, D.Y.; Kotkin, G.L.; Serbo, V.G. Complete description of polarization effects in e+e− pair production by a photon in the field of a strong laser wave. Eur. Phys. J. C 2005, 40, 27–40. [Google Scholar] [CrossRef]
- Krajewska, K.; Kaminski, J.Z. Breit-Wheeler process in intense short laser pulses. Phys. Rev. A 2012, 86, 052104. [Google Scholar] [CrossRef]
- Bragin, S.; Di Piazza, A. Electron-positron annihilation into two photons in an intense plane-wave field. Phys. Rev. D 2021, 102, 116012. [Google Scholar] [CrossRef]
- Titov, A.I.; Takabe, H.; Kämpfer, B. Nonlinear Breit-Wheeler process in short laser double pulses. Phys. Rev. D 2018, 98, 036022. [Google Scholar] [CrossRef]
- Titov, A.I.; Kämpfer, B. Non-linear Breit–Wheeler process with linearly polarized beams. Eur. Phys. J. D 2020, 74, 218. [Google Scholar] [CrossRef]
- Tang, S. Fully polarized nonlinear Breit-Wheeler pair production in pulsed plane waves. Phys. Rev. D 2022, 105, 056018. [Google Scholar] [CrossRef]
- Blackburn, T.G.; King, B. Higher fidelity simulations of nonlinear Breit–Wheeler pair creation in intense laser pulses. Eur. Phys. J. C 2022, 82, 44. [Google Scholar] [CrossRef]
- Seipt, D.; King, B. Spin-and polarization-dependent locally-constant-field-approximation rates for nonlinear Compton and Breit-Wheeler processes. Phys. Rev. A 2020, 102, 052805. [Google Scholar] [CrossRef]
- Pustyntsev, A.A.; Dubov, V.V.; Roshchupkin, S.P. Resonant Breit-Wheeler process in an external electromagnetic field. Mod. Phys. Lett. A 2020, 35, 2040027. [Google Scholar] [CrossRef]
- Serov, V.D.; Roshchupkin, S.P.; Dubov, V.V. Resonant Effect for Breit–Wheeler Process in the Field of an X-ray Pulsar. Universe 2020, 6, 190. [Google Scholar] [CrossRef]
- Nousch, T.; Seipt, D.; Kämpfer, B.; Titov, A.I. Spectral caustics in laser assisted Breit–Wheeler process. Phys. Lett. B 2016, 755, 162–167. [Google Scholar] [CrossRef]
- Jansen, M.J.A.; Müller, C. Strongly enhanced pair production in combined high- and low-frequency laser fields. Phys. Rev. A 2013, 88, 052125. [Google Scholar] [CrossRef]
- Chen, H.; Wilks, S.C.; Meyerhofer, D.D.; Bonlie, J.; Chen, C.D.; Chen, S.N.; Courtois, C.; Elberson, L.; Gregori, G.; Kruer, W.; et al. Relativistic Quasimonoenergetic Positron Jets from Intense Laser-Solid Interactions. Phys. Rev. Lett. 2010, 105, 015003. [Google Scholar] [CrossRef] [PubMed]
- Sarri, G.; Schumaker, W.; Di Piazza, A.; Vargas, M.; Dromey, B.; Dieckmann, M.E.; Chvykov, V.; Maksimchuk, A.; Yanovsky, V.; He, Z.H.; et al. Table-Top Laser-Based Source of Femtosecond, Collimated, Ultrarelativistic Positron Beams. Phys. Rev. Lett. 2013, 110, 255002. [Google Scholar] [CrossRef] [PubMed]
- Wan, F.; Shaisultanov, R.; Li, Y.F.; Hatsagortsyan, K.Z.; Keitel, C.H.; Li, J.X. Ultrarelativistic polarized positron jets via collision of electron and ultraintense laser beams. Phys. Lett. B 2020, 800, 135120. [Google Scholar] [CrossRef]
- Turcu, I.C.E.; Negoita, F.; Jaroszynski, D.A.; Mckenna, P.; Balascuta, S.; Ursescu, D.; Dancus, I.; Cernaianu, M.O.; Tataru, M.V.; Ghenuche, P.; et al. High field physics and QED experiments at ELI-NP. Rom. Rep. Phys. 2016, 68, S145–S231. [Google Scholar]
- Abramowicz, H.; Acosta, U.; Altarelli, M.; Aßmann, R.; Bai, Z.; Behnke, T.; Benhammou, Y.; Blackburn, T.; Boogert, S.; Borysov, O.; et al. Conceptual design report for the LUXE experiment. Eur. Phys. J. Spec. Top. 2021, 230, 2445–2560. [Google Scholar] [CrossRef]
- Salgado, F.C.; Grafenstein, K.; Golub, A.; Döpp, A.; Eckey, A.; Hollatz, D.; Müller, C.; Seidel, A.; Seipt, D.; Karsch, S.; et al. Towards pair production in the non-perturbative regime. New J. Phys. 2021, 23, 105002. [Google Scholar] [CrossRef]
- Volkov, D. On a class of solutions of the Dirac equation. Z. Phys. 1935, 94, 250–260. [Google Scholar]
- Wang, H.; Zhong, M.; Gan, L.F. Orthonormality of Volkov Solutions and the Sufficient Condition. Commun. Theor. Phys. 2019, 71, 1179–1186. [Google Scholar] [CrossRef]
- Schwinger, J. On Gauge Invariance and Vacuum Polarization. Phys. Rev. 1951, 82, 664–679. [Google Scholar] [CrossRef]
- Brown, L.S.; Kibble, T.W.B. Interaction of Intense Laser Beams with Electrons. Phys. Rev. 1964, 133, A705–A719. [Google Scholar] [CrossRef]
- Breit, G.; Wigner, E. Capture of Slow Neutrons. Phys. Rev. 1936, 49, 519–531. [Google Scholar] [CrossRef]
- Berestetskii, V.B.; Lifshitz, E.M.; Pitaevskii, L.P. Quantum Electrodynamics; Butterworth-Heinemann: Oxford, UK, 1982; pp. 1–652. [Google Scholar]
- Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Boezio, M.; Bogomolov, E.A.; Bonechi, L.; Bongi, M.; Bonvicini, V.; Bottai, S.; et al. An anomalous positron abundance in cosmic rays with energies 1.5–100 GeV. Nature 2009, 458, 607–609. [Google Scholar] [CrossRef]
- Aguilar, M.; Aisa, D.; Alvino, A.; Ambrosi, G.; Andeen, K.; Arruda, L.; Attig, N.; Azzarello, P.; Bachlechner, A.; Barao, F.; et al. Electron and Positron Fluxes in Primary Cosmic Rays Measured with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2014, 113, 121102. [Google Scholar] [CrossRef] [PubMed]
- Gus’kov, S.Y. Laser fusion and high energy density physics. Kvantovaya Elektron. 2022, 52, 1070–1078. [Google Scholar]


| () | ||||
|---|---|---|---|---|
| , , , | (1,1) | 0 | 0.56 | 47 |
| (1,2) | 0 | 3 | ||
| (2,1) | 0.12 | 0.76 | 31 | |
| (2,2) | 0.06 | 0.78 | 11 | |
| , , , | (1,1) | 0 | 0.70 | |
| (1,2) | 0 | |||
| (2,1) | 0.06 | 0.82 | ||
| (2,2) | 0.07 | 0.81 | ||
| , , , | (1,1) | 0 | 0.71 | |
| (1,2) | 0 | |||
| (2,1) | 0.03 | 0.8 | ||
| (2,2) | 0.08 | 0.79 | ||
| , , , | (4,1) | 0.22 | 0.47 | |
| (4,2) | 0.16 | 0.5 | ||
| (5,1) | 0.07 | 0.64 | ||
| (5,2) | 0.22 | 0.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roshchupkin, S.P.; Serov, V.D.; Dubov, V.V. Generation of Narrow Beams of Ultrarelativistic Positrons (Electrons) in the Breit–Wheeler Resonant Process Modified by the Field of a Strong Electromagnetic Wave. Photonics 2023, 10, 949. https://doi.org/10.3390/photonics10080949
Roshchupkin SP, Serov VD, Dubov VV. Generation of Narrow Beams of Ultrarelativistic Positrons (Electrons) in the Breit–Wheeler Resonant Process Modified by the Field of a Strong Electromagnetic Wave. Photonics. 2023; 10(8):949. https://doi.org/10.3390/photonics10080949
Chicago/Turabian StyleRoshchupkin, Sergei P., Vitalii D. Serov, and Victor V. Dubov. 2023. "Generation of Narrow Beams of Ultrarelativistic Positrons (Electrons) in the Breit–Wheeler Resonant Process Modified by the Field of a Strong Electromagnetic Wave" Photonics 10, no. 8: 949. https://doi.org/10.3390/photonics10080949
APA StyleRoshchupkin, S. P., Serov, V. D., & Dubov, V. V. (2023). Generation of Narrow Beams of Ultrarelativistic Positrons (Electrons) in the Breit–Wheeler Resonant Process Modified by the Field of a Strong Electromagnetic Wave. Photonics, 10(8), 949. https://doi.org/10.3390/photonics10080949






