Hyperspectral Channel-Modulated Static Birefringent Fourier Transform Imaging Spectropolarimeter with Zoomable Spectral Resolution

Abstract

A novel channel-modulated static birefringent Fourier transform imaging spectropolarimeter (CSBFTIS) is introduced, which is based on a double Wollaston prism (DWP). With an adjustable air gap (AG), the spectral resolution can be adjusted by changing the AG. The CSBFTIS combines the channel-modulated imaging spectropolarimeter and the slit-free static birefringent Fourier transform imaging spectrometer technology with adjustable spectral resolution. The device is compact and robust, with a wide spectral range and a large luminous flux. Compared with various previous spectropolarimeters, it can greatly reduce the size of the spectral image data to adapt to different application requirements. A prototype is built, and simulation and experiments are carried out, and the results prove the effectiveness of the method.

1. Introduction

Hyperspectral Fourier transform imaging spectroscopy (FTIS) enables the simultaneous acquisition of two-dimensional spatial information and one-dimensional spectral information, and has proven to be a critical tool in numerous scientific and industrial fields, including biomedicine [1,2,3], agriculture [4,5], remote sensing [6], and others. In recent years, several types of Fourier transform imaging spectroscopies (FTISs) have been developed, including interferometers based on Michelson interferometers [7,8,9,10], Sagnac interferometers [11,12,13,14,15,16,17], Mach–Zehnder interferometers [18,19,20], and Fabry–Perot interferometers [21,22]. The static birefringent Fourier transform imaging spectrometer (SBFTIS) [23,24,25] is particularly valued for its compact size, robustness, accuracy, and energy efficiency. However, traditional SBFTIS is limited by its fixed spectral resolution and the use of slits, resulting in large amounts of data [26,27] that must be captured, stored, transmitted, and analyzed, and a low luminous flux and signal-to-noise ratio (SNR).

An imaging polarimeter captures the two-dimensional spatial polarization information of the target, which is widely used in biomedicine [28,29], industrial detection [30,31,32], de-scattering imaging [33,34,35,36], and other fields due to its ability in describing the roughness and contour of targets. The channel-modulated imaging spectropolarimeter (CMIS) [37,38,39] developed on the basis of FTIS can simultaneously obtain the spectra and full polarization information of the target, which has attracted significant attention for its compact structure and high stability. Traditional CMIS also has the limits of a fixed spectral resolution, low luminous flux, and low SNR brought by slits.

In our previous work [40,41,42], a compact static Fourier transform imaging spectropolarimeter and a novel slit-free SBFTIS with a zoomable spectral resolution were proposed, respectively. However, the former still has a slit and a fixed spectral resolution, and the latter has no full polarization detection capability, thus the application of the two is still limited.

In this paper, a novel channel-modulated static birefringent Fourier transform imaging spectropolarimeter (CSBFTIS) with an adjustable spectral resolution is proposed, combining the CMIS and the slit-free SBFTIS technology with an adjustable spectral resolution. The CSBFTIS is stable, robust, and slit-free, making it capable of increasing luminous flux and reducing SNR. A prototype has been developed and experiments have been conducted to verify its zoomable spectral resolution and full polarization detection capabilities. The results prove the validity of the method.

2. Theory

2.1. System Structure

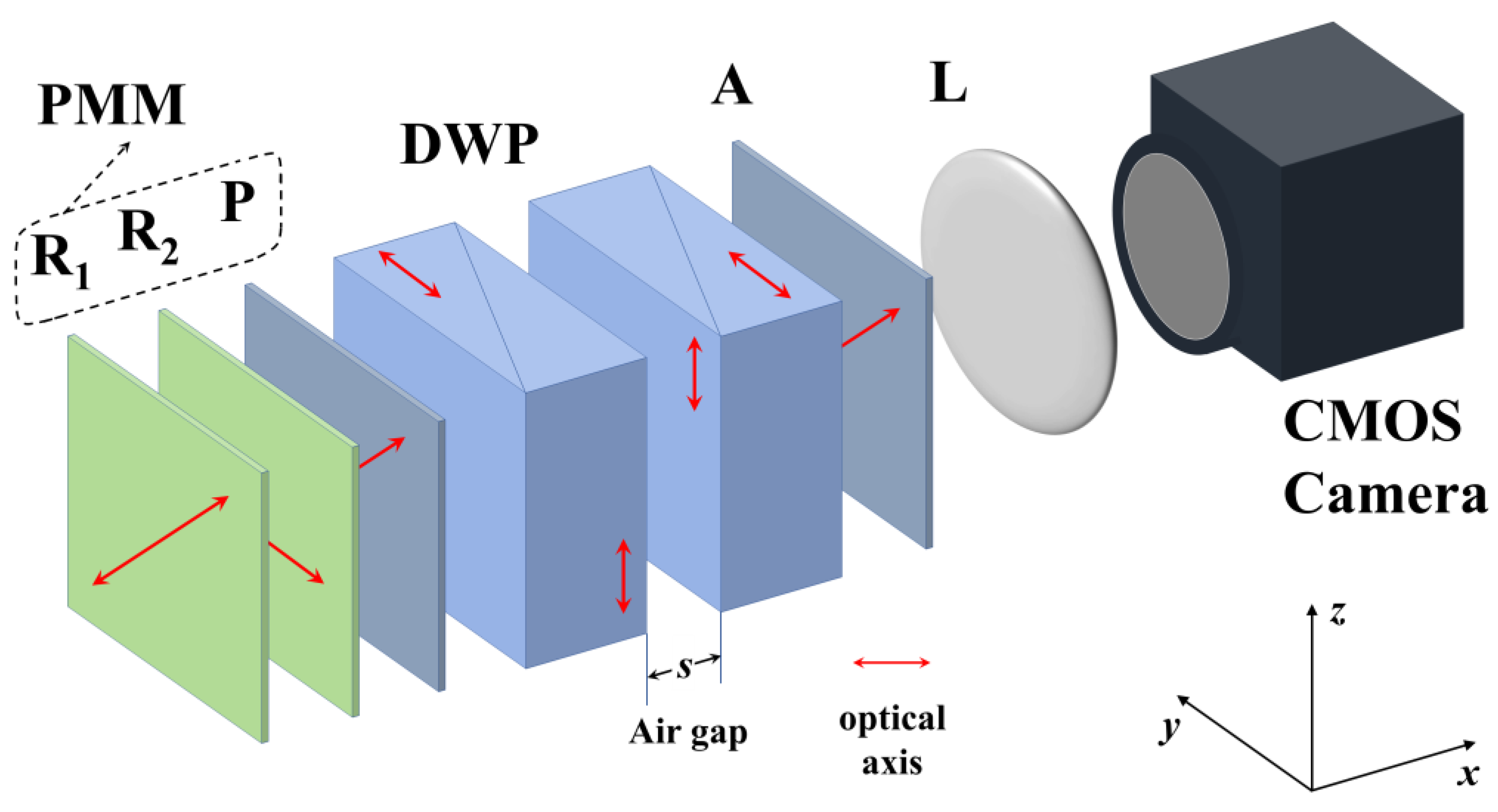
The optical schematic of CSBFTIS is shown in Figure 1. It consists of a pre-optical system (not marked in the figure), two-phase retarders (R₁ and R₂), a polarizer (P), a Double Wollaston Prism (DWP) with an adjustable air gap, an analyzer (A), an imaging lens (L), and a CMOS area array detector. R₁, R₂, and P form a phase modulation module (PMM). The polarizing directions of P and A (45°), the fast axis directions of R₁ (45°) and R₂ (0°), and the optical axis directions of each wedge (0° and 90°) in DWP are shown in Figure 1. The thicknesses of R₁ and R₂ are d₁ and d₂, respectively, and the ratio between them is 1:2.

2.2. Optical Principle

2.2.1. Phase Modulation Module

The light from the object is collected and collimated by the front optical device and the polarization information is modulated by PMM. The retardation of R₁ and R₂ can be expressed as:

$$\{\begin{array}{l}{\phi }_1=\frac{2\pi }{\lambda }(n_o-n_e)d_1\\ {\phi }_2=\frac{2\pi }{\lambda }(n_o-n_e)d_2\end{array},$$

(1)

The refractive indexes of calcite, n_o and n_e, for different wavelengths are obtained according to the Sellmeier formula [43]. The Mueller matrix of an ideal retarder, characterized by a retardation of φ and fast axis angle of θ, is given by [44]:

$$M_R=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& {\cos }^2\left(2\theta \right)+{\sin }^2\left(2\theta \right)\cos \phi & (1-\cos \phi )\sin \left(2\theta \right)\cos \left(2\theta \right)& -\sin \phi \sin \left(2\theta \right)\\ 0& (1-\cos \phi )\sin \left(2\theta \right)\cos \left(2\theta \right)& {\sin }^2\left(2\theta \right)+{\cos }^2\left(2\theta \right)\cos \phi & \sin \phi \cos \left(2\theta \right)\\ 0& \sin \phi \sin \left(2\theta \right)& -\sin \phi \cos \left(2\theta \right)& \cos \phi \end{array}\right],$$

(2)

The Mueller matrix of an ideal polarizer with polarization angle θ can be expressed as [44]:

$$M_P=\frac{1}{2}\left[\begin{array}{cccc}1& \cos \left(2\theta \right)& \sin \left(2\theta \right)& 0\\ \cos \left(2\theta \right)& {\cos }^2\left(2\theta \right)& \sin \left(2\theta \right)\cos \left(2\theta \right)& 0\\ \sin \left(2\theta \right)& \sin \left(2\theta \right)\cos \left(2\theta \right)& {\sin }^2\left(2\theta \right)& 0\\ 0& 0& 0& 0\end{array}\right],$$

(3)

The total Mueller matrix of the PMM can be obtained derived by multiplying the Mueller matrices of each component:

$$\begin{array}{ll}{M}_{PMM}& =M_{P_1}\cdot M_{R_2}\cdot M_{R_1}\hfill \\ & =\frac{1}{2}\left[\begin{array}{cccc}1& \sin {\phi }_1\sin {\phi }_2& \cos {\phi }_2& \cos {\phi }_1\sin {\phi }_2\\ 0& 0& 0& 0\\ 1& \sin {\phi }_1\sin {\phi }_2& \cos {\phi }_2& \cos {\phi }_1\sin {\phi }_2\\ 0& 0& 0& 0\end{array}\right],\hfill \end{array}$$

(4)

The relationship between the Stokes vectors of the input and output light from the PMM can be described as:

$$\begin{gathered} \left[\begin{array}{c}{S}_0^{\prime }\\ S_1^{\prime }\\ S_2^{\prime }\\ S_3^{\prime }\end{array}\right]=\frac{1}{2}\left[\begin{array}{cccc}1& \sin {\phi }_1\sin {\phi }_2& \cos {\phi }_2& \cos {\phi }_1\sin {\phi }_2\\ 0& 0& 0& 0\\ 1& \sin {\phi }_1\sin {\phi }_2& \cos {\phi }_2& \cos {\phi }_1\sin {\phi }_2\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}{S}_0\\ S_1\\ S_2\\ S_3\end{array}\right] \\ =\frac{1}{2}\left[\begin{array}{c}{S}_0+S_1\sin {\phi }_1\sin {\phi }_2+S_2\cos {\phi }_2+S_3\cos {\phi }_1\sin {\phi }_2\\ 0\\ S_0+S_1\sin {\phi }_1\sin {\phi }_2+S_2\cos {\phi }_2+S_3\cos {\phi }_1\sin {\phi }_2\\ 0\end{array}\right], \end{gathered}$$

(5)

where S₀–S₃ are the Stokes parameters of the input light and $S_0^{\prime }$–$S_3^{\prime }$ are the Stokes item of the output light. The $S_0^{\prime }$ parameters of the output light contain all the Stokes parameters of the input light, which are modulated by different modulation functions.

2.2.2. Interference Module

The output light is then split into two parallel lights by the DWP, which are orthogonally polarized and have equal amplitudes, with a small lateral displacement. According to the different polarization states inside the DWP, the two output lights are referred to as the eooe and oeeo lights, as shown in Figure 2.

The Mueller matrix of the DWP for each of these lights can be regarded as two polarizers, calculated by Equation (3) and expressed as:

$$M_{eooe}=\frac{1}{2}\left[\begin{array}{cccc}1& 1& 0& 0\\ 1& 1& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right],$$

(6)

$$M_{oeeo}=\frac{1}{2}\left[\begin{array}{cccc}1& -1& 0& 0\\ -1& 1& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right],$$

(7)

Then, after DWP beam splitting, taking the eooe light as an example, the Stokes vectors are:

$$\left[\begin{array}{c}{S}_{0e}^{\prime }\\ S_{1e}^{\prime }\\ S_{2e}^{\prime }\\ S_{3e}^{\prime }\end{array}\right]{=\mathrm{M}}_{eooe}\left[\begin{array}{c}{S}_0^{\prime }\\ S_1^{\prime }\\ S_2^{\prime }\\ S_3^{\prime }\end{array}\right]=\frac{1}{4}\left[\begin{array}{c}{S}_0+S_1\sin {\phi }_1\sin {\phi }_2+S_2\cos {\phi }_2+S_3\cos {\phi }_1\sin {\phi }_2\\ S_0+S_1\sin {\phi }_1\sin {\phi }_2+S_2\cos {\phi }_2+S_3\cos {\phi }_1\sin {\phi }_2\\ 0\\ 0\end{array}\right],$$

(8)

Subsequently, after passing through A, the Stokes vectors of the two lights are:

$$\begin{array}{ll}\left[\begin{array}{c}{S}_{0e}^{″}\\ S_{1e}^{″}\\ S_{2e}^{″}\\ S_{3e}^{″}\end{array}\right]& {=\mathrm{M}}_A\left[\begin{array}{c}{S}_{0e}^{\prime }\\ S_{1e}^{\prime }\\ S_{2e}^{\prime }\\ S_{3e}^{\prime }\end{array}\right]=\frac{1}{2}\left[\begin{array}{cccc}1& 0& 1& 0\\ 0& 0& 0& 0\\ 1& 0& 1& 0\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}{S}_{0e}^{\prime }\\ S_{1e}^{\prime }\\ S_{2e}^{\prime }\\ S_{3e}^{\prime }\end{array}\right]\hfill \\ & =\frac{1}{8}\left[\begin{array}{c}{S}_0+S_1\sin {\phi }_1\sin {\phi }_2+S_2\cos {\phi }_2+S_3\cos {\phi }_1\sin {\phi }_2\\ 0\\ S_0+S_1\sin {\phi }_1\sin {\phi }_2+S_2\cos {\phi }_2+S_3\cos {\phi }_1\sin {\phi }_2\\ 0\end{array}\right]\end{array},$$

(9)

As the states of the two lights output from A are identical, they can interact on the CMOS photosensitive surface to produce an image with an interference pattern. The complete target interference information of CSBFTIS cannot be obtained in a single measurement, but rather requires the scanning process to change the angle of the target and thus the optical path difference (OPD) to obtain the complete interference information of the target.

The detector can only detect light intensity I₀, which is equal to the first row of the Stokes vector of the output light:

$$I_0=\frac{1}{8}\left(S_0+S_1\sin {\phi }_1\sin {\phi }_2+S_2\cos {\phi }_2+S_3\cos {\phi }_1\sin {\phi }_2\right),$$

(10)

In practice, the incident light is typically polychromatic light, and the interference intensity is the superposition of the interference intensities corresponding to all wavelengths in the spectral range at the same OPD. The final interference intensity of the two beams can be expressed as:

$$\begin{array}{l}I(\Delta )=\frac{1}{8}{\displaystyle \underset{{\sigma }_1}{\overset{{\sigma }_2}{\int }}\left(S_0+S_1\sin {\phi }_1\sin {\phi }_2+S_2\cos {\phi }_2+S_3\cos {\phi }_1\sin {\phi }_2\right)}d\sigma \\ +\frac{1}{8}{\displaystyle \underset{{\sigma }_1}{\overset{{\sigma }_2}{\int }}\left(S_0+S_1\sin {\phi }_1\sin {\phi }_2+S_2\cos {\phi }_2+S_3\cos {\phi }_1\sin {\phi }_2\right)}\cos (2\pi \sigma \Delta )d\sigma \end{array},$$

(11)

where I(Δ) is final interference intensity, σ is the wavenumber, and Δ is the OPD, which is related to the thickness s of the air gap. The equation of Δ has been thoroughly analyzed using the wave normal tracing method in our previous work [45].

2.2.3. Restoration of Spectra

Equation (11) includes a background term and an interference term. The background item is the two-dimensional intensity information of the target, and the interference term is an expression of interference fringe that contains the spectral information of the target. After removing the background term, the interference term in exponential form and sorted can be expressed as:

$$I(\Delta )=\frac{1}{8}{\displaystyle \underset{{\sigma }_1}{\overset{{\sigma }_2}{\int }}\cos (2\pi \sigma \Delta )\left\{\begin{array}{l}{S}_0+\frac{1}{2}{S}_2\left(e^{i{\phi }_2}+e^{-i{\phi }_2}\right)\\ +\frac{1}{4}\left[S_{13}{e}^{i\left({\phi }_1-{\phi }_2\right)}+S_{13}^{*}{e}^{-i\left({\phi }_1-{\phi }_2\right)}\right]\\ -\frac{1}{4}\left[S_{13}{e}^{i\left({\phi }_1+{\phi }_2\right)}+S_{13}^{*}{e}^{-i\left({\phi }_1+{\phi }_2\right)}\right]\end{array}\right\}}d\sigma ,$$

(12)

where S₁₃ = S₁ + iS₃, * represents the complex conjugate. Equation (12) demonstrates that the four Stokes parameters of the incident light are modulated with different phase factors by the PMM, resulting in seven independent channels with a channel spacing equal to the retardation of the retarder.

$$\{\begin{array}{l}{C}_0=\frac{1}{8}{\displaystyle \underset{{\sigma }_1}{\overset{{\sigma }_2}{\int }}\cos (2\pi \sigma \Delta )S_0}d\sigma \\ C_1=\frac{1}{32}{\displaystyle \underset{{\sigma }_1}{\overset{{\sigma }_2}{\int }}\cos (2\pi \sigma \Delta )S_{13}{e}^{i\left({\phi }_1-{\phi }_2\right)}}d\sigma \\ C_1^{*}=\frac{1}{32}{\displaystyle \underset{{\sigma }_1}{\overset{{\sigma }_2}{\int }}\cos (2\pi \sigma \Delta )S_{13}^{*}{e}^{-i\left({\phi }_1-{\phi }_2\right)}}d\sigma \\ C_2=\frac{1}{16}{\displaystyle \underset{{\sigma }_1}{\overset{{\sigma }_2}{\int }}\cos (2\pi \sigma \Delta )S_2{e}^{i{\phi }_2}}d\sigma \\ C_2^{*}=\frac{1}{16}{\displaystyle \underset{{\sigma }_1}{\overset{{\sigma }_2}{\int }}\cos (2\pi \sigma \Delta )S_2{e}^{-i{\phi }_2}}d\sigma \\ C_3=-\frac{1}{32}{\displaystyle \underset{{\sigma }_1}{\overset{{\sigma }_2}{\int }}\cos (2\pi \sigma \Delta )S_{13}{e}^{i\left({\phi }_1+{\phi }_2\right)}}d\sigma \\ C_3^{*}=-\frac{1}{32}{\displaystyle \underset{{\sigma }_1}{\overset{{\sigma }_2}{\int }}\cos (2\pi \sigma \Delta )S_{13}^{*}{e}^{-i\left({\phi }_1+{\phi }_2\right)}}d\sigma \end{array},$$

(13)

Adjusting the prism spacing will increase the total OPD of the system, but the retardation of the phase retarder cannot be adjusted. Hence, at a high spectral resolution, the channel spacing becomes relatively narrow. Both C₁ and C₃ contain the information of S₁ and S₃, so only one of them needs to be processed. The demodulation process is actually purposed to perform Fourier inverse transform on the corresponding phase modulation information; the process is as follows:

$$\begin{array}{l}{S}_0=8F^{-1}\left\{C_0\right\}\\ S_2=16F^{-1}\left\{C_2\right\}{e}^{i{\phi }_2}\\ S_1=32real{F}^{-1}\left\{C_1\right\}{e}^{i\left({\phi }_1-{\phi }_2\right)}\\ S_3=32imag{F}^{-1}\left\{C_1\right\}{e}^{i\left({\phi }_1-{\phi }_2\right)}\end{array},$$

(14)

2.2.4. Data Acquisition Method

When there is a relative displacement between the CSBFTIS system and the target being measured, the angle of the target and the system changes, resulting in a corresponding movement of the target’s image in the captured pictures. However, during this process, all internal components of the instrument remain immobile, ensuring that the light transmission characteristics of the instrument do not change. Consequently, the OPD distribution on the photosensitive surface of the camera remains unchanged, leading to stationary interference fringes. This phenomenon is observed as the interference fringes remain static while the target traverses the entire image along the scanning direction, as shown in Figure 3.

In each frame captured during imaging, each target unit within the shooting area simultaneously enters the system at different incident angles. Therefore, each pixel in a frame of the interferogram captures information corresponding to the respective target unit at a specific angle. As the system moves relative to the target, the incident angle of each target unit changes in relation to its previous position. Throughout the scanning process of the system, the incident angle of each target unit undergoes a positive maximum incident angle, zero, and negative maximum incident angle, ultimately creating a data cube.

To obtain complete interference information of a specific target element, it is necessary to extract all the interference data belonging to that target element from the data cube and recombine it, as shown in Figure 4. Indeed, the information pertaining to the same target element is associated with both time (due to the pictures being taken at different times during the scanning process) and space (due to the different positions within the captured image). This unique combination of time and space modulation principles is referred to as the spatio-tempo hybrid modulated principle. The scanning process is essential for achieving comprehensive data collection using spatio-tempo hybrid modulated-type CSBFTIS.

3. Performance Analysis

3.1. Spectral Resolution

The spectral resolution of a spectrometer is a characteristic that determines its ability to separate two adjacent spectral lines. It is determined by two key factors: the maximum OPD of the system and the apodization function employed during restoration. The most common metric used to quantify spectral resolution is the full width at a half-maximum (FWHM) of the restored spectrum when the input spectrum is an ideal delta function spectrum.

In theory, an infinite OPD would lead to an ideal spectral resolution. However, the size of the detector limits the OPD, which is equivalent to imposing a rectangular apodization function on the obtained interference fringes:

$$\mathrm{A}(\Delta )=\{\begin{array}{l}1,|\Delta |\le {\Delta }_{\max }\\ 0,|\Delta |>{\Delta }_{\max }\end{array},$$

(15)

Its instrument function can be expressed as:

$$I(\sigma )=2{\Delta }_{\max }\sin \mathrm{c}(2\pi \sigma {\Delta }_{\max }),$$

(16)

The full width at a half-maximum is:

$$FWHM=\frac{1.20671}{2{\Delta }_{\max }},$$

(17)

which is intrinsic spectral resolution of the CSBFTIS. An example of the spectral resolution zooming capability of the CSBFTIS is presented in Figure 5. In the calculation, the material of DWP is made of calcite, with a structure angle of 1.5° and a thickness of 10.2 mm. The focal length of the imaging lens is 50 mm. The results demonstrate that as the thickness of the air gap (s) increases, the spectral resolution of the system improves rapidly. For instance, when s = 10 mm, the spectral resolution reaches 23 cm⁻¹, nearly 2.5 times higher than that of s = 0 mm.

Since the instrument function of the rectangular function has negative sidelobes and the captured interferogram needs to be segmented into different spectral channels, an additional apodization function needs to be implemented. The selection of the appropriate apodization function is dependent on the specific requirements of the experiment. Taking the Hanning function as an example, its expression is:

$$H=\{\begin{array}{ll}\frac{1}{2}[1+\cos \left(\frac{2\pi x}{T}\right)],& \left|x\right|\le \frac{T}{2}\\ 0,& \left|x\right|>\frac{T}{2}\end{array},$$

(18)

The FWHM of the restored spectrum is [46]:

$$FWHM=\frac{2}{T},$$

(19)

T is the width of the Hanning function. Therefore, for a specific spectrum, its spectral resolution also depends on the type and width of the apodization function selected during restoration.

However, it should be noted that the spectral resolution is limited by the effective number of pixels of the sampled interferogram according to the Nyquist criterion. According to the Nyquist criterion, the detector-limited spectral resolution can be expressed as:

$$\Delta {\sigma }_d={\sigma }_{\max }\frac{2}{N},$$

(20)

where ${\sigma }_{\max }$ is the maximum detectable wave number of the instrument and N is the maximum number of pixels for single-side sampling.

3.2. Signal-to-Noise Ratio

The SNR is another critical parameter of a spectrometer. The intrinsic SNR of CSBFTIS without using other apodization functions is also related to the maximum OPD, which can be expressed as [47]:

$$SNR(\lambda )\propto =\frac{S(\lambda )}{\overline{S}}\sqrt{\frac{1.20671}{2{\Delta }_{\max }({\sigma }_{\max }-{\sigma }_{\min })}},$$

(21)

where $\frac{S(\lambda )}{\overline{S}}$ is the ratio of the signal in a particular spectral band to the average signal over all spectral bands, ${\sigma }_{\max }$ and ${\sigma }_{\min }$, maximum and minimum wavenumbers, respectively. Figure 6 is the estimated theoretical relative SNR, taking $\frac{S(\lambda )}{\overline{S}}=1$, and other parameters are the same as the calculation shown ins Figure 5.

It can be seen that the SNR decreases with the increase in the air gap thickness, just opposite to the spectral resolution. Therefore, it is necessary to comprehensively consider the SNR and spectral resolution in the application.

4. Experimental Results and Discussion

4.1. Principle Verification System and Prototype

The structure of the CSBFTIS principle verification system is shown in Figure 7a. The thicknesses of the two-phase retarders R₁ and R₂ are 4.85 mm and 9.7 mm, respectively. DWP is made of calcite, with a structure angle of 27.15° and a thickness of 10.2 mm. The thickness of the air gap is controlled by a stepper motor and an optical switch. The focal length of the imaging lens, L, is 50 mm. Interferograms were captured by a 4024 × 3036 monochrome rolling shutter CMOS with a pixel size of 1.85 μm (Daheng MER2-1220-32U3M). The pre-optical system is not shown in Figure 7a, where the field diaphragm is placed to control the field of view FOV = 10° in the experiment. The independence of the pre-optical system from the core components of CSBFTIS allows for the replacement of various types of front-end optical systems without compromising imaging and interference, thereby satisfying the spectral detection needs in complex environments.

On the basis of the principle verification system, the front optical system and the CSBFTIS core are integrated, and the CSBFTIS prototype is designed and assembled, as shown in Figure 7b. The prototype system has a more compact structure and strong stability, and the imaging system has been redesigned to improve the imaging quality.

4.2. Verification of Spectral Zooming

The spectral resolution of the prototype was evaluated by performing a spectral interference imaging experiment using a triple-laser source with wavelengths of 450 nm, 532 nm, and 633 nm. The resulting data are presented in Figure 8, where (a) depicts the input spectrum, (b) displays the interferogram of CSBFTIS using an air gap thickness of s = 0 mm as an example, and (c) shows the intensity curve of the blue line in (b).

After the apodization of the Hanning function, which effectively removes the negative sidelobe, several restored spectra are presented in Figure 9, with an increasing value of s from (a) to (e). The FWHM of the spectra gradually decreases with the increase in s, which significantly reduces from 124.09 cm, 127.65 cm, and 127.90 cm to 50.44 cm, 49.68 cm, and 51.98 cm, at 450 nm, 534 nm, and 633 nm, respectively. This provides clear evidence of the zoomable spectral resolution of CSBFTIS. The noise also gradually increases, as previously calculated. A larger value of s results in a larger OPD, allowing for more information to be retained, which leads to a stronger relative intensity of the restored spectrum. But apodization inevitably leads to a loss of information, with more information lost at lower wavenumbers; thus, the restored spectrum intensity is smaller at lower wavenumbers.

4.3. Verification of Full Polarization

An experiment was performed to demonstrate the polarization channel modulation method of CSBFTIS using the polarized polychromatic light interferogram, as shown in Figure 10. Among them, Figure 10a is captured with s = 0 mm, and Figure 10b is captured with s = 10 mm. It can be seen that the number of channels in Figure 10a is less than in 10b, but the channel spacing is greater than in Figure 10b. According to Equation (12), changing the maximum OPD of CSBFTIS does not change the OPD between each channel, thus reducing the channel spacing, leading to an increase in the crosstalk between the channels and noise of the restored spectra. Hence, in practical applications, a balance between spectral resolution and channel crosstalk needs to be considered.

The full polarization detection capability of the SESFTS prototype was tested by a fully polarized incident light. Taking s = 0 mm as an example, Figure 11a is the input spectrum, Figure 11b is the CSBFTIS interferogram, and Figure 11c is the intensity curve of the blue line in Figure 11b. After the apodization of the Hanning function to remove the negative sidelobe and split different channels, the restored spectrum is presented in Figure 11d. The spectra of the four Stokes parameters are all effectively restored, which proves the full polarization detection capability of CSBFTIS. However, for polychromatic light interferograms, apodization also unavoidably leads to information loss. The information in the central part of the spectrum is relatively well-preserved, while the edge part is more lost. Nevertheless, unlike monochromatic light interferograms, the information in polychromatic light interferograms is more concentrated, resulting in less spectral information loss in apodization. At the same time, due to the existence of channel crosstalk, there is a certain distortion in the spectral lines of each parameter.

One of the contributing factors to the edge effect in the spectrum is the apodization function. While an ideal interferogram possesses an infinite range of OPDs, the apodization function can only intercept a portion of this information, leading to a loss of spectral information. Additionally, the issue of channel interference, although minor, does exist and can impact the accuracy of spectrum restoration.

Considering the instrument’s principle, the system’s ability to detect luminous flux is limited due to the multiple polarization devices it passes through. Consequently, the energy of different channels varies, with C₀ having the largest intensity, C₂ being half of C₀, and C₁₃ being only one-third of C₀. During spectrum restoration, C₀ exhibits the highest intensity and the highest signal-to-noise ratio for S₀. Conversely, C₁₃ exhibits the smallest intensity, resulting in lower signal-to-noise ratios for S₁ and S₃. Moreover, the stronger the channel, the less susceptible it is to crosstalk. Considering all these factors, S₃, S₂, and S₁ tend to have lower signal-to-noise ratios compared to S₀. Among these channels, S₃ is the most affected as its original signal is the weakest, leading to the most significant impact from various errors and consequently the lowest signal-to-noise ratio in each channel.

4.4. Verification of Environmental Target

To further validate the proposed method’s imaging performance, an additional experiment was conducted using a complex scene in a natural environment under sunlight as the imaging target, as depicted in Figure 12a. The scene included multiple targets such as trees, grass, cars, and roads. The pictures captured by the CSBFTIS are superimposed pictures of intensity information and interference fringes, with three example interferograms shown in Figure 12b–d.

The scanning process facilitated the capture of all target information by changing the target’s relative position with the spectrometer across the scanning direction. In all interferograms, the fringe position remained fixed while the target intensity image was moved. The fringe pattern in the image was slightly curved due to the Wollaston prism’s OPD distribution. As per the spatio-tempo hybrid modulated scanning principle, the interference data for a specific point in the image are solely dependent on the scanning direction angle change and are independent of the scanning’s vertical direction. Each shot can only capture the information of a column of geo-elements at a certain angle, so it is necessary to traverse all angles for a specific geo-element to obtain complete interference information. Data processing was conducted on the obtained interferogram to extract the spectral curve of each point of the target, and further reorganization was carried out to obtain the target spectral graph. The resulting spectrum image in the full working band range (400–1000 nm) is shown in Figure 13. The visible band has been color-restored, while the infrared band is displayed in grayscale. The light intensities of 400 and 950 nm are too weak, so there are more noise points. The pictures are arranged neatly, and the 1000 nm pictures are not shown.

Spectral curves of some specific targets are presented in Figure 14, including trees, grassland, cement road, and a white car.

All data in the 400–1000 nm band range were subjected to visible light color mapping, resulting in a hyperspectral pseudo-color image shown in Figure 15. Since the pseudo-color mapping maps the infrared part to red, the overall sample is reddish. The image clearly shows improved details of the spectral information, with a clear improvement in the ability to distinguish trees from grass.

Polarization information was also processed and analyzed. Due to the large amount of polarization data, specific bands at the wavelengths of 440 nm, 530 nm, and 630 nm were selected for display, shown in Figure 16. Unlike the intensity picture of a specific polarization state captured by a commercial polarization camera, the picture obtained by CSBFTIS is a grayscale image of the Stokes parameter. It is evident that the polarization information is more pronounced on the smooth surface of the car, and the outline of the car is displayed more clearly. Polarization imaging has the advantage of highlighting the outline of the target.

Figure 17 displays the degree of polarization (DOP) and the angle of polarization image. DOP can be described as:

$$DOP=\sqrt{\frac{S_1^2+S_2^2+S_3^2}{S_0}},$$

(22)

The angle of polarization (AOP) can be expressed as:

$$AOP=\frac{1}{2}\arctan (\frac{S_2}{S_1}),$$

(23)

The DOP of the image clearly enhances the outline of each target and better distinguishes between the trees and grass targets that are difficult to distinguish in the visible intensity image.

5. Discussion

Compared with the previous work of the team, the new CSBFTIS system has the following improvements:

The data acquisition method has been upgraded from the spatio-modulated type [40] to the spatio-tempo hybrid modulated type, so the system can be slit-free. Thus, the luminous flux and the spectral detection performance of the system under weak light conditions have been greatly improved.

Compared with the original FTIS principle verification experimental device with zoomable spectral resolution [41,42], a PMM was added, and the principle verification experimental device was further optimized and designed to be upgraded to a compact prototype. The electronic control system was designed to precisely control the air gap between the prisms, replacing the original mechanical manual adjustment device, and the accuracy was greatly improved.

The principle verification system only provides a rough interference experiment, and the spectrum was not restored. On the basis of accurate analysis of the optical path difference of the system, more accurate restoration of the spectrum can be realized.

6. Conclusions

We have proposed a novel channel-modulated static birefringent Fourier transform imaging spectropolarimeter (CSBFTIS) that allows for a scalable spectral resolution. The technique involves changing the air gap thickness of the DWP to obtain interferograms with different OPDs, which in turn alters the spectral resolution of the recovered spectrum to suit various complex working environments and reduce data size. Unlike common spatio-temporal mixed scanning modes that limit spectral resolution, the spectral resolution of CSBFTIS can be controlled by adjusting the spacing of the prisms. This makes it possible for the instrument to be used in a wider range of outdoor environments, scanning in full-band low-spectrum resolution or in characteristic bands of interest with high precision. Furthermore, the pre-optical system and core of CSBFTIS are independent of each other, allowing for an easy replacement of the front-end optical module meeting the needs of different scenarios.

The working principle of a CSBFTIS was introduced, and the intrinsic spectral resolution and signal-to-noise ratio of a CSBFTIS were calculated. Additionally, a prototype was developed, and its efficacy demonstrated. A spectral interference imaging experiment of monochromatic light was conducted to investigate the spectral resolution at different air gap thicknesses. The full width at a half-maximum (FWHM) changed from approximately 124 cm to 50 cm as the air gap thickness changed from s = 0 mm to 10 mm, thus substantiating its spectral zooming capability. To confirm its full polarization state detection ability, a spectral interference imaging experiment of polychromatic polarized light was conducted and all Stokes parameters of the input spectrum were effectively restored. The target object in the natural environment was photographed and the data were processed to display the spectral pictures of some bands and the spectral curves of some typical targets, which were compared with other spectrometers to verify its potential in improving spectral detection ability in remote sensing applications. A hyperspectral pseudo-color map was created to present the results. Moreover, the polarization images of some bands are displayed, and the degree of polarization (DOP) images were calculated, indicating the polarization detection function of the system in remote sensing applications.

In conclusion, our study presented a novel CSBFTIS, which was demonstrated to be feasible through both theoretical and experimental analyses. The slit-free design of the interferometer allowed for an increased light throughput and reduced signal-to-noise ratio, resulting in superior performance. Moreover, CSBFTIS is characterized by a linear optical path, compact size, stability, and robustness. It offers a straightforward and efficient means for accurately measuring polarized spectral features using high-performance spectrometers.