Optical Tunable Frequency-Doubling OEO Using a Chirped FBG Based on Orthogonally Polarized Double Sideband Modulation
Abstract
:1. Introduction
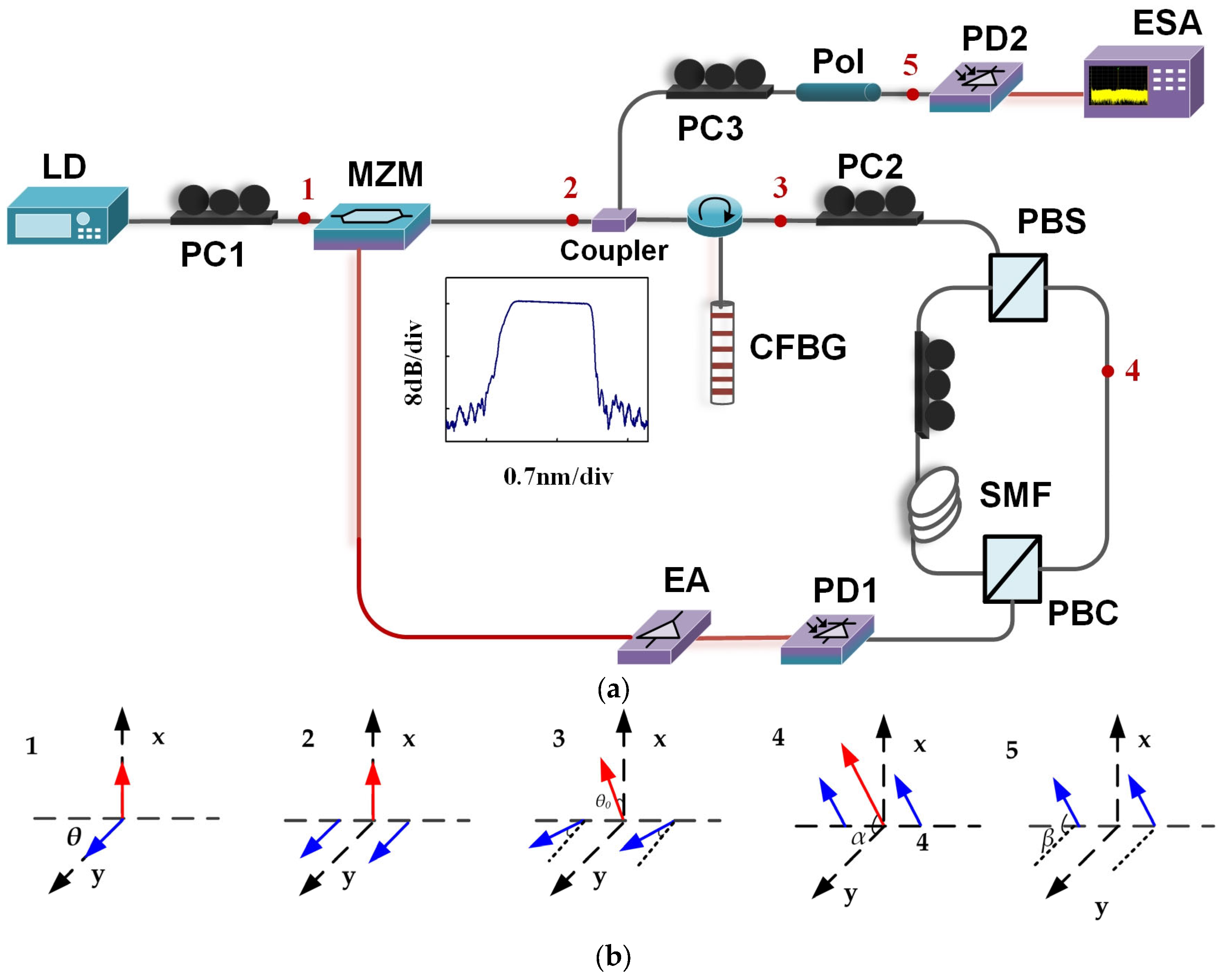
2. Materials and Methods
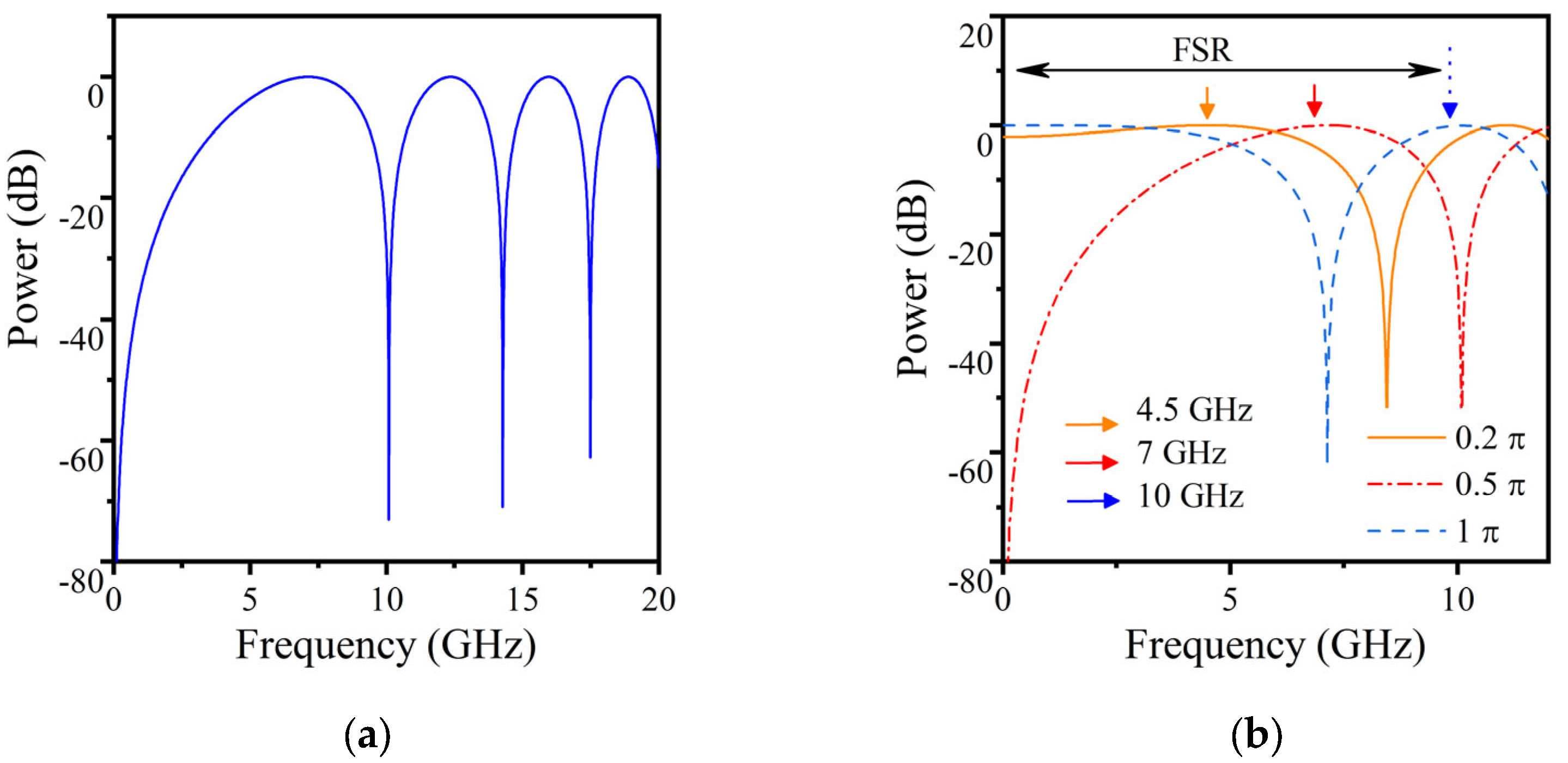
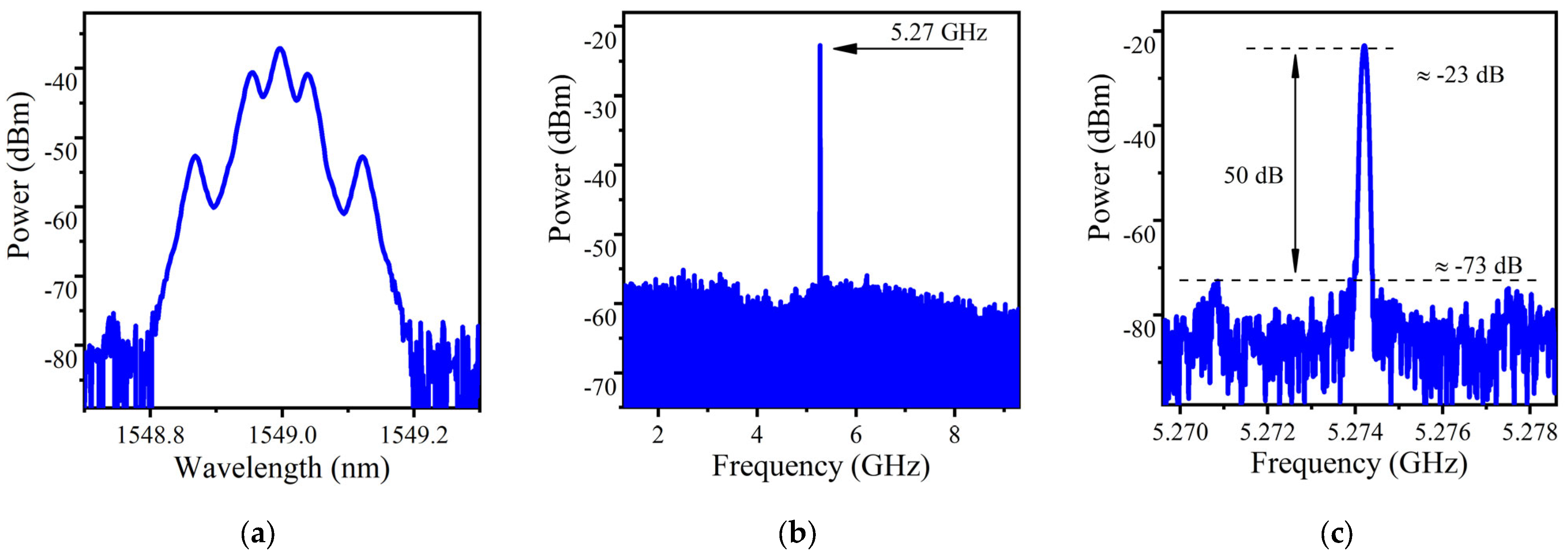
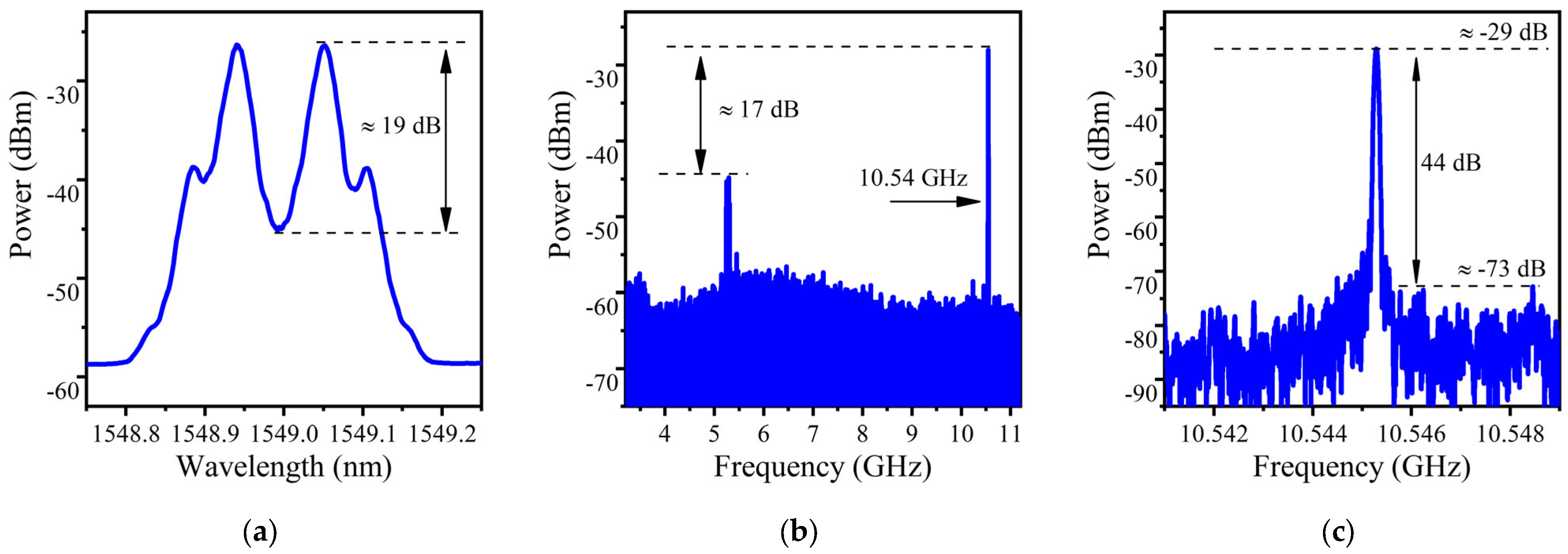
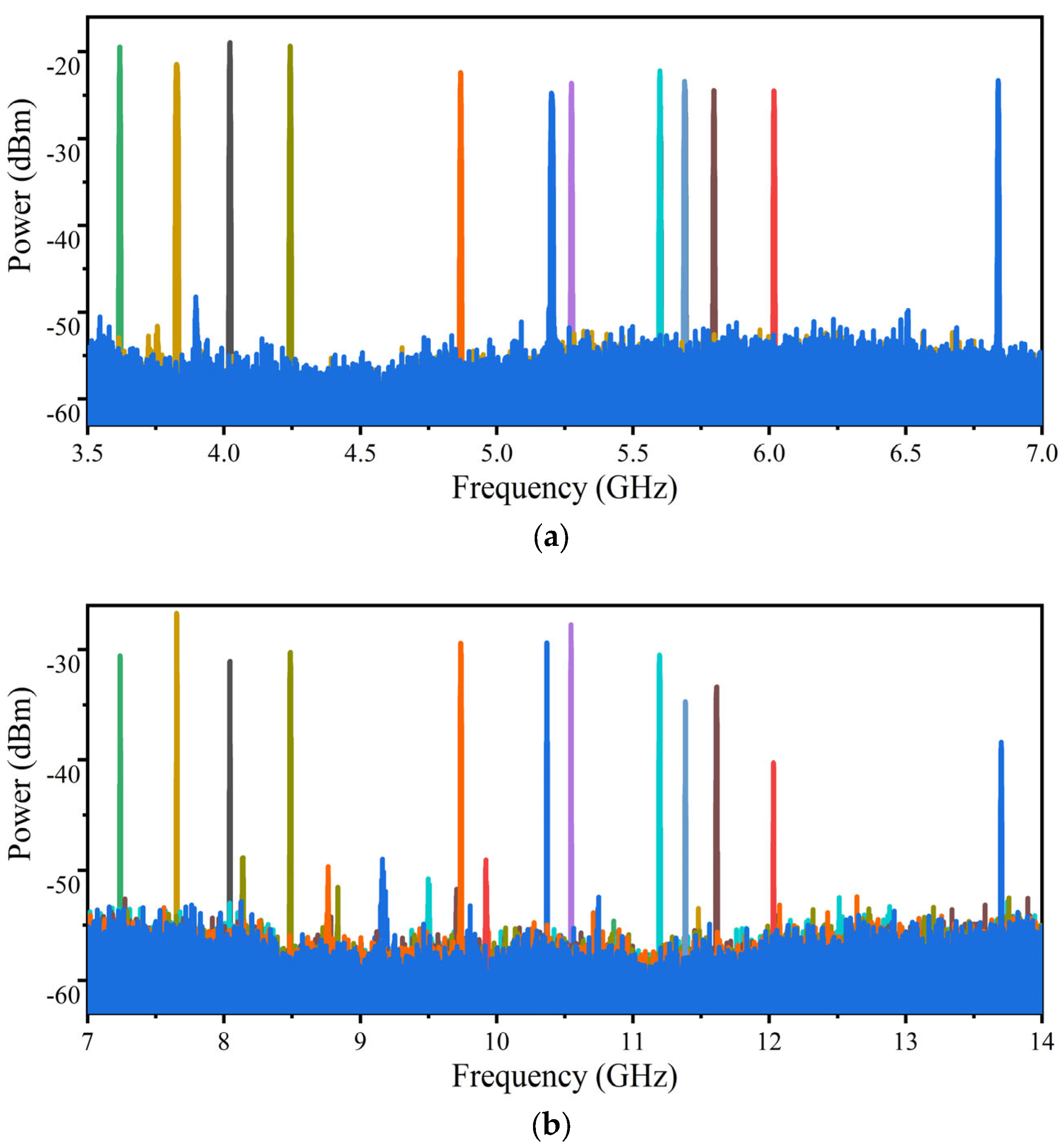
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yao, X.S.; Maleki, L. Converting light into spectrally pure microwave oscillation. Opt. Lett. 1996, 21, 483–485. [Google Scholar] [CrossRef] [PubMed]
- Yao, J. Microwave photonics. J. Light. Technol. 2009, 27, 314–335. [Google Scholar] [CrossRef]
- Tsuchida, H. Simultaneous clock recovery and serial-to-parallel conversion of data signals using a polarization modulator-based optoelectronic oscillator. J. Light. Technol. 2009, 27, 3777–3782. [Google Scholar] [CrossRef]
- Yao, J. Optoelectronic oscillators for high speed and high resolution optical sensing. J. Light. Technol. 2017, 35, 3489–3497. [Google Scholar] [CrossRef]
- Pan, S.; Yao, J. A frequency-doubling optoelectronic oscillator using a polarization modulator. IEEE Photonics Technol. Lett. 2009, 21, 929–931. [Google Scholar]
- Xue, Z.; Li, S.; Xue, X.; Zheng, X.; Zhou, B. Photonics-assisted joint radar and communication system based on an optoelectronic oscillator. Opt. Express 2021, 29, 22442–22454. [Google Scholar] [CrossRef]
- Yao, X.S.; Maleki, L. Optoelectronic microwave oscillator. JOSA B 1996, 13, 1725–1735. [Google Scholar] [CrossRef]
- Hao, P.; Niu, J.; Wang, X.; Yao, X.S. Dual-loop diode-tuned Fourier domain harmonically mode-locked opto-electronic oscillator with over 50 dB side-mode spur reduction. Opt. Express 2022, 30, 45569–45582. [Google Scholar] [CrossRef]
- Shifeng, L.; Xiaorui, X.; Fangzheng, Z.; Peng, L.; Xiaochen, K.; Huashan, Y.; Shilong, P. Ultralow phase noise optoelectronic oscillator and its application to a frequency synthesizer. J. Radar. 2019, 8, 243–250. [Google Scholar]
- Hao, T.; Tang, J.; Domenech, D.; Li, W.; Zhu, N.; Capmany, J.; Li, M. Toward monolithic integration of OEOs: From systems to chips. J. Light. Technol. 2018, 36, 4565–4582. [Google Scholar] [CrossRef]
- Tang, J.; Hao, T.; Li, W.; Domenech, D.; Baños, R.; Muñoz, P.; Zhu, N.; Capmany, J.; Li, M. Integrated optoelectronic oscillator. Opt. Express 2018, 26, 12257–12265. [Google Scholar] [CrossRef] [PubMed]
- Brunetti, G.; Armenise, M.N.; Ciminelli, C. Chip-scaled Ka-band photonic linearly chirped microwave waveform generator. Front. Phys. 2022, 10, 158. [Google Scholar] [CrossRef]
- Pan, S.; Yao, J. Optical NRZ to RZ format conversion based on a frequency-doubling optoelectronic oscillator. In Proceedings of the 2009 IEEE LEOS Annual Meeting Conference Proceedings, Antalya, Turkey, 4–8 October 2009. [Google Scholar]
- Lee, J.-Y.; Song, J.-I. Photonic frequency down-converter based on a frequency-doubling OEO using two cascaded EAMs. IEEE Photonics Technol. Lett. 2017, 29, 1529–1532. [Google Scholar] [CrossRef]
- Shin, M.; Kumar, P. Optical microwave frequency up-conversion via a frequency-doubling optoelectronic oscillator. IEEE Photonics Technol. Lett. 2007, 19, 1726–1728. [Google Scholar] [CrossRef]
- Pan, S.; Yao, J. Optical clock recovery using a polarization-modulator-based frequency-doubling optoelectronic oscillator. J. Light. Technol. 2009, 27, 3531–3539. [Google Scholar]
- Shin, M.; Grigoryan, V.; Kumar, P. Frequency-doubling optoelectronic oscillator for generating high-frequency microwave signals with low phase noise. Electron. Lett. 2007, 43, 242–244. [Google Scholar] [CrossRef]
- Liu, X.; Pan, W.; Zou, X.; Zheng, D.; Yan, L.; Luo, B. Frequency-doubling optoelectronic oscillator using DSB-SC modulation and carrier recovery based on stimulated Brillouin scattering. IEEE Photonics J. 2013, 5, 6600606. [Google Scholar]
- Wang, L.; Zhu, N.; Li, W.; Liu, J. A frequency-doubling optoelectronic oscillator based on a dual-parallel Mach–Zehnder modulator and a chirped fiber Bragg grating. IEEE Photonics Technol. Lett. 2011, 23, 1688–1690. [Google Scholar] [CrossRef]
- Zheng, J.; Sun, W.; Wang, W.; Tong, Y.; Wang, W.Y.; Wang, X.; Yuan, H.; Liu, J.; Zhu, N. Frequency-doubling OEO using the polarization property of LiNbO 3 modulator. IEEE Photonics Technol. Lett. 2015, 27, 1864–1867. [Google Scholar] [CrossRef]
- Yang, B.; Jin, X.; Chi, H.; Zhang, X.; Zheng, S.; Zou, S.; Chen, H.; Tangdiongga, E.; Koonen, T. Optically tunable frequency-doubling Brillouin optoelectronic oscillator with carrier phase-shifted double sideband modulation. IEEE Photonics Technol. Lett. 2012, 24, 1051–1053. [Google Scholar] [CrossRef]
- Qiao, Y.; Pan, M.; Zheng, S.; Chi, H.; Jin, X.; Zhang, X. An electrically tunable frequency-doubling optoelectronic oscillator with operation based on stimulated Brillouin scattering. J. Opt. 2013, 15, 035406. [Google Scholar] [CrossRef]
- Li, W.; Yao, J. An optically tunable frequency-doubling optoelectronic oscillator incorporating a phase-shifted-fiber-Bragg-grating-based frequency-tunable photonic microwave filter. In Proceedings of the 2011 International Topical Meeting on Microwave Photonics Jointly held with the 2011 Asia-Pacific Microwave Photonics Conference, Gold Coast, Australia, 18–21 October 2011. [Google Scholar]
- Li, W.; Yao, J. Optically tunable frequency-multiplying optoelectronic oscillator. IEEE Photonics Technol. Lett. 2012, 24, 812–814. [Google Scholar] [CrossRef]
- Li, W.; Liu, J.G.; Zhu, N.H. A widely and continuously tunable frequency doubling optoelectronic oscillator. IEEE Photonics Technol. Lett. 2015, 27, 1461–1464. [Google Scholar] [CrossRef]
- Zheng, J.; Wang, J.; Yu, J.; Zhu, M.; Dong, Z.; Wang, X.; Su, T.; Liu, J.; Zhu, N.; Chang, G.K. Photonic microwave-signal-mixing technique using phase-coherent orthogonal optical carriers for radio-over-fiber application. Opt. Lett. 2014, 39, 5263–5266. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Q.; Yang, J.; Cao, J.; Li, W. Reconfigurable multi-band microwave photonic radar transmitter with a wide operating frequency range. Opt. Express 2019, 27, 34519–34529. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhang, L.; Zhang, Y.; Zhang, Z.; Zhang, S.; Zhang, Y.; Sun, B.; Liu, Y. Frequency-definable linearly chirped microwave waveform generation by a Fourier domain mode locking optoelectronic oscillator based on stimulated Brillouin scattering. Opt. Express 2020, 28, 13861–13870. [Google Scholar] [CrossRef]
- Zhang, C.; Jin, X.; Jin, X.; Yu, X.; Feng, L.; Yang, H.; Chi, H.; Zhang, X. Photonic vector signal generation based on OEO and optical coherent QPSK modulation. IEEE Photonics Technol. Lett. 2018, 30, 1711–1714. [Google Scholar] [CrossRef]
- Zou, F.; Zou, L.; Yang, B.; Ma, Q.; Zou, X.; Zou, J.; Chen, S.; Milosevic, D.; Cao, Z.; Liu, H. Optoelectronic oscillator for 5G wireless networks and beyond. J. Phys. D Appl. Phys. 2021, 54, 423002. [Google Scholar] [CrossRef]
- Zhang, W.; Yao, J. Silicon Photonic Integrated Optoelectronic Oscillator for Frequency-Tunable Microwave Generation. J. Light. Technol. 2018, 36, 4655–4663. [Google Scholar] [CrossRef]
- Zhang, W.; Yao, J. A silicon photonic integrated frequency-tunable optoelectronic oscillator. In Proceedings of the Microwave Photonics (MWP), 2017 International Topical Meeting, Beijing, China, 23–26 October 2017. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wu, B.; Zhou, H.; Wang, W.; Xu, G. Optical Tunable Frequency-Doubling OEO Using a Chirped FBG Based on Orthogonally Polarized Double Sideband Modulation. Photonics 2023, 10, 1002. https://doi.org/10.3390/photonics10091002
Wang H, Wu B, Zhou H, Wang W, Xu G. Optical Tunable Frequency-Doubling OEO Using a Chirped FBG Based on Orthogonally Polarized Double Sideband Modulation. Photonics. 2023; 10(9):1002. https://doi.org/10.3390/photonics10091002
Chicago/Turabian StyleWang, Haiyang, Beilei Wu, Haoran Zhou, Wensheng Wang, and Guangluan Xu. 2023. "Optical Tunable Frequency-Doubling OEO Using a Chirped FBG Based on Orthogonally Polarized Double Sideband Modulation" Photonics 10, no. 9: 1002. https://doi.org/10.3390/photonics10091002
APA StyleWang, H., Wu, B., Zhou, H., Wang, W., & Xu, G. (2023). Optical Tunable Frequency-Doubling OEO Using a Chirped FBG Based on Orthogonally Polarized Double Sideband Modulation. Photonics, 10(9), 1002. https://doi.org/10.3390/photonics10091002





