A Systematic Summary and Comparison of Scalar Diffraction Theories for Structured Light Beams
Abstract
:1. Introduction
2. Scalar Fields of Typical Structured Light Beams in the Source Plane
2.1. Fundamental Gaussian Beams
2.2. Hermite–Gaussian Beams
2.3. Laguerre–Gaussian Beams
2.4. Bessel Beams
2.5. Airy Beams
3. Main Scalar Diffraction Theories of Light Beams
3.1. Fresnel Diffraction Integral
3.2. Collins Formula
3.3. Angular Spectrum Representation
3.4. Rayleigh–Sommerfeld Diffraction Integral
4. Analytical Propagation Expressions of Typical Structured Light Beams Described by Various Scalar Diffraction Theories
4.1. Fundamental Gaussian Beams
4.1.1. Fresnel Diffraction Integral
4.1.2. Collins Formula
4.1.3. Angular Spectrum Representation
4.1.4. Rayleigh–Sommerfeld Diffraction Integral
4.2. Hermite–Gaussian Beams
4.2.1. Fresnel Diffraction Integral
4.2.2. Collins Formula
4.2.3. Angular Spectrum Representation
4.2.4. Rayleigh–Sommerfeld Diffraction Integral
4.3. Laguerre–Gaussian Beams
4.3.1. Fresnel Diffraction Integral
4.3.2. Collins Formula
4.3.3. Angular Spectrum Representation
4.3.4. Rayleigh–Sommerfeld Diffraction Integral
4.4. Bessel Beams
4.4.1. Fresnel Diffraction Integral
4.4.2. Collins Formula
4.4.3. Angular Spectrum Representation
4.4.4. Rayleigh–Sommerfeld Diffraction Integral
4.5. Airy Beams
4.5.1. Fresnel Diffraction integral
4.5.2. Collins Formula
4.5.3. Angular Spectrum Representation
4.5.4. Rayleigh–Sommerfeld Diffraction Integral
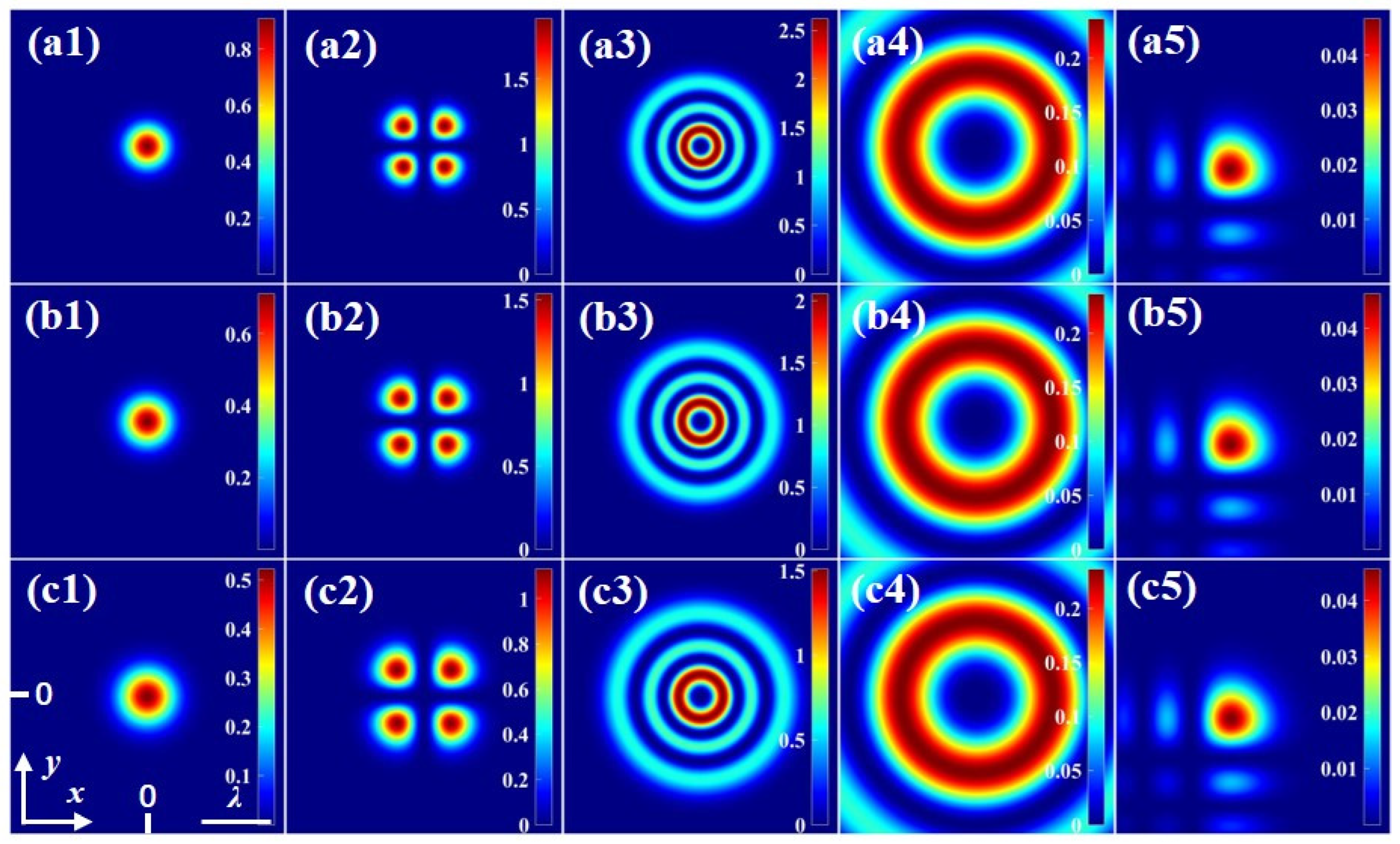
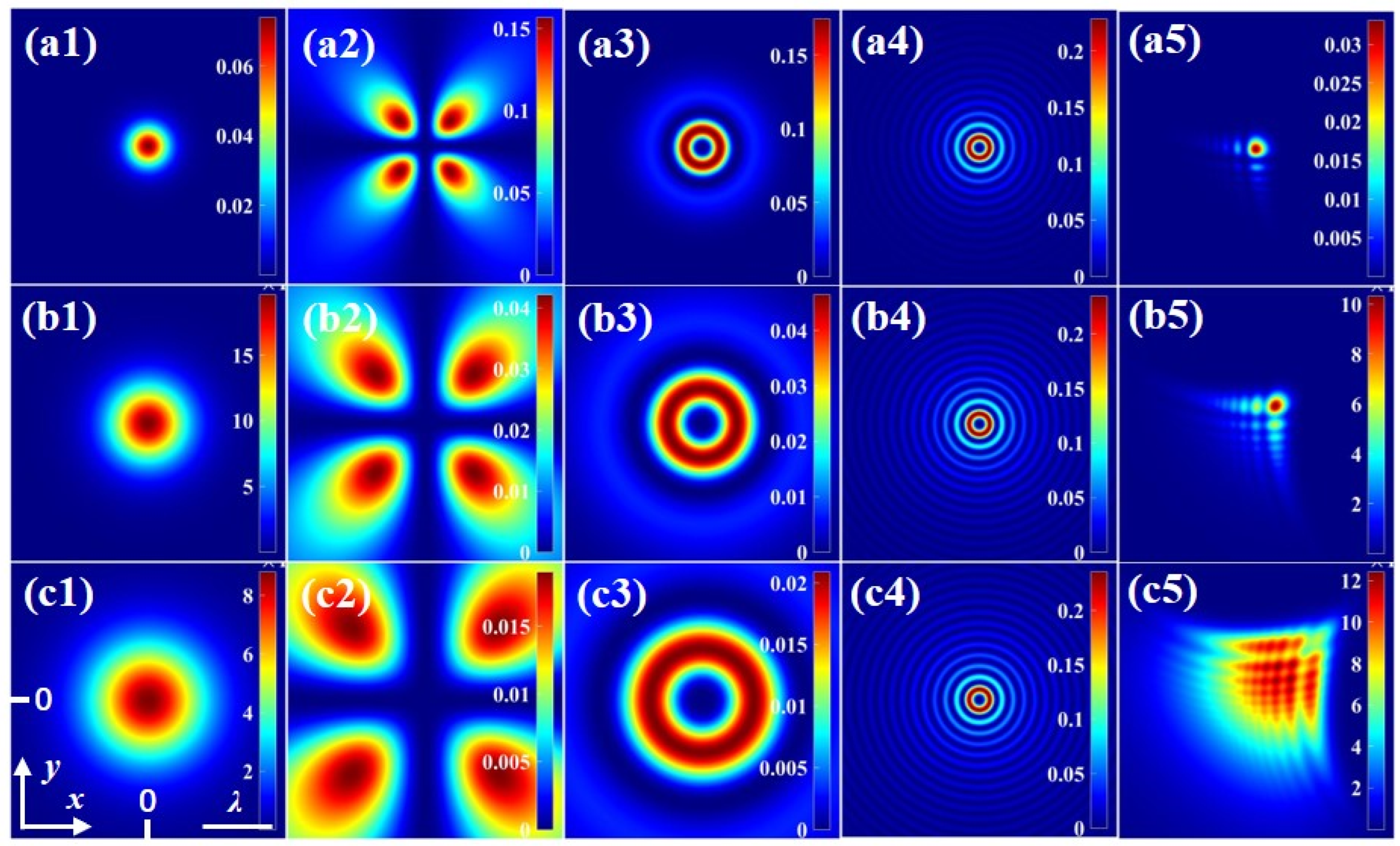
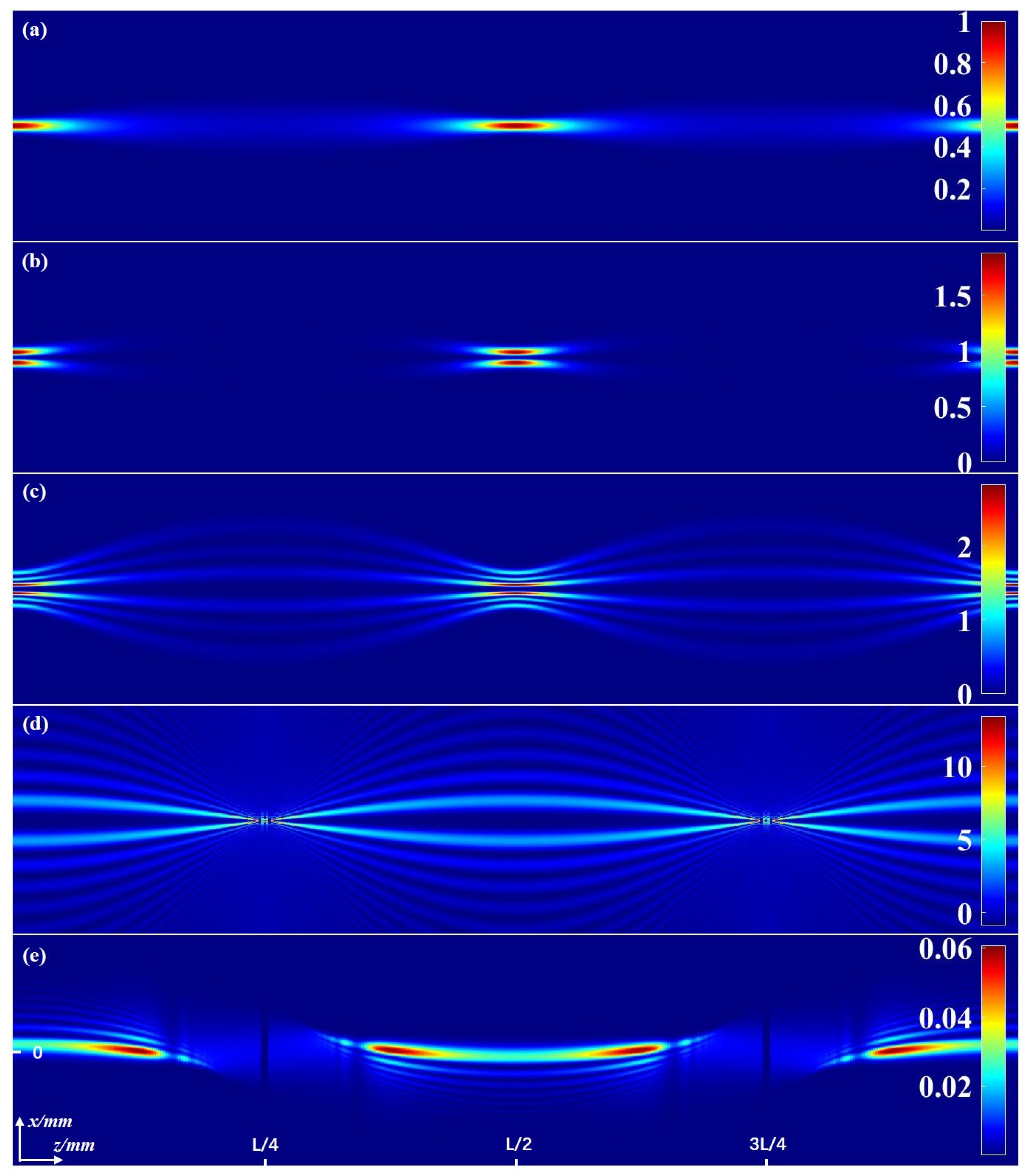
5. Numerical Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Siegman, A.E. Hermite–Gaussian Functions of Complex Argument as Optical-Beam Eigenfunctions. J. Opt. Soc. Am. 1973, 63, 1093–1094. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital Angular Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef]
- Durnin, J. Exact Solutions for Nondiffracting Beams. I. The Scalar Theory. J. Opt. Soc. Am. A 1987, 4, 651–654. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of Accelerating Airy Beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.; Wang, J.; Ma, W.; Zhao, W. Concise and Explicit Expressions for Typical Spatial-Structured Light Beams beyond the Paraxial Approximation. J. Opt. Soc. Am. A 2022, 39, 1794–1804. [Google Scholar] [CrossRef]
- Won, R. Structured Light Spiralling Up. Nat. Photonics 2017, 11, 619–622. [Google Scholar] [CrossRef]
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T.; et al. Roadmap on Structured Light. J. Opt. 2016, 19, 013001. [Google Scholar] [CrossRef]
- Forbes, A. Structured Light from Lasers. Laser Photonics Rev. 2019, 13, 1900140. [Google Scholar] [CrossRef]
- Angelsky, O.V.; Bekshaev, A.Y.; Hanson, S.G.; Zenkova, C.Y.; Mokhun, I.I.; Jun, Z. Structured Light: Ideas and Concepts. Front. Phys. 2020, 8, 114. [Google Scholar] [CrossRef]
- Forbes, A.; de Oliveira, M.; Dennis, M.R. Structured Light. Nat. Photonics 2021, 15, 253–262. [Google Scholar] [CrossRef]
- Cox, M.A.; Mphuthi, N.; Nape, I.; Mashaba, N.; Cheng, L.; Forbes, A. Structured Light in Turbulence. IEEE J. Sel. Top. Quant. 2020, 27, 1–21. [Google Scholar] [CrossRef]
- Yang, Y.; Ren, Y.; Chen, M.; Arita, Y.; Rosales-Guzmán, C. Optical Trapping with Structured Light: A Review. Adv. Photon. 2021, 3, 034001. [Google Scholar] [CrossRef]
- Wang, J.; Liang, Y. Generation and Detection of Structured Light: A Review. Front. Phys. 2021, 9, 688284. [Google Scholar] [CrossRef]
- Jun, Y.; Dian-Yuan, F.; Shi-Ji, W.; Yuan, G. Generalized Fresnel Diffraction Integral and Its Applications. Chin. Phys. 2000, 9, 119. [Google Scholar] [CrossRef]
- Ding, G.; Lü, B. Generalized Huygens–Fresnel Diffraction Integral for Misaligned Asymmetric First-Order Optical Systems and Decentered Anisotropic Gaussian Schell-Model Beams. J. Opt. Soc. Am. A 2002, 19, 485–490. [Google Scholar] [CrossRef]
- Cywiak, M.; Cywiak, D.; Yáñez, E. Finite Gaussian Wavelet Superposition and Fresnel Diffraction Integral for Calculating the Propagation of Truncated, Non-Diffracting and Accelerating Beams. Opt. Commun. 2017, 405, 132–142. [Google Scholar] [CrossRef]
- Feshchenko, R.M.; Vinogradov, A.V.; Artyukov, I.A. Propagation of Waves from an Arbitrary Shaped Surface—A Generalization of the Fresnel Diffraction Integral. Opt. Commun. 2018, 413, 291–294. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, X.; Fan, D. Collins Formula in Frequency-Domain and Fractional Fourier Transforms. Opt. Commun. 1998, 155, 7–11. [Google Scholar] [CrossRef]
- Zhao, D.M. Collins Formula in Frequency-Domain Described by Fractional Fourier Transforms or Fractional Hankel Transforms. Optik 2000, 111, 9–12. [Google Scholar]
- Zhao, D.; Wang, S. Collins Formula in Spatial-Domain Written in Terms of Fractional Fourier Transform or Fractional Hankel Transform. Optik 2000, 111, 371–374. [Google Scholar]
- Lin, Q.; Wang, L. Collins Formula and Tensor ABCD Law in Spatial-Frequency Domain. Opt. Commun. 2000, 185, 263–269. [Google Scholar] [CrossRef]
- Cai, L.Z.; Yang, X.L. Collins Formulae in Both Space and Frequency Domains for ABCD Optical Systems with Small Deformations. J. Mod. Opt. 2001, 48, 1389–1396. [Google Scholar] [CrossRef]
- Li, J.; Li, C. Algorithm Study of Collins Formula and Inverse Collins Formula. Appl. Opt. 2008, 47, A97–A102. [Google Scholar] [CrossRef] [PubMed]
- Chuan-Mei, X.; Hong-Yi, F. A Generalized Collins Formula Derived by Virtue of the Displacement-Squeezing Related Squeezed Coherent State Representation. Chin. Phys. B 2010, 19, 064207. [Google Scholar] [CrossRef]
- Fagerholm, J.; Friberg, A.T.; Huttunen, J.; Morgan, D.P.; Salomaa, M.M. Angular-Spectrum Representation of Nondiffracting X Waves. Phy. Rev. E 1996, 54, 4347. [Google Scholar] [CrossRef]
- Tervo, J.; Turunen, J. Angular Spectrum Representation of Partially Coherent Electromagnetic Fields. Opt. Commun. 2002, 209, 7–16. [Google Scholar] [CrossRef]
- Borghi, R. On the Angular-Spectrum Representation of Multipole Wave Fields. J. Opt. Soc. Am. A 2004, 21, 1805–1810. [Google Scholar] [CrossRef] [PubMed]
- Arnoldus, H.F. Angular Spectrum Representation of the Electromagnetic Multipole Fields, and Their Reflection at a Perfect Conductor. Surf. Sci. 2005, 590, 101–116. [Google Scholar] [CrossRef]
- Gbur, G.; Korotkova, O. Angular Spectrum Representation for the Propagation of Arbitrary Coherent and Partially Coherent Beams through Atmospheric Turbulence. J. Opt. Soc. Am. A 2007, 24, 745–752. [Google Scholar] [CrossRef]
- Korotkova, O.; Gbur, G. Angular Spectrum Representation for Propagation of Random Electromagnetic Beams in a Turbulent Atmosphere. J. Opt. Soc. Am. A 2007, 24, 2728–2736. [Google Scholar] [CrossRef]
- Veerman, J.A.; Rusch, J.J.; Urbach, H.P. Calculation of the Rayleigh–Sommerfeld Diffraction Integral by Exact Integration of the Fast Oscillating Factor. J. Opt. Soc. Am. A 2005, 22, 636–646. [Google Scholar] [CrossRef] [PubMed]
- Shen, F.; Wang, A. Fast-Fourier-Transform Based Numerical Integration Method for the Rayleigh-Sommerfeld Diffraction Formula. Appl. Opt. 2006, 45, 1102–1110. [Google Scholar] [CrossRef]
- Nascov, V.; Logofătu, P.C. Fast Computation Algorithm for the Rayleigh-Sommerfeld Diffraction Formula Using a Type of Scaled Convolution. Appl. Opt. 2009, 48, 4310–4319. [Google Scholar] [CrossRef] [PubMed]
- Sheppard, C.J.R.; Lin, J.; Kou, S.S. Rayleigh–Sommerfeld Diffraction Formula in k Space. J. Opt. Soc. Am. A 2013, 30, 1180–1183. [Google Scholar] [CrossRef] [PubMed]
- Pozzi, G. A Computer Algebra Derivation of the Rayleigh–Sommerfeld Diffraction Formula by a Plane Screen. Optik 2015, 126, 4405–4409. [Google Scholar] [CrossRef]
- Ochoa, N.A. Alternative Approach to Evaluate the Rayleigh-Sommerfeld Diffraction Integrals Using Tilted Spherical Waves. Opt. Express 2017, 25, 12008–12019. [Google Scholar] [CrossRef]
- Mehrabkhani, S.; Schneider, T. Is the Rayleigh-Sommerfeld Diffraction Always an Exact Reference for High Speed Diffraction Algorithms? Opt. Express 2017, 25, 30229–30240. [Google Scholar] [CrossRef]
- Buitrago-Duque, C.; Garcia-Sucerquia, J. Non-Approximated Rayleigh–Sommerfeld Diffraction Integral: Advantages and Disadvantages in the Propagation of Complex Wave Fields. Appl. Opt. 2019, 58, G11–G18. [Google Scholar] [CrossRef]
- Gao, Y.; Xie, J.; Yu, X. Rayleigh-Sommerfeld Diffraction on a Subwavelength Scale: Theories and a Resolution Criterion. Phys. Rew. A 2019, 99, 023814. [Google Scholar] [CrossRef]
- Chen, N.; Wang, C.; Heidrich, W. HTRSD: Hybrid Taylor Rayleigh-Sommerfeld Diffraction. Opt. Express 2022, 30, 37727–37735. [Google Scholar] [CrossRef]
- Tao, X.; Zhou, N.; Lü, B. Recurrence Propagation Equation of Hermite-Gaussian Beams through a Paraxial Optical ABCD System with Hard-Edge Aperture. Optik 2003, 114, 113–117. [Google Scholar] [CrossRef]
- Lu, B.; Wu, P. Analytical Propagation Equation of Astigmatic Hermite-Gaussian Beams through a 4x4 Paraxial Optical System and Their Symmetrizing Transformation. Opt. Laser Technol. 2003, 35, 497–504. [Google Scholar] [CrossRef]
- Cai, Y.; Chen, C. Paraxial Propagation of a Partially Coherent Hermite-Gaussian Beam through Aligned and Misaligned ABCD Optical Systems. J. Opt. Soc. Am. A 2007, 24, 2394–2401. [Google Scholar] [CrossRef]
- Ortiz-Acebedo, A.; Mata-Mendez, O.; Chavez-Rivas, F. Diffraction of Hermite-Gaussian Beams by Ronchi and Aperiodic Rulings. Rev. Mex. Fis. 2008, 54, 35–41. [Google Scholar]
- Lü, B.; Peng, R. Relative Phase Shift in Laguerre-Gaussian Beams Propagating through an Apertured Paraxial ABCD System. J. Mod. Optic. 2003, 50, 857–865. [Google Scholar] [CrossRef]
- Mei, Z.; Zhao, D.; Gu, J. Propagation of Elegant Laguerre–Gaussian Beams through an Annular Apertured Paraxial ABCD Optical System. Opt. Commun. 2004, 240, 337–343. [Google Scholar] [CrossRef]
- Cai, Y.; He, S. Propagation of a Laguerre–Gaussian Beam through a Slightly Misaligned Paraxial Optical System. Appl. Phys. B 2006, 84, 493–500. [Google Scholar] [CrossRef]
- Luo, H.; Ren, Z.; Shu, W.; Wen, S. Reversed Propagation Dynamics of Laguerre-Gaussian Beams in Left-Handed Materials. Phys. Rev. A 2008, 77, 023812. [Google Scholar] [CrossRef]
- Xu, Y. Propagation of Elegant Laguerre Gaussian Beam through a Misaligned Optical System. Opt. Commun. 2013, 308, 237–242. [Google Scholar] [CrossRef]
- Li, H.; Honary, F.; Wu, Z.; Bai, L. Reflection and Transmission of Laguerre-Gaussian Beams in a Dielectric Slab. J. Quant. Spectrosc. Ra. 2017, 195, 35–43. [Google Scholar] [CrossRef]
- Volyar, A.V.; Abramochkin, E.G.; Razueva, E.V.; Bretsko, M.V.; Akimova, Y.E. Geometry of spiral beams: 3D curved structured vortex beams and optical currents. J. Opt. 2021, 23, 044003. [Google Scholar] [CrossRef]
- Volyar, A.; Abramochkin, E.; Akimova, Y.; Bretsko, M. Destroying and recovering spiral vortex beams due to figured perturbations. J. Opt. Soc. Am. A 2021, 38, 1793–1802. [Google Scholar] [CrossRef]
- Volyar, A.; Akimova, Y. Structural stability of spiral vortex beams to sector perturbations. Appl. Opt. 2021, 60, 8865–8874. [Google Scholar] [CrossRef]
- Vahimaa, P.; Kettunen, V.; Kuittinen, M.; Turunen, J.; Friberg, A.T. Electromagnetic Analysis of Nonparaxial Bessel Beams Generated by Diffractive Axicons. J. Opt. Soc. Am. A 1997, 14, 1817–1824. [Google Scholar] [CrossRef]
- El Halba, E.M.; Boustimi, M.; Ez-zariy, L.; Hennani, S.; Belafhal, A. Propagation Characteristics of Bessel-like Beams through ABCD Optical System. Opt. Quant. Electron 2017, 49, 269. [Google Scholar] [CrossRef]
- Cao, Z.; Zhai, C.; Xu, S.; Chen, Y. Propagation of On-Axis and off-Axis Bessel Beams in a Gradient-Index Medium. J. Opt. Soc. Am. A 2018, 35, 230–235. [Google Scholar] [CrossRef]
- Cao, Z.; Zhai, C. Propagation of Bessel Beam in a Strongly Nonlocal Nonlinear Media. Optik 2019, 178, 301–309. [Google Scholar] [CrossRef]
- Torre, A. Airy Beams beyond the Paraxial Approximation. Opt. Commun. 2010, 283, 4146–4165. [Google Scholar] [CrossRef]
- Lin, H.-C.; Pu, J.-X. Propagation of Airy Beams from Right-Handed Material to Left-Handed Material. Chin. Phys. B 2012, 21, 054201. [Google Scholar] [CrossRef]
- Wen, W.; Lu, X.; Zhao, C.; Cai, Y. Propagation of Airy Beam Passing through the Misaligned Optical System with Hard Aperture. Opt. Commun. 2014, 313, 350–355. [Google Scholar] [CrossRef]
- Wen, W.; Chu, X. Propagation of Symmetric Tunable Dual Airy Beam through ABCD Optical System. Opt. Commun. 2014, 333, 38–44. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; Tang, M.; Cao, J.; Li, X. Propagation of Airy Beams in the Quadratic-Index Medium Based on Matrix Optics. Optik 2017, 149, 144–148. [Google Scholar] [CrossRef]
- Hui, Y.; Cui, Z.; Zhao, M.; Han, Y. Vector Wave Analysis of Airy Beams upon Reflection and Refraction. J. Opt. Soc. Am. A 2020, 37, 1480–1489. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, J.; Pang, Z.; Wang, L.; Zhong, T.; Yang, X.; Deng, D. Propagation Properties of the Chirped Airy Beams through the Gradient-Index Medium. Opt. Commun. 2017, 402, 60–65. [Google Scholar] [CrossRef]
- Zhao, R.; Deng, F.; Yu, W.; Huang, J.; Deng, D. Propagation Properties of Airy–Gaussian Vortex Beams through the Gradient-Index Medium. J. Opt. Soc. Am. A 2016, 33, 1025–1031. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhou, K.; Deng, D. Propagation of Cosine Complex Variable Function Airy–Gaussian Beams through the Gradient-Index Medium. Appl. Phys. B 2019, 125, 91. [Google Scholar] [CrossRef]
- Pei, S.; Xu, S.; Cui, F.; Pan, Q.; Cao, Z. Propagation of a Bessel–Gaussian Beam in a Gradient-Index Medium. Appl. Opt. 2019, 58, 920–926. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, F.; Luo, Y.; Cui, Z. A Systematic Summary and Comparison of Scalar Diffraction Theories for Structured Light Beams. Photonics 2023, 10, 1041. https://doi.org/10.3390/photonics10091041
Wu F, Luo Y, Cui Z. A Systematic Summary and Comparison of Scalar Diffraction Theories for Structured Light Beams. Photonics. 2023; 10(9):1041. https://doi.org/10.3390/photonics10091041
Chicago/Turabian StyleWu, Fuping, Yi Luo, and Zhiwei Cui. 2023. "A Systematic Summary and Comparison of Scalar Diffraction Theories for Structured Light Beams" Photonics 10, no. 9: 1041. https://doi.org/10.3390/photonics10091041
APA StyleWu, F., Luo, Y., & Cui, Z. (2023). A Systematic Summary and Comparison of Scalar Diffraction Theories for Structured Light Beams. Photonics, 10(9), 1041. https://doi.org/10.3390/photonics10091041





