Supercontinuum Generation from Airy-Gaussian Pulses in Photonic Crystal Fiber with Three Zero-Dispersion Points
Abstract
:1. Introduction
2. Theoretical Model
3. Analysis of Numerical Results
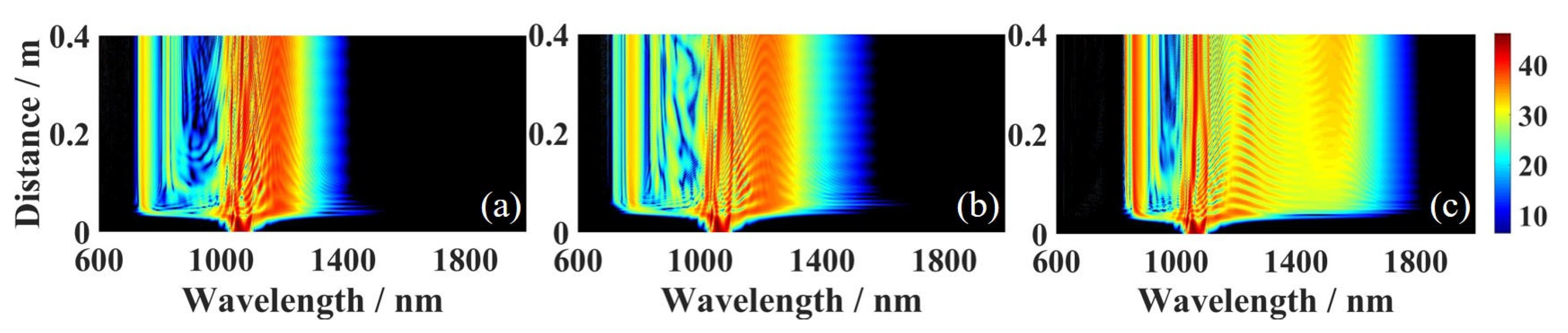
3.1. Effect of Barrier Width of Three-Zero-Dispersion-Point PCF
3.2. Effect of the Number of Zero-Dispersion Points in PCF
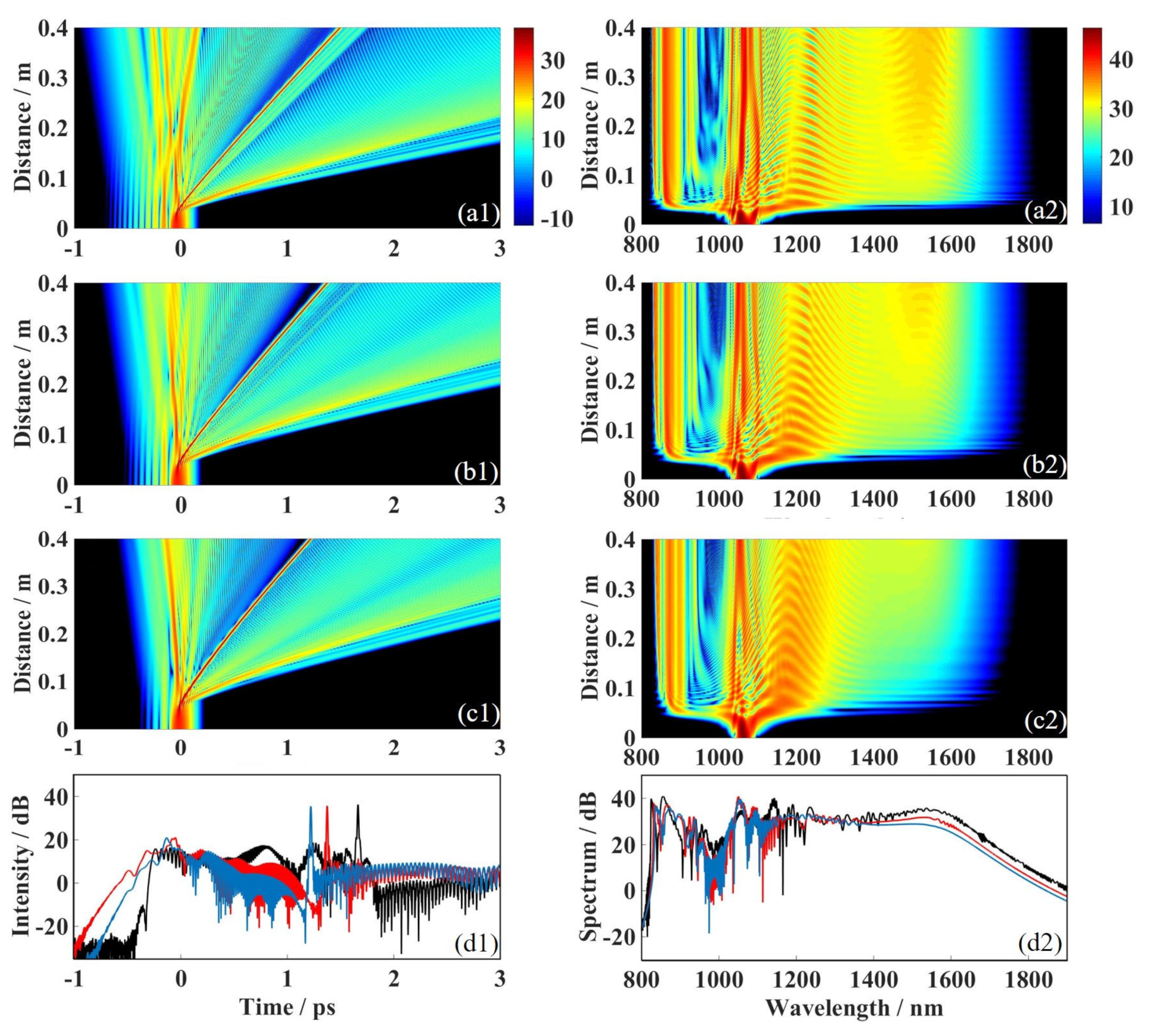
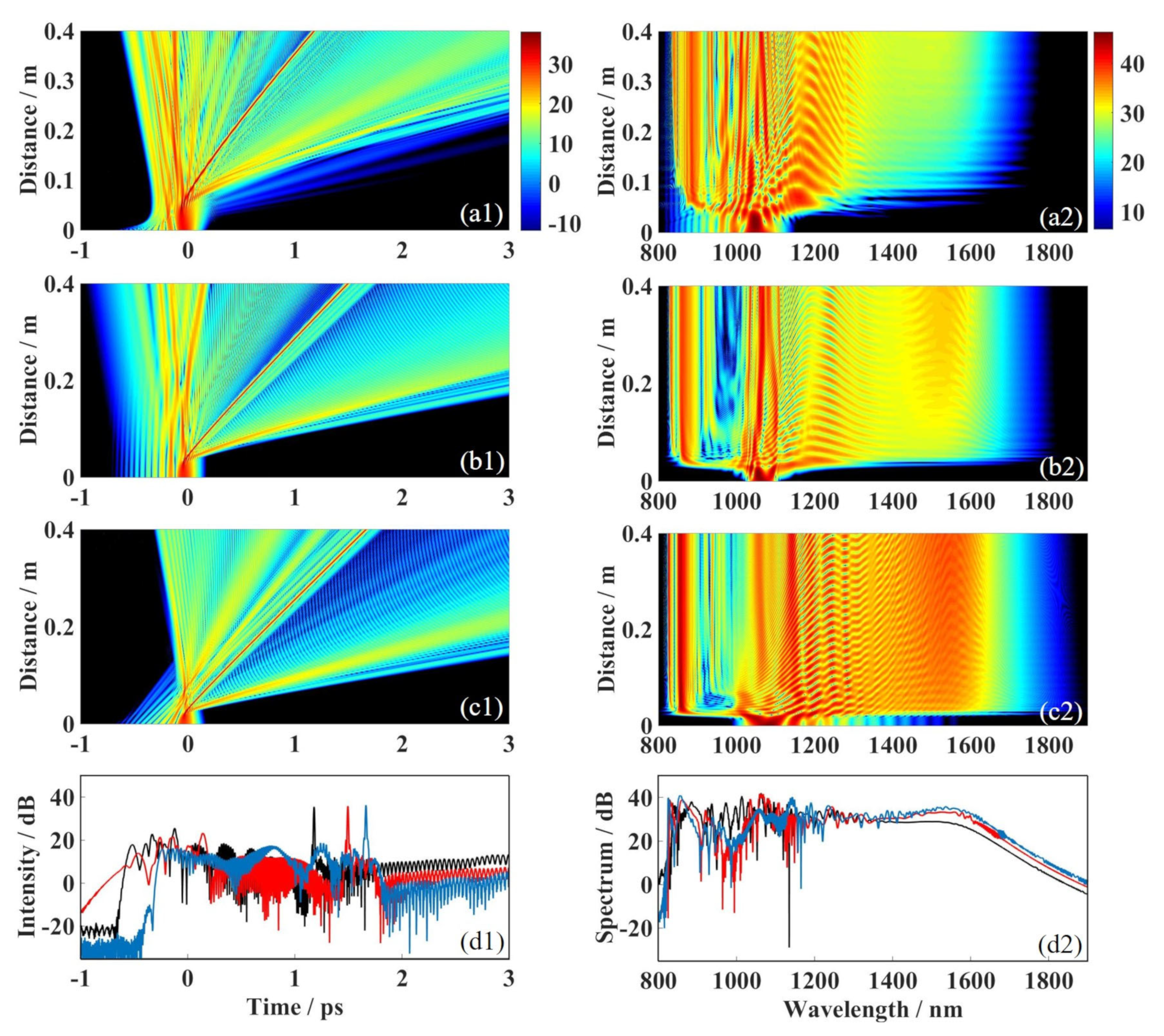
3.3. Influence of the Initial Parameters of the Airy-Gaussian Pulse
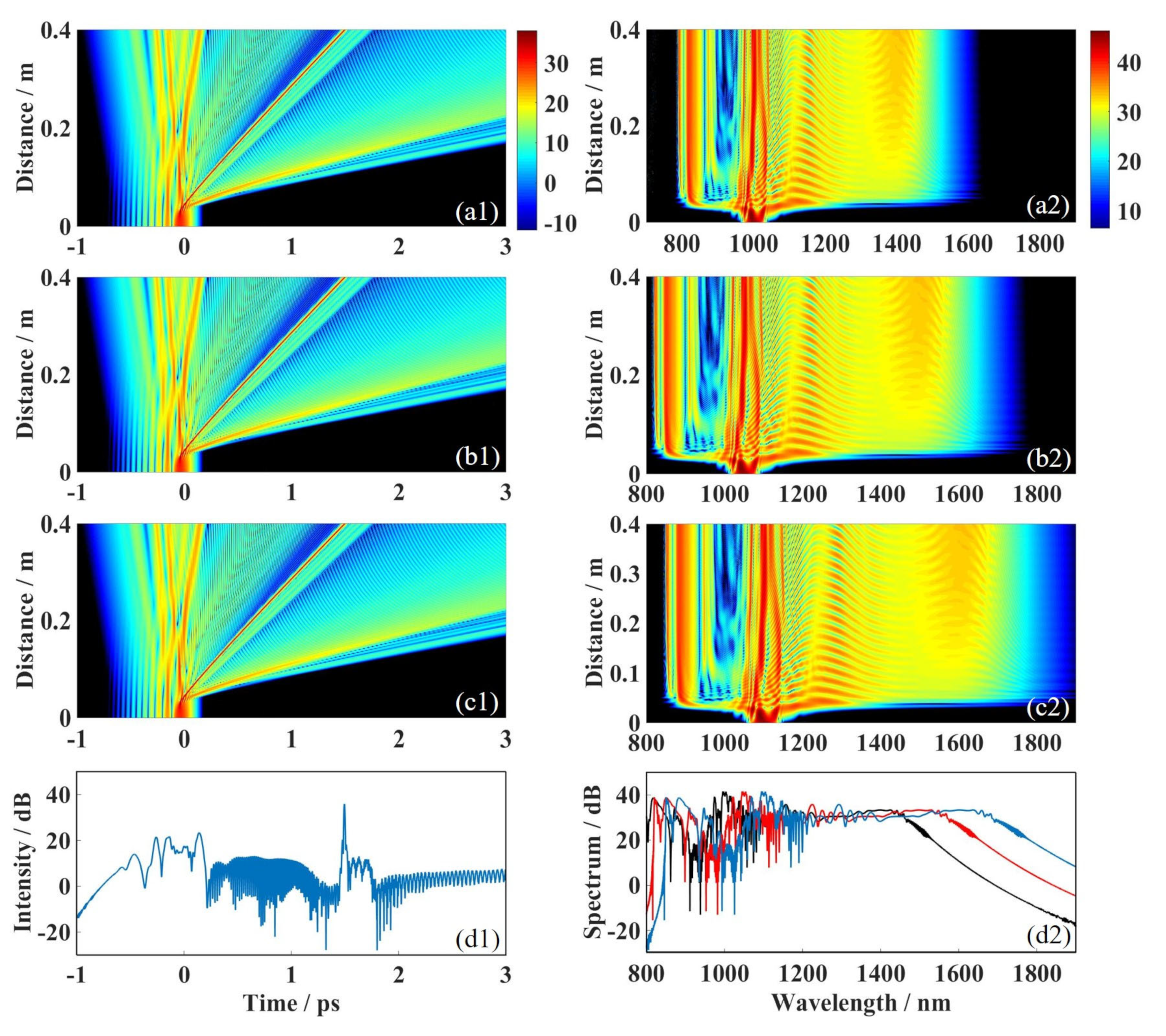
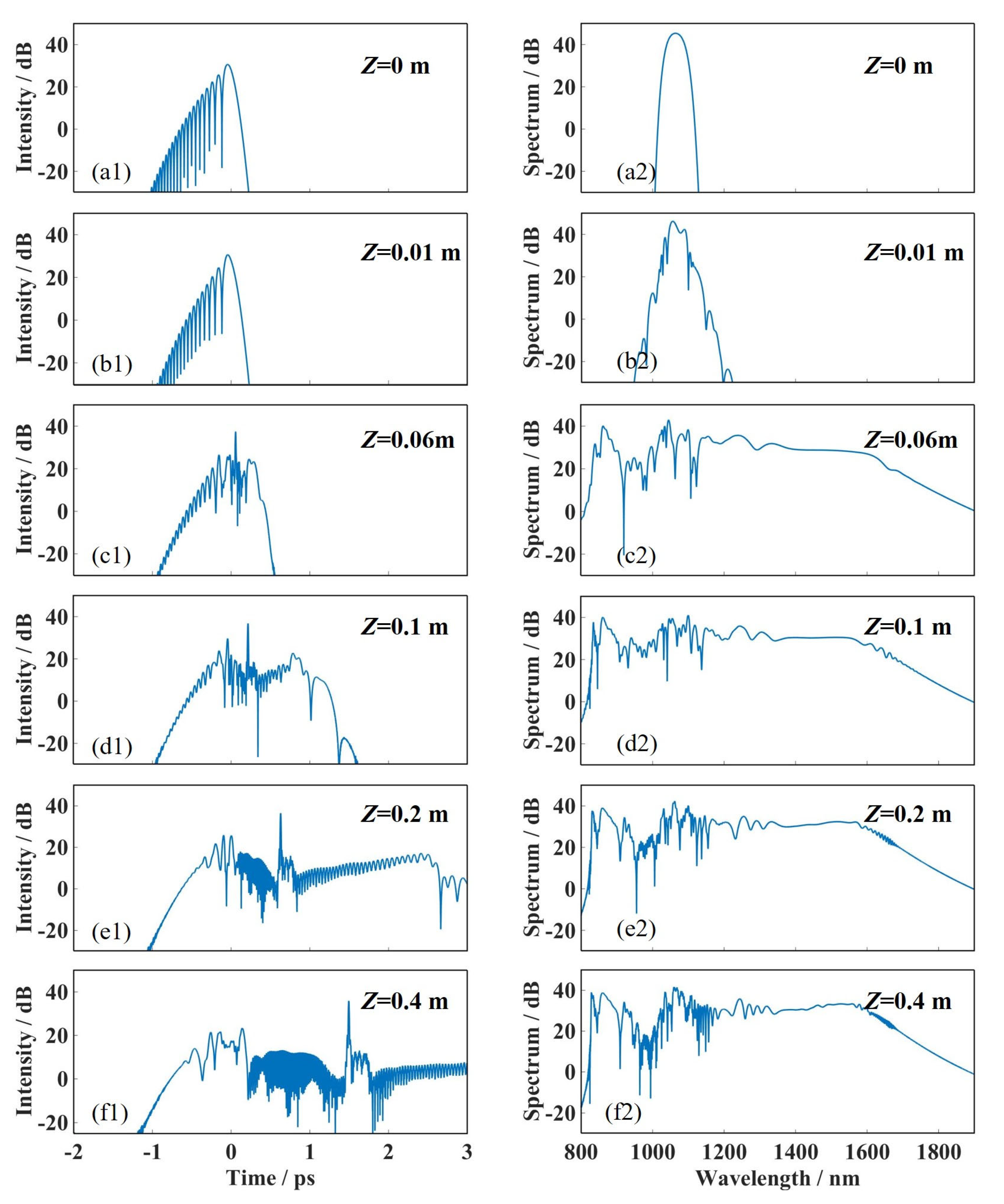
3.4. The Detailed Process of the Supercontinuum Formation of Airy-Gaussian Pulse in PCF2
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Siviloglou, G.A.; Christodoulides, D.N. Accelerating finite energy Airy beams. Opt. Lett. 2007, 32, 979–981. [Google Scholar] [CrossRef] [PubMed]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of Accelerating Airy Beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef] [PubMed]
- Kaminer, I.; Bekenstein, R.; Nemirovsky, J.; Segev, M. Nondiffracting Accelerating Wave Packets of Maxwell’s Equations. Phys. Rev. Lett. 2012, 108, 163901. [Google Scholar] [CrossRef] [PubMed]
- Broky, J.; Siviloglou, G.A.; Dogariu, A.; Christodoulides, D.N. Self-healing properties of optical Airy beams. Opt. Exp. 2008, 16, 12880–12891. [Google Scholar] [CrossRef] [PubMed]
- Ellenbogen, T.; Voloch-Bloch, N.; Ganany-Padowicz, A.; Arie, A. Nonlinear generation and manipulation of Airy beams. Nat. Photonics 2009, 3, 395–398. [Google Scholar] [CrossRef]
- Christodoulides, D.N. Optical trapping: Riding along an Airy beam. Nat. Photonics 2008, 2, 652–653. [Google Scholar] [CrossRef]
- Christodoulides, D.N. Airy plasmon: A nondiffracting surface wave. Opt. Lett. 2010, 35, 2082–2084. [Google Scholar]
- Polynkin, P.; Kolesik, M.; Moloney, J.V.; Siviloglou, G.A.; Christodoulides, D.N. Curved Plasma Channel Generation Using Ultraintense Airy Beams. Science 2009, 324, 229–232. [Google Scholar] [CrossRef]
- Minovich, A.; Klein, A.E.; Janunts, N.; Pertsch, T.; Neshev, D.N.; Kivshar, Y.S. Generation and near-field imaging of Airy surface plasmons. Phys. Rev. Lett. 2011, 107, 116802. [Google Scholar] [CrossRef]
- Deng, D.; Li, H. Propagation properties of Airy–Gaussian beams. Appl. Phys. B 2012, 106, 677–681. [Google Scholar] [CrossRef]
- Li, P.; Malomed, B.A.; Mihalache, D. Symmetry breaking of spatial Kerr-solitons in fractional dimension. Chaos Solitons Fract. 2020, 132, 109602. [Google Scholar] [CrossRef]
- Zeng, L.W.; Malomed, B.A.; Mihalache, D.; Cai, Y.; Lu, X.W.; Zhu, Q.F.; Li, J.Z. Bubbles and W-shaped solitons in Kerr media with fractional diffraction. Nonlinear Dyn. 2021, 104, 4253–4264. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, J.; Wang, P.X. Periodic evolution of Airy-Gaussian beams under linear potential. Chin. J. Lasers 2021, 48, 105002. [Google Scholar] [CrossRef]
- Chen, W.J.; Song, D.; Li, Y.; Wang, X.; Qin, X.L.; Liu, C.Y. Control on interaction of Airy-Gaussian beams in competing no nlinear medium. Acta Phys. Sin. 2019, 68, 94206. [Google Scholar] [CrossRef]
- Zhang, L.F.; Liu, K.; Zhong, H.Z.; Zhang, J.G.; Li, Y.; Fan, D.Y. Effect of initial frequency chirp on Airy pulse propagation in an optical fiber. Opt. Express 2015, 23, 2566–2576. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.F.; Zhong, H.Z. Modulation instability of finite energy Airy pulse in optical fiber. Opt. Express 2014, 22, 17107–17115. [Google Scholar] [CrossRef]
- Zhang, L.F.; Zhong, H.Z.; Li, Y.; Fan, D.Y. Manipulation of Raman-induced frequency shift by use of asymmetric self-accelerating Airy pulse. Opt. Express 2014, 22, 22598–22607. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.D.; Chen, B.; Peng, X.; Deng, D.M. Propagation of Airy-Gaussian beam in Kerr medium. J. Opt. 2015, 17, 35504. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, L.; Xu, C.; Deng, D. Propagation and Wigner distribution of the Airy–Gauss beam through an apertured paraxial optical system. Opt. Commun. 2020, 454, 124494. [Google Scholar] [CrossRef]
- Ranka, J.K.; Windeler, R.S.; Stentz, A.J. Visible continuum generation in air–silica microstructure optical fibers with anomalous dispersion at 800 nm. Opt. Lett. 2000, 25, 25–27. [Google Scholar] [CrossRef]
- Ranka, J.K.; Windeler, R.S.; Stentz, A.J. Nonlinear wavelength conversion in photonic crystal fibers with three zero-dispersion points. Phys. Rev. A 2011, 83, 23808. [Google Scholar]
- Barak, A.; Peleg, O.; Stucchio, C.; Segev, M. Observation of Soliton Tunneling Phenomena and Soliton Ejection. Phys. Rev. Lett. 2008, 100, 153901. [Google Scholar] [CrossRef] [PubMed]
- Tsoy, E.N.; De Sterke, C.M. Theoretical analysis of the self-frequency shift near zero-dispersion points: Soliton spectral tunneling. Phys. Rev. A 2007, 76, 43804. [Google Scholar] [CrossRef]
- Bache, M.; Bang, O.; Zhou, B.; Moses, J.; Wise, F.W. Optical Cherenkov radiation by cascaded nonlinear interaction: An efficient source of few-cycle energetic near- to mid-IR pulses. Opt. Express 2011, 19, 22557–22562. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.F.; Hu, J.G.; Guo, H.R.; Zeng, X.L. Optical Cherenkov radiation in an As2S3 slot waveguide with four zero-dispersion wavelengths. Opt. Express 2013, 21, 3067–3072. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Baquedano, N.; Torres-Gomez, M.; Arzate, N.; Ferrando, A.; Ceballos-Herrera, D.E. Pulse quality analysis on soliton pulse compression and soliton self-frequency shift in a hollow-core photonic bandgap fiber. Opt. Express 2013, 21, 9132–9143. [Google Scholar] [CrossRef] [PubMed]
- Li, H.Z.; Cai, W.Y.; Zhang, J.; Gao, Y.X.; Zhang, L.F.; Fan, D.Y. Manipulation of dispersive waves emission via quadratic spectral phase. Opt. Express 2021, 29, 12723–12735. [Google Scholar] [CrossRef] [PubMed]
- Peng, W.L.; Zhang, X.; Jing, L.Q.; Gao, Y.X.; Deng, Z.X.; Zhang, L.F.; Fan, D.Y. Soliton-sinc optical pulse propagation in the presence of high-order effects. Opt. Express 2023, 31, 9961–9972. [Google Scholar] [CrossRef]
- Li, H.Z.; Wang, Z.T.; Xie, Z.X.; Fan, D.Y.; Zhang, L.F. Manipulating dispersive wave emission via temporal sinusoidal phase modulation. Opt. Express 2023, 31, 6296–6303. [Google Scholar] [CrossRef]
- Ouahid, L.; Dalil, E.L.; Belafhal, A. Effect of light absorption and temperature on self-focusing of finite Airy Gaussian beams in plasma with relativistic and ponderomotive regime. Quantum Electron. 2018, 50, 216–232. [Google Scholar] [CrossRef]
- Marest, T.; Braud, F.; Conforti, M.; Wabnitz, S.; Mussot, A.; Kudlinski, A. Longitudinal soliton tunneling in optical fiber. Opt. Lett. 2017, 42, 2350–2353. [Google Scholar] [CrossRef]
- Peng, H.Y.; Li, Y.; Peng, J.; Wen, B.; Deng, Y.B.; Tang, P.H. Evolution of Airy-Gaussian pulses in photonic crystal fiber with two zero-dispersion wavelengths. Optik 2021, 250, 168324. [Google Scholar] [CrossRef]
- Luo, Y.P.; Yang, H.; Zhao, S.L.; Lv, J.; Hu, H. Impact of potential barriers on soliton spectral tunneling in photonic crystal fiber. Opt. Commun. 2020, 454, 124330. [Google Scholar] [CrossRef]
- Li, Y.; Peng, J.; Tan, C.; Tang, P.H. Numerical investigation on the dynamic propagation of finite-energy Airy pulses in photonic crystal fiber. J. Mod. Opt. 2020, 67, 445–453. [Google Scholar] [CrossRef]



| psk | PCFs with Three Zero-Dispersion Points | |||
|---|---|---|---|---|
| k | 1 | 2 | 3 | 4 |
| 2 | −15.8126 | −15.8126 | −15.8126 | −15.8126 |
| 3 | 0.10025 | 0.11025 | 0.11025 | 0.13025 |
| 4 | 1.0582 × 10−3 | 1.0382 × 10−3 | 0.9682 × 10−3 | 1.0382 × 10−3 |
| 5 | −1.5686 × 10−6 | −1.5686 × 10−6 | −1.5686 × 10−6 | −1.5686 × 10−6 |
| 6 | 2.4280 × 10−9 | 2.4280 × 10−9 | 2.4280 × 10−9 | 2.4280 × 10−9 |
| 7 | 4.0260 × 10−10 | 2.1260 × 10−10 | 0.5260 × 10−10 | −0.3260 × 10−10 |
| 8 | −1.7693 × 10−12 | −1.7693 × 10−12 | −1.7693 × 10−12 | −1.7693 × 10−12 |
| 9 | 6.4322 × 10−15 | 6.4322 × 10−15 | 6.4322 × 10−15 | 6.4322 × 10−15 |
| 10 | 3.1990 × 10−20 | 3.1990 × 10−20 | 3.1990 × 10−20 | 3.1990 × 10−20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Wen, B.; Deng, Y.; Gao, C.; Wei, J.; Zhang, S.; Zhu, Q. Supercontinuum Generation from Airy-Gaussian Pulses in Photonic Crystal Fiber with Three Zero-Dispersion Points. Photonics 2023, 10, 1061. https://doi.org/10.3390/photonics10091061
Yu X, Wen B, Deng Y, Gao C, Wei J, Zhang S, Zhu Q. Supercontinuum Generation from Airy-Gaussian Pulses in Photonic Crystal Fiber with Three Zero-Dispersion Points. Photonics. 2023; 10(9):1061. https://doi.org/10.3390/photonics10091061
Chicago/Turabian StyleYu, Xinyi, Bing Wen, Yangbao Deng, Chunhui Gao, Jiamou Wei, Saiwen Zhang, and Qiuxiang Zhu. 2023. "Supercontinuum Generation from Airy-Gaussian Pulses in Photonic Crystal Fiber with Three Zero-Dispersion Points" Photonics 10, no. 9: 1061. https://doi.org/10.3390/photonics10091061
APA StyleYu, X., Wen, B., Deng, Y., Gao, C., Wei, J., Zhang, S., & Zhu, Q. (2023). Supercontinuum Generation from Airy-Gaussian Pulses in Photonic Crystal Fiber with Three Zero-Dispersion Points. Photonics, 10(9), 1061. https://doi.org/10.3390/photonics10091061





