All-Metal Coding Metasurfaces for Broadband Terahertz RCS Reduction and Infrared Invisibility
Abstract
:1. Introduction
2. Materials and Methods
2.1. Methods of RCS Reduction
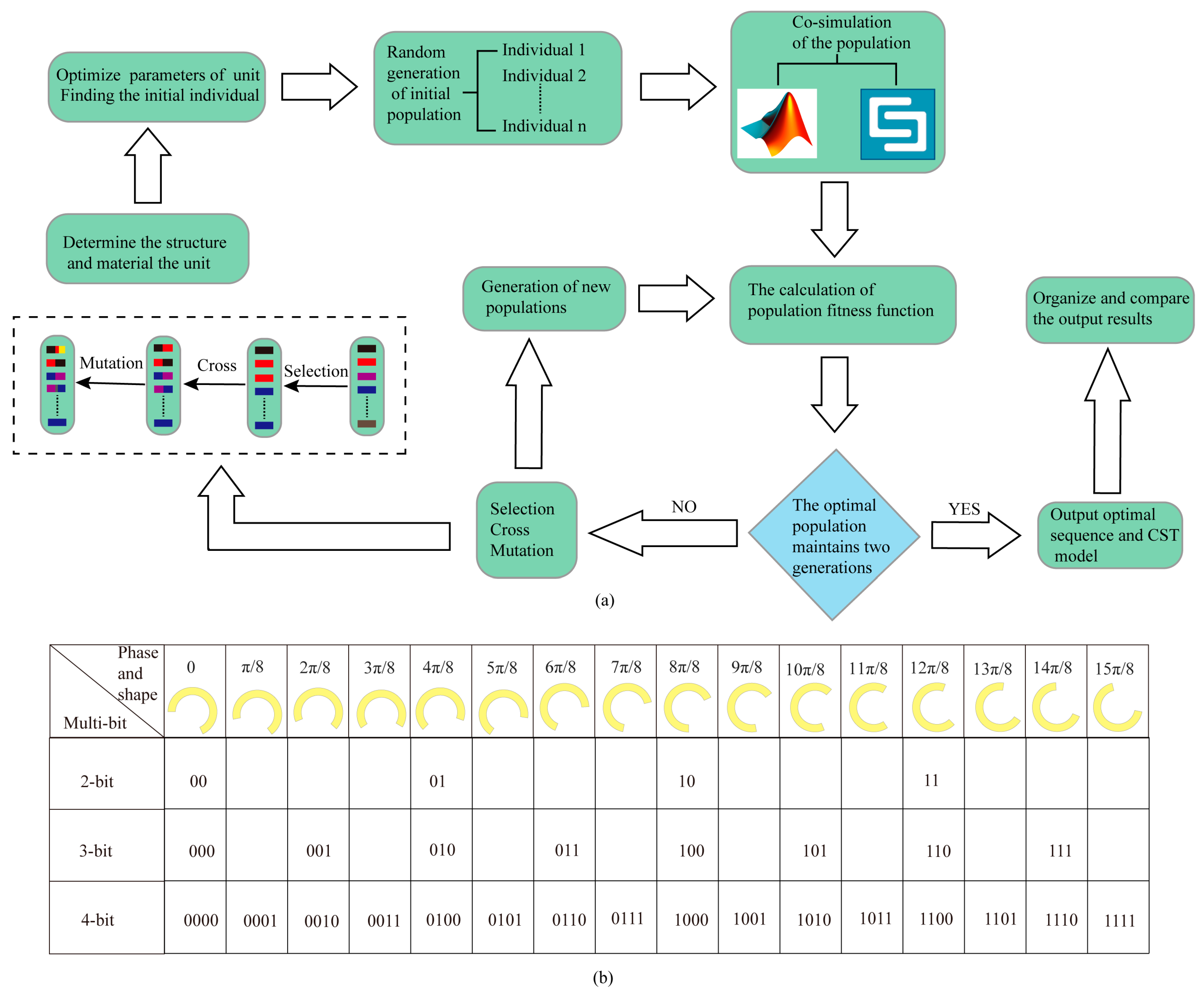
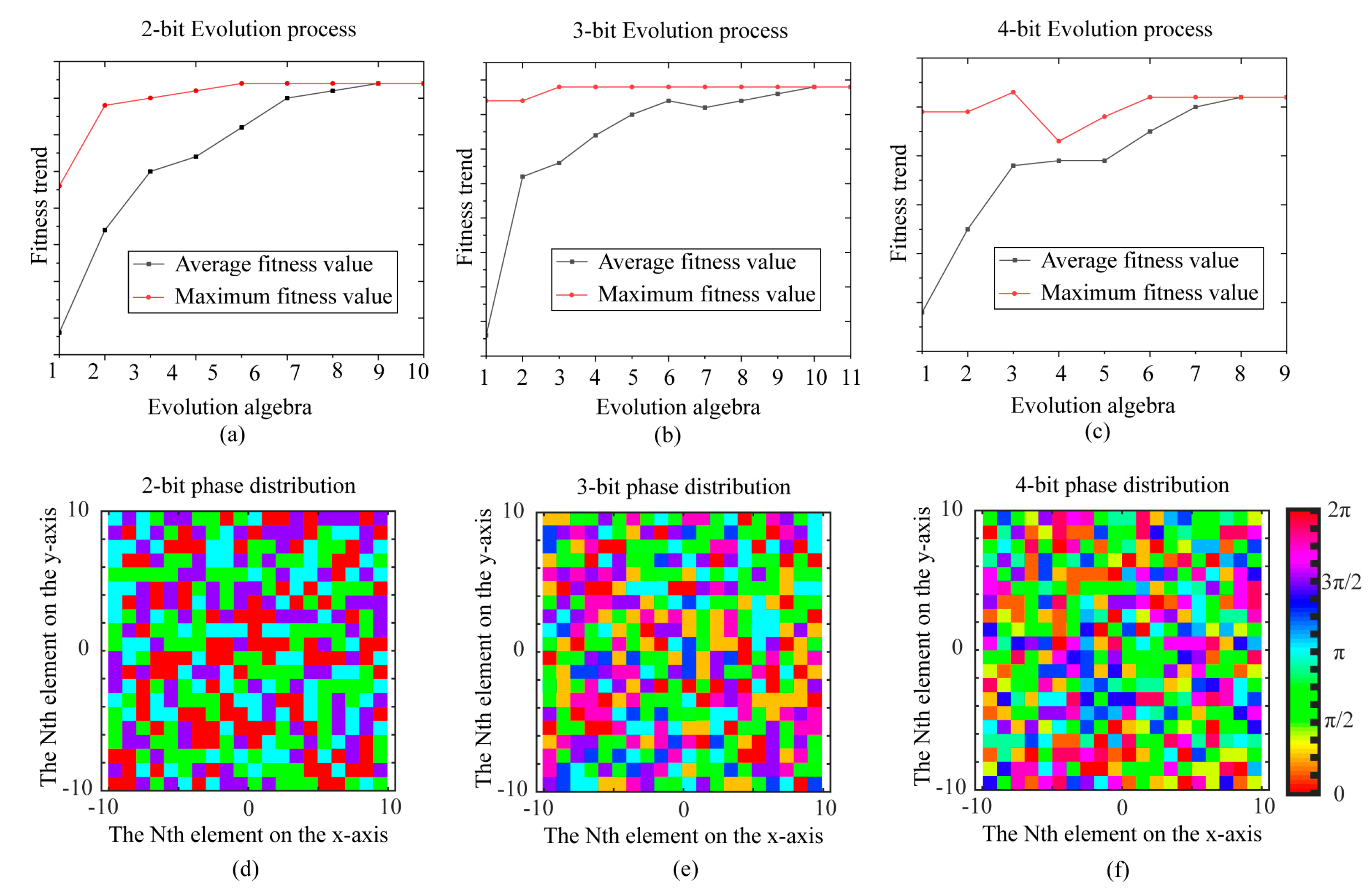
2.2. Multi-Bit Coding Metasurface
3. Results and Discussion
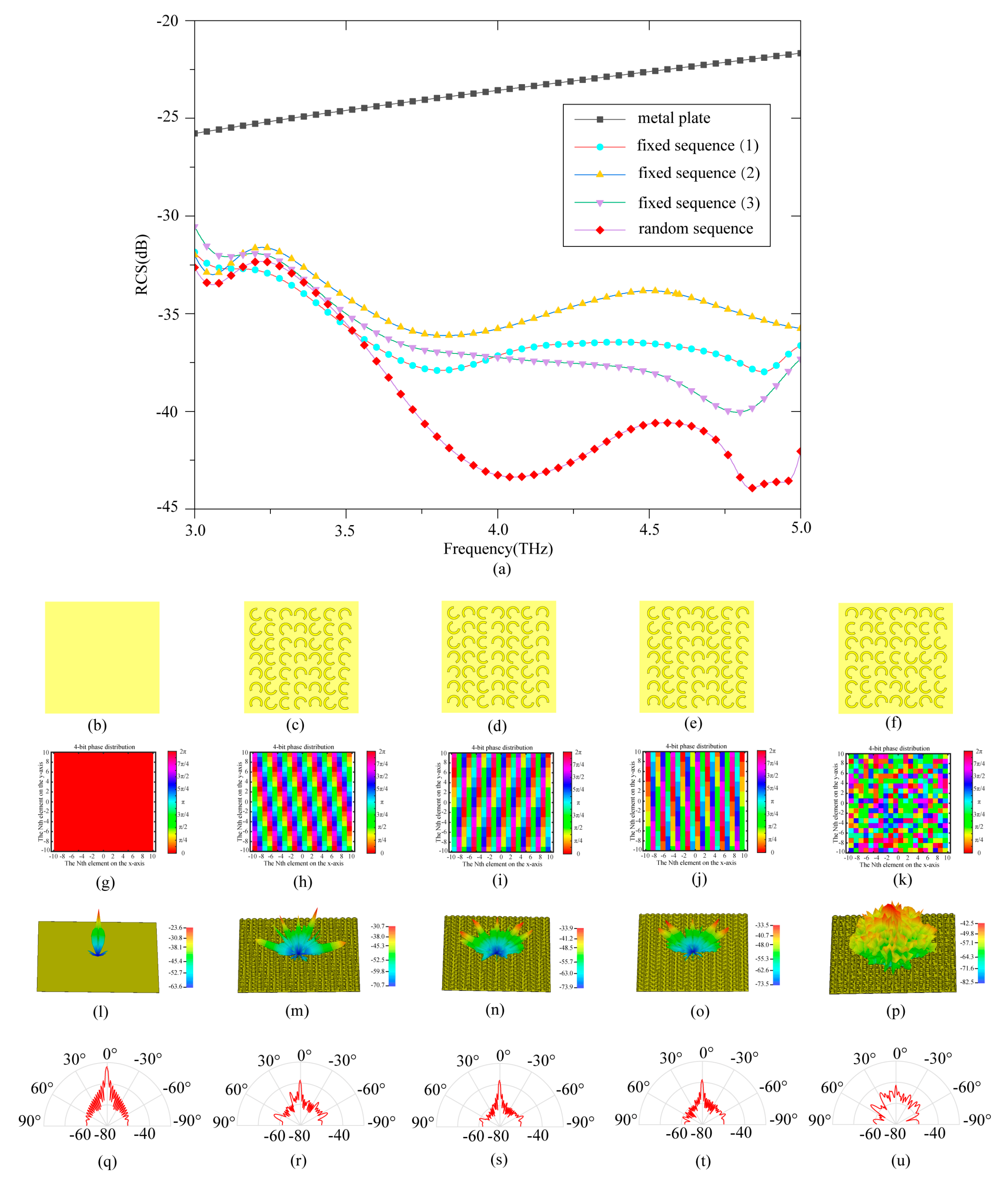
3.1. Design of Coding Metasurface
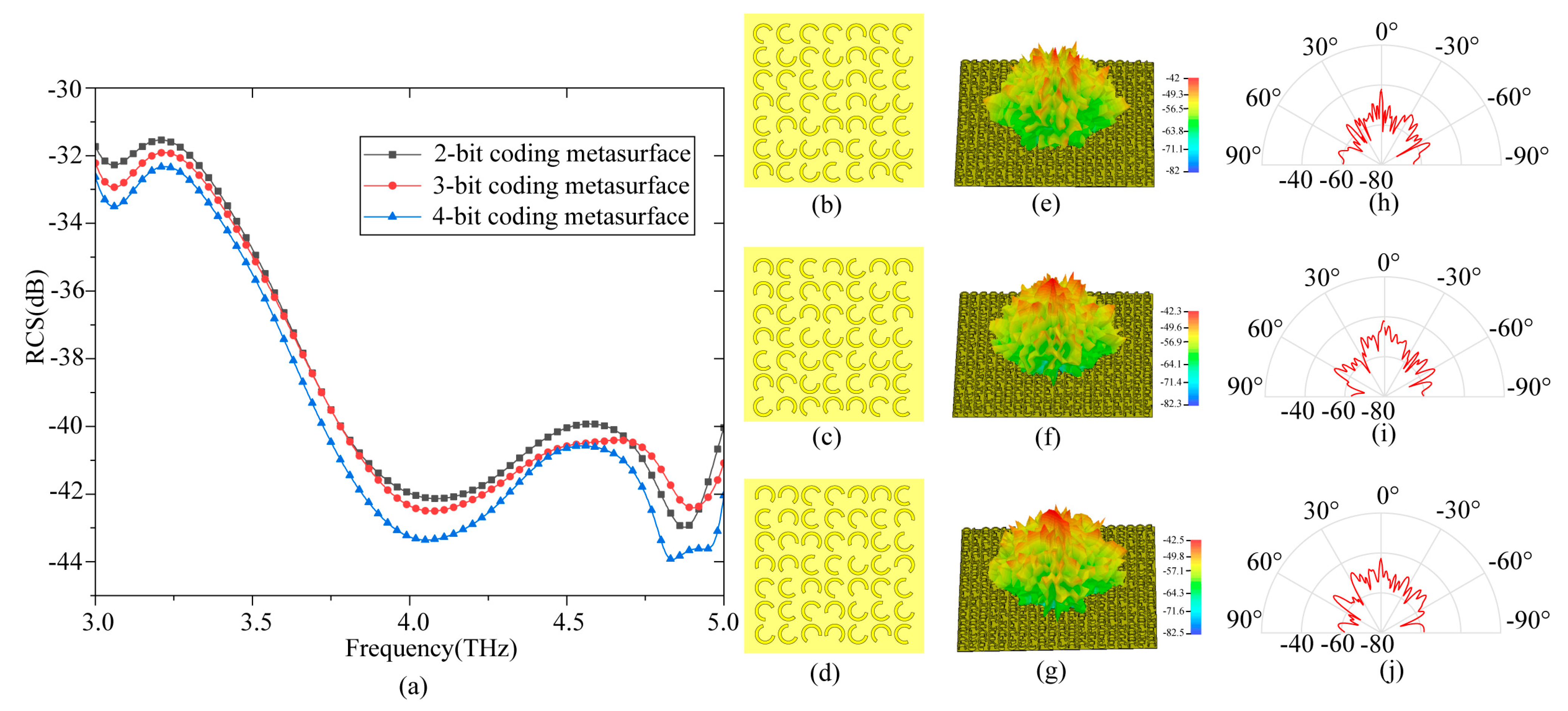
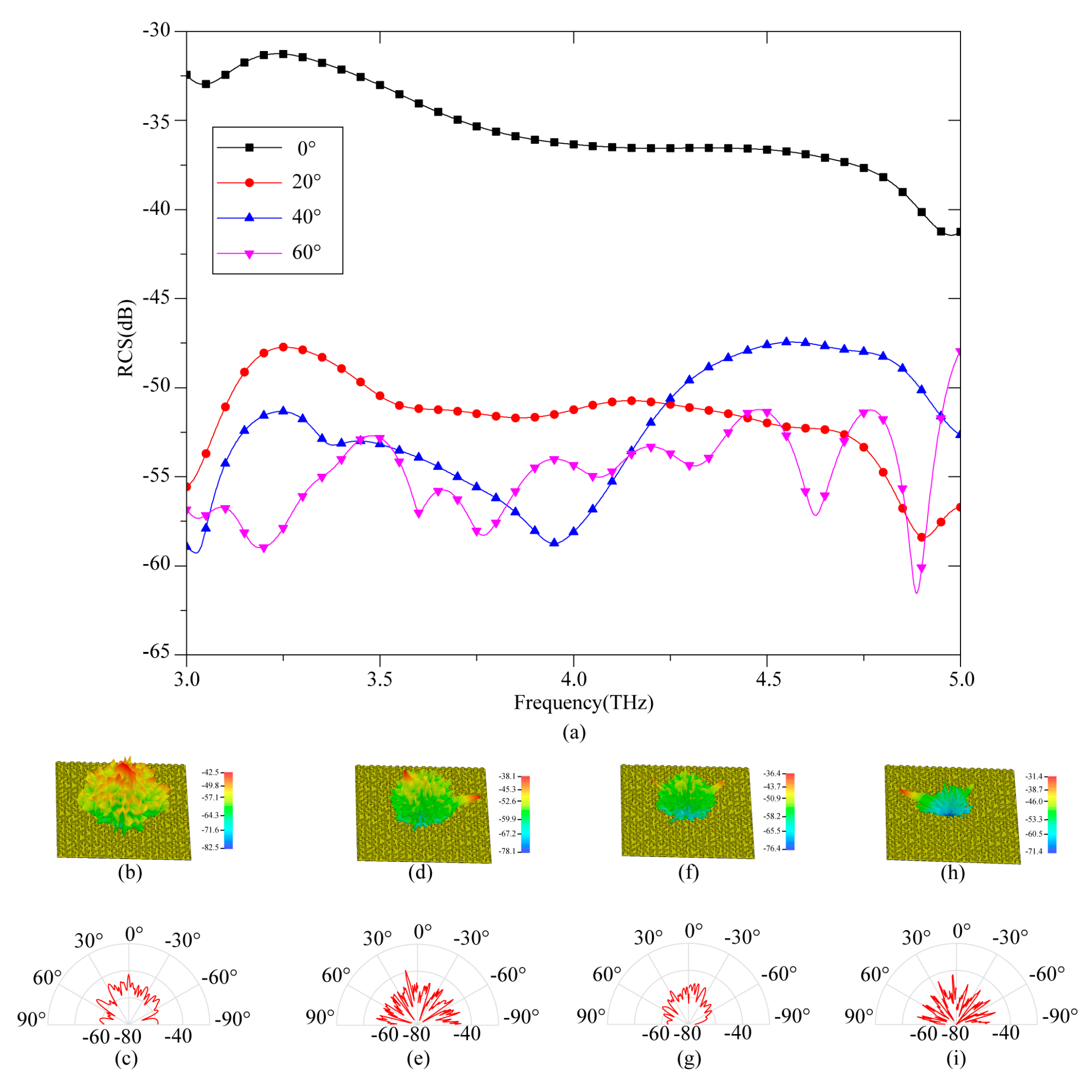
3.2. Simulation and Analysis of Coding Metasurface
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, P.; Tian, H.W.; Cai, X.; Jiang, W.X.; Cui, T.J. Radiation-Type Metasurfaces for Advanced Electromagnetic Manipulation. Adv. Funct. Mater. 2021, 31, 2100569. [Google Scholar] [CrossRef]
- Hestenes, D. Space-time structure of weak and electromagnetic interactions. Found. Phys. 1982, 12, 153–168. [Google Scholar] [CrossRef]
- Li, X.F.; Liu, C.; Zhou, F.; Chen, Z.C.; Iraklis, G.; Evert, S. Deep learning–based nondestructive evaluation of reinforcement bars using ground-penetrating radar and electromagnetic induction data. Comput.–Aided Civ. Infrastruct. Eng. 2022, 37, 1834–1853. [Google Scholar] [CrossRef]
- Zhang, L.; Mei, S.; Huang, K.; Qiu, C.-W. Advances in Full Control of Electromagnetic Waves with Metasurfaces. Adv. Opt. Mater. 2016, 4, 818–833. [Google Scholar] [CrossRef]
- Li, Y.; Shen, C.; Xie, Y.; Li, J.; Wang, W.; Cummer, S.A.; Jing, Y. Tunable Asymmetric Transmission via Lossy Acoustic Metasurfaces. Phys. Rev. Lett. 2017, 119, 035501. [Google Scholar] [CrossRef]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling Electromagnetic Fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef]
- Schurig, D.; Mock, J.J.; Justice, B.J.; Cummer, S.A.; Pendry, J.B.; Starr, A.F.; Smith, D.R. Metamaterial Electromagnetic Cloak at Microwave Frequencies. Science 2006, 314, 977–980. [Google Scholar] [CrossRef]
- Cheng, Q.; Jiang, W.X.; Cui, T.J. Spatial Power Combination for Omnidirectional Radiation via Anisotropic Metamaterials. Phys. Rev. Lett. 2012, 108, 213903. [Google Scholar] [CrossRef]
- Guo, Y.; Yan, J.; Pu, M.; Li, X.; Ma, X.; Zhao, Z.; Luo, X. Ultra-wideband manipulation of electromagnetic waves by bilayer scattering engineered gradient metasurface. RSC Adv. 2018, 8, 13061–13066. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Luo, J.; Pu, M.; Guo, Y.; Zhao, Z.; Ma, X.; Li, X.; Luo, X. Catenary Electromagnetics for Ultra-Broadband Lightweight Absorbers and Large-Scale Flat Antennas. Adv. Sci. 2019, 6, 1801691. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, T.; Chen, S.; Xie, Z.; Zheng, J.; Zhu, J.; Su, Y.; Chen, W.; Liu, K.; Tang, M.; et al. All-optical controlled-NOT logic gate achieving directional asymmetric transmission based on metasurface doublet. Opto-Electron. Adv. 2023, 6, 220073. [Google Scholar] [CrossRef]
- Tang, Z.; Li, L.; Zhang, H.; Yang, J.; Hu, J.; Lu, X.; Hu, Y.; Qi, S.; Liu, K.; Tian, M.; et al. Multifunctional Janus metasurfaces achieving arbitrary wavefront manipulation at dual frequency. Mater. Des. 2022, 223, 111264. [Google Scholar] [CrossRef]
- Xu, H.-X.; Ma, S.; Ling, X.; Zhang, X.-K.; Tang, S.; Cai, T.; Sun, S.; He, Q.; Zhou, L. Deterministic Approach to Achieve Broadband Polarization-Independent Diffusive Scatterings Based on Metasurfaces. ACS Photonics 2017, 5, 1691–1702. [Google Scholar] [CrossRef]
- Zhu, H.; Li, Q.; Tao, C.; Hong, Y.; Xu, Z.; Shen, W.; Kaur, S.; Ghosh, P.; Qiu, M. Multispectral camouflage for infrared, visible, lasers and microwave with radiative cooling. Nat. Commun. 2021, 12, 1805. [Google Scholar] [CrossRef] [PubMed]
- Bilal, R.M.H.; Naveed, M.A.; Baqir, M.A.; Ali, M.M.; Rahim, A.A. Design of a wideband terahertz metamaterial absorber based on Pythagorean-tree fractal geometry. Opt. Mater. Express 2020, 10, 3007–3020. [Google Scholar] [CrossRef]
- Naveed, M.A.; Bilal, R.M.; Rahim, A.A.; Baqir, M.A.; Ali, M.M. Polarization-insensitive dual-wideband fractal meta-absorber for terahertz applications. Appl. Opt. 2021, 60, 9160–9166. [Google Scholar] [CrossRef]
- Yin, W.; Shen, Z.; Li, S.; Gao, F.; Hao, H.; Zhang, L.; Chen, X. Flexible broadband terahertz absorbers for RCS reduction on conformal surfaces. Opt. Commun. 2022, 520, 128502. [Google Scholar] [CrossRef]
- Chen, Z.; Segev, M. Highlighting photonics: Looking into the next decade. eLight 2021, 1, 2. [Google Scholar] [CrossRef]
- Song, S.; Ma, X.; Pu, M.; Li, X.; Guo, Y.; Gao, P.; Luo, X. Tailoring active color rendering and multiband photodetection in a vanadium-dioxide-based metamaterial absorber. Photonics Res. 2018, 6, 492–497. [Google Scholar] [CrossRef]
- Sun, Z.; Yan, M.; Eric Mupona, T.; Xu, B. Control Electromagnetic Waves Based on Multi-Layered Transparent Metasurface. Front. Phys. 2019, 7, 181. [Google Scholar] [CrossRef]
- Fu, C.; Sun, Z.; Han, L.; Liu, C. Dual-Bandwidth Linear Polarization Converter Based on Anisotropic Metasurface. IEEE Photonics J. 2020, 12, 2962336. [Google Scholar] [CrossRef]
- Jia, M.; Wang, Z.; Li, H.; Wang, X.; Luo, W.; Sun, S.; Zhang, Y.; He, Q.; Zhou, L. Efficient manipulations of circularly polarized terahertz waves with transmissive metasurfaces. Light Sci. Appl. 2019, 8, 16. [Google Scholar] [CrossRef]
- Pang, Y.; Shen, Y.; Li, Y.; Wang, J.; Xu, Z.; Qu, S. Water-based metamaterial absorbers for optical transparency and broadband microwave absorption. J. Appl. Phys. 2018, 123, 155106. [Google Scholar] [CrossRef]
- Qi, D.; Wang, X.; Cheng, Y.; Gong, R.; Li, B. Design and characterization of one-dimensional photonic crystals based on ZnS/Ge for infrared-visible compatible stealth applications. Opt. Mater. 2016, 62, 52–56. [Google Scholar] [CrossRef]
- Xu, C.; Wang, B.; Pang, Y.; Wang, J.; Yan, M.; Wang, W.; Wang, A.; Jiang, J.; Qu, S. Hybrid Metasurfaces for Infrared-Multiband Radar Stealth-Compatible Materials Applications. IEEE Access 2019, 7, 147586–147595. [Google Scholar] [CrossRef]
- Fu, C.; Han, L.; Liu, C.; Lu, X.; Sun, Z. Combining Pancharatnam–Berry Phase and Conformal Coding Metasurface for Dual-Band RCS Reduction. IEEE Trans. Antennas Propag. 2022, 70, 2352–2357. [Google Scholar] [CrossRef]
- Liu, X.; Gao, J.; Xu, L.; Cao, X.; Zhao, Y.; Li, S. A Coding Diffuse Metasurface for RCS Reduction. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 724–727. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, Z.; Ma, H.; Du, T.; Luo, M.; Liu, D.; Yang, J. Tunable mid-infrared selective emitter based on inverse design metasurface for infrared stealth with thermal management. Opt. Express 2022, 30, 18250–18263. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Shi, J.M.; Zhang, J.K.; Li, Z.G.; Chen, Z.S.; Deng, X.S. Infrared stealth performance analysis of photonic crystal with high heat dissipation. Opt. Mater. 2021, 111, 110689. [Google Scholar] [CrossRef]
- Zhou, Y.-C.; Yang, J.; Bai, L.; Bao, R.-Y.; Yang, M.-B.; Yang, W. Flexible phase change hydrogels for mid-/low-temperature infrared stealth. Chem. Eng. J. 2022, 446, 137463. [Google Scholar] [CrossRef]
- Mei, P.; Zhang, S.; Cai, Y.; Lin, X.Q.; Pedersen, G.F. A Reflectarray Antenna Designed With Gain Filtering and Low-RCS Properties. IEEE Trans. Antennas Propag. 2019, 67, 5362–5371. [Google Scholar] [CrossRef]
- Huang, Q.; Zhao, Y.; Wu, Y.; Zhou, M.; Tan, S.; Tang, S.; Ji, G. A dual-band transceiver with excellent heat insulation property for microwave absorption and low infrared emissivity compatibility. Chem. Eng. J. 2022, 446, 137279. [Google Scholar] [CrossRef]
- Kim, S.H.; Yoon, Y.J. Wideband Radar Cross-Section Reduction on Checkerboard Metasurfaces With Surface Wave Suppression. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 896–900. [Google Scholar] [CrossRef]
- Xie, X.; Pu, M.; Huang, Y.; Ma, X.; Li, X.; Guo, Y.; Luo, X. Heat Resisting Metallic Meta-Skin for Simultaneous Microwave Broadband Scattering and Infrared Invisibility Based on Catenary Optical Field. Adv. Mater. Technol. 2019, 4, 1800612. [Google Scholar] [CrossRef]
- Cui, T.J.; Qi, M.Q.; Wan, X.; Zhao, J.; Cheng, Q. Coding metamaterials, digital metamaterials and programmable metamaterials. Light Sci. Appl. 2014, 3, e218. [Google Scholar] [CrossRef]
- Bai, G.D.; Ma, Q.; Iqbal, S.; Bao, L.; Jing, H.B.; Zhang, L.; Wu, H.T.; Wu, R.Y.; Zhang, H.C.; Yang, C.; et al. Multitasking Shared Aperture Enabled with Multiband Digital Coding Metasurface. Adv. Opt. Mater. 2018, 6, 1800657. [Google Scholar] [CrossRef]
- Gao, L.-H.; Cheng, Q.; Yang, J.; Ma, S.-J.; Zhao, J.; Liu, S.; Chen, H.-B.; He, Q.; Jiang, W.-X.; Ma, H.-F.; et al. Broadband diffusion of terahertz waves by multi-bit coding metasurfaces. Light Sci. Appl. 2015, 4, e234. [Google Scholar] [CrossRef]
- Li, L.L.; Cui, T.J.; Ji, W.; Liu, S.; Ding, J.; Wan, X.; Li, Y.B.; Jiang, M.H.; Qiu, C.W.; Zhang, S. Electromagnetic reprogrammable coding-metasurface holograms. Nat. Commun. 2017, 8, 197. [Google Scholar] [CrossRef]
- Liu, S.; Cui, T.; Zhang, L.; Xu, Q.; Wang, Q.; Wan, X.; Gu, J.; Tang, W.; Qi, M.; Han, J.; et al. Convolution Operations on Coding Metasurface to Reach Flexible and Continuous Controls of Terahertz. Adv. Sci. 2016, 3, 1600156. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, L.; Yang, Q.L.; Xu, Q.; Yang, Y.; Noor, A.; Zhang, Q.; Iqbal, S.; Wan, X.; Tian, Z.; et al. Frequency-Dependent Dual-Functional Coding Metasurfaces at Terahertz Frequencies. Adv. Opt. Mater. 2016, 4, 1965–1973. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, K.; Li, Y.; Cao, Q. Design of Nonresonant Metasurfaces for Broadband RCS Reduction. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 346–350. [Google Scholar] [CrossRef]
- Qi, Y.; Zhang, B.; Ding, J.; Zhang, T.; Wang, X.; Yi, Z. Efficient manipulation of terahertz waves by multi-bit coding metasurfaces and further applications of such metasurfaces. Chin. Phys. B 2021, 30, 024211. [Google Scholar]
- Salisbury, J.W.; Wald, A.; D’Aria, D.M. Thermal-infrared remote sensing and Kirchhoff’s law: 1. Laboratory measurements. J. Geophys. Res. Solid Earth 1994, 99, 11897–11911. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Liang, L.; Wei, M.; Yan, X.; Wei, D.; Liang, D.; Han, J.; Ding, X.; Zhang, G.; Yao, J. Broadband and wide-angle RCS reduction using a 2-bit coding ultrathin metasurface at terahertz frequencies. Sci. Rep. 2016, 6, 39252. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Li, J. Manipulating terahertz wave and reducing radar cross section (RCS) by combining a Pancharatnam–Berry phase with a coding metasurface. Laser Phys. 2019, 29, 075403. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, J.; Tian, M.; Liu, M.; Zhang, Y. 3-bit switchable terahertz coding metasurface based on Dirac semimetals. Opt. Commun. 2023, 527, 128958. [Google Scholar] [CrossRef]
- Jiu-sheng, L.; Shao-he, L.; Jian-quan, Y. Actively tunable terahertz coding metasurfaces. Opt. Commun. 2020, 461, 125186. [Google Scholar] [CrossRef]
- Zhou, C.; Peng, X.-Q.; Li, J.-S. Graphene-embedded coding metasurface for dynamic terahertz manipulation. Optik 2020, 216, 164937. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Zhang, N.; Dong, P.; Yang, L.; Wang, B.; Wu, R.; Hou, W. All-Metal Coding Metasurfaces for Broadband Terahertz RCS Reduction and Infrared Invisibility. Photonics 2023, 10, 962. https://doi.org/10.3390/photonics10090962
Zhang M, Zhang N, Dong P, Yang L, Wang B, Wu R, Hou W. All-Metal Coding Metasurfaces for Broadband Terahertz RCS Reduction and Infrared Invisibility. Photonics. 2023; 10(9):962. https://doi.org/10.3390/photonics10090962
Chicago/Turabian StyleZhang, Ming, Najiao Zhang, Peng Dong, Lin Yang, Baozhu Wang, Ruihong Wu, and Weimin Hou. 2023. "All-Metal Coding Metasurfaces for Broadband Terahertz RCS Reduction and Infrared Invisibility" Photonics 10, no. 9: 962. https://doi.org/10.3390/photonics10090962
APA StyleZhang, M., Zhang, N., Dong, P., Yang, L., Wang, B., Wu, R., & Hou, W. (2023). All-Metal Coding Metasurfaces for Broadband Terahertz RCS Reduction and Infrared Invisibility. Photonics, 10(9), 962. https://doi.org/10.3390/photonics10090962




