Next Article in Journal
Kalman Filter Based Pseudo-Code Ranging and Carrier Phase Measurement for Fiber Optical Time Transfer Method
Previous Article in Journal
Electron Paramagnetic Resonance Sensing of «Hidden» Atomistic and Cooperative Defects in Femtosecond Laser-Inscribed Photoluminescent Encoding Patterns in Diamond
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Photonics
Volume 10
Issue 9
10.3390/photonics10090980
photonics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Chiral Quasi-Bound States in the Continuum of a Dielectric Metasurface for Optical Monitoring and Temperature Sensing

by
Xu Du
1,
Suxia Xie
2,*,
Haoxuan Nan
1,
Siyi Sun
2,
Weiwei Shen
2,
Jingcheng Yang
2 and
Xin Guan
2
1
School of Energy and Power Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China
2
School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China
*
Author to whom correspondence should be addressed.
Photonics 2023, 10(9), 980; https://doi.org/10.3390/photonics10090980
Submission received: 30 July 2023 / Revised: 18 August 2023 / Accepted: 24 August 2023 / Published: 28 August 2023
(This article belongs to the Special Issue Optical Metasurfaces: Recent Advances and Future Directions)
Browse Figures
Versions Notes

Abstract

:
Chiral BIC can reach ultrahigh quality factors (Q-factor) based on its asymmetry, with broken mirror symmetries and in-plane inversion. Only by in-plane structural perturbation can chiral quasi-BIC (q-BIC) appear, so it is much more realizable and reasonable for the manufacturers in practical productions and fabrications considering the technology and means that are available. In this paper, we design a new dielectric metasurface employing H-shaped silica meta-atoms in the lattice, which is symmetrical in structure, obtaining chiral BIC with ultrahigh Q-factor (exceeding 105). In this process, we change the length of the limbs of the structure to observe the specific BICs. Previous scholars have focused on near-infrared-wavelength bands, while we concentrate on the terahertz wavelength band (0.8–1 THz). We found that there is more than one BIC, thus realizing multiple BICs in the same structure; all of them exhibit excellent circular dichroism (CD) (the maximum value of CD is up to 0.8127) for reflectance and transmittance, which provides significant and unique guidance for the design of multi-sensors. Meanwhile, we performed temperature sensing with chiral BIC; the sensitivity for temperature sensing can reach 13.5 nm/°C, which exhibits high accuracy in measuring temperature. As a consequence, the result proposed in this study will make some contributions to advanced optical imaging, chiral sensors with high frequency and spectral resolution, optical monitoring of environmental water quality, multiple sensors, temperature sensing, biosensing, substance inspection and ambient monitoring and other relevant optical applications.

1. Instruction

In optics, it is difficult but vital to obtain a high quality factor (Q-factor) with a terse structure, for which researchers and scholars have been questing and struggling for a long time. It is generally believed that bound states in the continuum (BICs) are a wonderful and unique resolution [1,2,3], providing inspiration for creative and valid ideas, which have been investigated and realized extensively in multitudinous photonic applications, covering advanced optical imaging, chiral sensors with high frequency and spectral resolution [4], optical monitoring of environmental water quality, and low-threshold circular polarized lasing [5,6,7]. In essence, BIC is the absolutely dark state which has an infinitely high Q-factor [5,8,9], and there are some other reasons like material breakage, finite sample sizes, and defects in the structure, aggravating the phenomenon. Considering the aforesaid condition, it is widely accepted that chiral quasi-BICs should be used for practical applications due to their conspicuously high Q-factors. Most previous works on chiral quasi-BICs in all-dielectric metasurfaces broke in-plane inversion symmetry photonic systems [5,8,9,10], while mirror symmetry was broken in this work.
Characterized by broken mirror symmetry, chiral metasurfaces [9,11,12] and metamaterials [13,14,15,16,17,18,19,20,21] have shown a prosperous future in photonic applications, which could be used for biosensing, selecting polarized light wavefronts, and some other circular dichroic nonlinear generations [22,23,24]. Many studies have been reported focusing on chiral metasurfaces and metamaterials, demonstrating they have made great progress in wide-band-width circular dichroism (CD). Judging from the existing experiments, it would be more scientific if CD with narrow bandwidth and high quality factor were used in photonic applications, and there is no doubt that this technology would stimulate the development of circularly polarized lasing with low threshold, boosting the prosperity of optical detection technology, providing a solid guarantee for secure optical communications [25]. Some current studies adopting chiral quasi-BIC in mirror symmetry-broken systems have proven effective, and it may offer us a promising solution. Hentschel et al. [26] proposed that the chirality effect of the duplex structure mainly depends on the vertical and horizontal distance between the two L-structures [27], but there are many factors disturbing the double-layer structure, and people have been exploring whether the chiral quasi-BIC can be realized in the single-layer structure. Tan Shi et al. [28] proposed a single-layer structure with a strong chiral effect, but with a different height, making fabrication of the structure complicated. Optimized metasurfaces can realize the enhancement of the third-harmonic generation and the amplitude optomechanical vibrations by a hundred times [29]. Previous studies have integrated single and multiple layers of graphene [30] into metal-based terahertz (THz) metamaterials to achieve complete modulation of the simulated resonance strength of EIT [31], while we applied terahertz to a monolayer of a semiconductor metasurface consisting of silica and silicon to seek better chiral quasi-BIC with high Q-factor and great CD. Tang et al. [32] introduced a new method for measuring the chiral density of electromagnetic fields. This optical chirality determines the asymmetry in the excitation rate between a small chiral molecule and its mirror image, and the continuity equation of optical chirality in the presence of a material current describes the flow of chirality, which is applicable to molecules in an electromagnetic field with arbitrary spatial dependence. Mohammadi et al. [33] revealed that chiral molecules can exhibit handedness when interacting with chiral light (such as circular-polarized light), and significantly enhanced the signal of the circular dichroism (CD) spectra as well as the local intensity of electric and magnetic fields by adopting dielectric structure as the best chiral sensing platform, providing constructive suggestions for chiral BIC. Fan et al. [34] found that CD spectra are very sensitive to the geometry and composition of chiral complexes, and that the helix geometry of the strongest CD signals is similar to the helix structure of many biomolecules. They also describe the mechanism of a plasma CD capable of producing a strong CD signal over the visible wavelength range, which provides a unique possibility for designing colloids and other nanostructures with strong optical chirality.
Through the above experiments and treatments, it has been revealed that breaking in-plane symmetry simultaneously will result in chiral BICs with strong CD and high Q-factor. It should be noted that the CD for the reflectance and transmittance of the metasurface increases and the Q-factor decreases with mirror asymmetries, and in-plane inversion increasing with mirror symmetry; original BICs appear in dielectric metasurfaces, while quasi-BICs only emerges as a result of breaking mirror and in-plane inversion symmetries simultaneously. In this process, we changed the length of the limbs of the structure to adjust the degree of asymmetry with the purpose of observing multiple chiral quasi-BICs, and we concentrated on the terahertz wavelength band (0.8–1 THz), where we found more than one BIC, making it possible to have multiple BICs in the same structure, all of them exhibiting excellent CD for reflectance and transmittance, which is a great breakthrough in the field of chiral quasi-BIC, boosting the design and development of multi-sensors. Furthermore, we bring temperature sensing in chiral BIC, which can reach 13.5 nm/°C, exhibiting conspicuous accuracy in measuring temperature, providing inspiration for the research of temperature sensing. Based on the chiral quasi-BIC, we explored its potential application areas, introducing and exploiting its application in the design of sensors such as temperature sensors, verifying its significant sensitivity, which can be used in temperature measurement. The results demonstrated in this paper make it clearer and more persuasive that quasi-BICs and multiple BICs can be extended into photonic applications, advanced optical imaging, chiral sensors with high frequency and spectral resolution, optical monitoring of temperature sensing, multi-sensors, and biolosensing.

2. Analysis and Discussion

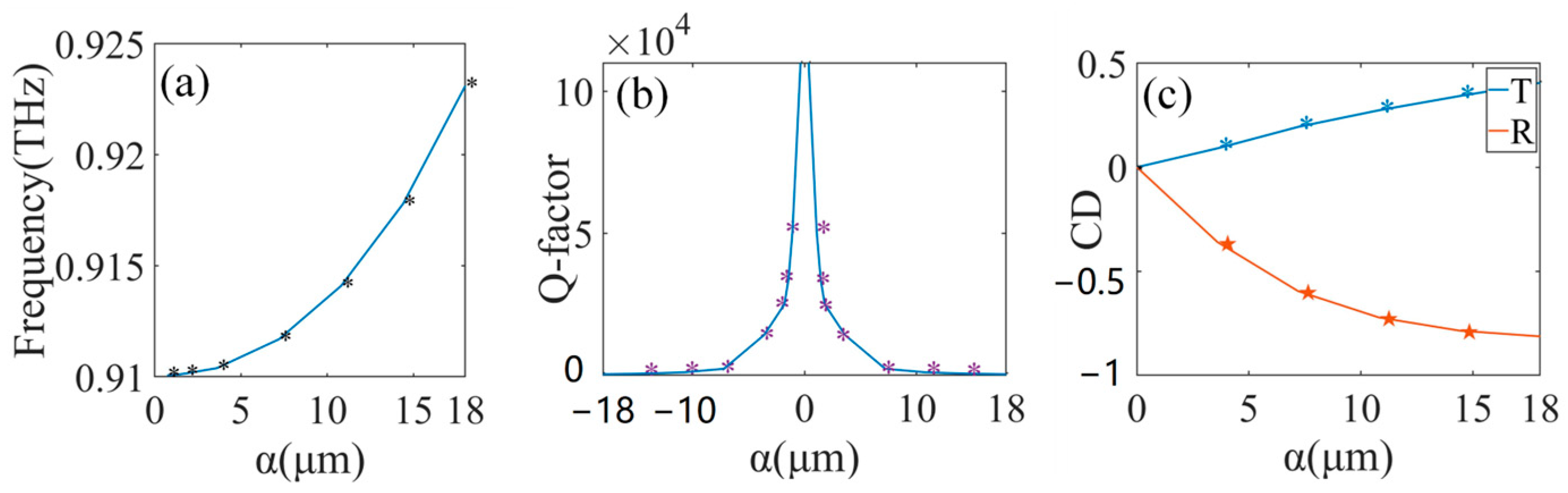
2.1. Multiple Chiral Quasi-BIC Depending on Breaking Mirror and In-Plane Inversion Symmetries Simultaneously

Currently, it is known that dielectric metasurfaces have drawn more and more attention in the field of applied optics for the reason that they are able to significantly reduce the intrinsic resistance loss resulting from high Q-factor, thus showing their vigorous power in exploring quasi-BIC, enabling efficient applications in nonlinear generation [35,36]. What should be noted is that broken mirror symmetry shows a chiral character, while dielectric chiral metasurfaces demonstrate intense CD [37,38], revealing photonic spin-Hall effects and radiation modulation [39] originating from photonic spin–orbit coupling [40]. The use of double layered structure [25] or the introduction of out-of-plane perturbations assist in achieving high-Q chiroptical responses [25], satisfied by sophisticated fabricating processes. A innovate scheme emerges as the time requires, which has proven that in-plane perturbations are capable of breaking mirror and in-plane inversion symmetry simultaneously, obtaining the desired chiral quasi-BICs, resulting in expected CD with narrower spectral characteristics. We have been trying to simplify the structure, preferably with asymmetric parameters only in the same plane. Most previous studies have focused on a single chiral quasi-BIC [26,33,34], while we have been trying to explore and design a structure with more than one chiral quasi-BIC.
Initially, we designed a new dielectric metasurface employing H-shaped silica meta-atoms in a lattice, supported by a silicon dioxide plate (see Figure 1). As is shown clearly in Figure 1, the thickness of the silicon dioxide plate (t1) is 135 μm, the thickness of the H-shaped silicon (t2) is 72 μm, the width of the four vertical arms is w1 = 34.75 μm, the lengths of the four vertical arms are l1 = L − 2α, l2 = L + 2α, l3 = L − α, l4 = L + α, where L = 56.25 μm and α = 18 μm, and the width and the length of the horizontal arm is w2 = 53 μm, l5 = 36 μm. The concrete dielectric functions of silica and silicon dioxide are 13.69 and 2.1904, respectively, according to the Handbook of Optical Properties of Solids [41].
As there is no perturbation (α = 0 μm) in the structure (Figure 1), it is obvious that l1 = l2 = l3 = l4 = L = 56.25 μm, signifying that mirror and in-plane inversion symmetries are satisfied simultaneously. When α ≠ 0 μm, whether it is positive or negative, the lengths of all four vertical arms, l1, l2, l3, and l4, differ from each other. For in-plane mirror symmetry, it is indispensable that the length of the four vertical arms ought to be identical with each other. Moreover, for in-plane inversion symmetry, what should be satisfied is l1 = l2, l3 = l4. Consequently, it cannot be denied that when α ≠ 0 μm, mirror and in-plane inversion symmetries of the structure have been broken simultaneously. The value α ranges from −18 μm to 18 μm, and each of them in correspondence to a different structure, so it is predictable that there are countless asymmetric structures. Vertically illuminated by incident light, owing to the broken mirror symmetry, the dielectric chiral metasurfaces show strong CD. It is reasonable to only take the normal incidence into account in this work, because nonvertical incidental light will complicate the situation. As the metasurface is illuminated by the normal incidental light perpendicularly, we find that it is a feasible idea to contrive all the potential simulations using the CST software, using the formulae CDR = (RLCP − RRCP)/(RLCP + RRCP) and CDT = (TLCP − TRCP)/(TLCP + TRCP) [42], in which R represents the reflectance and T represents the transmittance, and RCP is short for the right-hand circular polarizations (RCP) while LCP is short for the left-hand circular polarizations (LCP). According to the relation of the structural parameters above, α is the one and only determinant of the in-plane asymmetry of the metasurface. Increasing the magnitude of α, the asymmetry appears weakened. On the contrary, as the magnitude of α reduces to 0 μm, satisfied with mirror and inversion symmetries simultaneously, the dielectric metasurface seems completely symmetrical. Therefore, it is predictable and verifiable that the greatly resonant CD of the dielectric metasurface derives from quasi-BIC, while the original BIC is under symmetry protection. To further confirm the conjecture above, we adjusted and altered the asymmetry parameter α to explore the CD of reflectance and transmittance spectra shown in Figure 2.
The transmittance and reflectance spectra of RCP and LCP with perpendicular incidences are exhibited in Figure 2a,b,d,e, while Figure 2c,f display CDT (from transmittance) and CDR (from reflectance), and the asymmetry parameter α varies from −18 μm to 18 μm consecutively. As it is shown in Figure 2, the dielectric metasurfaces prove not to show chiral features as the α = 0 μm, for the reason that the mirror and inversion symmetries are satisfied simultaneously. The results indicate that the magnitude of α correlates positively with the spectral width of the resonant modes. Judging from the research investigated already, breaking mirror and inversion symmetries simultaneously results in chiral quasi-BIC, which excites the modes to be more polarization-dependent. For α = 0 μm, it is evident that the structure of the metasurface is symmetrical, so the distribution of the eigenmode is supposed to meet the conditions of mirror and inversion symmetries. When α = 0 μm, the marks I, II, III, IV in Figure 2 are chiral BICs.
In traditional quantum mechanics, bound states are states [43,44] whose energies are below the continuous energy spectrum, confined to a potential well or barrier. However, in some special cases, there is a phenomenon whereby the energy is in the range of continuous energy levels, but the particles remain bound in the system, which is called bound states in the continuum (BIC) [43,44]. The implementation of a BIC usually involves interference effects that can result in a complete or partial cancellation of some energy, leaving the particles trapped in the system. These interference effects may be caused by the symmetries of physical structures, microscopic local singularities, or other quantum mechanical effects. BIC has a wide range of applications in the field of optics and electronics. For example, in optics, the presence of BIC in the photon energy spectrum can be realized by precisely controlling the parameters of the structure. This phenomenon can be used to realize high-quality-factor microcavities and high-gain nanolasers and sensors. Reference [43] describes the concept and physical mechanism of BIC, and divides BIC into the following categories: (i) Bound states due to symmetry or separability: this includes symmetry-protected BICs and separable BICs, which are coupled to radiation modes where system symmetry or separability is prohibited. (ii) Bound states obtained by parameter tuning: when the number of radiation channels is small, the radiation can be completely inhibited from entering all channels by adjusting the system parameters. (iii) The bound states resulting from inverse construction: Starting with the expected BIC, a system can be designed that supports this bound state and includes it in a continuous spectrum.
The mass factor (Q-factor) of these three BICs is theoretically infinite. When a BIC evolves into a quasi-BIC and the conditions deviate from the requirements, its q factor becomes finite, but it still has an ultra-high value. In summary, BIC is a special quantum mechanical phenomenon in which a particle’s energy is in the range of continuous energy levels but is still bound to the system. This phenomenon usually involves interference effects and has important applications in several fields.
Chiral bound states in the continuum [4,14,45] (CBIC) is a special type of interaction between bound states and continuous states. Chiral properties represent systems with left- and right-handed symmetries. In some particular chiral structures, there may be a phenomenon in which the energy lies in the continuous energy level range, but the particles are still bound to the system, which is called chiral bound states in the continuum. The key to the realization of CBIC is the interaction between the asymmetric coupled structure and the chiral structure. This coupling can lead to interference between bound and continuous states with specific energies, so that particles with energies in the range of continuous energy levels are bound to the system. The realization of the CBIC usually requires the precise regulation of the chiral symmetry of the field structure and the interaction of the bound and continuous states through a specific coupling way. This can be achieved by designing chiral nanostructures, spin distributions, and electromagnetic field distributions. CBIC has important applications in optics and nanophotonics. For example, by constructing chiral optical structures, optical microcavities with high quality factors, selective transmission, and high-efficiency second harmonic generation can be realized. In short, CBIC is a special interaction between the continuous states, in which the interaction of the chiral structure and the asymmetric coupling structure results in the energy of the particles in the range of continuous energy levels being bound in the system. This phenomenon has a wide range of potential applications in optics and nanophotonics.
There are four chiral BICs in the 0.8–1 THz wavelength band, which are located as chiral BICs I, II, III, IV by frequency, and their frequencies are as follows: f1 = 0.86701 THz (corresponding to chiral BIC I), f2 = 0.91008 THz (corresponding to chiral BIC II), f1 = 0.96182 THz (corresponding to chiral BIC III), f1 = 0.98225 THz (corresponding to chiral BIC IV), and the CDT (from transmittance) and CDR (from reflectance) can be seen from Figure 3a,b. All of them demonstrate significant effect, and we chose chiral quasi-BIC II to analyze the character of chiral BIC. As Figure 3c,d show, the absolute value of CDT and CDR of the chiral BIC II increases with the increase in parameter α. When α = ±18 μm, CD reaches the maximum of its absolute value 0.8127. For the resonant frequency, the dependencies on the structural parameters (Figure 3) tend to be the same: the resonant frequency red-shifts with the decrease in degree of asymmetry α, reaching its minimum value when α = 0 μm, at which point chiral BICs occur. As exhibited in Figure 3, we draw the conclusion that choosing and altering the structural parameters simultaneously is capable of acquiring a preferable CD with a high Q-factor at the ideal frequency, which is of great significance in the practical application of photonics, making incredible progress in optical sensing and detecting.
Here, the polarized light waves are defined as E =   E 0 cos   ( ω   t   -   φ ) , where E is electric field intensity of the polarized light waves, E 0 is the amplitude of electric field intensity, ω represents the frequency of the polarized light waves, and φ represents the phase of polarized light waves. From the above equation, it can be seen that the only difference between RCP and LCP is φ , and the phase difference between them is Δ φ = kπ (k is odd), so the mode of RCP and LCP incidental waves are identical with each other, indicating that the Q-factors are also the same. There are four quasi-BICs in the frequency range of 0.8 THz to 1 THz; for the sake of better observation, it is feasible to investigate the chiral quasi-BIC II, whose frequency ranges from 0.91008 THz (α = 0 μm) to 0.9232 THz (α = 18 μm), and there are other BICs corresponding to respective frequencies and CD (Figure 2 and Figure 3). Remarkably, as α = 0 μm, CD appears when circularly polarized light rotating with opposite phase is incapable of coupling to the eigenmode. What is exhibited clearly in Figure 4a,b, respectively, is the reflectance spectra R and transmittance T with RCP and LCP. As Figure 4c shows, the frequency of the incidental light is 0.9232 THz (α = 18 μm), and its high CD is shown in the metasuraface (the CDT is short for the CD for transmittance and the CDR is short for the CD for reflectance). As it is shown clearly in Figure 4, when α = 18 μm, the CD proves greatest for both of the transmitted and reflected waves with the extreme values of CDT = 0.4058 and CDR = −0.8127, respectively. It is interesting to discover the rule that the peak of absolute value both of CDT and CDR enhances with the increase in α. If α = −18 μm, it turns out just the opposite.
Figure 5a shows the resonant frequency of the H-shaped metasurface as a function of α. The eigenmodes vary from 0.91008 THz to 0.9231 THz with the asymmetry parameter α ranging from −18 μm to 18 μm. To quantitatively characterize the sensing performance of the proposed structure, we calculated the Q-factor using the data of transmittance, which is defined as the ratio of the center frequency ( f ) to the full width at half maxima (FWHM) Q = f F W H M [43]. Figure 5b shows the Q-factor of the metasurface as a function of α. The inversion asymmetry of the metasurface surges with the asymmetry parameter α increasing, resulting in the values of Q-factor decreasing from 128,909 (α = 0.72 μm) to 372 (see from Figure 5b). It can be seen clearly from the mathematical definition that, as the values of α become arbitrarily close to 0, the values of the Q-factor approach infinity. Responsibly speaking, with the eigenmode and asymmetry of the dielectric metasurface increasing, the magnitude of Q-factor declines spontaneously, which is quite a common phenomenon in general photonic structures displaying symmetry-protected BIC. As α = 0 μm, given the conditions that there are no inherent and acquired optical losses in the components and the metasurface is fabricated precisely with an ideally symmetric structure, the magnitude of Q-factor ought to be infinite and the metasurface eigenmode cannot be coupled to the outer far-field as a result of the confined electromagnetic energy with no scattering or out-coupling. What is shown in Figure 5b is the dramatic and monotonous decrease in the Q-factor, convincingly demonstrating that the appearance of quasi-BIC above derives from symmetry-protected BIC instead of the accidental one.
Enhancing the intensity of incidental waves diversely with RCP and LCP, it is apparent that the peak values of transmitted and reflected waves are affected by the polarized light. It is interesting to discover the rule that the peak of absolute value both of CDT and CDR enhances with the increase in α (see Figure 5c). The parameter α embodies the asymmetry of mirror and inversion simultaneously, so it is convincing that the magnitude of CD is affected greatly by α, and the transmittance and reflectance spectra from the metasurface, depicted with blue and orange lines, respectively, are shown in Figure 5c, where CDR with reflected wave declines monotonously from 0 to −1 with increasing α, while the range of CDT with transmitted wave is comparatively gentle, remaining positive all the time. Furthermore, it is proven that quasi-BIC results from the breaking of inversion symmetry and the bandwidth of the excited state narrows markedly. Nevertheless, only by breaking the mirror and inversion symmetry simultaneously can the metasurface exhibit chiral quasi-BIC for vertical incident light. It is delightful to observe the chirality of the incident circularly polarized waves preserved by the transmitted and reflected ones. Significantly, no matter what magnitude of α is taken, the ellipticity remains practically constant.
Based on the above research, we find it is of great necessity for us to investigate and clarify the impact of structural and material parameters on circular dichroism in the dielectric metasurface exhibiting chiral quasi-BIC, applied in photonic sensing and monitoring.

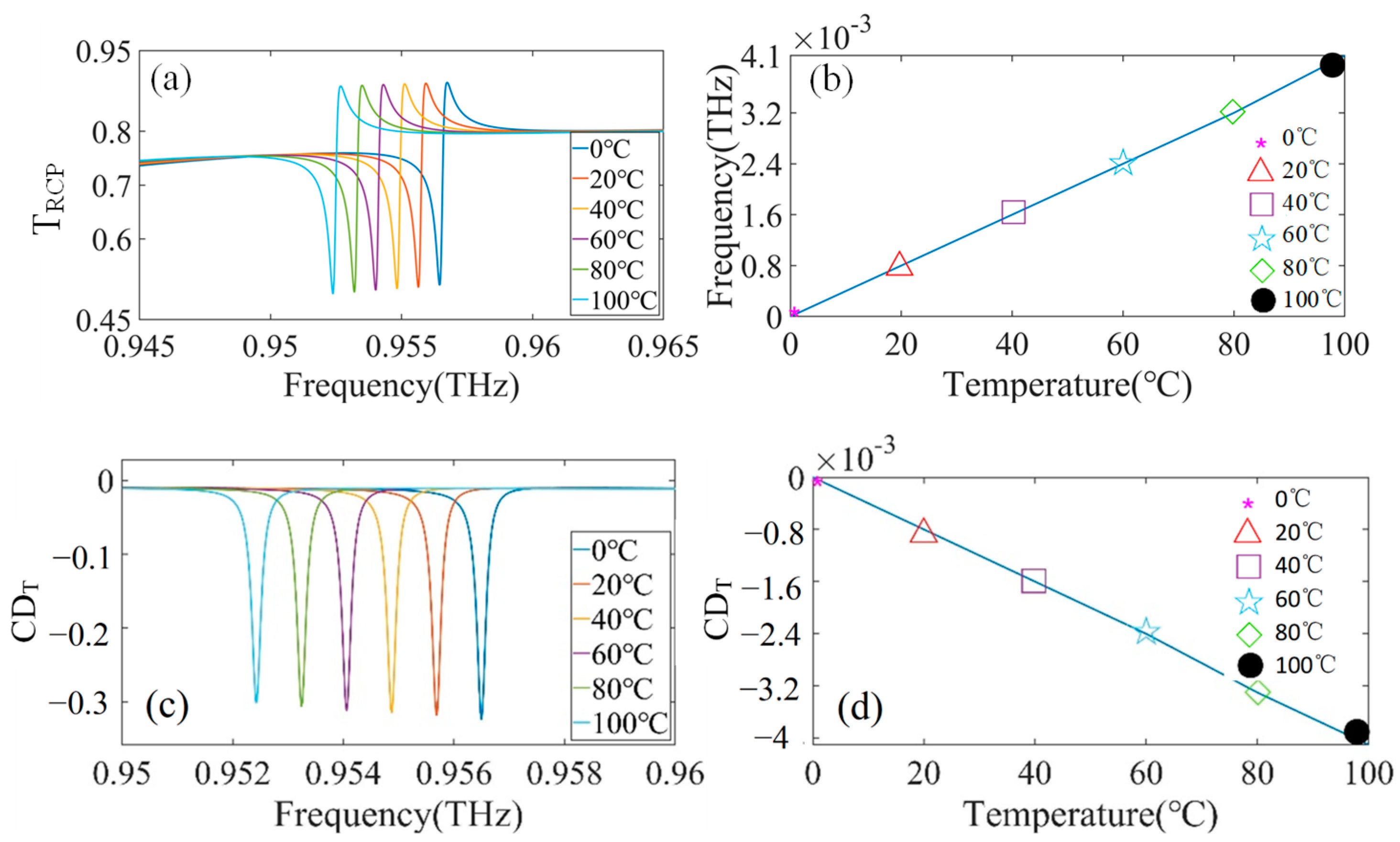
2.2. Exploration and Generalization of Chiral Quasi-BIC in Liquid Quality Monitoring and Temperature Sensing

Butt et al. [46] found that a hybrid metasurface perfect absorber (HMSPA) with hollow-square meta-atoms (HS-Mas) is very sensitive to slight changes in the refractive index of environmental media, and its sensing sensitivity is 355 nm/RIU, providing an ideal choice for biosensing applications. At the same time, due to the extraordinary thermo-optical coefficient of polydimethylsiloxane, the temperature sensitivity of HS-MA-based HMSPA in the range of 20 °C to 60 °C can reach −0.18 nm/°C, which could be used in filtration, biosensing, and temperature sensing. Zhao et al. [47] proposed a new terahertz (THz) perfect absorber (PA) with an absorbance of up to 99.8% at 0.221 THz at room temperature T = 300 K. The resonant absorption characteristics of the PA vary with the geometric parameters of the strontium titanate (STO) resonator structure, and the temperature sensing sensitivity is as high as 0.37 GHz K−1, which provides a lot of inspiration for the design of temperature sensors. Guo et al. [48] proposed an all-dielectric metasurface that can measure refractive index and temperature, which consists of silicon disks with tilted split gap, and they found that breaking the symmetry properties enables them to transform the symmetric protected bound state (BIC) into toroidal dipole (TD) quasi-BIC with a high quality-factor (Q-factor). Moreover, they also analyzed the spectral response at different incidence angles and obtained a sensitivity of up to 746 nm/RIU for the refractive index sensing, providing ideas and inspiration for the design of high-performance sensing applications. Li et al. [49] proposed a dual-frequency terahertz perfect absorber for indium-antimony arrays based on all-dielectric metamaterials. The simulation results showed that, at 1.265 THz and 1.436 THz, the absorbance was 99.9% and 99.8%, respectively, which accords with the theoretical predictions, and the absorption comes from the first- and second-order plasmon resonance modes. The designed absorber is not sensitive to polarization and can absorb transverse magnetic waves at a wide angle. The performance of the absorber can be adjusted by adjusting the parameters and the ambient temperature.
Predecessors have found the ability of chiral quasi-BIC to detect small frequency shifts caused by trace analytes or environmental changes [50], which has provided a great idea that extremely high Q-factor and strong field enhancement significantly could be used in the manufacture of the ultra-sensitive sensors. The structure adopted in this study is identical with previous, the asymmetric H-shaped silica, supported by silica substrate, but what is different from the previous model is that the structure is covered by material with a different refractive index. As it is shown in Figure 1, the materials fill the vacancy of the cube, whose thickness is the same with the silica substrate, t2 = 72 μm. Because of the unique relationship between refractive index and materials [51,52], it is feasible and scientific for us to select the materials by altering their refractive index. Generally speaking, the relation between the liquid refractive index and temperature is as follows: the liquid refractive index is inversely proportional to temperature, the higher the temperature, the more active the molecule, the smaller the molecular density, the smaller the refractive index.
Additionally, the refractive index is connected closely with the temperature in practical sensing applications [53]. As a consequence, what we should to do next is to ascertain the concrete electromagnetic response of metasurfaces to different temperatures. The thermal expansion and thermo-optical coefficients are two critical parameters, occupying a vital position in this process, and should be paid significant attention. Proceeding from the practical situation, the thermal expansion coefficient [54,55] of the designed metasurface with a small size could be negligible, so it is reasonable and scientific that the dependence of the refractive index on temperature is expressed as, n (T) = n (T0) + η (T − T0) [48], where T is the target temperature, T0 is the room temperature, and η is the thermo-optic coefficient. As before, the Si and SiO2 are adopted as the materials of the designed metasurface. Generally speaking, it is assumed that the room temperature is T0 = 20 °C, the refractive index of Si and SiO2 are n1 (T) = n1 (T0) + η1 (T − T0) and n2 (T) = n2 (T0) + η1 (T − T0), respectively, where n1 (T0) = 3.42, n2 (T0) = 2, η1 = 1.84 × 10−4/K [56], and η1 = 2.45 × 10−4/K [57]. The metasurface is covered with water of a different temperature to the surrounding material, whose refractive index is n3 (T) = n3 (T0) + η3 (T − T0), where n3 (T0) = 1.33, η3 = −1.02 × 10−4/K [58]. As shown in Figure 6a, the transmittance spectra of resonance vary with temperature. It can be revealed that the chiral quasi-BIC III has an incredible resonance, exhibiting a very narrow peak and significant blueshift with the temperature increasing. When the incident light illuminates from the top perpendicularly, the Q-factor can reach 99,873, which reveals its fabulous performance for temperature sensing. Figure 6b exhibits a linear fit of the frequency position shift corresponding to temperature, and the sensitivity for temperature can reach S ( T ) = Δ   λ / Δ T = 13.5   nm / ° C . As a consequence, the results show that the innovative dielectric metasurface can measure temperature accurately. To exhibit our novelty in temperature sensing compared with other sophisticated structures, we summarize the sensing performance in Table 1.
As Table 1 shows, this work has a high temperature-sensing degree and outstanding sensing performance, which can be used for high-precision temperature sensing.
It is demonstrated that chiral BICs with infinite Q-factor exhibit excellent resonances in an all-dielectric metasurface from the above research. The high Q-factor of resonance chiral quasi-BIC III (in Figure 6) enable the designed metasurface to be a promising sensing candidate. Therefore, it is promising to apply the excellent performance of chiral quasi-BIC III in resonance to the monitoring of ambient refractive index and temperature sensing.
As can be seen from Figure 6, CDT has a redshift with increasing temperature, and the redshift of CDT always maintains a stable linear relationship with temperature.
In summary, we have numerically studied an all-dielectric chiral metasurface composed of silicon and silica. After simulation and analysis in the terahertz band, we found that it has an excellent resonance effect, which has important application value in biosensing, biological monitoring, environmental detection, and so on. In the 0.8–1 THz wavelength band, we have revealed that there is more than one BIC, realizing multiple BICs in the same structure, all of which exhibited excellent CD (the maximum value of CD is 0.8127) for reflectance and transmittance, which provide significant and unique guidance for the design of multiple sensors. It is worth noting that all of them are symmetrical protected chiral BICs with a high Q-factor (128,909), which can be transformed into a quasi-BIC by breaking the symmetry. At the same time, due to its excellent temperature sensing coefficient, the extraordinary thermo-optical coefficient of the material used in the metasurface allows the designed metasurface to be used for temperature sensing with a sensitivity of up to 13.5 nm/°C. The results obtained in this study provide a new way for optical monitoring, multiple sensors, and temperature sensing, and it is convincing that chiral quasi-BIC and multiple-BICs can be applied to photonic applications, improving advanced optical imaging, chiral sensors with high frequency and strong spectral resolution, optical monitoring of environmental water quality, improvement of multiple sensors, and biosensing.

Author Contributions

X.D.: Conceptualization, Data curation, Formal analysis, Investigation, Writing original draft. S.X.: Funding acquisition, Investigation, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing original draft, Writing review and editing. H.N., S.S., W.S., J.Y. and X.G.: Methodology, Software, Investigation, Data curation. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by National Natural Science Foundation of China (Grant No. 11304094), Hunan Provincial Natural Science Foundation of China (Grant No. 2020JJ5153), Shanghai Undergraduate Training Program for Innovation and Entrepreneurship (Grant No. SH2023001).

Institutional Review Board Statement

All analyses were based on previous published studies and theoretical simulation, thus no ethical approval and patient consent are required.

Informed Consent Statement

Written informed consent for publication was obtained from all participants. The authors consented to participate and publish.

Data Availability Statement

All codes and data generated or analyzed during this study are included in this published article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Koshelev, K.; Bogdanov, A.; Kivshar, Y. Meta-optics and bound states in the continuum. Sci. Bull. 2019, 64, 836–842. [Google Scholar] [CrossRef]
  2. Koshelev, K.; Bogdanov, A.; Kivshar, Y. Engineering with bound states in the continuum. Opt. Photonics News 2020, 31, 38. [Google Scholar] [CrossRef]
  3. Koshelev, K.; Favraud, G.; Bogdanov, A.; Kivshar, Y.; Fratalocchi, A. Nonradiating photonics with resonant dielectric nanostructures. Nanophotonics 2019, 8, 725–745. [Google Scholar] [CrossRef]
  4. Zhang, Z.; Zhong, C.; Fan, F.; Liu, G.; Chang, S. Terahertz polarization and chirality sensing for amino acid solution based on chiral metasurface sensor. Sens. Actuators B Chem. 2021, 330, 129315. [Google Scholar] [CrossRef]
  5. Kodigala, A.; Lepetit, T.; Gu, Q.; Bahari, B.; Fainman, Y.; Kanté, B. Lasing action from photonic bound states in continuum. Nature 2017, 541, 196–199. [Google Scholar] [CrossRef] [PubMed]
  6. Pavlov, A.; Zabkov, I.; Klimov, V. Lasing threshold of the bound states in the continuum in the plasmonic lattices. Opt. Express 2018, 26, 28948–28962. [Google Scholar] [CrossRef] [PubMed]
  7. Wu, M.; Ha, S.T.; Shendre, S.; Durmusoglu, E.G.; Koh, W.-K.; Abujetas, D.R.; Sánchez-Gil, J.A.; Paniagua-Domínguez, R.; Demir, H.V.; Kuznetsov, A.I. Room-temperature lasing in colloidal nanoplatelets via Mie-resonant bound states in the continuum. Nano Lett. 2020, 20, 6005–6011. [Google Scholar] [CrossRef] [PubMed]
  8. Volkovskaya, I.; Xu, L.; Huang, L.; Smirnov, A.I.; Miroshnichenko, A.E.; Smirnova, D. Multipolar second-harmonic generation from high-Q quasi-BIC states in subwavelength resonators. Nanophotonics 2020, 9, 3953–3963. [Google Scholar] [CrossRef]
  9. Abujetas, D.R.; Barreda, Á.; Moreno, F.; Litman, A.; Geffrin, J.M.; Sánchez-Gil, J.A. High-Q transparency band in all-dielectric metasurfaces induced by a quasi bound state in the continuum. Laser Photonics Rev. 2021, 15, 2000263. [Google Scholar] [CrossRef]
  10. Koshelev, K.; Tang, Y.; Li, K.; Choi, D.-Y.; Li, G.; Kivshar, Y. Nonlinear metasurfaces governed by bound states in the continuum. ACS Photonics 2019, 6, 1639–1644. [Google Scholar] [CrossRef]
  11. Kilchoer, C.; Abdollahi, N.; Steiner, U.; Gunkel, I.; Wilts, B.D. Determining the complex Jones matrix elements of a chiral 3D optical metamaterial. APL Photonics 2019, 4, 126107. [Google Scholar] [CrossRef]
  12. Yang, S.; Liu, Z.; Yang, H.; Jin, A.; Zhang, S.; Li, J.; Gu, C. Intrinsic Chirality and Multispectral Spin-Selective Transmission in Folded Eta-Shaped Metamaterials. Adv. Opt. Mater. 2020, 8, 1901448. [Google Scholar] [CrossRef]
  13. Hu, J.; Zhao, X.; Lin, Y.; Zhu, A.; Zhu, X.; Guo, P.; Cao, B.; Wang, C. All-dielectric metasurface circular dichroism waveplate. Sci. Rep. 2017, 7, 41893. [Google Scholar] [CrossRef]
  14. Gorkunov, M.V.; Antonov, A.A.; Tuz, V.R.; Kupriianov, A.S.; Kivshar, Y.S. Bound states in the continuum underpin near-lossless maximum chirality in dielectric metasurfaces. Adv. Opt. Mater. 2021, 9, 2100797. [Google Scholar] [CrossRef]
  15. Chen, Y.; Gao, J.; Yang, X. Chiral grayscale imaging with plasmonic metasurfaces of stepped nanoapertures. Adv. Opt. Mater. 2019, 7, 1801467. [Google Scholar] [CrossRef]
  16. Gorkunov, M.V.; Rogov, O.Y.; Kondratov, A.V.; Artemov, V.V.; Gainutdinov, R.V.; Ezhov, A.A. Chiral visible light metasurface patterned in monocrystalline silicon by focused ion beam. Sci. Rep. 2018, 8, 11623. [Google Scholar] [CrossRef] [PubMed]
  17. Fasold, S.; Linß, S.; Kawde, T.; Falkner, M.; Decker, M.; Pertsch, T.; Staude, I. Disorder-enabled pure chirality in bilayer plasmonic metasurfaces. ACS Photonics 2018, 5, 1773–1778. [Google Scholar] [CrossRef]
  18. Zhang, R.; Zhao, Q.; Wang, X.; Gao, W.; Li, J.; Tam, W.Y. Measuring circular phase-dichroism of chiral metasurface. Nanophotonics 2019, 8, 909–920. [Google Scholar] [CrossRef]
  19. Kan, Y.; Andersen, S.K.; Ding, F.; Kumar, S.; Zhao, C.; Bozhevolnyi, S.I. Metasurface-enabled generation of circularly polarized single photons. Adv. Mater. 2020, 32, 1907832. [Google Scholar] [CrossRef]
  20. Liu, Z.; Du, H.; Li, J.; Lu, L.; Li, Z.-Y.; Fang, N.X. Nano-kirigami with giant optical chirality. Sci. Adv. 2018, 4, eaat4436. [Google Scholar] [CrossRef]
  21. Basiri, A.; Chen, X.; Bai, J.; Amrollahi, P.; Carpenter, J.; Holman, Z.; Wang, C.; Yao, Y. Nature-inspired chiral metasurfaces for circular polarization detection and full-Stokes polarimetric measurements. Light Sci. Appl. 2019, 8, 78. [Google Scholar] [CrossRef] [PubMed]
  22. Kim, K.H.; Kim, J.R. Dielectric Chiral Metasurfaces for Second-Harmonic Generation with Strong Circular Dichroism. Ann. Der Phys. 2020, 532, 2000078. [Google Scholar] [CrossRef]
  23. Kang, L.; Wang, C.-Y.; Guo, X.; Ni, X.; Liu, Z.; Werner, D.H. Nonlinear chiral meta-mirrors: Enabling technology for ultrafast switching of light polarization. Nano Lett. 2020, 20, 2047–2055. [Google Scholar] [CrossRef]
  24. Chen, Y.; Yang, X.; Gao, J. Spin-selective second-harmonic vortex beam generation with babinet-inverted plasmonic metasurfaces. Adv. Opt. Mater. 2018, 6, 1800646. [Google Scholar] [CrossRef]
  25. Overvig, A.; Yu, N.; Alù, A. Chiral quasi-bound states in the continuum. Phys. Rev. Lett. 2021, 126, 073001. [Google Scholar] [CrossRef] [PubMed]
  26. Hentschel, M.; Ferry, V.E.; Alivisatos, A.P. Optical Rotation Reversal in the Optical Response of Chiral Plasmonic Nanosystems: The Role of Plasmon Hybridization. ACS Photonics 2015, 2, 1253–1259. [Google Scholar] [CrossRef]
  27. Chen, T.; Mao, H.; Wang, J. Optical chirality of the double “L” structure. Opt. Quantum Electron. 2018, 50, 247. [Google Scholar] [CrossRef]
  28. Shi, T.; Deng, Z.-L.; Tu, Q.-A.; Cao, Y.; Li, X. Displacement-mediated bound states in the continuum in all-dielectric superlattice metasurfaces. PhotoniX 2021, 2, 7. [Google Scholar] [CrossRef]
  29. Xu, L.; Rahmani, M.; Ma, Y.; Smirnova, D.A.; Kamali, K.Z.; Deng, F.; Chiang, Y.K.; Huang, L.; Zhang, H.; Gould, S. Enhanced light–matter interactions in dielectric nanostructures via machine-learning approach. Adv. Photonics 2020, 2, 026003. [Google Scholar] [CrossRef]
  30. Masyukov, M.; Vozianova, A.; Grebenchukov, A.; Gubaidullina, K.; Zaitsev, A.; Khodzitsky, M. Optically tunable terahertz chiral metasurface based on multi-layered graphene. Sci. Rep. 2020, 10, 3157. [Google Scholar] [CrossRef]
  31. Xiao, S.; Wang, T.; Liu, T.; Yan, X.; Li, Z.; Xu, C. Active modulation of electromagnetically induced transparency analogue in terahertz hybrid metal-graphene metamaterials. Carbon 2018, 126, 271–278. [Google Scholar] [CrossRef]
  32. Tang, Y.; Cohen, A.E. Optical chirality and its interaction with matter. Phys. Rev. Lett. 2010, 104, 163901. [Google Scholar] [CrossRef] [PubMed]
  33. Mohammadi, E.; Tavakoli, A.; Dehkhoda, P.; Jahani, Y.; Tsakmakidis, K.L.; Tittl, A.; Altug, H. Accessible Superchiral Near-Fields Driven by Tailored Electric and Magnetic Resonances in All-Dielectric Nanostructures. ACS Photonics 2019, 6, 1939–1946. [Google Scholar] [CrossRef]
  34. Fan, Z.; Govorov, A.O. Plasmonic Circular Dichroism of Chiral Metal Nanoparticle Assemblies. Nano Lett. 2010, 10, 2580–2587. [Google Scholar] [CrossRef] [PubMed]
  35. Cai, W.; Vasudev, A.P.; Brongersma, M.L. Electrically controlled nonlinear generation of light with plasmonics. Science 2011, 333, 1720–1723. [Google Scholar] [CrossRef]
  36. Ellenbogen, T.; Voloch-Bloch, N.; Ganany-Padowicz, A.; Arie, A. Nonlinear generation and manipulation of Airy beams. Nat. Photonics 2009, 3, 395–398. [Google Scholar] [CrossRef]
  37. Ma, Z.; Li, Y.; Li, Y.; Gong, Y.; Maier, S.A.; Hong, M. All-dielectric planar chiral metasurface with gradient geometric phase. Opt. Express 2018, 26, 6067–6078. [Google Scholar] [CrossRef]
  38. Zhu, A.Y.; Chen, W.T.; Zaidi, A.; Huang, Y.-W.; Khorasaninejad, M.; Sanjeev, V.; Qiu, C.-W.; Capasso, F. Giant intrinsic chiro-optical activity in planar dielectric nanostructures. Light Sci. Appl. 2018, 7, 17158. [Google Scholar] [CrossRef]
  39. Harari, P.M.; Huang, S.-M. Modulation of molecular targets to enhance radiation. Clin. Cancer Res. 2000, 6, 323–325. [Google Scholar]
  40. Whittaker, C.; Cancellieri, E.; Walker, P.; Royall, B.; Rodriguez, L.T.; Clarke, E.; Whittaker, D.; Schomerus, H.; Skolnick, M.; Krizhanovskii, D. Effect of photonic spin-orbit coupling on the topological edge modes of a Su-Schrieffer-Heeger chain. Phys. Rev. B 2019, 99, 081402. [Google Scholar] [CrossRef]
  41. Palik, E. Handbook of Optical Properties of Solids; Academic: Orlando, FL, USA, 1985; pp. 41–70. [Google Scholar]
  42. Kim, K.H.; Kim, J.R. High-Q Chiroptical Resonances by Quasi-Bound States in the Continuum in Dielectric Metasurfaces with Simultaneously Broken In-Plane Inversion and Mirror Symmetries. Adv. Opt. Mater. 2021, 9, 2101162. [Google Scholar] [CrossRef]
  43. Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef]
  44. Fan, K.; Shadrivov, I.V.; Padilla, W.J. Dynamic bound states in the continuum. Optica 2019, 6, 169–173. [Google Scholar] [CrossRef]
  45. Chen, Y.; Deng, H.; Sha, X.; Chen, W.; Wang, R.; Chen, Y.-H.; Wu, D.; Chu, J.; Kivshar, Y.S.; Xiao, S.; et al. Observation of intrinsic chiral bound states in the continuum. Nature 2023, 613, 474–478. [Google Scholar] [CrossRef]
  46. Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L.; Piramidowicz, R. Hybrid metasurface perfect absorbers for temperature and biosensing applications. Opt. Mater. 2021, 123, 111906. [Google Scholar] [CrossRef]
  47. Zhao, J.; Cheng, Y. Temperature-Tunable Terahertz Perfect Absorber Based on All-Dielectric Strontium Titanate (STO) Resonator Structure. Adv. Theory Simul. 2022, 5, 202200520. [Google Scholar] [CrossRef]
  48. Linhui, G.; Zexuan, Z.; Qun, X.; Wenxuan, L.; Feng, X.; Mei, W.; He, F.; Chenglong, Y.; Maojin, Y. Toroidal dipole bound states in the continuum in all-dielectric metasurface for high-performance refractive index and temperature sensing. Appl. Surf. Sci. 2023, 615, 156408. [Google Scholar] [CrossRef]
  49. Li, Z.; Cheng, Y.; Luo, H.; Chen, F.; Li, X. Dual-band tunable terahertz perfect absorber based on all-dielectric InSb resonator structure for sensing application. J. Alloys Compd. 2022, 925, 166617. [Google Scholar] [CrossRef]
  50. Wang, Y.; Han, Z.; Du, Y.; Qin, J. Ultrasensitive terahertz sensing with high-Q toroidal dipole resonance governed by bound states in the continuum in all-dielectric metasurface. Nanophotonics 2021, 10, 1295–1307. [Google Scholar] [CrossRef]
  51. Hervé, P.; Vandamme, L. General relation between refractive index and energy gap in semiconductors. Infrared Phys. Technol. 1994, 35, 609–615. [Google Scholar] [CrossRef]
  52. Moss, T. A relationship between the refractive index and the infra-red threshold of sensitivity for photoconductors. Proc. Phys. Soc. Sect. B 1950, 63, 167. [Google Scholar] [CrossRef]
  53. Tan, C.-Y.; Huang, Y.-X. Dependence of refractive index on concentration and temperature in electrolyte solution, polar solution, nonpolar solution, and protein solution. J. Chem. Eng. Data 2015, 60, 2827–2833. [Google Scholar] [CrossRef]
  54. Roy, R.; Agrawal, D.K.; McKinstry, H.A. Very low thermal expansion coefficient materials. Annu. Rev. Mater. Sci. 1989, 19, 59–81. [Google Scholar] [CrossRef]
  55. Fei, Y.; Ahrens, T. Thermal expansion. Miner. Phys. Crystallogr. A Handb. Phys. Constants 1995, 2, 29–44. [Google Scholar]
  56. Zou, J.; Le, Z.; He, J.-J. Temperature self-compensated optical waveguide biosensor based on cascade of ring resonator and arrayed waveguide grating spectrometer. J. Lightwave Technol. 2016, 34, 4856–4863. [Google Scholar] [CrossRef]
  57. Elshaari, A.W.; Zadeh, I.E.; Jöns, K.D.; Zwiller, V. Thermo-optic characterization of silicon nitride resonators for cryogenic photonic circuits. IEEE Photonics J. 2016, 8, 2701009. [Google Scholar] [CrossRef]
  58. Hu, J.; Lang, T.; Shi, G.-h. Simultaneous measurement of refractive index and temperature based on all-dielectric metasurface. Opt. Express 2017, 25, 15241–15251. [Google Scholar] [CrossRef]
  59. Hu, J.; Huang, H.; Bai, M.; Zhan, T.; Yang, Z.; Yu, Y.; Qu, B. A high sensitive fiber-optic strain sensor with tunable temperature sensitivity for temperature-compensation measurement. Sci. Rep. 2017, 7, 42430. [Google Scholar] [CrossRef] [PubMed]
  60. Zhang, Y.; Liu, W.; Li, Z.; Li, Z.; Cheng, H.; Chen, S.; Tian, J. High-quality-factor multiple Fano resonances for refractive index sensing. Opt. Lett. 2018, 43, 1842–1845. [Google Scholar] [CrossRef]
  61. Hu, J.; Lang, T.; Hong, Z.; Shen, C.; Shi, G. Comparison of Electromagnetically Induced Transparency Performance in Metallic and All-dielectric Metamaterials. J. Light. Technol. 2018, 36, 2083–2093. [Google Scholar] [CrossRef]
  62. Su, W.; Ding, Y.; Luo, Y.; Liu, Y. A high figure of merit refractive index sensor based on Fano resonance in all-dielectric metasurface. Results Phys. 2019, 16, 102833. [Google Scholar] [CrossRef]
  63. Peng, W.; Zhang, G.; Lv, Y.; Qin, L.; Qi, K. Ultra-narrowband absorption filter based on a multilayer waveguide structure. Opt. Express 2021, 29, 14582–14600. [Google Scholar] [CrossRef]
  64. Wang, Y.; Zhang, J.; Yao, J. An Optoelectronic Oscillator for High Sensitivity Temperature Sensing. IEEE Photonics Technol. Lett. 2016, 28, 1458–1461. [Google Scholar] [CrossRef]
  65. Qu, J.; Zhang, H.; Shi, X.; Li, C.; Jia, D.; Liu, T.; Su, R. High Sensitivity Temperature Sensing of Long-Period Fiber Grating for the Ocean. Sensors 2023, 23, 4768. [Google Scholar] [CrossRef] [PubMed]
Photonics 10 00980 g001
Figure 1. Aerial view of the unit cell structure of metasurface consisting of H-shaped unit cells with simultaneously broken mirror symmetries and in-plane inversion and its chioptical responses. The silicon rod is supported by a silicon dioxide plate. The incident light illuminates from the top perpendicularly, and the structural parameters are as follows: The thickness t1 = 135 μm, t2 = 72 μm, the width and lengths of structure are w1 = 34.75 μm, w2 = 53 μm, l1 = L − 2α, l2 = L + 2α, l3 = L − α, l4 = L + α, l5 = 36 μm, where L = 56.25 μm, α = 18 μm, respectively. The lattice constants along the x and y directions are lx = ly = 225 μm, respectively.
Figure 1. Aerial view of the unit cell structure of metasurface consisting of H-shaped unit cells with simultaneously broken mirror symmetries and in-plane inversion and its chioptical responses. The silicon rod is supported by a silicon dioxide plate. The incident light illuminates from the top perpendicularly, and the structural parameters are as follows: The thickness t1 = 135 μm, t2 = 72 μm, the width and lengths of structure are w1 = 34.75 μm, w2 = 53 μm, l1 = L − 2α, l2 = L + 2α, l3 = L − α, l4 = L + α, l5 = 36 μm, where L = 56.25 μm, α = 18 μm, respectively. The lattice constants along the x and y directions are lx = ly = 225 μm, respectively.
Photonics 10 00980 g001
Photonics 10 00980 g002
Figure 2. (a,b,d,e) Transmittance (T) and reflectance (R) spectra for RCP and LCP incidences as the functions of asymmetry parameter α (chiral BICs I, II, III, IV). The magnitudes of CD are shown for both (c) CDT and (f) CDR (chiral BICs I, II, III, IV), respectively. The other structural and material parameters are the same as in Figure 1.
Figure 2. (a,b,d,e) Transmittance (T) and reflectance (R) spectra for RCP and LCP incidences as the functions of asymmetry parameter α (chiral BICs I, II, III, IV). The magnitudes of CD are shown for both (c) CDT and (f) CDR (chiral BICs I, II, III, IV), respectively. The other structural and material parameters are the same as in Figure 1.
Photonics 10 00980 g002
Photonics 10 00980 g003
Figure 3. (a,b) CD for transmittance and reflectance for different structural parameters of H-shaped meta-atom (chiral BICs I, II, III, IV). (c,d) CD for transmittance and reflectance for different structural parameters of H-shaped meta-atom (chiral BIC II). The other structural and material parameters are the same as in Figure 1.
Figure 3. (a,b) CD for transmittance and reflectance for different structural parameters of H-shaped meta-atom (chiral BICs I, II, III, IV). (c,d) CD for transmittance and reflectance for different structural parameters of H-shaped meta-atom (chiral BIC II). The other structural and material parameters are the same as in Figure 1.
Photonics 10 00980 g003
Photonics 10 00980 g004
Figure 4. The reflectance spectra R and transmittance T are exhibited in (a,b). RCP and LCP represent the incident waves with right- and left-handed circular polarizations, α = 18 μm. In (c), the magnitudes of CD are shown for transmitted (T) and reflected waves (R). The distribution of intensity enhancement |E/E0| for incident waves with (d) RCP and (e) LCP at the mid-thickness of the silicon meta-atoms in the frequency of 0.9232 THz and the distribution of intensity enhancement |H/H0| for incident waves with (f) RCP and (g) LCP at the mid-thickness of the silicon meta-atoms in the frequency of 0.9232 THz.
Figure 4. The reflectance spectra R and transmittance T are exhibited in (a,b). RCP and LCP represent the incident waves with right- and left-handed circular polarizations, α = 18 μm. In (c), the magnitudes of CD are shown for transmitted (T) and reflected waves (R). The distribution of intensity enhancement |E/E0| for incident waves with (d) RCP and (e) LCP at the mid-thickness of the silicon meta-atoms in the frequency of 0.9232 THz and the distribution of intensity enhancement |H/H0| for incident waves with (f) RCP and (g) LCP at the mid-thickness of the silicon meta-atoms in the frequency of 0.9232 THz.
Photonics 10 00980 g004
Photonics 10 00980 g005
Figure 5. (a) The frequency corresponding to eigenfrequency as a function of α. In (b,c), the magnitudes of Q-factor of the excited modes and circular dichroism CD of the waves transmitted and reflected from the metasurface at resonant frequencies are shown as a function of α. The other structural and material parameters are the same as in Figure 1.
Figure 5. (a) The frequency corresponding to eigenfrequency as a function of α. In (b,c), the magnitudes of Q-factor of the excited modes and circular dichroism CD of the waves transmitted and reflected from the metasurface at resonant frequencies are shown as a function of α. The other structural and material parameters are the same as in Figure 1.
Photonics 10 00980 g005
Photonics 10 00980 g006
Figure 6. (a) Transmittance spectra of the chiral BIC III for different temperatures of the same metasurface. (b) Frequency shifts of the chiral BIC III with different temperatures of the same metasurface. (c) CDT of the chiral BIC III for different temperatures of the same metasurface. (d) CDT shifts of the chiral BIC III with different temperatures of the same metasurface.
Figure 6. (a) Transmittance spectra of the chiral BIC III for different temperatures of the same metasurface. (b) Frequency shifts of the chiral BIC III with different temperatures of the same metasurface. (c) CDT of the chiral BIC III for different temperatures of the same metasurface. (d) CDT shifts of the chiral BIC III with different temperatures of the same metasurface.
Photonics 10 00980 g006
Table 1. Comparison of sensitivity and FOM of published works and the current study.
Table 1. Comparison of sensitivity and FOM of published works and the current study.
ReferenceStructureSensitivity (Refraction)Sensitivity (Temperature)FOM (RIU)
[59] 2017Cantilever——0.19 dB/°C——
[60] 2018Nanobar Paris370 nm/RIU——2846
[61] 2018Glass-shaped433.05 nm/RIU——116.7
[62] 2020Elliptical ring-disks544 nm/RIU——2409
[63] 2021multilayer waveguide462 nm/RIU——5250
[49] 2022vertical-square-split-ring1.0 THz/RIU——19.05
[64] 2022Minor-cross-shaped——0.37 GHz K−1——
[48] 2023Split-disk746 nm/RIU54 pm/°C18,650
[65] 2023LPEG——3.8 nm/°C——
This workH-shaped132.373 μm/RIU13.5 nm/°C1303
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Du, X.; Xie, S.; Nan, H.; Sun, S.; Shen, W.; Yang, J.; Guan, X. Chiral Quasi-Bound States in the Continuum of a Dielectric Metasurface for Optical Monitoring and Temperature Sensing. Photonics 2023, 10, 980. https://doi.org/10.3390/photonics10090980

AMA Style

Du X, Xie S, Nan H, Sun S, Shen W, Yang J, Guan X. Chiral Quasi-Bound States in the Continuum of a Dielectric Metasurface for Optical Monitoring and Temperature Sensing. Photonics. 2023; 10(9):980. https://doi.org/10.3390/photonics10090980

Chicago/Turabian Style

Du, Xu, Suxia Xie, Haoxuan Nan, Siyi Sun, Weiwei Shen, Jingcheng Yang, and Xin Guan. 2023. "Chiral Quasi-Bound States in the Continuum of a Dielectric Metasurface for Optical Monitoring and Temperature Sensing" Photonics 10, no. 9: 980. https://doi.org/10.3390/photonics10090980

APA Style

Du, X., Xie, S., Nan, H., Sun, S., Shen, W., Yang, J., & Guan, X. (2023). Chiral Quasi-Bound States in the Continuum of a Dielectric Metasurface for Optical Monitoring and Temperature Sensing. Photonics, 10(9), 980. https://doi.org/10.3390/photonics10090980

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop