Methods of Radiation Wavelength Tuning in Short-Pulsed Fibre Lasers
Abstract
:1. Introduction
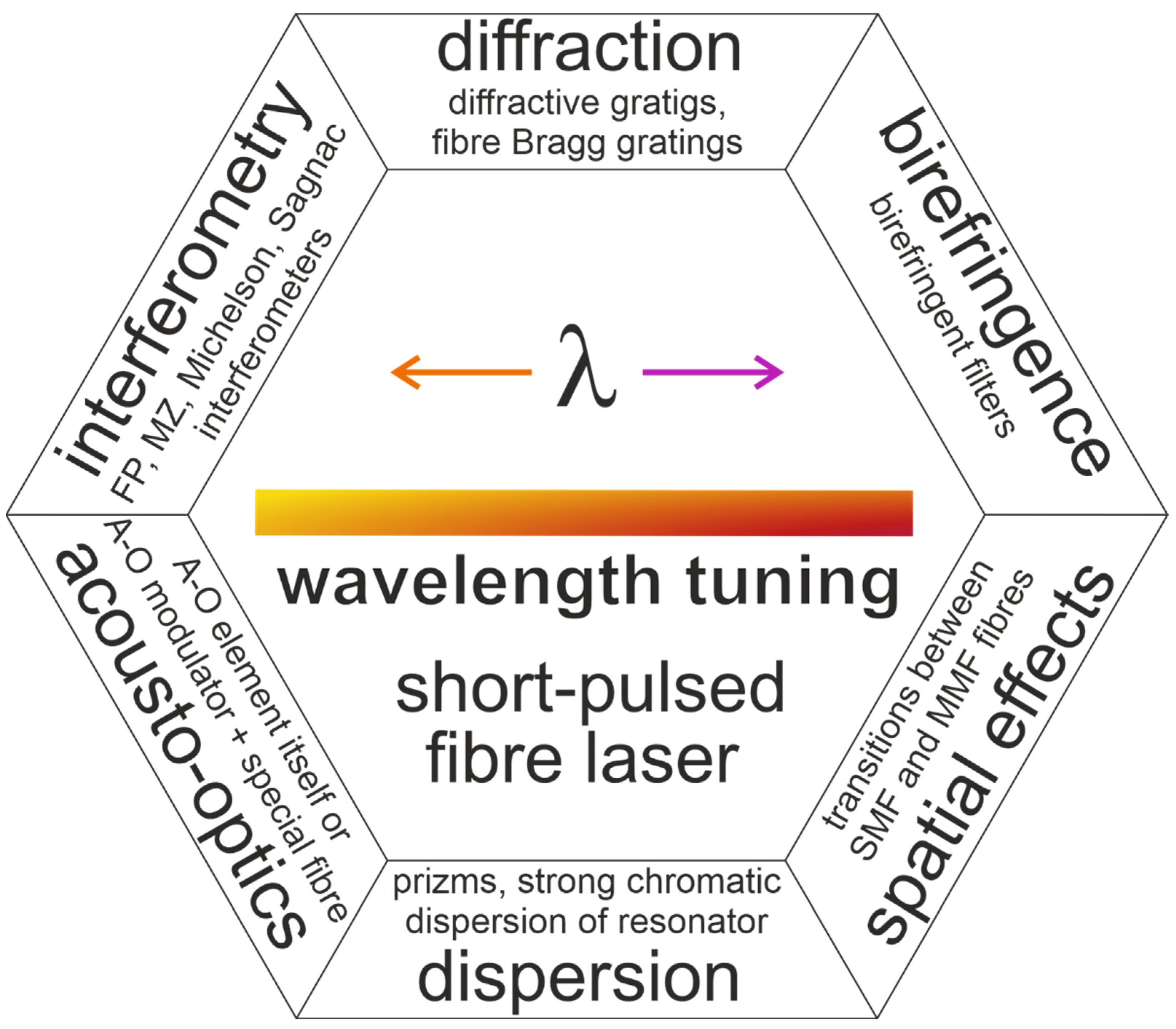
2. Elements for Output Wavelength Tuning in Short-Pulsed Fibre Lasers
3. Electrically Controlled Methods of Radiation Wavelength Tuning
4. Broad Wavelength Tuning Ranges of Mode-Locked Fibre Laser Radiation
5. Dependence of the Wavelength Tuning Range on the Output Pulse Duration
6. Unconventional Methods of Radiation Wavelength Tuning in Mode-Locked Fibre Lasers
7. Comments
8. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, D.; Jussila, H.; Wang, Y.; Hu, G.; Albrow-Owen, T.; Howe, R.; Ren, Z.; Bai, J.; Hasan, T.; Sun, Z. Wavelength and pulse duration tunable ultrafast fiber laser mode-locked with carbon nanotubes. Sci. Rep. 2018, 8, 2738. [Google Scholar] [CrossRef]
- Xiang, Y.; Luo, Y.; Liu, B.; Yan, Z.; Sun, Q.; Liu, D. Observation of wavelength tuning and bound states in fiber lasers. Sci. Rep. 2018, 8, 6049. [Google Scholar] [CrossRef]
- Chang, G.; Wei, Z. Ultrafast fiber lasers: An expanding versatile toolbox. iScience 2020, 23, 101101. [Google Scholar] [CrossRef]
- Chen, J.; Deng, G.; Yan, S.; Li, C.; Xi, K.; Xu, F.; Lu, Y. Microfiber-coupler-assisted control of wavelength tuning for Q-switched fiber laser with few-layer molybdenum disulfide nanoplates. Opt. Lett. 2015, 40, 3576–3579. [Google Scholar] [CrossRef]
- Tian, K.; Chen, G.; Gao, Y. Wavelength and bandwidth tunable passively mode-locked fiber laser based on semiconductor saturable absorber mirror and liquid crystal on silicon device. J. Phys. Conf. Ser. 2018, 1053, 012076. [Google Scholar] [CrossRef]
- Huang, F.; Si, J.; Chen, T.; Hou, L.; Hou, X. Wide-range wavelength-tunable mode-locked fiber laser based on fiber Bragg grating. IEEE Photonics Technol. Lett. 2020, 32, 1025–1028. [Google Scholar] [CrossRef]
- Yao, J.; Yao, J.; Wang, Y.; Tjin, S.; Zhou, Y.; Lam, Y.; Liu, J.; Lu, C. Active mode locking of tunable multi-wavelength fiber ring laser. Opt. Commun. 2001, 191, 341–345. [Google Scholar] [CrossRef]
- Wallmeier, K.; Würthwein, T.; Brinkmann, M.; Hellwig, T.; Fallnich, C. Fiber-based light source with multi-color output and fast wavelength tuning. EPJ Web Conf. 2022, 267, 02012. [Google Scholar] [CrossRef]
- Zuo, Z.; Wang, K.; Chen, H.; Lu, B.; Bai, J. Recent progress and development trend of self-sweeping fiber laser. Front. Phys. 2021, 9, 809049. [Google Scholar] [CrossRef]
- Comby, A.; Descamps, D.; Beauvarlet, S.; Gonzalez, A.; Guichard, F.; Petit, S.; Zaouter, Y.; Mairesse, Y. Cascaded harmonic generation from a fiber laser: A milliwatt XUV source. Opt. Express 2019, 27, 20383–20396. [Google Scholar] [CrossRef]
- Aporta, I.; Quintela, M.; López-Higuera, J. Broadband continuously tunable all-fiber laser based on OPG for CARS imaging. J. Light. Technol. 2021, 39, 2489–2496. [Google Scholar] [CrossRef]
- Kang, J.; Kong, C.; Feng, P.; Luo, Z.; Lam, E.; Wong, K. Broadband high-energy all-fiber laser at 1.6 μm. IEEE Photonics Technol. Lett. 2018, 30, 311–314. [Google Scholar] [CrossRef]
- Filion, J.; Olivier, M.; Burgoyne, B.; Villeneuve, A.; Piche, M. Tunable mode-locked fiber laser with a highly dispersive cavity. Proc. SPIE 2010, 7750, 775014. [Google Scholar] [CrossRef]
- Chmielowsk, I.P.; Nikodem, M. Widely tunable continuous-wave fiber laser in the 1.55–1.8 µm wavelength region. Opt. Express 2022, 30, 42300–42307. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, M.; Hou, L.; Tao, J.; Song, P.; Lu, B.; Bai, J. Wavelength-tunable dissipative soliton from Yb-doped fiber laser with nonlinear amplifying loop mirror. Chin. Opt. Lett. 2023, 21, 061402. [Google Scholar] [CrossRef]
- Tamura, K.; Doerr, C.; Haus, H.; Ippen, E. Soliton fiber ring laser stabilization and tuning with a broad intracavity filter. IEEE Photonics Technol. Lett. 1994, 6, 697–699. [Google Scholar] [CrossRef]
- Özgören, K.; Ilday, F. All-fiber all-normal dispersion laser with a fiber-based Lyot filter. Opt. Lett. 2010, 35, 1296–1298. [Google Scholar] [CrossRef]
- Han, D.; Mei, L.; Hui, Z.; Soliman, A.; Ren, K.; Zheng, Y.; Li, T.; Gong, J. Flexible wavelength-, pulse-controlled mode-locked all-fiber laser based on a fiber Lyot filter. Opt. Express 2022, 30, 41271–41278. [Google Scholar] [CrossRef]
- Kobtsev, S.; Kukarin, S.; Fedotov, Y. Wide-spectrally-tunable CW and femtosecond linear fiber lasers with ultrabroadband loop mirrors based on fiber circulators. Laser Phys. 2010, 20, 347–350. [Google Scholar] [CrossRef]
- Davydov, B.; Krylov, A. 30-W Yb3+-pulsed fiber laser with wavelength tuning. Laser Phys. 2017, 17, 1404–1415. [Google Scholar] [CrossRef]
- Li, S.; Chan, K. Electrical wavelength-tunable actively mode-locked fiber ring laser with a linearly chirped fiber Bragg grating. IEEE Photonics Technol. Lett. 1998, 10, 799–801. [Google Scholar] [CrossRef]
- Jiang, J.; Huang, Q.; Ma, Y.; Liao, D.; Huang, Z.; Dai, L.; Liu, Y.; Mou, C.; Araimi, M.; Rozhin, A. Wavelength-tunable L-band mode-locked fiber laser using a long-period fiber grating. Opt. Express 2021, 29, 26332–26339. [Google Scholar] [CrossRef]
- Dai, L.; Zou, C.; Huang, Q.; Huang, Z.; Ling, Y.; Xing, Z.; Yan, Z.; Mou, C. Continuously tunable mode-locked fiber laser based on tilted fiber grating. Chin. J. Lasers 2019, 46, 0508026. [Google Scholar] [CrossRef]
- Hou, L.; Li, M.; He, X.; Lin, Q.; Guo, H.; Lu, B.; Qi, X.; Chen, H.; Bai, J. Wavelength-tunable dissipative pulses from Yb-doped fiber laser with Sagnac filter. Laser Phys. Lett. 2016, 13, 125302. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, H.; Liu, B.; Miao, Y. Tilted fiber Bragg gratings: Principle and sensing applications. Photonic Sens. 2011, 1, 6–30. [Google Scholar] [CrossRef]
- Zou, M.; Zou, M.; Ran, Y.; Hu, J.; Xing, Z.; Yan, Z.; Liu, C.; Sun, Q.; Liu, D. Multiwavelength mode-locked fiber laser based on an all fiber Lyot filter. IEEE Photonics Technol. Lett. 2020, 32, 1419–1422. [Google Scholar] [CrossRef]
- Huang, L.; Song, X.; Chang, P.; Peng, W.; Zhang, W.; Gao, F.; Bo, F.; Zhang, G.; Xu, J. All-fiber tunable laser based on an acousto-optic tunable filter and a tapered fiber. Opt. Express 2016, 24, 7449–7455. [Google Scholar] [CrossRef]
- Han, X.; Hu, Y.; Li, J.; Chang, P.; Gao, F.; Dong, X.; Bo, F.; Zhang, W.; Zhang, G.; Xu, J. All-fiber frequency shifter based on an acousto-optic tunable filter cascaded with a tapered fiber-coupled microcavity. Crystals 2021, 11, 497. [Google Scholar] [CrossRef]
- Delgado-Pinar, M.; Zalvidea, D.; Díez, A.; Pérez-Millán, P.; Andrés, M. Q-switching of an all-fiber laser by acousto-optic modulation of a fiber Bragg grating. Opt. Express 2006, 14, 1106–1112. [Google Scholar] [CrossRef]
- Henderson-Sapir, O.; Bawden, N.; Theodosiou, A.; Majewski, M.; Kalli, K.; Jackson, S.; Ottaway, D. Mode-locked and tunable 3.5 µm fiber laser using an acousto-optic modulator. J. Light. Technol. 2023, 41, 716–725. [Google Scholar] [CrossRef]
- Pohl, A.; Oliveira, R.; Silva, R.; Marques, C.; Neves, P.; Cook, K.; Caning, J.; Noguera, R. Advances and new applications using the acousto-optic effect in optical fibers. Photonic Sens. 2013, 3, 1–25. [Google Scholar] [CrossRef]
- Lu, J.; Shi, F.; Xu, J.; Meng, L.; Zhang, L.; Cheng, P.; Zhou, X.; Pang, F.; Zeng, X. Recent progress of dynamic mode manipulation via acousto-optic interactions in few-mode fiber lasers: Mechanism, device and applications. Nanophotonics 2020, 10, 983–1010. [Google Scholar] [CrossRef]
- Demırbas, U. Off-surface optic axis birefringent filters for smooth tuning of broadband lasers. Appl. Opt. 2017, 56, 7815–7825. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, L.; Bai, C.; Ren, S.; Tian, Z.; Yao, Y.; Wang, M. Yb-doped mode-locked fiber laser based on an all-fiber interferometer filter. Photonics 2023, 10, 203. [Google Scholar] [CrossRef]
- Available online: https://www.fltphotonics.com/products.htm (accessed on 1 January 2020).
- Hill, K.; Meltz, G. Fiber Bragg grating technology fundamentals and overview. J. Light. Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef]
- Akulov, V.; Afanasiev, D.; Babin, S.; Churkin, D.; Kablukov, S.; Rybakov, M.; Vlasov, A. Frequency tuning and doubling in Yb-doped fiber lasers. Laser Phys. 2007, 17, 124–129. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, Y.; Wang, M.; Huang, Q.; Dai, L.; Huang, Z.; Liu, Y.; Mou, C. L-band filter-less wavelength tunable mode-locked fiber laser incorporating a long-period fiber grating. Results Opt. 2023, 10, 100360. [Google Scholar] [CrossRef]
- Han, P.; Liu, T.; Gao, X.; Ren, S. Thermal tuning on narrow linewidth fiber laser. Proc. SPIE 2010, 7655, 765516. [Google Scholar] [CrossRef]
- Selvas, R.; Torres-Gomez, I.; Martinez-Rios, A.; Avarez-Chavez, J.; May-Arrioja, D.A.; LiKamWa, P.; Mehta, A.; Johnson, E. Wavelength tuning of fiber lasers using multimode interference effects. Opt. Express 2005, 13, 9439–9445. [Google Scholar] [CrossRef]
- Guzman-Sepulveda, J.; Castillo-Guzman, A. Wavelength tuning of multimode interference fiber lasers: A review. Adv. Photonics Res. 2021, 2, 2100051. [Google Scholar] [CrossRef]
- Salceda-Delgado, G.; Martinez-Rios, A.; Sierra-Hernandez, J.; Rodríguez-Carreón, V.; Selvas-Aguilar, R.; Álvarez-Tamayo, R.; Durán-Sánchez, M.; Castillo-Guzman, A.; Rojas-Laguna, R. Wavelength switching and tuning of fiber lasers by using a modifiable intra-cavity filter based on a modal Michelson interferometer. Laser Phys. 2019, 29, 065104. [Google Scholar] [CrossRef]
- Wu, P.; Zhou, Q.; Wang, Y.; Deng, G.; Fan, Y.; Shen, S.; Xu, Q.; Wang, Y.; Song, H.; Wang, Y. Wavelength-tunable passively mode-locked all-fiber laser at 1.5 μm. Appl. Opt. 2019, 58, 5143–5147. [Google Scholar] [CrossRef]
- Armas-Rivera, I.; Rodriguez-Morales, L.; Durán-Sánchez, M.; Avazpour, M.; Carrascosa, A.; Silvestre, E.; Kuzin, E.; Andrés, M.; Ibarra-Escamilla, B. Wide wavelength-tunable passive mode-locked Erbium-doped fiber laser with a SESAM. Opt. Laser Technol. 2021, 134, 106593. [Google Scholar] [CrossRef]
- Yan, Z.; Sun, B.; Li, X.; Luo, J.; Shum, P.; Yu, X.; Wang, Y.Z.Q. Widely tunable Tm-doped mode-locked all-fiber laser. Sci. Rep. 2016, 6, 27245. [Google Scholar] [CrossRef]
- Hofer, M.; Ober, M.; Haber, F.; Fermann, M. Characterization of ultrashort pulse formation in passively mode-locked fiber lasers. IEEE J. Quantum Electron. 1992, 28, 720. [Google Scholar] [CrossRef]
- Koptev, M.; Anashkina, E.; Andrianov, A.; Dorofeev, V.; Kosolapov, A.; Muravyev, S.; Kim, A. Widely tunable mid-infrared fiber laser source based on soliton self-frequency shift in microstructured tellurite fiber. Opt. Lett. 2015, 40, 4094–4097. [Google Scholar] [CrossRef]
- Anashkina, E.; Andrianov, A.; Muravyev, S.; Kim, A. All-fiber design of erbium-doped laser system for tunable two-cycle pulse generation. Opt. Express 2011, 19, 20141–20150. [Google Scholar] [CrossRef]
- Henderson-Sapir, O.; Bawden, N.; Majewski, M.; Woodward, R.; Ottaway, D.; Jackson, S. Mode-locked and tunable fiber laser at the 3.5 µm band using frequency-shifted feedback. Opt. Lett. 2020, 45, 224–227. [Google Scholar] [CrossRef]
- Jeon, M.; Lee, H.; Kim, K.; Lee, E.; Yun, S.; Kim, B.; Koh, Y. An electronically wavelength-tunable mode-locked fiber laser using an all-fiber acoustooptic tunable filter. IEEE Photonics Technol. Lett. 1996, 8, 1618–1620. [Google Scholar] [CrossRef]
- Noronen, T.; Okhotnikov, O.; Gumenyuk, R. Electronically tunable thulium-holmium mode-locked fiber laser for the 1700–1800 nm wavelength band. Opt. Express 2016, 24, 14703–14708. [Google Scholar] [CrossRef]
- Kivistö, S.; Herda, R.; Okhotnikov, O. Electronically tunable Yb-doped mode-locked fiber laser. IEEE Photonics Technol. Lett. 2008, 20, 51–53. [Google Scholar] [CrossRef]
- Zhang, H.; Xia, H.; Fan, M.; Zheng, J.; Li, J.; Tian, X.; Zhou, D.; Huang, Z.; Zhang, F.; Zhang, R.; et al. Observation of wavelength tuning in a mode-locked figure-9 fiber laser. Photonics 2023, 10, 184. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, H.; Wu, Z.; Shen, L.; Wang, S.; Deng, G.; Zhou, S. Electrically tunable mode-locked fiber laser using laser induced graphene assisted long-period fiber grating. Laser Phys. Lett. 2023, 20, 035102. [Google Scholar] [CrossRef]
- Nishiura, M.; Shioda, T. Wavelength and pulse width programmable mode-locked Yb fiber laser. Opt. Express 2023, 31, 5347–5362. [Google Scholar] [CrossRef]
- Kobtsev, S. Noise-like pulses: Useful or harmful? Proc. SPIE 2021, 11905, 119051K. [Google Scholar] [CrossRef]
- Duan, L.; Dagenais, M.; Goldhar, J. Smoothly wavelength-tunable picosecond pulse generation using a harmonically mode-locked fiber ring laser. J. Light. Technol. 2003, 21, 930–937. [Google Scholar] [CrossRef]
- Lin, S.; Yu, J.; Li, W.; Ke, J. All-PM wavelength-tunable and harmonically mode-locking Yb-doped fiber laser. Apl. Opt. 2018, 57, 7410–7414. [Google Scholar] [CrossRef]
- Yamashita, S.; Asano, M. Wide and fast wavelength-tunable mode-locked fiber laser based on dispersion tuning. Opt. Express 2006, 14, 9299–9306. [Google Scholar] [CrossRef]
- Yang, S.; Zheng, J.; Qi, Y.; Shi, Y.; Li, D.; Nie, X. Widely-tunable harmonic mode-locked fiber laser by the combination of spectral filtering and gain management. Opt. Laser Technol. 2023, 157, 108726. [Google Scholar] [CrossRef]
- Jang, Y.; Park, J.; Jin, J. Wavelength Tunable All Polarization Maintaining Fiber Mode Locked Laser at C Band with High Repetition Rate of 126 MHz. SSRN. Available online: https://ssrn.com/abstract=4147706 (accessed on 1 January 2020).
- Chen, H.; Chen, S.; Jiang, Z.; Hou, J. Versatile long cavity widely tunable pulsed Yb-doped fiber laser with up to 27655th harmonic mode locking order. Opt. Express 2015, 23, 1308–1318. [Google Scholar] [CrossRef]
- Okhotnikov, O.; Gomes, L.; Xiang, N.; Jouhti, T. Mode-locked ytterbium fiber laser tunable in the 980–1070-nm spectral range. Opt. Lett. 2003, 28, 1522–1524. [Google Scholar] [CrossRef]
- Guo, H.; Hou, L.; Wang, Y.; Sun, J.; Lin, Q.; Bai, Y.; Bai, J. Tunable Ytterbium-doped mode-locked fiber laser based on single-walled carbon nanotubes. J. Light. Technol. 2019, 37, 2370–2374. [Google Scholar] [CrossRef]
- Lin, J.; Dong, T.; Zhang, Y.; Yao, P.; Gu, C.; Xu, L. All-fiber wavelength-tunable Ytterbium-doped mode-locked lasers based on fiber loop mirror. Proc. SPIE 2021, 12060, 120600U. [Google Scholar] [CrossRef]
- Nishiura, M.; Shioda, T. 1020–1064 nm wavelength-tunable all polarization maintaining mode-locked fiber laser with a programmable optical filter. Proc. SPIE 2020, 11260, 112600T. [Google Scholar] [CrossRef]
- Thipparapu, N.; Alam, S.; Wang, Y.; Pidishety, S.; Richardson, D.; Sahu, J. Widely tunable actively mode-locked Bi-doped fiber laser operating in the O-band. IEEE Photonics Technol. Lett. 2022, 34, 711–714. [Google Scholar] [CrossRef]
- Nyushkov, B.; Kobtsev, S.; Antropov, A.; Kolker, D.; Pivtsov, V. Femtosecond 78-nm tunable Er:fibre laser based on drop-shaped resonator topology. J. Light. Technol. 2019, 37, 1359–1363. [Google Scholar] [CrossRef]
- Meng, Y.; Salhi, M.; Niang, A.; Guesmi, K.; Semaan, G.; Sanchez, F. Mode-locked Er:Yb-doped double-clad fiber laser with 75-nm tuning range. Opt. Lett. 2015, 40, 1153–1156. [Google Scholar] [CrossRef]
- Gao, G.; Zhao, Z.; Cong, Z.; Zhao, Q.; Liu, Z. Widely wavelength-tunable mode locked Er-doped fiber oscillator from 1532 nm to 1594 nm with high signal-to-noise ratio. Opt. Laser Technol. 2021, 135, 106688. [Google Scholar] [CrossRef]
- Jang, Y.; Park, J.; Jin, J. Full C-band wavelength-tunable, 250 MHz repetition rate mode-locked polarization-maintaining fiber laser. Sci. Rep. 2023, 13, 3623. [Google Scholar] [CrossRef]
- Meng, Y.; Li, Y.; Xu, Y.; Wang, F. Carbon nanotube mode-locked Thulium fiber laser with 200 nm tuning range. Sci. Rep. 2017, 7, 45109. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, M.; Wu, J.; Cheng, F.; Liu, J.; Ruan, D.; Chen, Y. Ultra-broadband tunable and switchable multi-wavelength mode-locking Tm-doped all-fiber laser. Opt. Laser Technol. 2021, 143, 107364. [Google Scholar] [CrossRef]
- Tamura, K.; Haus, H.; Ippen, E. Self-starting additive pulse mode-locked erbium fiber ring laser. Electron. Lett. 1992, 28, 2226–2228. [Google Scholar] [CrossRef]
- Xu, Z.; Dou, Z.; Hou, J.; Xu, X. All-fiber wavelength-tunable Tm-doped fiber laser mode locked by SESAM with 120 nm tuning range. Appl. Opt. 2017, 56, 5978–5981. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, Y.; Chen, H.; Luan, K.; Tao, M.; Si, J. Wavelength-tunable passively mode-locked mid-infrared Er3+-doped ZBLAN fiber laser. Sci. Rep. 2017, 7, 14913. [Google Scholar] [CrossRef]
- Woodward, R.; Majewski, M.; Jackson, S. Mode-locked dysprosium fiber laser: Picosecond pulse generation from 2.97 to 3.30 μm. APL Photonics 2018, 3, 116106. [Google Scholar] [CrossRef]
- Gao, G.; Wang, S.; Zhao, Q.; Cong, Z.; Liu, Z.; Zhao, Z. Consecutive 1015–1105-nm wavelength tunable “figure-of-9” mode-locked Yb:fiber oscillator. Opt. Lett. 2022, 47, 5869–5872. [Google Scholar] [CrossRef]
- Gao, K.; Liu, Y.; Qiao, W.; Song, Y.; Zhao, X.; Wang, A.; Li, T. Wavelength-tunable 1104 nm nonlinear amplifier loop mirror laser based on a polarization-maintaining double-cladding fiber. Opt. Lett. 2022, 47, 5–8. [Google Scholar] [CrossRef]
- Chen, S.; Chen, Y.; Liu, K.; Sidharthan, R.; Li, H.; Chang, C.; Wang, Q.; Tang, D.; Yoo, S. All-fiber short-wavelength tunable mode-locked fiber laser using normal dispersion thulium-doped fiber. Opt. Express 2020, 28, 17570–17580. [Google Scholar] [CrossRef]
- Sun, B.; Luo, J.; Yan, Z.; Liu, K.; Ji, J.; Zhang, Y.; Wang, Q.; Yu, X. 1867–2010 nm tunable femtosecond thulium-doped all-fiber laser. Opt. Express 2017, 25, 8997–9002. [Google Scholar] [CrossRef]
- Dai, R.; Meng, Y.; Li, Y.; Qin, J.; Zhu, S.; Wang, F. Nanotube mode-locked, wavelength and pulsewidth tunable thulium fiber laser. Opt. Express 2019, 27, 3518–3527. [Google Scholar] [CrossRef]
- Wei, K.; Zhang, H.; Yang, K.; Zhu, H.; Yan, P.; Ruan, S.; Wang, J. Tunable thulium-doped mode-locked fiber laser with watt-level average power. Opt. Lett. 2022, 47, 1545–1548. [Google Scholar] [CrossRef]
- Koptev, M.; Anashkina, E.; Andrianov, A.; Dorofeev, V.; Kosolapov, A.; Muravyev, S.; Kim, A. Broadband wavelength tuning of hybrid femtosecond Er/Tm fiber laser system in microstructured suspended-core tellurite fiber. Proc. SPIE 2016, 9728, 97281N. [Google Scholar] [CrossRef]
- Wang, J.; Lin, S.; Liang, X.; Wang, M.; Yan, P.; Hu, G.; Albrow-Owen, T.; Ruan, S.; Sun, Z.; Hasan, T. High-energy and efficient Raman soliton generation tunable from 1.98 to 2.29 µm in an all-silica-fiber thulium laser system. Opt. Lett. 2017, 42, 3518–3521. [Google Scholar] [CrossRef]
- Wei, J.; Su, J.; Lu, H.; Peng, K. A review of progress about birefringent filter design and application in Ti:sapphire laser. Photonics 2023, 10, 1217. [Google Scholar] [CrossRef]
- Li, R.; Shi, H.; Tian, H.; Li, Y.; Liu, B.; Song, Y.; Hu, M. All-polarization-maintaining dual-wavelength mode-locked fiber laser based on Sagnac loop filter. Opt. Express 2018, 26, 28302–28311. [Google Scholar] [CrossRef]
- Wey, J.; Goldhar, J.; Burdge, G. Active harmonic modelocking of an Erbium fiber laser with intracavity Fabry–Perot filters. J. Light. Technol. 1997, 15, 1171–1180. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, L.; Wang, M.; Chen, N.; Yao, Y.; Tian, Z.; Bai, C. Wavelength-tunable mode-locked fiber laser based on an all-fiber Mach–Zehnder interferometer filter. Chin. Opt. Lett. 2023, 21, 041401. [Google Scholar] [CrossRef]
- Hanna, D.; Percival, R.; Perry, I.; Smart, R.; Sunit, P.J.; Tropper, A.C. An ytterbium-doped monomode fibre laser: Broadly tunable operation from 1010 µm to 1162 µm and three-level operation at 974 nm. J. Mod. Opt. 1990, 37, 517–525. [Google Scholar] [CrossRef]
- Agnesi, A.; Carrà, L.; Marco, C.; Piccoli, R.; Reali, G. Fourier-limited 19-ps Yb-Fiber seeder stabilized by spectral filtering and tunable between 1015 and 1085 nm. IEEE Photonics Technol. Lett. 2012, 24, 927–929. [Google Scholar] [CrossRef]
- Lia, S.; Chan, K. Electrical wavelength tunable and multiwavelength actively mode-locked fiber ring laser. Appl. Phys. Lett. 1998, 72, 1954–1956. [Google Scholar] [CrossRef]
- Chan, K.; Shu, C. Compensated dispersion tuning in harmonically mode-locked fiber laser. Appl. Phys. Lett. 1999, 75, 891–893. [Google Scholar] [CrossRef]
- Yamashita, S.; Nishihara, M. Widely tunable Erbium-doped fiber ring laser covering both C-band and L-band. IEEE J. Quantum Electron. 2001, 7, 41–43. [Google Scholar] [CrossRef]
- Lin, G.; Chang, J. Femtosecond mode-locked Erbium-doped fiber ring laser with intra-cavity loss controlled full L-band wavelength tunability. Opt. Express 2007, 15, 97–103. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, D.; Knize, R.; Zhao, L.; Bao, Q.; Loh, K. Graphene mode locked, wavelength-tunable, dissipative soliton fiber laser. Appl. Phys. Lett. 2010, 96, 111112. [Google Scholar] [CrossRef]
- Sun, Z.; Popa, D.; Hasan, T.; Torrisi, F.; Wang, F.; Kelleher, E.; Travers, J.; Nicolosi, V.; Ferrari, A. A stable, wideband tunable, near transform-limited, graphene-mode-locked, ultrafast laser. Nano Res. 2010, 3, 653–660. [Google Scholar] [CrossRef]
- Going, R.; Popa, D.; Torrisi, F.; Sun, Z.; Hasan, T.; Wang, F.; Ferrari, A.C. 500 fs wideband tunable fiber laser mode-locked by nanotubes. Phys. E Low Dimens. 2012, 44, 1078–1081. [Google Scholar] [CrossRef]
- He, X.; Liu, Z.; Wang, D. Wavelength-tunable, passively mode-locked fiber laser based on graphene and chirped fiber Bragg grating. Opt. Lett. 2012, 37, 2394–2396. [Google Scholar] [CrossRef]
- Jain, A.; Chandra, N.; Anchal, A.; Kumar, P. Tunable multiwavelength mode-locked fiber laser using intra-cavity polarization and wavelength dependent loss. Opt. Laser Technol. 2016, 83, 189–194. [Google Scholar] [CrossRef]
- Ryser, M.; Bacher, C.; Lätt, C.; Heidt, A.; Raisin, P.; Feurer, T.; Romano, V. Self-optimizing additive pulse mode-locked fiber laser: Wavelength tuning and selective operation in continuous-wave or mode-locked regime. Proc. SPIE 2018, 10512, 105121C. [Google Scholar] [CrossRef]
- Fu, B.; Popa, D.; Zhao, Z.; Hussain, S.; Flahaut, E.; Hasan, T.; Soavi, G.; Ferrari, A. Wavelength tunable soliton rains in a nanotube-mode locked Tm-doped fiber laser. Appl. Phys. Lett. 2018, 113, 193102. [Google Scholar] [CrossRef]
- Yun, L.; Zhao, W. Nanotube mode locked, wavelength-tunable, conventional and dissipative solitons fiber laser. Opt. Commun. 2018, 406, 205–208. [Google Scholar] [CrossRef]
- Lu, B.; Zou, C.; Huang, Q.; Yan, Z.; Xing, Z.; Araimi, M.; Rozhin, A.; Zhou, K.; Zhang, L.; Mou, C. Widely wavelength-tunable mode-locked fiber laser based on a 45°-tilted fiber grating and polarization maintaining fiber. J. Light. Technol. 2019, 37, 3571–3578. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, Z.; Wang, D.; Yang, F.; Li, L. Generation of wavelength-tunable and coherent dual-wavelength solitons in the C + L band by controlling the intracavity loss. Photonics Res. 2019, 7, 853–861. [Google Scholar] [CrossRef]
- Lin, J.; Dong, Z.; Dong, T.; Zhang, Y.; Dai, C.; Yao, P.; Gu, C.; Xu, L. All-fiber figure-eight wavelength-tunable noise-like pulse lasers. Opt. Laser Technol. 2021, 141, 107146. [Google Scholar] [CrossRef]
- Liu, L.; Li, X.; Zhang, S.; Liu, J.; Yan, D.; Xin, Y.; Wang, C.; Yang, Z. Wavelength-changeable thulium-doped fiber laser based on monolayer graphene. Opt. Laser Technol. 2021, 139, 106980. [Google Scholar] [CrossRef]
- Ding, J.; Wen, Z.; Lu, B.; Wang, K.; Chen, H.; Bai, J. Wavelength switchable dissipative soliton mode-locked fiber laser based on Lyot filter. Opt. Laser Technol. 2021, 144, 107460. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, P.; Wang, P. A tunable nanosecond pulse mode-locking fiber laser. Opto-Electron. Eng. 2021, 48, 210195. [Google Scholar] [CrossRef]
- Chang, S.; Wang, Z.; Wang, D.; Zhu, T.; Hua, K.; Gao, F. Tunable and dual-wavelength mode-locked Yb-doped fiber laser based on graded-index multimode fiber device. Opt. Laser Technol. 2021, 140, 107081. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, R.; Jiang, X.; Evans, J.; He, S. 1.7 µm–1.73 µm tunable ultrafast Raman fiber laser pumped by 1.6 µm dissipative soliton pulses. Opt. Express 2022, 30, 45970–45979. [Google Scholar] [CrossRef]
- Tao, J.; Fang, Y.; Song, Y.; Song, P.; Hou, L.; Lu, B.; Lin, Q.; Bai, J. Sideband-free tunable and switchable dual-wavelength mode-locked fiber laser based on the Lyot filter and spontaneous radiation peaks. Opt. Express 2022, 30, 17465–17475. [Google Scholar] [CrossRef]
- Huang, S.; Zheng, S.; Wang, J.; Chen, H.; Dong, F.; Yu, L.; Luo, X.; Guo, X.; Yan, P.; Wang, J.; et al. Tunable mode-locked Tm-doped fiber laser based upon cross-phase modulation. Opt. Express 2022, 30, 32256–32266. [Google Scholar] [CrossRef]
- Ahmad, H.; Ooi, S.; Samion, M.; Reduan, S. Tunable mode-locked pulsed laser generation at longer 2.0 μm region. IEEE J. Quantum Electron. 2022, 58, 1600410. [Google Scholar] [CrossRef]
- Tao, Z.; Li, X.; Ma, W.; Ding, X.; Wang, T.; Jiang, H.; Wang, Y.; Lou, Y. All-fiber 2.1 um band tunable continuous-wave and soliton mode-locked Ho-doped fiber laser. Opt. Commun. 2022, 515, 128157. [Google Scholar] [CrossRef]
- Shang, J.; Zhao, S.; Liu, Y.; Zhao, Y.; Song, Y.; Li, T.; Feng, T. The design of >2000-nm, ~100-MHz ultrafast Tm-doped fiber soliton laser source. J. Light. Technol. 2022, 40, 2116–2122. [Google Scholar] [CrossRef]
- Kirsch, D.; Bednyakova, A.; Varak, P.; Honzatko, P.; Cadier, B.; Robin, T.; Fotiadi, A.; Peterka, P.; Chernysheva, M. Gain-controlled broadband tuneability in self-mode-locked Thulium-doped fibre laser. Commun. Phys. 2022, 5, 219. [Google Scholar] [CrossRef]
- Liu, X.; Sahu, J.; Gumenyuk, R. Tunable dissipative soliton Tm-doped fiber laser operating from 1700 nm to 1900 nm. Opt. Lett. 2023, 48, 612–615. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Li, M.; Hou, X.; Du, L.; Xiao, L.; Wang, T.; Ma, W. Generation of mode-locked states of conventional solitons and bright-dark solitons in graphene mode-locked fiber laser. Front. Optoelectron. 2023, 16, 12. [Google Scholar] [CrossRef]
- Liu, X.; Gumenyuk, R. Short-wavelength-band tunable high-power Tm-doped fiber laser. Proc. SPIE 2023, 12400, 1240009. [Google Scholar] [CrossRef]
- Bednyakova, A.; Khudozhitkova, D.; Turitsyn, S. Nonlinear spectral tunability of pulsed fiber laser with semiconductor optical amplifier. Sci. Rep. 2022, 12, 13799. [Google Scholar] [CrossRef]
- Bednyakova, A.; Khudozhitkova, D.; Kokhanovskiy, A.; Turitsyn, S. Nonlinear spectral blueshift in semiconductor optical amplifiers. Opt. Lett. 2021, 46, 4757–4760. [Google Scholar] [CrossRef]
- Fermann, M.; Haberl, F.; Hofer, M.; Hochreiter, H. Nonlinear amplifying loop mirror. Opt. Lett. 1990, 15, 752–754. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Huang, Y.; Song, Z.; Wei, J.; Pei, J.; Ruan, S. Two-micron all-fiberized passively mode-locked fiber lasers with high-energy nanosecond pulse. High Power Laser Sci. Eng. 2020, 8, e14. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, B.; He, Q.; Guo, J.; Jiao, Z. Wavelength-tunable mode-locked Yb-doped fiber laser based on nonlinear Kerr beam clean-up effect. Chin. Opt. Lett. 2022, 20, 041403. [Google Scholar] [CrossRef]
- Fang, L.; Huang, C.; Liu, T.; Gogneau, N.; Bourhis, E.; Gierak, J.; Oudar, J. Wavelength tunable ultrafast fiber laser via reflective mirror with taper structure. Appl. Opt. 2016, 55, 10463–10468. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Liu, Y.; Wang, Z.; Lou, J.; Wang, Z.; Liu, Z. Broadband wavelength tunable modelocked thulium-doped fiber laser operating in the 2 μm region by using a graphene saturable absorber on microfiber. Laser Phys. Lett. 2016, 13, 065105. [Google Scholar] [CrossRef]
- Kobtsev, S.; Sventsitskaya, N. Application of birefringent filters in continuous-wave tunable lasers: A review. Opt. Spectrosc. 1992, 73, 114–123. [Google Scholar]
- Fedotov, Y.; Kobtsev, S.; Arif, R.; Rozhin, A.; Mou, C.; Turitsyn, S. Spectrum-, pulsewidth-, and wavelength-switchable all-fiber mode-locked Yb laser with fiber based birefringent filter. Opt. Express 2012, 20, 17797–17805. [Google Scholar] [CrossRef]
- Guo, Z.; Hao, Q.; Huang, K.; Zeng, H. All-normal-dispersion mode-locked fiber laser with a tunable angle-spliced polarization-maintaining fiber Lyot filter. IEEE Photonics J. 2021, 13, 1501108. [Google Scholar] [CrossRef]
- Zhang, S.; Meng, Q.; Zhao, G. All-fiber wavelength tunable passively mode-locked erbium-doped ring laser. Eur. Phys. J. D 2010, 60, 383–387. [Google Scholar] [CrossRef]
- Man, W.; Tam, H.; Demokan, M.; Wai, P.; Tang, D. Mechanism of intrinsic wavelength tuning and sideband asymmetry in a passively mode-locked soliton fiber ring laser. J. Opt. Soc. Am. B 2000, 17, 28–33. [Google Scholar] [CrossRef]
- Zhou, J.; Pan, W.; Qi, W.; Cao, X.; Cheng, Z.; Feng, Y. Ultrafast Raman fiber laser: A review and prospect. PhotoniX 2022, 3, 18. [Google Scholar] [CrossRef]
- Alfano, R.R. (Ed.) The Supercontinuum Laser Source. The Ultimate White Light, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2022; ISBN 978-3-031-06197-4. [Google Scholar]
- Jang, Y.; Park, J.; Jin, J. Linear-cavity Er-doped fiber mode-locked laser with large wavelength tunability. Appl. Opt. 2022, 61, 10116–10120. [Google Scholar] [CrossRef] [PubMed]

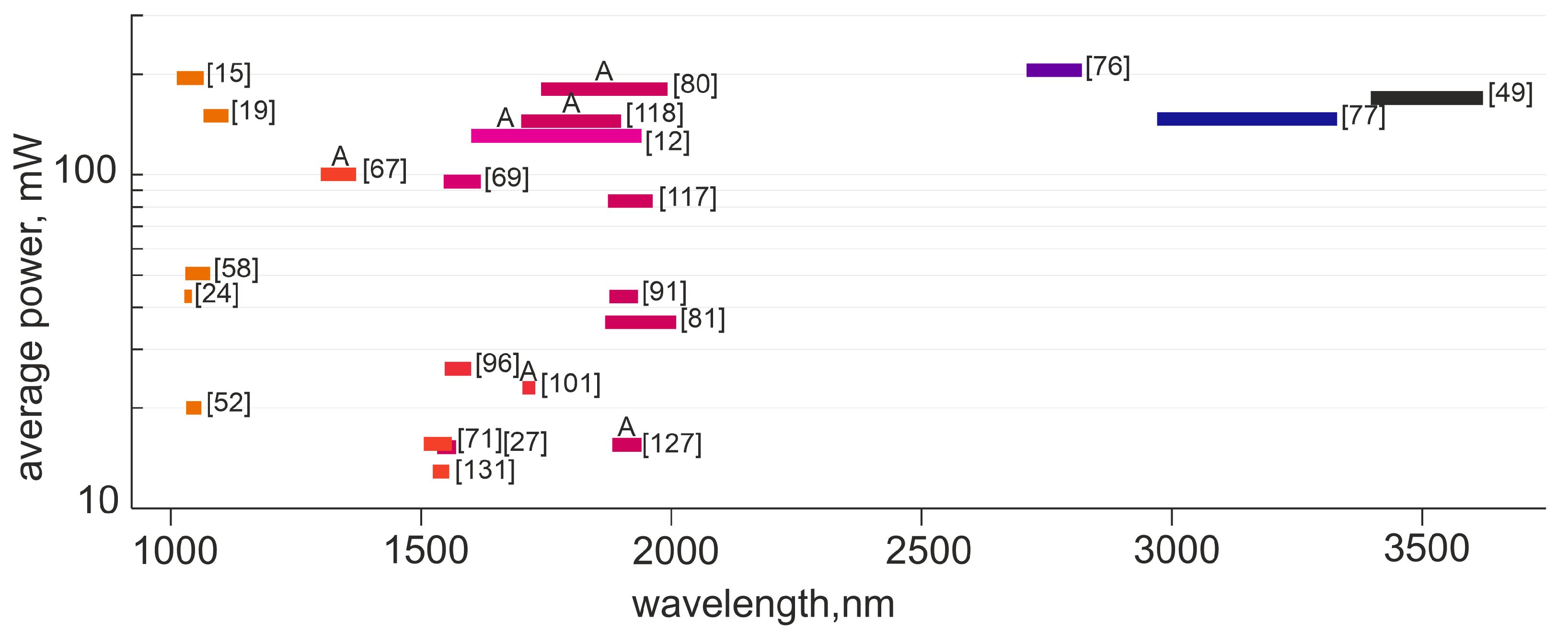
| ∆λ, nm | AM | ∆t, ps | PRR, MHz | Out, mW | M/S | REF |
|---|---|---|---|---|---|---|
| 90 (980–1070) | YDFL | 1.6–2 | 30 | 3 | Tilting of the HR mirror | [63] |
| 54.44 (1004.99–1059.43) | YDFL | 2.43 | 27.2 | ~4 | Free-space reflective grating | [64] |
| 53 (1023–1076) | YDFL | ~1 | 5.814 | ~0.01 | Adjusting PCs | [65] |
| 44 (1020–1064) | YDFL | 2–8 | 6.12 | ~0.7 | Programmable optical filter | [66] |
| 90 (1015–1105) | YDFL | 0.616–0.895 | 47.71 | 15.2 | Tilting the resonator mirror | [78] |
| 170 (1034–1104) | YDFL | 0.187–0.192 | 24.7 | 7.61 | Tuning the intra-cavity loss | [79] |
| 70 (1300–1370) | BDFL | 1300 | 1.683 | 7 | Tuneable filter | [67] |
| 78 (1524–1602) | EDFL | 0.5–0.94 | 17.5 | 2.4–3.1 | Free-space reflective grating | [68] |
| 75 (1545–1620) | EYDFL | 0.64–1.3 | ~4.4 | 22–95 | Adjusting PCs | [69] |
| 62 (1532–1594) | EDFL | 0.9–1.4 | 32.8 | 1.6–5.3 | Adjusting the width of a slit | [70] |
| 56 (1505–1561) | EDFL | 0.6–2.6 | 250 | 5–15 | Spectral filter | [71] |
| 152 (1740–1892) | TDFL | 2.76 | 3 | ~180 | Bending-induced filtering effect | [80] |
| 200 (1860–2060) | THDFL | <5 | 18.4 | 0.4–1.5 | Free-space reflective grating | [72] |
| 152.9 (1828.45–1981.35) | TDFL | <1000 | 4.866 | 3.2 | Adjusting PCs | [73] |
| 143 (1867–2010) | TDFL | <0.4 | 247.98 | 35 | Adjusting PC | [81] |
| 136 (1842–1978) | TDFL | several ps | 2.6 | 1–3 | Adjusting PCs | [45] |
| 121 (1862–1983) | TDFL | ~200 | 3.82 | 0.1–6.12 | Fibre tuneable filter | [75] |
| 300 (1733–2033) | TDFL | 0.91–6.43 | 14.83 | 1 | Free-space reflective grating | [82] |
| 113 (1918–2031) | TDFL | 509.7 | <0.2 | 1314 | Adjusting the intra-cavity waveplates | [83] |
| 310 (1980–2290) | TDFA | ~100 | 55.42 | 140.8–968 | Pump power | [84] |
| 339 (2007–2346) | TDFL + TDFA | 0.229 | 96 | 3300 | Pump power | [85] |
| 110 (2710–2820) | EZBLAN | 6.4 | 28.9 | 203 | Blazed grating | [76] |
| 330 (2970–3300) | DZBLAN | ~33 | 44.5 | 140 | Acousto-optic tunable filter | [77] |
| 215 (3397–3612) | Er3+:ZrF4 | 53 | 14.5–15.5 | 167 | Acousto-optic tunable filter | [49] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kobtsev, S. Methods of Radiation Wavelength Tuning in Short-Pulsed Fibre Lasers. Photonics 2024, 11, 28. https://doi.org/10.3390/photonics11010028
Kobtsev S. Methods of Radiation Wavelength Tuning in Short-Pulsed Fibre Lasers. Photonics. 2024; 11(1):28. https://doi.org/10.3390/photonics11010028
Chicago/Turabian StyleKobtsev, Sergey. 2024. "Methods of Radiation Wavelength Tuning in Short-Pulsed Fibre Lasers" Photonics 11, no. 1: 28. https://doi.org/10.3390/photonics11010028
APA StyleKobtsev, S. (2024). Methods of Radiation Wavelength Tuning in Short-Pulsed Fibre Lasers. Photonics, 11(1), 28. https://doi.org/10.3390/photonics11010028





