Abstract
Monte Carlo techniques have been extensively used for planning laser-based clinical procedures such as photobiomodulation. However, the effects of several biological tissue characteristics regarding its morphological structure and physiological parameters have not been carefully addressed in many applications. Specifically, many questions remain concerning the effect of skin phototype and body mass index on the effectiveness of photobiomodulation for extraoral therapies. To address these questions, a Monte Carlo simulation model of the effects of body mass index-dependent skin structure on different Fitzpatrick skin types was developed, specifically tailored for the morphological characteristics of cheek tissue. The model describes the settings of a typical oral photobiomodulation treatment protocol for pain relief, namely the use of 660 nm and 808 nm laser wavelengths and a therapeutic dose of on the masseter muscle. The simulations were used to train a machine learning predictive model aimed at accelerating the treatment planning stage and assessing the importance of patient-specific parameters. A multiple-regression approach was adopted to predict muscle dose and treatment time for effective delivered dose. Body mass index had little effect on epidermal energy deposition, but an important impact on muscle dose parameters. Phototype also influenced muscle dose, but to a lesser extent than body mass index. The results of this study can be used to develop customized dosimetry phototherapy protocols to promote more effective and safe clinical outcomes.
1. Introduction
Orofacial diseases are among the several pathological conditions that affect people’s quality of life in the world. Notably, temporomandibular disorder (TMD) is a group of conditions that cause symptoms like maxillary pain, headache, and facial pain [1]. Another painful condition is oral mucositis (OM), a complication of chemotherapy or head and neck radiotherapy causing soreness, redness and smoothness on oral tissues early after treatment onset [2]. Management of TMD- and OM-related pain may require opioid analgesia, which may cause addiction and other side effects. Photobiomodulation therapy (PBMT) is a safer alternative solution that uses lasers or other light sources to stimulate therapeutic biological responses including analgesic and anti-inflammatory effects, and also promoting healing and tissue repair. Clinical applications of PBMT have been found in diverse conditions such as neuromuscular pathologies, musculoskeletal pain, dermatological conditions, oral irritation and in different areas in dentistry. The PBMT is considered a non-thermal and non-ablative treatment, since the energy density levels associated with this therapeutic regimen are typically below the threshold associated with irreversible cell damage [3]. Highly penetrating red or near-infrared light must be absorbed by the target cells, specifically by cytochrome C oxidase that lies within mitochondria. A modulation of oxidative stress is then promoted through the release of nitric oxide, which increases adenosine triphosphate production, and the regulation of reactive oxygen species [4].
The successful application of PBMT relies on the choice of optimal treatment parameters from which wavelength, energy density expressed as (dose), number of points of application and their location, and treatment frequency and duration are among the most relevant. They should combine to obtain an effective penetration of light through different skin layers to reach the intended target tissue. For example, the laser can be applied intra- or extraorally and this has implications in the choice of laser wavelength and delivered dose [5]. Since there is a great variability in patient morphological and physiological characteristics, individual laser dosimetry planning may be recommended.
The layers of facial tissues are commonly categorized into five levels, progressing from outer to inner: (1) the dermis, (2) the subcutaneous layer, (3) the musculoaponeurotic layer, (4) the spaces and retaining ligament, and (5) the deep fascia. Bone and periosteum are disregarded since they can be avoided during extraoral PBMT administration, preventing additional dose attenuation. From a photobiological standpoint, simplifying the orofacial tissue layers into skin, fat, and muscle is feasible. Each of these layers displays distinct optical characteristics. Among the three tissues, the skin acts as the most absorptive layer, playing a significant role in light absorption and scattering due to the melanin chromophore.
In the case of PBMT for pain relief, light has to penetrate to as deep as the muscle layer to deploy a therapeutic effect. For this purpose, red and infrared light wavelengths can be used due to their longer mean-free-path. However, darker skin phototypes may still absorb a significant portion of the incident light and cause discomfort or even burn wounds in the patient. On the other hand, reducing the laser power to comply with safety regulations will also reduce the amount of light reaching the target sites, thus compromising the effectiveness of the intended treatment. To model the effect of skin tone, some quantitative assessment method that can be easy to implement in a clinical setting is preferable. Currently, the Fitzpatrick’s skin type classification scale is the preferred method [6]. It indicates not only the individual’s skin color but also their perception of the tendency to burn or tan or the risk of developing skin cancer when exposed to sunlight. Another factor affecting the amount of light delivered to the target tissue is the thickness of the upper layers. Particularly, the thickness of subcutaneous fat has to be taken into account due to its high scattering coefficient at therapeutic wavelengths. A quantitative assessment of skin layers and underlying tissue thicknesses can be conducted using ultrasonography [7] or in vivo Harmonic Generation Microscopy (HGM) [8]. However, in most clinical settings, these instruments may not be available, which makes the evaluation of body mass index (BMI) a much easier and practical tool. Thus, the correlation between BMI and tissue thickness [9] can be useful in laser treatment planning.
Monte Carlo (MC) techniques have been extensively used to model the propagation of light in biological tissues for the purpose of predicting the outcomes of therapeutic procedures and the sensitivity of diagnosis methods [10]. Both therapeutic and diagnostic applications share important methodological aspects with respect to the modeling of skin structure and physiological features, so some attention will be dedicated to them in the following overview.
In a recent paper, an MC analysis of the effect of skin tone and obesity on the photoplethysmography signal in wearable devices used by volunteers, with a BMI range of 20 to 45 and a Fitzpatrick scale between I and VI, was described [11]. They reported significant changes, leading to a loss of the reflected optical signal from visible light-emitting diodes (LEDs) () and near-infrared LEDs (), which penetrate the wrist skin of individuals with increased BMI and skin pigmentation.
Recent experimental studies on the effect of skin color and layer thickness on reflectance, transmittance and skin temperature at two different wavelengths ( and nm) revealed important changes in these quantities [12]. The authors concluded that skin thickness and color must be accounted for when selecting laser parameters such as energy dose and wavelength for successful therapeutic outcomes at the target tissue. It would be interesting to verify if these changes can be predicted using MC simulations since it would help in the development of a validation tool for laser dosimetry.
A validation study of an MC model for extraoral photobiomodulation dosimetry planning was carried out with a limited number of volunteers [13]. Interestingly, the role of an individual’s cheek morphology on laser penetration using Magnetic Resonance Imaging (MRI) and extraoral light transmission measurements at nm was addressed. No appreciable dependence was observed between the measured transmittance and the skin type, while total cheek thickness produced variations of over across the four volunteers.
The primary objective of this study is to develop a PBMT dosimetry model specific to cheek and oral cavity tissues, in external application mode, that can be adapted to patients’ morphological and physiological characteristics, with a focus on skin optical properties and layer structure. The model is built upon three main stages. First, an optical model relates skin optical properties with a widely used phototype classification scale using information from the literature. Tissue structure is modeled according to updated references reporting facial measurements of skin layer thicknesses that can be associated with different BMI values. Second, a laser treatment setup is simulated with a fixed-beam spatial configuration and irradiance targeted at an efficacious dose of that is delivered to the masseter muscle, as reported in previous studies, by varying the treatment duration. Care is taken to limit the incident irradiance to the maximum permissible exposure (MPE) for skin at the selected 660 nm and 808 nm laser wavelengths. The simulations are performed with the Monte Carlo method in order to predict the laser fluence at the muscle layer and compute the treatment duration required to achieve the therapeutic dose for a wide range of skin phototypes and BMIs. Finally, a third stage aims at amplifying the usability of Monte Carlo simulations and assessing the importance of patient-specific parameters to the dosimetry model using machine learning techniques. In this study, a bi-target multiple-regression model, trained with MC simulations, is designed to compute estimates of muscle and epidermal energy density deposition, so that efficacious dose conditions are met and, at the same time, laser safety considerations are warranted. The model is able to predict dose parameters for a new set of features that lie within the parameter space covered by the MC simulations in a much faster but nevertheless reliable way.
2. Materials and Methods
The dosimetry model is based upon empirically derived energy density values that have been found to deploy biological responses when laser light is used in PBMT for pain relief in orofacial tissues. According to [14], an efficacious dose of about at the target tissue, i.e., the muscle in this case, defines the onset of therapeutic effects. Thus, the aim of the planning model is to predict how the laser power and treatment duration time should be adjusted to ensure the right dose for a fixed laser setup (wavelength and spatial profile) and the individual physiological/morphological characteristics of a given patient. While a short treatment duration is preferred for clinical management reasons, care must be taken so as to not exceed the skin maximum permissible exposure (MPE) for the selected wavelength. Here, the guidelines of ANSI z136.1 standard [15] are followed for continuous wave lasers in the red-infrared region:
where () is the incident irradiance and (nm) is the laser wavelength. The correction factor is defined as for nm, and for nm.
2.1. Tissue Structure and Optical Properties
The propagation of light inside a biological tissue depends on its morphological as well as optical/physiological characteristics. Given that the spectral region of interest lies within the therapeutic window, the muscle layer is also included in the simulated tissue model. The facial tissue model consists of four layers, namely, the epidermis, dermis, subcutaneous fat, and muscle.
2.1.1. Skin Thickness
The variability of skin thickness at various facial locations can be assessed using diverse methods, such as in vivo ultrasound analysis, 3D structured light scanning, biopsy, and computerized or histological measurements. Skin thickness is directly influenced by factors like sex, age, and race, impacting both the epidermal and dermal layers. Accurate estimation of topographic skin thickness is crucial for optimizing medical and cosmetic outcomes while minimizing potential adverse events during facial photobiomodulation procedures.
Drawing upon a diverse population sample, a compendium of recent studies has employed the aforementioned techniques to ascertain skin thickness in regions comprising the head, cheek, and neck. Employing these data as a foundation, it has been observed that the average thickness of the epidermis in the cheek region is approximately 0.2 mm, while the dermis has an average thickness of 1.4 mm. Additionally, the subcutaneous layer exhibits an average thickness of 10 mm and 5 mm for the muscle layer in this specific facial area. It becomes feasible to estimate the thickness of each skin layer, as delineated in Table 1, where specific range values can be found, according to [16]. Considering the great variability of thickness values, we chose values consistent with recent publications employing four-layer models, including the muscle layer, targeting dosimetry applications [13,16,17].

Table 1.
Tissue layer structure and optical absorption defining chromophore composition.
2.1.2. Absorption Coefficient
We follow a model for the optical properties described in the work of Steven Jacques [18], where the spectrally dependent absorption coefficient of each layer can be computed given variable amounts of its main absorbing chromophores according to the formula:
where B is the average blood volume fraction, S is the oxygen saturation, W is the fractional water content, F is the fat content, and finally, M is the melanosome volume fraction. Each absorbing chromophore has its own spectral signature, as illustrated in Figure 1, from which the total absorption for each layer can be estimated (Figure 2).
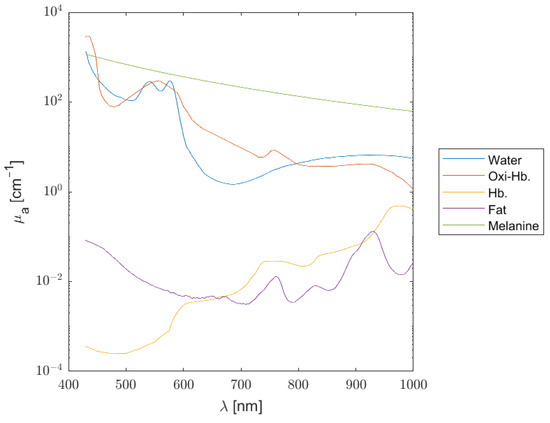
Figure 1.
Absorption coefficient spectra of main chromophores considered in the tissue model.
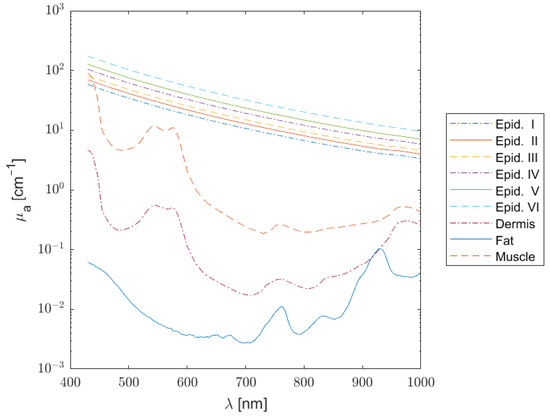
Figure 2.
Absorption coefficient spectra of the epidermis (phototypes I to VI), dermis, subcutaneous fat, and muscle.
The optical absorption coefficient of blood varies with oxygen saturation and can be calculated from its components and , where and in are the deoxy-hemoglogin and oxy-hemoglobin molar extinction coefficients, respectively. Due to the variation in blood fraction in a given tissue, the apparent molar concentrations, and , in also vary. Considering pure blood with a concentration given by , the blood volume fraction B in a tissue is defined by
In turn, the concentration of oxy-hemoglobin relates to oxygen saturation, S, as follows:
Here, we assume a value of for the hemoglobin concentration in the bloodstream and using as the molecular weight of hemoglobin.
Melanin is the most absorbing chromophore present in the epidermis and it is produced by specialized organelles called melanosomes which are present in melanocytes. Human skin color is classified according to the widely used Fitzpatrick scale [6], ranging from I to VI levels, also known as phototypes. The correspondence between the skin phototypes and melanosome volume fraction M inside the epidermis has been studied by several authors, but there is a certain lack of agreement between the adopted models. For example, Colas et al. [19] adapted the results from Karsten et al. [20], where four different melanosome volume fraction classes of values were selected: very fair to fair skin (phototypes I–II) have 1–4%, moderately fair skin types (phototype III) contain about , and dark skin (phototype IV) has about of melanosome volume fraction. On the other hand, some authors referred to a wider span of melanosome fraction values, establishing a correspondence between the six Fitzpatrick classes and the values , , , , , and [11]. In vivo measurements in dorsal forearm and volar arm, using both multiphoton microscopy and spatial frequency domain spectroscopy, gave smaller volume fraction results, between (skin type I) and (skin type VI) [21]. The latter results proved to be consistent, since a comparison between two modern measurement techniques for in vivo melanin inspection were assessed, and as such, they were adopted in this work.
A single dermal layer, comprising the papillary dermis and the reticular dermis, was considered. To simplify the model, the total amounts of oxy-hemoglobin and deoxy-hemoglobin molar concentrations, as well as fat and water fractions, were kept constant with average values as in [18].
Subcutaneous fat was considered a bloodless layer, with variable thickness representing different BMIs, as mentioned above. A small fraction of water, , and a larger part of fat, , were defined in this model.
Finally, a muscle layer with 70% of water and 0.50 µM for both the oxy-hemoglobin and deoxy-hemoglobin molar concentrations was included.
Table 1 shows the chromophore contents of each layer, defining the respective absorption coefficients.
2.1.3. Scattering, Anisotropy, and Refractive Index
The scattering coefficient has an important role in the distribution of fluence within the tissue. The reduced scattering coefficient is defined by the following empirical formula [18]:
with the wavelength in nm. This equation was parameterized by the scaling factor , in units of , and the dimensionless scattering power b. The parameters specifying in each tissue layer are given in Table 2. For the epidermis and dermis, a and b were fitted to the data found in [22]. Fat parameters were based on average values compiled by several authors of [18]. Muscle parameters a and b were fitted to ex vivo data from [23] for a spectral range of 620–1000 nm. The anisotropy coefficient g for epidermis and dermis for wavelengths in the range nm was found in the comprehensive review of [24]:
where a contribution of isotropic scattering at nm is assumed and the wavelength is given in nanometers. The muscle spectral dependence of g assumes a different shape:

Table 2.
Tissue layer structure and other optical parameters: scattering coefficient, anisotropy, and refractive index.
2.2. Monte Carlo Model
The propagation of light in biological tissue can be simulated by different approaches depending on tissue properties for the spectral characteristics of the laser radiation. The red-infrared portions of the spectrum can penetrate deeper into the tissue and be significantly scattered, in which case the Monte Carlo method offers the most versatile and accurate approach to solving the radiative transfer equation. In this method, a large number of photon packets travel through the medium in a random walk fashion and are allowed to suffer the events of scattering, absorption, and reflection/transmission at layer boundaries. Such events occur at a rate that depend on the local optical properties of the medium as well as its morphological structure. Since the early 1980s, many MC algorithms have been developed for different diagnosis and therapeutic applications. The MC implementation used in this study is based on the code MCMatlab, a user-friendly version of Steven Jacques’ “mcxyz.c” [25] developed by Marti et al. for MATLAB users [26].
The geometry of our MC implementation is illustrated in Figure 3. It consisted of a tissue block of wide, and variable thickness (up to cm), obtained by summing up the thickness of each layer presented in Table 1. There were up to voxels for the thickest simulated tissue, where photon packets were launched and tracked while propagating through the tissue. The software ran on a GPU-accelerated configuration using a I7 CPU and a NVIDEA GeForce RTX 4080 graphics card (Nvidia Corporation, Santa Clara, CA, USA).
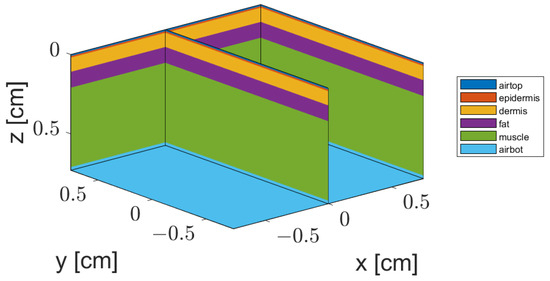
Figure 3.
Illustration of the geometry model of a four-layer tissue structure representing a cheek cross-section. A section on plane () illustrates the simplified skin structure with homogeneous parallel layers.
Data Set
The machine learning predictive model (MLPM) was designed to provide estimates of the epidermal and muscle average fluence. The reason underlying this choice is two-fold: on one hand, it is desirable to assess the treatment times to deliver an efficacious dose to the muscle and its dependence on the individual phototype and BMI; on the other hand, the epidermal energy deposition should be studied as well to make sure that safe levels of laser radiation are employed and no significant temperature rise occurs during the treatment time interval.
According to the model explained in the Tissue Structure and Optical Properties section, a data set representing a range of phototype levels between I and IV and BMI values between 20 and 45 was set up by varying the melanin fraction [21] between and in intervals and letting the fat layer and muscle layer thicknesses [13,16] vary in the ranges 0.1–1.2 cm and 0.2–0.8 cm, with cm spacing, respectively. The data set yielded samples for each simulated wavelength, 660 and 808 nm, corresponding to a total number of 3360 MC simulations obtained in this study. Table 3 presents absorption coefficients for the epidermal layers at the selected wavelengths and median melanin fractions (M) for each Fitzpatrick skin type to give an idea of the influence of skin color on optical properties used in the current work’s simulations.

Table 3.
Epidermis absorption coefficients at wavelengths 660 nm and 808 nm using median melanin fractions (M) for each Fitzpatrick skin type.
2.3. Predictive Model of Average Dose
Several MLPMs were constructed and tested within the scope of this study as multiple-regression problems with three features, (1) melanin fraction, (2) fat thickness, and (3) muscle thickness; and two response variables, epidermal and muscle energy incident fluences. For the purpose of estimating both variables, what could be understood as a bi-target regression problem was, in fact, decomposed into two independent single-target regression problems. Here, predictions of one parameter value from the predictor values were obtained from ground-truth MC simulations with known parameters, as presented in Table 1 and described above. These allowed for the analysis of feature importance, using feature selection algorithms to further simplify the regression procedure. Considering the characteristics of epidermal and muscle fluence plots observed in the preliminary analysis of the MC simulations, the most appropriate candidate MLPM models were Decision Trees for regression and linear regression models. The most promising results were obtained by applying linear regression to the logarithm of epidermal fluence and of muscle fluence. The details of the MLPM approach are described hereafter.
2.3.1. Design of the Predictive Model
The predictive model for each single-target task fits a linear model with a set of coefficients to minimize the residual sum of squares between the observed targets in the data set and the targets predicted by the linear approximation. To train the model, we used LinearRegression from Scikit-Learn [27].
2.3.2. Validation and Testing
The data were divided into a training set () and a test set (). To select optimal parameters and assess model performance during the training phase, 5-fold cross-validation (CV) was performed. The predictive performance was assessed using the training and test sets. For each fluence model j, the corresponding root-mean-squared error () was calculated as follows:
where is the predicted value of the response variable (epidermis or muscle) for sample number i from a given set, and is the corresponding true value, assuming a total of N samples. The mean absolute error () was also evaluated:
The relationship between the predicted and true energy density values was quantified by calculating the coefficient of determination for each single-target regression task :
where is the mean true response variable value. Note that, ideally, should approximate 1 for the best model.
3. Results
3.1. Monte Carlo Simulation Results
A preliminary literature survey of the optical and morphological parameters of a diversity of subject characteristics allowed for the construction of a model of the skin in the orofacial regions suitable for conducting realistic Monte Carlo simulations of laser treatment protocols. An extensive simulation study was conducted for laser light sources with Gaussian cross-sectional distribution, an aperture diameter of cm, and 660 nm and 808 nm laser wavelengths. Incident-laser radiant power and treatment duration were selected in a way that they would deliver a total dose of J at the skin surface, while respecting the maximum permissible exposure (MPE) for each wavelength. The total dose was selected as a reference configuration for a given tissue model ( cm, cm and —Fitzpatrick I), with minimal epidermal melanin influence, where an efficacious dose of would be achieved at the fat/muscle interface. This configuration, combined with the most penetrating wavelength of this study, nm, gives a treatment time of min for a safe laser radiant flux adjusted to , and an incident irradiance of , which is below the skin MPE () for this wavelength. Then, the treatment time was computed using this incident irradiance and the fluence rates at the muscle interface obtained from the MC simulations for each combination of thickness and optical parameters. The procedure described above was replicated for the wavelength 660 nm, where the skin MPE has a lower value (). This led to a laser radiant flux of , and an incident irradiance of for safe exposure levels, increasing the treatment time to 10 min when a total dose of J at the skin surface is to be delivered.
Figure 4 illustrates the fluence rate () and absorbed energy () density distributions for a laser with a wavelength of 808 nm across a cheek tissue section () with the following model parameters: , cm, and cm. The differences between absorbed energy and incident fluence show that the influence of a high absorption at the thin epidermal layer should be analyzed in comparison with a much more translucent but thicker fat layer. Both layers have a high impact in the amount of light that reaches the muscle layer. When the fat layer thickness is cm, the melanin fraction has a high influence on muscle dose.
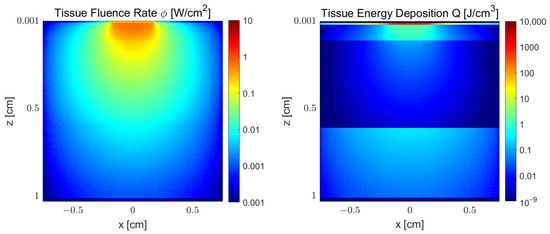
Figure 4.
Monte Carlo simulation results of fluence rate () and absorbed energy () density distribution of wavelength 808 nm in a cheek tissue section with the following model parameters: , cm, and cm.
Fluence (or delivered dose) is compared in Figure 5 and Figure 6 between the beginning of the epidermal and muscle layers for each wavelength and a reference tissue model. The corresponding heat deposition energy density plots are also presented in Figure 7 and Figure 8, for each wavelength. In Figure 6, a variation of over (from about to ) is observed when M varies across to . Similar relative decays are obtained for the remaining fat thickness values. However, fixed melanin values and varying fat thicknesses, between and cm, have a higher impact on muscle dose; when , a variation of over occurs (from about to ), and similar decays are found for the remaining melanin fractions. This happens because the fat layer has a large scattering coefficient and a much larger thickness than the epidermal layer, spreading the laser beam away from the target tissue. The behaviour for 660 nm is similar with respect to fat thickness and melanin variation. However, fluence is already slightly lower at the epidermal top when compared to 808 nm light, since absorption is larger at 660 nm. This difference accentuates as light propagates inside the tissue, increasing the difference in muscle delivered dose. It becomes evident that treatment time will have to be increased when using a 660 nm laser. For example, using a 10 mW laser, 10 min will be necessary to deliver a total dose of 6 J at the skin surface. However, only will be available at the muscle surface for this laser, so the time should be increased to min to achieve a dose of for the onset of PBM effects (or even higher, for analgesia responses). It can be compared to a treatment time of about min when similar conditions are used for a 808 nm wavelength. These simulations, combined with the machine learning prediction model, allow for the computation of the treatment time for any combination of tissue parameters within the simulation domain, as will be described in the following section.
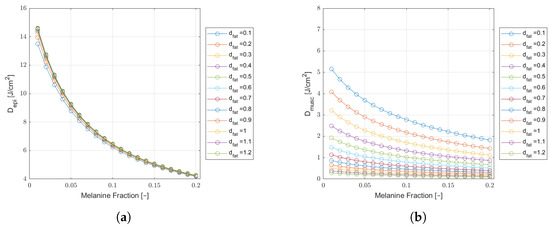
Figure 5.
Monte Carlo simulation results of epidermal (a) and muscle (b) fluence () as a function of melanin fraction, for a wavelength of 660 nm, in a cheek tissue with cm and varying fat thicknesses. Results for a safe incident laser power of and an extraoral delivered dose of J.
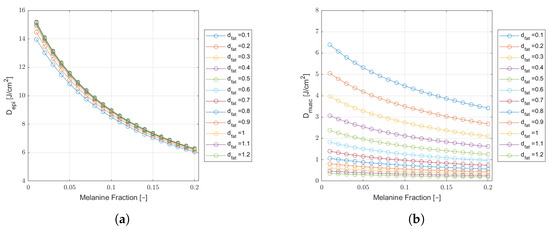
Figure 6.
Monte Carlo simulation results of epidermal (a) and muscle (b) fluence () as a function of melanin fraction, for a wavelength of 808 nm, in a cheek tissue with cm and varying fat thicknesses. Results for a safe incident laser power of and an extraoral delivered dose of J.
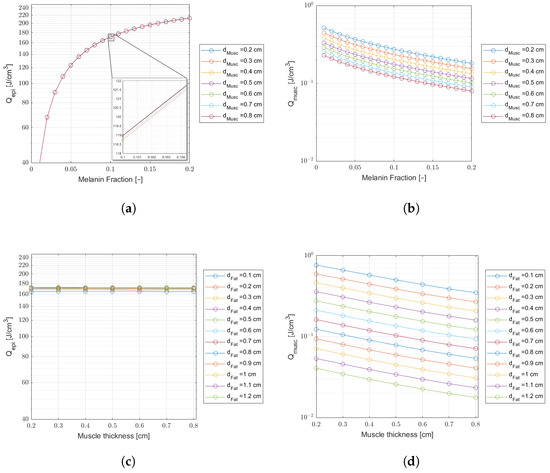
Figure 7.
Comparing laser energy density deposition at the epidermis and muscle for a wavelength of 660 nm and an incident laser power of 10 mW ( J delivered dose). Plots (a,b)—Curves of variable melanin fraction for different muscle thicknesses, and a fat thickness cm. The inset on (a) shows tiny differences in energy density. Plots (c,d)—Curves of variable muscle thicknesses for different fat thicknesses, and a melanin fraction .
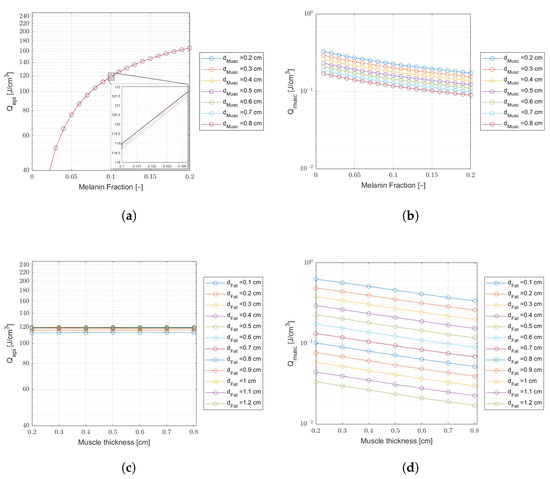
Figure 8.
Comparing laser energy density deposition at the epidermis and muscle for a wavelength of 808 nm, an incident laser power of 30 mW, and a treatment time of min ( J delivered dose). Plots (a,b)—Curves of variable melanin fractions for different muscle thicknesses, and a fat thickness cm. The inset on (a) shows tiny differences in energy density. Plots (c,d)—Curves of variable muscle thicknesses for different fat thicknesses, and a melanin fraction .
3.2. Predictive Model Results
The predictive model has been trained with the data set described above. To illustrate its potential as a tool for dosimetry planning, the average muscle dose was predicted for a range of typical melanin fractions related to phototype levels as listed in Table 3. Fat layer and muscle layer thickness values were selected in the ranges of 0.1–1.2 cm and 0.2–0.8 cm, with cm spacing, respectively, in accordance to the domain of MC simulated values. Figure 9 shows a comparison between the predicted doses and the respective MC simulations for these conditions. The laser power is adjusted according to safety exposure considerations mentioned before (10 min duration for a power of 10 mW at 660 nm, and 3 min duration for a power of 30 mW at 808 nm) and the total delivered dose at skin surface remains at 6 J. The plots represent the variations across the fat thicknesses, since the predictive model revealed that fat thickness is more important than phototype for muscle dose calculation. Epidermal dose is also given for comparison and safety considerations.
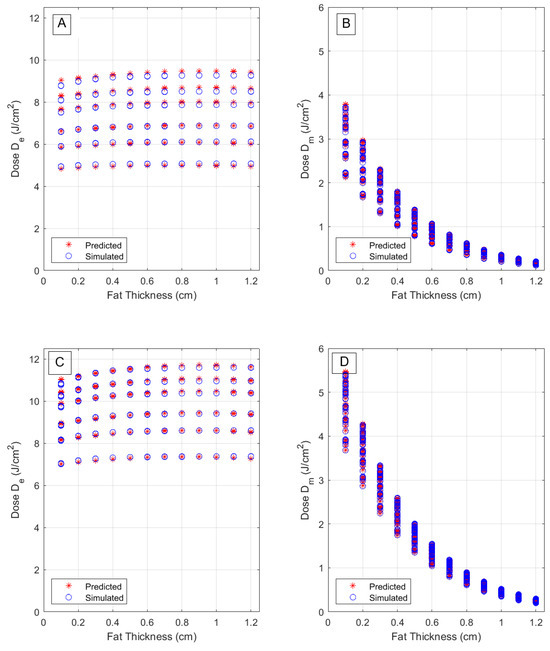
Figure 9.
Comparison of predicted and true fluence at epidermis and muscle layers, for a wavelength of 660 nm (A,B) and for a wavelength of 808 nm (C,D) as functions of fat layer thickness. A J delivered dose is assumed.
These plots also illustrate the overlap between predicted and true fluence values, under different optical and morphological parameters. The separation of different phototypes becomes clear in the epidermal dose (left) plots, where six groups of data, pertaining to six melanin fractions, are separated, but the variation with fat thickness is much slower. A better overlap is observed, however, for the longer wavelength, 808 nm, due to lower absorption coefficients, leading to less sensitivity of the response variable on phototype-related effects. Conversely, there is a much larger dependence on fat thickness in muscle fluence as can be seen in the (right) plot of the same figures. In this case, the epidermal absorption effect becomes diluted in the variations (along the vertical axis) caused by different muscle thicknesses that increase the available fluence, at the fat/muscle interface, due to scattering contributions.
3.2.1. Performance Assessment
The performance results of regression MLPM, described before, are summarized in Table 4. As mentioned before, linear regression was applied to the logarithm of epidermal and muscle fluence rates. The best performing linear regression (LR) models allowed for linear interactions with quadratic terms. Feature importance algorithms revealed that the melanin fraction was most important among the three features included (muscle and fat thickness, and melanin fraction) for predicting epidermal doses, while, as expected, fat thickness was most important when predicting muscle doses. However, removing one of the other two features did not yield consistent and performing models that would perform similarly for both response variables and laser wavelengths. Both training and test RMSEs, as well as the MAE, are low, indicating that overfitting is unlikely to occur. Mean Bias Error was computed from the residuals of the training and test sets to assess bias, yielding very small values of the order of in both cases. Response plots for a subset of the training set (corresponding to melanin fractions given in Table 3) are presented in Figure 9 for wavelengths of 660 and 808 nm. Figure 10A,B present the LR predicted versus the true (MC simulated) fluences, at epidermis and muscle layers, for each wavelength. The muscle dose plots reveal a more consistent structure with the linear model even though the values are practically 1 in both cases.

Table 4.
Summary of results for performance evaluation of the LR model for predicting the epidermis and muscle layers’ delivered doses from at each wavelength.
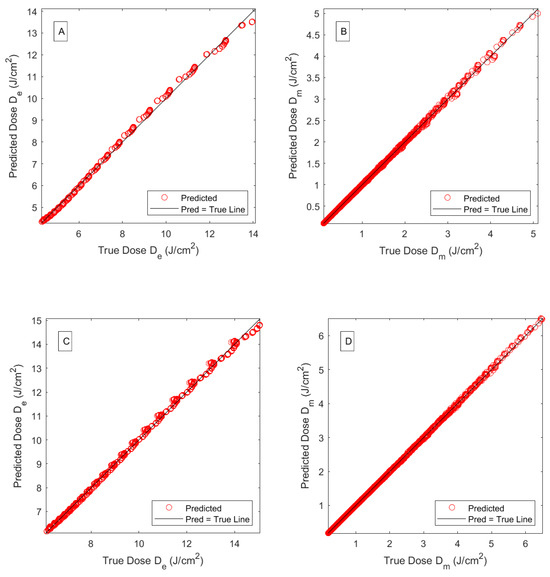
Figure 10.
Predicted versus the actual simulated fluences, as functions of fat layer thickness, at the epidermis and muscle layers (A,B) for a wavelength of 660 nm and (C,D) a wavelength of 808 nm. A J delivered total dose is assumed.
3.2.2. Predicting the Treatment Duration
Figure 11a,b present maps of the delivered dose at the entrance of the muscle layer, for laser wavelengths of 660 nm and 808 nm, respectively. Note that, although laser powers are different across wavelengths for laser safety considerations, the delivered fluences are the same. This is so in order to focus on the elicited biological response, herein, 2 , taken as the onset of PBM, as reported in the literature. That can be achieved by adjusting the treatment time (and incident total dose at the skin surface) in a way that the muscle dose remains equal to the aimed dose. Thus, the conversion of these maps to treatment time maps is quite straightforward, as depicted in Figure 11c,d for an illustration of the time scales involved in this study. Values selected from these maps are presented in Table 5 and Table 6 to exemplify the variation in treatment times with BMI and phototype, respectively.
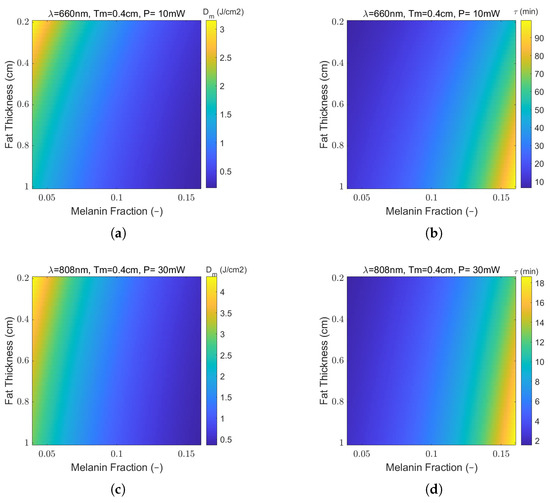
Figure 11.
The effect of variable fat layer thickness and skin color on (a,c) predicted average muscle dose () and (b,d) treatment time (min) at the fat/muscle interface for wavelengths of 660 nm and 808 nm, respectively. A muscle thickness of cm and reference total delivered dose at the skin surface, , are assumed.

Table 5.
Predicted muscle doses (and prediction errors, ) at laser wavelengths of 660 nm and 808 nm for the 6 J total delivered dose reference at the skin surface, using six fat thickness values, ; the fixed melanin fraction ; muscle thickness cm; and adjusted treatment time (and prediction errors, ) for delivering a dose of to the muscle.

Table 6.
Predicted muscle doses (and prediction errors, ) at laser wavelengths of 660 nm and 808 nm for the 6 J total delivered dose reference at the skin surface, using six levels of the Fitzpatrick skin type scale with melanin fractions (M). The fixed fat and muscle thicknesses of cm and cm, respectively, were used, as well as adjusted treatment time (and prediction errors, ) for delivering a dose of to the muscle.
4. Discussion and Outlook
A Monte Carlo-based dosimetry model for extraoral PBMT of temporomandibular disorders was designed and comprehensively evaluated for two laser wavelengths in the red-infrared region, focusing on the effects of tissue thickness and melanin contents on the delivered epidermal and muscle doses. Few clinical and computational studies have addressed the problem of PBMT dosimetry for extraoral applications, under patient-specific characteristics, and many questions remain to be answered. The availability of clinical data is often limited to small samples, with insufficient and/or uneven sample sizes in each BMI or phototype group to yield significant comparisons and meaningful correlations. Computational studies are able to fill some of these gaps and reveal important trends, but only few have addressed the combined effect of tissue thickness and skin pigmentation, and none, to our knowledge, have used a wide range of parameters, the wavelengths studied herein, and a predictive model approach to reduce the computational time and reveal the important features. Performing experimental studies can be lengthy and expensive. Due to its flexibility in generating large samples of hypothetical data, MLPM trained with MC simulations could stay ahead of clinical studies, revealing the important features and help in selecting meaningful explanatory variables to plan experimental work. It is, nevertheless, indispensable to conduct clinical trials to validate the computational approach, and further refine the model by updating the correlations between features and inspecting the impact of additional anthropometric and hemodynamic factors [28]. The model developed in this work constitutes an important stage of a larger project, involving a clinical trial [29], aiming at the development and clinical validation of a personalized laser dosimetry model.
The MC simulations presented herein reveal how much the dose delivered to the muscle can divert from the effective therapeutic value due to patient-specific parameters when adhering to a protocol of a fixed normative value, using a typical total dose of J. It has been found that the dose is higher when using a wavelength of 808 nm compared to 660 nm, but the variation in fat thickness is similar for both wavelengths, accounting for a decrease of over of delivered dose when fat thickness varies form to cm. This behavior does not change with phototype. However, different wavelengths generate different variations in muscle dose with phototype. The decrease in muscle dose is about across the span of simulated melanin fractions for 660 nm of light, while for 808 nm, it only decreases around . Examples of these figures can be easily calculated from Table 5 and Table 6.
Similar effects were observed in experimental studies on the effect of skin color and layer thickness on the transmittance of a skin fold, at the wavelengths 635 and 808 nm [12]. The authors reported that dark skin reduced transmittance for both red and near-infrared light, but the reduction was higher for red light. They also observed that this effect was partially lost when skin thickness increased. Experimental transmittance measurements across the skin fold can be somehow related to our simulated results on muscle fluence, since it is also affected by adipose layer thickness and skin color. However, only hemispherical contributions are measured in the former case, while simulations account for integrated photon contributions from all directions, including the muscle layer underneath. These findings highlight the contributions of epidermal melanin at red wavelengths, an effect that has a higher impact at shorter wavelengths, due to increased absorption and scattering coefficients. Fat also shows a small decrease in a reduced scattering coefficient with wavelength, thus reinforcing this effect.
These results suggest that, provided that the total delivered dose is carefully adjusted, in the function of the selected wavelength, to a median value for individuals of a given BMI range, phototype differences are less likely to produce different clinical results when using a 808 nm laser, while for 660 nm, the dose may have to be increased for darker skin subjects. When considering the biological responses to each wavelengths in terms of pain relief, inflammation reduction, and tissue repair, several studies at the cellular level suggest that, when the effect of photon penetration can be discarded, both red and infrared light produce identical therapeutic responses [30,31]. Therefore, light attenuation due to absorption and path length may be dominant factors when deciding which wavelength to use. For example, it might be advised to opt for an intraoral procedure with red light treatment for a patient with high BMI and phototype for better treatment efficacy, but at the cost of increased patient discomfort. However, when near-infrared laser is available, an extraoral procedure may be recommended for the same patient.
Although the emphasis of this study is on muscle dose for treatment planning, the epidermal delivered dose is also presented. Here, the phototype is more important than BMI, as expected, and although the mean incident dose decreases with melanin fraction due to increasing levels of absorption, leaving less back-scattered for the tissues underneath, the plots presented in Figure 5 and Figure 6 must be interpreted in conjunction with MC simulated heat deposition energy density plots displayed in Figure 7 and Figure 8. In fact, epidermal delivered dose decreases with phototype level, but the absorbed energy increases, which may require taking measures regarding laser duration and frequency to avoid patient discomfort or unwanted biological responses at the epidermal surface, since absorbed energy densities can be above in darker skin types. For example, PBMT relies on reactive oxygen species modulation to activate protective cellular responses and help to reduce oxidative stress. However, absorbed energy densities within the skin are several orders of magnitude higher than at the target tissue, even though the epidermal thickness is only about and heat might be easily dissipated. Nevertheless, since too high a dose of energy can lead to cellular stress or inhibition, according to the biphasic dose–response of PBM [14], the problem of eventual damage to skin tissue should also be carefully addressed in future clinical studies.
In a related study [13], an MC-based dosimetry model was applied to PBMT for OM and was experimentally tested. Their study included measurements of collimated transmittance through the cheek in four volunteers, using a 850 nm light-emitting diode. The authors found a larger effect of tissue thickness when compared to skin phototype, but the latter had a negligible impact on laser fluence rate, contrarily to what was found in our study. A subsequent study from the same authors [17], with a larger sample, reported fluence rate variations of up to , which agree better with our findings regarding the muscle’s delivered dose variations with melanin fraction. However, significant difference separates this study from ours, since the optical model and measurement conditions used in their MC simulation model is not the same. Absorption coefficients are lower than those presented herein, and the relation between optical parameters and melanin concentration remains unclear. The collimated transmitted fluence rate was measured (and simulated) at the cheek mucosa, while in our case, it made more sense to predict the delivered dose (fluence) at the fat/muscle interface, so that the results could be interpreted more easily in relation to the current evidence regarding biological responses and optimum dose selection.
A recent review on PBMT for TMD clinical trials [1] reported laser wavelengths between 635 and 980 nm, fluences in the range of 0.9–300 , and treatment times between 9 s and 15 min in each treatment section. Our results indicate that, while 808 nm light allows for treatment times within 3–5 min across all skin types, and a median fat thickness, which is within the reported range, less penetrating 660 nm light takes much longer to be effective. Only phototypes I and II allow for treatment times under 15 min, rising up to around 90 min for thicker cheek tissues, while for 808 nm, it can take up to 18 min at most. In another study [32], wavelengths ranging from 790 to 905 nm, with low doses of 3 to , showed the best results in TMDs. This study reported laser power in the range of 25 to 120 mW for these doses, but no mention is made to the phototype and laser beam spatial profile, which leads to the question of whether safe levels can be observed. This is a concern especially for darker skin types.
A limitation of the proposed approach could be the absence of statistically modeled data that take real data measured from patients, where the interactions between features can be unveiled. For example, it can be argued that the correlations between fat and muscle layer thicknesses should be considered when comparing the effects of different BMIs. To minimize the uncertainties in this matter, the emphasis was placed on the delivered muscle dose, not the absorbed dose across the whole muscle layer, so that the influence of its thickness can be minimized. However, skin thickness lies in the path of optical photons delivered to the target tissue and is directly influenced by factors like sex, age, and race, impacting both the epidermal and dermal layers. Accurate estimation of topographic skin thickness is crucial for optimizing medical outcomes, while minimizing potential adverse events during facial PBMT procedures. While skin thickness can be measured using diverse methods, such as in vivo ultrasound analysis, 3D structured light scanning, biopsy, and MRI, such measurements will increase treatment time and cost. It is, therefore, important to perform more studies on the relations between skin morphological characteristics and clinical data, particularly with respect to facial regions. The relations between optical properties and hemodynamic variables such as oxygen saturation and hemoglobin were out of the scope of this study. It is, nevertheless, the intent of our team to pursue future investigations on the impact of these variables on clinical outcomes and, eventually, improve the PBMT dosimetry model. This would help to build a database with anthropometric, morphological, and hemodynamic data, combined with the respective clinical outcomes, collected from several patients. It would then be possible to input parameters such as phototype, BMI, age, gender, and results from hemodynamic clinical analysis, and match the appropriate morphological and optical model from the database to yield a personalized dose prediction.
5. Conclusions
The MC simulations revealed the trends for the dependence of laser fluence rate and dose delivered at the muscle on skin color and obesity. BMI had little impact on epidermal heat deposition. Both BMI and phototype had significant impact on muscle dose. However, fat thickness is more important than phototype for muscle dose calculation. For a laser wavelength of 808 nm, muscle dose values decreased over , from to cm of fat thicknesses and considering phototype I, while they decreased less than across phototypes I to IV for median fat/muscle thickness. Similar variations are obtained at 660 nm, but for less penetrating red light, the treatment time (for an efficacious dose of ) can be 4 to 5 times longer, rendering the treatment less practical for extraoral treatments.
The predictive model is much faster than Monte Carlo and allows for the selection of laser parameters, based on patient-specific morphological and physiological characteristics, to ensure therapeutic effectiveness at the target muscle tissue while preventing unwanted biological responses at superficial layers. Once the fluence rate maps have been simulated and used to train the predictive model, at a reference total dose value delivered at the cheek skin surface (), they can be used to adjust the treatment time for patient-specific parameters and other laser powers within safe limits, since the target mean delivered dose D () at the muscle is proportional to the initial simulated value. This is useful for planning the dosimetry in function of the type of desired PBM response, whether it is healing- or pain-related.
In the future, the simulation results will be experimentally tested, keeping in mind the validation of the laser dosimetry planning tool.
Author Contributions
A.C.: Conceptualization, methodology, visualization, investigation, and writing—original draft preparation; L.J.M.: conceptualization, investigation, and writing—review and editing; P.F.: project administration, funding acquisition, visualization, and writing—review and editing; E.F.: conceptualization, methodology, investigation, software, writing—original draft preparation, and supervision. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are very grateful for the support granted by the Research Unit of Fiber Materials and Environmental Technologies (FibEnTech-UBI), through the project reference UIDB/00195/2020, funded by the Fundação para a Ciência e a Tecnologia, IP/MCTES through national funds (PIDDAC) (https://doi.org/10.54499/UIDB/00195/2020).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Farshidfar, N.; Farzinnia, G.; Samiraninezhad, N.; Assar, S.; Firoozi, P.; Rezazadeh, F.; Hakimiha, N. The Effect of Photobiomodulation on Temporomandibular Pain and Functions in Patients with Temporomandibular Disorders: An Updated Systematic Review of the Current Randomized Controlled Trials: Photobiomodulation in temporomandibular disorders. J. Lasers Med. Sci. 2023, 14, e24. [Google Scholar] [CrossRef] [PubMed]
- Cronshaw, M.; Parker, S.; Anagnostaki, E.; Mylona, V.; Lynch, E.; Grootveld, M. Photobiomodulation and oral mucositis: A systematic review. Dent. J. 2020, 8, 87. [Google Scholar] [CrossRef] [PubMed]
- Glass, G.E. Photobiomodulation: The clinical applications of low-level light therapy. Aesthetic Surg. J. 2021, 41, 723–738. [Google Scholar] [CrossRef] [PubMed]
- Dompe, C.; Moncrieff, L.; Matys, J.; Grzech-Leśniak, K.; Kocherova, I.; Bryja, A.; Bruska, M.; Dominiak, M.; Mozdziak, P.; Skiba, T.H.I.; et al. Photobiomodulation—Underlying mechanism and clinical applications. J. Clin. Med. 2020, 9, 1724. [Google Scholar] [CrossRef]
- Treister, N.S.; London, W.B.; Guo, D.; Malsch, M.; Verrill, K.; Brewer, J.; Margossian, S.; Duncan, C. A feasibility study evaluating extraoral photobiomodulation therapy for prevention of mucositis in pediatric hematopoietic cell transplantation. Photomed. Laser Surg. 2016, 34, 178–184. [Google Scholar] [CrossRef]
- Fitzpatrick, T.B. The validity and practicality of sun-reactive skin types I through VI. Arch. Dermatol. 1988, 124, 869–871. [Google Scholar] [CrossRef]
- Jeong, K.M.; Seo, J.Y.; Kim, A.; Kim, Y.C.; Baek, Y.S.; Oh, C.H.; Jeon, J. Ultrasonographic analysis of facial skin thickness in relation to age, site, sex, and body mass index. Ski. Res. Technol. 2023, 29, e13426. [Google Scholar] [CrossRef]
- Liao, Y.H.; Chen, S.Y.; Chou, S.Y.; Wang, P.H.; Tsai, M.R.; Sun, C.K. Determination of chronological aging parameters in epidermal keratinocytes by in vivo harmonic generation microscopy. Biomed. Opt. Express 2012, 4, 77–88. [Google Scholar] [CrossRef]
- Kobayashi, R.; Haga, S.; Umehara, A.; Takakaze, M.; Akatsuka, K.; Nakano, H. Quantitative and qualitative evaluation of the masseter muscle by ultrasonography and correlation with whole body health status. J. Phys. Ther. Sci. 2024, 36, 136–141. [Google Scholar] [CrossRef]
- Flock, S.T.; Patterson, M.S.; Wilson, B.C.; Wyman, D.R. Monte Carlo modeling of light propagation in highly scattering tissues. I. Model predictions and comparison with diffusion theory. IEEE Trans. Biomed. Eng. 1989, 36, 1162–1168. [Google Scholar] [CrossRef]
- Boonya-Ananta, T.; Rodriguez, A.J.; Du Le, V.; Ramella-Roman, J.C. Monte Carlo analysis of optical heart rate sensors in commercial wearables: The effect of skin tone and obesity on the photoplethysmography (PPG) signal. Biomed. Opt. Express 2021, 12, 7445–7457. [Google Scholar] [CrossRef]
- Souza-Barros, L.; Dhaidan, G.; Maunula, M.; Solomon, V.; Gabison, S.; Lilge, L.; Nussbaum, E.L. Skin color and tissue thickness effects on transmittance, reflectance, and skin temperature when using 635 and 808 nm lasers in low intensity therapeutics. Lasers Surg. Med. 2018, 50, 291–301. [Google Scholar] [CrossRef] [PubMed]
- Yaroslavsky, A.N.; Juliano, A.F.; Adnan, A.; Selting, W.J.; Iorizzo, T.W.; Carroll, J.D.; Sonis, S.T.; Duncan, C.N.; London, W.B.; Treister, N.S. Validation of a monte carlo modelling based dosimetry of extraoral photobiomodulation. Diagnostics 2021, 11, 2207. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.Y.; Chen, A.C.H.; Carroll, J.D.; Hamblin, M.R. Biphasic dose response in low level light therapy. Dose-Response 2009, 7. [Google Scholar] [CrossRef] [PubMed]
- ANSI Z136.1—2007; American National Standard for Safe Use of Lasers. Laser Institute of America: Orlando, FL, USA, 2007.
- Weersink, R.; White, R.; Lilge, L. Light dosimetry for low-level laser therapy: Accounting for differences in tissue and depth. In Proceedings of the Mechanisms for Low-Light Therapy II, San Jose, CA, USA, 21 January 2007; SPIE: Bellingham, DC, USA, 2007; Volume 6428, pp. 23–30. [Google Scholar]
- Yaroslavsky, A.N.; Iorizzo, T.W.; Juliano, A.F.; Adnan, A.; Carroll, J.D.; Sonis, S.T.; Duncan, C.N.; London, W.B.; Treister, N.S. Monte Carlo based dosimetry of extraoral photobiomodulation for prevention of oral mucositis. Sci. Rep. 2023, 13, 20425. [Google Scholar] [CrossRef]
- Jacques, S.L. Optical properties of biological tissues: A review. Phys. Med. Biol. 2013, 58, R37. [Google Scholar] [CrossRef]
- Colas, V.; Blondel, W.; Khairallah, G.; Daul, C.; Amouroux, M. Proposal for a skin layer-wise decomposition model of spatially-resolved diffuse reflectance spectra based on maximum depth photon distributions: A numerical study. Photonics 2021, 8, 444. [Google Scholar] [CrossRef]
- Karsten, A.E.; Smit, J.E. Modeling and verification of melanin concentration on human skin type. Photochem. Photobiol. 2012, 88, 469–474. [Google Scholar] [CrossRef]
- Saager, R.B.; Balu, M.; Crosignani, V.; Sharif, A.; Durkin, A.J.; Kelly, K.M.; Tromberg, B.J. In vivo measurements of cutaneous melanin across spatial scales: Using multiphoton microscopy and spatial frequency domain spectroscopy. J. Biomed. Opt. 2015, 20, 066005. [Google Scholar] [CrossRef]
- Salomatina, E.; Jiang, B.; Novak, J.; Yaroslavsky, A.N. Optical properties of normal and cancerous human skin in the visible and near-infrared spectral range. J. Biomed. Opt. 2006, 11, 064026. [Google Scholar] [CrossRef]
- Simpson, C.R.; Kohl, M.; Essenpreis, M.; Cope, M. Near-infrared optical properties of ex vivo human skin and subcutaneous tissues measured using the Monte Carlo inversion technique. Phys. Med. Biol. 1998, 43, 2465. [Google Scholar] [CrossRef] [PubMed]
- Bashkatov, A.N.; Genina, E.A.; Tuchin, V.V. Optical properties of skin, subcutaneous, and muscle tissues: A review. J. Innov. Opt. Health Sci. 2011, 4, 9–38. [Google Scholar] [CrossRef]
- Tran, A.P.; Jacques, S.L. Modeling voxel-based Monte Carlo light transport with curved and oblique boundary surfaces. J. Biomed. Opt. 2020, 25, 2. [Google Scholar] [CrossRef] [PubMed]
- Marti, D.; Aasbjerg, R.N.; Andersen, P.E.; Hansen, A.K. MCmatlab: An open-source, user-friendly, MATLAB-integrated three-dimensional Monte Carlo light transport solver with heat diffusion and tissue damage. J. Biomed. Opt. 2018, 23, 1. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Feng, Z.; Wang, P.; Song, Y.; Wang, H.; Jin, Z.; Xiong, D. Photobiomodulation for knee osteoarthritis: A model-based dosimetry study. Biomed. Opt. Express 2023, 14, 1800–1817. [Google Scholar] [CrossRef]
- Schuler, S.; Campos, M.; Lacerda, A.; Mazzoni, A.; Silva, T.; Silva, F.; Martins, M.; Fernandes, K.; Fonseca, E.; Mesquita-Ferrari, R.; et al. Dosimetry model for photobiomodulation based on anthropometric and hemodynamic variables in patients with orofacial pain post-Covid-19: Study protocol for randomized clinical trial. PLoS ONE 2024, 19, e0309073. [Google Scholar] [CrossRef]
- Almeida-Lopes, L.; Rigau, J.; Amaro Zângaro, R.; Guidugli-Neto, J.; Marques Jaeger, M.M. Comparison of the low level laser therapy effects on cultured human gingival fibroblasts proliferation using different irradiance and same fluence. Lasers Surg. Med. Off. J. Am. Soc. Laser Med. Surg. 2001, 29, 179–184. [Google Scholar] [CrossRef]
- de Lima Luna, C.A.; Guimarães, D.M.; e Silva, E.S.; do Couto, M.F.N.; Oliveira, G.L.; Alves, M.S.A.; Brazão-Silva, M.T.; de Andrade Hage, C. Photobiomodulation in the treatment of oral diseases. Res. Soc. Dev. 2023, 12, e9512338070. [Google Scholar] [CrossRef]
- de França, A.; Borges, A.G.; Daitx, R.B.; Ferrer, R.M.; Dohnert, M.B.; Durigan, J.L.Q. Photobiomodulation in Temporomandibular Dysfunction: A Systematic Review. Muscles Ligaments Tendons J. 2021, 11, 463. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).