BDCOA: Wavefront Aberration Compensation Using Improved Swarm Intelligence for FSO Communication
Abstract
:1. Introduction
- The SLAO system is used as an important module for compensating the losses caused by WA in the FSO;
- In SLAO, the BDCOA is used for searching optimum control signals for the actuators in the DM. The Brownian Motion (BM) and Directional Mutation Scheme (DMS) are integrated into the BDCOA for avoiding the suboptimal solutions and enhancing the search space efficiency while searching for an optimum control signal;
- The wavefront distortions are compensated by selecting the control signals using BDCOA, which further helps enhance the quality of the received signal and coupling efficiency. The enhanced quality of received signals aids in minimizing the BER and RMS.
2. BDCOA Based Optimum Control Signal
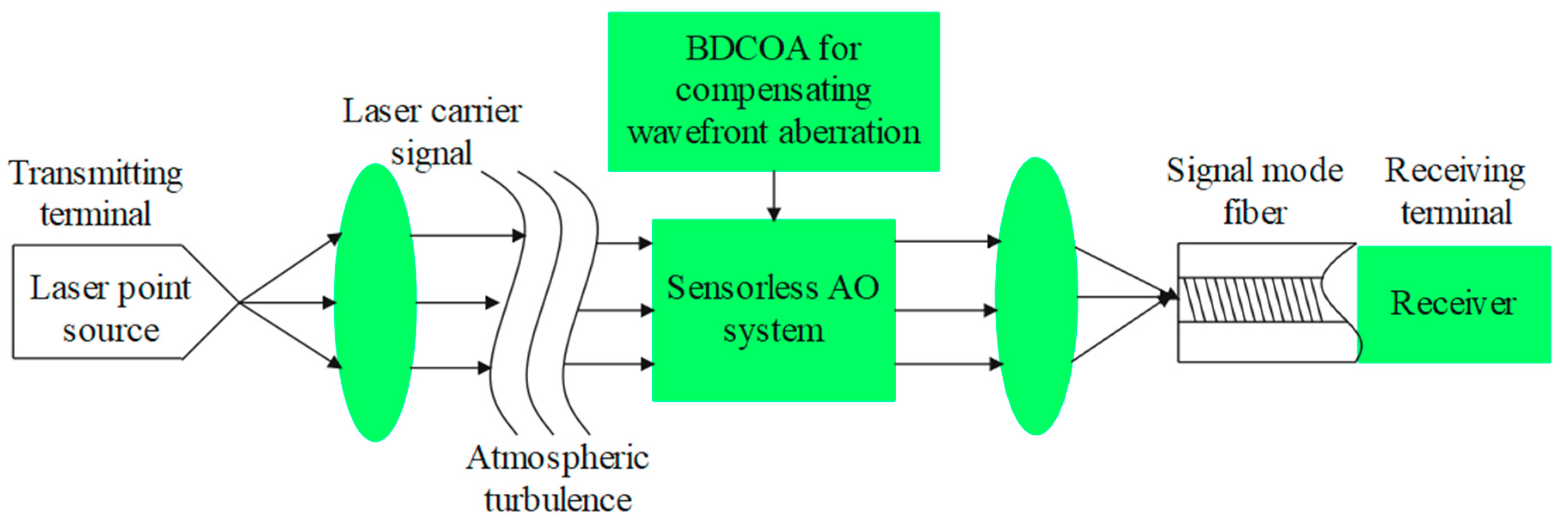
2.1. FSO System Model
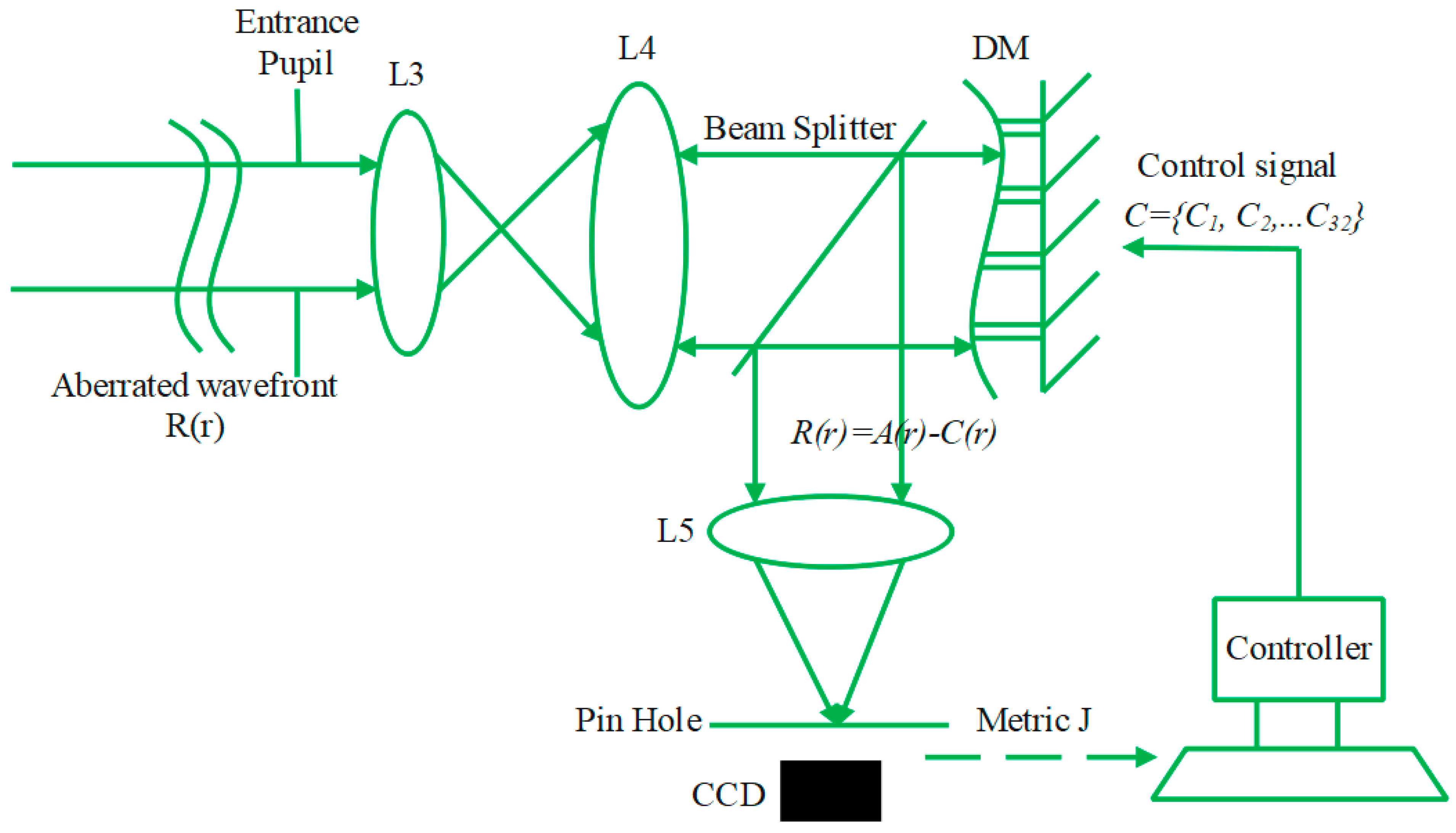
2.2. Model of SLAO System
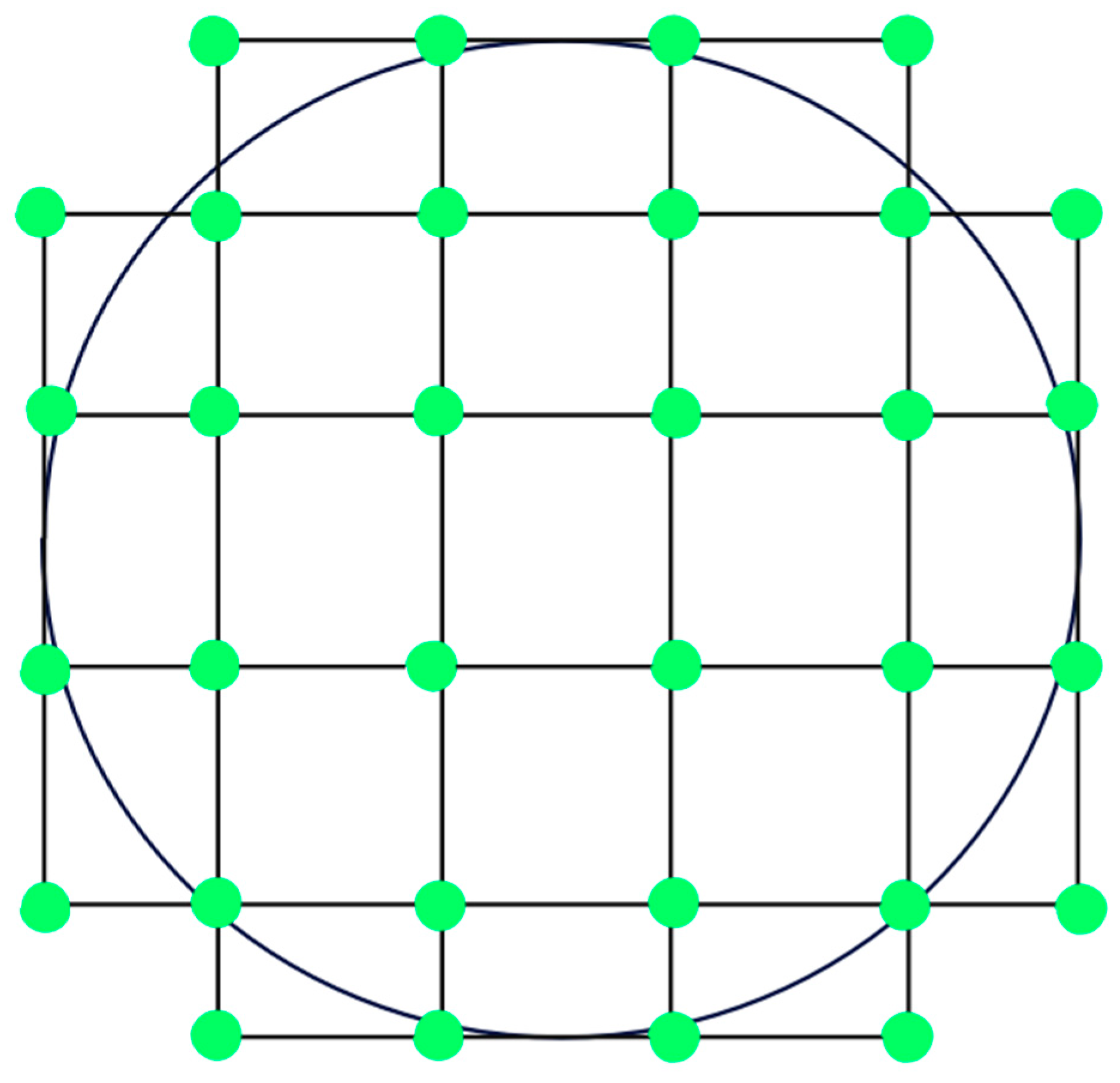
2.3. DM Model
2.4. Wavefront Aberration Using BDCOA
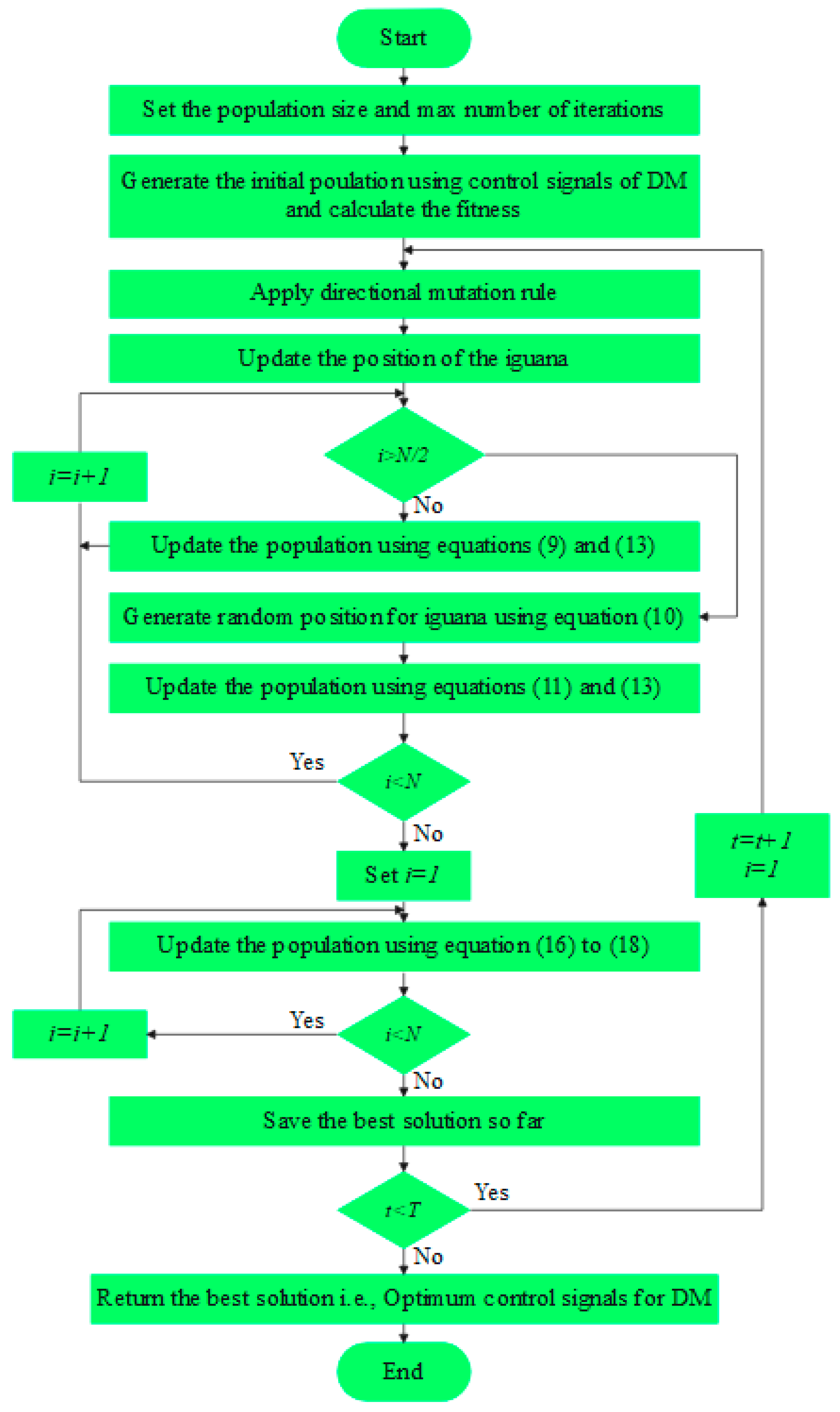
2.4.1. Algorithm Initialization Process
2.4.2. Directional Mutation
2.4.3. Exploration Phase (Hunting and Attacking)
2.4.4. Exploitation Phase (Escaping from the Predators)
3. Simulation Results
3.1. Performance Metrics
3.2. Performance Analysis
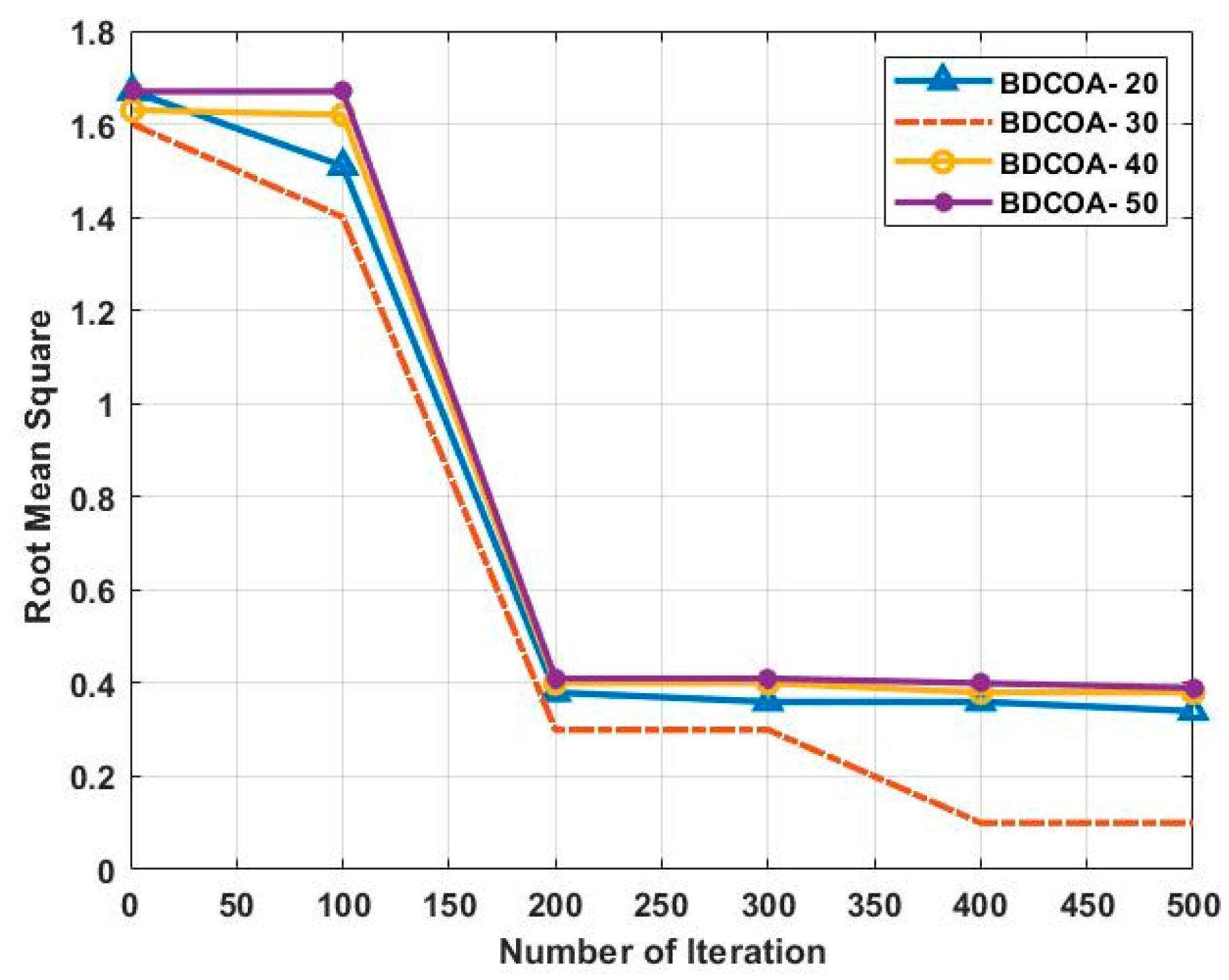
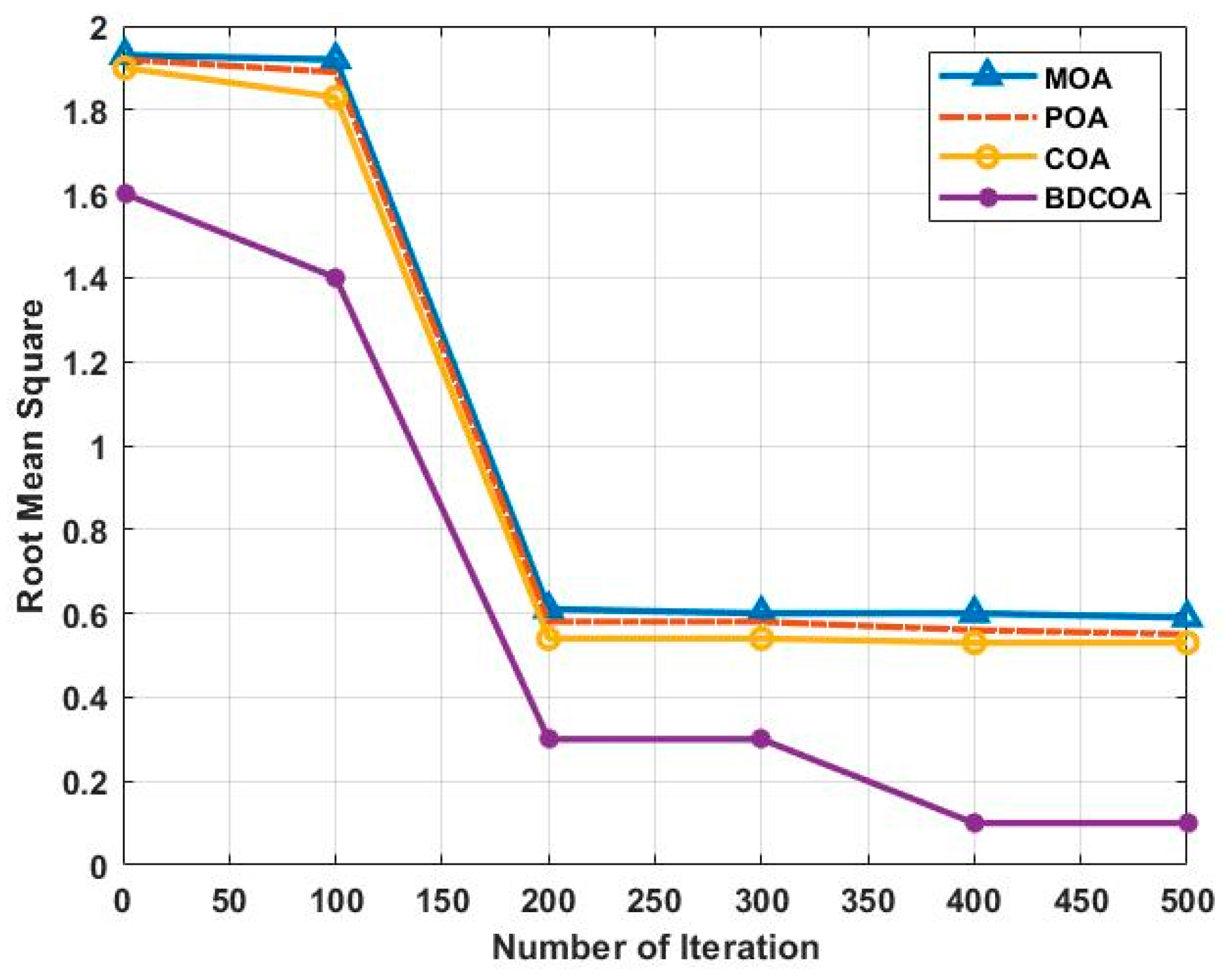
3.3. Root Mean Square
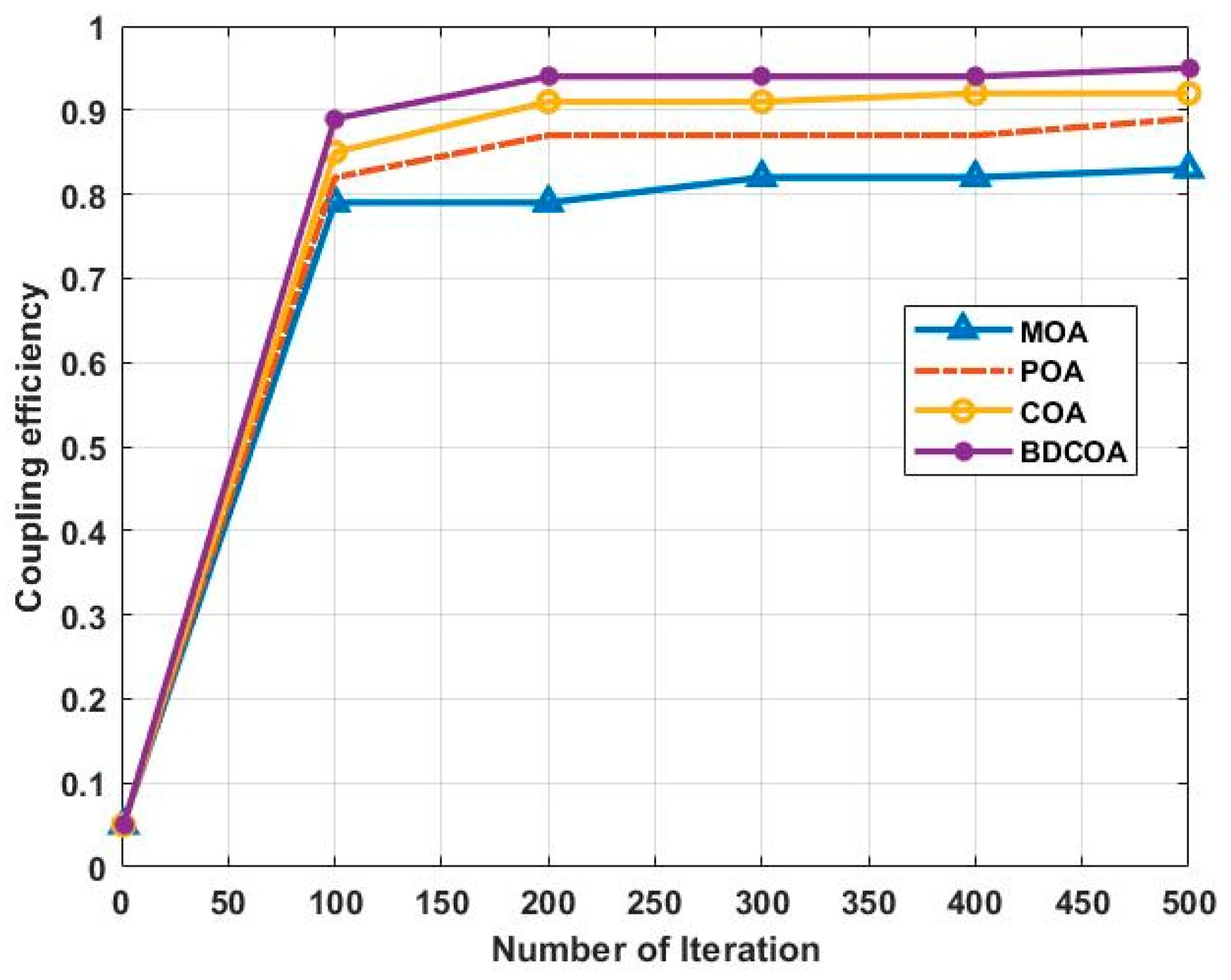
3.4. Coupling Efficiency
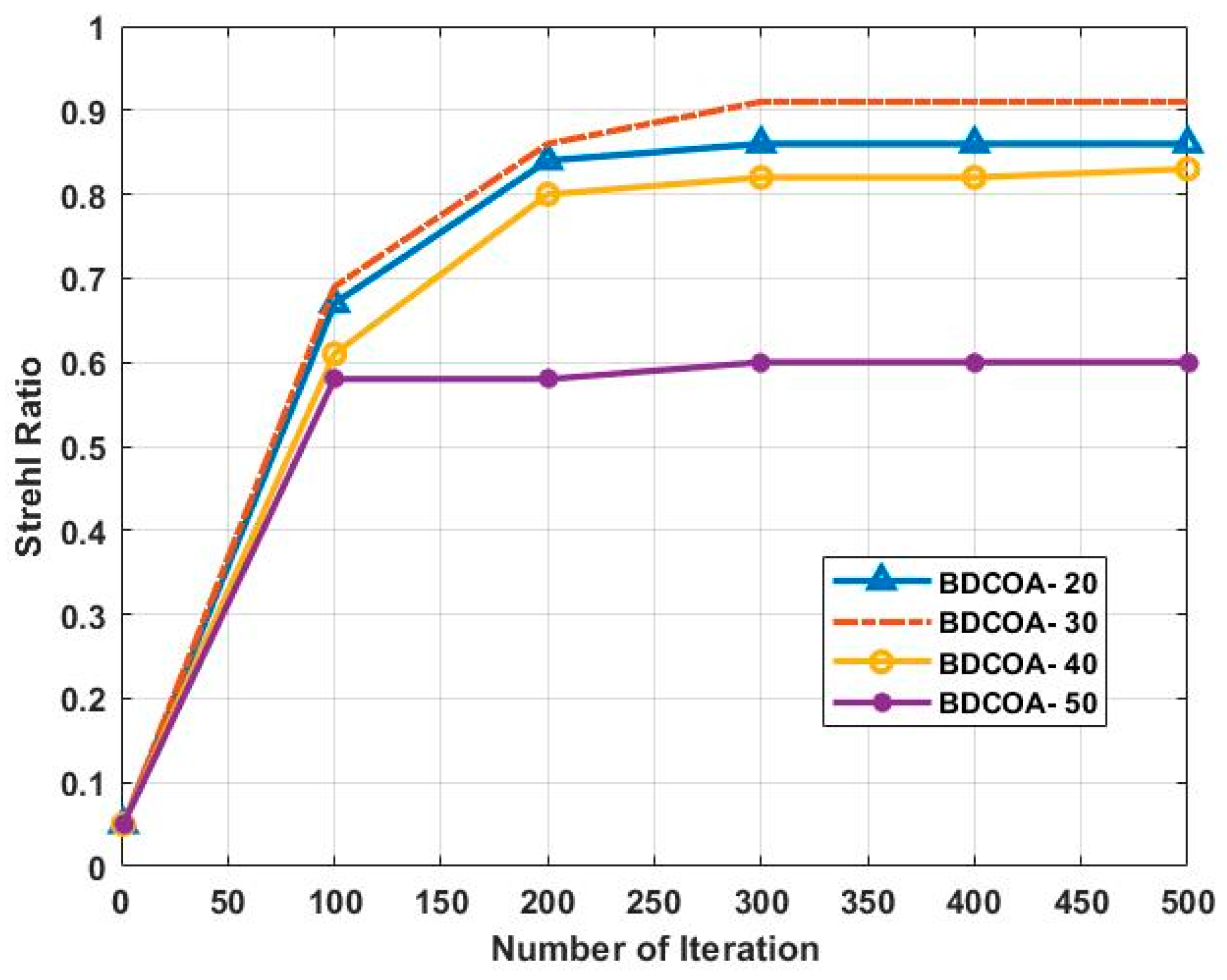
3.5. Strehl Ratio
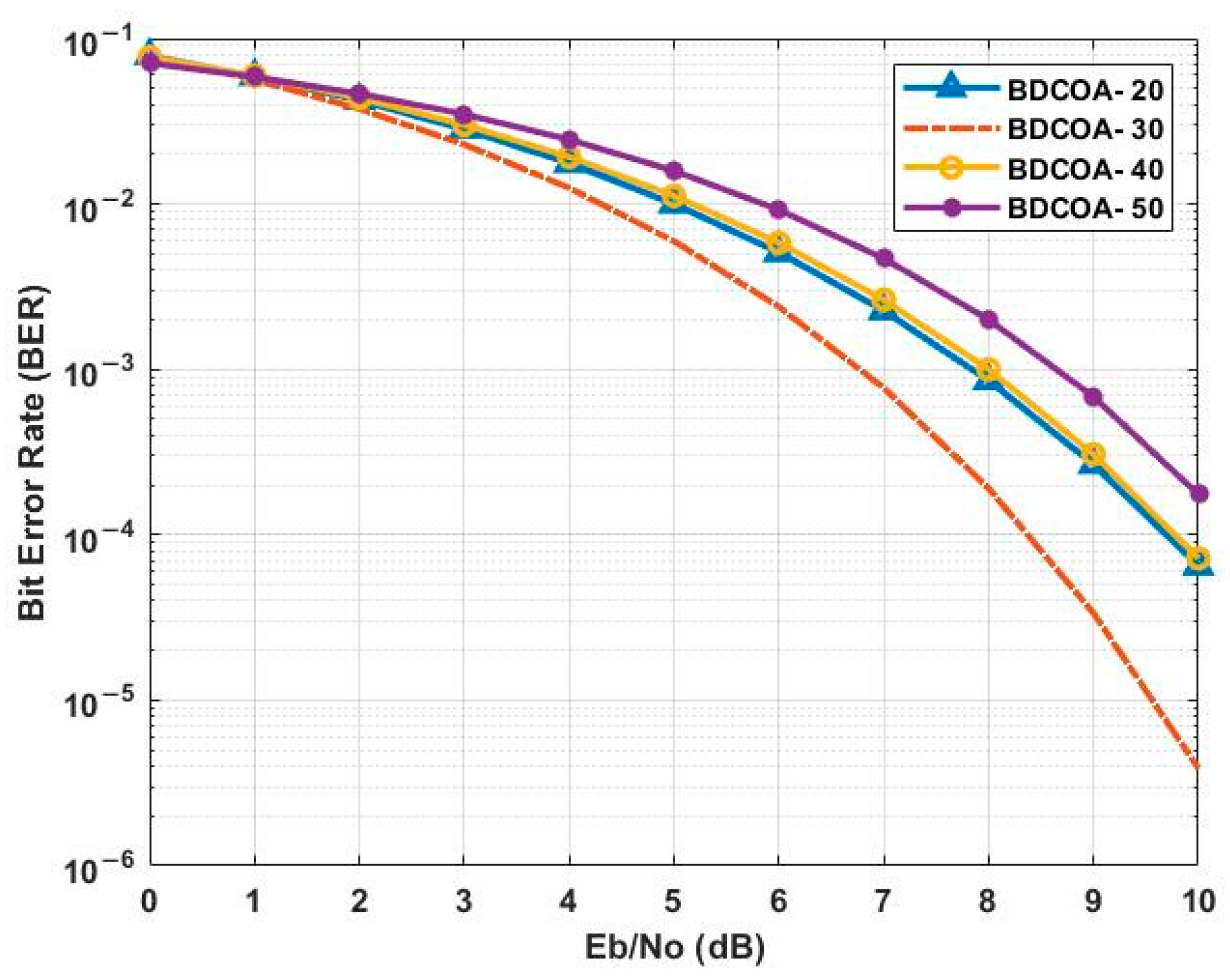
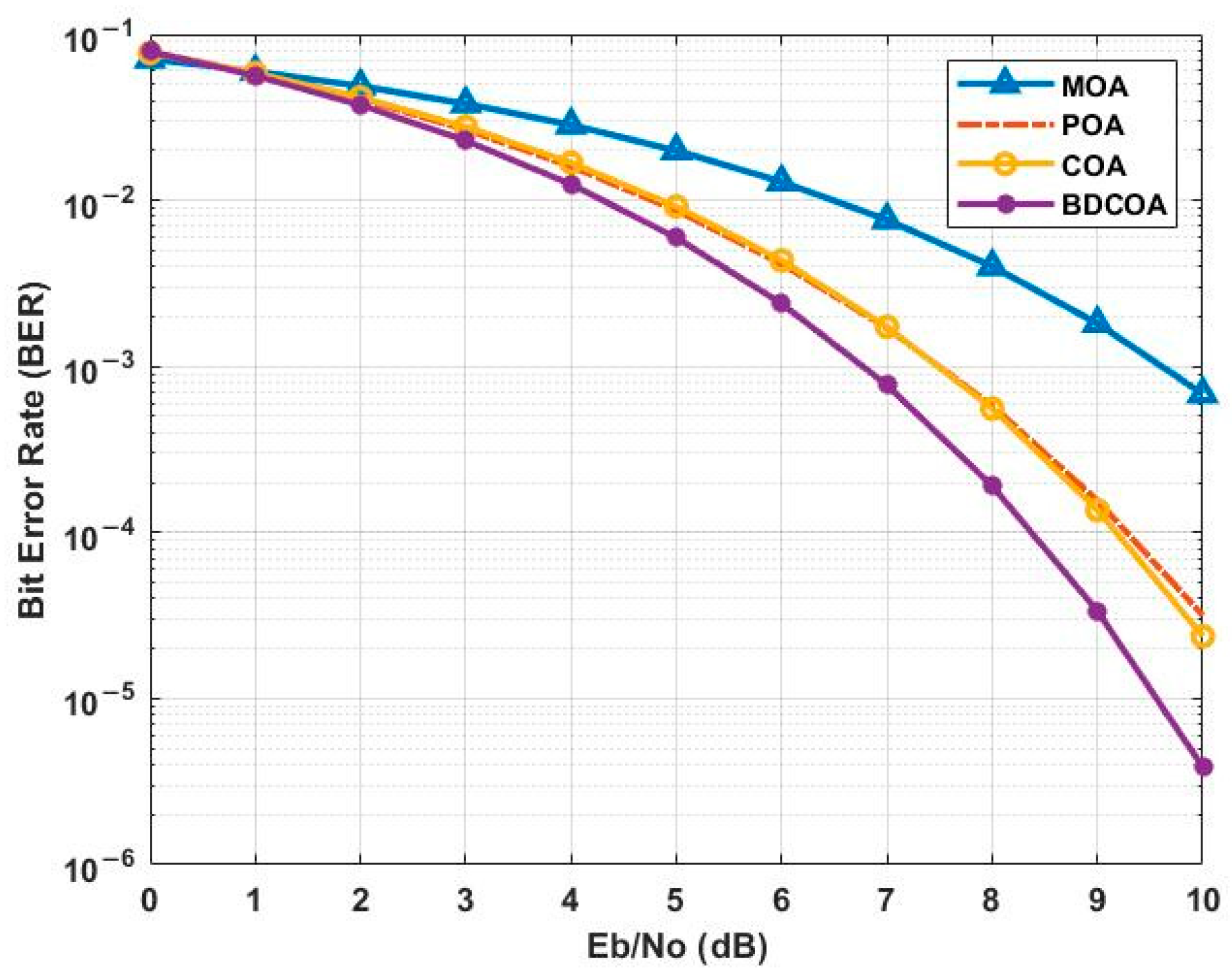
3.6. Bit Error Rate
3.7. Comparative Analysis
3.8. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, W.; Zhang, M.; Wang, D.; Zhan, Y.; Cai, S.; Yang, H.; Zhang, Z.; Chen, X.; Wang, D. Deep Learning-Based Channel Modeling for Free Space Optical Communications. J. Light. Technol. 2023, 41, 183–198. [Google Scholar] [CrossRef]
- Hayle, S.T.; Manie, Y.C.; Yao, C.-K.; Yeh, T.-Y.; Yu, C.-H.; Peng, P.-C. Hybrid of Free Space Optics Communication and Sensor System Using IWDM Technique. J. Light. Technol. 2022, 40, 5862–5869. [Google Scholar] [CrossRef]
- Agarwal, H.; Mishra, D.; Kumar, A. A Deep-Learning Approach for Turbulence Correction in Free Space Optical Communication with Laguerre–Gaussian Modes. Opt. Commun. 2024, 556, 130249. [Google Scholar] [CrossRef]
- Mirza, J.; Aljohani, A.J.; Raza, A.; Iqbal, S.; Ghafoor, S. A Multi-Hop Free Space Optical Link Based on a Regenerative Relay. Alex. Eng. J. 2022, 61, 1459–1467. [Google Scholar] [CrossRef]
- D’Amico, A.A.; Morelli, M. Blind Estimation of Timing Error, Channel Attenuation and Noise Parameters in OOK Free-Space Optical Communications. IEEE Trans. Commun. 2024, 1. [Google Scholar] [CrossRef]
- Mai, V.; Kim, H. Beaconless Angle-of-Arrival Tracking with Improved Receiver Sensitivity and Tracking Precision for Free-Space Optical Communications. Opt. Commun. 2023, 527, 128963. [Google Scholar] [CrossRef]
- Li, M.; Li, Y.; Han, J. Gerchberg–Saxton Algorithm Based Phase Correction in Optical Wireless Communication. Phys. Commun. 2017, 25, 323–327. [Google Scholar] [CrossRef]
- Ata, Y.; Alouini, M.-S. HAPS Based FSO Links Performance Analysis and Improvement with Adaptive Optics Correction. IEEE Trans. Wirel. Commun. 2023, 22, 4916–4929. [Google Scholar] [CrossRef]
- Yu, X.; Xu, G.; Zhang, Q.; Song, Z. Dual-Hop Optical Communication Systems Over Málaga Turbulence Under Pointing Error Impairments With Decode-and-Forward Protocol. IEEE Photonics J. 2022, 14, 7358215. [Google Scholar] [CrossRef]
- Altalbe, A.A.; Khan, M.N.; Tahir, M. Error Analysis of Free Space Communication System Using Machine Learning. IEEE Access 2023, 11, 7195–7207. [Google Scholar] [CrossRef]
- Narayanan, S.S.L.; Devappa, B.S.D.; Pawar, K.; Jain, S.; Venkata Ramana Murthy, A. Implementation of Forward Error Correction for Improved Performance of Free Space Optical Communication Channel in Adverse Atmospheric Conditions. Results Opt. 2024, 16, 100689. [Google Scholar] [CrossRef]
- He, X.; Zhao, X.; Cui, S.; Gu, H. A Rapid Hybrid Wave Front Correction Algorithm for Sensor-Less Adaptive Optics in Free Space Optical Communication. Opt. Commun. 2018, 429, 127–137. [Google Scholar] [CrossRef]
- Amirabadi, M.A.; Kahaei, M.H.; Nezamalhosseni, S.A. Low Complexity Deep Learning Algorithms for Compensating Atmospheric Turbulence in the Free Space Optical Communication System. IET Optoelectron. 2022, 16, 93–105. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, X. BP Artificial Neural Network Based Wave Front Correction for Sensor-Less Free Space Optics Communication. Opt. Commun. 2017, 385, 219–228. [Google Scholar] [CrossRef]
- Cao, J.; Zhao, X.; Li, Z.; Liu, W.; Gu, H. Modified Artificial Fish School Algorithm for Free Space Optical Communication with Sensor-Less Adaptive Optics System. J. Korean Phys. Soc. 2017, 71, 636–646. [Google Scholar] [CrossRef]
- Zheng, J.; Li, X.; Qiang, S.; Wang, Y. Decoding Scheme Based on CNN for Differential Free Space Optical Communication System. Opt. Commun. 2024, 559, 130449. [Google Scholar] [CrossRef]
- Hu, Z.; Li, Y.; Chen, Z.; Benton, D.M.; Ali, A.A.I.; Patel, M.; Lavery, M.P.J.; Ellis, A.D. Aiming for High-Capacity Multi-Modal Free-Space Optical Transmission Leveraging Complete Modal Basis Sets. Opt. Commun. 2023, 541, 129531. [Google Scholar] [CrossRef]
- Li, Z.; Cao, J.; Zhao, X.; Liu, W. Swarm Intelligence for Atmospheric Compensation in Free Space Optical Communication—Modified Shuffled Frog Leaping Algorithm. Opt. Laser Technol. 2015, 66, 89–97. [Google Scholar] [CrossRef]
- Liu, C.; Chen, M.; Chen, S.; Xian, H. Adaptive Optics for the Free-Space Coherent Optical Communications. Opt. Commun. 2016, 361, 21–24. [Google Scholar] [CrossRef]
- Wang, R.; Wang, Y.; Jin, C.; Yin, X.; Wang, S.; Yang, C.; Cao, Z.; Mu, Q.; Gao, S.; Xuan, L. Demonstration of Horizontal Free-Space Laser Communication with the Effect of the Bandwidth of Adaptive Optics System. Opt. Commun. 2019, 431, 167–173. [Google Scholar] [CrossRef]
- Chen, M.; Liu, C.; Rui, D.; Xian, H. Highly Sensitive Fiber Coupling for Free-Space Optical Communications Based on an Adaptive Coherent Fiber Coupler. Opt. Commun. 2019, 430, 223–226. [Google Scholar] [CrossRef]
- Ata, Y.; Gökçe, M.C.; Baykal, Y. Mitigation of Atmospheric Turbulence on up and Downlink Optical Communication Systems Using Receiver Diversity and Adaptive Optics. Opt. Quant. Electron. 2022, 54, 659. [Google Scholar] [CrossRef]
- Peng, J.; Qi, B.; Li, H.; Mao, Y. AS-SPGD Algorithm to Improve Convergence Performance for Fiber Coupling in Free Space Optical Communication. Opt. Commun. 2022, 519, 128397. [Google Scholar] [CrossRef]
- Sridhar, B.; Sridhar, S.; Nanchariah, V. Performance Evaluation of FSO System under Atmospheric Turbulence and Noise. J. Inst. Eng. India Ser. B 2022, 103, 2085–2095. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, L.; Guo, Y.; Cao, J.; Liu, W.; Yang, L. Application of AdamSPGD Algorithm to Sensor-Less Adaptive Optics in Coherent Free-Space Optical Communication System. Opt. Express 2022, 30, 7477. [Google Scholar] [CrossRef] [PubMed]
- Lv, P.-F.; Hong, Y.-Q. Self-Pilot Tone Based Adaptive Threshold RZ-OOK Decision for Free-Space Optical Communications. Photonics 2023, 10, 714. [Google Scholar] [CrossRef]
- Liu, W.; Jin, D.; Shi, W.; Cao, J. Performance Analysis of Coherent Optical Communication Based on Hybrid Algorithm. Opt. Laser Technol. 2022, 149, 107878. [Google Scholar] [CrossRef]
- Li, Z.; Shang, T.; Liu, X.; Qian, P.; Zhang, Y. Advanced Multi-Feedback Stochastic Parallel Gradient Descent Wavefront Correction in Free-Space Optical Communication. Opt. Commun. 2023, 533, 129268. [Google Scholar] [CrossRef]
- Kumar, N.; Khandelwal, V. Compensation of Wavefront Aberration Using Oppositional-Breeding Artificial Fish Swarm Algorithm in Free Space Optical Communication. J. Opt. 2023, 52, 1370–1380. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovský, P. Coati Optimization Algorithm: A New Bio-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Knowl.-Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
- Emam, M.M.; Houssein, E.H.; Samee, N.A.; Alohali, M.A.; Hosney, M.E. Breast cancer diagnosis using optimized deep convolutional neural network based on transfer learning technique and improved Coati optimization algorithm. Expert Syst. Appl. 2024, 255, 124581. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mostafa, R.R.; Hussien, A.G.; Helmy, F. An efficient adaptive-mutated coati optimization algorithm for feature selection and global optimization. Alex. Eng. J. 2023, 85, 29–48. [Google Scholar] [CrossRef]



| Author | Methodology | Advantages | Limitations |
|---|---|---|---|
| Ata et al. [22] | An uplink and downlink communication system was developed by using AO correction in the transmitter and MRC diversity approach in the receiver. | The performance of BER was minimized based on the AO correction and MRC receiver. | Signal distortion was caused during communication because of the failure in performing phase compensation. |
| Peng, J et al. [23] | The convergence in the fiber coupling of FSO was enhanced by using the AS-SPGD. | The incorporation of Staged SPGD was used to enhance the local convergence in FSO. | Reduction of WA was required to be done based on the selection of optimum control signal. |
| Sridhar et al. [24] | The performance of data broadcasting in FSO was examined with different modulation approaches such as MPSK, BPSK, OOK and M-QAM in transmitters and APD in receivers. | The M-PSK was designed for maximizing the data rate to enhance the transmission quality and BER. | The FSO performance in atmospheric turbulence was affected due to small routing error. |
| Zhang et al. [25] | The correction of wavefront was achieved by integrating the Adam from deep learning and AdamSPGD in FSO. | A precise depiction of WA was obtained by utilizing the Zernike polynomial modes. | In communication phase, the signal distortion occurred due to processing of DM with an inappropriate control signal in SLAO. |
| Lv and Hong [26] | An adaptive threshold RZ-OOK decision was developed according to the self-pilot tone to obtain the CSI of FSO. | The power of CSI signal was enhanced by assigning the optimum weight factors to achieve ATD. | In this work, there was a probability of signal distortion occurrence when the WA compensation was not done in FSO. |
| Liu et al. [27] | A hybrid approach of SA with SPGD was developed to perform error correction. | The integration of SA and SPGD reduced the probability of local optimization, supporting the reliability in correction. | Phase compensation was required to be done for further minimizing the errors in communication. |
| Li et al. [28] | The AMFSPGD was presented for improving the correction of WA. | The integration of global and local gradient in AMF-SPGD was used to effectively adjust the search gradient and obtain an optimal value for WA correction. | Corrections in FSO were unstable due to hard max recognition. |
| Kumar and Khandelwal [29] | The WA correction in SLAO system was developed by using OBAFS. | The control parameters selection was utilized to compensate the WA which improved FSO performances. | However, the selection of appropriate control signals was required to be obtained for additionally minimizing the error performances. |
| Parameter | Names/Values |
|---|---|
| Communication channel | Free space |
| Optical power | 10 dBm |
| Modulation | DPSK |
| Number of actuators | 32 |
| Wavelength of laser | 1550 nm |
| Bit rate | 1.25 Gb/s |
| Turbulence Model | Kolmogorov turbulence model |
| Noise | Atmospheric turbulence noise |
| Refractive structure parameter | |
| Length of FSO link | 1000 |
| Performances | Methods | Iterations | ||||
|---|---|---|---|---|---|---|
| 100 | 200 | 300 | 400 | 500 | ||
| RMS | SA-SPGD [27] | 1.65 | 0.9 | 0.45 | 0.2 | 0.15 |
| OBAFS [29] | 1.7 | 0.42 | 0.42 | 0.41 | 0.41 | |
| BDCOA | 1.49 | 0.36 | 0.35 | 0.15 | 0.12 | |
| Coupling efficiency | SA-SPGD [27] | 0.77 | 0.785 | 0.795 | 0.798 | 0.8 |
| OBAFS [29] | 0.87 | 0.93 | 0.93 | 0.93 | 0.93 | |
| BDCOA | 0.89 | 0.94 | 0.94 | 0.94 | 0.95 | |
| SR | OBAFS [29] | 0.66 | 0.83 | 0.86 | 0.86 | 0.86 |
| BDCOA | 0.69 | 0.86 | 0.91 | 0.91 | 0.91 | |
| BER | SA-SPGD [27] | 6.30 × 10−10 | 1.99 × 10−10 | 1.58 × 10−10 | 1.41 × 10−10 | 1.25 × 10−10 |
| BDCOA | 5.21 × 10−10 | 1.71 × 10−10 | 1.49 × 10−10 | 1.23 × 10−10 | 1.07 × 10−10 | |
| Performances | Methods | Iterations | |||
|---|---|---|---|---|---|
| 50 | 100 | 150 | 200 | ||
| SR | AMFSPGD [28] | 0.83 | 0.88 | 0.89 | 0.89 |
| BDCOA | 0.89 | 0.90 | 0.93 | 0.93 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shankarnahalli Krishnegowda, S.; Ganesh, A.K.; Bidare Divakarachari, P.; Shankarappa, V.Y.; Gollara Siddappa, N. BDCOA: Wavefront Aberration Compensation Using Improved Swarm Intelligence for FSO Communication. Photonics 2024, 11, 1045. https://doi.org/10.3390/photonics11111045
Shankarnahalli Krishnegowda S, Ganesh AK, Bidare Divakarachari P, Shankarappa VY, Gollara Siddappa N. BDCOA: Wavefront Aberration Compensation Using Improved Swarm Intelligence for FSO Communication. Photonics. 2024; 11(11):1045. https://doi.org/10.3390/photonics11111045
Chicago/Turabian StyleShankarnahalli Krishnegowda, Suhas, Arvind Kumar Ganesh, Parameshachari Bidare Divakarachari, Veena Yadav Shankarappa, and Nijaguna Gollara Siddappa. 2024. "BDCOA: Wavefront Aberration Compensation Using Improved Swarm Intelligence for FSO Communication" Photonics 11, no. 11: 1045. https://doi.org/10.3390/photonics11111045
APA StyleShankarnahalli Krishnegowda, S., Ganesh, A. K., Bidare Divakarachari, P., Shankarappa, V. Y., & Gollara Siddappa, N. (2024). BDCOA: Wavefront Aberration Compensation Using Improved Swarm Intelligence for FSO Communication. Photonics, 11(11), 1045. https://doi.org/10.3390/photonics11111045






