Wavelength Locking and Calibration of Fiber-Optic Ultrasonic Sensors Using Single-Sideband-Modulated Laser
Abstract
1. Introduction
2. Principle of Operation
2.1. Sideband Locking for Edge-Filter Detection
2.2. Real-Time In Situ Sensor Calibration
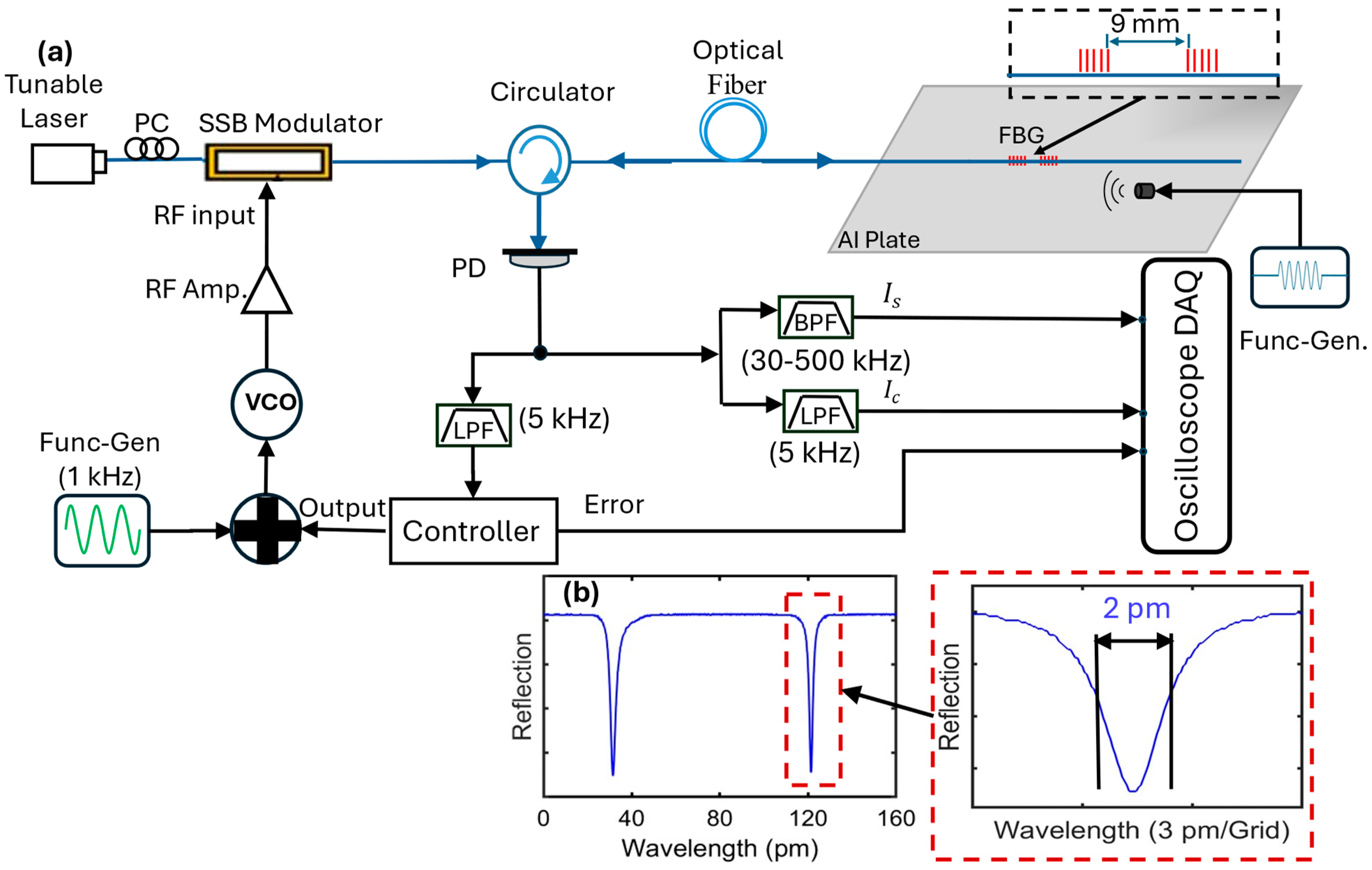
3. Experiment
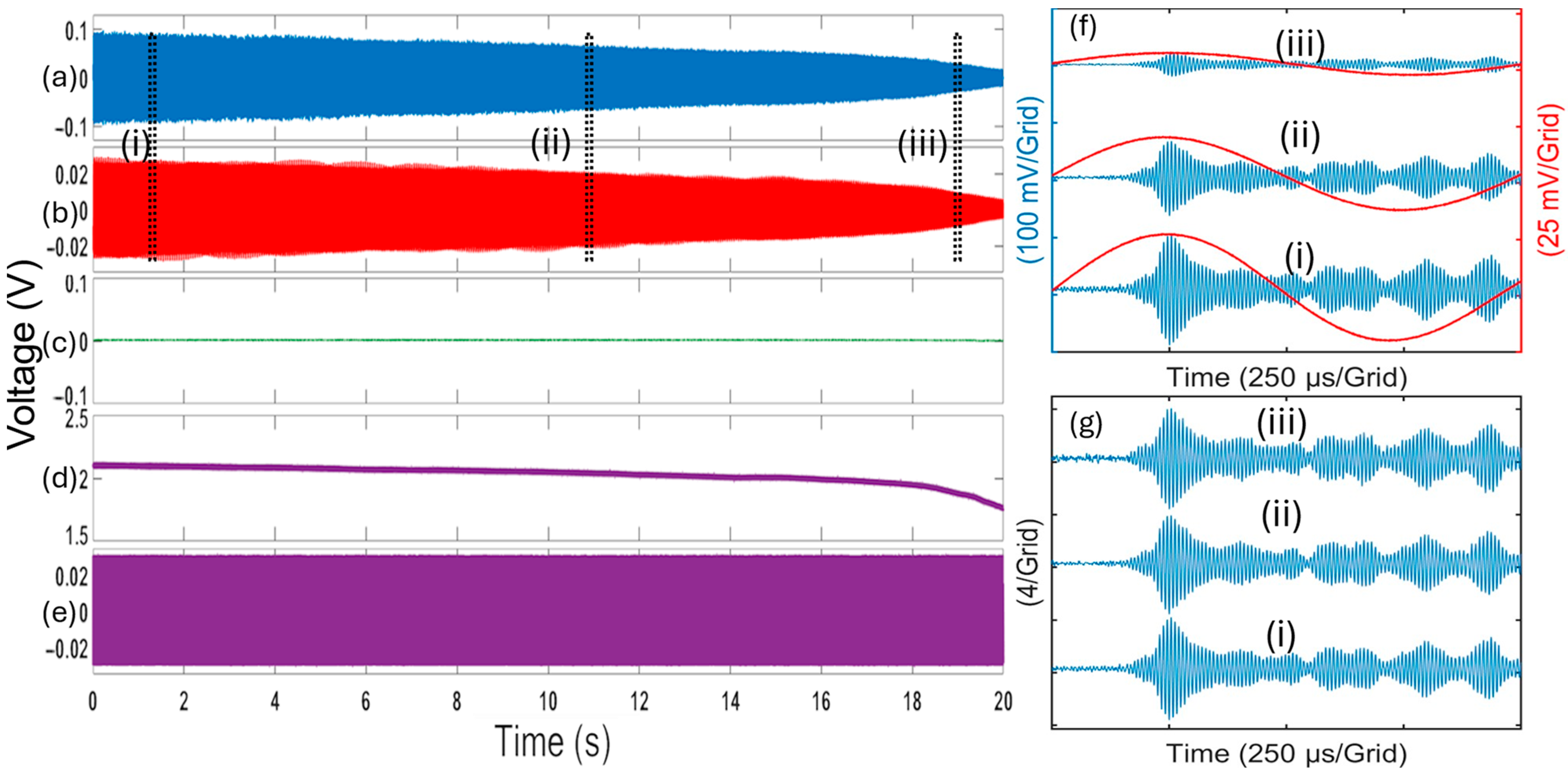
4. Results
4.1. Sideband Locking for Edge-Filter Detection
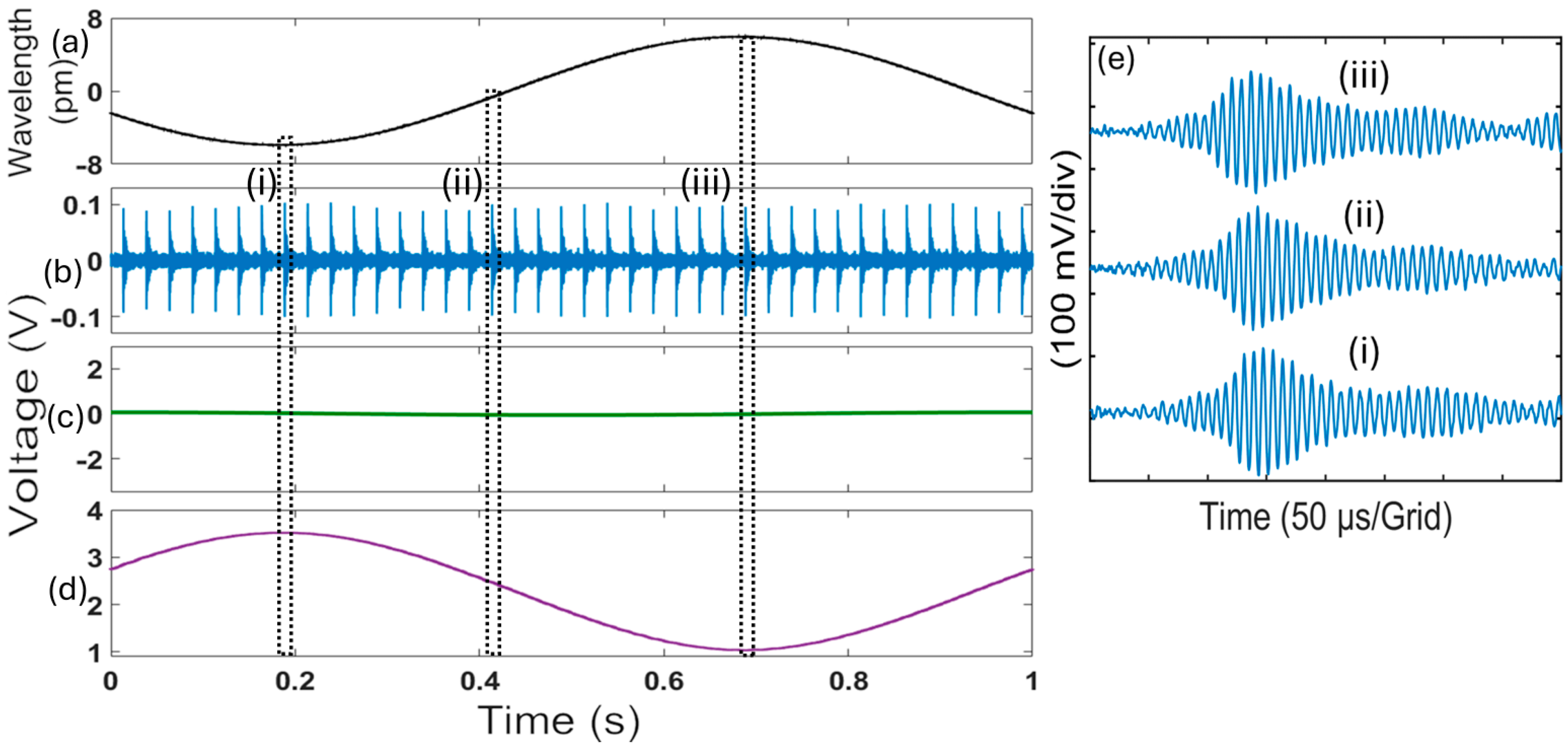
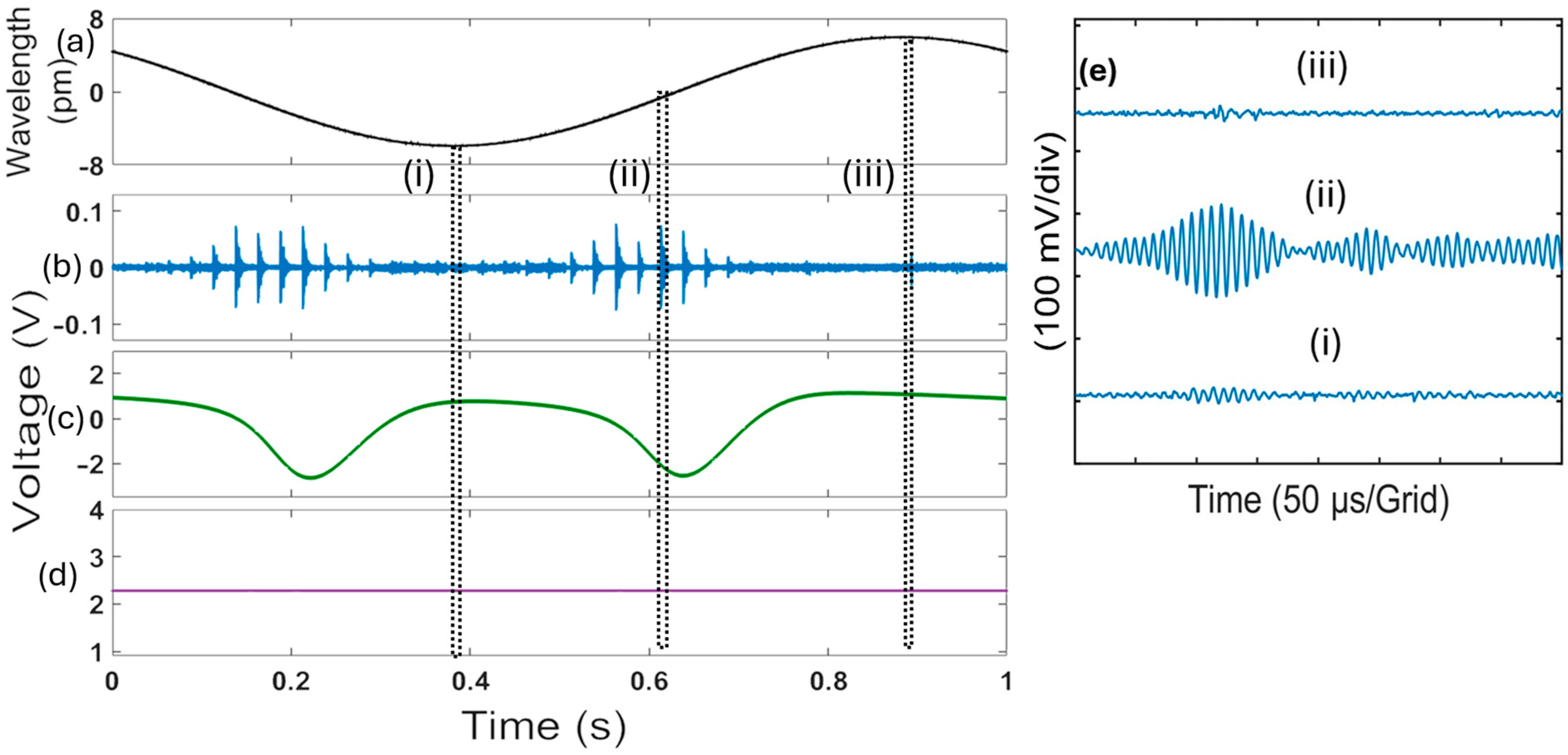
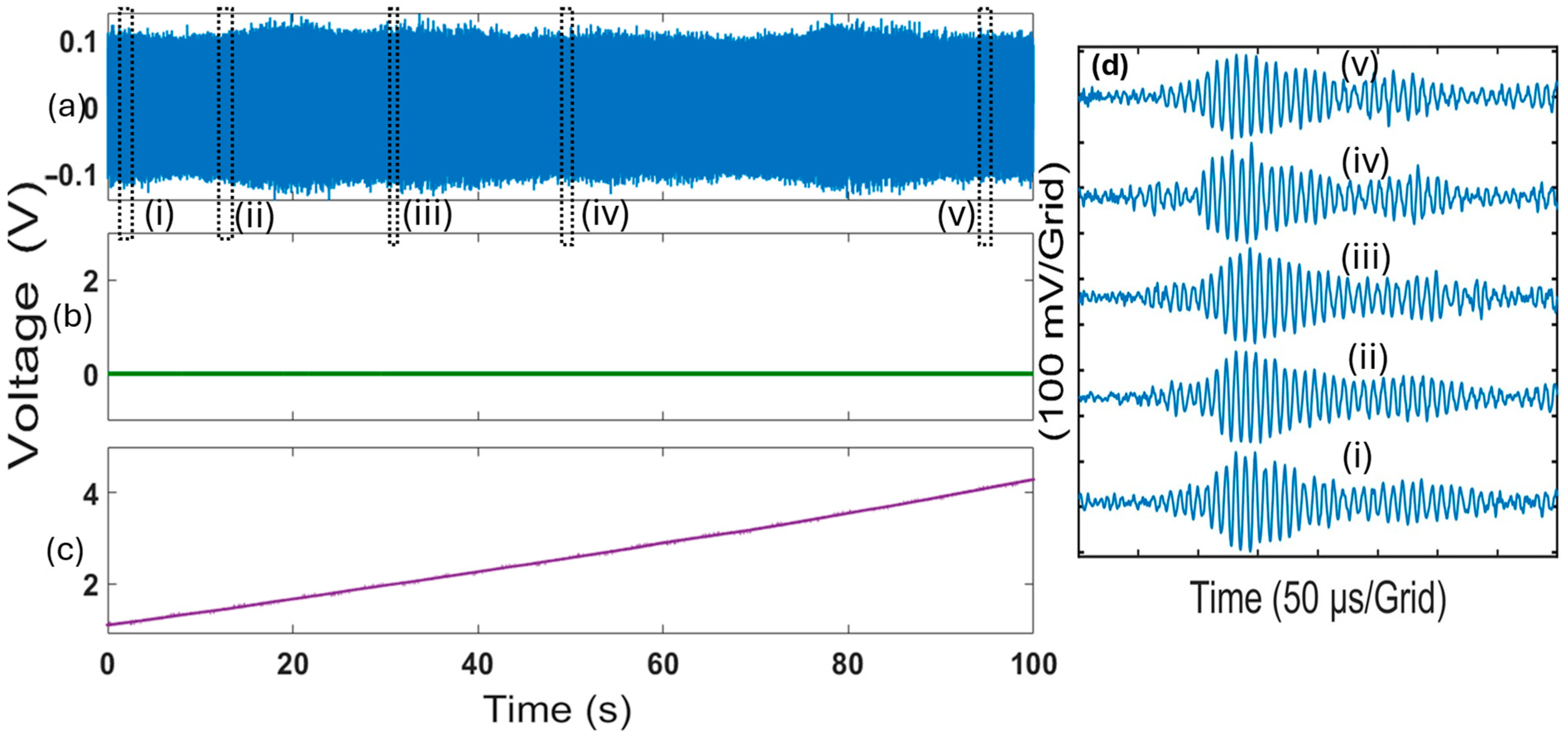
4.2. Real-Time In Situ Sensor Calibration
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Soman, R.; Wee, J.; Peters, K. Optical fiber sensors for ultrasonic structural health monitoring: A review. Sensors 2021, 21, 7345. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Jokerst, J.V. Photoacoustic imaging with fiber optic technology: A review. Photoacoustics 2020, 20, 100211. [Google Scholar] [CrossRef]
- Rosenthal, A.; Razansky, D.; Ntziachristos, V. High-sensitivity compact ultrasonic detector based on a pi-phase-shifted fiber Bragg grating. Opt. Lett. 2011, 36, 1833–1835. [Google Scholar] [CrossRef]
- Wu, Q.; Okabe, Y. High-sensitivity ultrasonic phase-shifted fiber Bragg grating balanced sensing system. Opt. Express 2012, 20, 28353–28362. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, Y.; Luo, X.; Liu, G.; Han, M. Acoustic emission sensor system using a chirped fiber-Bragg-grating Fabry–Perot interferometer and smart feedback control. Opt. Lett. 2017, 42, 631–634. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.; Krishnaswamy, S. Polymer micro-ring resonator integrated with a fiber ring laser for ultrasound detection. Opt. Lett. 2017, 42, 2655–2658. [Google Scholar] [CrossRef]
- Li, A.; Jing, Z.; Liu, Y.; Liu, Q.; Huang, Z.; Cheung, Y.; Zhang, Y.; Han, M.; Peng, W. Quadrature operating point stabilizing technique for fiber-optic Fabry–Perot sensors using Vernier-tuned distributed Bragg reflectors laser. IEEE Sens. J. 2020, 21, 2084–2091. [Google Scholar] [CrossRef]
- Mao, X.; Yuan, S.; Zheng, P.; Wang, X. Stabilized fiber-optic Fabry–Perot acoustic sensor based on improved wavelength tuning technique. J. Light. Technol. 2017, 35, 2311–2314. [Google Scholar] [CrossRef]
- Tsuda, H.; Kumakura, K.; Ogihara, S. Ultrasonic sensitivity of strain-insensitive fiber Bragg grating sensors and evaluation of ultrasound-induced strain. Sensors 2010, 10, 11248–11258. [Google Scholar] [CrossRef]
- Yu, F.; Okabe, Y. Fiber-Optic Sensor-Based Remote Acoustic Emission Measurement in a 1000° C Environment. Sensors 2017, 17, 2908. [Google Scholar] [CrossRef]
- Yu, F.; Okabe, Y.; Wu, Q.; Shigeta, N. Fiber-optic sensor-based remote acoustic emission measurement of composites. Smart Mater. Struct. 2016, 25, 105033. [Google Scholar] [CrossRef]
- Qiao, Y.; Zhou, Y.; Krishnaswamy, S. Adaptive demodulation of dynamic signals from fiber Bragg gratings using two-wave mixing technology. Appl. Opt. 2006, 45, 5132–5142. [Google Scholar] [CrossRef] [PubMed]
- Kirikera, G.R.; Balogun, O.; Krishnaswamy, S. Adaptive fiber Bragg grating sensor network for structural health monitoring: Applications to impact monitoring. Struct. Health Monit. 2011, 10, 5–16. [Google Scholar] [CrossRef]
- Hulme, J.; Doylend, J.; Bowers, J. Widely tunable Vernier ring laser on hybrid silicon. Opt. Express 2013, 21, 19718–19722. [Google Scholar] [CrossRef] [PubMed]
- Barton, J.S.; Skogen, E.J.; Masanovic, M.L.; DenBaars, S.P.; Coldren, L.A. A widely tunable high-speed transmitter using an integrated SGDBR laser-semiconductor optical amplifier and Mach-Zehnder modulator. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 1113–1117. [Google Scholar] [CrossRef]
- Bustillos-Barcaya, M.C.; Rinalde, G.F.; Bulus-Rossini, L.A.; Costanzo-Caso, P.A. Y-branch tunable laser design: Modeling, control and experimental validation. Opt. Laser Technol. 2021, 140, 107040. [Google Scholar] [CrossRef]
- Alshammari, M.; Chu, Y.; Han, M. Real-time in situ phase sensitivity calibration of interferometric fiber-optic ultrasonic sensors. Opt. Lett. 2024, 49, 5336–5339. [Google Scholar] [CrossRef] [PubMed]
- Higuma, K.; Oikawa, S.; Hashimoto, Y.; Nagata, H.; Izutsu, M. X-cut lithium niobate optical single-sideband modulator. Electron. Lett. 2001, 37, 515–516. [Google Scholar] [CrossRef]
- Janner, D.; Tulli, D.; Belmonte, M.; Pruneri, V. Waveguide electro-optic modulation in micro-engineered LiNbO3. J. Opt. A Pure Appl. Opt. 2008, 10, 104003. [Google Scholar] [CrossRef]
- Izutsu, M.; Shikama, S.; Sueta, T. Integrated optical SSB modulator/frequency shifter. IEEE J. Quantum Electron. 1981, 17, 2225–2227. [Google Scholar] [CrossRef]
- Erkılınç, M.S.; Li, Z.; Pachnicke, S.; Griesser, H.; Thomsen, B.C.; Bayvel, P.; Killey, R.I. Spectrally efficient WDM Nyquist pulse-shaped 16-QAM subcarrier modulation transmission with direct detection. J. Light. Technol. 2015, 33, 3147–3155. [Google Scholar] [CrossRef]
- Zhang, L.; Zuo, T.; Mao, Y.; Zhang, Q.; Zhou, E.; Liu, G.N.; Xu, X. Beyond 100-Gb/s transmission over 80-km SMF using direct-detection SSB-DMT at C-band. J. Light. Technol. 2015, 34, 723–729. [Google Scholar] [CrossRef]
- Li, Z.; Erkılınç, M.S.; Shi, K.; Sillekens, E.; Galdino, L.; Thomsen, B.C.; Bayvel, P.; Killey, R.I. SSBI mitigation and the Kramers–Kronig scheme in single-sideband direct-detection transmission with receiver-based electronic dispersion compensation. J. Light. Technol. 2017, 35, 1887–1893. [Google Scholar] [CrossRef]
- Qu, S.; Xu, Y.; Huang, S.; Sun, M.; Wang, C.; Shang, Y. Recent advancements in optical frequency-domain reflectometry: A review. IEEE Sens. J. 2022, 23, 1707–1723. [Google Scholar] [CrossRef]
- Drever, R.W.; Hall, J.L.; Kowalski, F.V.; Hough, J.; Ford, G.; Munley, A.; Ward, H. Laser phase and frequency stabilization using an optical resonator. Appl. Phys. B 1983, 31, 97–105. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Huang, X.; Notcutt, M.; Zanon-Willette, T.; Foreman, S.; Boyd, M.; Blatt, S.; Ye, J. Compact, thermal-noise-limited optical cavity for diode laser stabilization at 1 × 10−15. Opt. Lett. 2007, 32, 641–643. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshammari, M.; Han, M. Wavelength Locking and Calibration of Fiber-Optic Ultrasonic Sensors Using Single-Sideband-Modulated Laser. Photonics 2024, 11, 1063. https://doi.org/10.3390/photonics11111063
Alshammari M, Han M. Wavelength Locking and Calibration of Fiber-Optic Ultrasonic Sensors Using Single-Sideband-Modulated Laser. Photonics. 2024; 11(11):1063. https://doi.org/10.3390/photonics11111063
Chicago/Turabian StyleAlshammari, Mohammed, and Ming Han. 2024. "Wavelength Locking and Calibration of Fiber-Optic Ultrasonic Sensors Using Single-Sideband-Modulated Laser" Photonics 11, no. 11: 1063. https://doi.org/10.3390/photonics11111063
APA StyleAlshammari, M., & Han, M. (2024). Wavelength Locking and Calibration of Fiber-Optic Ultrasonic Sensors Using Single-Sideband-Modulated Laser. Photonics, 11(11), 1063. https://doi.org/10.3390/photonics11111063




