Logic Gate Generation in a Monostable Optical System: Improving the Erbium-Doped Fiber Laser Reconfigurable Logic Operation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Model
2.2. Experimental Set-Up
2.3. Procedures
3. Results
3.1. Numerical Results
3.2. Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bostock, G. Programmable Logic Devices: Technology and Applications; McGraw-Hill Companies: New York, NY, USA, 1988. [Google Scholar]
- Awschalom, D.; Loss, D. Semiconductor Spintronics and Quantum Computation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Brown, S.D.; Francis, R.J.; Rose, J.; Vranesic, Z.G. Field-Programmable Gate Arrays; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 180. [Google Scholar]
- Ditto, W.L.; Murali, K.; Sinha, S. Chaos computing: Ideas and implementations. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2008, 366, 653–664. [Google Scholar] [CrossRef] [PubMed]
- Murali, K.; Sinha, S.; Ditto, W.L.; Bulsara, A.R. Reliable logic circuit elements that exploit nonlinearity in the presence of a noise floor. Phys. Rev. Lett. 2009, 102, 104101. [Google Scholar] [CrossRef] [PubMed]
- Murali, K.; Rajamohamed, I.; Sinha, S.; Ditto, W.L.; Bulsara, A.R. Realization of reliable and flexible logic gates using noisy nonlinear circuits. Appl. Phys. Lett. 2009, 95. [Google Scholar] [CrossRef]
- Murali, K.; Sinha, S.; Bulsara, A.R.; Dari, A.; Ditto, W.L. Noise enhanced logic gates. In Proceedings of the AIP Conference Proceedings, Lake Louise, AB, Canada, 21–24 September 2010; American Institute of Physics: College Park, MD, USA, 2011; Volume 1339, pp. 67–77. [Google Scholar]
- Ditto, W.L.; Miliotis, A.; Murali, K.; Sinha, S.; Spano, M.L. Chaogates: Morphing logic gates that exploit dynamical patterns. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 037107. [Google Scholar] [CrossRef]
- Cafagna, D.; Grassi, G. Chaos-based SR flip–flop via chua’s circuit. Int. J. Bifurc. Chaos 2006, 16, 1521–1526. [Google Scholar] [CrossRef]
- Munakata, T.; Sinha, S.; Ditto, W.L. Chaos computing: Implementation of fundamental logical gates by chaotic elements. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2002, 49, 1629–1633. [Google Scholar] [CrossRef]
- Murali, K.; Sinha, S.; Mohamed, I.R. Chaos computing: Experimental realization of NOR gate using a simple chaotic circuit. Phys. Lett. A 2005, 339, 39–44. [Google Scholar] [CrossRef]
- Campos-Cantón, I.; Pecina-Sánchez, J.; Campos-Cantón, E.; Rosu, H.C. A simple circuit with dynamic logic architecture of basic logic gates. Int. J. Bifurc. Chaos 2010, 20, 2547–2551. [Google Scholar] [CrossRef]
- Diaz-Diaz, I.A.; Campos, E. An Analog Voltage Reconfigurable Logic Gate. In Proceedings of the 2023 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 18–20 October 2023; Volume 7, pp. 1–5. [Google Scholar]
- Murali, K.; Sinha, S.; Kohar, V.; Kia, B.; Ditto, W.L. Chaotic attractor hopping yields logic operations. PLoS ONE 2018, 13, e0209037. [Google Scholar] [CrossRef]
- Murali, K.; Sinha, S.; Kohar, V.; Ditto, W.L. Harnessing tipping points for logic operations. Eur. Phys. J. Spec. Top. 2021, 230, 3403–3409. [Google Scholar] [CrossRef]
- Singh, K.P.; Sinha, S. Enhancement of “logical” responses by noise in a bistable optical system. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2011, 83, 046219. [Google Scholar] [CrossRef] [PubMed]
- Perrone, S.; Vilaseca, R.; Masoller, C. Stochastic logic gate that exploits noise and polarization bistability in an optically injected VCSEL. Opt. Express 2012, 20, 22692–22699. [Google Scholar] [CrossRef] [PubMed]
- Zhong, D.; Yang, G.; Xiao, Z.; Ding, Y.; Xi, J.; Zeng, N.; Yang, H. Optical chaotic data-selection logic operation with the fast response for picosecond magnitude. Opt. Express 2019, 27, 23357–23367. [Google Scholar] [CrossRef] [PubMed]
- Zhong, D.; Yang, G.; Zeng, N.; Yang, H.; Xu, Z.; Xi, J. Optical chaotic flip-flop operations with multiple triggering under clock synchronization in the VCSEL with polarization-preserved optical injection. Opt. Express 2020, 28, 10363–10377. [Google Scholar] [CrossRef] [PubMed]
- Shahi, M.; Khatib, F. Design, simulation and optimization of all-optical NOT/XOR logic gates for use in the new photonic crystal 4 × 2 encoder. Int. J. Nonlinear Anal. Appl. 2021, 12, 1035–1045. [Google Scholar]
- Mehdizadeh, F.; Soroosh, M. Designing of all optical NOR gate based on photonic crystal. Indian J. Pure Appl. Phys. 2016, 54, 35–39. [Google Scholar]
- Moniem, T.A. All-optical digital 4 × 2 encoder based on 2D photonic crystal ring resonators. J. Mod. Opt. 2016, 63, 735–741. [Google Scholar] [CrossRef]
- Kouddad, E.; Naoum, R. Optimization of an all-optical photonic crystal NOT logic gate using switch based on nonlinear Kerr effect and ring resonator. Sens. Lett. 2020, 18, 89–94. [Google Scholar] [CrossRef]
- Jindal, P.; Abou Houran, M.; Goyal, D.; Choudhary, A. A review of different techniques used to design photonic crystal-based logic gates. Optik 2023, 280, 170794. [Google Scholar] [CrossRef]
- Afanador Delgado, S.M.; Echenausía Monroy, J.L.; Huerta Cuellar, G.; García López, J.H.; Reátegui, R.J. Implementation of logic gates in an erbium-doped fiber laser (EDFL): Numerical and experimental analysis. Photonics 2022, 9, 977. [Google Scholar] [CrossRef]
- Pisarchik, A.N.; Kir’yanov, A.V.; Barmenkov, Y.O.; Jaimes-Reátegui, R. Dynamics of an erbium-doped fiber laser with pump modulation: Theory and experiment. JOSA B 2005, 22, 2107–2114. [Google Scholar] [CrossRef]
- Gupta, N. Logic gates based on optical transistors. J. Opt. Commun. 2024, 44, s367–s377. [Google Scholar] [CrossRef]
- Murali, K.; Rajasekar, S.; Aravind, M.V.; Kohar, V.; Ditto, W.; Sinha, S. Construction of logic gates exploiting resonance phenomena in nonlinear systems. Philos. Trans. R. Soc. A 2021, 379, 20200238. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Liu, C.; Fang, Y.; Zhou, J.; Glasser, R.T.; Chen, L.; Jing, J.; Zhang, W. Optical logic gates using coherent feedback. Appl. Phys. Lett. 2012, 101, 191113. [Google Scholar] [CrossRef]




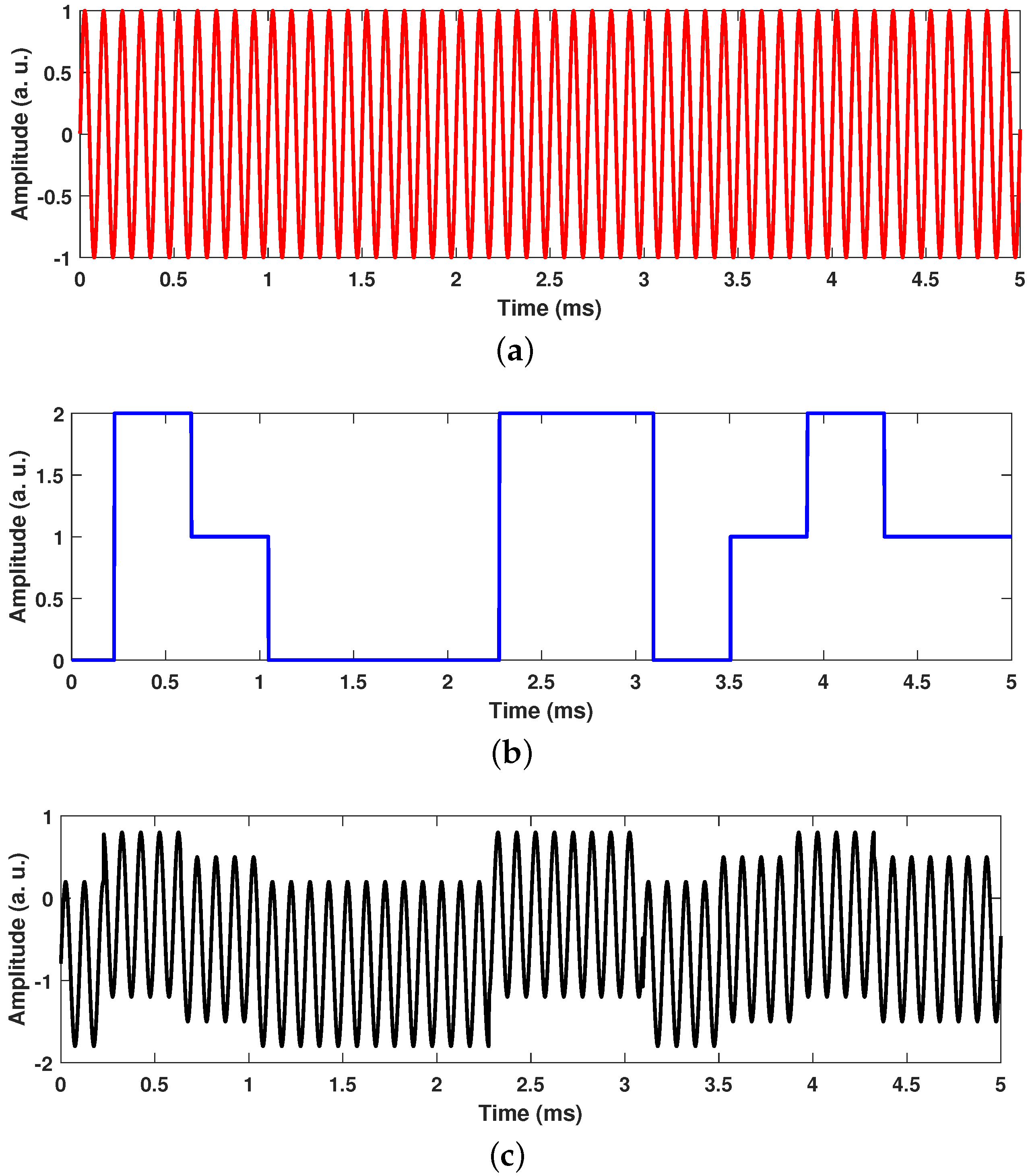
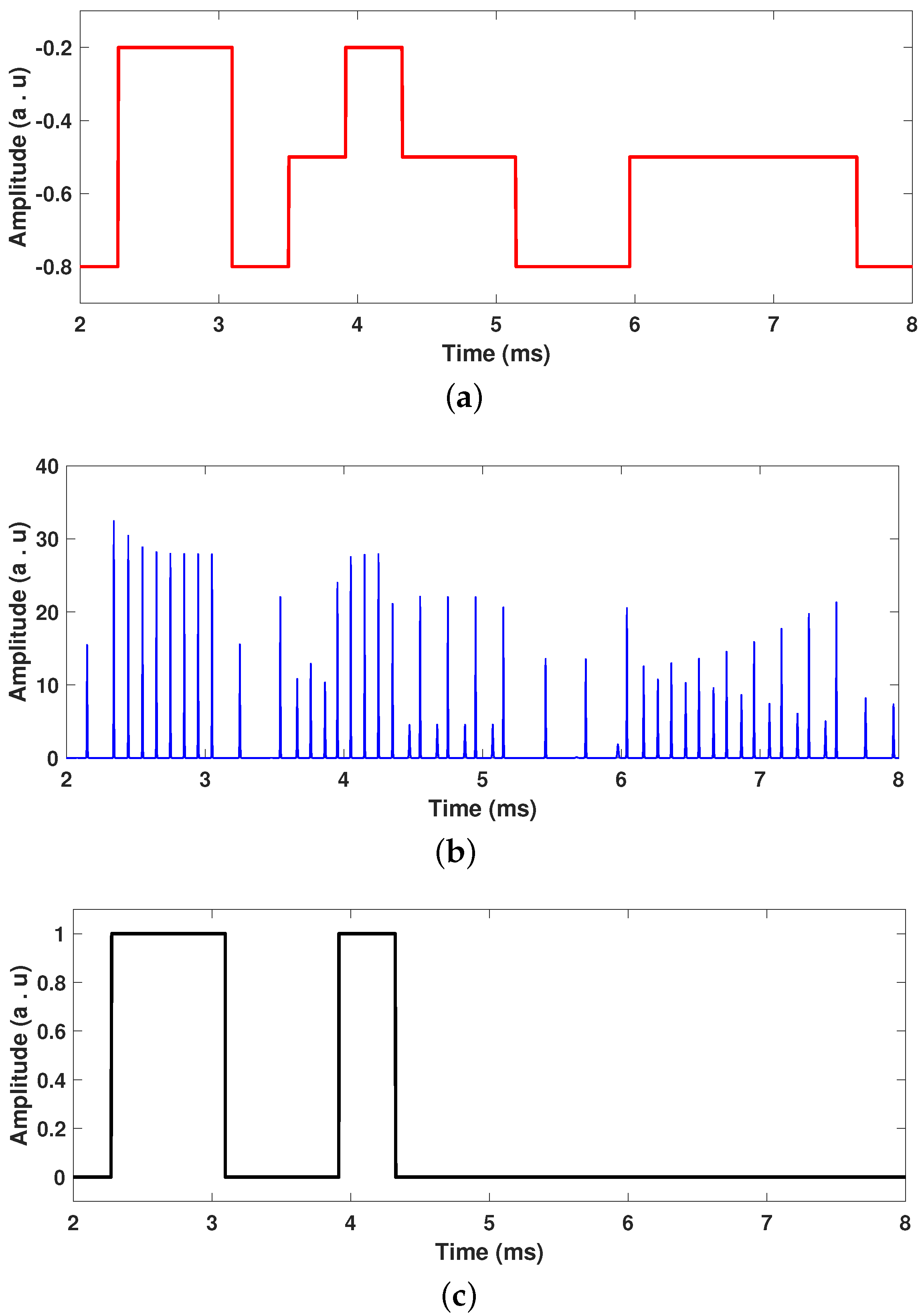




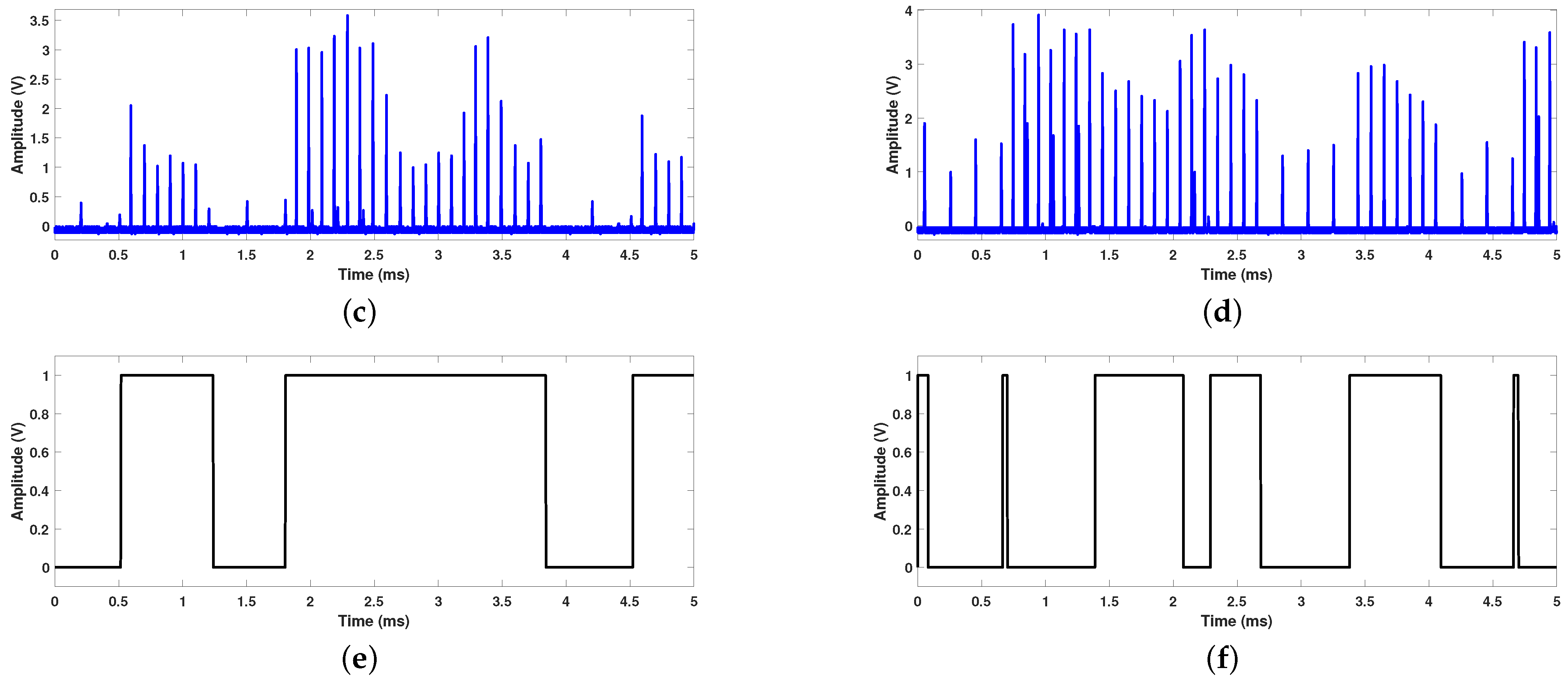
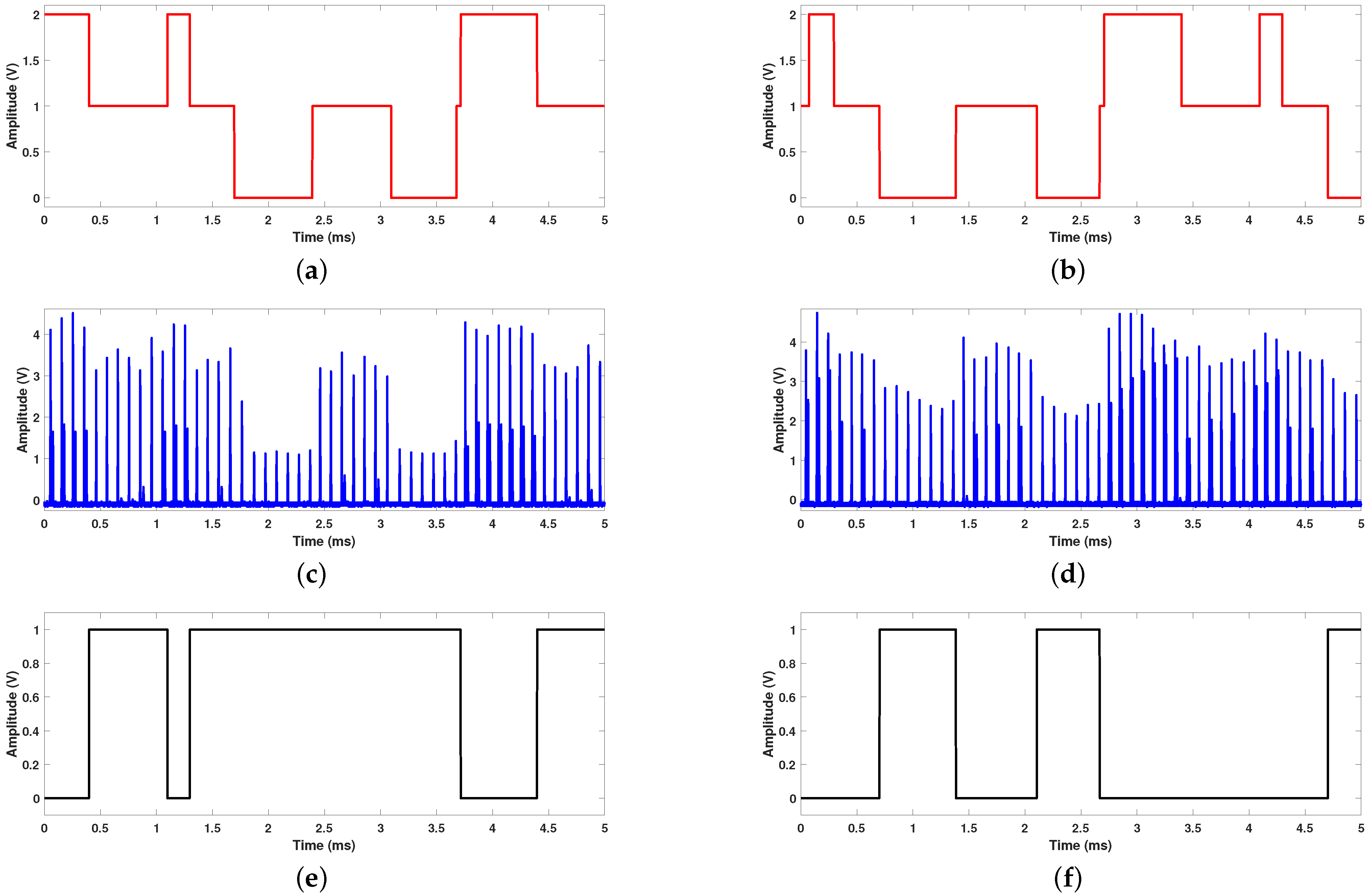
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| a | b | ||
| c | 0.016 | d | |
| e | 506 | 0.307 | |
| 0.615 | −18 |
| DC (a.u.)/ (a.u.) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
|---|---|---|---|---|---|---|
| −0.8 | NG | AND | AND | XOR | XOR | XOR |
| −0.7 | NG | AND | OR | XOR | XOR | XOR |
| −0.6 | AND | OR | XOR | XOR | XOR | NG |
| −0.5 | OR | OR | XOR | XOR | NG | NG |
| −0.4 | NG | NAND | NAND | NOR | NOR | NOR |
| −0.3 | NG | NAND | NOR | NOR | NOR | NOR |
| DC(V)/ | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
|---|---|---|---|---|---|---|---|---|---|
| −0.5 | NG | NG | NG | NG | NG | NOR | NOR | NOR | NOR |
| −0.4 | NG | NG | NG | NOR | NG | NOR | NOR | NOR | NOR |
| −0.3 | NG | NOR | NOR | NOR | NOR | NOR | NOR | NG | NG |
| −0.2 | NG | NAND | NAND | NAND | XOR | NG | NG | NG | NG |
| −0.1 | OR | OR | XOR | XOR | XOR | XOR | XOR | XOR | XOR |
| 0.0 | AND | AND | OR | OR | OR | XOR | XOR | XOR | XOR |
| 0.1 | NG | NG | AND | AND | AND | NG | NG | NG | NG |
| Inputs | AND | NAND | OR | NOR | XOR | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| (0,0) | - | 0 | P1 | 1 | - | 0 | P1 | 1 | - | 0 |
| (0,1)/(1,0) | - | 0 | P1 | 1 | P1 | 1 | - | 0 | P1 | 1 |
| (1,1) | P1 | 1 | - | 0 | P1 | 1 | - | 0 | - | 0 |
| [16] | OR, NOR, AND, NAND | Yes | No | No |
| [17] | OR | No | No | No |
| [20] | NOT, XOR | No | No | No |
| [21] | 3-input NOR | No | No | No |
| [27] | OR, AND, NOT | No | No | No |
| [28] | OR, AND, NOR, NAND, XNOR | Yes | No | No |
| [29] | OR, NOR | No | No | Yes |
| [25] | NOR, NAND, XNOR | Yes | Yes | Yes |
| This work | OR, AND, NOR, NAND, XOR | Yes | Yes | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afanador-Delgado, S.M.; Echenausía-Monroy, J.L.; Huerta-Cuellar, G.; García-López, J.H.; Lopez-Muñoz, E.E.; Jaimes-Reátegui, R. Logic Gate Generation in a Monostable Optical System: Improving the Erbium-Doped Fiber Laser Reconfigurable Logic Operation. Photonics 2024, 11, 1103. https://doi.org/10.3390/photonics11121103
Afanador-Delgado SM, Echenausía-Monroy JL, Huerta-Cuellar G, García-López JH, Lopez-Muñoz EE, Jaimes-Reátegui R. Logic Gate Generation in a Monostable Optical System: Improving the Erbium-Doped Fiber Laser Reconfigurable Logic Operation. Photonics. 2024; 11(12):1103. https://doi.org/10.3390/photonics11121103
Chicago/Turabian StyleAfanador-Delgado, Samuel Mardoqueo, José Luis Echenausía-Monroy, Guillermo Huerta-Cuellar, Juan Hugo García-López, Erick Emiliano Lopez-Muñoz, and Rider Jaimes-Reátegui. 2024. "Logic Gate Generation in a Monostable Optical System: Improving the Erbium-Doped Fiber Laser Reconfigurable Logic Operation" Photonics 11, no. 12: 1103. https://doi.org/10.3390/photonics11121103
APA StyleAfanador-Delgado, S. M., Echenausía-Monroy, J. L., Huerta-Cuellar, G., García-López, J. H., Lopez-Muñoz, E. E., & Jaimes-Reátegui, R. (2024). Logic Gate Generation in a Monostable Optical System: Improving the Erbium-Doped Fiber Laser Reconfigurable Logic Operation. Photonics, 11(12), 1103. https://doi.org/10.3390/photonics11121103








