Bidirectional Propagation Properties of Partially Coherent Laguerre–Gaussian Beams in Atmospheric Turbulence and Plasma
Abstract
1. Introduction
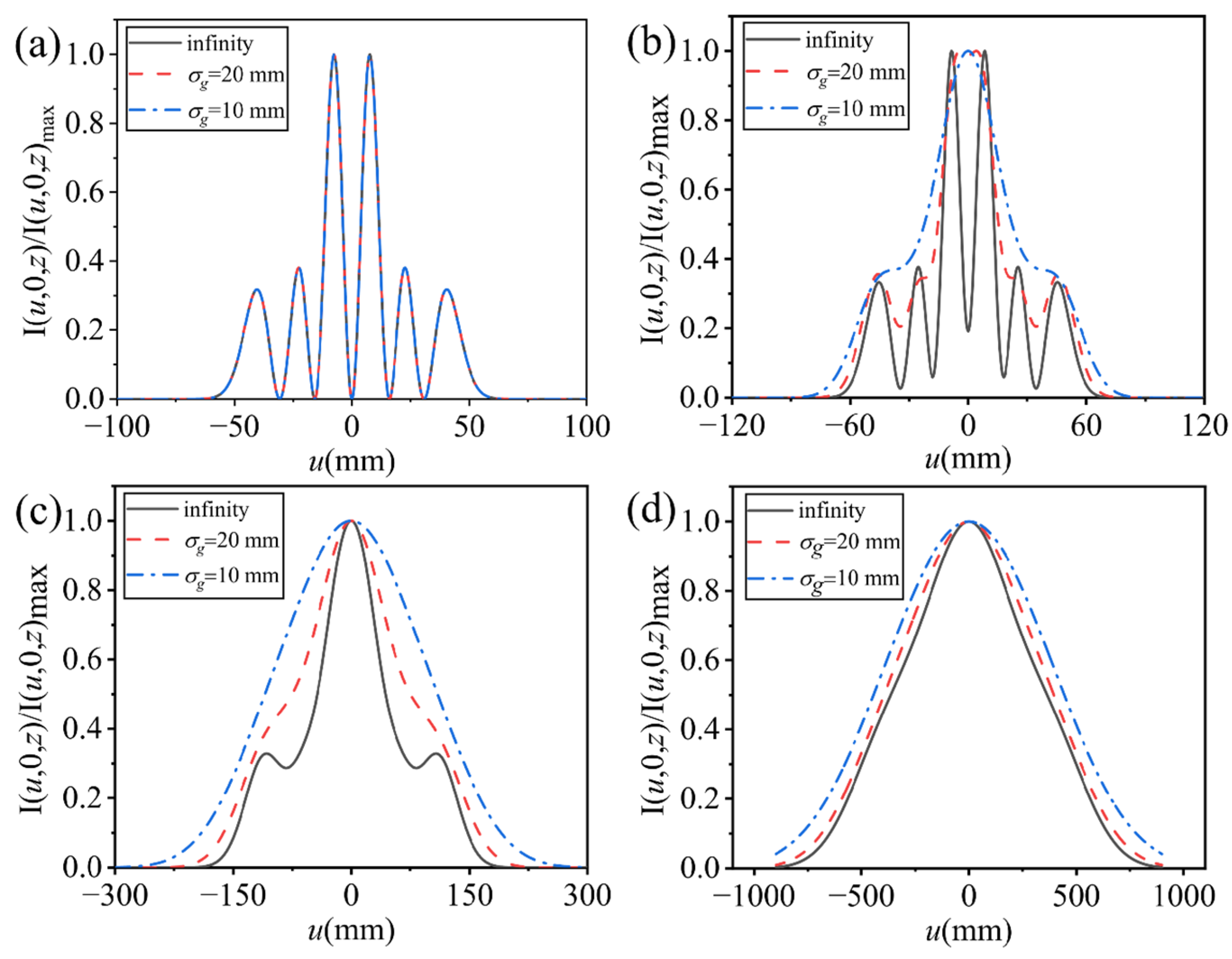
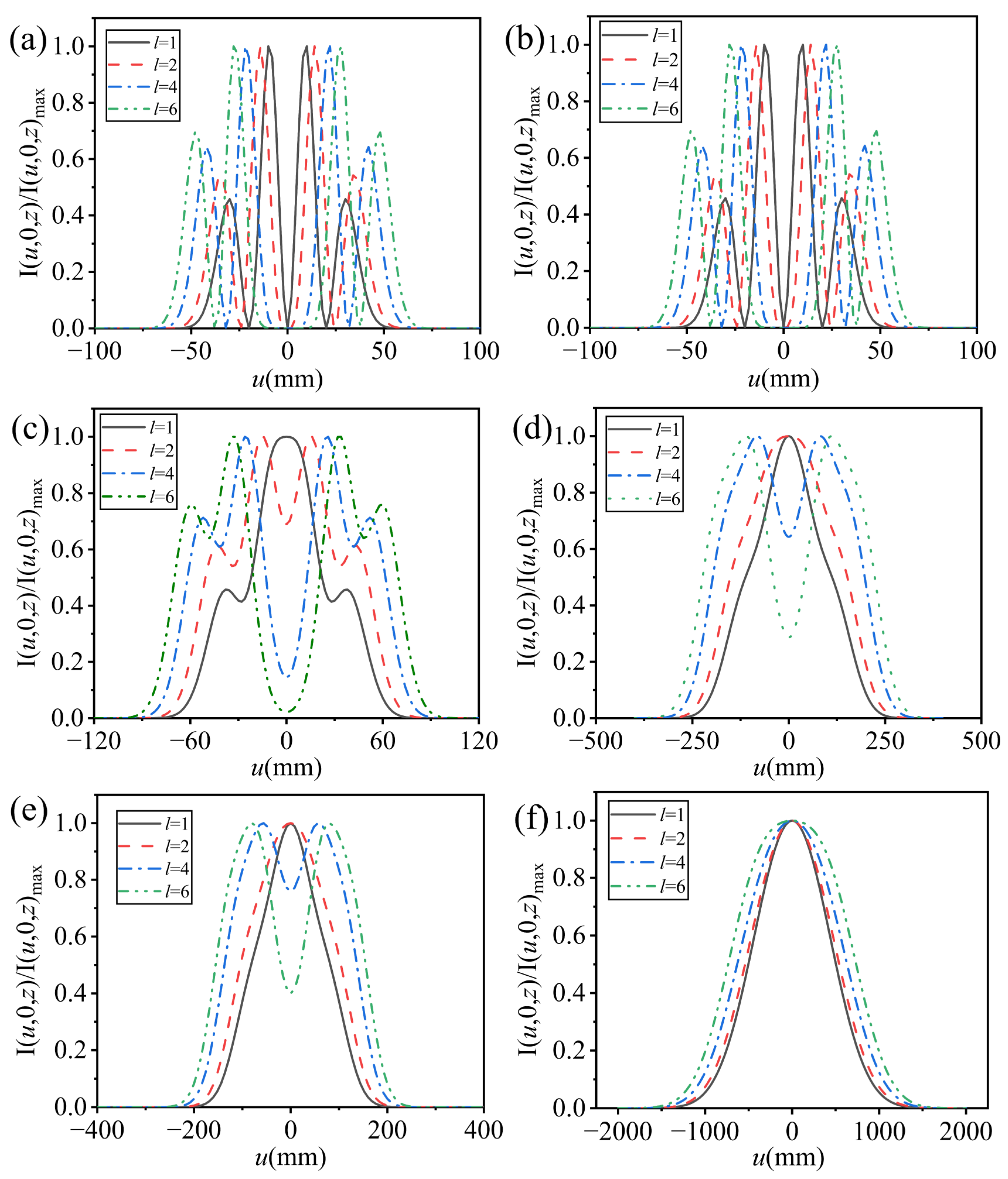
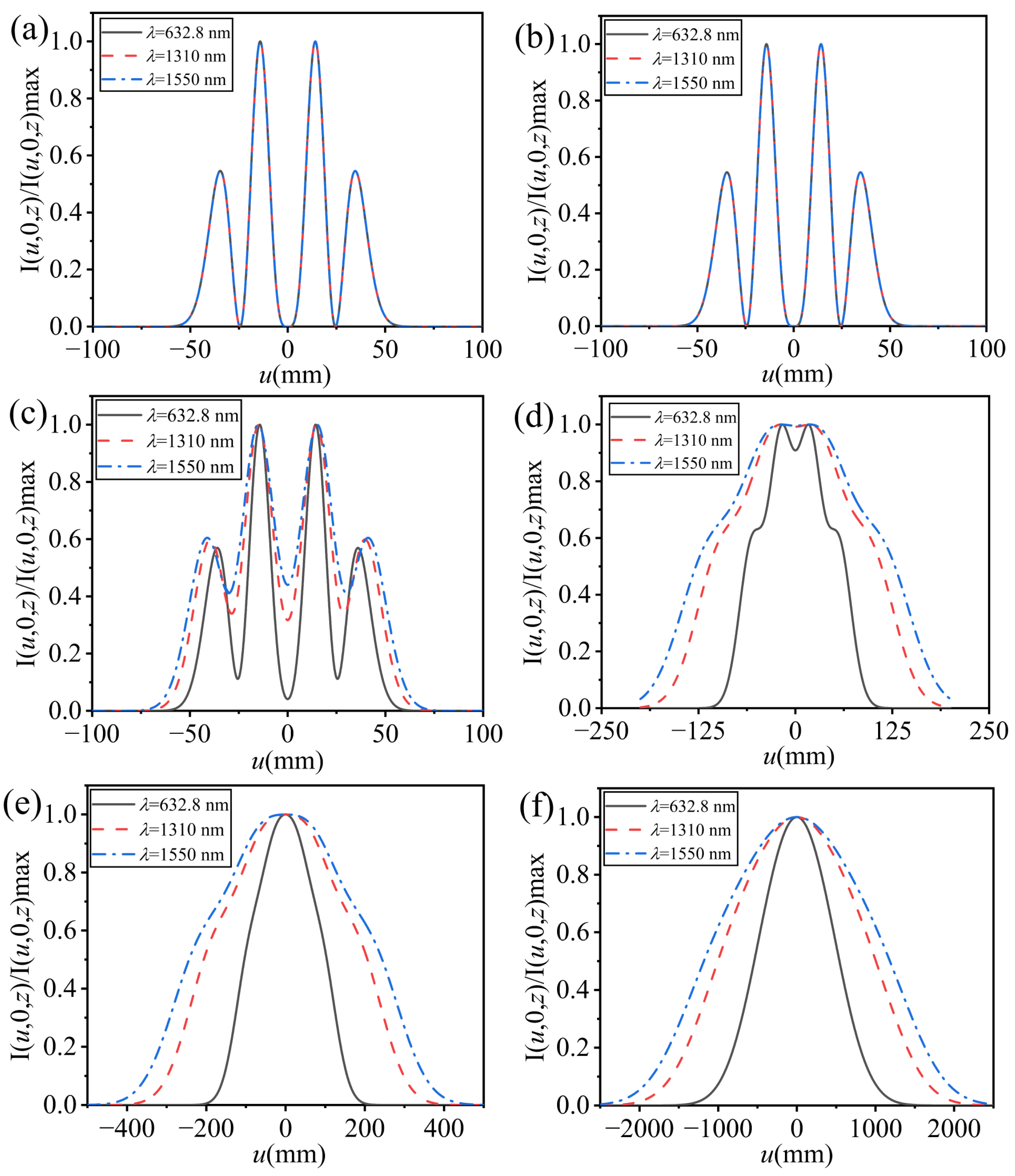
2. Intensity Distribution
3. Effective Beam Width
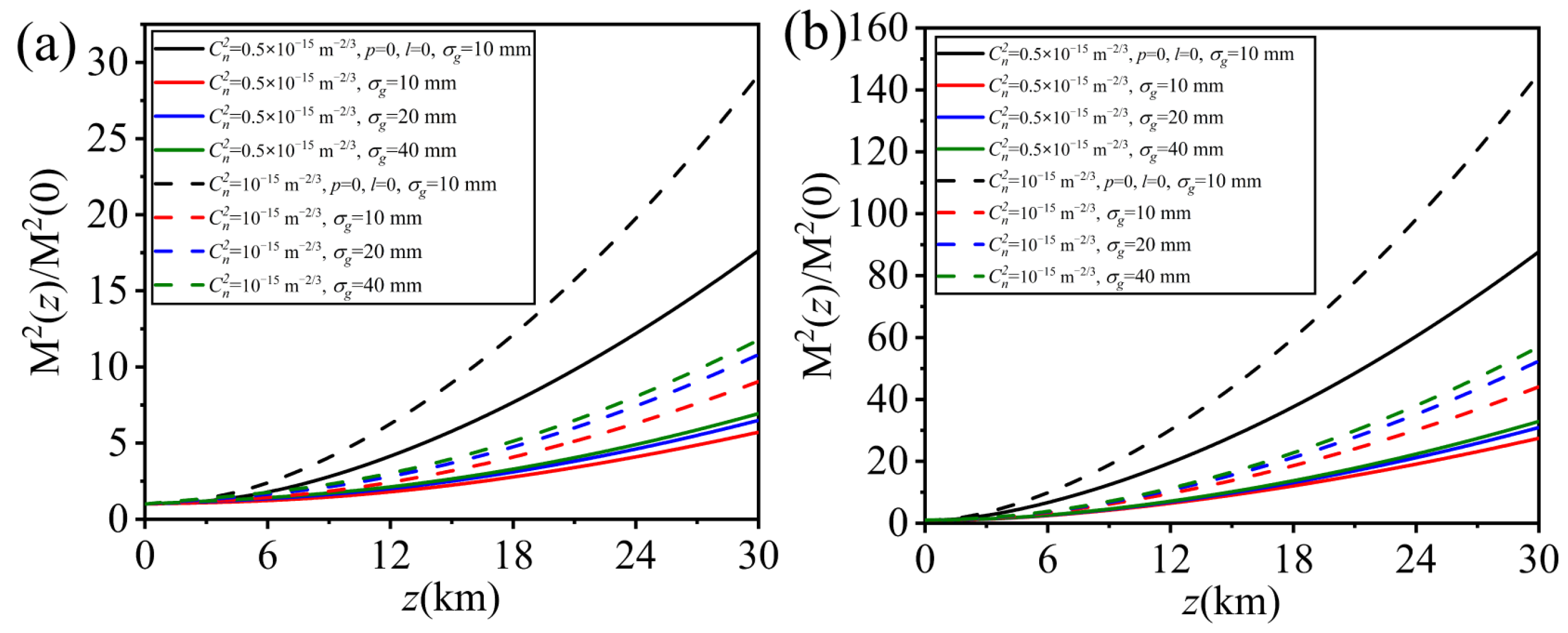
4. M2 Factor
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yuan, Y.; Zhang, J.; Dang, J.; Zheng, W.; Zheng, G.; Fu, P.; Qu, J.; Hoenders, B.; Zhao, Y.; Cai, Y. Enhanced fiber-coupling efficiency via high-order partially coherent flat-topped beams for free-space optical communications. Opt. Express 2022, 30, 5634–5643. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Cheng, B.; Wang, Q.; Wu, B.; Shen, X.; Zheng, L.; Xu, Y.; Lin, Q. Atom cooling by partially spatially coherent lasers. Phys. Rev. A 2013, 88, 023416. [Google Scholar] [CrossRef]
- Pesonen, H.; Halder, A.; Huusko, J.; Friberg, A.; Setala, T.; Turunen, J. Spatial coherence effects in second-harmonic generation of scalar light fields. J. Optics-UK 2021, 23, 035501. [Google Scholar] [CrossRef]
- Cai, Y.; Peschel, U. Second-harmonic generation by an astigmatic partially coherent beam. Opt. Express. 2007, 15, 15480–15492. [Google Scholar] [CrossRef] [PubMed]
- Domanski, A.; Cieslak, R.; Karpierz, M.; Budaszewski, D.; Wolinski, T. Efficiency of second harmonic generation for partially coherent light in anisotropic crystals. Open Phys. 2008, 6, 628–633. [Google Scholar] [CrossRef]
- Kato, Y.; Mima, K.; Miyanaga, N.; Arinaga, S.; Kitagawa, Y.; Nakatsuaka, M.; Yamanaka, C. Random phasing of high-power lasers for uniform target acceleration and plasma-instability suppression. Phys. Rev. Lett. 1984, 53, 1057–1060. [Google Scholar] [CrossRef]
- Deng, H.; Wu, P.; Tao, Z.; Li, X.; Li, Y.; Ruizhong, R.; Ren, Y. Scintillation of Computational Ghost Imaging with a Finite Bucket Detector through Atmospheric Turbulence. Photonics. 2023, 10, 542. [Google Scholar] [CrossRef]
- Luo, M.; Zhu, W.; Zhao, D. Ghost imaging and its visibility with partially coherent elliptical Gaussian Schell-model beams. Phy. Lett. A 2015, 379, 2789–2794. [Google Scholar] [CrossRef]
- Dawkins, R.; Hong, M.; You, C.; Magana-Loaiza, O. The quantum Gaussian–Schell model: A link between classical and quantum optics. Opt. Lett. 2024, 49, 4242–4245. [Google Scholar] [CrossRef]
- Alkelly, A.A.; Khaled, M.A.H.; Hassan, L.F. Propagation of Partially Coherent Flat-Topped Vortex Hollow Beams in Anisotropic Turbulent Plasma. Int. J. Opt. 2022, 2022, 7798053. [Google Scholar] [CrossRef]
- Wu, Z.; Feng, Z.; Ye, S.; Song, B.; Wei, R.; Yu, C. Beam properties of a partially coherent beam propagating horizontally in atmospheric turbulence. Photonics 2023, 10, 477. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, B. Turbulence distance for laser beams propagating through non-Kolmogorov turbulence. J. Opt. Soc. Am. A 2013, 30, 2339–2346. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Z. Characteristics of a partially coherent Gaussian Schell-model beam propagating in slanted atmospheric turbulence. Chinese Phys. B. 2012, 21, 054203. [Google Scholar] [CrossRef]
- Ji, X.; Lü, B. Turbulence-induced quality degradation of partially coherent beams. Opt. Commun. 2005, 251, 231–236. [Google Scholar] [CrossRef]
- Zhou, Z.; Qu, J. Self-splitting and propagation factors of a superimposed Hermite-Gaussian correlated Schell-model beam in turbulent atmosphere. Results Phys. 2021, 28, 104609. [Google Scholar] [CrossRef]
- Wang, C.; Liu, L.; Liu, L.; Yu, J.; Wang, F.; Cai, Y.; Peng, X. Second-order statistics of a Hermite-Gaussian correlated Schell-model beam carrying twisted phase propagation in turbulent atmosphere. Opt. Express 2023, 31, 13255–13268. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Suo, Q.; Chen, L. Analysis to beam quality of partially coherent flat-topped vortex beams propagating through atmospheric turbulence. Optik 2016, 127, 11342–11348. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Qian, X.; Zhu, W.; Li, J. Orbital angular momentum evolution of twisted multi-Gaussian Schell model beams in anisotropic turbulence. Opt. Commun. 2022, 520, 128454. [Google Scholar] [CrossRef]
- Hu, J.; Ji, X.; Wang, H.; Deng, Y.; Li, X.; Wang, T.; Zhang, H. Influence of Kerr nonlinearity on propagation characteristics of twisted Gaussian Schell-model beams. Opt. Express 2021, 29, 23393–23407. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, Y.; Wang, T. Evolution properties of a partially coherent twisted laguerre-gaussian pulsed beam propagating through anisotropic atmospheric turbulence. Photonics 2022, 9, 707. [Google Scholar] [CrossRef]
- Zhong, Y.; Cui, Z.; Shi, J.; Qu, J. Propagation properties of partially coherent Laguerre–Gaussian beams in turbulent atmosphere. Opt. Laser Technol. 2011, 43, 741–747. [Google Scholar] [CrossRef]
- Huang, K.; Xu, Y.; Li, Y. Average Intensity of a Laguerre–Gaussian Vector Vortex Beam through Inhomogeneous Atmospheric Turbulence. Photonics 2023, 10, 1189. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Z.; Lin, Q. Atom interferometers manipulated through the toroidal trap realized by the interference patterns of Laguerre-Gaussian beams. Eur. Phys. J. D 2009, 53, 127–131. [Google Scholar] [CrossRef]
- Bradshaw, D.; Andrews, D. Interactions between spherical nanoparticles optically trapped in Laguerre–Gaussian modes. Opt. Lett. 2005, 30, 3039–3041. [Google Scholar] [CrossRef] [PubMed]
- Arlt, J.; Hitomi, T.; Dholakia, K. Atom guiding along Laguerre-Gaussian and Bessel light beams. Appl. Phys. B 2000, 71, 549–554. [Google Scholar] [CrossRef]
- Rhodes, D.; Gherardi, D.; Livesey, J.; Mcgloin, D.; Melvilie, H.; Freegarde, T.; Dholakia, K. Atom guiding along high order Laguerre–Gaussian light beams formed by spatial light modulation. J. Mod. Optic. 2006, 53, 547–556. [Google Scholar] [CrossRef]
- Kuga, T.; Torii, Y.; Shiokawa, N.; Hirano, T. Novel optical trap of atoms with a doughnut beam. Phys. Rev. Lett. 1997, 78, 4713–4716. [Google Scholar] [CrossRef]
- Song, H.; Pae, K.; Won, J.; Song, J.; Lee, S.; Kim, C.; Ryu, C.; Bang, W.; Nam, C. Characteristics of electron beams accelerated by parallel and antiparallel circularly polarized Laguerre–Gaussian laser pulses. Appl. Phys. B 2023, 129, 56. [Google Scholar] [CrossRef]
- Cai, Y.; He, S. Propagation of a Laguerre–Gaussian beam through a slightly misaligned paraxial optical system. Appl. Phys. B 2006, 84, 493–500. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.; Xu, Y.; Qian, X. Intensity and polarization properties of the partially coherent Laguerre–Gaussian vector beams with vortices propagating through turbulent atmosphere. Opt. Laser Technol. 2014, 56, 1–6. [Google Scholar] [CrossRef]
- Alkelly, A.; Khaled, M.; Hassan, L. Angular width and beam quality of a partially coherent standard Laguerre–Gaussian vortex beam in turbulent plasma. J. Opt. Soc. Am. A 2024, 41, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Lv, C.; Cui, Z.; Han, Y. Light propagation characteristics of turbulent plasma sheath surrounding the hypersonic aerocraft. Chinese Phys. B 2019, 28, 074203. [Google Scholar] [CrossRef]
- Li, J.; Yang, S.; Guo, L. Propagation characteristics of Gaussian beams in plasma sheath turbulence. IET Microw. Antenna. P 2017, 11, 280–286. [Google Scholar] [CrossRef]
- Hassan, L.; Alkelly, A.; Khaled, M. Polarization and coherence properties of a partially coherent elegant Laguerre–Gaussian vortex beam in turbulent plasma. J. Appl. Phys. 2024, 135, 193107. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.; Gao, Y.; Wei, D.; Cai, Y.; Yuan, Y. Distribution of intensity and M2 factor for a partially coherent flat-topped beam in bidirectional turbulent atmosphere and plasma connection. Opt. Express 2024, 32, 5982–5995. [Google Scholar] [CrossRef]
- Li, J.; Yang, S.; Guo, L.; Cheng, M. Anisotropic power spectrum of refractive-index fluctuation in hypersonic turbulence. Appl. Optics. 2016, 55, 9137–9144. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Guo, L.; Cheng, M.; Xi, L. Polarization characteristics of radially polarized partially coherent vortex beam in anisotropic plasma turbulence. Wave Random Complex 2021, 31, 1931–1944. [Google Scholar] [CrossRef]
- Alkelly, A.; Khaled, M.; Hassan, L. Spreading properties of partially coherent multi-Gaussian Schell-model and modified Bessel-correlated vortex beams in anisotropic turbulent plasma. Phys. Scr. 2023, 98, 075518. [Google Scholar] [CrossRef]
- Wang, Y.; Bai, L.; Zhang, D.; Xie, J.; Guo, Y.; Guo, L. Spiral spectrum of a Laguerre-Gaussian beam propagating in anisotropic turbulent plasma. IEEE Photonics J. 2021, 13, 1–10. [Google Scholar] [CrossRef]
- Lv, C.; Han, Y. Analysis of propagation characteristics of Gaussian beams in turbulent plasma sheaths. Acta Phys. Sin. 2019, 68, 094201. [Google Scholar]
- Wang, F.; Cai, Y.; Korotkova, O. Partially coherent standard and elegant Laguerre-Gaussian beams of all orders. Opt. Express 2009, 17, 22366–22379. [Google Scholar] [CrossRef] [PubMed]
- Kimel, I.; Elias, L. Relations between hermite and laguerre gaussian modes. IEEE. J. Quantum. Electron. 1993, 29, 2562–2567. [Google Scholar] [CrossRef]
- Wang, F.; Cai, Y.; Eyyuboglu, H.; Baykal, Y. Average intensity and spreading of partially coherent standard and elegant Laguerre-Gaussian beams in turbulent atmosphere. Prog. Electromagn. Res. 2010, 103, 33–56. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Zhao, X. Intensity and effective beam width of partially coherent Laguerre–Gaussian beams through a turbulent atmosphere. J. Opt. Soc. Am. A. 2015, 32, 1623–1630. [Google Scholar] [CrossRef] [PubMed]
- Shirai, T.; Dogariu, A.; Wolf, E. Mode analysis of spreading of partially coherent beams propagating through atmospheric turbulence. J. Opt. Soc. Am. A. 2003, 20, 1094–1102. [Google Scholar] [CrossRef]
- Gradshteyn, I.; Ryzhik, I. Table of Integrals, Series, and Products, 7th ed.; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Dan, Y.; Zhang, B. Beam propagation factor of partially coherent flat-topped beams in a turbulent atmosphere. Opt. Express 2008, 16, 15563–15575. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yao, L.; Zhao, Y.; Zhang, H.; Cai, Y.; Yuan, Y.; Gao, Y. Bidirectional Propagation Properties of Partially Coherent Laguerre–Gaussian Beams in Atmospheric Turbulence and Plasma. Photonics 2024, 11, 1111. https://doi.org/10.3390/photonics11121111
Zhang Y, Yao L, Zhao Y, Zhang H, Cai Y, Yuan Y, Gao Y. Bidirectional Propagation Properties of Partially Coherent Laguerre–Gaussian Beams in Atmospheric Turbulence and Plasma. Photonics. 2024; 11(12):1111. https://doi.org/10.3390/photonics11121111
Chicago/Turabian StyleZhang, Yuelei, Linxuan Yao, Yuanhao Zhao, Hui Zhang, Yangjian Cai, Yangsheng Yuan, and Yaru Gao. 2024. "Bidirectional Propagation Properties of Partially Coherent Laguerre–Gaussian Beams in Atmospheric Turbulence and Plasma" Photonics 11, no. 12: 1111. https://doi.org/10.3390/photonics11121111
APA StyleZhang, Y., Yao, L., Zhao, Y., Zhang, H., Cai, Y., Yuan, Y., & Gao, Y. (2024). Bidirectional Propagation Properties of Partially Coherent Laguerre–Gaussian Beams in Atmospheric Turbulence and Plasma. Photonics, 11(12), 1111. https://doi.org/10.3390/photonics11121111





