Chromatic Aberration in Wavefront Coding Imaging with Trefoil Phase Mask
Abstract
:1. Introduction
2. Methodology
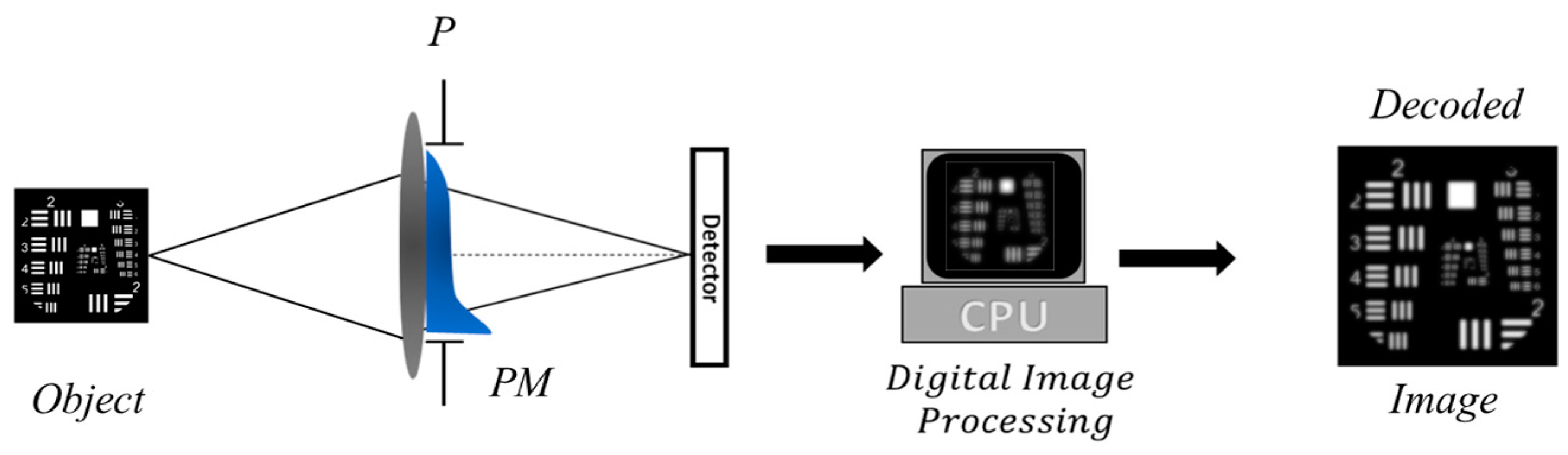
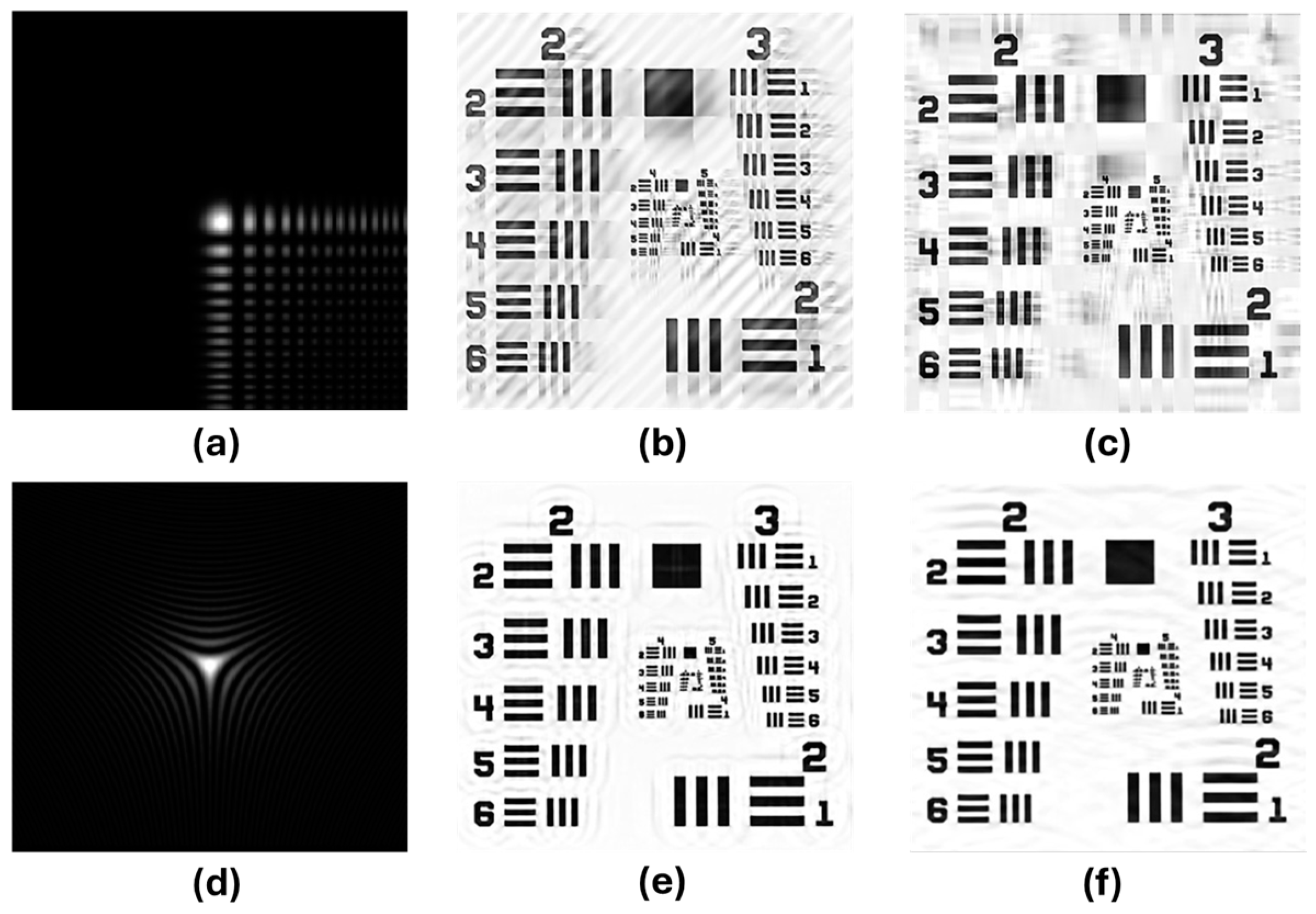
2.1. Theoretical Bakcground
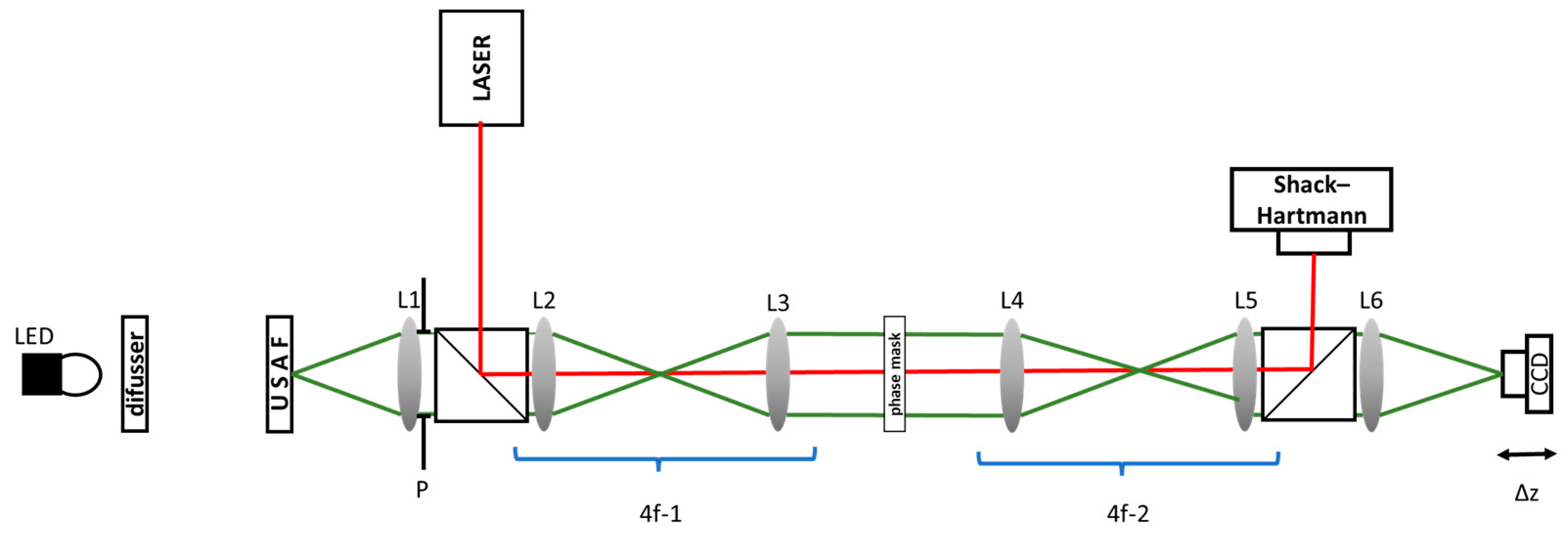
2.2. Experimental Setup
3. Results
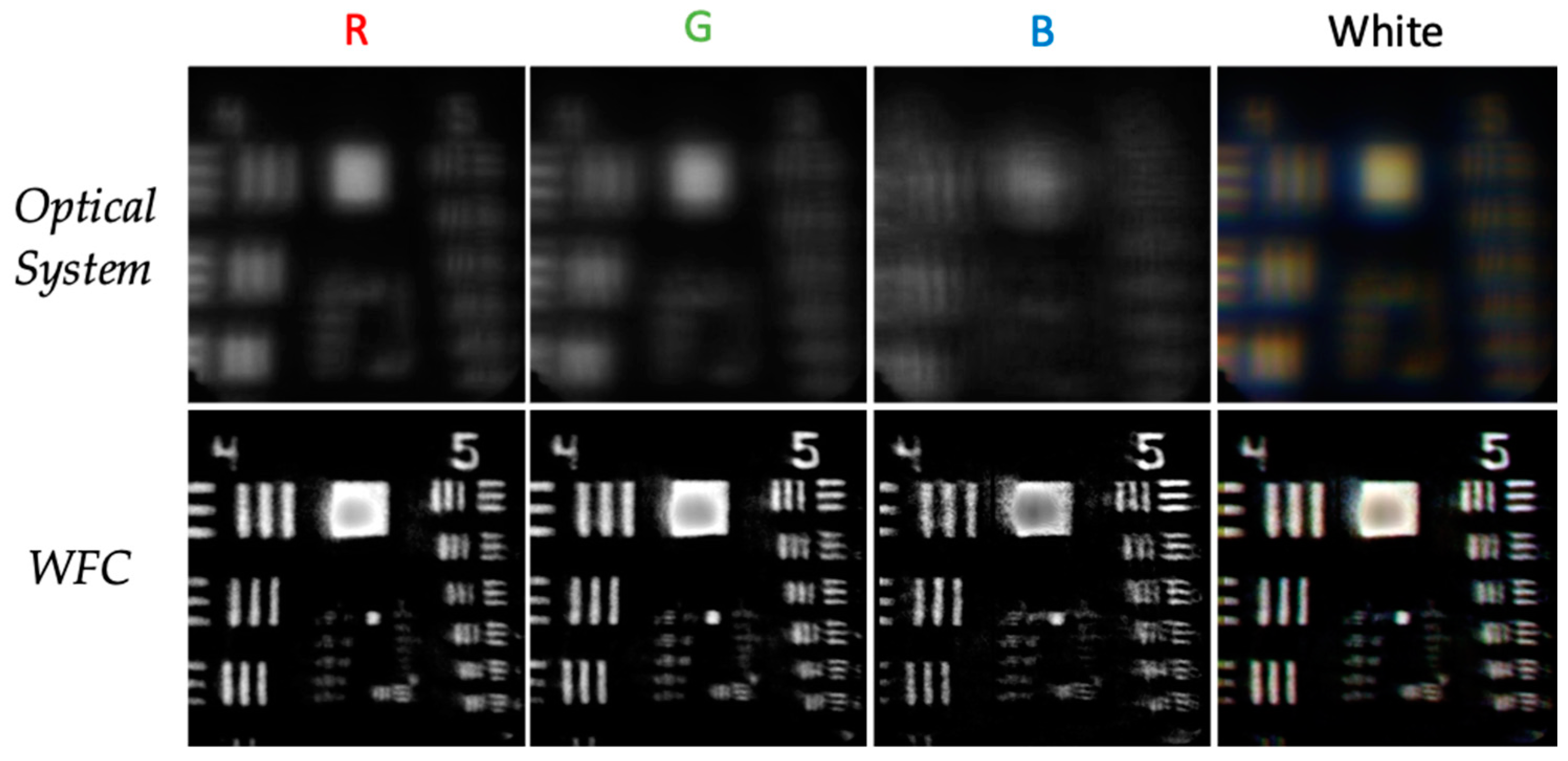
3.1. RGB LEDs
3.2. White Light
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kingslake, R.; Johnson, B.B. Lens Design Fundamentals, 2nd ed.; Academic Press: Burlington, VT, USA, 2010; pp. 137–163. [Google Scholar]
- Korneliussen, J.T.; Hirakawa, K. Camera processing with chromatic aberration. IEEE Trans. Image Process. 2014, 23, 4539–4552. [Google Scholar] [CrossRef] [PubMed]
- Dowski, E.R.; Cathey, W.T. Extended depth of field through wave-front coding. Appl. Opt. 1995, 34, 1859–1886. [Google Scholar] [CrossRef] [PubMed]
- Kubala, k.; Dowski, E.R.; Cathey, W.T. Reducing complexity in computational imaging systems. Opt. Express 2003, 11, 2102–2108. [Google Scholar] [CrossRef] [PubMed]
- Ye, Q.; Wu, Y.M.; Zhang, H.; Li, Y.; Wang, L.; Sun, K. Experimental damage thresholds of a laser suppression imaging system using a cubic phase plate. Chin. Opt. Lett. 2023, 21, 041403. [Google Scholar] [CrossRef]
- Niu, Z.; Wang, J.; Tian, Y.; Wu, Z.; Wei, C.; Shao, J. Wavefront-coded phase measuring deflectometry for the all-focused measurement. Opt. Lett. 2022, 47, 4770–4773. [Google Scholar] [CrossRef] [PubMed]
- Arnison, M.R.; Cogswell, C.J.; Sheppard, C.J.R.; Török, P. Wavefront Coding Fluorescence Microscopy Using High Aperture Lenses. In Optical Imaging and Microscopy; Springer Series in Optical Sciences; Springer: Berlin/Heidelberg, Germany, 2003; Volume 87. [Google Scholar] [CrossRef]
- Fontbonne, A.; Trouvé-Peloux, P.; Tartas, E.; Druart, G. Depth of Focus Extension Wavefront Coding Methods for Fast Imaging Systems. In Optica Design and Fabrication Congress 2023 (IODC, OFT); Technical Digest Series; Optica Publishing Group: Washington, DC, USA, 2023; p. 127981M. [Google Scholar] [CrossRef]
- Wach, H.B.; Dowski, E.R.; Cathey, W.T. Control of chromatic focal shift through wave-front coding. Appl. Opt. 1998, 37, 5359–5367. [Google Scholar] [CrossRef] [PubMed]
- Akpinar, U.; Sahin, E.; Meem, M.; Menon, R.; Gotchev, A. Learning Wavefront Coding for Extended Depth of Field Imaging. IEEE Trans. Image Process. 2021, 30, 3307–3320. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 4th ed.; Pearson: New York, NY, USA, 2018; pp. 317–368. [Google Scholar]
- Wei, S.; Cheng, H.; Xue, B.; Shao, X.; Xi, L. Low-cost and simple optical system based on wavefront coding and deep learning. Appl. Opt. 2023, 62, 6171–6179. [Google Scholar] [CrossRef] [PubMed]
- Fontbonne, A.; Sauer, H.; Goudail, F. Comparison of methods for end-to-end co-optimization of optical systems and image processing with commercial lens design software. Opt. Express 2022, 30, 13556–13571. [Google Scholar] [CrossRef] [PubMed]
- Diaz, F.; Goudail, F.; Loiseaux, B.; Huignard, J.-P. Increase in depth of field taking into account deconvolution by optimization of pupil mask. Opt. Lett. 2009, 34, 2970–2972. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Bao, M.; Sun, L.; Liu, Y.; Zheng, J. Wavefront coding image reconstruction via physical prior and frequency attention. Opt. Express 2023, 31, 32875–32886. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Li, Y. Optimized logarithmic phase masks used to generate defocus invariant modulation transfer function for wavefront coding system. Opt. Lett. 2010, 35, 2630–2632. [Google Scholar] [CrossRef] [PubMed]
- Le, V.N.; Chen, S.; Fan, Z. Optimized asymmetrical tangent phase mask to obtain defocus invariant modulation transfer function in incoherent imaging systems. Opt. Lett. 2014, 39, 2171–2174. [Google Scholar] [CrossRef] [PubMed]
- Scrymgeour, D.A.; Adelsberger, K.; Boye, R. Advanced Imaging Optics Utilizing Wavefront Coding; Sandia Report SAND2015-4431; Office of Scientific and Technical Information: Oak Ridge, TN, USA, 2015. [CrossRef]
- Demenikov, M.; Harvey, A.R. Image artifacts in hybrid imaging systems with a cubic phase mask. Opt. Express 2010, 18, 8207–8212. [Google Scholar] [CrossRef] [PubMed]
- Demenikov, M.; Harvey, A.R. A technique to remove image artefacts in optical systems with wavefront coding. In Novel Optical Systems Design and Optimization XII; SPIE: Bellingham, WA, USA, 2009; Volume 7429. [Google Scholar] [CrossRef]
- Prasad, S.; Torgersen, T.C.; Pauca, V.P.; Plemmons, R.J.; van der Gracht, J. Engineering the pupil phase to improve image quality. In Visual Information Processing XII; SPIE: Bellingham, WA, USA, 2003; Volume 5108. [Google Scholar] [CrossRef]
- Acosta, E. Adaptive phase plates for optical encoding systems invariant to second-order aberrations. Opt. Commun. 2011, 284, 3862–3866. [Google Scholar] [CrossRef]
- Demenikov, M.; Muyo, G.; Harvey, A.R. Experimental demonstration of continuously variable optical encoding in a hybrid imaging system. Opt. Lett. 2010, 35, 2100–2102. [Google Scholar] [CrossRef] [PubMed]
- Olvera-Angeles, M.; Padilla-Vivanco, A.; Ortega, K.; Sasian, J.; Schwiegerling, J.; Arines, J. Eva Acosta Optimizing trefoil phase plates design for color wavefront coding. In Current Developments in Lens Design and Optical Engineering XIX; SPIE: Bellingham, WA, USA, 2018; Volume 1074. [Google Scholar] [CrossRef]
- Shi, Y.; Chen, S.; Le, V.N.; Fan, Z.; Zhang, W. Performance analysis of wavefront coding system with spherical aberration by using ray aberration approach. Optik 2017, 130, 1266–1271. [Google Scholar] [CrossRef]
- Utsugi, A.; Ishiga, K. Correcting lateral chromatic aberrations by image processing. In International Optical Design Conference; SPIE: Bellingham, WA, USA, 2010; Volume 76520. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olvera-Angeles, M.; Arines, J.; Acosta, E. Chromatic Aberration in Wavefront Coding Imaging with Trefoil Phase Mask. Photonics 2024, 11, 1117. https://doi.org/10.3390/photonics11121117
Olvera-Angeles M, Arines J, Acosta E. Chromatic Aberration in Wavefront Coding Imaging with Trefoil Phase Mask. Photonics. 2024; 11(12):1117. https://doi.org/10.3390/photonics11121117
Chicago/Turabian StyleOlvera-Angeles, Miguel, Justo Arines, and Eva Acosta. 2024. "Chromatic Aberration in Wavefront Coding Imaging with Trefoil Phase Mask" Photonics 11, no. 12: 1117. https://doi.org/10.3390/photonics11121117
APA StyleOlvera-Angeles, M., Arines, J., & Acosta, E. (2024). Chromatic Aberration in Wavefront Coding Imaging with Trefoil Phase Mask. Photonics, 11(12), 1117. https://doi.org/10.3390/photonics11121117




