Single-Frequency Ring Fiber Laser with Random Distributed Feedback Provided by Artificial Rayleigh Scattering
Abstract
:1. Introduction
2. Experiment
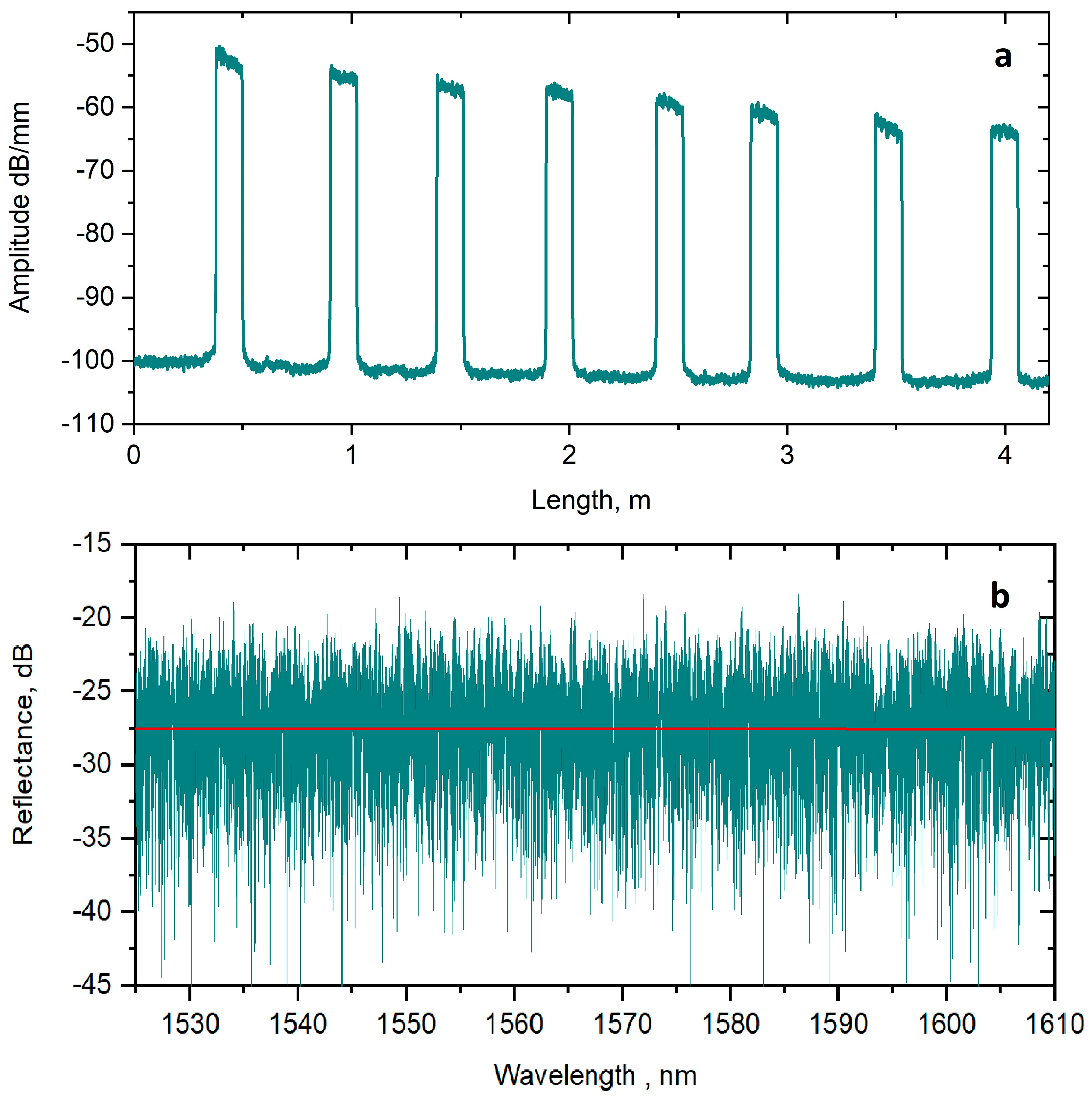
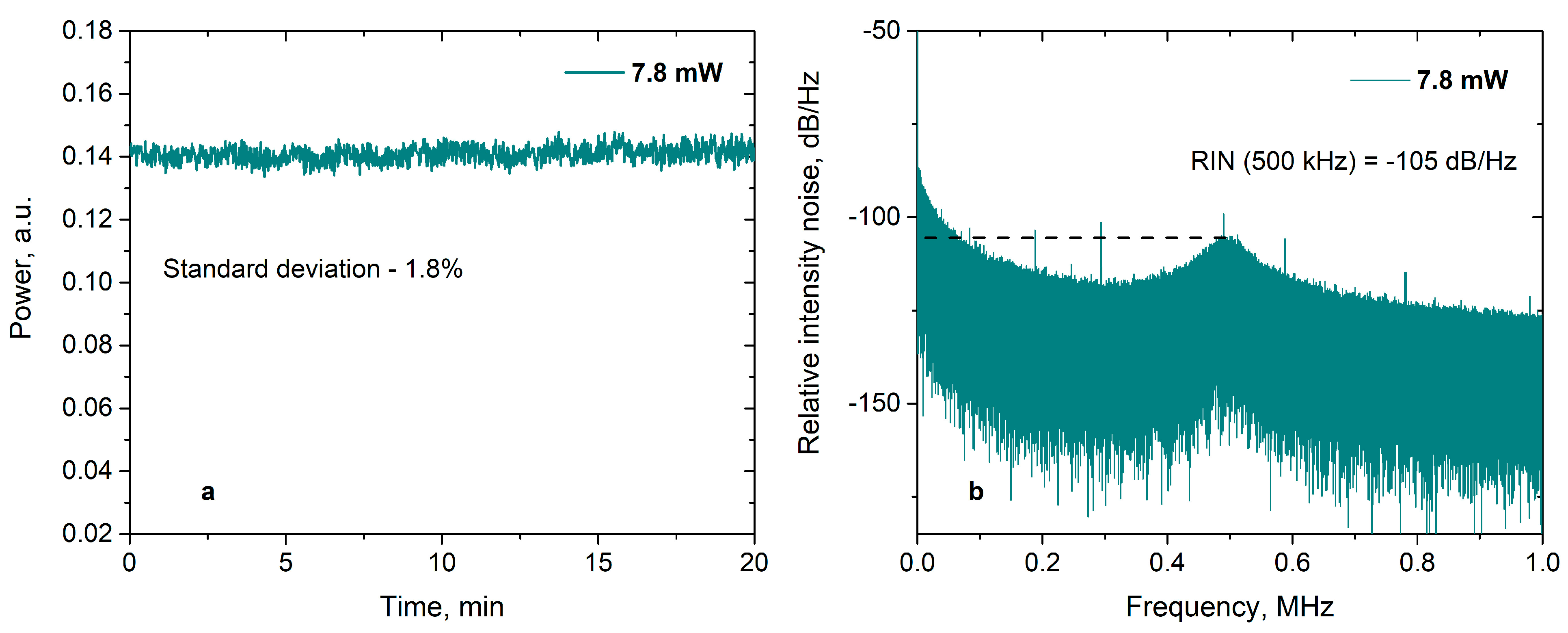
3. Results
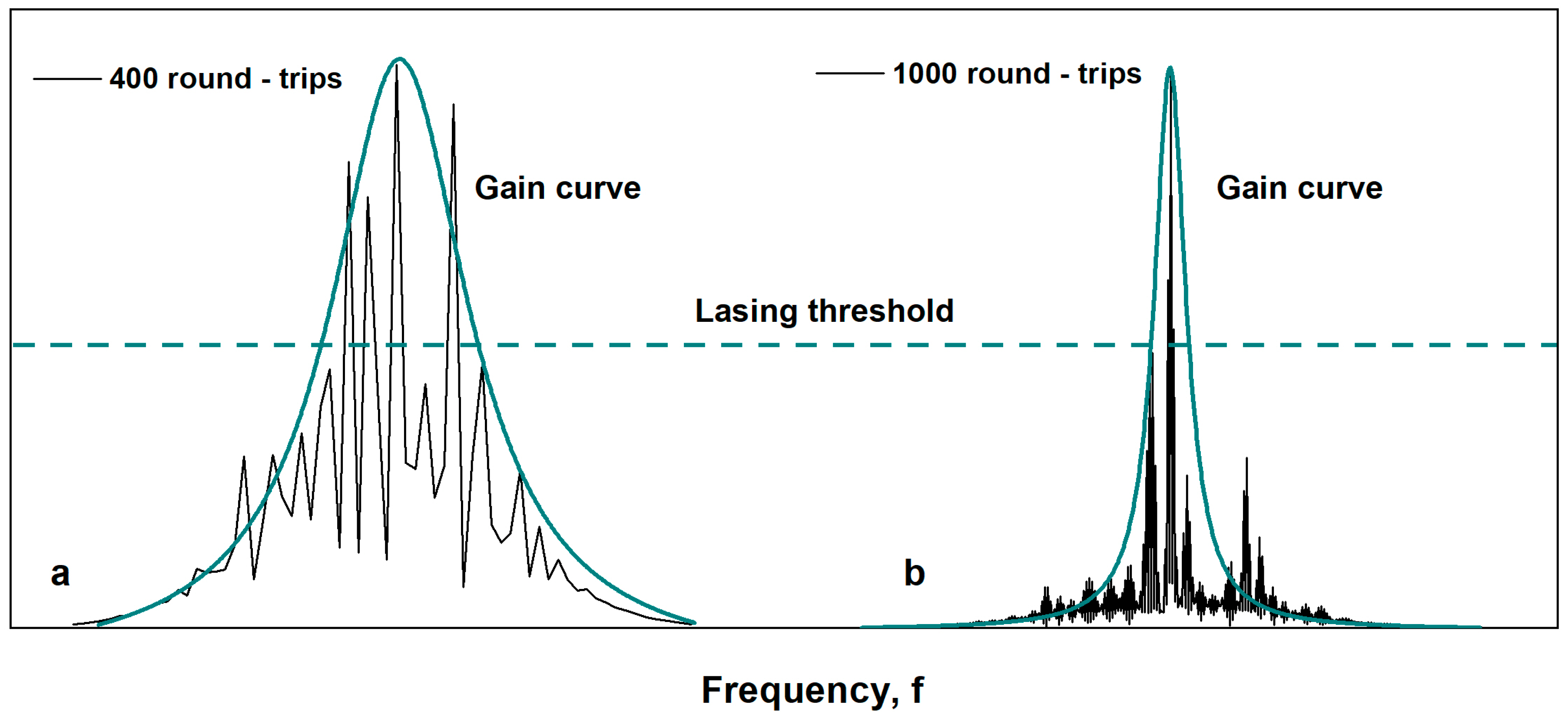
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Z.N.; Rao, Y.J.; Wu, H.; Li, P.Y.; Jiang, Y.; Jia, X.H.; Zhang, W.L. Long-Distance Fiber-Optic Point-Sensing Systems Based on Random Fiber Lasers. Opt. Express 2012, 20, 17695–17700. [Google Scholar] [CrossRef] [PubMed]
- Wiersma, D.S.; Cavalieri, S. A Temperature-Tunable Random Laser. Nature 2001, 414, 708–709. [Google Scholar] [CrossRef] [PubMed]
- Han, B.; Wu, H.; Liu, Y.; Dong, S.; Rao, Y.; Wang, Z.; Xu, J.; Ma, L. Ultralong Single-Ended Random Fiber Laser and Sensor. Laser Photonics Rev. 2023, 17, 2200797. [Google Scholar] [CrossRef]
- Wu, H.; Wang, W.; Hu, B.; Li, Y.; Tian, K.; Ma, R.; Li, C.; Liu, J.; Liang, H. Widely tunable continuous-wave visible and mid-infrared light generation based on a dual-wavelength switchable and tunable random Raman fiber laser. Photonics Res. 2023, 11, 808–816. [Google Scholar] [CrossRef]
- Dontsova, E.I.; Kablukov, S.I.; Vatnik, I.D.; Babin, S.A. Frequency Doubling of Raman Fiber Lasers with Random Distributed Feedback. Opt. Lett. 2016, 41, 1439–1442. [Google Scholar] [CrossRef] [PubMed]
- Turitsyn, S.K.; Babin, S.A.; El-Taher, A.E.; Harper, P.; Churkin, D.V.; Kablukov, S.I.; Ania-Castañón, J.D.; Karalekas, V.; Podivilov, E.V. Random Distributed Feedback Fibre Laser. Nat. Photonics 2010, 4, 231–235. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, L.; Chen, L.; Bao, X. Single-Mode SOA-Based 1kHz-Linewidth Dual-Wavelength Random Fiber Laser. Opt. Express 2017, 25, 15828–15837. [Google Scholar] [CrossRef] [PubMed]
- Gagné, M.; Kashyap, R. Random Fiber Bragg Grating Raman Fiber Laser. Opt. Lett. 2014, 39, 2755–2758. [Google Scholar] [CrossRef]
- Abdullina, S.R.; Skvortsov, M.I.; Vlasov, A.A.; Podivilov, E.V.; Babin, S.A. Coherent Raman Lasing in a Short Polarization-Maintaining Fiber with a Random Fiber Bragg Grating Array. Laser Phys. Lett. 2019, 16, 105001. [Google Scholar] [CrossRef]
- Deng, J.; Han, M.; Xu, Z.; Du, Y.; Shu, X. Stable and Low-Threshold Random Fiber Laser via Anderson Localization. Opt. Express 2019, 27, 12987–12997. [Google Scholar] [CrossRef]
- Abdullina, S.R.; Vlasov, A.A.; Lobach, I.A.; Belai, O.V.; Shapiro, D.A.; Babin, S.A. Single-Frequency Yb-Doped Fiber Laser with Distributed Feedback Based on a Random {FBG}. Laser Phys. Lett. 2016, 13, 75104. [Google Scholar] [CrossRef]
- Popov, S.M.; Butov, O.V.; Bazakutsa, A.P.; Vyatkin, M.Y.; Chamorovskii, Y.K.; Fotiadi, A.A. Random Lasing in a Short Er-Doped Artificial Rayleigh Fiber. Results Phys. 2020, 16, 102868. [Google Scholar] [CrossRef]
- Skvortsov, M.; Wolf, A.; Dostovalov, A.; Egorova, O.; Semjonov, S.L.; Babin, S. Narrow-Linewidth Er-Doped Fiber Lasers with Random Distributed Feedback Provided by Artificial Rayleigh Scattering. J. Light. Technol. 2021, 40, 1829–1835. [Google Scholar] [CrossRef]
- Li, Y.; Lu, P.; Baset, F.; Ou, Z.; Song, J.; Alshehri, A.; Bhardwaj, V.R.; Bao, X. Narrow Linewidth Low Frequency Noise Er-Doped Fiber Ring Laser Based on Femtosecond Laser Induced Random Feedback. Appl. Phys. Lett. 2014, 105, 101105. [Google Scholar] [CrossRef]
- Dostovalov, A.V.; Wolf, A.A.; Parygin, A.V.; Zyubin, V.E.; Babin, S.A. Femtosecond Point-by-Point Inscription of Bragg Gratings by Drawing a Coated Fiber through Ferrule. Opt. Express 2016, 24, 16232–16237. [Google Scholar] [CrossRef] [PubMed]
- Yan, A.; Huang, S.; Li, S.; Chen, R.; Ohodnicki, P.; Buric, M.; Lee, S.; Li, M.-J.; Chen, K.P. Distributed Optical Fiber Sensors with Ultrafast Laser Enhanced Rayleigh Backscattering Profiles for Real-Time Monitoring of Solid Oxide Fuel Cell Operations. Sci. Rep. 2017, 7, 9360. [Google Scholar] [CrossRef] [PubMed]
- Shimotsuma, Y.; Kazansky, P.G.; Qiu, J.; Hirao, K. Self-Organized Nanogratings in Glass Irradiated by Ultrashort Light Pulses. Phys. Rev. Lett. 2003, 91, 247405. [Google Scholar] [CrossRef] [PubMed]
- Taylor, R.; Hnatovsky, C.; Simova, E. Applications of Femtosecond Laser Induced Self-Organized Planar Nanocracks inside Fused Silica Glass. Laser Photon. Rev. 2008, 2, 26–46. [Google Scholar] [CrossRef]
- Rybaltovsky, A.A.; Egorova, O.N.; Zhuravlev, S.G.; Galagan, B.I.; Sverchkov, S.E.; Denker, B.I.; Semjonov, S.L. Distributed Bragg Reflector Fiber Laser Directly Written in a Composite Fiber Manufactured by Melting Phosphate Glass in a Silica Tube. Opt. Lett. 2019, 44, 3518–3521. [Google Scholar] [CrossRef]
- Egorova, O.N.; Semjonov, S.L.; Velmiskin, V.V.; Yatsenko, Y.P.; Sverchkov, S.E.; Galagan, B.I.; Denker, B.I.; Dianov, E.M. Phosphate-Core Silica-Clad Er/Yb-Doped Optical Fiber and Cladding Pumped Laser. Opt. Express 2014, 22, 7632. [Google Scholar] [CrossRef]
- Egorova, O.N.; Semjonov, S.L.; Medvedkov, O.I.; Astapovich, M.S.; Okhrimchuk, A.G.; Galagan, B.I.; Denker, B.I.; Sverchkov, S.E.; Dianov, E.M. High-Beam Quality, High-Efficiency Laser Based on Fiber with Heavily Yb 3+-Doped Phosphate Core and Silica Cladding. Opt. Lett. 2015, 40, 3762. [Google Scholar] [CrossRef]
- Karlsson, G.; Laurell, F.; Tellefsen, J.; Denker, B.; Galagan, B.; Osiko, V.; Sverchkov, S. Development and Characterization of Yb-Er Laser Glass for High Average Power Laser Diode Pumping. Appl. Phys. B Lasers Opt. 2002, 75, 41–46. [Google Scholar] [CrossRef]
- Okoshi, T.; Kikuchi, K.; Nakayama, A. Novel Method for High Resolution Measurement of Laser Output Spectrum. Electron. Lett. 1980, 16, 630–631. [Google Scholar] [CrossRef]
- Hui, R.; Sullivan, M.O. Fiber Optic Measurement Techniques British Library Cataloguing in Publication Data; Academic Press: Cambridge, MA, USA, 2009; ISBN 9780123738653. [Google Scholar]
- Skvortsov, M.I.; Wolf, A.A.; Dostovalov, A.V.; Vlasov, A.A.; Akulov, V.A.; Babin, S.A. Distributed Feedback Fiber Laser Based on a Fiber Bragg Grating Inscribed Using the Femtosecond Point-by-Point Technique. Laser Phys. Lett. 2018, 15, 035103. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skvortsov, M.I.; Proskurina, K.V.; Golikov, E.V.; Dostovalov, A.V.; Wolf, A.A.; Munkueva, Z.E.; Abdullina, S.R.; Terentyev, V.S.; Egorova, O.N.; Semjonov, S.L.; et al. Single-Frequency Ring Fiber Laser with Random Distributed Feedback Provided by Artificial Rayleigh Scattering. Photonics 2024, 11, 103. https://doi.org/10.3390/photonics11020103
Skvortsov MI, Proskurina KV, Golikov EV, Dostovalov AV, Wolf AA, Munkueva ZE, Abdullina SR, Terentyev VS, Egorova ON, Semjonov SL, et al. Single-Frequency Ring Fiber Laser with Random Distributed Feedback Provided by Artificial Rayleigh Scattering. Photonics. 2024; 11(2):103. https://doi.org/10.3390/photonics11020103
Chicago/Turabian StyleSkvortsov, Mikhail I., Kseniya V. Proskurina, Evgeniy V. Golikov, Alexander V. Dostovalov, Alexey A. Wolf, Zhibzema E. Munkueva, Sofia R. Abdullina, Vadim S. Terentyev, Olga N. Egorova, Sergey L. Semjonov, and et al. 2024. "Single-Frequency Ring Fiber Laser with Random Distributed Feedback Provided by Artificial Rayleigh Scattering" Photonics 11, no. 2: 103. https://doi.org/10.3390/photonics11020103
APA StyleSkvortsov, M. I., Proskurina, K. V., Golikov, E. V., Dostovalov, A. V., Wolf, A. A., Munkueva, Z. E., Abdullina, S. R., Terentyev, V. S., Egorova, O. N., Semjonov, S. L., & Babin, S. A. (2024). Single-Frequency Ring Fiber Laser with Random Distributed Feedback Provided by Artificial Rayleigh Scattering. Photonics, 11(2), 103. https://doi.org/10.3390/photonics11020103




