Abstract
In this paper, we propose an asymmetric cryptosystem based on dynamic foveated imaging and bidimensional empirical mode decomposition (BEMD). Firstly, a novel dynamic foveated imaging algorithm is developed to transform a plaintext image to a globally ambiguous and locally clear image. Then, the image is passed through a phase-truncated Fourier transform system to generate a white noise image. The resulting image is encoded using BEMD to produce an encrypted image. The proposed cryptosystem offers two distinct decryption methods, allowing the receiver to obtain a decrypted image from a specific frame or a combination of frames, depending on the unique keys. This encryption scheme significantly expands the key space and strengthens the system’s anti-iterative attack capability. Numerical simulation results demonstrate the effectiveness, security and robustness of the proposed cryptosystem.
1. Introduction
As the Internet and modern communication technology continue to develop rapidly, the security of optical image transmission has become an increasingly prominent concern. Given its parallel signal processing and high-dimensional wavefront adjustment ability, optical encryption technology has been extensively researched in information security and optical fields [1]. The first optical cryptosystem was double random phase encoding (DRPE) encryption [2]. In this system, phase information is superimposed in the spatial and frequency domains through two random phase masks, and a white noise image is finally obtained. Since then, many optical encryption schemes, such as the phase-truncated Fourier transform (PTFT) [3], fractional Fourier transform [4], Fresnel transform [5,6], linear canonical transform [7], gyrator transform [8,9], Radon transform [10], ghost imaging [11,12,13] and deep learning [14,15,16,17], have been developed. Because the encryption and decryption processes of DRPE are linear, it is vulnerable to various attacks [18,19]. Some asymmetric encryption algorithms, such as PTFT, are easily cracked when using iterative algorithms [20,21]. To expand the key space and improve the security of image data, several other optical imaging techniques [22,23,24,25,26,27,28] are introduced into optical image encryption, especially optical wavefront aberration encryption [29] and equal modulus decomposition (EMD) encryption [30].
In EMD-based cryptosystems, the complex value image encrypted by the front-end encryption system is disassembled into two complex value mask images. The amplitude of EMD is calculated in accordance with a specific formula as ciphertext; the phase angle of the first mask is used as the public key, and the phase angle of the second mask is used as the private key [6,9,30,31]. The silhouette problem is effectively solved by EMD-based cryptosystems. However, before the mode decomposition, determining the phase of one mask for the complex value image and then obtaining another mask through the modulus decomposition rule are necessary steps. Once the attacker knows the public key, the corresponding private key will also be known. Thus, the encoding method is cumbersome, and the security is difficult to guarantee.
In optical wavefront aberration cryptosystems, the plane wave is shaped into a distorted wavefront by superimposing Zernike aberration. The Zernike coefficient is introduced into optical encryption systems as a new type of key. Each order of the Zernike coefficients and each direction coefficient are key, which tremendously increases the key space [29]. The distorted wavefront and the ideal wavefront are used as public and private keys. For the decryption process, only when both wavefronts are known can the decryption image be correct. Later, Xu et al. [32] studied the influences of various optical aberrations on optical encryption systems and proposed two methods to solve the problem of aberration in optical encryption systems. The above cryptosystems can only realize the encryption of the whole image but cannot achieve local encryption. Once the cryptosystem is cracked, the information will be lost completely.
In this paper, we propose an innovative asymmetric encryption scheme that combines dynamic foveated imaging and bidimensional empirical mode decomposition (BEMD) to provide enhanced security. Unlike traditional encryption schemes that rely on a single decryption method, our proposed scheme allows the receiver to select from two different decryption methods on the basis of the keys sent by the sender. To encrypt a plaintext image, the sender uses dynamic foveated imaging technology to transform it into a globally ambiguous and locally clear image. The resulting image is then passed through a PTFT system to generate a white noise image. To further strengthen the system’s anti-iterative attack capability, BEMD is applied to produce an encrypted image. When the dynamic foveated regions fill the whole plaintext image, the sender can encrypt ciphertext frames into a video. Depending on the key used, the receiver can obtain a decrypted image from a specific frame or a combination of frames. This approach significantly expands the key space and enhances the security of the cryptosystem. Furthermore, the cryptosystem offers added security features, such as the ability to select the size, location and arrangement of foveated regions as the key. The addition of spoofing frames to the encrypted video can be used to mislead attackers, further strengthening the security of the system. In summary, our proposed asymmetric encryption scheme, which combines dynamic foveated imaging and BEMD, offers a highly secure and flexible approach to encryption, greatly enhancing information security.
The rest of this paper is arranged in the following manner. The algorithm of the cryptosystem is elucidated in Section 2. In Section 3, the simulation results and the security analysis of the cryptosystem are presented. The discussion section is presented in Section 4. Concluding remarks are given in Section 5.
2. Principle and Methods
2.1. Process of Dynamic Foveated Regions Imaging
All optical systems contain wavefront aberration, which can describe the difference between ideal and real wavefronts. The difference between the wavefronts can be combined with the optical path difference (OPD) of each point on the pupil plane. The optical path lengths are as follows.
When ,
where represents the optical path from object point to real wavefront and ideal wavefront at the pupil, as shown in Figure 1; and denote the Gaussian ideal image point and real image point, respectively; represents the optical path in K direction; refers to pupil coordinates; is the OPD distribution at the pupil. Therefore, the phase difference between actual and ideal wavefronts can be expressed as follows:
where is the ideal wavefront phase, is the distorted wavefront phase, is the wave number, and is the wavelength of incident light. We can express wave aberration by a normalized pupil function as follows:
where represents the pupil diameter.
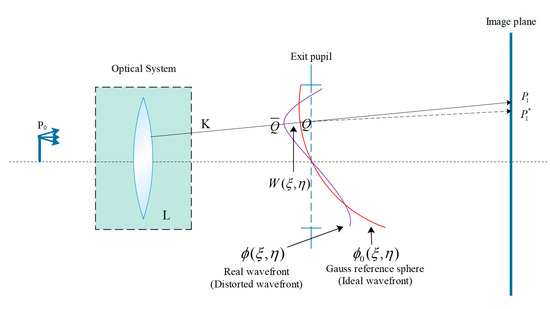
Figure 1.
Wavefront aberration and ray aberration.
By adding locally distributed aberrations to the parallel plane beam carrying plaintext information, the preconstructed wavefront distortion can be introduced. The foveated region imaging method, which is consistent with the imaging characteristics of the human eye, can be used to make the local image clear and the rest fuzzy. Zernike aberration theory is a mathematical theory describing wavefront aberrations in optical systems. The foveated region imaging method constructs aberration in accordance with Zernike aberration theory and adds preconstructed aberration to the plane wave to obtain a wavefront with aberration, as shown as follows:
where is the initial plane wave, is the output wavefront with added overall aberration, is the Fourier transform operation, is the inverse Fourier transform operation, and is the phase with global aberration. Aberrations can be expressed by using Zernike polynomials as follows:
where refers to the aberrations, is the Zernike term, and is its co-efficient [33].
To obtain a wavefront with foveated aberration, we need to process the wavefront with global aberration. Assuming that the complex amplitude of each point on the input plane wave is , we need to restore the foveated region of the output wavefront to , as described in the following formula:
where is the wavefront of the modified foveated aberration, and represents the foveated regions. The number, size and position of the foveated regions can be changed at will. The transformation process from to can be expressed as follows:
means optical transfer function. The phase of the foveated aberration can be expressed as follows:
where means the operation of taking phase of OTF. In our proposed asymmetric encryption scheme, is first converted to an 8-bit grayscale image, which is subsequently loaded onto the phase-based spatial light modulator (SLM) so that the plaintext image can be attached with foveated aberration.
2.2. BEMD Process
Empirical mode decomposition (EMD) is commonly used for analyzing nonlinear and nonstationary data [34]. It has good performance in analyzing nonstationary signals. Some researchers have extended EMD to 2D and proposed the BEMD method to process image information [35,36]. Compared with some cryptosystems based on wavelet transform [23,37], BEMD can adaptively handle nonlinear and nonstationary signal noises without constructing wavelet functions, thus avoiding ciphertext cracking after the wavelet function is obtained. PTFT and BEMD are used to realize double encryption of image information, which improves the ability of the optical encryption system to resist statistical and iterative attacks.
In an asymmetric optical encryption system, there is usually a pair of asymmetric keys (a public key and a private key). Different keys are used in the encryption and decryption processes. The public key is used to encrypt a message, while the private key is used for decryption. This asymmetric key generation and use is the basis for the security of the encryption system. The PTFT system is implemented based on a 4f system using two Fourier lenses with a focal length of and two random phase plates to achieve asymmetric encryption effects. The spacing in the elements of the system is also . In the PTFT optical encryption system, the incident parallel plane beam achieves [0, 2π] random phase superposition when it passes through RM1 in the spatial domain. Then, the wavefront continues to propagate forward and undergo Fourier transform when it passes through Len1, and the result of the Fourier transform will be in the form of a complex amplitude. The amplitude of the wavefront is taken as the output to continue the subsequent processing, while its phase is kept as the private key to be used when decrypting. The process is as follows:
where refers to the parallel plane beam carrying image information; refers to the random phase in the spatial domain, with the value range of [0, 2π]; represents the phase truncation operation; represents the amplitude part of the output complex amplitude; represents the phase reservation operation; and represents the phase part of the output complex amplitude. is reserved as the first phase key.
realizes [0, 2π] random phase superposition when it passes through RM2 on the spectrum plane, then it is transformed into the spatial domain via inverse Fourier transform when it passes through Len2. The phase of the complex amplitude is extracted as the private key for the parallel plane beam after the inverse Fourier transform into the spatial domain. The amplitude part of the complex amplitude is retained as a multiple real value encrypted image. The process is as follows.
where refers to the random phase in the frequency domain, with the value range of [0, 2π]. represents the amplitude part of the output complex amplitude, and represents its phase part. is reserved as the second phase key.
If the encrypted image is regarded as a bidimensional signal, the BEMD method, which can adaptively separate various frequency components in the data effectively, can be used to decompose the signal. Firstly, we calculate the maximum and minimum of the 2D signal envelope surface via the eight-neighborhood algorithm [38]. The set of maximum and minimum points is then fitted to a surface envelope by using a bilinear interpolation algorithm [39]. We record the maximum and minimum points as and , respectively, and take their mean value as the mean envelope of the encrypted image. The calculation process is as follows:
The mean envelope of the original signal is subtracted to obtain the residual quantity. If the residual quantity meets the preset screening criteria, the first-order component of the original signal is obtained. The calculation process is shown as follows:
where is the residual quantity, is the first-order residual term, and indicates the screening criteria. Generally, . If the screening criteria are met, is defined as the first-order component image of the encrypted image.
Thus, the remainder can be calculated as follows:
Then, the remainder is taken as a new signal, and the above process is repeated until the residual term is a monotone function or constant. Finally, the encrypted image is decomposed as follows:
Through the BEMD method, the encrypted image after PTFT is decomposed into multiple component images. The component image with the least amount of information is taken as the final output encrypted image. The amplitude, as a property of light, can be realized in the actual optical path by loading it on an amplitude-type SLM and, thus, in the actual optical system. Therefore, the remaining components are loaded onto an amplitude-based SLM and used as the public key in the asymmetric optical encryption system to achieve double encryption.
2.3. Encryption Processes of the Proposed Cryptosystem
By utilizing dynamic foveated imaging and BEMD, we achieve the effect that one encryption scheme corresponds to two decryption methods. The entire setup of the cryptosystem is shown in Figure 2. In our proposed cryptosystem, the whole encryption process can be divided into three parts. The first part is to load foveated aberration on plaintext information through SLM. The second part involves the use of the 4f system to build a PTFT system to acquire a white noise image. The final part is to adopt another SLM to implement BEMD. As shown in Figure 3, the encryption process involves the following steps:
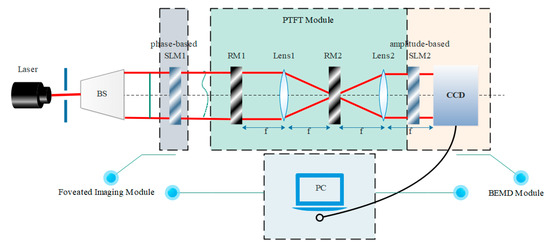
Figure 2.
Optical setup of the proposed encryption system.
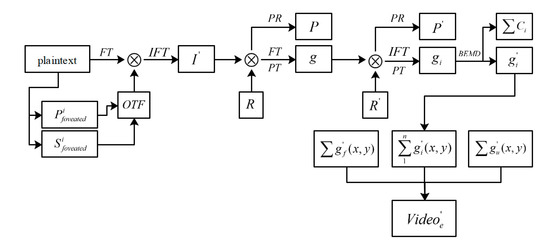
Figure 3.
Flowchart of the encryption process of the proposed cryptosystem.
Step 1: The preconstructed aberration is added to the original plaintext image to obtain a blurred image in accordance with Zernike aberration theory on a computer. The specific area and the size of the area are selected to restore to obtain a locally clear and residual blurred image . The position of the foveated region and the size are recorded and reserved as the keys. Subsequently, the phase change is calculated between and . In addition, the optical path difference (OPD) converted from plaintext to encrypted image is saved as a secret key. The phase change is loaded into the SLM to add the plaintext to the foveated aberration.
Step 2: In PTFT, the image is passed through the 4f system to obtain . The random phase plates and are reserved as public keys to encrypt . The phases and are reserved as private keys to decrypt the images. The image is decomposed into multiple component images through BEMD. The component image with the least amount of information is taken as the final output , and the remaining components are used as the public key.
Step 3: The SLM is used to change the position of the foveated region and the size . Then, the above process is repeated. The encrypted images of each frame are recorded as , and the encrypted images of each frame are combined into an optical encrypted video . Invalid frames and spoofed frames can be added to the video to further improve the dimension of the key space and the security and scalability of the optical information security system. The video can be expressed as follows:
2.4. Decryption Processes of the Proposed Cryptosystem
The first decryption method is for encrypting a single valid frame, and the decryption process is the inverse process of encrypting a single image, as shown in Figure 4. The keys consist of the remaining components obtained in BEMD, two random phases ( and ) in PTFT, two private keys ( and ) and the OPD in dynamic foveated imaging encryption. The single ciphertext image is first superimposed on from BEMD, then reversed through the PTFT system and finally superimposed on the OPD to obtain a decrypted image. The decryption process can be written as
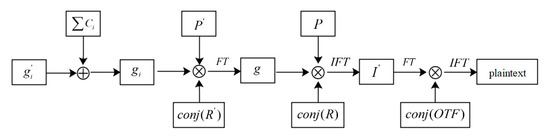
Figure 4.
Flowchart of the first decryption process of the proposed cryptosystem.
The second decryption method is for all valid frames in the ciphertext video stream. The key includes the remaining components obtained in BEMD, two random phases ( and ) in PTFT and two private keys ( and ) without using OPD, as shown in Figure 5. Firstly, we decrypt the foveated part of the decrypted image by following the same steps as in Decryption Method 1. Then, the final decrypted image is obtained by dividing and combining the foveated areas. If the correct location of the valid frames in the video and their corresponding plaintext patterns are obtained, the Decryption Method 2 can yield lossless plaintext, and the range of invalid frames and spoofed frames does not affect the decryption result. Decryption Method 1 is suitable for scenarios with high practicability requirements, such as video surveillance, real-time video transmission, military optical communication, etc. Decryption Method 2 is suitable for scenarios with low real-time requirements but high data quality requirements, such as regular data backup and batch transmission.
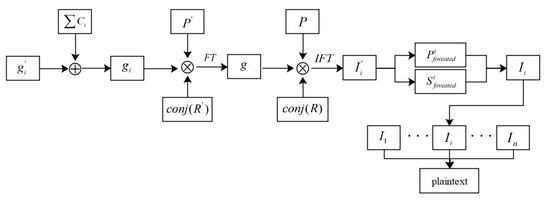
Figure 5.
Flowchart of the second decryption process of the proposed cryptosystem.
3. Results
In consideration of the limited laboratory conditions, in this study, only numerical simulation experiments are conducted on the computer. The aberrations, stray light effects and systematic errors of the optical system are ignored during the simulation experiments. The proposed encryption scheme is analyzed in this section to verify its good security and stability.
The encryption process is simulated. Firstly, the aberration is constructed by inputting a laser beam wavelength of 532 nm into the encryption system and setting the eighth coefficient of the Zernike coefficients to . The plaintext image ‘iris’ (image size = 512 × 512) is input into the encryption system. The plaintext is added to the computer, and the data type of plaintext image is first converted from uint8 type to double float type, followed by normalization process scaling it to the range of 0–1 for subsequent numerical simulation. The blurred image is obtained by adding the preconstructed aberration, as shown in Figure 6b. Afterwards, a specific region of certain size is selected and recovered as the initial image to obtain a locally clear image with the rest being blurred, as shown in Figure 7a. The region position is selected as in the form of a line scan from left to right, and the size is a rectangular region of 128 × 128. The OPD can be calculated in accordance with Fourier optical theory, as shown in Figure 6c. , and OPD are saved as keys, which are loaded into the liquid crystal SLM capable of introducing foveated aberrations into the actual optical path. Subsequently, the random phase of [0, 2π] is superimposed on the space and frequency domains by the PTFT system, and the phase truncation operation is performed to obtain . The random phase , and the phase information , are retained as keys. Finally, through the BEMD module, the encrypted image is obtained, as shown in Figure 8f. The remaining components are used as the public key. The above encryption process is repeated until the complete plaintext image is scanned. All the ciphertext groups are synthesised into a video and sent to the receiver in the form of a video to complete the encryption process.
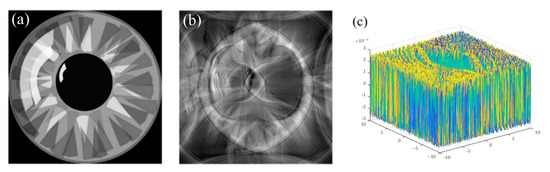
Figure 6.
(a) Plaintext image ‘iris’; (b) blurred image with Zernike aberration; (c) OPD.
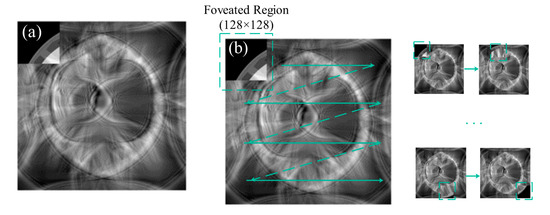
Figure 7.
(a) Foveated image; (b) scanning schematic (the green arrow indicates the scanning process).


Figure 8.
(a,b) Random phase and ; (c) ciphertext image after PTFT; (d,e) private keys and ; (f) ciphertext after BEMD.
The proposed method is characterized by the ability to decrypt in two ways. According to the first decryption method, a single image can be decrypted to obtain a plaintext image, and the decryption process is the inverse of the encryption process. The final decrypted image is shown in Figure 9a. According to the second decryption method, the whole video can be decrypted to generate a plaintext image, as shown in Figure 9b. To analyze the effect of the cryptosystem proposed in this paper, the correlation coefficient value CC is introduced. The CC value is used to describe the correlation between plaintext and decrypted images.
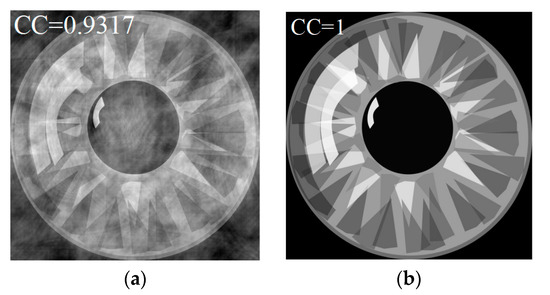
Figure 9.
(a) Decrypted image by the first decryption method; (b) decrypted image by the second decrypted method.
means the expected value operator, and means the absolute value operator.
The CC values of the decrypted images calculated by the two decryption methods are 0.9371 and 1, which demonstrate that the proposed method decrypts well. Specifically, the second decryption method can restore completely under ideal conditions.
3.1. Sensitivity of Secret Keys
In addition, we analyze the effect of the difference in OPD on the decrypted image. To simulate such variation, Gaussian noise with different standard deviations is added to the OPD. The decryption effect is evaluated by comparing the CC value of the final decrypted image with that of the plaintext, and the results are shown in Figure 10. Only the correct OPD can generate the correct image.
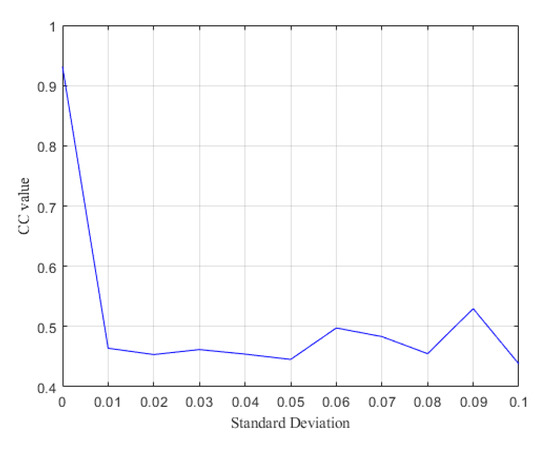
Figure 10.
Dependence of CC value on the change in OPD.
3.2. Security Analysis
The statistical properties of the ciphertext image and the distribution of grayscales can be one of the main focuses of an attacker, which can allow them to obtain useful information from some disordered information. The security of the system is evaluated through grayscale histograms and adjacent pixel correlations. Grayscale histograms can effectively reflect whether an image contains intuitive information. As shown in Figure 11, the grayscale histogram of the plaintext has a more fragmented grayscale distribution, whilst the statistical distribution of the ciphertext is close to Gaussian white noise and conforms to a normal distribution. In addition to grayscale histograms, adjacent pixel correlations are introduced. The analysis of adjacent pixel correlations is performed in three directions (horizontally, vertically and diagonally), which can be described as
where and are a pair of pixels.

Figure 11.
(a,b) Histograms of the plaintext and ciphertext.
To illustrate the impact of BEMD, three stages are analyzed from the plaintext image, after PTFT and after BEMD. The correlations of adjacent pixels in the horizontal, vertical and diagonal directions are shown in Figure 12. The difference between adjacent pixels in the plaintext image is relatively large, whereas the difference between adjacent pixels in is small and almost negligible. The adjacent pixel difference in becomes large again, which can make the attacker confused when intercepting and analyzing the ciphertext, thus deceiving the attacker. Moreover, some characteristics of the PTFT encryption system can be changed by using BEMD.
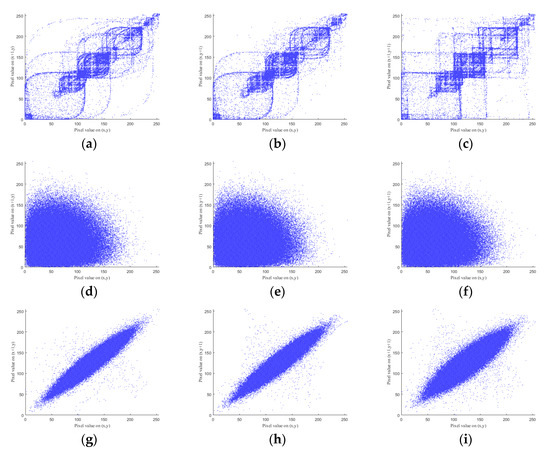
Figure 12.
Correction of two adjacent pixels: (a–c) correlation of two horizontally, vertically and diagonally adjacent pixels for plaintext; (d–f) correlation of two horizontally, vertically and diagonally adjacent pixels for ; (g–i) correlation of two horizontally, vertically and diagonally adjacent pixels for .
3.3. Robustness Analysis
In an optical encryption system, the robustness of the cryptosystem refers to whether the ciphertext can be successfully decrypted when it may be affected by some external factors. The process of ciphertext transmission is easily affected by noise, so the effect of random noise on the proposed cryptosystem is analyzed here. Random noise with a standard deviation of 0.02, 0.05 and 0.1 is introduced into the ciphertext image, and the decrypted image obtained via the first decryption method is shown in Figure 13d–f. The evaluation of CC values shows that the encrypted image can be decrypted even when it is affected by noise, and a lower degree of noise has less impact on the decryption method.

Figure 13.
(a–c) Ciphertexts contaminated by Gaussian noise with 0.02, 0.05, 0.1 standard deviation; (d–f) corresponding decrypted image with ciphertext contaminated by Gaussian noise with 0.02 standard deviation (CC value is 0.9294), 0.05 standard deviation (CC value is 0.9287) and 0.1 standard deviation (CC value is 0.9282).
In addition to the effect of noise, the effect of final decryption when the ciphertext is subjected to an occlusion attack should be analyzed. A rectangular area of 128 × 128 is selected to mask the five regions of the ciphertext, as shown in Figure 14a–e. The first decryption method is then selected for recovery, and the final decrypted image is shown in Figure 14f–j. Although the ciphertext is masked, it has a minimal effect on the decryption process, and the CC value does not change much. If the second decryption method is used, the final CC values obtained by masking the ciphertext are 0.9991, 0.9995, 0.9996, 0.9996 and 0.9988, which are close to those by lossless decryption.

Figure 14.
(a–e) Five regions of the ciphertext is occluded; (f–j) Decrypted image by the first decryption method with (a–e), and the CC values are 0.9284, 0.9266, 0.9267, 0.9274 and 0.9261.
3.4. Comparison of Attacking a Conventional PTFT Cryptosystem and Proposed Cryptosystems with APRA-Based Attacks
The conventional PTFT system is vulnerable to iterative attacks, and a two-step special iterative attack based on APRA in reference [20] can effectively break the PTFT system. On the contrary, BEMD can improve resistance to iterative attacks. Under the assumption that all the keys (except one of ) are known to the attacker, the two-step iterative method is used to break the traditional PTFT and the proposed cryptosystem in this paper, with 1000 iterations for each of the two steps. The results are shown in Figure 15 and Figure 16. The traditional PTFT system is breached, and some information is already visible. By contrast, BEMD is able to effectively prevent information leakage, and the iterative attack is ineffective.

Figure 15.
Simulation of attacking the proposed cryptosystem with APRA: (a) correct image, (b) decrypted image of the conventional PFTF (CC = 0.6641), (c) decrypted image of the proposed method (CC = 0.4534).
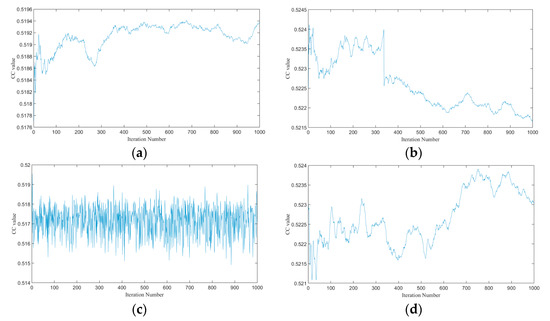
Figure 16.
Decrypted private keys’ CC values against iteration number in two iterative steps for attacking the conventional PTFT cryptosystem and the proposed cryptosystem: (a) CC value of decrypted and right in the first step for attacking the conventional PTFT cryptosystem, (b) CC value of decrypted and right in the second step for attacking the conventional PTFT cryptosystem, (c) CC value of decrypted and right in the first step for attacking the proposed cryptosystem and (d) CC value of decrypted and right in the second step for attacking the proposed cryptosystem.
4. Discussion
In the encryption process, as can be seen in Figure 11, the distribution of gray values of the encrypted image conforms to the Gaussian distribution, which makes it difficult to obtain the information from the perspective of statistical law. As shown in Figure 12, the encrypted image is not correlated with the adjacent pixels in the horizontal, vertical, and diagonal directions. Therefore, it is not possible to obtain encryption information from the correlation of pixels. In addition, due to the dynamic foveated imaging, if the attacker only captures a single frame, they can only obtain part of the information but not completely decrypt it. In the decryption process, as shown in Figure 10, after adding different degrees of Gaussian noise to the OPD, there is basically no correlation between the decrypted image and the plaintext image, which means that the decryption cannot be carried out if the secret key is just a little bit wrong. As shown in Figure 13 and Figure 14, if the encrypted image introduces noise during transmission or receives partial occlusion, when the receiver holds the correct secret key, it is also able to correctly decrypt to obtain the information, and the image quality of the decrypted image has not been seriously impacted.
The whole cryptosystem can be realized by using optical components and a PC and can be decrypted through the use of two decryption methods. In addition, as shown in Figure 15, compared with traditional PTFT-based asymmetric cryptosystem, the proposed cryptosystem introduces the BEMD, which can effectively resist APRA-based attacks. The proposed cryptosystem can be widely used in some information security fields, such as communication security, image security, and intelligence transmission. In optical communication systems, invalid frames and spoofed frames can be introduced into the encrypted video to ensure that sensitive information is not intercepted or eavesdropped on by unauthorized visitors.
However, there are some limitations in our work. The time consumption of the two decryption methods is different when performing the decryption operation. As shown in Figure 17, we carry out a numerical simulation process on ten different images in the CPU platform (12th Gen Intel(R) Core(TM) i9-12900H). The average time consumption of the two decryption methods is 0.31 s and 0.86 s, respectively. The results may be due to the fact that Decryption Method 2 needs to decrypt multiple encrypted images and thus needs to improve the algorithm subsequently to increase the decryption speed. Therefore, Decryption Method 1 is more suitable for video surveillance, real-time video transmission, military optical communication, and other applications with high real-time requirements, while Decryption Method 2 is more suitable for regular data backup, batch transmission, and other applications with low real-time requirements. In addition, our cryptosystem is designed to cope with the scenario of optical encryption for a single image and to realize one encryption and one series of secret keys at a time so as to increase the number of secret keys and improve security. In the future, we will improve our work and hope to realize the encryption of different images with the same series of secret keys.

Figure 17.
Decryption time.
5. Conclusions
In this paper, we propose an asymmetric cryptosystem based on dynamic foveated imaging and BEMD. Subsequently, the basic theories of dynamic foveated imaging, BEMD and PTFT are introduced. Using these methods, we develop an asymmetric optical encryption system that utilizes two decryption methods for decryption. The first decryption method is the inverse process of the encryption method, which can obtain a better-decrypted image. The second method decrypts multiple video frames and utilizes the foveated area’s characteristics for cropping and stitching to obtain a lossless decrypted image. The security analysis of the encryption system reveals its stability during the transmission process. Compared with the traditional PTFT system, the proposed system can effectively resist APRA attacks through the introduction of BEMD and greatly expands the key space to enhance the encryption system’s security. Furthermore, the addition of spoof or invalid frames to the video increases the difficulty for attackers to decrypt the ciphertext. Numerical simulation results validate the effectiveness, security and robustness of the proposed cryptosystem. The proposed method can be used in the fields of optical communication security, real-time image security, and military optical communication.
Author Contributions
Conceptualization, J.C.; methodology, Y.W.; software, Y.W.; validation, Y.W. and Z.J.; formal analysis, Y.W. and Y.H.; investigation, Y.W. and J.W.; resources, Y.W. and S.Z.; data curation, Y.W.; writing—original draft preparation, Y.W.; writing—review and editing, Y.W. and J.C.; visualization, Y.W.; supervision, J.C. and S.Z.; project administration, J.C.; funding acquisition, S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (2021YFC2202100).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The available data have been provided in the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Matoba, O.; Nomura, T.; Pérez-Cabré, E.; Millán, M.; Javidi, B. Optical Techniques for Information Security. Proc. IEEE 2009, 97, 1128–1148. [Google Scholar] [CrossRef]
- Refregier, P.; Javidi, B. Optical Image Encryption Based on Input Plane and Fourier Plane Random Encoding. Opt. Lett. 1995, 20, 767–769. [Google Scholar] [CrossRef] [PubMed]
- Qin, W.; Peng, X. Asymmetric Cryptosystem Based on Phase-Truncated Fourier Transforms. Opt. Lett. 2010, 35, 118–120. [Google Scholar] [CrossRef] [PubMed]
- Unnikrishnan, G.; Joseph, J.; Singh, K. Optical Encryption by Double-Random Phase Encoding in the Fractional Fourier Domain. Opt. Lett. 2000, 25, 887–889. [Google Scholar] [CrossRef] [PubMed]
- Situ, G.; Zhang, J. Double Random-Phase Encoding in the Fresnel Domain. Opt. Lett. 2004, 29, 1584–1586. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhang, X.; Shan, M.; Zhong, Z.; Liu, B.; Yu, L.; Liu, L. Asymmetric Double-Image Encryption via Wavelength Multiplexing. Appl. Opt. 2022, 61, 1248–1253. [Google Scholar] [CrossRef]
- Huang, Z.-J.; Cheng, S.; Gong, L.-H.; Zhou, N.-R. Nonlinear Optical Multi-Image Encryption Scheme with Two-Dimensional Linear Canonical Transform. Opt. Lasers Eng. 2020, 124, 105821. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, H.; Liu, T.; Li, P.; Dai, J.; Sun, X.; Liu, S. Double-Image Encryption Based on the Affine Transform and the Gyrator Transform. J. Opt. 2010, 12, 035407. [Google Scholar] [CrossRef]
- Yadav, P.L.; Singh, H. Security Enrichment of Optical Image Cryptosystem Based on Superposition Technique Using Fractional Hartley and Gyrator Transform Domains Deploying Equal Modulus Decomposition. Opt. Quant. Electron. 2019, 51, 140. [Google Scholar] [CrossRef]
- Wu, J.; Li, S. Optical Multiple-Image Compression-Encryption via Single-Pixel Radon Transform. Appl. Opt. 2020, 59, 9744–9754. [Google Scholar] [CrossRef] [PubMed]
- Katz, O.; Bromberg, Y.; Silberberg, Y. Compressive Ghost Imaging. Appl. Phys. Lett. 2009, 95, 131110. [Google Scholar] [CrossRef]
- Du, J.; Xiong, Y.; Wu, C.; Quan, C. Optical Image Encryption with High Efficiency Based on Variable-Distance Ghost Imaging. Optik 2022, 252, 168484. [Google Scholar] [CrossRef]
- Yuan, S.; Wang, L.; Liu, X.; Zhou, X. Forgery Attack on Optical Encryption Based on Computational Ghost Imaging. Opt. Lett. 2020, 45, 3917–3920. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.-T.C.; Fang, Y.-C.; Tien, C.-H. Deep Neural Network for Coded Mask Cryptographical Imaging. Appl. Opt. 2021, 60, 1686–1693. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, X.; Wang, W.; Wei, H.; Xu, B.; Dai, C. Holographic and Speckle Encryption Using Deep Learning. Opt. Lett. 2021, 46, 5794–5797. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, X.; Wei, H.; Jin, M.; Xu, B.; Chen, J. Experimental Optical Encryption Based on Random Mask Encoding and Deep Learning. Opt. Express 2022, 30, 11165–11173. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Liao, M.; He, W.; Zhang, Y.; Peng, X. Untrained Neural Network for Cryptanalysis of a Phase-Truncated-Fourier-Transform-Based Optical Cryptosystem. Opt. Express 2021, 29, 42642. [Google Scholar] [CrossRef]
- Sachin; Kumar, R.; Singh, P. Modified Plaintext Attacks in a Session for an Optical Cryptosystem Based on DRPE with PFS. Appl. Opt. 2022, 61, 623–628. [Google Scholar] [CrossRef]
- Wu, H.; Li, Q.; Meng, X.; Yang, X.; Liu, S.; Yin, Y. Cryptographic Analysis on an Optical Random-Phase-Encoding Cryptosystem for Complex Targets Based on Physics-Informed Learning. Opt. Express 2021, 29, 33558. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, D. A Special Attack on the Asymmetric Cryptosystem Based on Phase-Truncated Fourier Transforms. Opt. Commun. 2012, 285, 1078–1081. [Google Scholar] [CrossRef]
- Wang, Y.; Quan, C.; Tay, C.J. Improved Method of Attack on an Asymmetric Cryptosystem Based on Phase-Truncated Fourier Transform. Appl. Opt. 2015, 54, 6874–6881. [Google Scholar] [CrossRef]
- Dejean, M.; Nourrit, V.; de Bougrenet de la Tocnaye, J.-L. Optical Scrambling System for Document Authentication by Image Decryption. Opt. Lett. 2020, 45, 347–350. [Google Scholar] [CrossRef]
- Shen, Y.; Tang, C.; Zhou, L.; Lei, Z. Optical Single-Channel Cryptosystem Based on the Discrete Wavelet Transform and the Chaotic Standard Map for Multi-Image. Appl. Opt. 2020, 59, 9558–9567. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Tang, C.; Zhou, L.; Lei, Z. Optical Asymmetric Cryptosystem for Multi-Image in Cyan–Magenta–Yellow–Black Color Space. Appl. Opt. 2020, 59, 1854–1863. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Chang, J.; Quan, C.; Zhang, Y. Optical Cryptosystem Model Based on the Keyspace Transformation. Opt. Commun. 2020, 462, 125347. [Google Scholar] [CrossRef]
- DhiyaEddine, C.M.; Rachid, H.; Alfalou, A.; Abderezzaq, H.; Badr-Eddine, B. Tailored Dual Polarization Encryption-Coherence Modulation-Based Decryption Scheme for a Predefined Uniformly Distributed Noisy Output Image. Opt. Express 2022, 30, 17400. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, T.; Liao, Y.; Li, D.-H.; Li, X. 3D Medical Images Security via Light-Field Imaging. Opt. Lett. 2022, 47, 3535–3538. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.-H.; Hwang, Y.-S.; Wang, H.-C.; Wang, Y.-L.; Tsai, K.-Y. Microstructure Overlapping Image Application with Optical Decryption. J. Opt. Soc. Am. A 2020, 37, 1361–1368. [Google Scholar] [CrossRef]
- Yu, H.; Chang, J.; Liu, X.; Wu, C.; He, Y.; Zhang, Y. Novel Asymmetric Cryptosystem Based on Distorted Wavefront Beam Illumination and Double-Random Phase Encoding. Opt. Express 2017, 25, 8860–8871. [Google Scholar] [CrossRef]
- Cai, J.; Shen, X.; Lei, M.; Lin, C.; Dou, S. Asymmetric Optical Cryptosystem Based on Coherent Superposition and Equal Modulus Decomposition. Opt. Lett. 2015, 40, 475–478. [Google Scholar] [CrossRef]
- Kumar, R.; Bhaduri, B.; Nishchal, N.K. Nonlinear QR Code Based Optical Image Encryption Using Spiral Phase Transform, Equal Modulus Decomposition and Singular Value Decomposition. J. Opt. 2018, 20, 015701. [Google Scholar] [CrossRef]
- Xu, X.; Chang, J.; Wu, C.; Liu, X.; Zhang, X.; Zhang, Y. Influences of Aberrations on Double Random Phase Encoding System. In Proceedings of the Optical Design and Testing X; Wu, R., Matoba, O., Wang, Y., Kidger, T.E., Eds.; SPIE, China, 10 October 2020; SPIE: Bellingham, WA, USA, 2020; p. 5. [Google Scholar]
- Atchison, D.A.; Scott, D.H.; Cox, M.J. Mathematical Treatment of Ocular Aberrations: A User’s Guide. In Proceedings of the Vision Science and its Applications; OSA: Santa Fe, NM, USA, 2000; p. NW2. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Nunes, J.C.; Niang, O.; Bouaoune, Y.; Delechelle, E.; Bunel, P. Texture Analysis Based on the Bidimensional Empirical Mode Decomposition with Gray-Level Co-Occurrence Models. In Proceedings of the Seventh International Symposium on Signal Processing and Its Applications, Paris, France, 4 July 2003; Volume 2, pp. 633–635. [Google Scholar]
- Nunes, J.C.; Bouaoune, Y.; Delechelle, E.; Niang, O.; Bunel, P. Image Analysis by Bidimensional Empirical Mode Decomposition. Image Vis. Comput. 2003, 21, 1019–1026. [Google Scholar] [CrossRef]
- Mehra, I.; Nishchal, N.K. Optical Asymmetric Image Encryption Using Gyrator Wavelet Transform. Opt. Commun. 2015, 354, 344–352. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 4th ed.; Pearson: Indianapolis, IN, USA, 2017; ISBN 978-0-13-335672-4. [Google Scholar]
- Bovik, A.C. Chapter 3—Basic Gray Level Image Processing. In The Essential Guide to Image Processing; Bovik, A., Ed.; Academic Press: Boston, MA, USA, 2009; pp. 43–68. ISBN 978-0-12-374457-9. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).