Fully Phase-Locked Fiber Dual Comb Enables Accurate Frequency and Phase Detection in Multidimensional Coherent Spectroscopy
Abstract
:1. Introduction
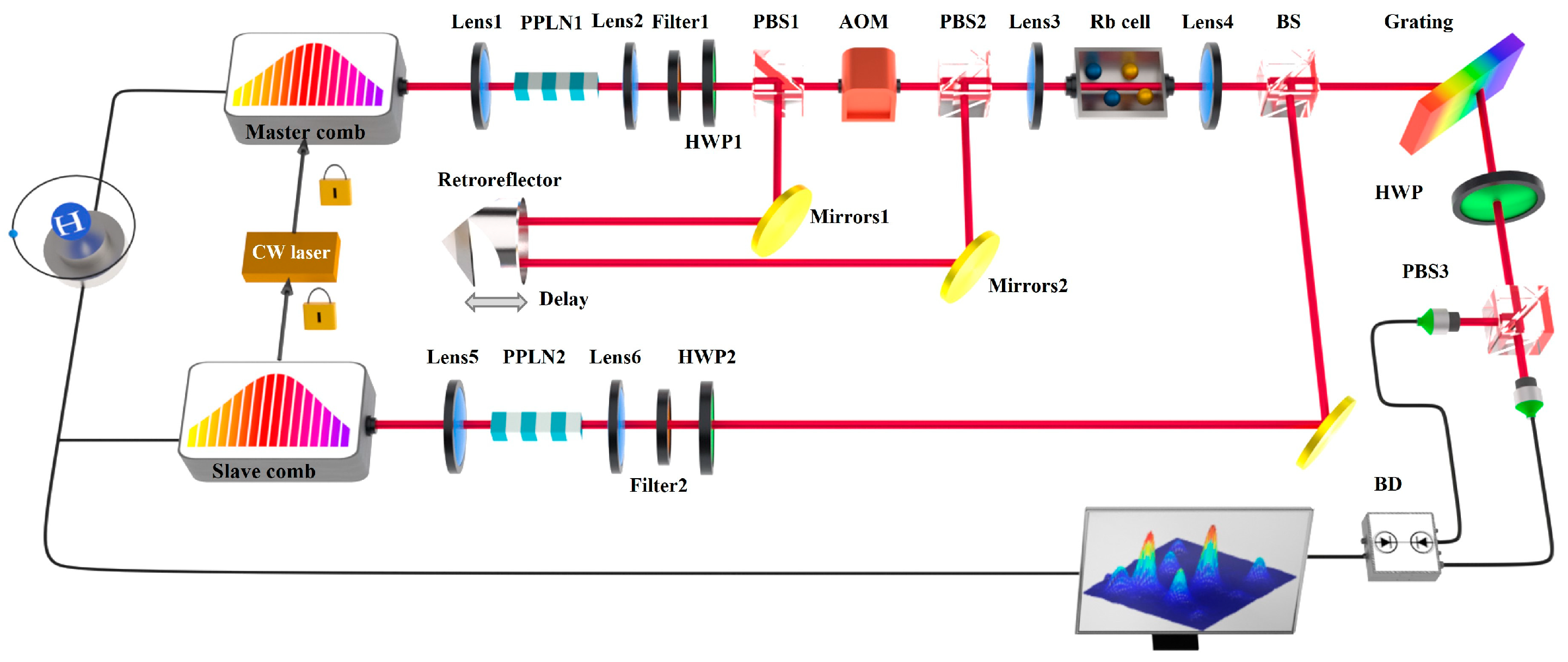
2. Experimental Setup and Principle
2.1. MDCS System Based on the Fully Phase-Locked Fiber DCS
2.2. The Principle of Photon Echo and Double-Quantum Signal
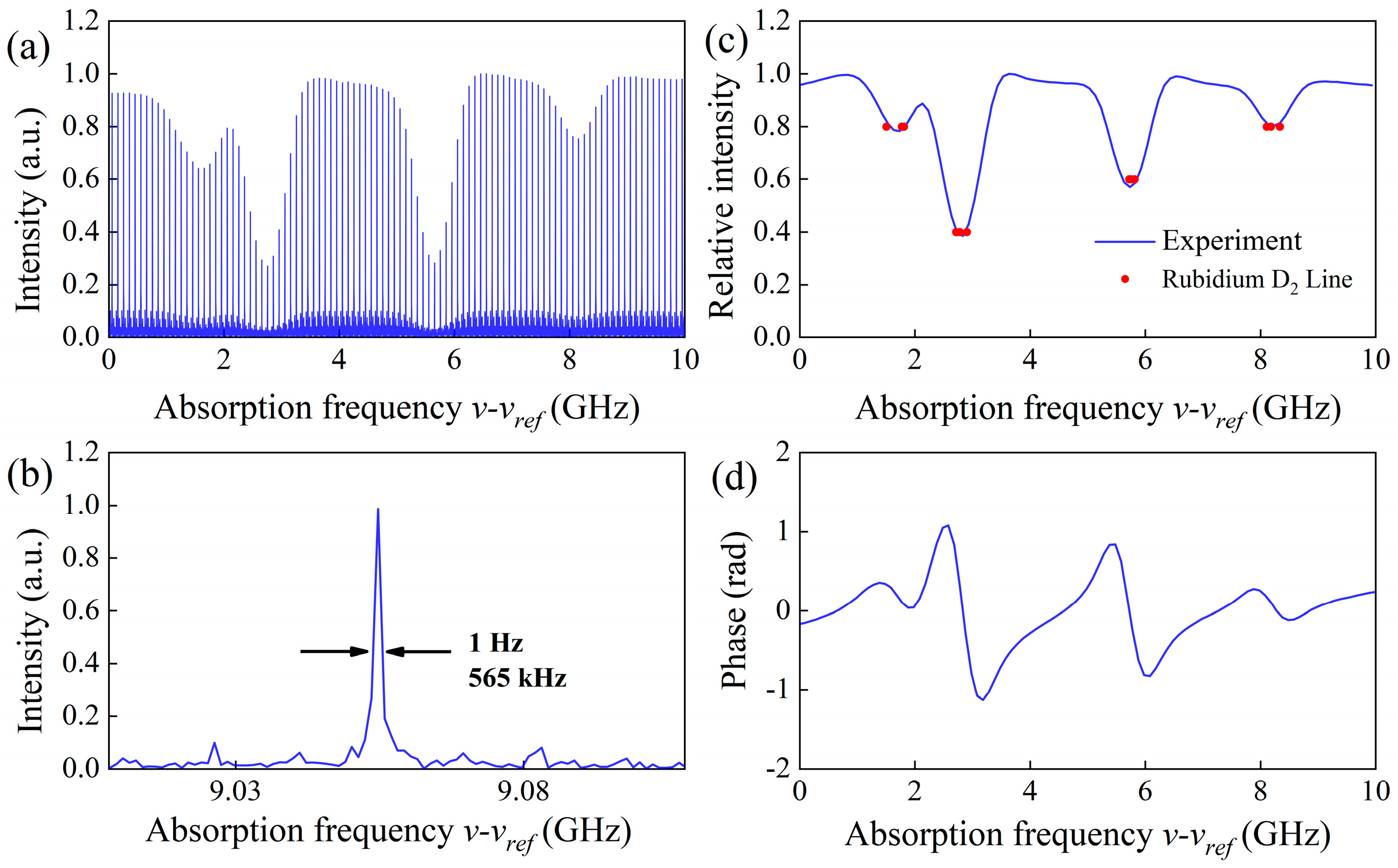
2.3. The Data Acquisition of Photon Echo and Double-Quantum Spectrum
3. Results and Discussion
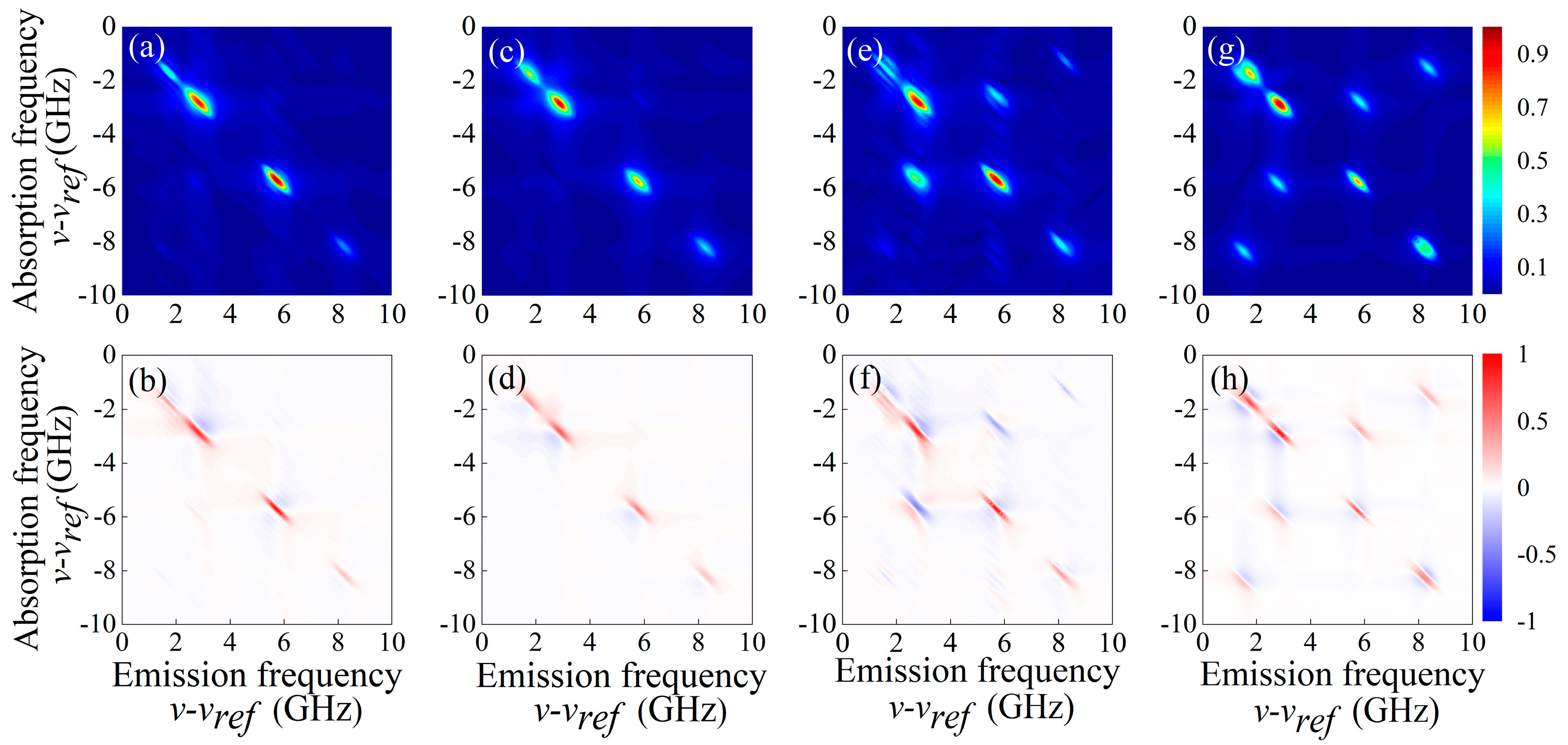
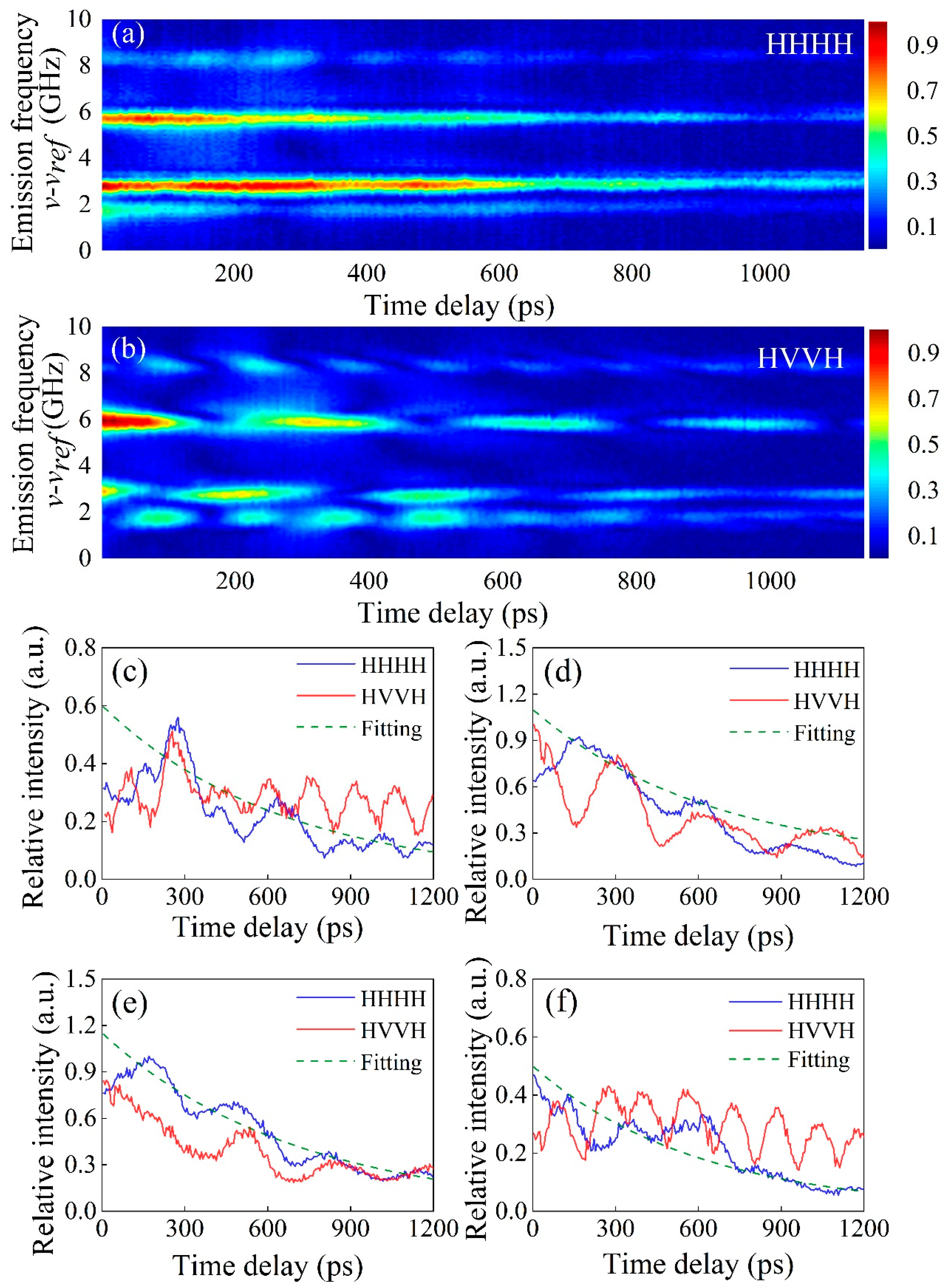
3.1. Photon Echo 2DCS
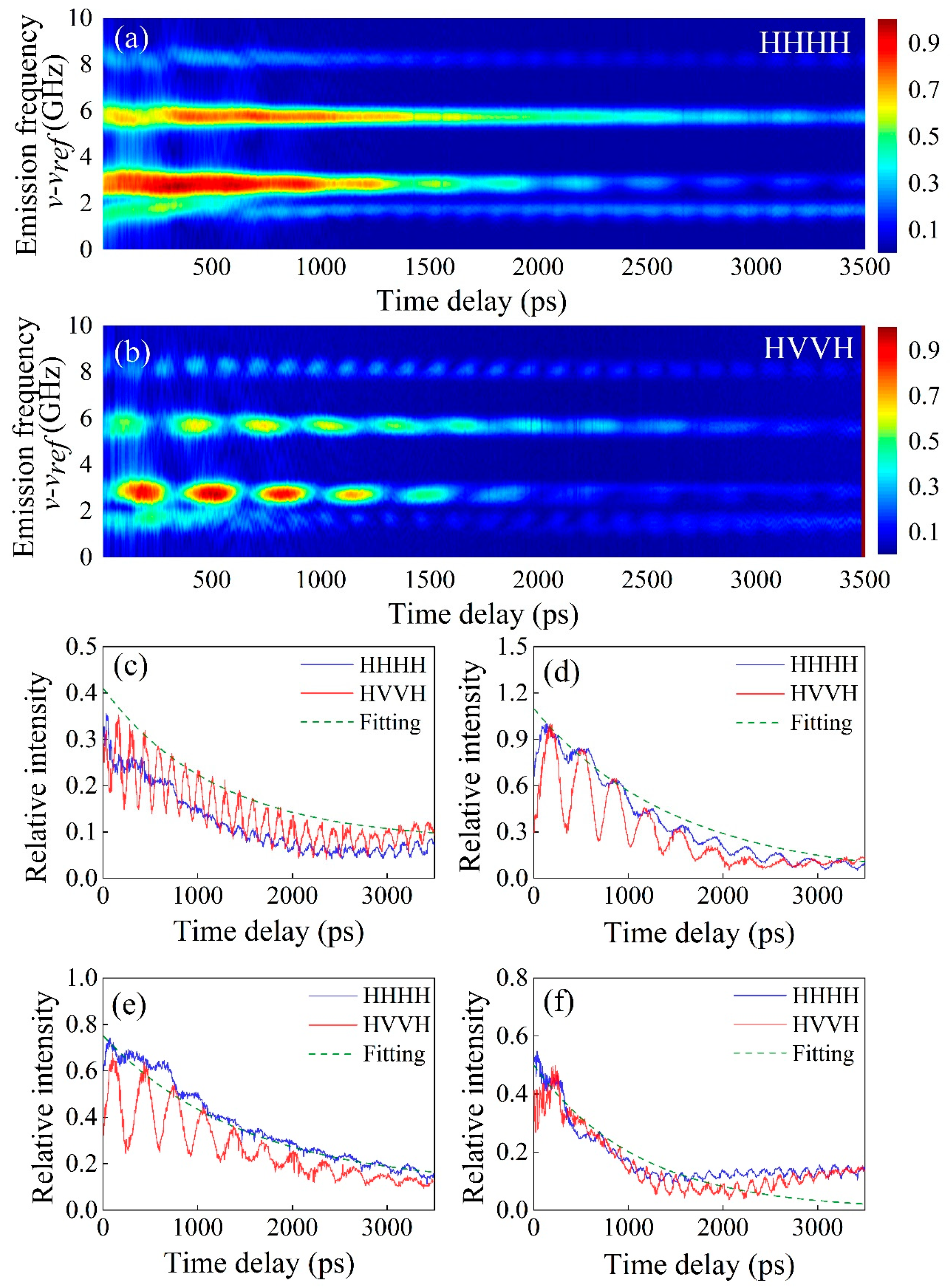
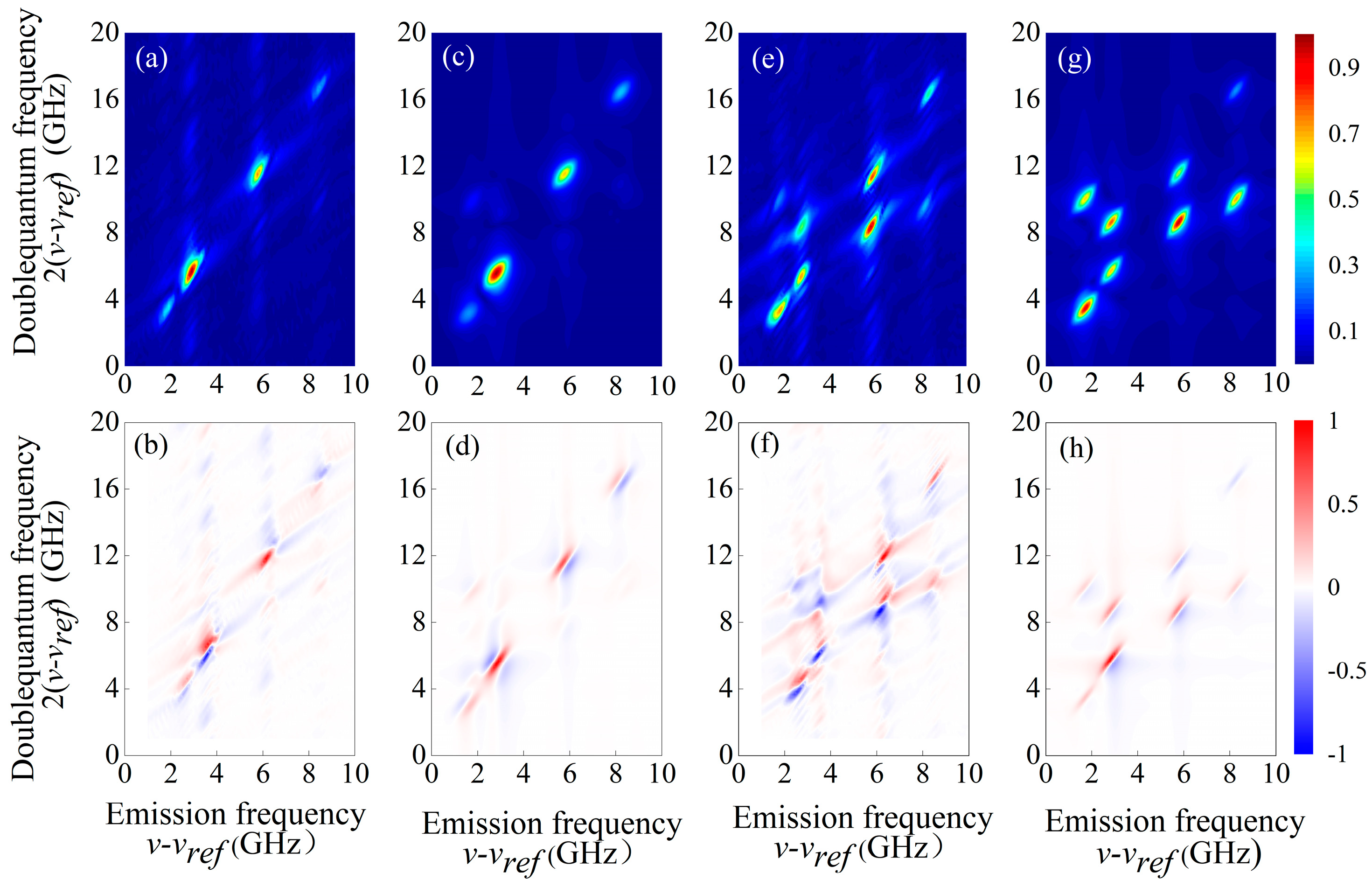
3.2. Double-Quantum 2DCS
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ernst, R.R.; Bodenhausen, G.; Wokaun, A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions; International Series of Monographs on Chemistry; Oxford University Press: Oxford, UK; New York, NY, USA, 1990; ISBN 978-0-19-855647-3. [Google Scholar]
- Wei, Z.; Yang, J.; Chen, Y.; Chen, L.; Cao, S.; Cai, S.; Lin, Y.; Chen, Z. Ultrafast Multidimensional Nuclear Magnetic Resonance Technique: A Proof of Concept Based on Inverse-k-Space for Convenient and Efficient Performance. Appl. Phys. Lett. 2016, 108, 084102. [Google Scholar] [CrossRef]
- Hamm, P.; Zanni, M. Concepts and Methods of 2D Infrared Spectroscopy; Cambridge University Press: Cambridge, UK, 2011; ISBN 978-1-107-00005-6. [Google Scholar]
- Chemla, D.S.; Shah, J. Many-Body and Correlation Effects in Semiconductors. Nature 2001, 411, 549–557. [Google Scholar] [CrossRef] [PubMed]
- Cundiff, S.T.; Zhang, T.; Bristow, A.D.; Karaiskaj, D.; Dai, X. Optical Two-Dimensional Fourier Transform Spectroscopy of Semiconductor Quantum Wells. Acc. Chem. Res. 2009, 42, 1423–1432. [Google Scholar] [CrossRef] [PubMed]
- Moody, G.; Cundiff, S.T. Advances in Multi-Dimensional Coherent Spectroscopy of Semiconductor Nanostructures. Adv. Phys. X 2017, 2, 641–674. [Google Scholar] [CrossRef] [PubMed]
- Bristow, A.D.; Karaiskaj, D.; Dai, X.; Mirin, R.P.; Cundiff, S.T. Polarization Dependence of Semiconductor Exciton and Biexciton Contributions to Phase-Resolved Optical Two-Dimensional Fourier-Transform Spectra. Phys. Rev. B 2009, 79, 161305. [Google Scholar] [CrossRef]
- Li, X.; Zhang, T.; Borca, C.N.; Cundiff, S.T. Many-Body Interactions in Semiconductors Probed by Optical Two-Dimensional Fourier Transform Spectroscopy. Phys. Rev. Lett. 2006, 96, 057406. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Trovatello, C.; Dal Conte, S.; Nuß, M.; Soavi, G.; Wang, G.; Ferrari, A.C.; Cerullo, G.; Brixner, T. Exciton–Phonon Coupling Strength in Single-Layer MoSe2 at Room Temperature. Nat. Commun. 2021, 12, 954. [Google Scholar] [CrossRef]
- Shacklette, J.M.; Cundiff, S.T. Role of Excitation-Induced Shift in the Coherent Optical Response of Semiconductors. Phys. Rev. B 2002, 66, 045309. [Google Scholar] [CrossRef]
- Wang, H.; Ferrio, K.; Steel, D.G.; Hu, Y.Z.; Binder, R.; Koch, S.W. Transient Nonlinear Optical Response from Excitation Induced Dephasing in GaAs. Phys. Rev. Lett. 1993, 71, 1261–1264. [Google Scholar] [CrossRef]
- Zheng, J.; Kwak, K.; Asbury, J.; Chen, X.; Piletic, I.R.; Fayer, M.D. Ultrafast Dynamics of Solute-Solvent Complexation Observed at Thermal Equilibrium in Real Time. Science 2005, 309, 1338–1343. [Google Scholar] [CrossRef]
- Ghosh, A.; Hochstrasser, R.M. A Peptide’s Perspective of Water Dynamics. Chem. Phys. 2011, 390, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Luo, Y.; Zhang, Y.; Yu, Y.-J.; Kuang, Y.-M.; Zhang, L.; Meng, Q.-S.; Luo, Y.; Yang, J.-L.; Dong, Z.-C.; et al. Visualizing Coherent Intermolecular Dipole–Dipole Coupling in Real Space. Nature 2016, 531, 623–627. [Google Scholar] [CrossRef] [PubMed]
- Abramavicius, D.; Palmieri, B.; Voronine, D.V.; Šanda, F.; Mukamel, S. Coherent Multidimensional Optical Spectroscopy of Excitons in Molecular Aggregates; Quasiparticle versus Supermolecule Perspectives. Chem. Rev. 2009, 109, 2350–2408. [Google Scholar] [CrossRef] [PubMed]
- Cannizzo, A. Ultrafast UV Spectroscopy: From a Local to a Global View of Dynamical Processes in Macromolecules. Phys. Chem. Chem. Phys. 2012, 14, 11205–11223. [Google Scholar] [CrossRef] [PubMed]
- Russo, M.; McGhee, K.E.; Virgili, T.; Lidzey, D.G.; Cerullo, G.; Maiuri, M. Dephasing Processes in the Molecular Dye Lumogen-F Orange Characterized by Two-Dimensional Electronic Spectroscopy. Molecules 2022, 27, 7095. [Google Scholar] [CrossRef]
- Policht, V.R.; Russo, M.; Liu, F.; Trovatello, C.; Maiuri, M.; Bai, Y.; Zhu, X.; Dal Conte, S.; Cerullo, G. Dissecting Interlayer Hole and Electron Transfer in Transition Metal Dichalcogenide Heterostructures via Two-Dimensional Electronic Spectroscopy. Nano Lett. 2021, 21, 4738–4743. [Google Scholar] [CrossRef] [PubMed]
- Zhu, R.; Zou, J.; Wang, Z.; Chen, H.; Weng, Y. Electronic State-Resolved Multimode-Coupled Vibrational Wavepackets in Oxazine 720 by Two-Dimensional Electronic Spectroscopy. J. Phys. Chem. A 2020, 124, 9333–9342. [Google Scholar] [CrossRef]
- Nardin, G.; Autry, T.M.; Silverman, K.L.; Cundiff, S.T. Multidimensional Coherent Photocurrent Spectroscopy of a Semiconductor Nanostructure. Opt. Express 2013, 21, 28617–28627. [Google Scholar] [CrossRef]
- Tekavec, P.F.; Lott, G.A.; Marcus, A.H. Fluorescence-Detected Two-Dimensional Electronic Coherence Spectroscopy by Acousto-Optic Phase Modulation. J. Chem. Phys. 2007, 127, 214307. [Google Scholar] [CrossRef]
- Bristow, A.D.; Karaiskaj, D.; Dai, X.; Zhang, T.; Carlsson, C.; Hagen, K.R.; Jimenez, R.; Cundiff, S.T. A Versatile Ultrastable Platform for Optical Multidimensional Fourier-Transform Spectroscopy. Rev. Sci. Instrum. 2009, 80, 073108. [Google Scholar] [CrossRef]
- Munoz, M.F.; Medina, A.; Autry, T.M.; Moody, G.; Siemens, M.E.; Bristow, A.D.; Cundiff, S.T.; Li, H. Fast Phase Cycling in Non-Collinear Optical Two-Dimensional Coherent Spectroscopy. Opt. Lett. 2020, 45, 5852–5855. [Google Scholar] [CrossRef]
- Wagner, W.; Li, C.; Semmlow, J.; Warren, W.S. Rapid Phase-Cycled Two-Dimensional Optical Spectroscopy in Fluorescence and Transmission Mode. Opt. Express 2005, 13, 3697–3706. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, V. Multidimensional Electronic Spectroscopy in High-Definition—Combining Spectral, Temporal, and Spatial Resolutions. J. Chem. Phys. 2021, 154, 230901. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Kuznetsova, I.; Meier, T.; Li, X.; Mirin, R.P.; Thomas, P.; Cundiff, S.T. Polarization-Dependent Optical 2D Fourier Transform Spectroscopy of Semiconductors. Proc. Natl. Acad. Sci. USA 2007, 104, 14227–14232. [Google Scholar] [CrossRef] [PubMed]
- Bristow, A.D.; Karaiskaj, D.; Dai, X.; Cundiff, S.T. All-Optical Retrieval of the Global Phase for Two-Dimensional Fourier-Transform Spectroscopy. Opt. Express 2008, 16, 18017–18027. [Google Scholar] [CrossRef] [PubMed]
- Jonas, D.M. Two-Dimensional Femtosecond Spectroscopy. Annu. Rev. Phys. Chem. 2003, 54, 425–463. [Google Scholar] [CrossRef] [PubMed]
- Keusters, D.; Tan, H.-S. Warren Role of Pulse Phase and Direction in Two-Dimensional Optical Spectroscopy. J. Phys. Chem. A 1999, 103, 10369–10380. [Google Scholar] [CrossRef]
- Zhu, Z.; Yang, S.; He, C.; Lin, X. Cavity-Birefringence-Dependent Vector Pure-Quartic Soliton Fiber Laser. Opt. Express 2023, 31, 35529–35541. [Google Scholar] [CrossRef]
- Zhu, Z.; Yang, S.; He, C.; Lin, X. Vector Pure-Quartic Soliton Molecule Fiber Laser. Chaos Solitons Fractals 2023, 175, 113978. [Google Scholar] [CrossRef]
- Ideguchi, T.; Bernhardt, B.; Guelachvili, G.; Hänsch, T.W.; Picqué, N. Raman-Induced Kerr-Effect Dual-Comb Spectroscopy. Opt. Lett. 2012, 37, 4498–4500. [Google Scholar] [CrossRef]
- Ideguchi, T.; Holzner, S.; Bernhardt, B.; Guelachvili, G.; Picqué, N.; Hänsch, T.W. Coherent Raman Spectro-Imaging with Laser Frequency Combs. Nature 2013, 502, 355–358. [Google Scholar] [CrossRef] [PubMed]
- Coluccelli, N.; Howle, C.R.; McEwan, K.; Wang, Y.; Fernandez, T.T.; Gambetta, A.; Laporta, P.; Galzerano, G. Fiber-Format Dual-Comb Coherent Raman Spectrometer. Opt. Lett. 2017, 42, 4683–4686. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Wu, T.; Chen, T.; Wei, H.; Yang, H.; Zhou, T.; Li, Y. Spectral Focusing Dual-Comb Coherent Anti-Stokes Raman Spectroscopic Imaging. Opt. Lett. 2017, 42, 3634–3637. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Yoon, T.H.; Cho, M. Time-Resolved Impulsive Stimulated Raman Spectroscopy with Synchronized Triple Mode-Locked Lasers. J. Phys. Chem. Lett. 2020, 11, 2864–2869. [Google Scholar] [CrossRef] [PubMed]
- Asahara, A.; Minoshima, K. Development of Ultrafast Time-Resolved Dual-Comb Spectroscopy. APL Photon. 2017, 2, 041301. [Google Scholar] [CrossRef]
- Cho, M. Coherent Nonlinear Spectroscopy with Multiple Mode-Locked Lasers. J. Phys. Chem. Lett. 2021, 12, 10284–10294. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Cho, B.; Yoon, T.H.; Cho, M. Dual-Frequency Comb Transient Absorption: Broad Dynamic Range Measurement of Femtosecond to Nanosecond Relaxation Processes. J. Phys. Chem. Lett. 2018, 9, 1866–1871. [Google Scholar] [CrossRef]
- Kim, J.; Yoon, T.H.; Cho, M. Interferometric Measurement of Transient Absorption and Refraction Spectra with Dual Frequency Comb. J. Phys. Chem. B 2018, 122, 9775–9785. [Google Scholar] [CrossRef]
- Kim, J.; Jeon, J.; Yoon, T.H.; Cho, M. Dual Frequency-Comb Spectroscopy of Chromophores in Condensed Phases. Chem. Phys. 2019, 520, 122–137. [Google Scholar] [CrossRef]
- Lomsadze, B.; Cundiff, S.T. Frequency Combs Enable Rapid and High-Resolution Multidimensional Coherent Spectroscopy. Science 2017, 357, 1389–1391. [Google Scholar] [CrossRef]
- Lomsadze, B.; Smith, B.C.; Cundiff, S.T. Tri-Comb Spectroscopy. Nat. Photon. 2018, 12, 676–680. [Google Scholar] [CrossRef]
- Lomsadze, B.; Cundiff, S.T. Frequency Comb-Based Four-Wave-Mixing Spectroscopy. Opt. Lett. 2017, 42, 2346–2349. [Google Scholar] [CrossRef] [PubMed]
- Lomsadze, B.; Cundiff, S.T. Frequency-Comb Based Double-Quantum Two-Dimensional Spectrum Identifies Collective Hyperfine Resonances in Atomic Vapor Induced by Dipole-Dipole Interactions. Phys. Rev. Lett. 2018, 120, 233401. [Google Scholar] [CrossRef] [PubMed]
- Ideguchi, T.; Poisson, A.; Guelachvili, G.; Picqué, N.; Hänsch, T.W. Adaptive Real-Time Dual-Comb Spectroscopy. Nat. Commun. 2014, 5, 3375. [Google Scholar] [CrossRef] [PubMed]
- Ideguchi, T.; Poisson, A.; Guelachvili, G.; Hänsch, T.W.; Picqué, N. Adaptive Dual-Comb Spectroscopy in the Green Region. Opt. Lett. 2012, 37, 4847–4849. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Ivanov, E.; Kitching, J.; Donley, E.A. Frequency Shift Mitigation in a Cold-Atom CPT Clock. In Proceedings of the 2016 IEEE International Frequency Control Symposium (IFCS), New Orleans, LA, USA, 9–12 May 2016; pp. 1–3. [Google Scholar]
- Eckner, W.J.; Darkwah Oppong, N.; Cao, A.; Young, A.W.; Milner, W.R.; Robinson, J.M.; Ye, J.; Kaufman, A.M. Realizing Spin Squeezing with Rydberg Interactions in an Optical Clock. Nature 2023, 621, 734–739. [Google Scholar] [CrossRef] [PubMed]
- Aeppli, A.; Chu, A.; Bothwell, T.; Kennedy, C.J.; Kedar, D.; He, P.; Rey, A.M.; Ye, J. Hamiltonian Engineering of Spin-Orbit–Coupled Fermions in a Wannier-Stark Optical Lattice Clock. Sci. Adv. 2022, 8, eadc9242. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Yan, M.; Hänsch, T.W.; Picqué, N. A Phase-Stable Dual-Comb Interferometer. Nat. Commun. 2018, 9, 3035. [Google Scholar] [CrossRef]
- Deng, Z.; Liu, Y.; Zhu, Z.; Luo, D.; Gu, C.; Zhou, L.; Xie, G.; Li, W. Ultra-Precise Optical Phase-Locking Approach for Ultralow Noise Frequency Comb Generation. Opt. Laser Technol. 2021, 138, 106906. [Google Scholar] [CrossRef]
- Asahara, A.; Nishiyama, A.; Yoshida, S.; Kondo, K.; Nakajima, Y.; Minoshima, K. Dual-Comb Spectroscopy for Rapid Characterization of Complex Optical Properties of Solids. Opt. Lett. 2016, 41, 4971–4974. [Google Scholar] [CrossRef]
- Benko, C.; Ruehl, A.; Martin, M.J.; Eikema, K.S.E.; Fermann, M.E.; Hartl, I.; Ye, J. Full Phase Stabilization of a Yb:Fiber Femtosecond Frequency Comb via High-Bandwidth Transducers. Opt. Lett. 2012, 37, 2196–2198. [Google Scholar] [CrossRef] [PubMed]
- Ascarrunz, F.G.; Dudin, Y.O.; Delgado Aramburo, M.C.; Ascarrunz, L.I.; Savory, J.; Banducci, A.; Jefferts, S.R. A Portable Cold 87Rb Atomic Clock with Frequency Instability at One Day in the 10−15 Range. In Proceedings of the 2018 IEEE International Frequency Control Symposium (IFCS), Olympic Valley, CA, USA, 21–24 May 2018; pp. 1–3. [Google Scholar]
- Chabbra, N.; Wade, A.R.; Rose Rees, E.; Sutton, A.J.; Stochino, A.; Ward, R.L.; Shaddock, D.A.; McKenzie, K. High Stability Laser Locking to an Optical Cavity Using Tilt Locking. Opt. Lett. 2021, 46, 3199–3202. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Aeppli, A.; Bothwell, T.; Ye, J. Evaluation of Lattice Light Shift at Low 10−19 Uncertainty for a Shallow Lattice Sr Optical Clock. Phys. Rev. Lett. 2023, 130, 113203. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Spencer, A.P.; Kortyna, A.; Moody, G.; Jonas, D.M.; Cundiff, S.T. Pulse Propagation Effects in Optical 2D Fourier-Transform Spectroscopy: Experiment. J. Phys. Chem. A 2013, 117, 6279–6287. [Google Scholar] [CrossRef] [PubMed]
- DA Steck Rubidium 85 and 87 D Line Data (2008). Available online: http://steck.us/alkalidata (accessed on 30 April 2008).
- Tokmakoff, A. Two-Dimensional Line Shapes Derived from Coherent Third-Order Nonlinear Spectroscopy. J. Phys. Chem. A 2000, 104, 4247–4255. [Google Scholar] [CrossRef]
- Siemens, M.E.; Moody, G.; Li, H.; Bristow, A.D.; Cundiff, S.T. Resonance Lineshapes in Two-Dimensional Fourier Transform Spectroscopy. In Frontiers in Optics 2010/Laser Science XXVI; Optica Publishing Group: Washington, DC, USA, 2010; p. LThA3. [Google Scholar]
- Lomsadze, B.; Weight, S.C.; Hovland, P.K.D. Effects of Phase Accumulation in Frequency-Comb-Based Multidimensional Coherent Spectroscopy. Phys. Rev. A 2022, 106, 033704. [Google Scholar] [CrossRef]
- Lomsadze, B.; Cundiff, S.T. Line-Shape Analysis of Double-Quantum Multidimensional Coherent Spectra. Phys. Rev. A 2020, 102, 043514. [Google Scholar] [CrossRef]
- Zuo, Z.; Gu, C.; Wang, S.; Xiong, S.; Deng, Z.; Di, Y.; Luo, D.; Wu, J.; Li, W. Phase-Stable Multidimensional Coherent Spectroscopy Based on Dual-Comb Interferometry. Adv. Optical Mater. 2024, 2303130. [Google Scholar] [CrossRef]
- Coddington, I.; Swann, W.C.; Nenadovic, L.; Newbury, N.R. Rapid and Precise Absolute Distance Measurements at Long Range. Nat. Photon. 2009, 3, 351–356. [Google Scholar] [CrossRef]
- Cundiff, S.T. Effects of Correlation between Inhomogeneously Broadened Transitions on Quantum Beats in Transient Four-Wave Mixing. Phys. Rev. A 1994, 49, 3114–3118. [Google Scholar] [CrossRef]
- Li, H.; Lomsadze, B.; Moody, G.; Smallwood, C.; Cundiff, S. Optical Multidimensional Coherent Spectroscopy; Oxford University Press: Oxford, UK, 2023; ISBN 978-0-19-284386-9. [Google Scholar]
- Yi, Z.; Begzjav, T.K.; Ariunbold, G.O.; Zheltikov, A.M.; Sokolov, A.V.; Scully, M.O. Multiple Pathway Quantum Beat Spectroscopy. Front. Phys. 2022, 10, 921499. [Google Scholar] [CrossRef]
- Dai, X.; Richter, M.; Li, H.; Bristow, A.D.; Falvo, C.; Mukamel, S.; Cundiff, S.T. Two-Dimensional Double-Quantum Spectra Reveal Collective Resonances in an Atomic Vapor. Phys. Rev. Lett. 2012, 108, 193201. [Google Scholar] [CrossRef]
- Bott, K.; Heller, O.; Bennhardt, D.; Cundiff, S.T.; Thomas, P.; Mayer, E.J.; Smith, G.O.; Eccleston, R.; Kuhl, J.; Ploog, K. Influence of Exciton-Exciton Interactions on the Coherent Optical Response in GaAs Quantum Wells. Phys. Rev. B 1993, 48, 17418–17426. [Google Scholar] [CrossRef]
- Yetzbacher, M.K.; Belabas, N.; Kitney, K.A.; Jonas, D.M. Propagation, Beam Geometry, and Detection Distortions of Peak Shapes in Two-Dimensional Fourier Transform Spectra. J. Chem. Phys. 2007, 126, 044511. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, S.; Deng, Z.; Zuo, Z.; Pan, J.; Zhao, Z.; Xie, G.; Li, W. Fully Phase-Locked Fiber Dual Comb Enables Accurate Frequency and Phase Detection in Multidimensional Coherent Spectroscopy. Photonics 2024, 11, 120. https://doi.org/10.3390/photonics11020120
Xiong S, Deng Z, Zuo Z, Pan J, Zhao Z, Xie G, Li W. Fully Phase-Locked Fiber Dual Comb Enables Accurate Frequency and Phase Detection in Multidimensional Coherent Spectroscopy. Photonics. 2024; 11(2):120. https://doi.org/10.3390/photonics11020120
Chicago/Turabian StyleXiong, Shiping, Zejiang Deng, Zhong Zuo, Jiayi Pan, Zilin Zhao, Gehui Xie, and Wenxue Li. 2024. "Fully Phase-Locked Fiber Dual Comb Enables Accurate Frequency and Phase Detection in Multidimensional Coherent Spectroscopy" Photonics 11, no. 2: 120. https://doi.org/10.3390/photonics11020120
APA StyleXiong, S., Deng, Z., Zuo, Z., Pan, J., Zhao, Z., Xie, G., & Li, W. (2024). Fully Phase-Locked Fiber Dual Comb Enables Accurate Frequency and Phase Detection in Multidimensional Coherent Spectroscopy. Photonics, 11(2), 120. https://doi.org/10.3390/photonics11020120



