Design of an Achromatic Graphene Oxide Metalens with Multi-Wavelength for Visible Light
Abstract
:1. Introduction
2. Theoretical Model
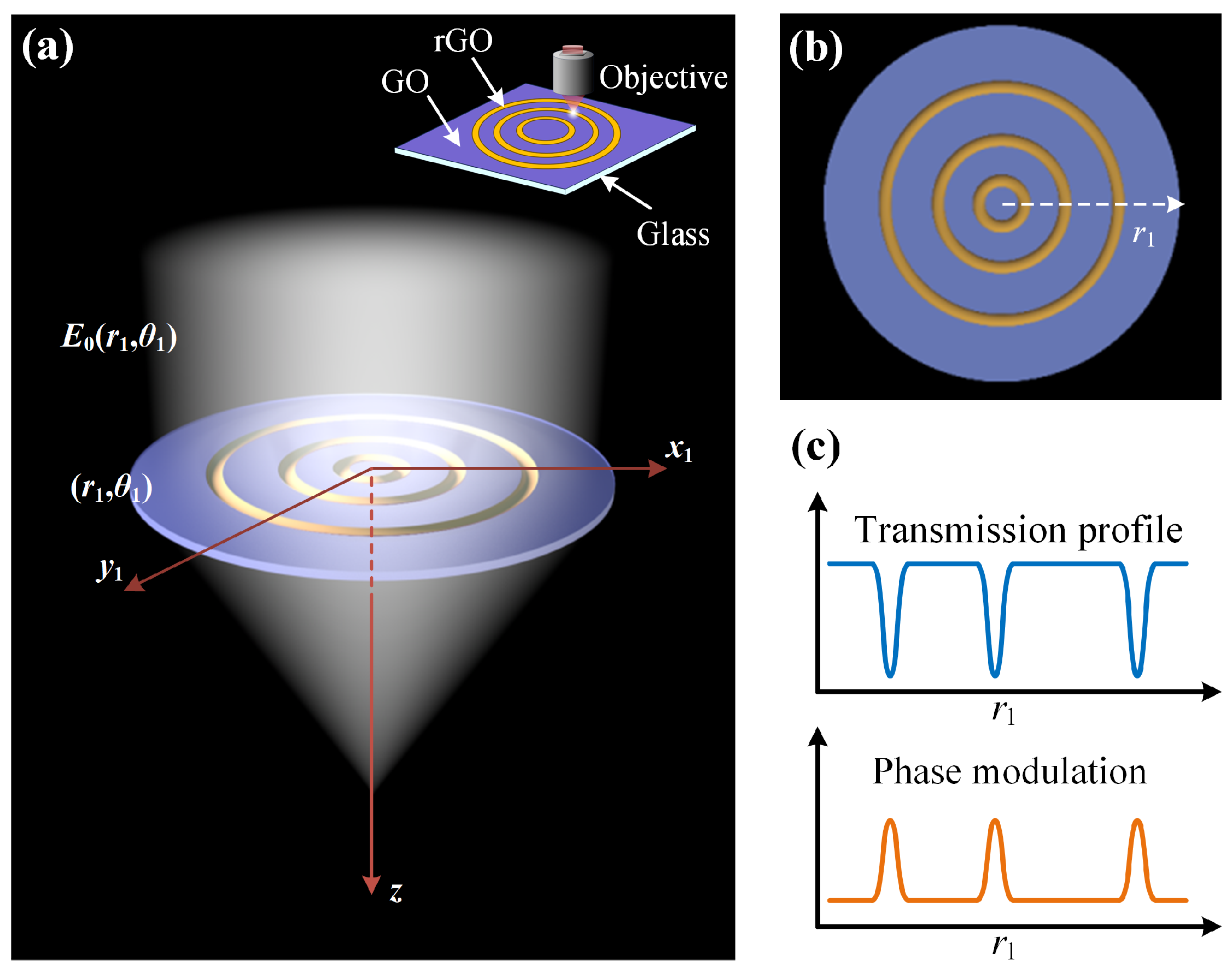
2.1. Imaging Principle of Graphene Oxide Metalens
2.2. Model of Multi-Wavelength Achromatic Aberration GO Metalens
3. Results and Discussion
3.1. Optimized Design of Achromatic Graphene Oxide Metalens
3.2. Achromatic Focusing Characterization
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, W.; Duan, F.; Tatsumi, K.; Beaucamp, A. Monolithic topological honeycomb lens for achromatic focusing and imaging. Optica 2022, 9, 100–107. [Google Scholar] [CrossRef]
- Pinilla, S.; Rostami, S.R.M.; Shevkunov, I.; Katkovnik, V.; Egiazarian, K. Hybrid diffractive optics design via hardware-in-the-loop methodology for achromatic extended-depth-of-field imaging. Opt. Express 2022, 30, 32633–32649. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Yang, L.; Yang, Y.; Wu, R.; Zhang, L.; Chen, L.; Wu, D.; She, J. Improved optical camera communication systems using a freeform lens. Opt. Express 2021, 29, 34066–34076. [Google Scholar] [CrossRef] [PubMed]
- Dholakia, K.; Drinkwater, B.W.; Ritsch-Marte, M. Comparing acoustic and optical forces for biomedical research. Nat. Rev. Phys. 2020, 2, 480–491. [Google Scholar] [CrossRef]
- Luo, Y.; Chu, C.H.; Vyas, S.; Kuo, H.Y.; Chia, Y.H.; Chen, M.K.; Shi, X.; Tanaka, T.; Misawa, H.; Huang, Y.Y.; et al. Varifocal metalens for optical sectioning fluorescence microscopy. Nano Lett. 2021, 21, 5133–5142. [Google Scholar] [CrossRef] [PubMed]
- Coste, A.; Oktay, M.H.; Condeelis, J.S.; Entenberg, D. Intravital imaging techniques for biomedical and clinical research. Cytom. Part A 2020, 97, 448–457. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Zheng, Y.; Li, J.; Cheng, Y.; Wang, J.; Zhou, Z.K.; Chen, L. High-resolution metalens imaging polarimetry. Nano Lett. 2023, 23, 10991–10997. [Google Scholar] [CrossRef] [PubMed]
- Bai, J.; Li, X.; Wang, X.; Wang, J.; Ni, K.; Zhou, Q. Self-reference dispersion correction for chromatic confocal displacement measurement. Opt. Lasers Eng. 2021, 140, 106540. [Google Scholar] [CrossRef]
- Hecht, E. Optics; Pearson Education India: Delhi, India, 2012. [Google Scholar]
- Sun, W.S.; Tien, C.L.; Liang, S.S.; Lin, J.S. A Cost-Effective Triplet Lens Design with Chromatic Aberration Correction Based on Optimization Algorithm and Illustration Method. Appl. Sci. 2022, 12, 11881. [Google Scholar] [CrossRef]
- Shrestha, S.; Overvig, A.C.; Lu, M.; Stein, A.; Yu, N. Broadband achromatic dielectric metalenses. Light Sci. Appl. 2018, 7, 85. [Google Scholar] [CrossRef]
- Ndao, A.; Hsu, L.; Ha, J.; Park, J.H.; Chang-Hasnain, C.; Kanté, B. Octave bandwidth photonic fishnet-achromatic-metalens. Nat. Commun. 2020, 11, 3205. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.K.; Wu, Y.; Feng, L.; Fan, Q.; Lu, M.; Xu, T.; Tsai, D.P. Principles, functions, and applications of optical meta-lens. Adv. Opt. Mater. 2021, 9, 2001414. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, C.; Wei, Y.; Lin, Y.; Han, Y.; Deng, Y. High-Efficiency Achromatic Metalens Topologically Optimized in the Visible. Nanomaterials 2023, 13, 890. [Google Scholar] [CrossRef] [PubMed]
- Dou, K.; Xie, X.; Pu, M.; Li, X.; Ma, X.; Wang, C.; Luo, X. Off-axis multi-wavelength dispersion controlling metalens for multi-color imaging. Opto-Electron. Adv. 2020, 3, 190005-1. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Shi, Z.; Zhu, A.Y.; Chen, W.T.; Sanjeev, V.; Zaidi, A.; Capasso, F. Achromatic metalens over 60 nm bandwidth in the visible and metalens with reverse chromatic dispersion. Nano Lett. 2017, 17, 1819–1824. [Google Scholar] [CrossRef] [PubMed]
- Aiello, M.D.; Backer, A.S.; Sapon, A.J.; Smits, J.; Perreault, J.D.; Llull, P.; Acosta, V.M. Achromatic varifocal metalens for the visible spectrum. ACS Photonics 2019, 6, 2432–2440. [Google Scholar] [CrossRef]
- Baek, S.; Kim, J.; Kim, Y.; Cho, W.S.; Badloe, T.; Moon, S.W.; Rho, J.; Lee, J.L. High numerical aperture RGB achromatic metalens in the visible. Photonics Res. 2022, 10, B30–B39. [Google Scholar] [CrossRef]
- Qian, Z.; Tian, S.; Zhou, W.; Wang, J.; Guo, H. Broadband achromatic longitudinal bifocal metalens in the visible range based on a single nanofin unit cell. Opt. Express 2022, 30, 11203–11216. [Google Scholar] [CrossRef]
- Chung, H.; Miller, O.D. High-NA achromatic metalenses by inverse design. Opt. Express 2020, 28, 6945–6965. [Google Scholar] [CrossRef]
- Li, Z.; Pestourie, R.; Park, J.S.; Huang, Y.W.; Johnson, S.G.; Capasso, F. Inverse design enables large-scale high-performance meta-optics reshaping virtual reality. Nat. Commun. 2022, 13, 2409. [Google Scholar] [CrossRef]
- Shen, S.; Li, S.; Yuan, Y.; Tan, H. High-efficiency broadband achromatic metalenses for visible full-stokes polarization imaging. Opt. Express 2023, 31, 28611–28623. [Google Scholar] [CrossRef]
- Huang, L.; Colburn, S.; Zhan, A.; Majumdar, A. Full-Color Metaoptical Imaging in Visible Light. Adv. Photonics Res. 2022, 3, 2100265. [Google Scholar] [CrossRef]
- Pan, M.; Fu, Y.; Zheng, M.; Chen, H.; Zang, Y.; Duan, H.; Li, Q.; Qiu, M.; Hu, Y. Dielectric metalens for miniaturized imaging systems: Progress and challenges. Light Sci. Appl. 2022, 11, 195. [Google Scholar] [CrossRef] [PubMed]
- Fan, Z.B.; Qiu, H.Y.; Zhang, H.L.; Pang, X.N.; Zhou, L.D.; Liu, L.; Ren, H.; Wang, Q.H.; Dong, J.W. A broadband achromatic metalens array for integral imaging in the visible. Light Sci. Appl. 2019, 8, 67. [Google Scholar] [CrossRef] [PubMed]
- Elsawy, M.M.; Gourdin, A.; Binois, M.; Duvigneau, R.; Felbacq, D.; Khadir, S.; Genevet, P.; Lanteri, S. Multiobjective statistical learning optimization of RGB metalens. ACS Photonics 2021, 8, 2498–2508. [Google Scholar] [CrossRef]
- Wang, F.; Geng, G.; Wang, X.; Li, J.; Bai, Y.; Li, J.; Wen, Y.; Li, B.; Sun, J.; Zhou, J. Visible achromatic metalens design based on artificial neural network. Adv. Opt. Mater. 2022, 10, 2101842. [Google Scholar] [CrossRef]
- Chen, W.T.; Zhu, A.Y.; Sanjeev, V.; Khorasaninejad, M.; Shi, Z.; Lee, E.; Capasso, F. A broadband achromatic metalens for focusing and imaging in the visible. Nat. Nanotechnol. 2018, 13, 220–226. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.T.; Zhu, A.Y.; Sisler, J.; Bharwani, Z.; Capasso, F. A broadband achromatic polarization-insensitive metalens consisting of anisotropic nanostructures. Nat. Commun. 2019, 10, 355. [Google Scholar] [CrossRef]
- Dai, X.; Dong, F.; Zhang, K.; Liao, D.; Li, S.; Shang, Z.; Zhou, Y.; Liang, G.; Zhang, Z.; Wen, Z.; et al. Holographic super-resolution metalens for achromatic sub-wavelength focusing. ACS Photonics 2021, 8, 2294–2303. [Google Scholar] [CrossRef]
- Koppens, F.; Mueller, T.; Avouris, P.; Ferrari, A.; Vitiello, M.; Polini, M. Photodetectors based on graphene, other two-dimensional materials and hybrid systems. Nat. Nanotechnol. 2014, 9, 780–793. [Google Scholar] [CrossRef]
- Cao, G.; Lin, H.; Fraser, S.; Zheng, X.; Del Rosal, B.; Gan, Z.; Wei, S.; Gan, X.; Jia, B. Resilient graphene ultrathin flat lens in aerospace, chemical, and biological harsh environments. ACS Appl. Mater. Interfaces 2019, 11, 20298–20303. [Google Scholar] [CrossRef]
- Lin, H.; Sturmberg, B.C.; Lin, K.T.; Yang, Y.; Zheng, X.; Chong, T.K.; de Sterke, C.M.; Jia, B. A 90-nm-thick graphene metamaterial for strong and extremely broadband absorption of unpolarized light. Nat. Photonics 2019, 13, 270–276. [Google Scholar] [CrossRef]
- Yang, D.; Cheng, Y.; Chen, F.; Luo, H.; Wu, L. Efficiency tunable broadband terahertz graphene metasurface for circular polarization anomalous reflection and plane focusing effect. Diam. Relat. Mater. 2023, 131, 109605. [Google Scholar] [CrossRef]
- Wei, S.; Cao, G.; Lin, H.; Yuan, X.; Somekh, M.; Jia, B. A varifocal graphene metalens for broadband zoom imaging covering the entire visible region. ACS Nano 2021, 15, 4769–4776. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Jia, B.; Lin, H.; Qiu, L.; Li, D.; Gu, M. Highly efficient and ultra-broadband graphene oxide ultrathin lenses with three-dimensional subwavelength focusing. Nat. Commun. 2015, 6, 8433. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wei, S.; Cao, G.; Lin, H.; Zhao, Y.; Jia, B. Graphene metalens for particle nanotracking. Photonics Res. 2020, 8, 1316–1322. [Google Scholar] [CrossRef]
- Zhang, S.; Li, Y.; Pan, N. Graphene based supercapacitor fabricated by vacuum filtration deposition. J. Power Sources 2012, 206, 476–482. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, Z.; Li, B.; Wang, C.; Liu, Q. Progresses on new generation laser direct writing technique. Mater. Today Nano 2021, 16, 100142. [Google Scholar] [CrossRef]
- Li, X.; Meng, F.; Chen, Y.; Xu, Y. Designer graphene oxide ultrathin flat lens with versatile focusing property. Opt. Express 2024, 32, 6531–6539. [Google Scholar] [CrossRef]
- Aarts, E.; Korst, J.; Michiels, W. Simulated annealing. In Search Methodologies: Introductory Tutorials in Optimization and Decision Support Techniques; Springer: New York, NY, USA, 2005; pp. 187–210. [Google Scholar]
- Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Lambora, A.; Gupta, K.; Chopra, K. Genetic algorithm—A literature review. In Proceedings of the 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019; IEEE: San Francisco, CA, USA, 2019; pp. 380–384. [Google Scholar]
- Cao, G.; Gan, X.; Lin, H.; Jia, B. An accurate design of graphene oxide ultrathin flat lens based on Rayleigh-Sommerfeld theory. Opto-Electron. Adv. 2018, 1, 180012-1. [Google Scholar] [CrossRef]
- Delahaye, D.; Chaimatanan, S.; Mongeau, M. Simulated annealing: From basics to applications. In Handbook of Metaheuristics; Springer: Cham, Switzerland, 2019; pp. 1–35. [Google Scholar]
- Çetin, G.; Keçebaş, A. Optimization of thermodynamic performance with simulated annealing algorithm: A geothermal power plant. Renew. Energy 2021, 172, 968–982. [Google Scholar] [CrossRef]
- Otubamowo, K.; Egunjobi, T.; Adewole, A. A comparative study of simulated annealing and genetic algorithm for solving the travelling salesman problem. Int. J. Appl. Inf. Syst. 2012, 4, 6–12. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Ding, Y.; Yu, H.; Li, X. Design of an Achromatic Graphene Oxide Metalens with Multi-Wavelength for Visible Light. Photonics 2024, 11, 249. https://doi.org/10.3390/photonics11030249
Chen Y, Ding Y, Yu H, Li X. Design of an Achromatic Graphene Oxide Metalens with Multi-Wavelength for Visible Light. Photonics. 2024; 11(3):249. https://doi.org/10.3390/photonics11030249
Chicago/Turabian StyleChen, Yuxi, Yongchang Ding, Haowen Yu, and Xueyan Li. 2024. "Design of an Achromatic Graphene Oxide Metalens with Multi-Wavelength for Visible Light" Photonics 11, no. 3: 249. https://doi.org/10.3390/photonics11030249
APA StyleChen, Y., Ding, Y., Yu, H., & Li, X. (2024). Design of an Achromatic Graphene Oxide Metalens with Multi-Wavelength for Visible Light. Photonics, 11(3), 249. https://doi.org/10.3390/photonics11030249




