Rapid Fabrication of Yttrium Aluminum Garnet Microhole Array Based on Femtosecond Bessel Beam
Abstract
:1. Introduction
2. Materials and Methods
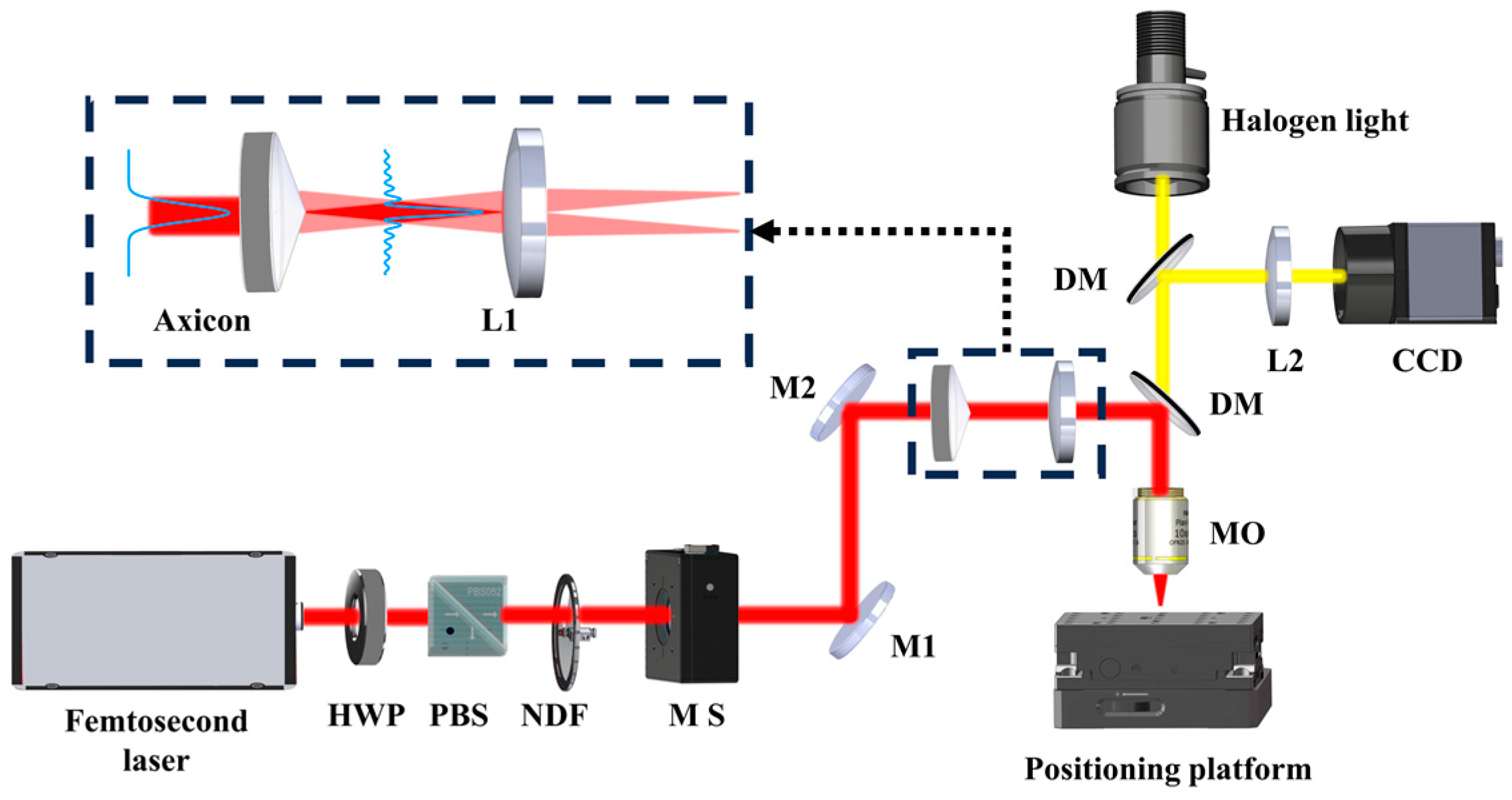
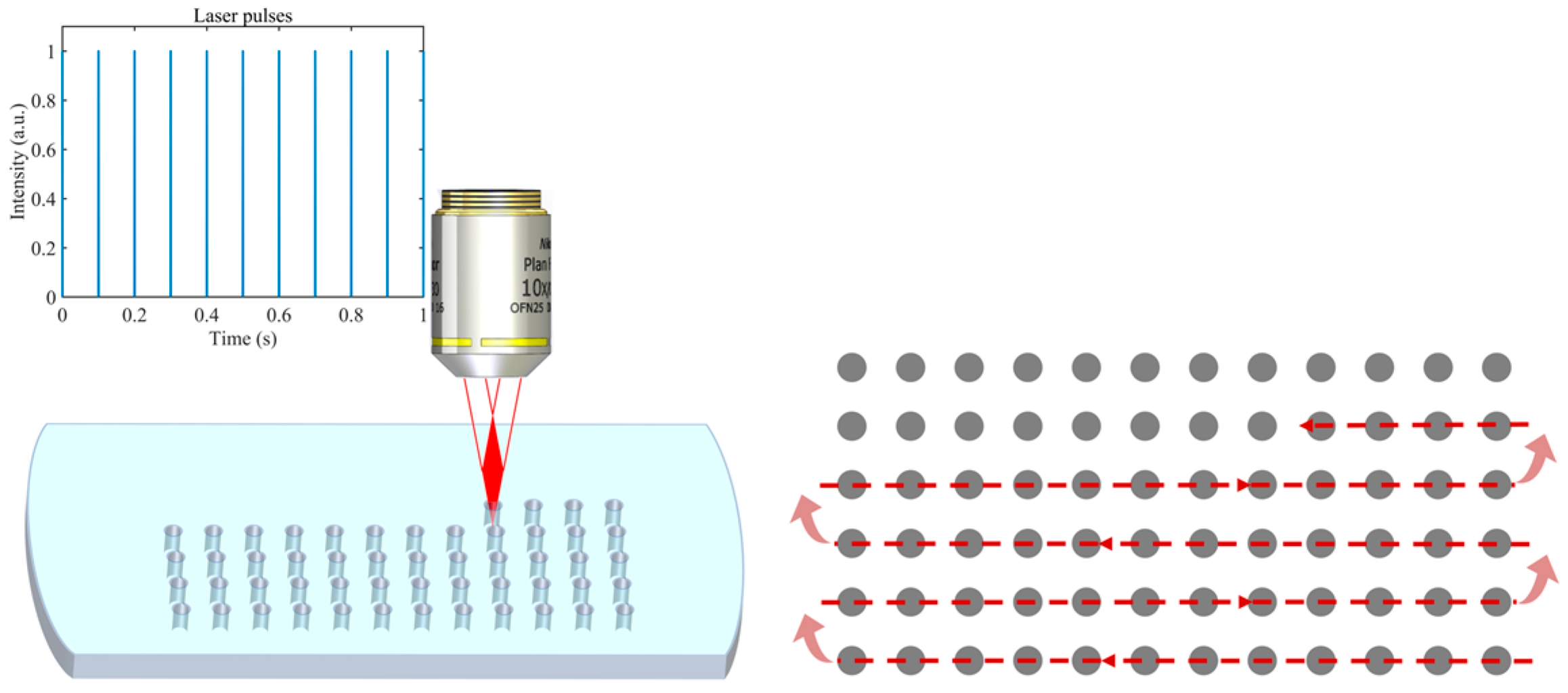
2.1. Experimental Setup
2.2. Materials
2.3. Methods
3. Results and Discussion
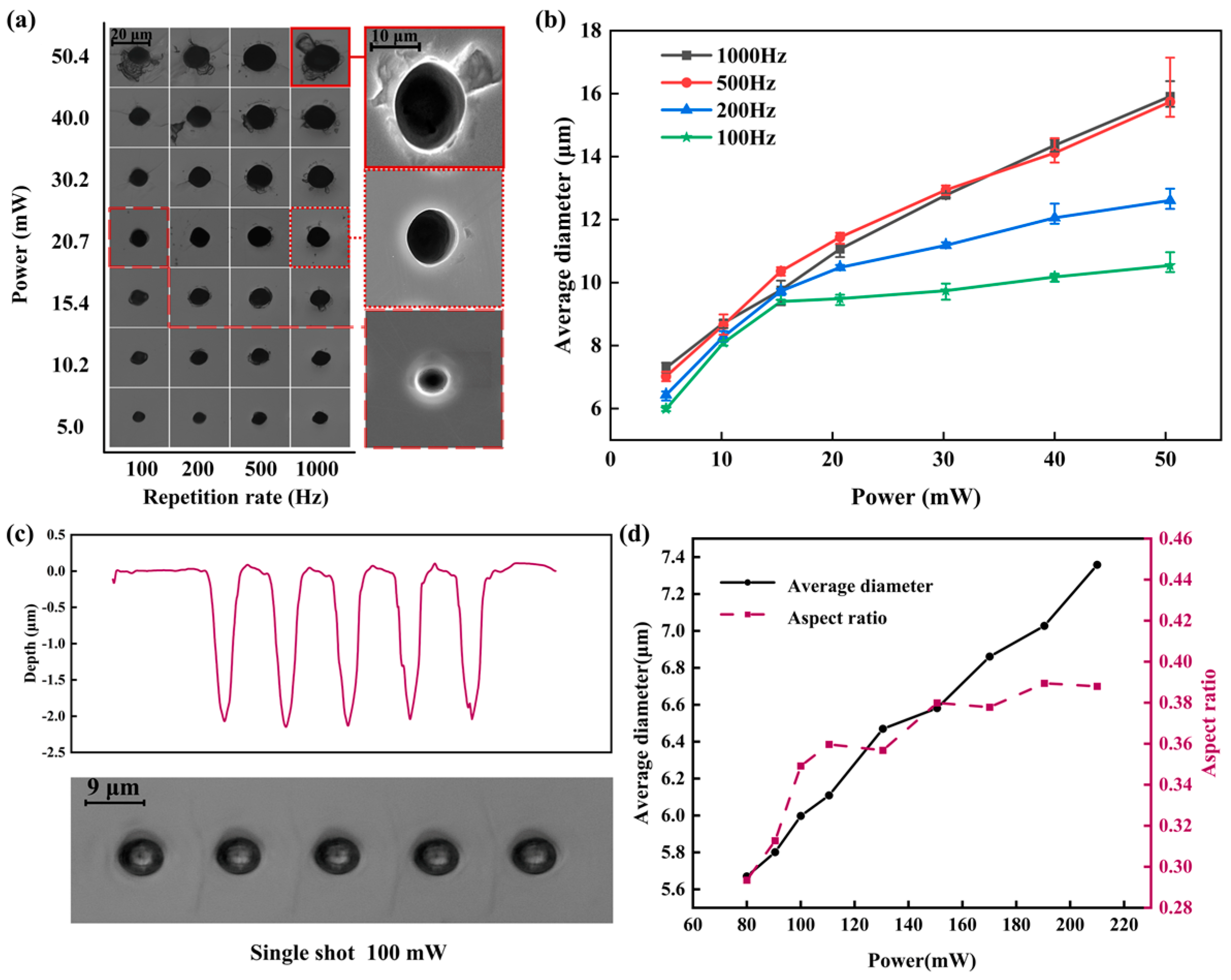
3.1. Ultrafast Gaussian Beam Machining of YAG Crystals
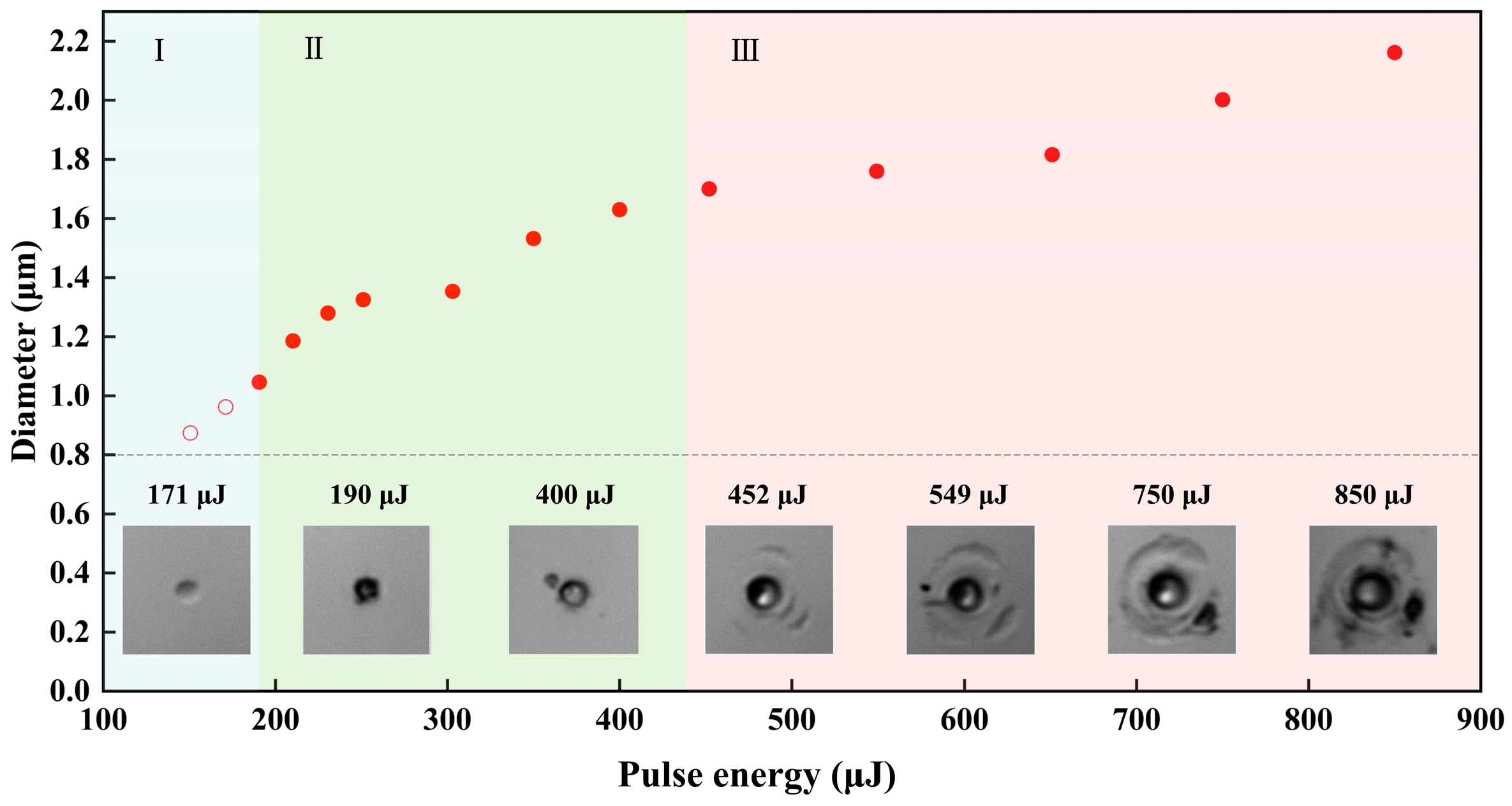
3.2. Ultrafast Bessel Beam Machining of YAG Crystals
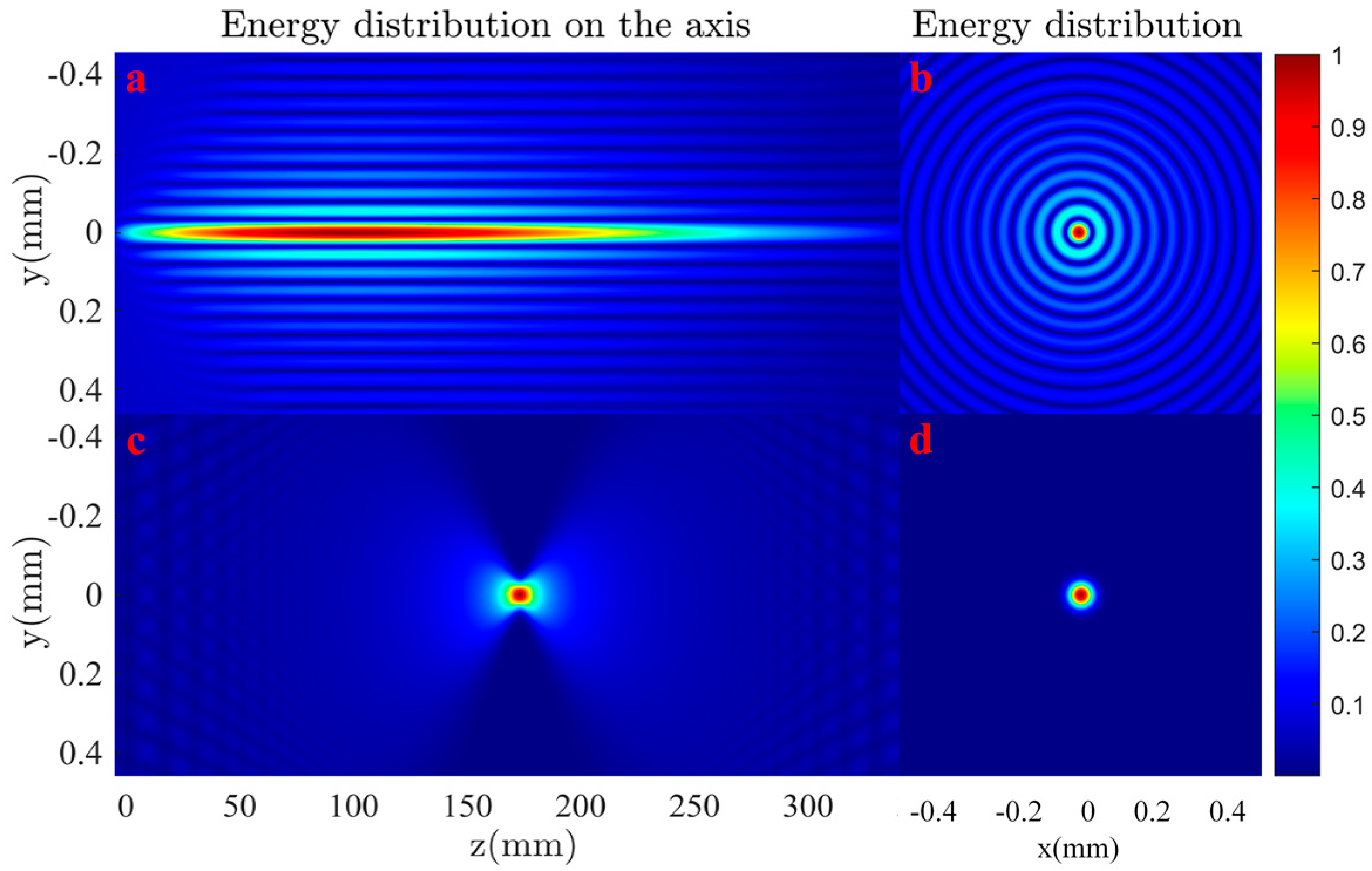
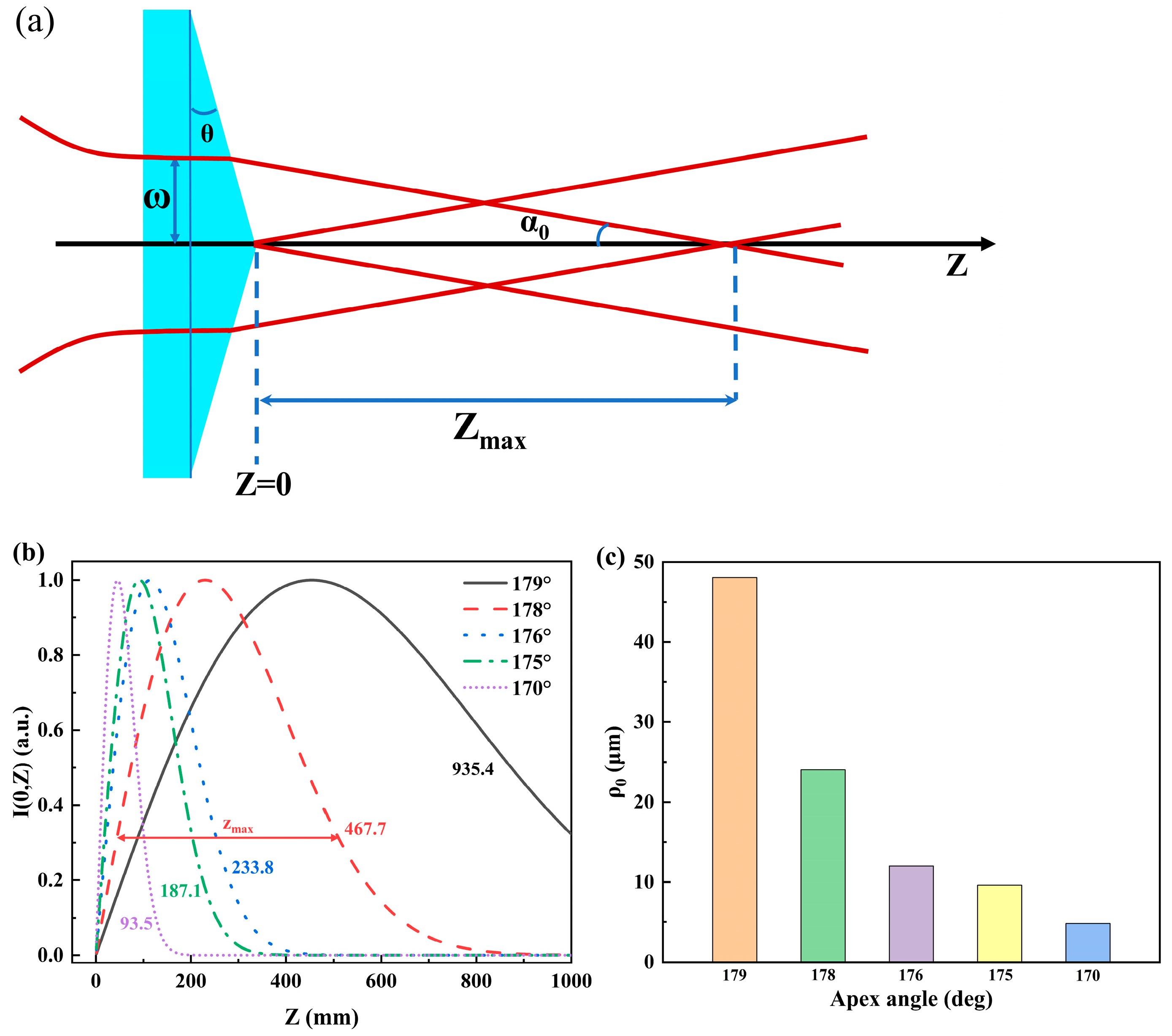
3.2.1. Generation of Bessel Beam
3.2.2. Experiment of Femtosecond Bessel Beam Fabrication on YAG Crystals
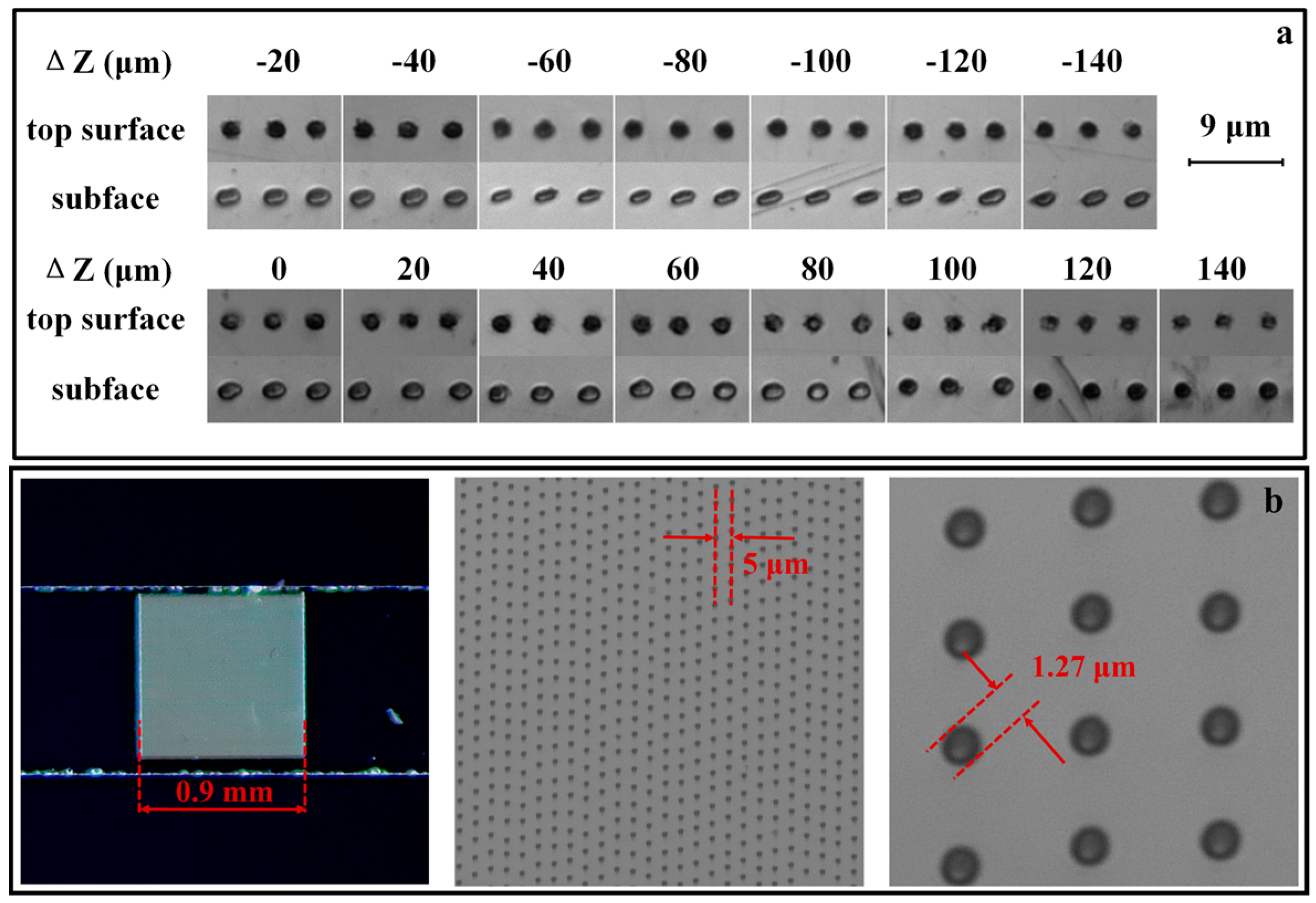
3.2.3. Fabrication of Microhole Array
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, Y.M.; Duan, Y.Z.; Liu, X.Q.; Chen, Q.D.; Sun, H.B. High-quality rapid laser drilling of transparent hard materials. Opt. Lett. 2022, 47, 921–924. [Google Scholar] [CrossRef]
- An, R.; Hoffman, M.D.; Donoghue, M.A.; Hunt, A.J.; Jacobson, S.C. Water-assisted femtosecond laser machining of electrospray nozzles on glass microfluidic devices. Opt. Express 2008, 16, 15206–15211. [Google Scholar] [CrossRef] [PubMed]
- Vong, T.; Schoffelen, S.; van Dongen, S.F.M.; van Beek, T.A.; Zuilhof, H.; van Hest, J.C.M. A DNA-based strategy for dynamic positional enzyme immobilization inside fused silica microchannels. Chem. Sci. 2011, 2, 1278–1285. [Google Scholar] [CrossRef]
- Leng, N.; Jiang, L.; Li, X.; Xu, C.C.; Liu, P.J.; Lu, Y.F. Femtosecond laser processing of fused silica and aluminum based on electron dynamics control by shaping pulse trains. Appl. Phys. A Mater. 2012, 109, 679–684. [Google Scholar] [CrossRef]
- Baheri, S.; Tabrizi, S.P.A.; Jubran, B.A. Film cooling effectiveness from trenched shaped and compound holes. Heat. Mass. Transfer 2008, 44, 989–998. [Google Scholar] [CrossRef]
- Fei, Z.Z.; Hu, X.; Choi, H.W.; Wang, S.N.; Farson, D.; Lee, L.J. Micronozzle Array Enhanced Sandwich Electroporation of Embryonic Stem Cells. Anal. Chem. 2010, 82, 353–358. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.F.; Zhu, S.H.; Hong, M.H.; Chen, F.; Liu, H.L. Specklegram temperature sensor based on femtosecond laser inscribed depressed cladding waveguides in Nd:YAG crystal. Opt. Laser Technol. 2019, 113, 11–14. [Google Scholar] [CrossRef]
- Lai, M.F.; Li, S.W.; Shih, J.Y.; Chen, K.N. Wafer-level three-dimensional integrated circuits (3D IC): Schemes and key technologies. Microelectron. Eng. 2011, 88, 3282–3286. [Google Scholar] [CrossRef]
- Jia, C.L.; Tang, W.J.; Liu, K.; Liao, Y. Transparent Ho,Yb:YAG crystal waveguide inscribed by direct femtosecond laser writing. Opt. Mater. 2023, 135, 113314. [Google Scholar] [CrossRef]
- Egashira, K.; Mizutani, K. Micro-drilling of monocrystalline silicon using a cutting tool. Precis. Eng. 2002, 26, 263–268. [Google Scholar] [CrossRef]
- Cao, X.D.; Kim, B.H.; Chu, C.N. Micro-structuring of glass with features less than 100 μm by electrochemical discharge machining. Precis. Eng. 2009, 33, 459–465. [Google Scholar] [CrossRef]
- Ahn, S.H.; Ryu, S.H.; Choi, D.K.; Chu, C.N. Electro-chemical micro drilling using ultra short pulses. Precis. Eng. 2004, 28, 129–134. [Google Scholar] [CrossRef]
- Spinney, P.S.; Howitt, D.G.; Smith, R.L.; Collins, S.D. Nanopore formation by low-energy focused electron beam machining. Nanotechnology 2010, 21, 375301. [Google Scholar] [CrossRef]
- Sebastiani, M.; Eberl, C.; Bemporad, E.; Pharr, G.M. Depth-resolved residual stress analysis of thin coatings by a new FIB-DIC method. Mat. Sci. Eng. A-Struct. 2011, 528, 7901–7908. [Google Scholar] [CrossRef]
- Wu, J.H.; Chantiwas, R.; Amirsadeghi, A.; Soper, S.A.; Park, S. Complete plastic nanofluidic devices for DNA analysis direct imprinting with polymer stamps. Lab. Chip 2011, 11, 2984–2989. [Google Scholar] [CrossRef]
- Sugioka, K.; Cheng, Y. Fabrication of 3D microfluidic structures inside glass by femtosecond laser micromachining. Appl. Phys. A Mater. 2014, 114, 215–221. [Google Scholar] [CrossRef]
- Lu, Y.; Li, Y.F.; Wang, G.; Yu, Y.; Bai, Z.X.; Wang, Y.L.; Lu, Z.W. Femtosecond Laser Fabrication of Microchannels in Transparent Hard Materials. Adv. Mater. Technol. 2023, 8, 2300015. [Google Scholar] [CrossRef]
- Jiang, C.Y.; Zhou, G.Q.; Xu, J.; Deng, P.Z.; Gan, F.X. Femtosecond laser irradiation on YAG and sapphire crystals. J. Cryst. Growth 2004, 260, 181–185. [Google Scholar] [CrossRef]
- Liu, H.L.; de Aldana, J.R.V.; Hong, M.H.; Chen, F. Femtosecond Laser Inscribed Y-Branch. Waveguide in Nd:YAG Crystal: Fabrication and Continuous-Wave Lasing. IEEE J. Sel. Top. Quantum 2016, 22, 227–230. [Google Scholar] [CrossRef]
- Ren, Y.Y.; Zhang, L.M.; Romero, C.; de Aldana, J.R.V.; Chen, F. Femtosecond laser irradiation on Nd:YAG crystal: Surface ablation and high-spatial-frequency nanograting. Appl. Surf. Sci. 2018, 441, 372–380. [Google Scholar] [CrossRef]
- Ródenas, A.; Gu, M.; Corrielli, G.; Paiè, P.; John, S.; Kar, A.K.; Osellame, R. Three-dimensional femtosecond laser nanolithography of crystals. Nat. Photonics 2019, 13, 105–109. [Google Scholar] [CrossRef]
- Courvoisier, F.; Stoian, R.; Couairon, A. Ultrafast laser micro-and nano-processing with nondiffracting and curved beams: Invited paper for the section: Hot topics in ultrafast lasers. Opt. Laser Technol. 2016, 80, 125–137. [Google Scholar] [CrossRef]
- Meyer, R.; Jacquot, M.; Giust, R.; Safioui, J.; Rapp, L.; Furfaro, L.; Lacourt, P.A.; Dudley, J.M.; Courvoisier, F. Single-shot ultrafast laser processing of high-aspect-ratio nanochannels using elliptical Bessel beams. Opt. Lett. 2017, 42, 4307–4310. [Google Scholar] [CrossRef] [PubMed]
- Rapp, L.; Meyer, R.; Giust, R.; Furfaro, L.; Jacquot, M.; Lacourt, P.-A.; Dudley, J.M.; Courvoisier, F. High aspect ratio micro-explosions in the bulk of sapphire generated by femtosecond Bessel beams. Sci. Rep. 2016, 6, 34286. [Google Scholar] [CrossRef] [PubMed]
- Xie, Q.; Li, X.; Jiang, L.; Xia, B.; Yan, X.; Zhao, W.; Lu, Y. High-aspect-ratio, high-quality microdrilling by electron density control using a femtosecond laser Bessel beam. Appl. Phys. A 2016, 122, 136. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, G.; Wang, Y.; Li, X.; Stoian, R.; Cheng, G. Reconstructing of embedded high-aspect-ratio nano-voids generated by ultrafast laser bessel beams. Micromachines 2020, 11, 671. [Google Scholar] [CrossRef] [PubMed]
- Vetter, C.; Giust, R.; Furfaro, L.; Billet, C.; Froehly, L.; Courvoisier, F. High aspect ratio structuring of glass with ultrafast Bessel beams. Materials 2021, 14, 6749. [Google Scholar] [CrossRef] [PubMed]
- Fernelius, N.C.; Graves, G.A.; Knecht, W.L. Characterization of Candidate Laser Window Materials. Proc. Soc. Photo Opt. Instrum. 1981, 297, 188–195. [Google Scholar]
- Zhang, N.; Ye, J.-S.; Feng, S.-F.; Wang, X.-K.; Han, P.; Sun, W.-F.; Zhang, Y.; Zhang, X.-C. Generation of long-distance stably propagating Bessel beams. OSA Contin. 2021, 4, 1223–1233. [Google Scholar] [CrossRef]
- Cizmár, T. Optical Traps Generated by Non-Traditional Beams. Ph.D. Thesis, Masaryk University in Brno, Brno, Czech Republic, 2006. [Google Scholar]


| Property | Detail | Note |
|---|---|---|
| Crystal structure | Cubic | |
| Refractive index | 1.8197 | @1064 nm |
| Density | 4.55 | g/cm3 |
| Mohs hardness | 8~8.5 | |
| Thermal conductivity | 13.1 | W/m/K, @20 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Yu, Y.; Zhang, T.; Ma, S.; Chen, L.; Xu, B.; Wang, Z. Rapid Fabrication of Yttrium Aluminum Garnet Microhole Array Based on Femtosecond Bessel Beam. Photonics 2024, 11, 408. https://doi.org/10.3390/photonics11050408
Yang H, Yu Y, Zhang T, Ma S, Chen L, Xu B, Wang Z. Rapid Fabrication of Yttrium Aluminum Garnet Microhole Array Based on Femtosecond Bessel Beam. Photonics. 2024; 11(5):408. https://doi.org/10.3390/photonics11050408
Chicago/Turabian StyleYang, Heng, Yuan Yu, Tong Zhang, Shufang Ma, Lin Chen, Bingshe Xu, and Zhiyong Wang. 2024. "Rapid Fabrication of Yttrium Aluminum Garnet Microhole Array Based on Femtosecond Bessel Beam" Photonics 11, no. 5: 408. https://doi.org/10.3390/photonics11050408
APA StyleYang, H., Yu, Y., Zhang, T., Ma, S., Chen, L., Xu, B., & Wang, Z. (2024). Rapid Fabrication of Yttrium Aluminum Garnet Microhole Array Based on Femtosecond Bessel Beam. Photonics, 11(5), 408. https://doi.org/10.3390/photonics11050408




