Generation of Propagation-Dependent OAM Self-Torque with Chirped Spiral Gratings
Abstract
1. Introduction
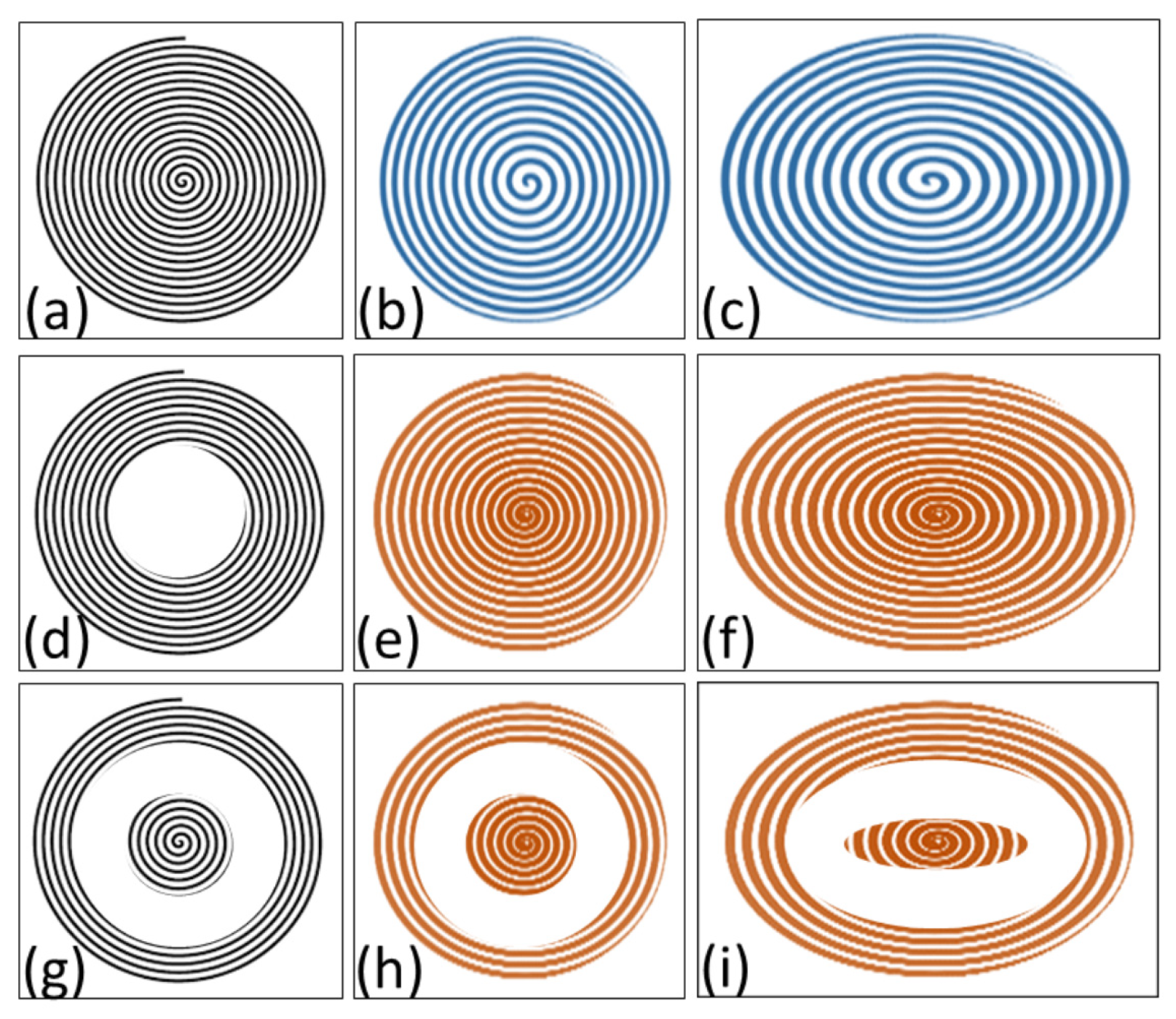
2. Spiral Phase Gratings
- (A)
- Grating completely filling a circle;
- (B)
- Grating completely filling an ellipse;
- (C)
- Toroidal grating filling a single annulus (one ring);
- (D)
- Grating filling the center and annulus (center, one ring);
- (E)
- Multi-toroidal grating filling multiple annuli (N rings).
- (1)
- Constant grating period (uniform Archimedean grating);
- (2)
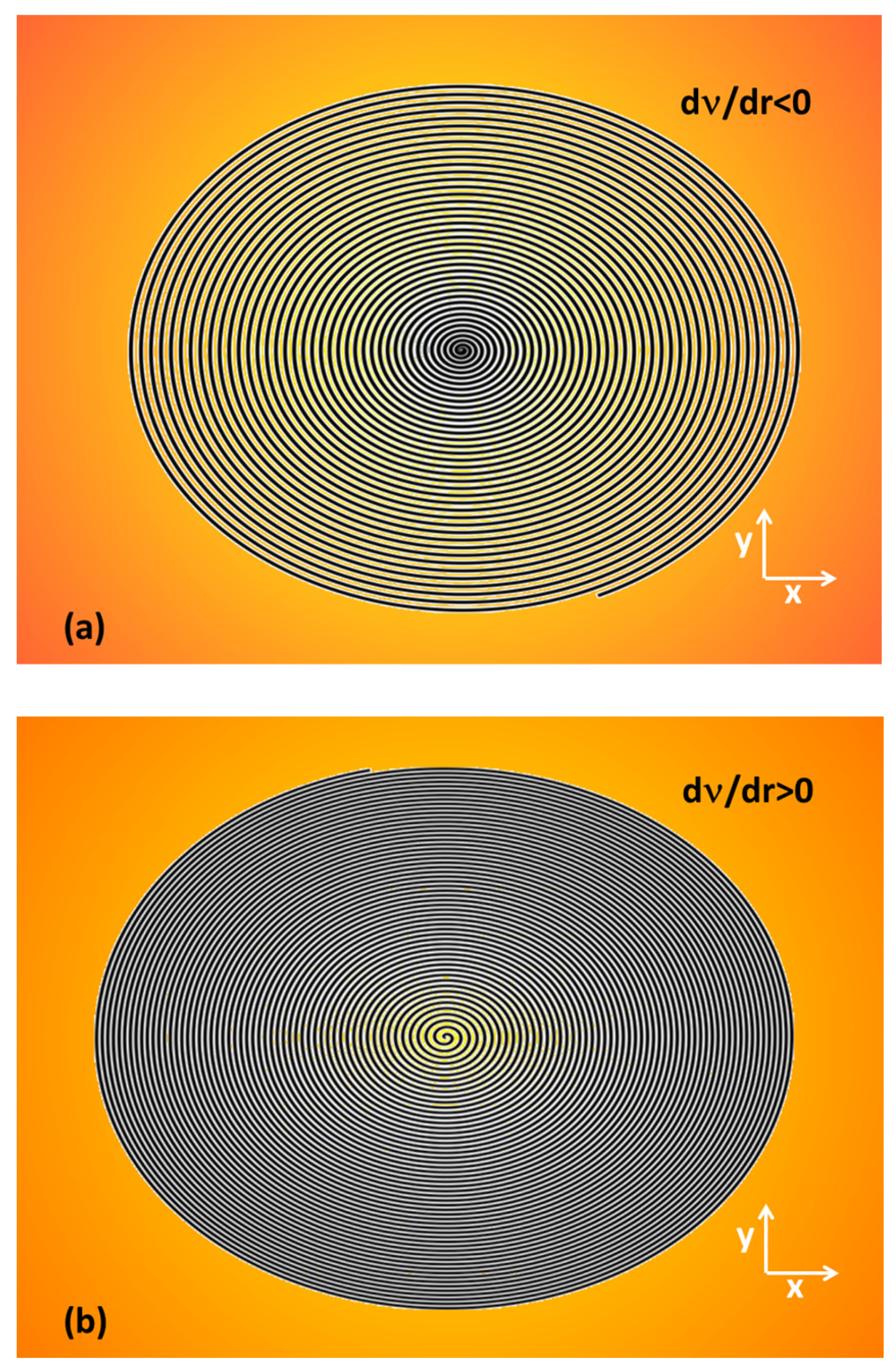
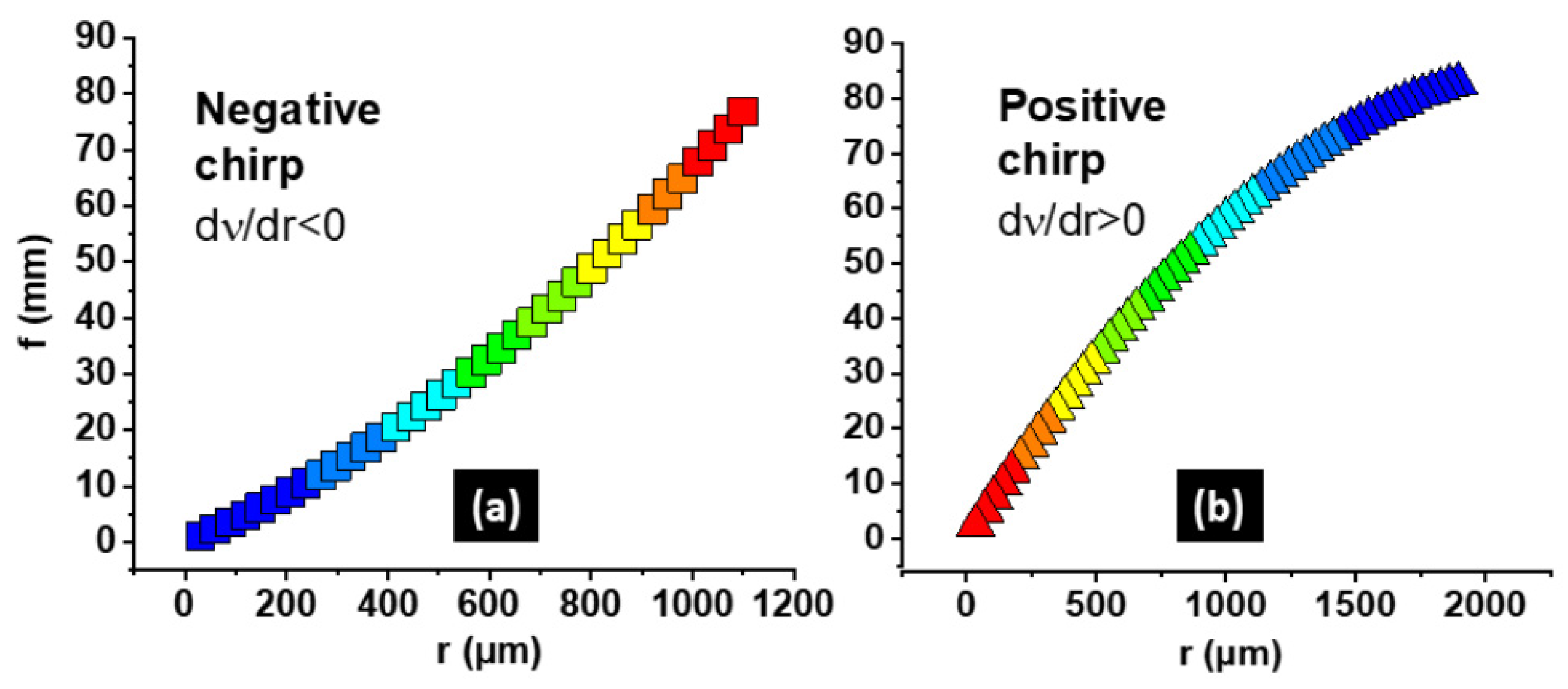
- Radially monotonically increasing spatial frequency (positive chirp);
- (3)
- Radially monotonically decreasing spatial frequency (negative chirp);
- (4)
- Grating period depending on θ (oscillating chirp).
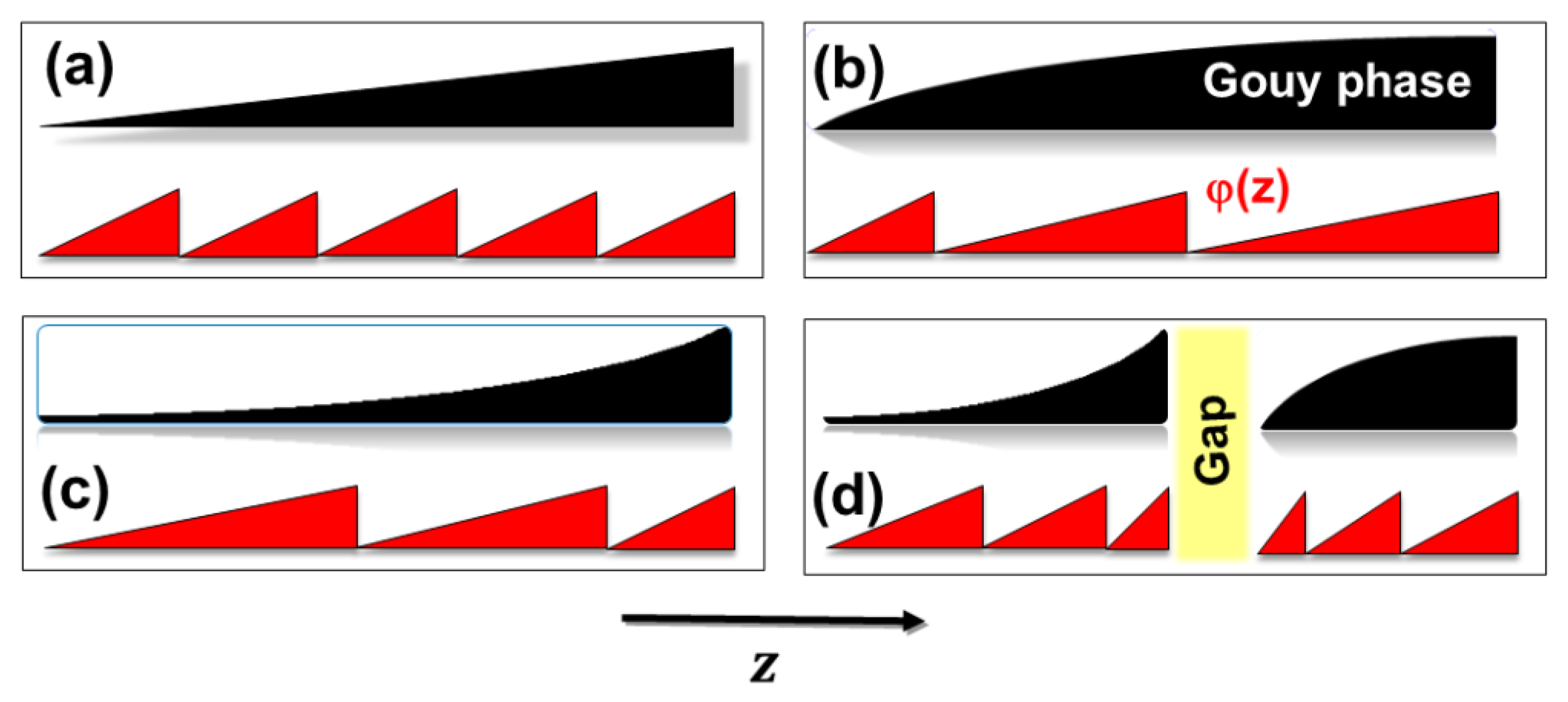
3. Propagation-Dependent Self-Torque
- (i)
- A local, interference-type, superposition-generated self-torque (SST);
- (ii)
- A nonlocal, propagation-type self-torque (PST).
4. Experimental Techniques
4.1. Experimental Setup
4.2. Elliptical Continuously Chirped Gratings
4.3. Non-Uniform Toroidal Gratings
5. Experimental Results
5.1. Spectral Filtering
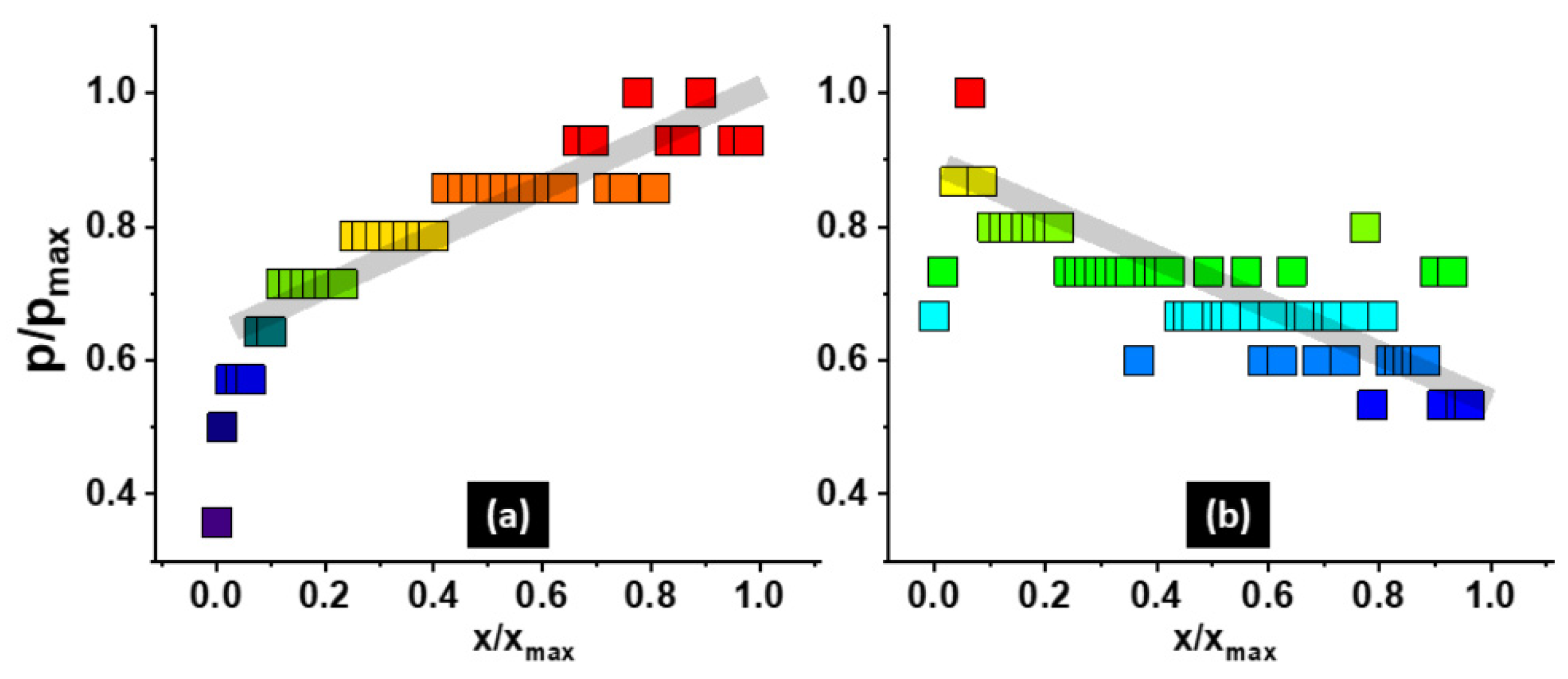
5.2. Grating Aberrations at Oblique Incidence
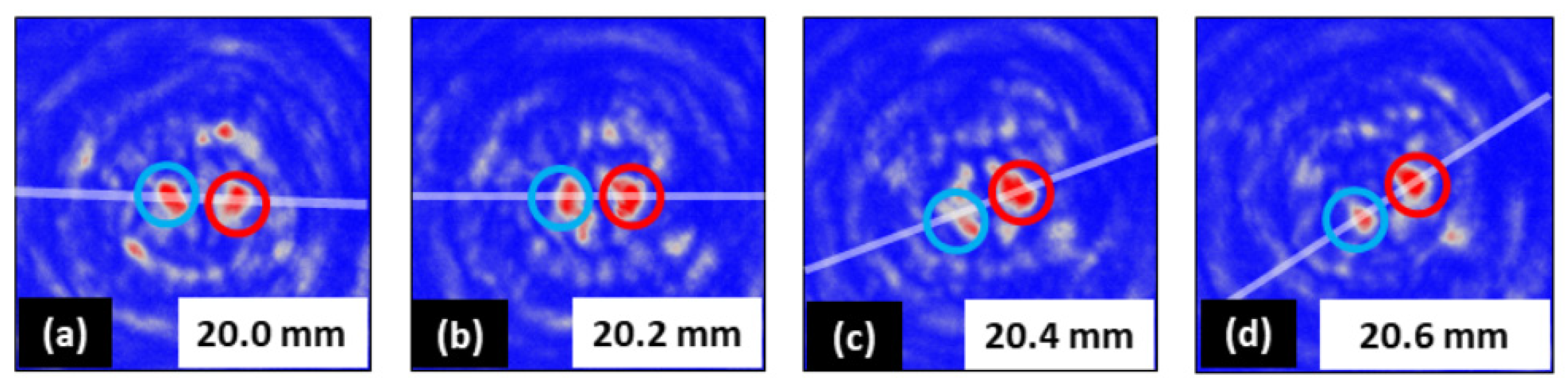
5.3. Propagation-Dependent Self-Torque
5.4. Influence of Grating Talbot Effect
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Design Parameters for Linearly Chirped SPGs
References
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T.; et al. Roadmap on structured light. J. Opt. 2017, 19, 133001. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Karimi, E.; Padgett, M.J.; Alonso, M.A.; Dennis, M.R.; Dudley, A.; Forbes, A.; Zahedpour, S.; Hancock, S.W.; Milchberg, H.M.; et al. Roadmap on structured waves. J. Opt. 2023, 25, 103001. [Google Scholar] [CrossRef]
- Nye, J.F.; Berry, M.V. Dislocations in wave trains. Proc. R. Soc. Lond. 1974, 336, 165–190. [Google Scholar] [CrossRef]
- Coullet, P.; Gil, L.; Rocca, F. Optical vortices. Opt. Commun. 1989, 73, 403–408. [Google Scholar] [CrossRef]
- Soskin, M.S.; Vasnetsov, M.V. Singular optics. Prog. Opt. 2001, 42, 219–276. [Google Scholar] [CrossRef]
- Dennis, M.R.; O’Holleran, K.; Padgett, M.J. Singular optics: Optical vortices and polarization singularities. Prog. Opt. 2009, 53, 293–363. [Google Scholar] [CrossRef]
- Yao, A.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Wang, X.; Nie, Z.; Liang, Y.; Wang, J.; Li, T.; Jia, B. Recent advances on optical vortex generation. Nanophotonics 2018, 7, 1533–1556. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, Y.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Life Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Zhou, H.; Moretti, M.; Wang, X.; Li, J. Orbital angular momentum waves: Generation, detection and emerging applications. IEEE Commun. Surv. Tutor. 2020, 22, 840–868. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, Y.; Yuan, Y.; Burokur, S.N. A review of orbital angular momentum vortex beams generation: From traditional methods to metasurfaces. Appl. Sci. 2020, 10, 1015. [Google Scholar] [CrossRef]
- Fatkhiev, D.M.; Butt, M.A.; Grakhova, E.P.; Kutluyarov, R.V.; Stepanov, I.V.; Kazanskiy, N.L.; Khonina, S.N.; Lyubopytov, V.S.; Sultanov, A.K. Recent advances in generation and detection of orbital angular momentum optical beams—A review. Sensors 2021, 21, 4988. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Lv, H.; Fu, X.; Yang, Y. Vortex beam: Generation and detection of orbital angular momentum. Chin. Opt. Lett. 2022, 20, 012601. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, J. A review of multiple optical vortices generation: Methods and application. Front. Optoelectron. 2019, 12, 52–68. [Google Scholar] [CrossRef]
- Forbes, A. Advances in orbital angular momentum lasers. IEEE J. Light. Technol. 2023, 41, 2079–2086. [Google Scholar] [CrossRef]
- Berry, M.V. Coloured phase singularities. New J. Phys. 2002, 4, 66. [Google Scholar] [CrossRef]
- Gbur, G.; Visser, T.D.; Wolf, E. Anomalous behavior of spectra near phase singularities of focus waves. Phys. Rev. Lett. 2002, 88, 013901. [Google Scholar] [CrossRef] [PubMed]
- Popescu, G.; Dogariu, A. Spectral anomalies at wave-front dislocations. Phys. Rev. Lett. 2002, 88, 183902. [Google Scholar] [CrossRef]
- Berry, M.V. Exploring the colours of dark light. New J. Phys. 2002, 4, 74. [Google Scholar] [CrossRef]
- Leach, J.; Padgett, M.J. Observation of chromatic effects near a white-light vortex. New J. Phys. 2003, 5, 154. [Google Scholar] [CrossRef]
- Zapata-Rodríguez, C.J. Analytical characterization of spectral anomalies in polychromatic aperture beams. Opt. Commun. 2006, 257, 9–15. [Google Scholar] [CrossRef]
- Liebmann, M.; Treffer, A.; Bock, M.; Elsaesser, T.; Grunwald, R. Spectral anomalies and Gouy rotation around the singularity of ultrashort vortex pulses. Opt. Express 2017, 25, 26076–26088. [Google Scholar] [CrossRef] [PubMed]
- Liebmann, M.; Treffer, A.; Bock, M.; Wallrabe, U.; Grunwald, R. Ultrashort vortex pulses with controlled spectral Gouy rotation. Appl. Sci. 2020, 10, 4288. [Google Scholar] [CrossRef]
- Bock, M.; Liebmann, M.; Elsaesser, T.; Grunwald, R. Gouy phase rotation in spectral maps of ultrashort vortex pulses. In Proceedings of the Conference on Lasers and Electro-Optics/CLEO Europe-Conference on Lasers and Electro-Optics/Europe—European Quantum Electronics/EQEC, Munich, Germany, 25–29 June 2017. [Google Scholar]
- Liebmann, M.; Treffer, A.; Bock, M.; Seiler, T.; Jahns, J.; Elsaesser, T.; Grunwald, R. Spectral meta-moments reveal hidden signatures of vortex pulses. EPJ Web Conf. 2019, 205, 01005. [Google Scholar] [CrossRef]
- Bock, M.; Brunne, J.; Treffer, A.; König, S.; Wallrabe, U.; Grunwald, R. Sub-3-cycle vortex pulses of tunable topological charge. Opt. Lett. 2013, 38, 3642–3645. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Fang, Z.-X.; Ren, Y.-X.; Gong, L.; Lu, R.-D. Generation and characterization of a perfect vortex beam with a large topological charge through a digital micromirror device. Appl. Opt. 2015, 54, 8030–8035. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.F.; Liu, K.; Sun, H.X.; Zhang, J.X.; Gao, J.R. Generation of high-order Laguerre-Guassian beams by liquid crystal spatial light modulators. J. Quantum Opt. 2015, 21, 86–92. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, J. Arbitrary manipulation of spatial amplitude and phase using phase-only spatial light modulators. Sci. Rep. 2014, 4, 7441. [Google Scholar] [CrossRef] [PubMed]
- Grunwald, R.; Jurke, M.; Bock, M.; Liebmann, M.; Bruno, B.P.; Gowda, H.; Wallrabe, U. High-flexibility control of structured light with combined adaptive optical systems. Photonics 2022, 9, 42. [Google Scholar] [CrossRef]
- Grunwald, R.; Jurke, M.; Bock, M.; Liebmann, M.; Bruno, B.P.; Gowda, H.; Wallrabe, U. Structuring light by combining spatial modulation and fast angular shaping. In Proceedings of the Complex Light and Optical Forces XVII, Photonics West, San Francisco, CA, USA, 28 January–2 February 2023; Volume 12436, p. 1243606. [Google Scholar] [CrossRef]
- Brand, G.F. Phase singularities in beams. Am. J. Phys. 1999, 67, 55–60. [Google Scholar] [CrossRef] [PubMed]
- Dyson, J. Circular and spiral diffraction gratings. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1958, 248, 93–106. [Google Scholar] [CrossRef]
- Vasara, A.; Turunen, J.; Friberg, A.T. Realization of general nondiffracting beams with computer-generated holograms. J. Opt. Soc. Am. A 1989, 6, 1748–1754. [Google Scholar] [CrossRef]
- Abramochkin, E.; Volostnikov, V. Spiral-type beams. Opt. Commun. 1993, 102, 336–350. [Google Scholar] [CrossRef]
- Pereiro-García, J.; García-de-Blas, M.; Geday, M.A.; Quintana, X.; Caño-García, M. Flat variable liquid crystal diffractive spiral axicon enabling perfect vortex beams generation. Sci. Rep. 2023, 13, 2385. [Google Scholar] [CrossRef] [PubMed]
- Musigmann, M.; Jahns, J.; Bock, M.; Grunwald, R. Refractive-diffractive dispersion compensation for optical vortex beams with ultrashort pulse durations. Appl. Opt. 2014, 53, 7304–7311. [Google Scholar] [CrossRef] [PubMed]
- Supp, S.; Jahns, J. Coaxial superposition of Bessel beams by discretized spiral axicons. J. Eur. Opt. Soc.-Rapid Publ. 2018, 14, 18. [Google Scholar] [CrossRef]
- Li, X.; Shen, Z.; Tan, Q.; Hu, W. High efficient metadevices for terahertz beam shaping. Front. Phys. 2021, 9, 659747. [Google Scholar] [CrossRef]
- Jiménez, N.; Picó, R.; Sánchez-Morcillo, V.; Romero-García, V.; García-Raffi, L.M.; Staliunas, K. Formation of high-order acoustic Bessel beams by spiral diffraction gratings. Phys. Rev. E 2016, 94, 053004. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Ke, M.; Li, W.; Yang, Q.; Qiu, C.; Liu, Z. Particle manipulation with acoustic vortex beam induced by a brass plate with spiral shape structure. Appl. Phys. Lett. 2016, 109, 123506. [Google Scholar] [CrossRef]
- Li, W.; Ke, M.; Peng, S.; Liu, F.; Qiu, C.; Liu, Z. Rotational manipulation by acoustic radiation torque of high-order vortex beams generated by an artificial structured plate. Appl. Phys. Lett. 2018, 113, 051902. [Google Scholar] [CrossRef]
- Zhou, H.; Li, J.; Guo, K.; Guo, Z. Generation of acoustic vortex beams with designed Fermat’s spiral diffraction grating. J. Acoust. Soc. Am. 2019, 146, 4237–4243. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.; Sun, Z.; Li, J.; Zhao, L.; Liu, H.; Li, T.; Liu, S. MEMS Bessel beam acoustic transducer (MEMS-BBAT) with air-cavity lens based on spiral diffraction grating for particle trapping. In Proceedings of the 2022 IEEE International Ultrasonics Symposium (IUS), Venice, Italy, 10–13 October 2022. [Google Scholar] [CrossRef]
- Li, J.; Sun, Z.; Jia, Y.; Li, T.; Lu, H.; Zhao, L.; Liu, H.; Liu, S. MEMS first-order Bessel beam acoustic transducer for particle trapping and controllable rotating. In Proceedings of the 2023 IEEE 36th International Conference on Micro Electro Mechanical Systems (MEMS), Munich, Germany, 15–19 January 2023. [Google Scholar] [CrossRef]
- Muelas-Hurando, R.D.; Ealo, J.L.; Volke-Sepúlveda, K. Electro-active diffraction gratings for the generation of acoustic vortex beams. In Proceedings of the 2021 IEEE International Ultrasonics Symposium (IUS), Xi’an, China, 11–16 September 2021. [Google Scholar] [CrossRef]
- Muelas-Hurtado, R.D.; Ealo, J.L.; Pazos-Ospina, J.F.; Volke-Sepúlveda, K. Generation of multiple vortex beam by means of active diffraction gratings. Appl. Phys. Lett. 2018, 112, 084101. [Google Scholar] [CrossRef]
- Muelas-Hurtado, R.D.; Ealo, J.L.; Pazos-Ospina, J.F.; Volke-Sepulveda, K. Acoustic analysis of a broadband spiral source for the simultaneous generation of multiple Bessel vortices in air. J. Acoust. Soc. Am. 2018, 144, 3252–3261. [Google Scholar] [CrossRef] [PubMed]
- Ketchum, R.S.; Blanche, P.A. Diffraction efficiency characteristics for MEMS-based phase-only spatial light modulator with nonlinear phase distribution. Photonics 2021, 8, 62. [Google Scholar] [CrossRef]
- Serati, S.A.; Ewing, T.K.; Stockley, J.E. New developments in high-resolution liquid crystal spatial light modulators for wavefront control. Proc. SPIE 2002, 4825, 46–55. [Google Scholar] [CrossRef]
- Ohtake, Y.; Ando, T.; Fukuchi, N.; Matsumoto, N.; Ito, H.; Hara, T. Universal generation of higher-order multiringed Laguerre-Gaussian beams by using a spatial light modulator. Opt. Lett. 2007, 32, 1411–1413. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, N.; Ando, T.; Inoue, T.; Ohtake, Y.; Fukuchi, N.; Hara, T. Generation of high-quality higher-order Laguerre-Gaussian beams using liquid-crystal-on-silicon spatial light modulators. J. Opt. Soc. Am. A 2008, 25, 1642–1651. [Google Scholar] [CrossRef] [PubMed]
- Lazarev, G.; Hermerschmidt, A.; Krüger, S.; Osten, S. LCOS spatial light modulators: Trends and applications. In Optical Imaging and Metrology: Advanced Technologies, 1st ed.; Osten, W., Reingand, N., Eds.; Wiley-VCH: Weinheim, Germany; Berlin, Germany, 2012; pp. 1–28. [Google Scholar] [CrossRef]
- Gongjian, Z.; Man, Z.; Yang, Z. Wave front control with SLM and simulation of light wave diffraction. Opt. Express 2018, 26, 33543–33564. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Chen, Z.; Ding, J.; Wang, H.-T. Single ultra-high-definition spatial light modulation enabling highly efficient generation of fully structured vector beams. Appl. Opt. 2019, 58, 6591–6596. [Google Scholar] [CrossRef] [PubMed]
- Liebmann, M.; Treffer, A.; Bock, M.; Jurke, M.; Wallrabe, U.; Grunwald, R. Tailored spectral rotation of vortex pulses by non-uniform spiral phase gratings. Proc. SPIE 2021, 11701, 117010V. [Google Scholar] [CrossRef]
- Padgett, M.J.; Miatto, F.M.; Lavery, M.P.; Zeilinger, A.; Boyd, R.W. Divergence of an orbital-angular-momentum-carrying beam upon propagation. New J. Phys. 2015, 17, 023011. [Google Scholar] [CrossRef]
- Liu, W.; Cheng, J.; Wan, C. Generation of optical toroidal vortex with circular asymmetric gratings. arXiv 2024, arXiv:2404.11921. [Google Scholar] [CrossRef]
- Dorney, K.M.; Rego, L.; Brooks, N.J.; Nguyen, Q.; Liao, C.; Román, J.S.; Couch, D.E.; Liu, A.; Pisanty, E.; Lewenstein, M.; et al. Attosecond extreme ultraviolet beams with time-varying orbital angular momentum: The Self-Torque of Light. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San José, CA, USA, 5–10 May 2019. [Google Scholar] [CrossRef]
- Rego, L.; Dorney, K.M.; Brooks, N.J.; Nguyen, Q.; Liao, C.-T.; Román, J.S.; Couch, D.E.; Liu, A.; Pisanty, E.; Lewenstein, M.; et al. Generation of extreme-ultraviolet beams with time-varying orbital angular momentum. Science 2019, 364, eaaw9486. [Google Scholar] [CrossRef] [PubMed]
- Yamane, K.; Sakamoto, M.; Murakami, N.; Morita, R.; Oka, K. Picosecond rotation of a ring-shaped optical lattice by using a chirped vortex-pulse pair. Opt. Lett. 2016, 41, 4597–4600. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Yu, P.; Liu, Y.; Wang, Z.; Li, Y.; Gong, L. Time-varying optical spin-orbit interactions in tight focusing of self-torqued beams. J. Light. Technol. 2023, 41, 2252–2258. [Google Scholar] [CrossRef]
- Grunwald, R.; Bock, M. Characterization of orbital angular momentum beams by polar mapping and Fourier Transform. Photonics 2024, 11, 296. [Google Scholar] [CrossRef]
- Kim, M.-S.; Scharf, T.; da Costa Assafrao, A.; Rockstuhl, C.; Pereira, S.F.; Urbach, H.P.; Herzig, H.P. Phase anomalies in Bessel-Gauss beams. Opt. Express 2012, 20, 28929–28940. [Google Scholar] [CrossRef]
- Berry, M.V.; Klein, S. Integer, fractional and fractal Talbot effects. J. Mod. Opt. 1996, 43, 2139–2164. [Google Scholar] [CrossRef]
- Elson, J.M. Mathematical analysis of gratings with circularly concentric grooves. J. Opt. Soc. Am. 1983, 73, 702–706. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grunwald, R.; Jurke, M.; Liebmann, M.; Treffer, A.; Bock, M. Generation of Propagation-Dependent OAM Self-Torque with Chirped Spiral Gratings. Photonics 2024, 11, 463. https://doi.org/10.3390/photonics11050463
Grunwald R, Jurke M, Liebmann M, Treffer A, Bock M. Generation of Propagation-Dependent OAM Self-Torque with Chirped Spiral Gratings. Photonics. 2024; 11(5):463. https://doi.org/10.3390/photonics11050463
Chicago/Turabian StyleGrunwald, Ruediger, Mathias Jurke, Max Liebmann, Alexander Treffer, and Martin Bock. 2024. "Generation of Propagation-Dependent OAM Self-Torque with Chirped Spiral Gratings" Photonics 11, no. 5: 463. https://doi.org/10.3390/photonics11050463
APA StyleGrunwald, R., Jurke, M., Liebmann, M., Treffer, A., & Bock, M. (2024). Generation of Propagation-Dependent OAM Self-Torque with Chirped Spiral Gratings. Photonics, 11(5), 463. https://doi.org/10.3390/photonics11050463





