The Generation of Equal-Intensity and Multi-Focus Optical Vortices by a Composite Spiral Zone Plate
Abstract
:1. Introduction
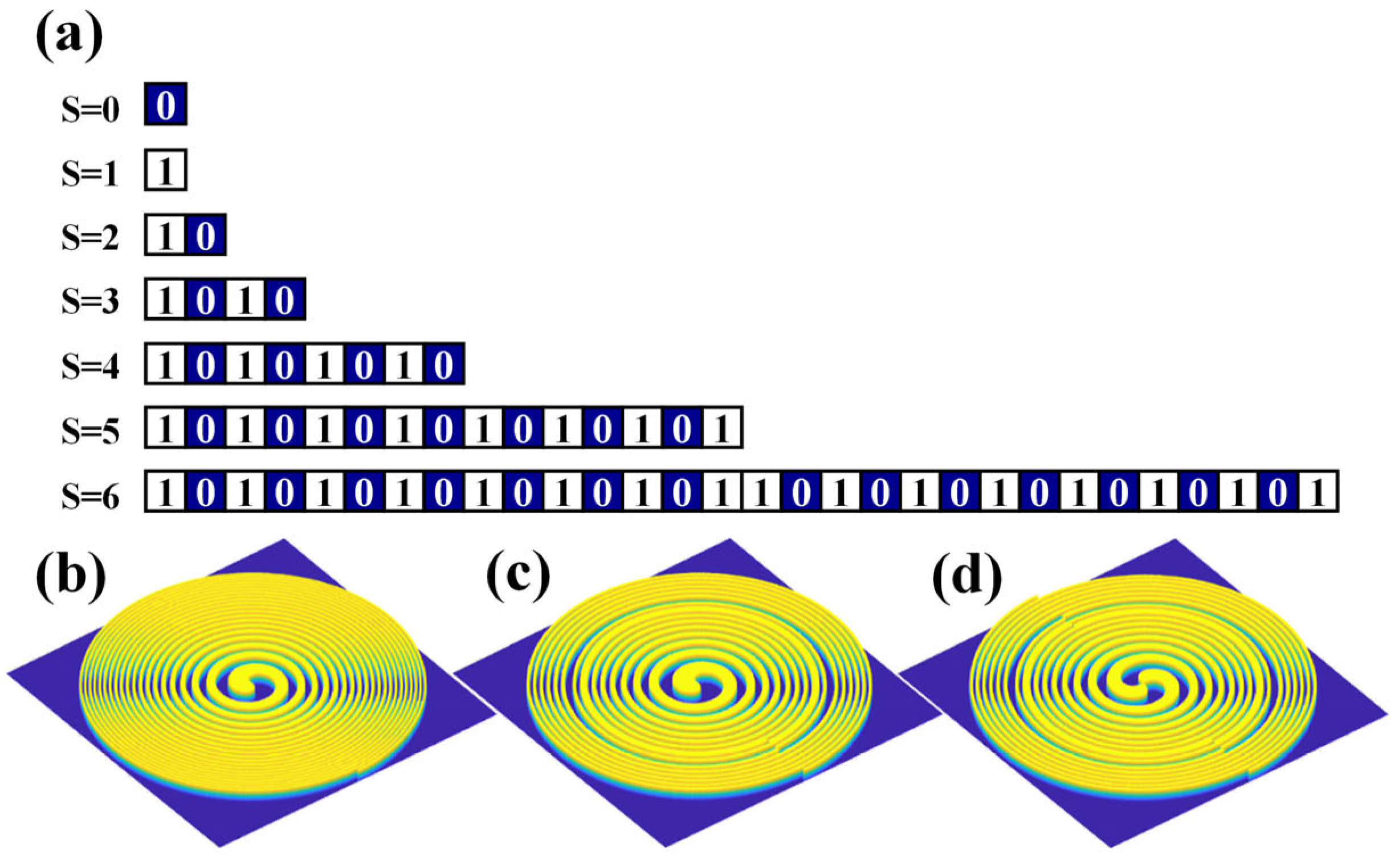
2. Design and Method
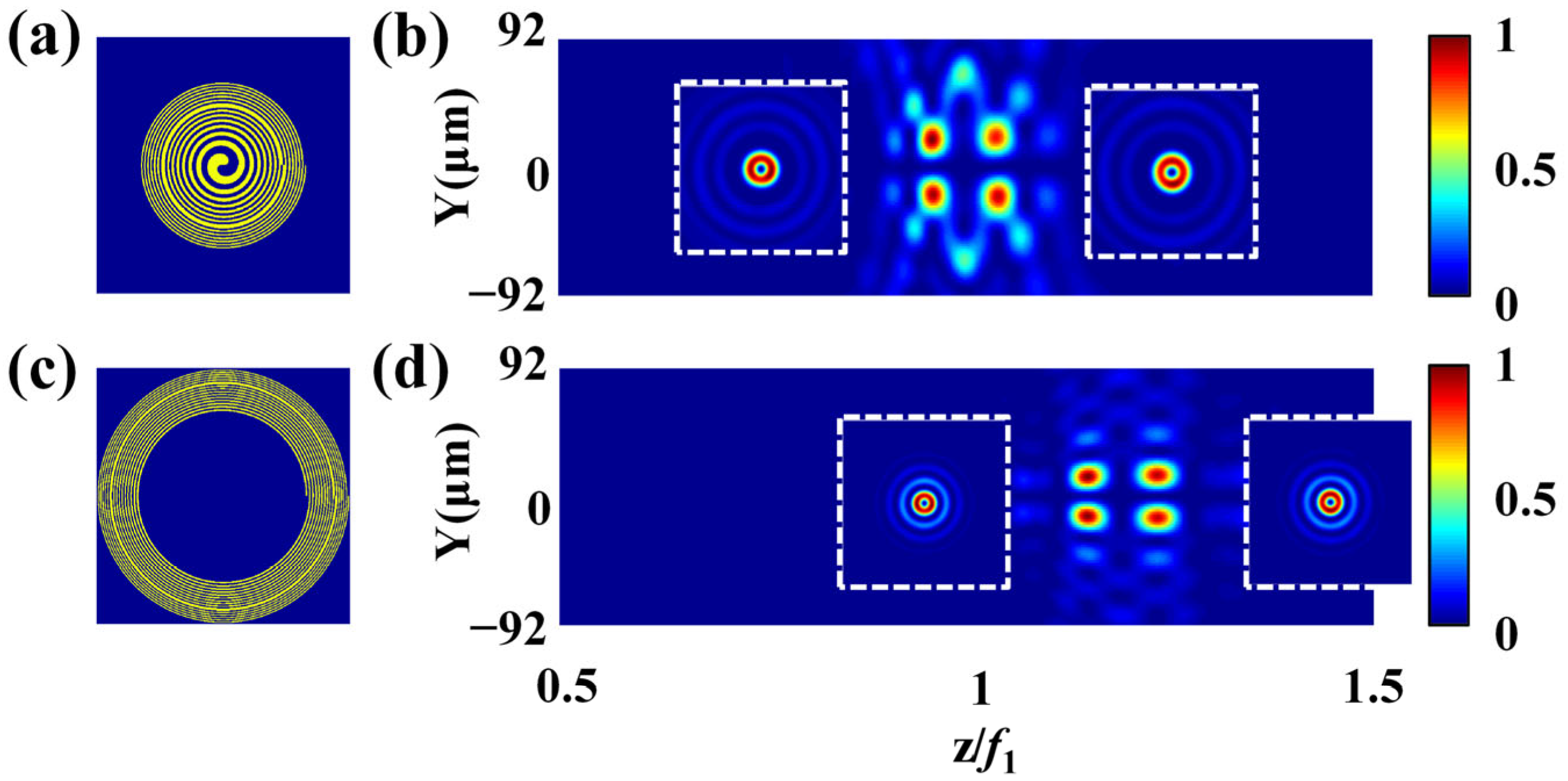
3. Focusing Properties of the EMCSZPs
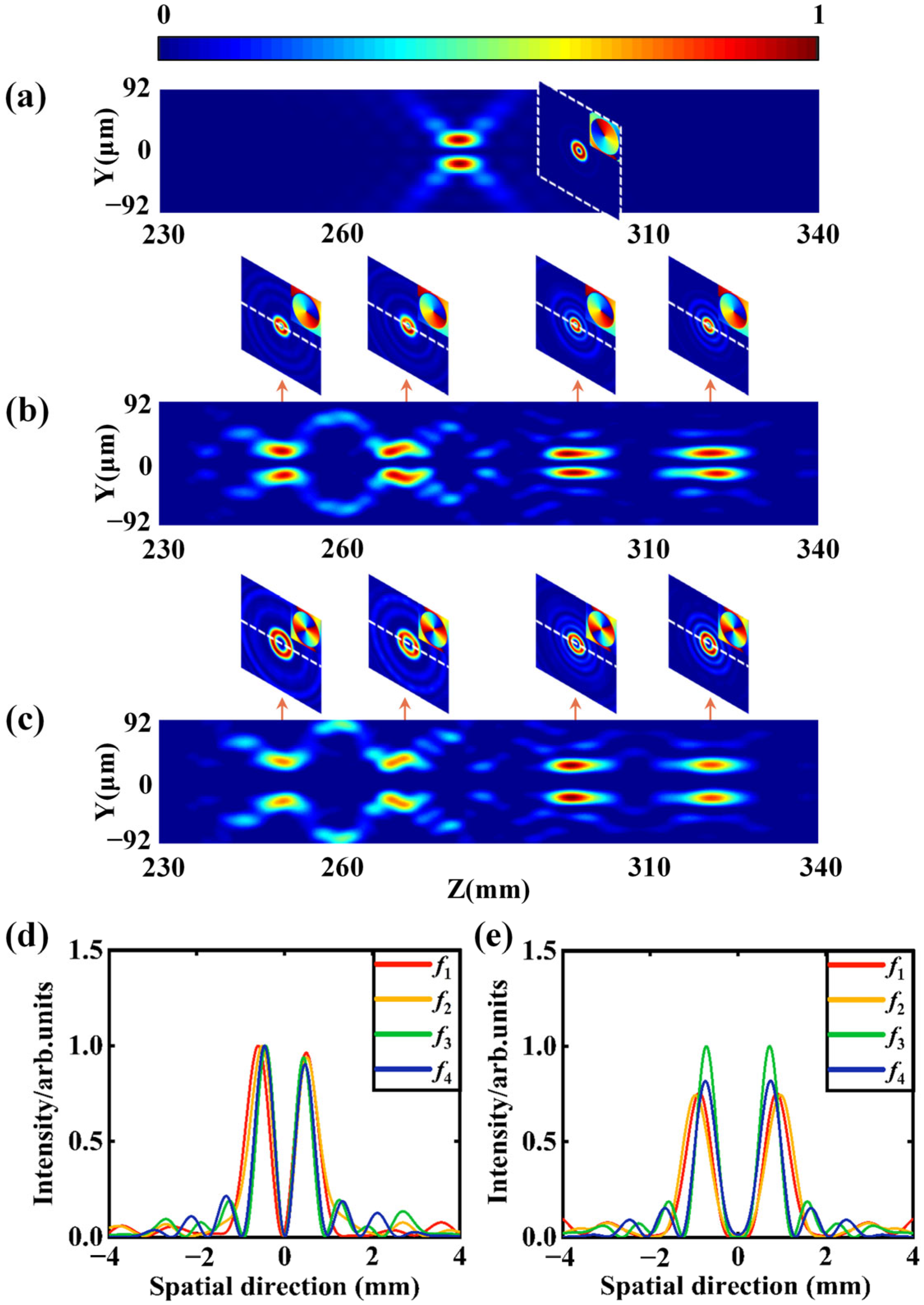
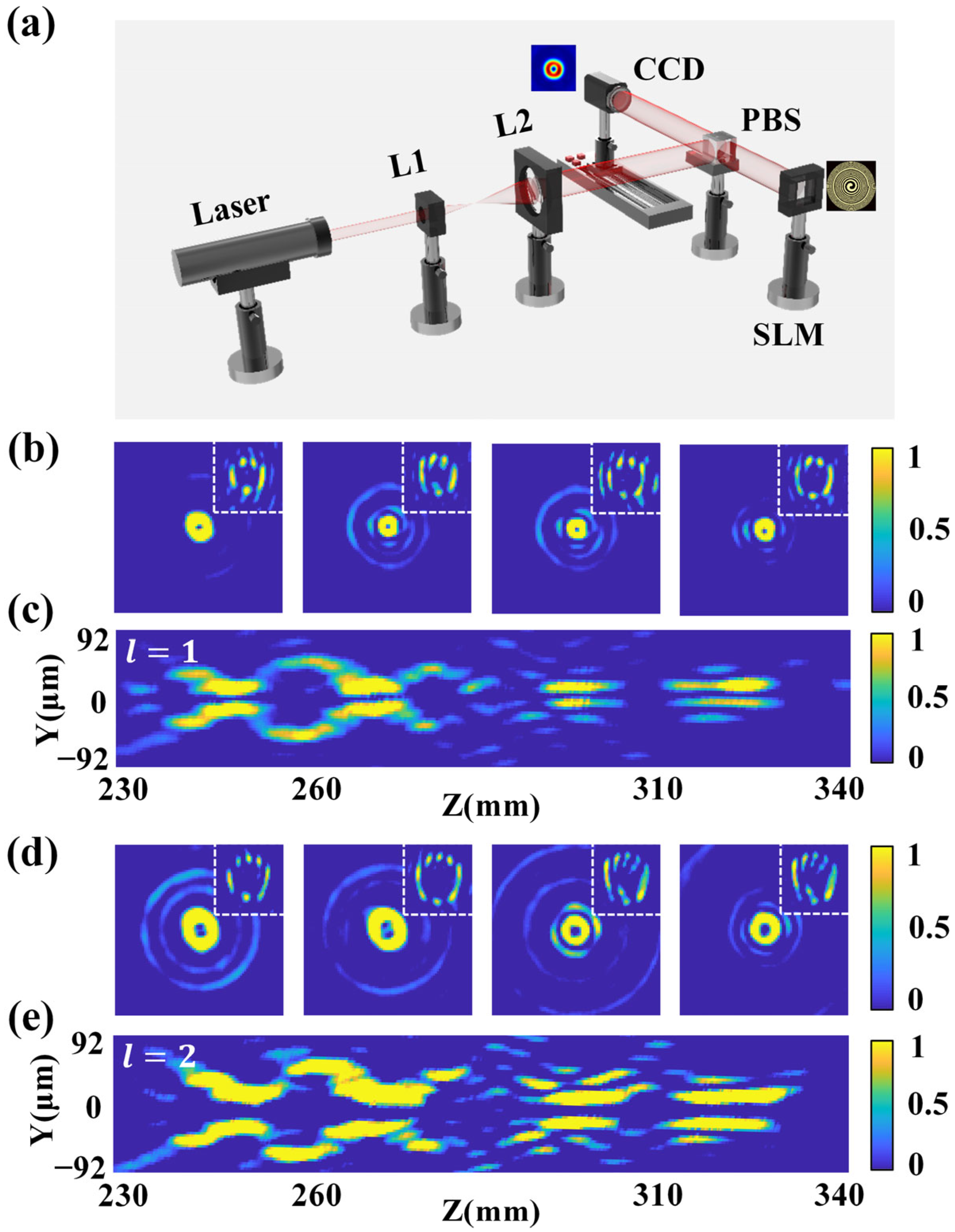
4. Experimental Results
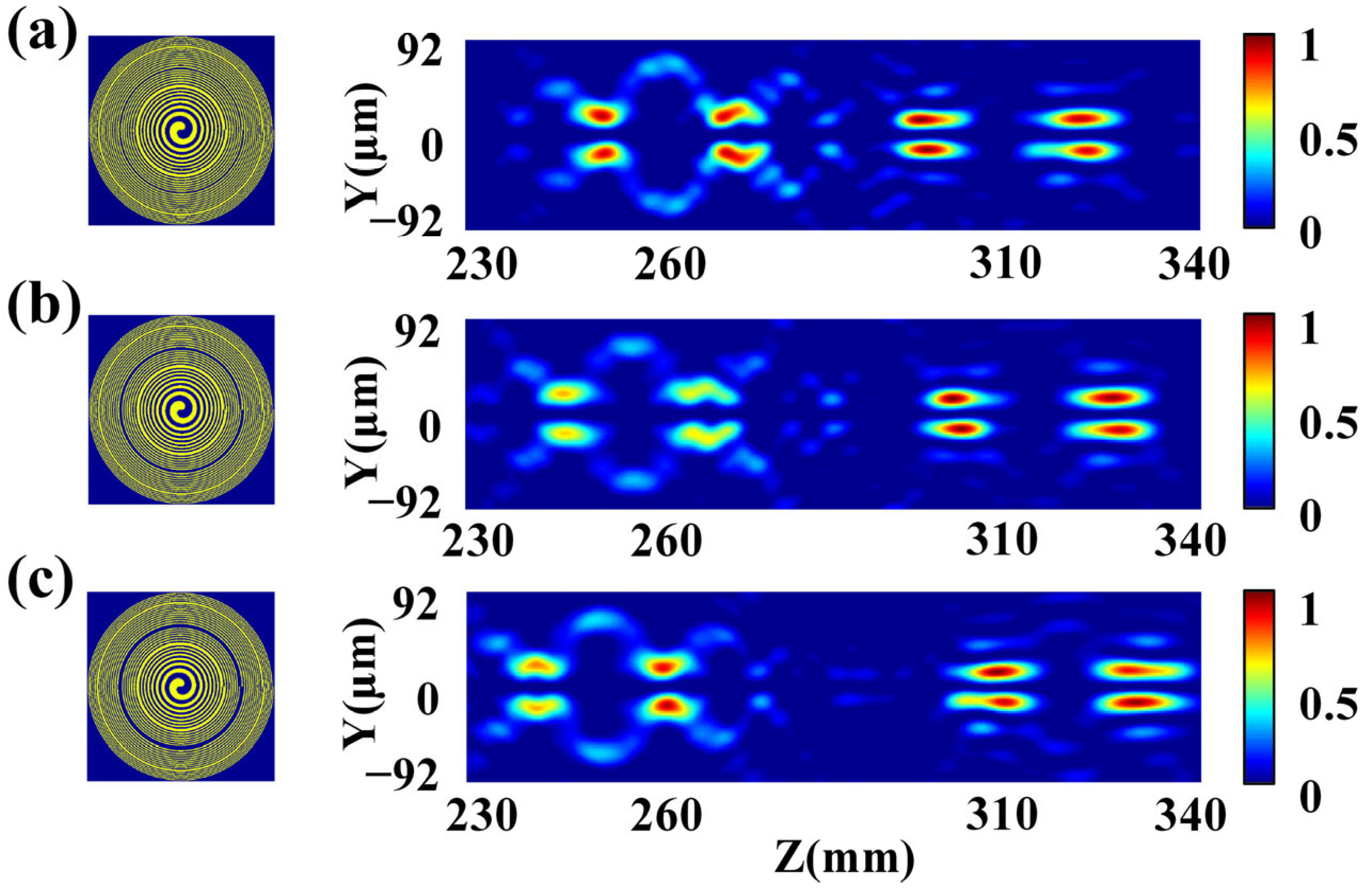
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ashkin, A.; Dziedzic, J.M. Optical trapping and manipulation of viruses and bacteria. Science 1987, 235, 1517–1520. [Google Scholar] [CrossRef] [PubMed]
- The Nobel Prize in Physics 2018. Nobel Prize Outreach AB 2022. 2022. Available online: https://www.nobelprize.org/prizes/physics/2018/summary/ (accessed on 1 August 2023).
- Zang, H.; Miao, Z.; Wang, M.; Fan, Q.; Wei, L.; Wang, C.; Zhou, W.; Hua, Y.; Cao, L.; Xue, X.; et al. Generation of single-focus phase singularity by the annulus-quadrangle-element coded binary square spiral zone plates. Sci. China Phys. Mech. Astron. 2022, 65, 294212. [Google Scholar] [CrossRef]
- Ni, J.; Huang, C.; Zhou, L.; Gu, M.; Song, Q.; Kivshar, Y.; Qiu, C. Multidimensional phase singularities in nanophotonics. Science 2021, 374, eabj0039. [Google Scholar] [CrossRef] [PubMed]
- Verbeeck, J.; Tian, H.; Schattschneider, P. Production and application of electron vortex beams. Nature 2010, 467, 301–304. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Zhao, C.; Zeng, Y.; Chen, Y.; Zhao, C.; Qiu, C. Evolution and nonreciprocity of loss-induced topological phase singularity pairs. Phys. Rev. Lett. 2021, 127, 266101. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef] [PubMed]
- Bliokh, K.Y. Orbital angular momentum of optical, acoustic, and quantum-mechanical spatiotemporal vortex pulses. Phys. Rev. A 2023, 107, L031501. [Google Scholar] [CrossRef]
- Min, C.; Shen, Z.; Shen, J.; Zhang, Y.; Fang, H.; Yuan, G.; Du, L.; Zhu, S.; Lei, T.; Yuan, X. Focused plasmonic trapping of metallic particles. Nat. Commun. 2013, 4, 2891. [Google Scholar] [CrossRef] [PubMed]
- Xia, T.; Cheng, S.; Tao, S. The generalized mean zone plate. Laser Phys. 2018, 28, 066201. [Google Scholar] [CrossRef]
- Pascucci, M.; Tessier, G.; Emiliani, V.; Guillon, M. Superresolution imaging of optical vortices in a speckle pattern. Phys. Rev. Lett. 2016, 116, 093904. [Google Scholar] [CrossRef]
- Gao, N.; Xie, C.; Li, C.; Jin, C.; Liu, M. Square optical vortices generated by binary spiral zone plates. Appl. Phys. Lett. 2011, 98, 151106. [Google Scholar] [CrossRef]
- Zang, H.; Wang, B.; Zheng, C.; Wei, L.; Fan, Q.; Wang, S.; Yang, Z.; Zhou, W.; Cao, L.; Guo, H. Performance analysis of single-focus phase singularity based on elliptical reflective annulus quadrangle-element coded spiral zone plates. Chin. Phys. B 2023, 33, 014209. [Google Scholar] [CrossRef]
- Yang, Y.; Forbes, A.; Cao, L. A review of liquid crystal spatial light modulators: Devices and applications. Opto-Electron. Sci. 2023, 2, 230026-1–230026-29. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Logachev, V.I.; Porfirev, A.P. Properties of vortex light fields generated by generalized spiral phase plates. Phys. Rev. A 2020, 101, 043829. [Google Scholar] [CrossRef]
- Nassiri, M.G.; Brasselet, E. Multispectral management of the photon orbital angular momentum. Phys. Rev. Lett. 2018, 121, 213901. [Google Scholar] [CrossRef] [PubMed]
- Géneaux, R.; Camper, A.; Auguste, T.; Gobert, O.; Caillat, J.; Taïeb, R.; Ruchon, T. Synthesis and characterization of attosecond light vortices in the extreme ultraviolet. Nat. Commun. 2016, 7, 12583. [Google Scholar] [CrossRef]
- Rego, L.; San Román, J.; Picón, A.; Plaja, L.; Hernández-García, C. Nonperturbative twist in the generation of extreme-ultraviolet vortex beams. Phys. Rev. Lett. 2016, 117, 163202. [Google Scholar] [CrossRef]
- Aleksanyan, A.; Brasselet, E. Spin–orbit photonic interaction engineering of Bessel beams. Optica 2016, 3, 167–174. [Google Scholar] [CrossRef]
- Pu, J.; Jones, P.H. Devil’s lens optical tweezers. Opt. Express 2015, 23, 8190–8199. [Google Scholar] [CrossRef]
- Singh, H.; Yadav, A.K.; Vashisth, S.; Singh, K. Optical image encryption using devil’s vortex toroidal lens in the Fresnel transform domain. Int. J. Opt. 2015, 2015, 926135. [Google Scholar] [CrossRef]
- Zang, H.; Zhou, X.; Yang, Z.; Yu, Q.; Zheng, C.; Yao, J. Polarization multiplexed multifunctional metasurface for generating longitudinally evolving vector vortex beams. Phys. Lett. A 2024, 497, 129336. [Google Scholar] [CrossRef]
- Zheng, C.; Liu, J.; Li, H.; Wang, M.; Zang, H.; Zhang, Y.; Yao, J. Terahertz metasurface polarization detection employing vortex pattern recognition. Photonics Res. 2023, 11, 2256–2263. [Google Scholar] [CrossRef]
- Karabchevsky, A. On-chip optical vortex-based nanophotonic detectors. Light Sci. Appl. 2020, 9, 115. [Google Scholar] [CrossRef] [PubMed]
- White, A.D.; Su, L.; Shahar, D.I.; Yang, K.Y.; Ahn, G.H.; Skarda, J.L.; Ramachandran, S.; Vučković, J. Inverse design of optical vortex beam emitters. ACS Photonics 2022, 10, 803–807. [Google Scholar] [CrossRef]
- Heckenberg, N.R.; McDuff, R.; Smith, C.P.; White, A.G. Generation of optical phase singularities by computer-generated holograms. Opt. Lett. 1992, 17, 221–223. [Google Scholar] [CrossRef] [PubMed]
- Tsukamoto, Y.; Yoshida, H.; Ozaki, M. Generation of a focused optical vortex beam using a liquid crystal spiral zone plate. Opt. Express 2022, 30, 8667–8675. [Google Scholar] [CrossRef]
- Yi, S.; Mu, B.; Wang, X.; Zhang, Z.; Zhu, J.; Wang, Z.; He, P.; Cao, Z.; Dong, J.; Liu, S.; et al. Large-field high-resolution Kirkpatrick–Baez amélioré-Kirkpatrick–Baez mixed microscope for multi-keV time-resolved X-ray imaging diagnostics of laser plasma. Opt. Eng. 2014, 53, 053114. [Google Scholar] [CrossRef]
- Gao, N.; Zhang, Y.; Xie, C. Circular Fibonacci gratings. Appl. Opt. 2011, 50, G142–G148. [Google Scholar] [CrossRef] [PubMed]
- Monsoriu, J.A.; Calatayud, A.; Remón, L.; Furlan, W.D.; Saavedra, G.; Andrés, P. Bifocal Fibonacci diffractive lenses. IEEE Photonics J. 2013, 5, 3400106. [Google Scholar] [CrossRef]
- Calatayud, A.; Ferrando, V.; Remón, L.; Furlan, W.D.; Monsoriu, J.A. Twin axial vortices generated by Fibonacci lenses. Opt. Express 2013, 21, 10234–10239. [Google Scholar] [CrossRef]
- Teng, S.; Wang, J.; Li, F.; Zhang, W. Talbot image of two-dimensional fractal grating. Opt. Commun. 2014, 315, 103–107. [Google Scholar] [CrossRef]
- Verma, R.; Banerjee, V.; Senthilkumaran, P. Fractal signatures in the aperiodic Fibonacci grating. Opt. Lett. 2014, 39, 2557–2560. [Google Scholar] [CrossRef] [PubMed]
- Verma, R.; Sharma, M.K.; Senthilkumaran, P.; Banerjee, V. Analysis of Fibonacci gratings and their diffraction patterns. J. Opt. Soc. Am. A 2014, 31, 1473–1480. [Google Scholar] [CrossRef] [PubMed]
- Ferrando, V.; Calatayud, A.; Andrés, P.; Torroba, R.; Furlan, W.D.; Monsoriu, J.A. Imaging properties of Kinoform Fibonacci lenses. IEEE Photonics J. 2014, 6, 6500106. [Google Scholar] [CrossRef]
- Monsoriu, J.A.; Giménez, M.H.; Furlan, W.D.; Barreiro, J.C.; Saavedra, G. Diffraction by m-bonacci gratings. Eur. J. Phys. 2015, 36, 065005. [Google Scholar] [CrossRef]
- Machado, F.; Ferrando, V.; Furlan, W.D.; Monsoriu, J.A. Diffractive m-bonacci lenses. Opt. Express 2017, 25, 8267–8273. [Google Scholar] [CrossRef] [PubMed]
- Pérez-López, S.; Fuster, J.M.; Candelas, P. M-Bonacci zone plates for ultrasound focusing. Sensors 2019, 19, 4313. [Google Scholar] [CrossRef] [PubMed]
- Perez-Lopez, S.; Fuster, J.M.; Candelas, P.; Rubio, C. Fractal lenses based on Cantor binary sequences for ultrasound focusing applications. Ultrasonics 2019, 99, 105967. [Google Scholar] [CrossRef] [PubMed]
- Xia, T.; Cheng, S.; Yu, W.; Tao, S. Tailorable polygon-like beams generated by modified spiral petal-like zone plates. Results Phys. 2021, 21, 103823. [Google Scholar] [CrossRef]
- Ferrando, V.; Calatayud, A.; Giménez, F.; Furlan, W.D.; Monsoriu, J.A. Cantor dust zone plates. Opt. Express 2013, 21, 2701–2706. [Google Scholar] [CrossRef]
- Ma, W.; Tao, S.; Cheng, S. Composite Thue-Morse zone plates. Opt. Express 2016, 24, 12740–12747. [Google Scholar] [CrossRef]
- Ferrando, V.; Giménez, F.; Furlan, W.D.; Monsoriu, J.A. Bifractal focusing and imaging properties of Thue-Morse Zone Plates. Opt. Express 2015, 23, 19846–19853. [Google Scholar] [CrossRef] [PubMed]
- Cheng, S.; Liu, M.; Xia, T.; Tao, S. Fibonacci-like zone plate. Laser Phys. 2018, 28, 066203. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, P.; Yang, H.; Qin, Y.; Zheng, Y. Multi-focus composite spiral zone plate to generate focused vortices with the comparable intensity based on genetic algorithm. Opt. Express 2023, 31, 35363–35376. [Google Scholar] [CrossRef]
- Waddill, M.E. The Tetranacci sequence and generalizations. Fibonacci Q. 1992, 30, 9–20. [Google Scholar]
- Sharma, K.K.; Panwar, V. On Tetranacci Functions and Tetranacci Numbers. Int. J. Math. Comput. Sci. 2020, 15, 923–932. [Google Scholar]
- Iemmi, C.; Campos, J.; Escalera, J.C.; López-Coronado, O.; Gimeno, R.; Yzuel, M.J. Depth of focus increase by multiplexing programmable diffractive lenses. Opt. Express 2006, 14, 10207–10219. [Google Scholar] [CrossRef] [PubMed]
- Vergara, M.; Iemmi, C. Multiple quasi-perfect vector vortex beams with arbitrary 3D position on focus. Appl. Opt. 2022, 61, 5926–5933. [Google Scholar] [CrossRef]
- Zang, H.; Wang, Y.; Zheng, C.; Zhou, W.; Wei, L.; Cao, L.; Fan, Q. Generalized binary spiral zone plates with a single focus obtained by feedforward neural network. Opt. Express 2023, 31, 30486–30494. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zang, H.; Li, J.; Zheng, C.; Tian, Y.; Wei, L.; Fan, Q.; Wang, S.; Wang, C.; Xie, J.; Cao, L. The Generation of Equal-Intensity and Multi-Focus Optical Vortices by a Composite Spiral Zone Plate. Photonics 2024, 11, 466. https://doi.org/10.3390/photonics11050466
Zang H, Li J, Zheng C, Tian Y, Wei L, Fan Q, Wang S, Wang C, Xie J, Cao L. The Generation of Equal-Intensity and Multi-Focus Optical Vortices by a Composite Spiral Zone Plate. Photonics. 2024; 11(5):466. https://doi.org/10.3390/photonics11050466
Chicago/Turabian StyleZang, Huaping, Jingzhe Li, Chenglong Zheng, Yongzhi Tian, Lai Wei, Quanping Fan, Shaoyi Wang, Chuanke Wang, Juan Xie, and Leifeng Cao. 2024. "The Generation of Equal-Intensity and Multi-Focus Optical Vortices by a Composite Spiral Zone Plate" Photonics 11, no. 5: 466. https://doi.org/10.3390/photonics11050466
APA StyleZang, H., Li, J., Zheng, C., Tian, Y., Wei, L., Fan, Q., Wang, S., Wang, C., Xie, J., & Cao, L. (2024). The Generation of Equal-Intensity and Multi-Focus Optical Vortices by a Composite Spiral Zone Plate. Photonics, 11(5), 466. https://doi.org/10.3390/photonics11050466





