Analysis of the Effective and Actual Lens Position by Different Formulas. Postoperative Application of a Ray-Tracing-Based Simulated Optical Model
Abstract
:1. Introduction
2. Methods
2.1. Subjects and Procedures
2.2. Surgery Procedure
2.3. IOLP and ELP Calculation
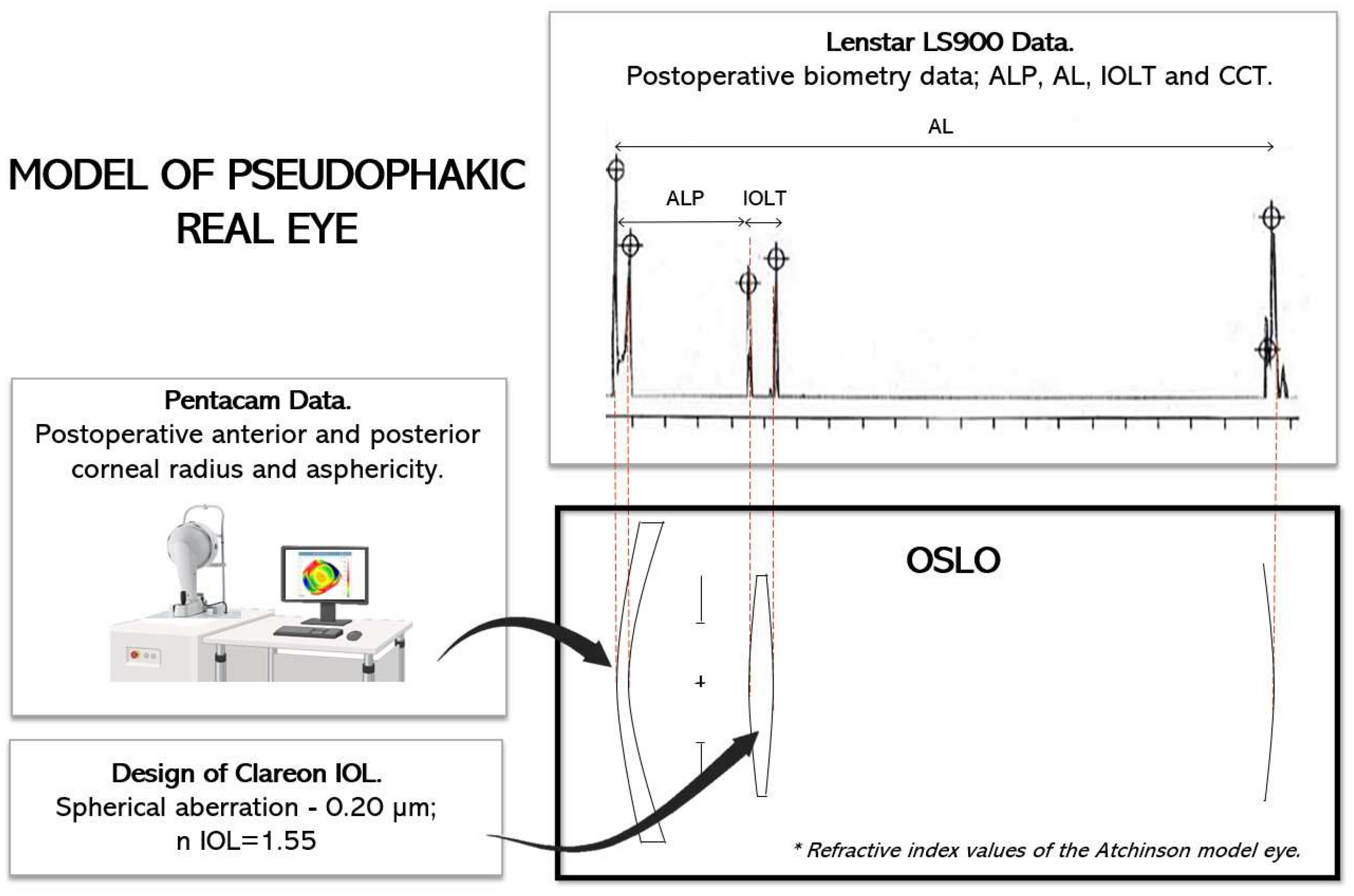
2.4. Optical Modeling
- (1)
- Firstly, Clareon IOL was designed with a power range between 16.50 and 26.50 D and a spherical aberration on the anterior surface equal to −0.20 µm for a 6.00 mm pupil.
- (2)
- Secondly, all real eyes were modeled using the refractive index values of the Atchison model eye [18]. To model each cornea, we used the postoperative tomography measurements obtained with Pentacam. The postoperative values of CCT, ALP, and AL were obtained from the Lenstar, and the position of the iris in each case was assumed from the measurement of the preoperative ACD with the Lenstar, which represented the distance from the anterior corneal vertex to the position of the crystalline lens.
- (3)
- Thirdly, the operated eyes were simulated in the software, including the IOLP and the ALP.
2.5. Data Analysis
3. Results
3.1. Intraocular Lens Power
3.2. Effective Lens Position and Actual Lens Position
3.3. Optical Modeling
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davis, G. The Evolution of Cataract Surgery. Mo. Med. 2016, 113, 58–62. [Google Scholar]
- Olsen, T. Calculation of intraocular lens power: A review. Acta Ophthalmol. Scand. 2007, 85, 472–485. [Google Scholar] [CrossRef]
- Norrby, S. Sources of error in intraocular lens power calculation. J. Cataract. Refract. Surg. 2008, 34, 368–376. [Google Scholar] [CrossRef] [PubMed]
- Retzlaff, J.A.; Sanders, D.R.; Kraff, M.C. Development of the SRK/T intraocular lens implant power calculation formula. J. Cataract. Refract. Surg. 1990, 16, 333–340. [Google Scholar] [CrossRef] [PubMed]
- Holladay, J.T.; Musgrove, K.H.; Prager, T.C.; Lewis, J.W.; Chandler, T.Y.; Ruiz, R.S. A three-part system for refining intraocular lens power calculations. J. Cataract. Refract. Surg. 1988, 14, 17–24. [Google Scholar] [CrossRef] [PubMed]
- Hoffer, K.J. The Hoffer Q formula: A comparison of theoretic and regression formulas. J. Cataract. Refract. Surg. 1993, 19, 700–712. [Google Scholar] [CrossRef] [PubMed]
- Barrett, G.D. An improved universal theoretical formula for intraocular lens power prediction. J. Cataract. Refract. Surg. 1993, 19, 713–720. [Google Scholar] [CrossRef]
- Haigis, W. The Haigis formula. In Intraocular Lens Power Calculations; Shammas, H., Ed.; SLACK Incorporated: San Francisco, CA, USA, 2004; pp. 41–57. [Google Scholar]
- Olsen, T.; Olesen, H.; Thim, K.; Corydon, L. Prediction of postoperative intraocular lens chamber depth. J. Cataract. Refract. Surg. 1990, 16, 587–590. [Google Scholar] [CrossRef] [PubMed]
- Einighammer, J.; Oltrup, T.; Bende, T.; Jean, B. Calculating intraocular lens geometry by real ray tracing. J. Refract. Surg. 2007, 23, 393–404. [Google Scholar] [CrossRef]
- Li, T.; Stein, J.; Nallasamy, N. AI-powered effective lens position prediction improves the accuracy of existing lens formulas. Br. J. Ophthalmol. 2022, 106, 1222–1226. [Google Scholar] [CrossRef]
- Li, T.; Reddy, A.; Stein, J.D.; Nallasamy, N. Ray tracing intraocular lens calculation performance improved by AI-powered postoperative lens position prediction. Br. J. Ophthalmol. 2023, 107, 483–487. [Google Scholar] [CrossRef] [PubMed]
- Kothari, S.S.; Reddy, J.C. Recent developments in the intraocular lens formulae: An update. Semin. Ophthalmol. 2022, 38, 143–150. [Google Scholar] [CrossRef] [PubMed]
- Melles, R.B.; Kane, J.X.; Olsen, T.; Chang, W.J. Update on intraocular lens calculation formulas. Ophthalmology 2019, 126, 1334–1335. [Google Scholar] [CrossRef]
- Holzer, M.P.; Mamusa, M.; Auffarth, G.U. Accuracy of a new partial coherence interferometry analyser for biometric measurements. Br. J. Ophthalmol. 2009, 93, 807–810. [Google Scholar] [CrossRef]
- Cruysberg, L.P.J.; Doors, M.; Verbakel, F.; Berendschot, T.T.J.M.; De Brabander, J.; Nuijts, R.M.M.A. Evaluation of the Lenstar LS 900 non-contact biometer. Br. J. Ophthalmol. 2010, 94, 106–110. [Google Scholar] [CrossRef] [PubMed]
- Castro-Alonso, F.J.; Bordonaba-Bosque, D.; Piñero, D.P.; Latre-Rebled, B. Predictive value of intracrystalline interphase point measured by optical low-coherence reflectometry for the estimation of the anatomical position of an intraocular lens after cataract surgery. J. Cataract. Refract. Surg. 2019, 45, 1294–1304. [Google Scholar] [CrossRef] [PubMed]
- Atchison, D.A. Optical models for human myopic eyes. Vis. Res. 2006, 46, 2236–2250. [Google Scholar] [CrossRef] [PubMed]
- Thibos, L.N.; Hong, X.; Bradley, A.; Cheng, X. Statistical variation of aberration structure and image quality in a normal population of healthy eyes. J. Opt. Soc. Am. A 2002, 19, 2329–2348. [Google Scholar] [CrossRef]
- Thibos, L.N.; Horner, D. Power vector analysis of the optical outcome of refractive surgery. J. Cataract. Refract. Surg. 2001, 27, 80–85. [Google Scholar] [CrossRef] [PubMed]
- Iskander, D.R.; Davis, B.A.; Collins, M.J.; Franklin, R. Objective refraction from monochromatic wavefront aberrations via Zernike power polynomials. Ophthalmic Physiol. Opt. 2007, 27, 245–255. [Google Scholar] [CrossRef]
- Shammas, J.H.; Shammas, M.C. Improving the preoperative prediction of the anterior pseudophakic distance for intraocular lens power calculation. J. Cataract. Refract. Surg. 2015, 41, 2379–2386. [Google Scholar] [CrossRef] [PubMed]
- Goto, S.; Maeda, N.; Koh, S.; Ohnuma, K.; Hayashi, K.; Iehisa, I.; Noda, T.; Nishida, K. Prediction of postoperative intraocular lens position with angle-to-angle depth using anterior segment optical coherence tomography. Ophthalmology 2016, 123, 2474–2480. [Google Scholar] [CrossRef] [PubMed]
- Fernández, J.; Rodríguez-Vallejo, M.; Martínez, J.; Tauste, A.; Piñero, D.P. New approach for the calculation of the intraocular lens power based on the fictitious corneal refractive index estimation. J. Ophthalmol. 2019, 2019, 2796126. [Google Scholar] [CrossRef] [PubMed]
- Gatinel, D.; Debellemanière, G.; Saad, A.; Dubois, M.; Rampat, R. Determining the theoretical effective lens position of thick intraocular lenses for machine learning–based iol power calculation and simulation. Transl. Vis. Sci. Technol. 2021, 10, 27. [Google Scholar] [CrossRef] [PubMed]
- Holladay, J.T.; Maverick, K.J. Relationship of the actual thick intraocular lens optic to the thin lens equivalent. Arch. Ophthalmol. 1998, 126, 339–347. [Google Scholar] [CrossRef] [PubMed]
- Olsen, T.; Hoffmann, P. C constant: New concept for ray tracing–assisted intraocular lens power calculation. J. Cataract. Refract. Surg. 2014, 40, 764–773. [Google Scholar] [CrossRef] [PubMed]
- Hirnschall, N.; Amir-Asgari, S.; Maedel, S.; Findl, O. Predicting the postoperative intraocular lens position using continuous intraoperative optical coherence tomography measurements. Investig. Ophthalmol. Vis. Sci. 2013, 54, 5196–5203. [Google Scholar] [CrossRef]
- Pereira, S.; Ganesh, S.; Umarani, R.; Sute, S.S. Prediction of effective lens position (ELP) and its changes in different monofocal intraocular lens (IOL’s). Glob. J. Cataract. Surg. Res. Ophthalmol. 2023, 1, 93–98. [Google Scholar] [CrossRef]


| Preoperative Data | Postoperative Data | p-Value | |
|---|---|---|---|
| AL (mm) | 23.52 ± 0.96 [22.18–25.97] | 23.46 ± 1.05 [22.06–25.97] | 0.123 |
| CCT (µm) | 550 ± 37 [478–661] | 550 ± 37 [475–654] | 0.972 |
| WTW (mm) | 11.93 ± 0.36 [11.14–12.60] | 11.95 ± 0.96 [10.9–12.89] | 0.701 |
| Km anterior (D) | 43.23 ± 1.38 [40.65–46.44] | 43.14 ± 1.44 [40.31–46.44] | 0.572 |
| Km posterior (D) | −5.97 ± 1.29 [(−6.5)–(−5.97)] | −6.16 ± 1.50 [(−6.60)–(−5.55)] | 0.692 |
| ACD (mm) | 3.11 ± 0.38 [2.48–3.85] | ||
| LT (mm) | 4.52 ± 0.44 [3.470–5.450] | - | |
| ALP (mm) | - | 4.53 ± 0.25 [3.81–5.24] | |
| IOLT (mm) | - | 0.67 ± 0.06 [0.55–0.96] | |
| REOBJ (D) | −0.05 ± 0.35 [(−1.25)–(+1.00)] | ||
| RESUBJ (D) | −0.02 ± 0.39 [(−0.62)–(+1.00)] | ||
| IOLP Hoffer Q [21.29 ± 2.79 D] | IOLP Holladay I [21.12 ± 2.72 D] | IOLP SRK/T [21.32 ± 2.50 D] | IOLP Haigis [21.12 ± 2.66 D] | ||
|---|---|---|---|---|---|
| Mean dif. ± SD (mm) | IOLP Implanted | 0.31 ± 0.91 | 0.48 ± 1.01 | 0.28 ± 0.78 | 0.49 ± 0.83 |
| LoAs (mm) | (−1.48, 2.10) | (−1.50, 2.47) | (−1.25, 1.81) | (−1.15, 2.12) | |
| p-value (t-test) | 0.030 * | 0.003 * | 0.023 * | p < 0.001 * |
| ELP Hoffer Q | ELP Holladay I | ELP SRK/T | ||
|---|---|---|---|---|
| Mean dif. ± SD (mm) | ELP Holladay I | 0.02 ± 0.18 | - | - |
| LoAs (mm) | (−0.32, 0.38) | |||
| p-value (t-test) | 0.320 | |||
| Mean dif. ± SD (mm) | ELP SRK/T | −0.04 ± 0.19 | −0.07 ± 0.23 | - |
| LoAs (mm) | (−0.42, 0.33) | (−0.52, 0.38) | ||
| p-value (t-test) | 0.139 | 0.055 | ||
| Mean dif. ± SD (mm) | ELP Haigis | 0.61 ± 0.09 | 0.58 ± 0.22 | 0.65 ± 0.27 |
| LoAs (mm) | (0.42, 0.79) | (0.14, 1.01) | (0.12, 1.17) | |
| p-value (t-test) | 0.001 * | p < 0.001 * | p < 0.001 * | |
| Mean ± SD (mm) range (mm) | ALP | 4.53 ± 0.25 | ||
| (3.80–5.02) | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gargallo Yebra, D.; Remón Martín, L.; Pérez Escorza, I.; Castro Alonso, F.J. Analysis of the Effective and Actual Lens Position by Different Formulas. Postoperative Application of a Ray-Tracing-Based Simulated Optical Model. Photonics 2024, 11, 711. https://doi.org/10.3390/photonics11080711
Gargallo Yebra D, Remón Martín L, Pérez Escorza I, Castro Alonso FJ. Analysis of the Effective and Actual Lens Position by Different Formulas. Postoperative Application of a Ray-Tracing-Based Simulated Optical Model. Photonics. 2024; 11(8):711. https://doi.org/10.3390/photonics11080711
Chicago/Turabian StyleGargallo Yebra, Diana, Laura Remón Martín, Iván Pérez Escorza, and Francisco Javier Castro Alonso. 2024. "Analysis of the Effective and Actual Lens Position by Different Formulas. Postoperative Application of a Ray-Tracing-Based Simulated Optical Model" Photonics 11, no. 8: 711. https://doi.org/10.3390/photonics11080711
APA StyleGargallo Yebra, D., Remón Martín, L., Pérez Escorza, I., & Castro Alonso, F. J. (2024). Analysis of the Effective and Actual Lens Position by Different Formulas. Postoperative Application of a Ray-Tracing-Based Simulated Optical Model. Photonics, 11(8), 711. https://doi.org/10.3390/photonics11080711






