Rapid Focused Spot Scanning Imaging Using Multimode Fiber with a Convolutional Neural Network-Based Phase Modulation
Abstract
1. Introduction
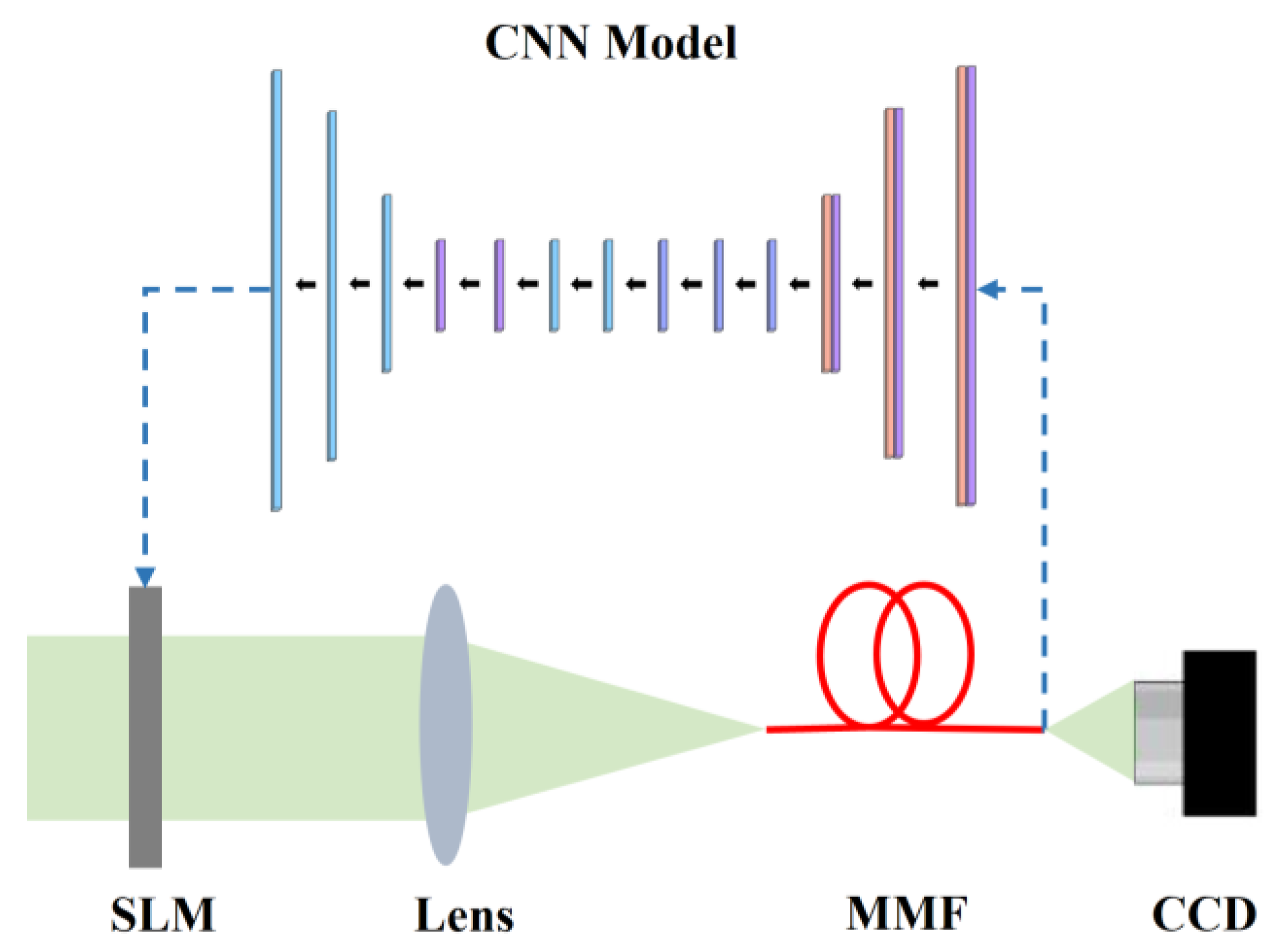
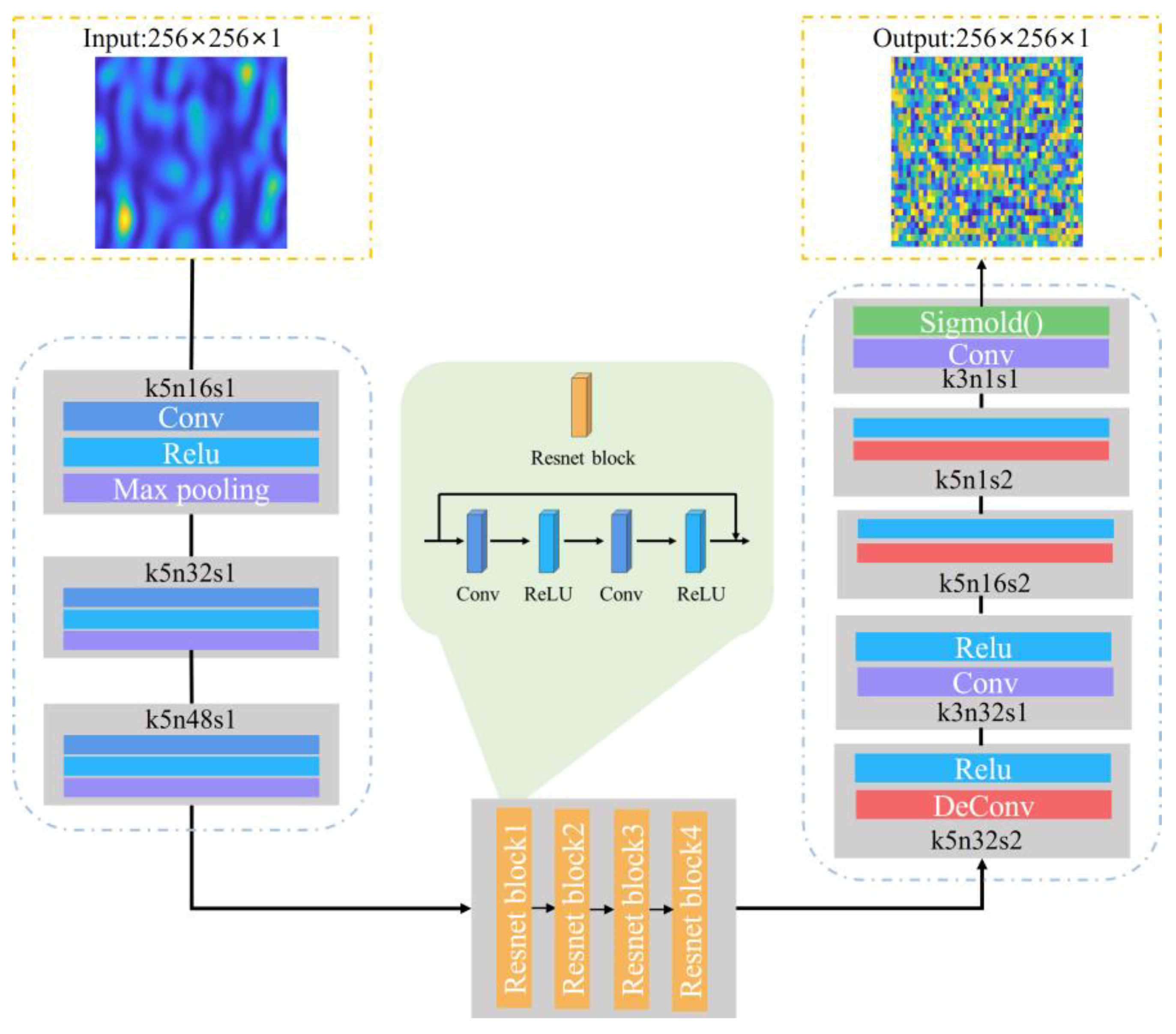
2. Principle and Model
3. Simulation and Results
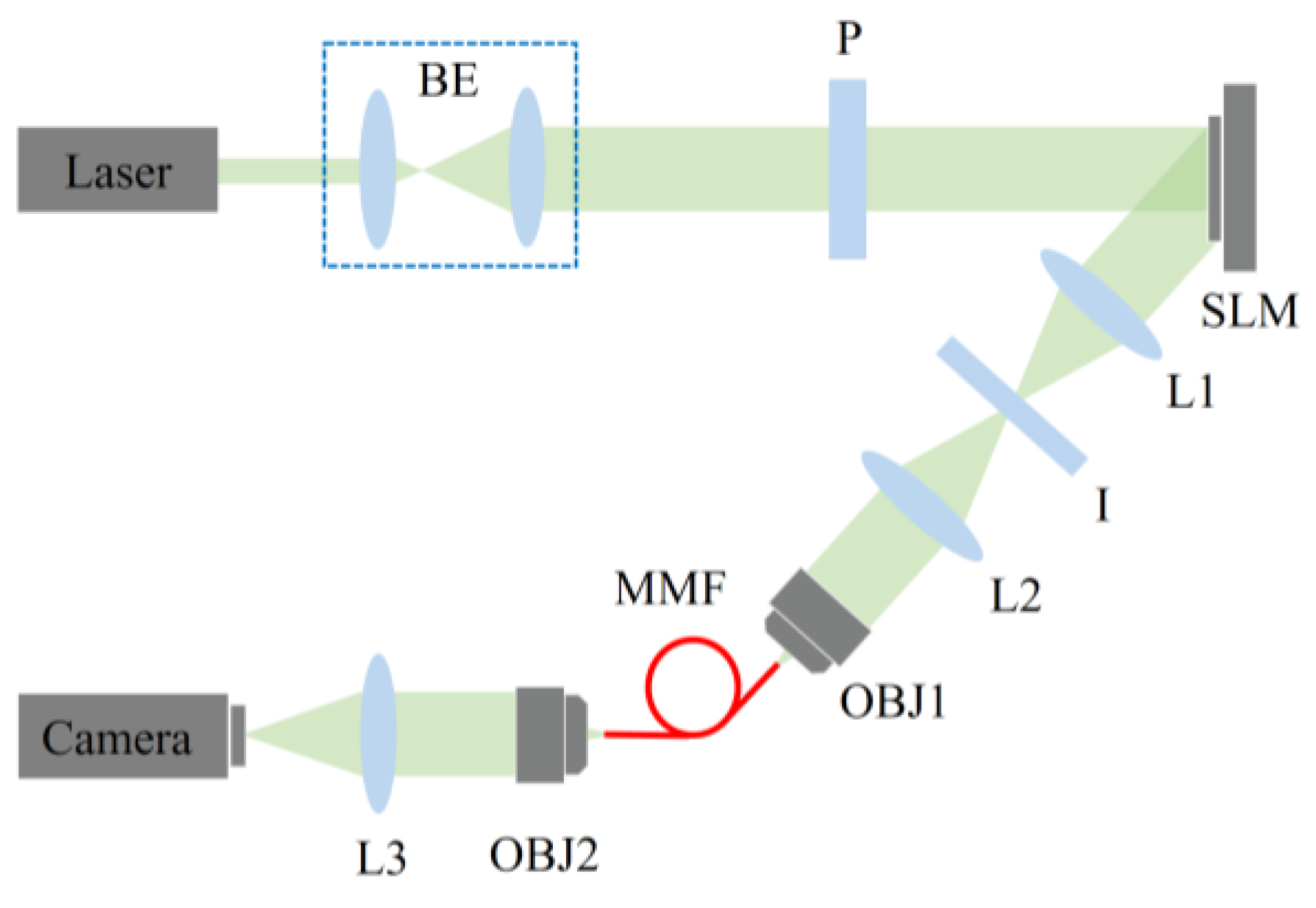
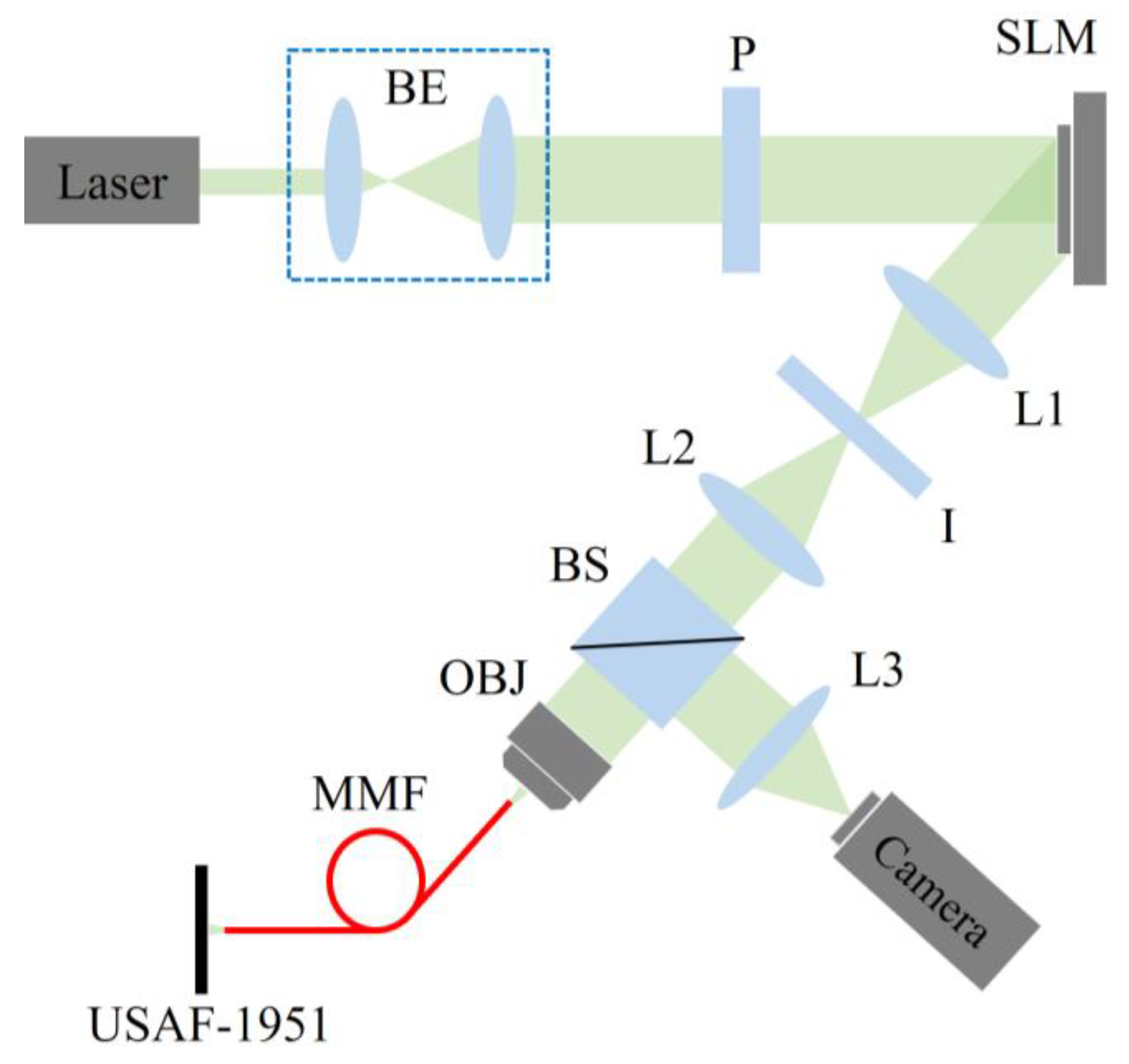
4. Experiment Results and Discussion
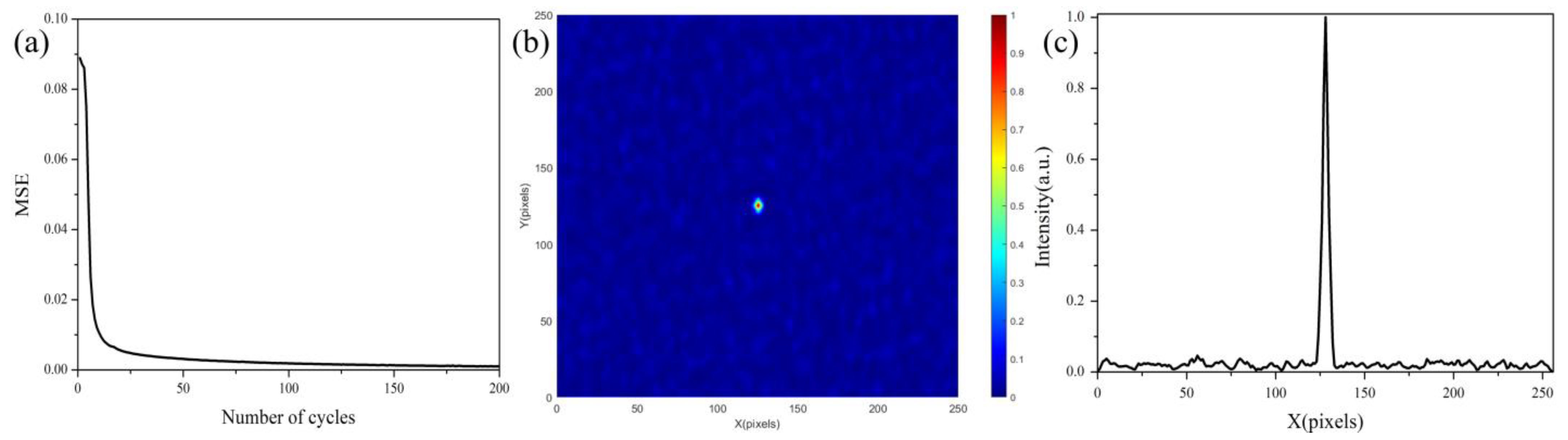
4.1. The Experiment on Multimode Fiber Beam Focusing
4.2. The Experiment on Multimode Fiber Scanning Imaging
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stellinga, D.; Phillips, D.; Mekhail, S.; Selyem, A.; Turtaev, S.; Čižmár, T.; Padgett, M. Time-of-Flight 3D Imaging through Multimode Optical Fibers. Science 2021, 374, 1395–1399. [Google Scholar] [CrossRef]
- Moussa, N.O.; Mansuryan, T.; Hage, C.-H.; Fabert, M.; Krupa, K.; Tonello, A.; Ferraro, M.; Leggio, L.; Zitelli, M.; Mangini, F.; et al. Spatiotemporal Beam Self-Cleaning for High-Resolution Nonlinear Fluorescence Imaging with Multimode Fiber. Sci. Rep. 2021, 11, 18240. [Google Scholar] [CrossRef] [PubMed]
- Caramazza, P.; Moran, O.; Murray-Smith, R.; Faccio, D. Transmission of Natural Scene Images through a Multimode Fibre. Nat. Commun. 2019, 10, 2029. [Google Scholar] [CrossRef]
- Shekel, R.; Lib, O.; Gutiérrez-Cuevas, R.; Popoff, S.M.; Ling, A.; Bromberg, Y. Shaping Single Photons through Multimode Optical Fibers Using Mechanical Perturbations. APL Photonics 2023, 8, 096109. [Google Scholar] [CrossRef]
- Chapalo, I.; Stylianou, A.; Mégret, P.; Theodosiou, A. Advances in Optical Fiber Speckle Sensing: A Comprehensive Review. Photonics 2024, 11, 299. [Google Scholar] [CrossRef]
- Wen, Z.; Dong, Z.; Deng, Q.; Pang, C.; Kaminski, C.F.; Xu, X.; Yan, H.; Wang, L.; Liu, S.; Tang, J.; et al. Single Multimode Fibre for in Vivo Light-Field-Encoded Endoscopic Imaging. Nat. Photonics 2023, 17, 679–687. [Google Scholar] [CrossRef]
- Leite, I.T.; Turtaev, S.; Boonzajer Flaes, D.E.; Čižmár, T. Observing Distant Objects with a Multimode Fiber-Based Holographic Endoscope. APL Photonics 2021, 6, 036112. [Google Scholar] [CrossRef]
- Du, Y.; Turtaev, S.; Leite, I.T.; Lorenz, A.; Kobelke, J.; Wondraczek, K.; Čižmár, T. Hybrid Multimode—Multicore Fibre Based Holographic Endoscope for Deep-Tissue Neurophotonics. Light Adv. Manuf. 2022, 3, 408–416. [Google Scholar] [CrossRef]
- Choutagunta, K.; Kahn, J.M. Designing High-Performance Multimode Fibers Using Refractive Index Optimization. J. Light. Technol. 2021, 39, 233–242. [Google Scholar] [CrossRef]
- Mondal, P.; Mishra, V.; Varshney, S.K. Nonlinear Interactions in Multimode Optical Fibers. Opt. Fiber Technol. 2020, 54, 102041. [Google Scholar] [CrossRef]
- Rademacher, G.; Luís, R.S.; Puttnam, B.J.; Ryf, R.; van der Heide, S.; Eriksson, T.A.; Fontaine, N.K.; Chen, H.; Essiambre, R.-J.; Awaji, Y.; et al. A Comparative Study of Few-Mode Fiber and Coupled-Core Multi-Core Fiber Transmission. J. Light. Technol. 2022, 40, 1590–1596. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, R.; Wang, K.; Xu, B.; Chen, R.; Sarwar, R.; Zhang, D. Research on Image Transmission Mechanism through a Multimode Fiber Based on Principal Component Analysis. Opt. Lasers Eng. 2020, 134, 106197. [Google Scholar] [CrossRef]
- Resisi, S.; Popoff, S.M.; Bromberg, Y. Image Transmission Through a Dynamically Perturbed Multimode Fiber by Deep Learning. Laser Photonics Rev. 2021, 15, 2000553. [Google Scholar] [CrossRef]
- Li, S.; Saunders, C.; Lum, D.J.; Murray-Bruce, J.; Goyal, V.K.; Čižmár, T.; Phillips, D.B. Compressively Sampling the Optical Transmission Matrix of a Multimode Fibre. Light Sci. Appl. 2021, 10, 88. [Google Scholar] [CrossRef]
- Tran, V.; Wang, T.; Nazirkar, N.P.; Bassène, P.; Fohtung, E.; N’Gom, M. On the Exploration of Structured Light Transmission through a Multimode Fiber in a Reference-Less System. APL Photonics 2023, 8, 126111. [Google Scholar] [CrossRef]
- Resisi, S.; Viernik, Y.; Popoff, S.M.; Bromberg, Y. Wavefront Shaping in Multimode Fibers by Transmission Matrix Engineering. APL Photonics 2020, 5, 036103. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, E.H.; Brake, J.; Ruan, H.; Jang, M.; Yang, C. Focusing through Dynamic Tissue with Millisecond Digital Optical Phase Conjugation. Optica 2015, 2, 728–735. [Google Scholar] [CrossRef] [PubMed]
- Büttner, L.; Thümmler, M.; Czarske, J. Velocity Measurements with Structured Light Transmitted through a Multimode Optical Fiber Using Digital Optical Phase Conjugation. Opt. Express 2020, 28, 8064–8075. [Google Scholar] [CrossRef]
- Ma, C.; Di, J.; Li, Y.; Xiao, F.; Zhang, J.; Liu, K.; Bai, X.; Zhao, J. Rotational Scanning and Multiple-Spot Focusing through a Multimode Fiber Based on Digital Optical Phase Conjugation. Appl. Phys. Express 2018, 11, 062501. [Google Scholar] [CrossRef]
- Cui, M. Parallel Wavefront Optimization Method for Focusing Light through Random Scattering Media. Opt. Lett. 2011, 36, 870–872. [Google Scholar] [CrossRef] [PubMed]
- Cheng, S.; Zhong, T.; Woo, C.M.; Zhao, Q.; Hui, H.; Lai, P. Long-Distance Pattern Projection through an Unfixed Multimode Fiber with Natural Evolution Strategy-Based Wavefront Shaping. Opt. Express 2022, 30, 32565. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Yao, Z.; Sui, X.; Gu, G.; Chen, Q. Focusing through Disturbed Multimode Optical Fiber Based on Self-Adaptive Genetic Algorithm. Optik 2022, 261, 169129. [Google Scholar] [CrossRef]
- Fayyaz, Z.; Mohammadian, N.; Salimi, F.; Fatima, A.; Tabar, M.R.R.; Avanaki, M.R.N. Simulated Annealing Optimization in Wavefront Shaping Controlled Transmission. Appl. Opt. 2018, 57, 6233–6242. [Google Scholar] [CrossRef] [PubMed]
- Di Leonardo, R.; Bianchi, S. Hologram Transmission through Multi-Mode Optical Fibers. Opt. Express 2011, 19, 247. [Google Scholar] [CrossRef]
- Mahalati, R.N.; Askarov, D.; Wilde, J.P.; Kahn, J.M. Adaptive Control of Input Field to Achieve Desired Output Intensity Profile in Multimode Fiber with Random Mode Coupling. Opt. Express 2012, 20, 14321. [Google Scholar] [CrossRef]
- Yin, Z.; Liu, G.; Chen, F.; Liu, B. Fast-Forming Focused Spots through a Multimode Fiber Based on an Adaptive Parallel Coordinate Algorithm. Chin. Opt. Lett. 2015, 13, 071404. [Google Scholar] [CrossRef]
- Geng, Y.; Zhao, G.; Chen, H.; Xu, C.; Zhuang, B.; Ren, L. High-Speed Focusing and Scanning Light through a Multimode Fiber Based on Binary Amplitude-Only Modulation Parallel Coordinate Algorithm. Appl. Phys. B 2019, 125, 83. [Google Scholar] [CrossRef]
- Rahmani, B.; Loterie, D.; Konstantinou, G.; Psaltis, D.; Moser, C. Multimode Optical Fiber Transmission with a Deep Learning Network. Light Sci. Appl. 2018, 7, 69. [Google Scholar] [CrossRef] [PubMed]
- Rothe, S.; Zhang, Q.; Koukourakis, N.; Czarske, J.W. Deep Learning for Computational Mode Decomposition in Optical Fibers. Appl. Sci. 2020, 10, 1367. [Google Scholar] [CrossRef]
- Xu, R.; Zhang, L.; Chen, Z.; Wang, Z.; Zhang, D. High Accuracy Transmission and Recognition of Complex Images through Multimode Fibers Using Deep Learning. Laser Photonics Rev. 2023, 17, 2200339. [Google Scholar] [CrossRef]
- Zhu, R.; Luo, J.; Zhou, X.; Feng, H.; Xu, F. Anti-Perturbation Multimode Fiber Imaging Based on the Active Measurement of the Fiber Configuration. ACS Photonics 2023, 10, 3476–3483. [Google Scholar] [CrossRef]
- Fan, P.; Wang, Y.; Ruddlesden, M.; Wang, X.; Thaha, M.A.; Sun, J.; Zuo, C.; Su, L. Deep Learning Enabled Scalable Calibration of a Dynamically Deformed Multimode Fiber. Adv. Photonics Res. 2022, 3, 2100304. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, Z.; Wei, Y.; Wang, Z.; Hao, J.; Zhang, J. Image Transmission through a Multimode Fiber Based on Transfer Learning. Opt. Fiber Technol. 2023, 79, 103362. [Google Scholar] [CrossRef]
- Chen, H.; Geng, Y.; Xu, C.; Zhuang, B.; Ju, H.; Ren, L. Efficient Light Focusing through an MMF Based on Two-Step Phase Shifting and Parallel Phase Compensating. Appl. Opt. 2019, 58, 7552–7557. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; Stern, R.; Zhang, H.; Pang, L. Speedy Light Focusing through Scattering Media by a Cooperatively FPGA-Parameterized Genetic Algorithm. Opt. Express 2022, 30, 36414–36428. [Google Scholar] [CrossRef] [PubMed]
- Farahi, S.; Ziegler, D.; Papadopoulos, I.N.; Psaltis, D.; Moser, C. Dynamic Bending Compensation While Focusing through a Multimode Fiber. Opt. Express 2013, 21, 22504. [Google Scholar] [CrossRef] [PubMed]


| Method | Average Generation Time of Light Field (s) | Focusing Efficiency (%) |
|---|---|---|
| Adaptive Parallel Coordinate algorithm [26] | 3.36 | 17.5 |
| Two-Step Phase-Shifting Method [31] | 0.65 | 21.6 |
| FPGA-parameterized genetic algorithm [32] | 14 | / |
| Our work | 0.2 | 27.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, R.; Xu, A.; Shen, H. Rapid Focused Spot Scanning Imaging Using Multimode Fiber with a Convolutional Neural Network-Based Phase Modulation. Photonics 2025, 12, 41. https://doi.org/10.3390/photonics12010041
Tong R, Xu A, Shen H. Rapid Focused Spot Scanning Imaging Using Multimode Fiber with a Convolutional Neural Network-Based Phase Modulation. Photonics. 2025; 12(1):41. https://doi.org/10.3390/photonics12010041
Chicago/Turabian StyleTong, Rongjing, Anni Xu, and Hua Shen. 2025. "Rapid Focused Spot Scanning Imaging Using Multimode Fiber with a Convolutional Neural Network-Based Phase Modulation" Photonics 12, no. 1: 41. https://doi.org/10.3390/photonics12010041
APA StyleTong, R., Xu, A., & Shen, H. (2025). Rapid Focused Spot Scanning Imaging Using Multimode Fiber with a Convolutional Neural Network-Based Phase Modulation. Photonics, 12(1), 41. https://doi.org/10.3390/photonics12010041




