A Review of Pointing Modules and Gimbal Systems for Free-Space Optical Communication in Non-Terrestrial Platforms
Abstract
1. Introduction
2. Existing Technologies and Implementations
2.1. Literature Survey
2.2. Motivations and Contributions
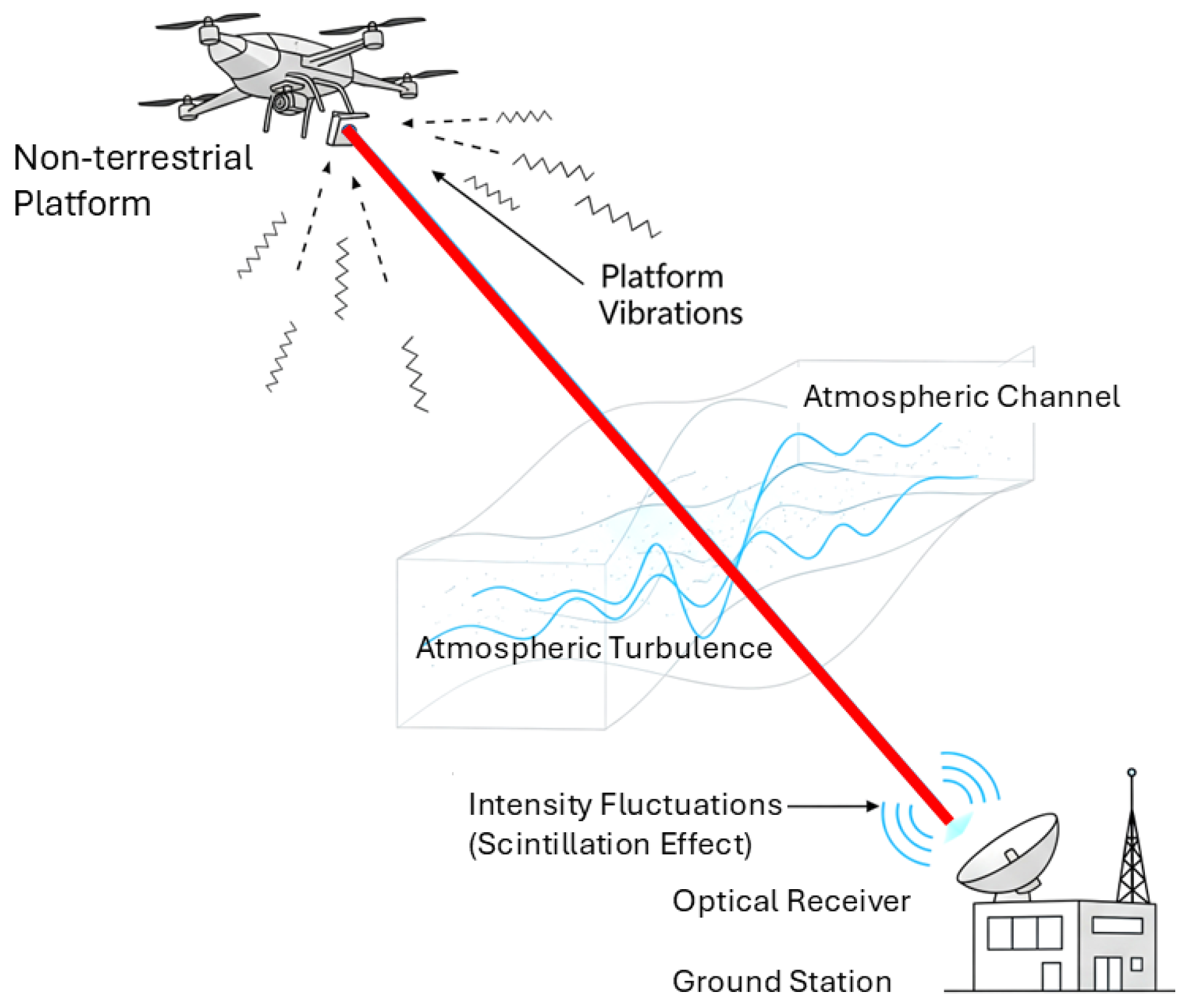
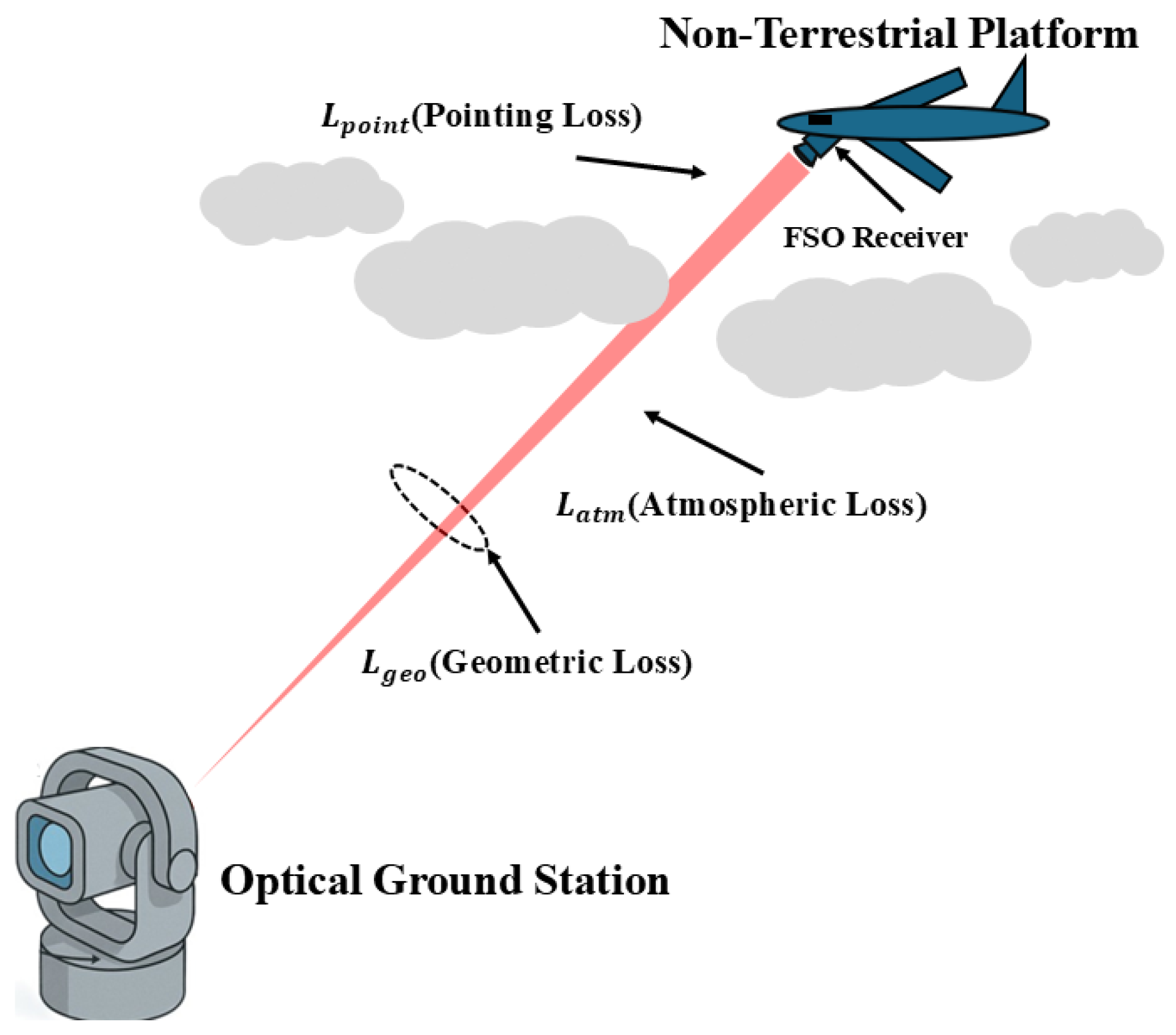
3. Fundamentals of FSO Communication for Non-Terrestrial Platforms
3.1. UAV–Ground FSO Link
3.2. HAPS–Ground FSO Links
3.3. Satellite–Ground FSO Links
3.4. Satellite–HAPS FSO Links
3.5. Inter-Satellite FSO Links
4. Coarse vs. Fine Pointing in Non-Terrestrial FSO Links
4.1. Coarse Pointing: Mechanical Beam Acquisition
4.2. Fine Pointing: High-Precision Optical Stabilization
4.3. Need for Combined Operation
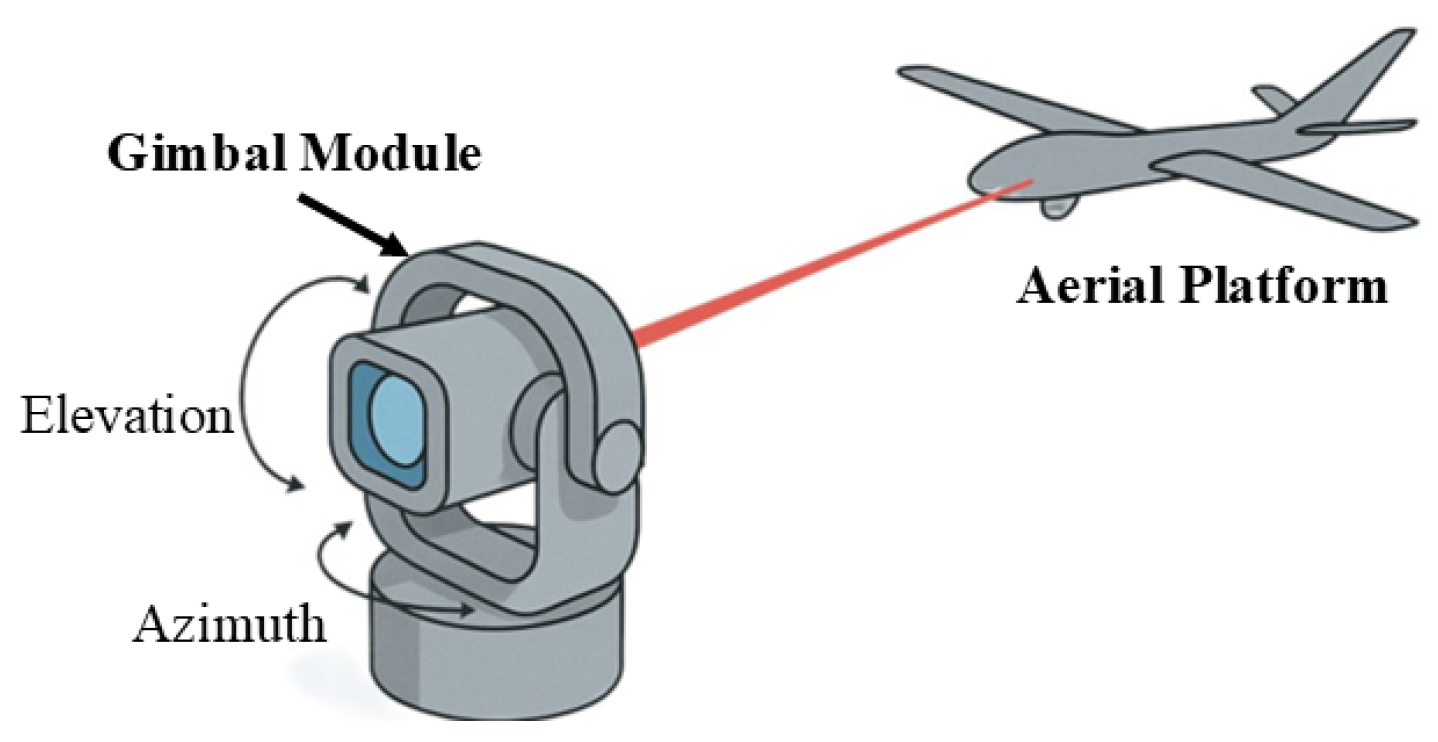
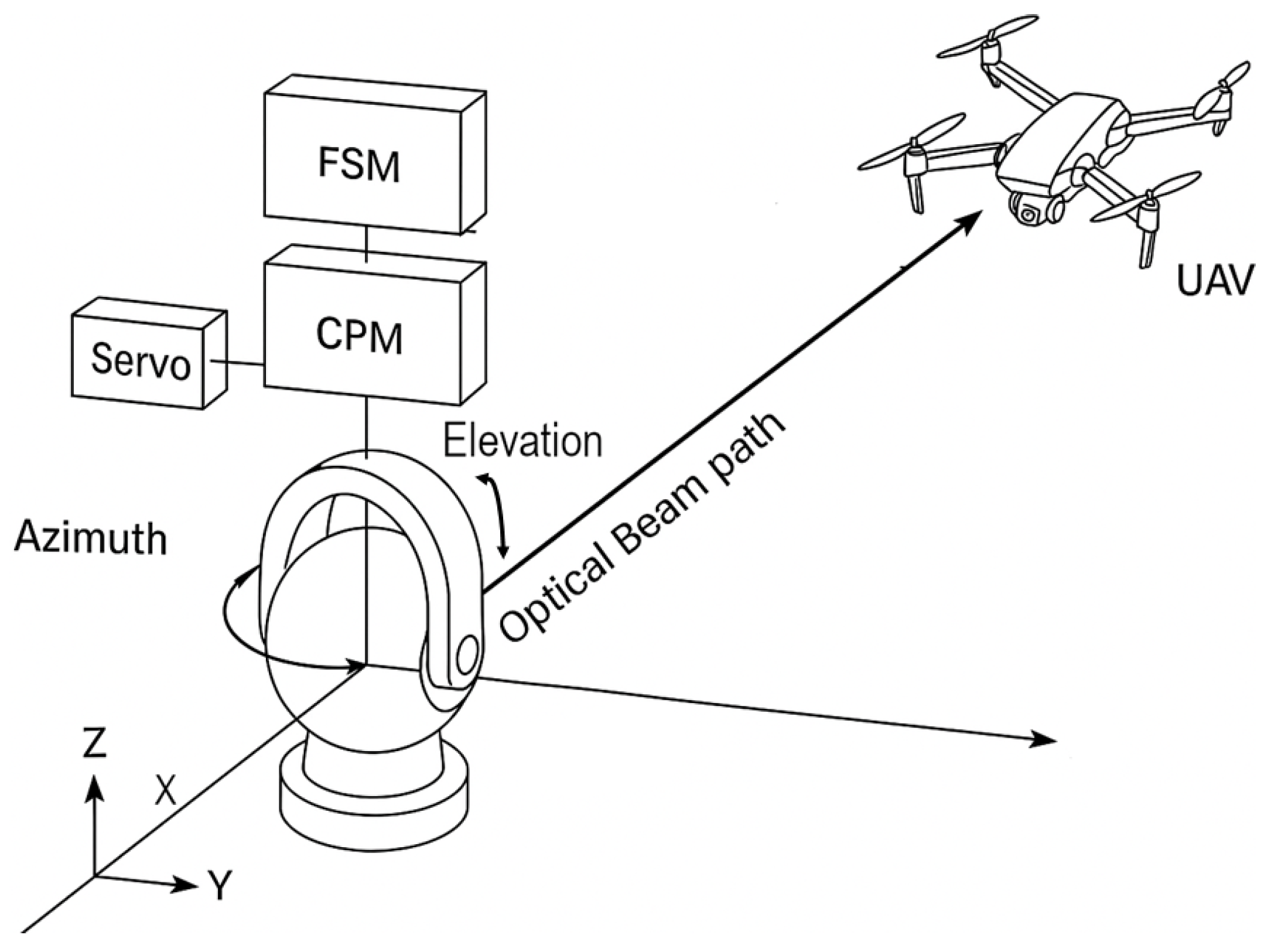
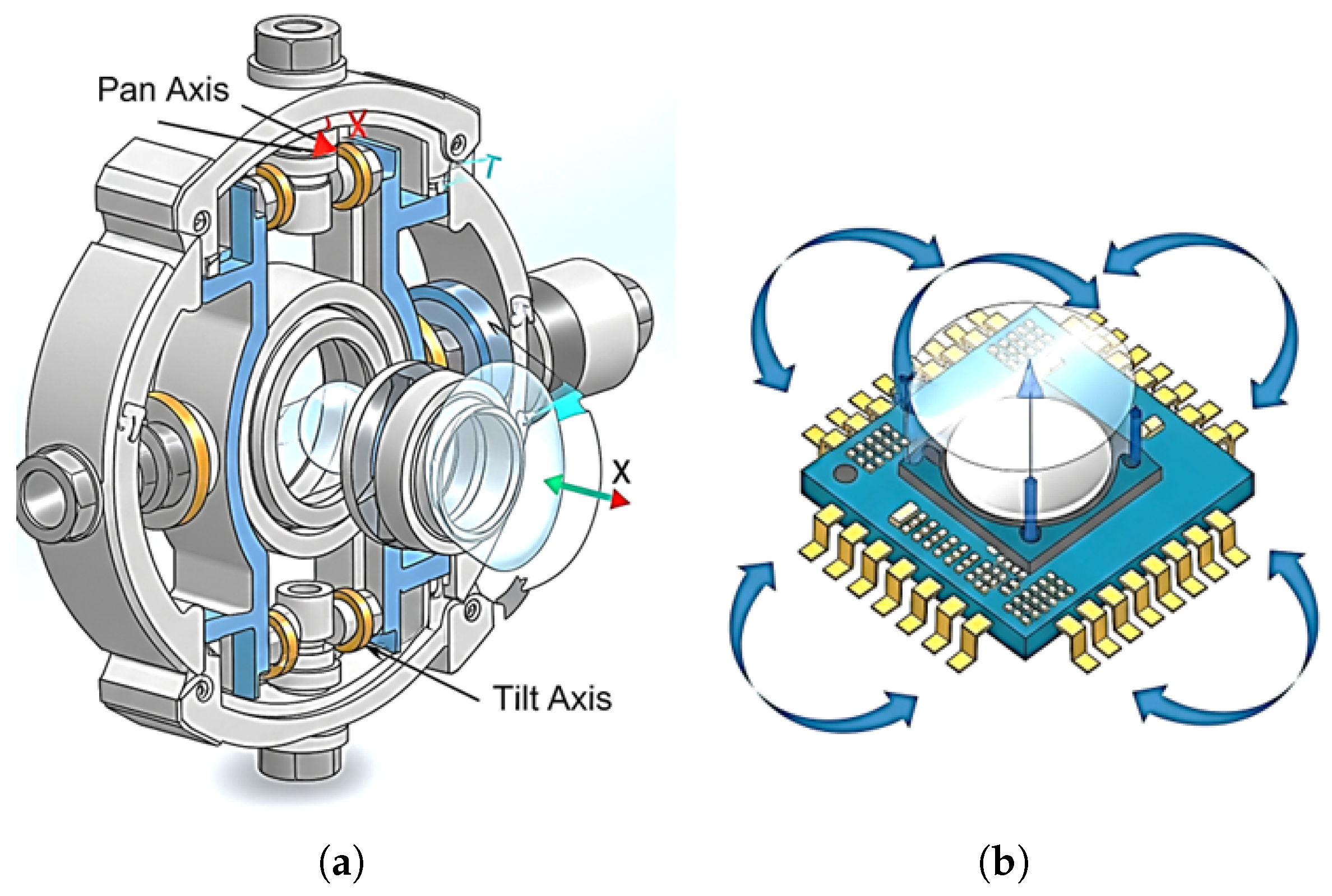
5. Gimbal Architectures and Technologies for Non-Terrestrial FSO Communication
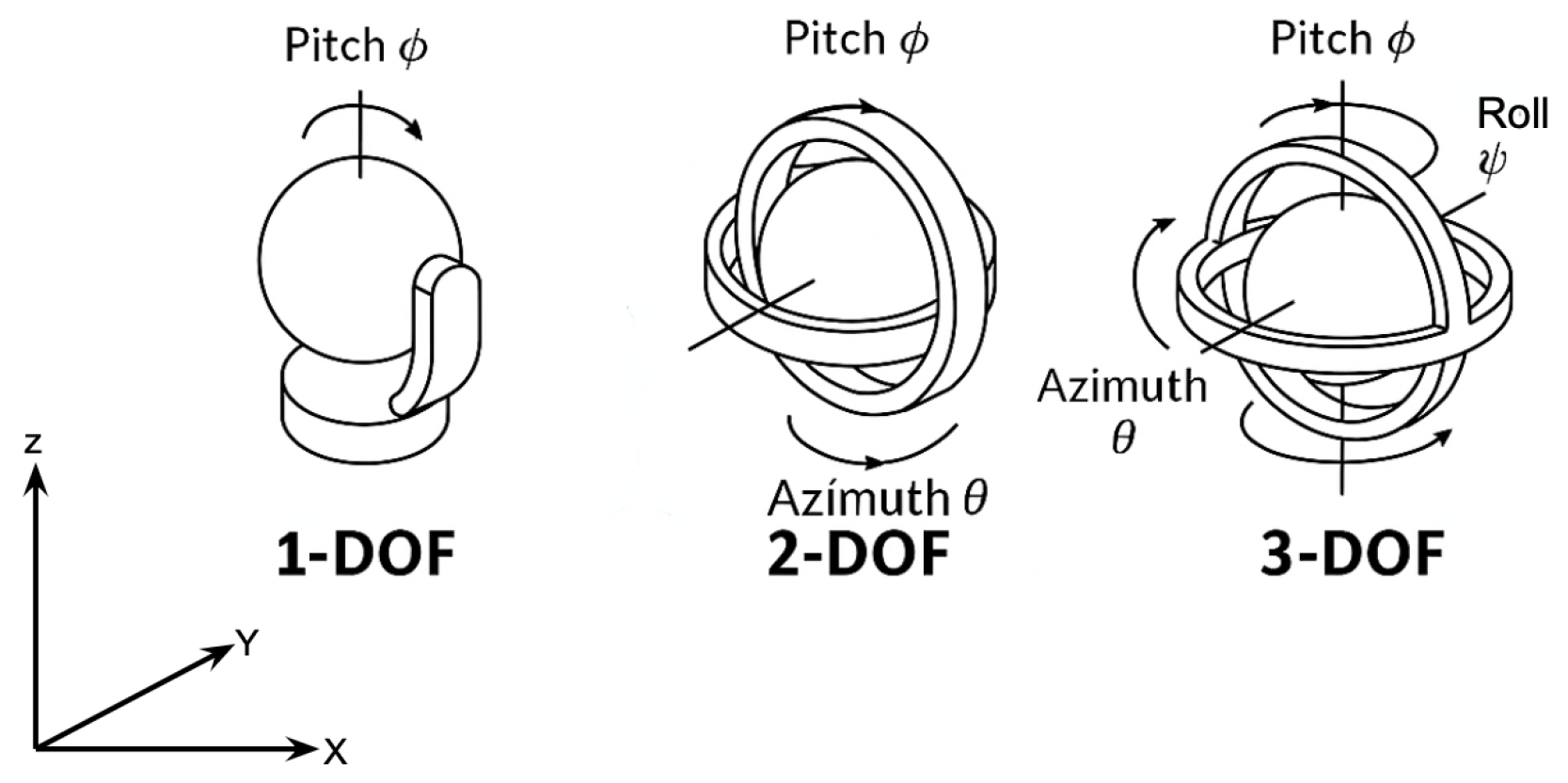
5.1. Classification of Gimbal Architectures
5.2. Actuation Technologies
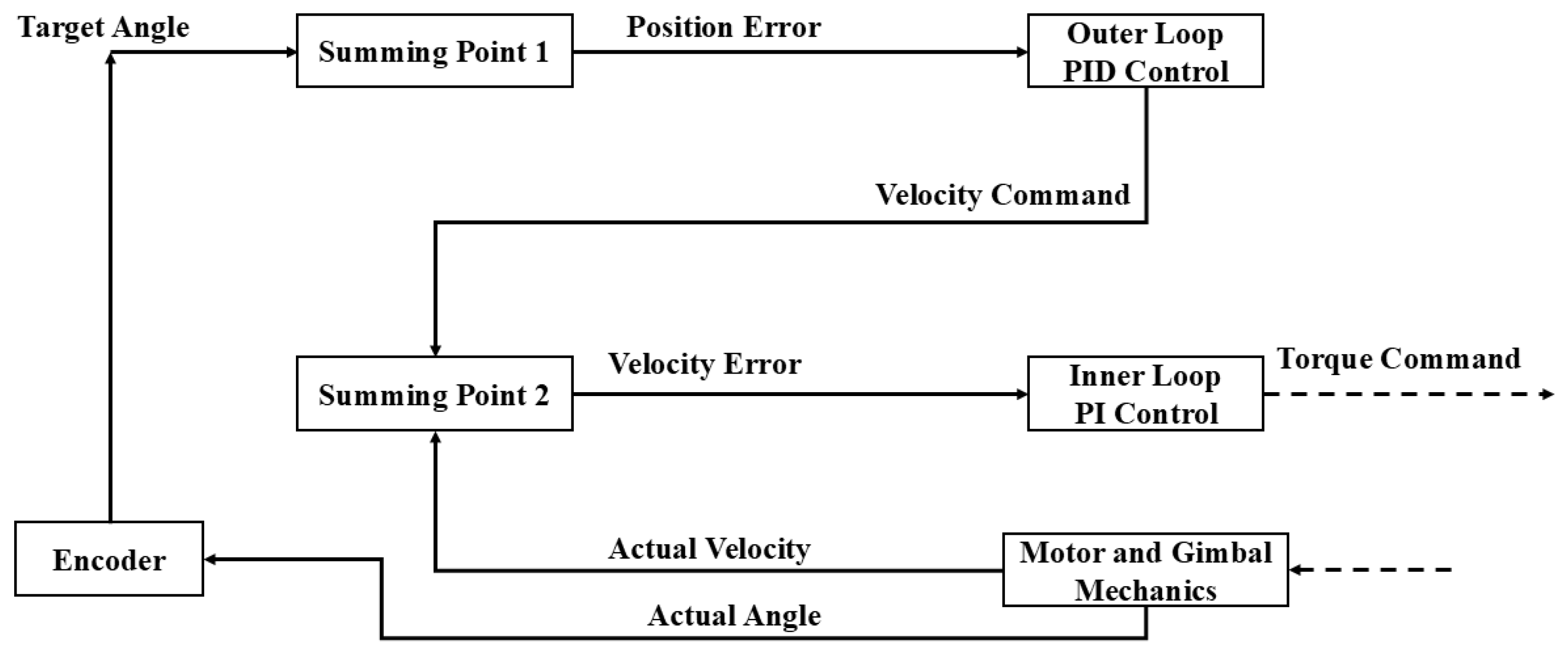
6. Control Algorithms Used in Pointing
6.1. Coarse Pointing Control Algorithms
6.1.1. Proportional Integral Derivative (PID)
6.1.2. Linear Quadratic Regulator (LQR)
6.1.3. Extended Kalman Filter (EKF)
6.1.4. Hybrid Approaches PID and Kalman/LQR and Kalman
6.2. Fine Pointing Control Algorithms
6.2.1. Adaptive PID
6.2.2. Model Predictive Control (MPC)
6.2.3. Linear Quadratic Gaussian (LQG)
6.2.4. Sliding Mode Control (SMC)
6.2.5. AI/ML-Based Predictive Control
7. Future Directions and Open Research Questions
8. Conclusions
Funding
Conflicts of Interest
References
- Gupta, L.; Jain, R.; Vaszkun, G. Survey of important issues in UAV communication networks. IEEE Commun. Surv. Tutor. 2015, 18, 1123–1152. [Google Scholar] [CrossRef]
- Li, B.; Fei, Z.; Zhang, Y. UAV Communications for 5G and Beyond: Recent Advances and Future Trends. IEEE Internet Things J. 2018, 6, 2241–2263. [Google Scholar] [CrossRef]
- Kaushal, H.; Jain, V.; Kar, S. Free Space Optical Communication; Springer: Berlin/Heidelberg, Germany, 2017; Volume 60. [Google Scholar]
- Hemmati, H. Near-Earth Laser Communications, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2020; pp. 1–40. [Google Scholar]
- Khalighi, M.A.; Uysal, M. Survey on Free Space Optical Communication: A Communication Theory Perspective. IEEE Commun. Surv. Tutor. 2014, 16, 2231–2258. [Google Scholar] [CrossRef]
- Mondal, A.; Hossain, A. Channel Characterization and Performance Analysis of Unmanned Aerial Vehicle-Operated Communication System with Multihop Radio Frequency–Free-Space Optical Link in Dynamic Environment. Int. J. Commun. Syst. 2020, 33, e4568. [Google Scholar] [CrossRef]
- Toyoshima, M.; Kuri, T.; Werner, K.; Toyoda, M.; Takenaka, H.; Shoji, Y.; Takayama, Y.; Koyama, Y.; Kunimori, H.; Jono, T.; et al. Overview of the Laser Communication System for the NICT Optical Ground Station and Laser Communication Experiments on Ground-to-Satellite Links. J. Natl. Inst. Inf. Commun. Technol. 2012, 59, 53–75. [Google Scholar]
- Chaudhary, H.; Khatoon, S.; Singh, R.; Pandey, A. Fast Steering Mirror for Optical Fine Pointing Applications: A Review Paper Applications: A Review Paper. In Proceedings of the 2018 3rd International Innovative Applications of Computational Intelligence on Power, Energy and Controls with their Impact on Humanity (CIPECH), Ghaziabad, India, 1–2 November 2018; pp. 1–5. [Google Scholar]
- Harris, A.; Sluss, J.J.; Refai, H.H.; LoPresti, P.G. Alignment and Tracking of a Free-Space Optical Communications Link to a UAV. In Proceedings of the 24th Digital Avionics Systems Conference, 2005, Washington, DC, USA, 30 October–3 November 2005; IEEE: New York, NY, USA; Volume 1, p. 1.C.2-1.1. [Google Scholar]
- Giggenbach, D.; Horwath, J. Optical Free-Space Communications Downlinks from Stratospheric Platforms-Overview on Stropex, the Optical Communications Experiment of Capanina. In Proceedings of the IST Summit Dresden, Dresden, Germany, 19–23 June 2005. [Google Scholar]
- Wikipedia Contributors. NASA Pathfinder. 2025. Available online: https://en.wikipedia.org/wiki/NASA_Pathfinder (accessed on 13 September 2025).
- Wikipedia Contributors. Airbus Zephyr. 2025. Available online: https://en.wikipedia.org/wiki/Airbus_Zephyr (accessed on 13 September 2025).
- Cap, G.A.; Refai, H.H.; Sluss, J.J., Jr. FSO Tracking and Auto-Alignment Transceiver System. In Proceedings of the Unmanned/Unattended Sensors and Sensor Networks V, Cardiff, UK, 16–18 September 2008; SPIE: Bellingham, WA, USA, 2008; Volume 7112, pp. 71–82. [Google Scholar]
- Locke, M.; Czarnomski, M.; Qadir, A.; Setness, B.; Baer, N.; Meyer, J.; Semke, W.H. High-Performance Two-Axis Gimbal System for Free Space Laser Communications Onboard Unmanned Aircraft Systems. In Proceedings of the Free-Space Laser Communication Technologies XXIII, San Francisco, CA, USA, 22–27 January 2011; SPIE: Bellingham, WA, USA; Volume 7923, pp. 141–148. [Google Scholar]
- Talmor, A.G.; Harding, H., Jr.; Chen, C.C. Two-Axis Gimbal for Air-to-Air and Air-to-Ground Laser Communications. In Proceedings of the Free-Space Laser Communication and Atmospheric Propagation XXVIII, San Francisco, CA, USA, 15–16 February 2016; SPIE: Bellingham, WA, USA, 2016; Volume 9739, pp. 129–135. [Google Scholar]
- Carrasco-Casado, A.; Vergaz, R.; Pena, J.M.S. Design and Early Development of a UAV Terminal and a Ground Station for Laser Communications. In Proceedings of the Unmanned/Unattended Sensors and Sensor Networks VIII, Prague, Czech Republic, 20–21 September 2011; SPIE: Bellingham, WA, USA, 2011; Volume 8184, pp. 89–97. [Google Scholar]
- Teledyne FLIR. Pan Tilts. 2025. Available online: https://oem.flir.com/categories/pan-tilts/ (accessed on 4 October 2025).
- Rowen, D.; Dolphus, R.; Doyle, P.; Faler, A. OCSD-A/AeroCube-7: A Status Update. In Proceedings of the 13th Cal Poly CubeSat Developer’s Workshop, San Luis Obispo, CA, USA, 20–22 April 2016; pp. 20–22. [Google Scholar]
- Welle, R.; Venturini, C.; Hinkley, D.; Gangestad, J.; Bellardo, J.; Johnson, P.; Rowen, D. On-Orbit Results of the AeroCube-10 Mission: Proximity Operations and In-Space Inspection. In Proceedings of the 34th Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 5–10 August 2019; Utah State University: Logan, UT, USA, 2020. SSC20-III-01. [Google Scholar]
- Safi, H.; Dargahi, A.; Cheng, J. Spatial Beam Tracking and Data Detection for an FSO Link to a UAV in the Presence of Hovering Fluctuations. arXiv 2019, arXiv:1904.03774. [Google Scholar] [CrossRef]
- Safi, H.; Dargahi, A.; Cheng, J. Beam Tracking for UAV-Assisted FSO Links with a Four-Quadrant Detector. IEEE Commun. Lett. 2021, 25, 3908–3912. [Google Scholar] [CrossRef]
- Ge, H.; Dong, K.; An, Y.; Gao, L.; Li, X. Joint channel model of unmanned aerial vehicle laser communication based on Hoyt distribution. Chin. J. Lasers 2023, 50, 1106004. [Google Scholar] [CrossRef]
- Jia, H.; Chen, G.; Huang, C.; Dang, S.; Chambers, J.A. Trajectory and Phase Shift Optimization for RIS-equipped UAV in FSO Communications with Atmospheric and Pointing Error Loss. Electronics 2023, 12, 4275. [Google Scholar] [CrossRef]
- Nguyen, T.V.; Le, H.D.; Pham, A.T. On the Design of RIS–UAV Relay-Assisted Hybrid FSO/RF Satellite–Aerial–Ground Integrated Network. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 757–771. [Google Scholar] [CrossRef]
- AbdElKader, A.G.; Allam, A.; Kato, K.; Shalaby, H.M. Performance Analysis of a UAV-Integrated RIS-Aided MRR-FSO System Utilizing Wavelength and Time Diversity Techniques. Photonic Netw. Commun. 2025, 50, 1–16. [Google Scholar] [CrossRef]
- Seong, K.j.; Kang, H.g.; Yeo, B.y.; Lee, H.p. The Stabilization Loop Design for a Two-Axis Gimbal System Using LQG/LTR Controller. In Proceedings of the 2006 SICE-ICASE International Joint Conference, Busan, Republic of Korea, 18–21 October 2006; pp. 755–759. [Google Scholar] [CrossRef]
- Yang, S.; Li, X. High-Accuracy Model Predictive Control with Inverse Hysteresis for High-Speed Trajectory Tracking of Piezoelectric Fast Steering Mirror. arXiv 2024, arXiv:2412.14511. [Google Scholar]
- Moon, H.J.; Chae, C.B.; Wong, K.K.; Alouini, M.S. A Generalized Pointing Error Model for FSO Links with Fixed-Wing UAVs for 6G: Analysis and Trajectory Optimization. IEEE Trans. Wirel. Commun. 2025, 24, 5723–5737. [Google Scholar] [CrossRef]
- National Aeronautics and Space Administration. OCSD Project. 2025. Available online: https://www.nasa.gov/smallspacecraft/ocsd-project/ (accessed on 28 August 2025).
- Schieler, C.M.; Riesing, K.M.; Bilyeu, B.C.; Chang, J.S.; Garg, A.S.; Gilbert, N.J.; Horvath, A.J.; Reeve, R.S.; Robinson, B.S.; Wang, J.P.; et al. On-Orbit Demonstration of 200-Gbps Laser Communication Downlink from the TBIRD CubeSat. In Proceedings of the Free-Space Laser Communications XXXV, San Francisco, CA, USA, 30 January–1 February 2023; SPIE: Bellingham, WA, USA, 2023; Volume 12413, p. 1241302. [Google Scholar]
- Tong, Q.; Hu, J.; Chen, Y.; Guo, D.; Liu, X. Long-Term Trajectory Prediction Model Based on Transformer. IEEE Access 2023, 11, 143695–143703. [Google Scholar] [CrossRef]
- Lee, J.K. Transformer-Based Vehicle-Trajectory Prediction at Urban Low-Speed T-Intersection. Sensors 2025, 25, 4256. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Xia, J.; Chen, X.; Tan, Y.; Chen, J. SIT: A Apatial Interaction-Aware Transformer-Based Model for Freeway Trajectory Prediction. ISPRS Int. J. Geo-Inf. 2022, 11, 79. [Google Scholar] [CrossRef]
- Chen, Y. Federated Learning in Hybrid RF/FSO Communication for Space-Aerial-Ground Networks 2025. Available online: https://trepo.tuni.fi/bitstream/handle/10024/228928/ChenYuehua.pdf?sequence=3 (accessed on 1 May 2025).
- Song, S.; He, Q.; Liu, Y.; Wu, P.; Sun, Q.; Zhao, L.; Wu, T.; Guo, L. Personalized Federated Learning Based Adaptive Optical Compensation for Atmospheric Turbulence. J. Light. Technol. 2025, 43, 177–189. [Google Scholar] [CrossRef]
- Wang, G.; Yang, F.; Song, J.; Han, Z. Dynamic Laser Inter-Satellite Link Scheduling Based on Federated Reinforcement Learning: An Asynchronous Hierarchical Architecture. IEEE Trans. Wirel. Commun. 2024, 23, 14273–14288. [Google Scholar] [CrossRef]
- Abdelfatah, R.; Alshaer, N.; Ismail, T. A Review on Pointing, Acquisition, and Tracking Approaches in UAV-Based FSO Communication Systems. Opt. Quantum Electron. 2022, 54, 571. [Google Scholar] [CrossRef]
- Petkovic, M.; Narandzic, M. Overview of UAV based free-space optical communication systems. In Proceedings of the International Conference on Interactive Collaborative Robotics, Istanbul, Turkey, 20–25 August 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 270–277. [Google Scholar]
- Leitgeb, E.; Zettl, K.; Muhammad, S.S.; Schmitt, N.; Rehm, W. Investigation in Free Space Optical Communication Links Between Unmanned Aerial Vehicles (UAVs). In Proceedings of the 2007 9th International Conference on Transparent Optical Networks, Rome, Italy, 1–5 July 2007; IEEE: New York, NY, USA, 2007; Volume 3, pp. 152–155. [Google Scholar]
- Andrews, L.C.; Beason, M.K. Laser Beam Propagation in Random Media: New and Advanced Topics; SPIE: Bellingham, WA, USA, 2023. [Google Scholar]
- Elsayed, E.E. Investigations on OFDM UAV-Based Free-Space Optical Transmission System with Scintillation Mitigation for Optical Wireless Communication-to-Ground Links in Atmospheric Turbulence. Opt. Quantum Electron. 2024, 56, 837. [Google Scholar] [CrossRef]
- Takahashi, K.; Arimoto, Y. Compact Optical Antennas using Free-Form Surface Optics for Ultrahigh-Speed Laser Communication Systems. Opt. Eng. 2008, 47, 016002. [Google Scholar] [CrossRef]
- Mohan, S.; Alvarez-Salazar, O.; Birnbaum, K.; Biswas, A.; Farr, W.; Hemmati, H.; Johnson, S.; Ortiz, G.; Quirk, K.; Rahman, Z.; et al. Pointing, Acquisition, and Tracking Architecture Tools for Deep-Space Optical Communications. In Proceedings of the Free-Space Laser Communication and Atmospheric Propagation XXVI, San Francisco, CA, USA, 2–4 February 2014; SPIE: Bellingham, WA, USA, 2014; Volume 8971, pp. 112–122. [Google Scholar]
- Fidler, F.; Knapek, M.; Horwath, J.; Leeb, W.R. Optical Communications for High-Altitude Platforms. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1058–1070. [Google Scholar] [CrossRef]
- Indraganti, V.; Gupta, A.; Sharma, R. Attitude Estimation of HAPs using Fused Global Positioning System and Inertial Navigation System. In Proceedings of the 2022 8th International Conference on Signal Processing and Communication (ICSC), Noida, India, 1–3 December 2022; pp. 54–57. [Google Scholar] [CrossRef]
- R, S.; Sharma, S.; Vishwakarma, N.; Madhukumar, A.S. HAPS-Based Relaying for Integrated Space–Air–Ground Networks with Hybrid FSO/RF Communication: A Performance Analysis. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1581–1599. [Google Scholar] [CrossRef]
- Anddrews, L.; Phillips, R. Laser Beam Propagation Through Random Media; SPIE: Bellingham, WA, USA, 2005. [Google Scholar]
- Celik, U.; Yasar, H.A.; Yigitoglu Keskin, M.; Bayar, C.; Aslantas, I.; Midilli, Y. Estimation of Ground-Based Atmospheric Turbulence Strength (C n 2) by Neural Network Architecture. Appl. Opt. 2024, 63, 7402–7409. [Google Scholar] [CrossRef]
- Birnir, B. The Kolmogorov–Obukhov Statistical Theory of Turbulence. J. Nonlinear Sci. 2013, 23, 657–688. [Google Scholar] [CrossRef]
- Pak, J.H.; Joo, J.Y.; Lee, J.H.; Kim, J.I.; Cho, S.H.; Park, K.S.; Son, E.S. Evaluating Laser Beam Parameters for Ground-to-Space Propagation Through Atmospheric Turbulence at the Geochang SLR Observatory. Curr. Opt. Photonics 2024, 8, 382–390. [Google Scholar]
- Korotkova, O.; Toselli, I. Non-Classic Atmospheric Optical Turbulence. Appl. Sci. 2021, 11, 8487. [Google Scholar] [CrossRef]
- Mai, V.V.; Kim, H. Beam Size Optimization and Adaptation for High-Altitude Airborne Free-Space Optical Communication Systems. IEEE Photonics J. 2019, 11, 1–13. [Google Scholar] [CrossRef]
- European Space Agency. Low Earth Orbit. Image/ESA Multimedia Page, 2020. Credit: ESA–L. Boldt-Christmas. Available online: https://www.esa.int/ESA_Multimedia/Images/2020/03/Low_Earth_orbit (accessed on 15 September 2025).
- Ma, J.; Zheng, P.; Liu, X.; Zhang, Y.; Al-Naffouri, T.Y. Integrated Positioning and Communication via LEO Satellites: Opportunities and Challenges. arXiv 2024, arXiv:2411.14360. [Google Scholar] [CrossRef]
- Ophir Optronics Solutions Ltd. Laser Beam Measurement Vocabulary: Wavelength. 2025. Available online: https://www.ophiropt.com/en/t/laser-measurement-vocabulary (accessed on 15 September 2025).
- Cantore, C.; Monopoli, D.; Altamura, A.; Mengali, A.; Grande, M.; D’Orazio, A. Link Budget Analysis of Bi-Directional LEO and GEO Optical Feeder Links Advancing the Beam Wander Model’s Accuracy. Sci. Rep. 2024, 14, 8579. [Google Scholar] [CrossRef]
- Chan, V.W. Free-Space Optical Communications. J. Light. Technol. 2006, 24, 4750–4762. [Google Scholar] [CrossRef]
- Knopp, M.T.; Spoerl, A.; Gnat, M.; Rossmanith, G.; Huber, F.; Fuchs, C.; Giggenbach, D. Towards the Utilization of Optical Ground-to-Space Links for Low Earth Orbiting Spacecraft. Acta Astronaut. 2020, 166, 147–155. [Google Scholar] [CrossRef]
- Fernandez-Nino, E.; Fraire, J.A.; Camps, A.; Ruiz-De-Azua, J.A. RF-Assisted Uncertainty Cone Reduction in Free-Space Optical Inter-Satellite Links. IEEE Open J. Commun. Soc. 2024, 5, 7598–7612. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, Q. Mixed RF/FSO Deep Space Communication System Under Solar Scintillation Effect. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3237–3251. [Google Scholar] [CrossRef]
- Xu, G. BER and Channel Capacity of a Deep Space FSO Communication System Using L-PPM-MSK-SIM Scheme During Superior Solar Conjunction. Opt. Express 2019, 27, 24610–24623. [Google Scholar] [CrossRef]
- Beam Divergence. 2023. Available online: https://en.wikipedia.org/wiki/Beam_divergence (accessed on 15 September 2025).
- Böhmer, K.; Gregory, M.; Heine, F.; Kämpfner, H.; Lange, R.; Lutzer, M.; Meyer, R. Laser Communication Terminals for The European Data Relay System. In Proceedings of the Free-Space Laser Communication Technologies XXIV, San Francisco, CA, USA, 21–26 January 2012; SPIE: Bellingham, WA, USA, 2012; Volume 8246, pp. 79–85. [Google Scholar]
- Kaushal, H.; Kaddoum, G. Optical Communication in Space: Challenges and Mitigation Techniques. IEEE Commun. Surv. Tutor. 2017, 19, 57–96. [Google Scholar] [CrossRef]
- Liu, X.; Li, X.; Deng, Z.; Sun, H. High-Precision Point-Ahead Angle Real-Time Prediction Algorithm for Inter-Satellite Laser Links. Photonics 2025, 12, 886. [Google Scholar] [CrossRef]
- Lou, Y.; Zhao, Y.W.; Chen, C.; Tong, S.; Han, C. Analysis of Sun Outages Influence on GEO to LEO Communication. In Wireless Communications, Networking and Applications: Proceedings of WCNA 2014; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1017–1025. [Google Scholar]
- Ren, W.; Qiao, Q.; Nie, K.; Mao, Y. Robust DOBC for Stabilization Loop of a Two-Axes Gimbal System. IEEE Access 2019, 7, 110554–110562. [Google Scholar] [CrossRef]
- Cui, Y.; Zhu, Y.; Liu, J.; Wang, C.; Zhao, L. Analysis, Estimation, and Rejection of Multi-Frequency Unknown Disturbances in CMG Gimbal Servo Systems. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 4501–4505. [Google Scholar] [CrossRef]
- Carrasco-Casado, A.; Shiratama, K.; Trinh, P.V.; Kolev, D.; Ishola, F.; Fuse, T.; Tsuji, H.; Toyoshima, M. NICT’s Versatile Miniaturized Lasercom Terminals for Moving Platforms. In Proceedings of the 2022 IEEE International Conference on Space Optical Systems and Applications (ICSOS), Kyoto, Japan, 28–31 March 2022; pp. 213–217. [Google Scholar] [CrossRef]
- Graham, C.; Bramall, D.; Younus, O.; Riaz, A.; Binns, R.; Scullion, E.; Wicks, R.T.; Bourgenot, C. Steering Mirror System with Closed-Loop Feedback for Free-Space Optical Communication Terminals. Aerospace 2024, 11, 330. [Google Scholar] [CrossRef]
- CubeSpace. Gen2 CubeStar Miniature Star Tracker. 2024. Available online: https://satsearch.co/products/cubespace-gen2-cubestar-miniature-star-tracker (accessed on 9 August 2024).
- Ding, J.; Mei, H.; I, C.L.; Zhang, H.; Liu, W. Frontier Progress of Unmanned Aerial Vehicles Optical Wireless Technologies. Sensors 2020, 20, 5476. [Google Scholar] [CrossRef]
- Kaymak, Y.; Rojas-Cessa, R.; Feng, J.; Ansari, N.; Zhou, M.; Zhang, T. A Survey on Acquisition, Tracking, and Pointing Mechanisms for Mobile Free-Space Optical Communications. IEEE Commun. Surv. Tutor. 2018, 20, 1104–1123. [Google Scholar] [CrossRef]
- Majumdar, A.K. Advanced Free Space Optics (FSO): A Systems Approach; Springer: Berlin/Heidelberg, Germany, 2014; Volume 186. [Google Scholar]
- Eguri, S.V.K.; Raj A, A.B.; Sharma, N. Survey on Acquisition, Tracking and Pointing (ATP) Systems and Beam Profile Correction Techniques in FSO Communication Systems. J. Opt. Commun. 2024, 45, 881–904. [Google Scholar] [CrossRef]
- Hemmati, H. Deep Space Optical Communications; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Truex, T.; Bent, A.A.; Hagood, N.W. Beam Steering Optical Switch Fabric Utilizing Piezoelectric Actuation Technology. In Proceedings of the Proceedings NFOEC, Orlando, FL, USA, 8–11 September 2003. [Google Scholar]
- Li, Q.; Liu, L.; Ma, X.; Chen, S.L.; Yun, H.; Tang, S. Development of Multitarget Acquisition, Pointing, and Tracking System for Airborne Laser Communication. IEEE Trans. Ind. Inf. 2018, 15, 1720–1729. [Google Scholar] [CrossRef]
- Ke, C.; Shu, Y.; Ke, X.; Han, M.; Chen, R. Design and Implementation of a Non-Common-View Axis Alignment System for Airborne Laser Communication. Photonics 2023, 10, 1037. [Google Scholar] [CrossRef]
- Li, X.M.; Zhang, L.z.; Meng, L.X. Airborne Space Laser Communication System and Experiments. In Proceedings of the Selected Papers of the Photoelectronic Technology Committee Conferences, Harbin, China, 14–19 June 2015; SPIE: Bellingham, WA, USA, 2015; Volume 9795, pp. 98–108. [Google Scholar]
- Lahari, S.A.; Raj, A.; Soumya, S. Control of Fast Steering Mirror for Accurate Beam Positioning in FSO Communication System. In Proceedings of the 2021 International Conference on System, Computation, Automation and Networking (ICSCAN), Puducherry, India, 30–31 July 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Miyata, K.; van der Ha, J.C. Atitude Control by Magnetic Torquer. Adv. Astronaut. Sci. 2009, 134, 1041–1060. [Google Scholar]
- Milaševičius, M.; Mačiulis, L. A Review of Mechanical Fine-Pointing Actuators for Free-Space Optical Communication. Aerospace 2023, 11, 5. [Google Scholar] [CrossRef]
- Hasha, M.D. High-Performance Reaction Wheel Optimization for Fine-Pointing Space Platforms: Minimizing Induced Vibration Effects on Jitter Performance Plus Lessons Learned From Hubble Space Telescope for Current and Future Spacecraft Applications. In Proceedings of the 43rd Aerospace Mechanisms Symposium, Santa Clara, CA, USA, 4–6 May 2016. [Google Scholar]
- Vitelli, M.; Specht, B.; Boquet, F. A Process to Verify the Microvibration and Pointing Stability Requirements for the BepiColombo Mission. In Proceedings of the International Workshop on Instrumentation for Planetary Missions, Greenbelt, MD, USA, 10–12 October 2012; Voume 1683, p. 1023. [Google Scholar]
- Wu, X.; Chen, S.; Shi, B.; Chen, W.; Xiong, X.; Chen, S. High-Powered Voice Coil Actuator for Fast Steering Mirror. Opt. Eng. 2011, 50, 023002. [Google Scholar] [CrossRef]
- Bednarski, S.T. CubeSat Attitude Determination and Control System (ADACS) Characterization and Testing for Rendezvous and Proximity Operations (RPO). 2021. Available online: https://scholar.afit.edu/cgi/viewcontent.cgi?article=5973&context=etd (accessed on 9 August 2025).
- Wikipedia Contributors. High-Altitude Platform Station—Wikipedia, The Free Encyclopedia. 2025. Available online: https://en.wikipedia.org/wiki/High-altitude_platform_station (accessed on 9 August 2025).
- Şahin, M. Stabilization of Two Axis Gimbal System with Self Tuning PID Control. Politeknik Dergisi 2024, 27, 1441–1452. [Google Scholar] [CrossRef]
- Maaruf, M.; Mahmoud, M.S.; Ma’arif, A. A Survey of Control Methods for Quadrotor UAV. Int. J. Robot. Control Syst. 2022, 2, 652–665. [Google Scholar] [CrossRef]
- Safi, H.; Dargahi, A.; Cheng, J.; Safari, M. Analytical Channel Model and Link Design Optimization for Ground-to-HAP Free-Space Optical Communications. J. Light. Technol. 2020, 38, 5036–5047. [Google Scholar] [CrossRef]
- Panomrattanarug, B.; Higuchi, K.; Mora-Camino, F. Attitude Control of a Quadrotor Aircraft using LQR State Feedback Controller with Full Order State Observer. In Proceedings of the SICE Annual Conference 2013, Nagoya, Japan, 14–17 September 2013; pp. 2041–2046. [Google Scholar]
- Marković, L.; Kovač, M.; Milijas, R.; Car, M.; Bogdan, S. Error State Extended Kalman Filter Multi-Sensor Fusion for Unmanned Aerial Vehicle Localization in GPS and Magnetometer Denied Indoor Environments. In Proceedings of the 2022 International Conference on Unmanned Aircraft Systems (ICUAS), Dubrovnik, Croatia, 21–24 June 2022; pp. 184–190. [Google Scholar] [CrossRef]
- Wakitani, S.; Nakanishi, H.; Ashida, Y.; Yamamoto, T. Study on a Kalman Filter based PID Controller. IFAC-PapersOnLine 2018, 51, 422–425. [Google Scholar] [CrossRef]
- Gómez Gómez, J.A.; Moncada Guayazán, C.E.; Roa Prada, S.; Gonzalez Acevedo, H. Design and Experimental Validation of a LQG Control System for the Stabilization of a 2DOF Commercial Gimbal Using Physical Modelling Techniques. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Virtual, 16–19 November 2020; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 84546, p. V07AT07A019. [Google Scholar]
- Liu, Y. Review of Self-Stabilization Algorithms in UAV Electro-Optical Pods. Appl. Comput. Eng. 2024, 93, 56–60. [Google Scholar] [CrossRef]
- Wikipedia Contributors. Spacecraft Attitude Determination and Control—Wikipedia, The Free Encyclopedia. 2025. Available online: https://en.wikipedia.org/wiki/Spacecraft_attitude_determination_and_control (accessed on 31 August 2025).
- Maharjan, N.; Kim, B.W. Machine Learning-Based Beam Pointing Error Reduction for Satellite-Ground FSO Links. Electronics 2024, 13, 3466. [Google Scholar] [CrossRef]
- Noordin, A.; Mohd Basri, M.A.; Mohamed, Z. Adaptive PID Control via Sliding Mode for Position Tracking of Quadrotor MAV: Simulation and Real-Time Experiment Evaluation. Aerospace 2023, 10, 512. [Google Scholar] [CrossRef]
- Obiora, V.; Achumba, I.E. Adaptive Control of Aerial Vehicle Gimbal Using Fuzzy-PID Compensator. In Proceedings of the 2017 IEEE 3rd International Conference on Electro-Technology for National Development (NIGERCON), Owerri, Nigeria, 7–10 November 2017; pp. 451–456. [Google Scholar] [CrossRef]
- Proportional–Integral–Derivative Controller. 2025. Available online: https://en.wikipedia.org/wiki/Proportional-integral-derivative_controller (accessed on 15 September 2025).
- Guru, C. Using Signal Filters in Our PID Loop. 2015. Available online: https://controlguru.com/using-signal-filters-in-our-pid-loop/ (accessed on 15 September 2025).
- Şahin, M. Gimbal Axes Control with PID Controllers. Gazi Üniversitesi Fen Bilim. Derg. Pt C Tasarım Ve Teknol. 2023, 11, 143–152. [Google Scholar] [CrossRef]
- Segovia, V.R.; Hägglund, T.; Åström, K.J. Noise Filtering in PI and PID Control. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 1763–1770. [Google Scholar] [CrossRef]
- Monolithic Power Systems. Model Predictive Control (MPC). 2025. Available online: https://www.monolithicpower.com/en/learning/mpscholar/power-electronics/control-of-power-electronic-systems/model-predictive-control-mpc (accessed on 17 September 2025).
- Wikipedia Contributors Model Predictive Control. 2025. Available online: https://en.wikipedia.org/wiki/Model_predictive_control (accessed on 17 September 2025).
- The MathWorks, Inc. What is Model Predictive Control? 2025. Available online: https://www.mathworks.com/help/mpc/gs/what-is-mpc.html (accessed on 17 September 2025).
- Qin, H.; Xu, P.; Zhang, F.; Xue, Y. An Improved LOS Guidance and Sail-Rudder Cooperative Controller for the Path Tracking of Unmanned Sailboats. IEEE Trans. Intell. Veh. 2024, 9, 6610–6623. [Google Scholar] [CrossRef]
- Clouse, P.S. Vibration Reduction Algorithms Based on Model Predictive Control for Large Flexible Space Structures. 2023. Available online: https://apps.dtic.mil/sti/html/trecms/AD1224965/ (accessed on 1 December 2023).
- El Haj, Y.; Sood, V.K. Linear Quadratic Gaussian Controller for Single-Ended Primary Inductor Converter via Integral Linear Quadratic Regulator Merged with an Offline Kalman Filter. Energies 2024, 17, 3385. [Google Scholar] [CrossRef]
- Baskin, M.; Leblebicioğlu, M.K. Robust Control for Line-of-Sight Stabilization of a Two-Axis Gimbal System. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 3839–3853. [Google Scholar] [CrossRef]
- Obando, C.; Rojas, R.; Ulloa, F.; Camacho, O. Dual-Mode Based Sliding Mode Control Approach for Non-Linear Chemical Processes. ACS Omega 2023, 8, 9511–9525. [Google Scholar] [CrossRef]
- Uppal, A.A.; Azam, M.R.; Iqbal, J. Sliding Mode Control in Dynamic Systems. Electronics 2023, 12, 2970. [Google Scholar] [CrossRef]
- JuliaHub; DyadControl Contributors. DyadControl.jl: A Julia Package for Controlling Quantum Systems. 2023. Available online: https://juliaquantumcontrol.github.io/QuantumControl.jl/stable/ (accessed on 16 September 2025).
- Perruquetti, W.; Barbot, J.P. Sliding Mode Control in Engineering; Marcel Dekker: New York, NY, USA, 2002; Volume 11. [Google Scholar]
- Ermilov, A.S.; Saltykova, O.A. Application of Machine Learning for Adaptive Trajectory Control of UAVs Under Cyberleninka. RUDN J. Eng. Res. 2025, 26, 7–16. [Google Scholar]
- Liang, X.l.; Yao, Z.k.; Ge, Y.w.; Yao, J.y. Reinforcement Learning Based Adaptive Control for Uncertain Mechanical Systems with Asymptotic Tracking. Def. Technol. 2024, 34, 19–28. [Google Scholar] [CrossRef]
- Cloud, G. What Is Reinforcement Learning? 2023. Available online: https://cloud.google.com/discover/what-is-reinforcement-learning (accessed on 17 September 2025).
- Park, S.; Yeo, C.I.; Heo, Y.S.; Ryu, J.H.; Kang, H.S.; Lee, D.S.; Jang, J.H. Tracking Efficiency Improvement According to Incident Beam Size in QPD-Based PAT System for Common Path-Based Full-Duplex FSO Terminals. Sensors 2022, 22, 7770. [Google Scholar] [CrossRef] [PubMed]
- Nzekwu, N.J.; Fernandes, M.A.; Fernandes, G.M.; Monteiro, P.P.; Guiomar, F.P. A Comprehensive Review of UAV-Assisted FSO Relay Systems. Photonics 2024, 11, 274. [Google Scholar] [CrossRef]
- Luo, D.; Xiong, X.; Chen, W.; Huang, R. Design of Two-Dimensional Piezoelectric Laser Scanner System for Precision Laser Beam Steering. Rev. Sci. Instrum. 2023, 94, 105003. [Google Scholar] [CrossRef]
- Liu, C.; Yuan, W.; Wei, Z.; Liu, X.; Ng, D.W.K. Location-Aware Predictive Beamforming for UAV Communications: A Deep Learning Approach. IEEE Wirel. Commun. Lett. 2020, 10, 668–672. [Google Scholar] [CrossRef]
- Lee, J.H.; Park, J.; Bennis, M.; Ko, Y.C. Integrating LEO Satellites and Multi-UAV Reinforcement Learning for Hybrid FSO/RF Non-Terrestrial Networks. IEEE Trans. Veh. Technol. 2022, 72, 3647–3662. [Google Scholar] [CrossRef]
- Hou, J.; Li, H.; Qian, L.; Yu, H.; Shen, W. Control of a Micro-Electro-Mechanical System Fast Steering Mirror with an Input Shaping Algorithm. Micromachines 2024, 15, 1215. [Google Scholar] [CrossRef]
- Kim, J.G. System Integration Design of High-Performance Piezo-Actuated Fast-Steering Mirror for Laser Beam Steering System. Sensors 2024, 24, 6775. [Google Scholar] [CrossRef]
- Wu, H.; Wang, W.; Wang, T.; Suzuki, S. Sliding Mode Control Approach for Vision-Based High-Precision Unmanned Aerial Vehicle Landing System Under Disturbances. Drones 2024, 9, 3. [Google Scholar] [CrossRef]
- Chugh, T.; Bruzelius, F.; Kulcsár, B. Robust H-infinity Position Controller for Steering Systems. arXiv 2024, arXiv:2412.19161. [Google Scholar]
- Farajzadeh, A.; Yadav, A.; Yanikomeroglu, H. Federated Learning in NTN: Design, Architecture, and Challenges. IEEE Commun. Mag. 2025, 63, 26–33. [Google Scholar] [CrossRef]
- Wikipedia Contributors. Sliding Mode Control. 2025. Available online: https://en.wikipedia.org/wiki/Sliding_mode_control (accessed on 8 August 2025).
- Han, K.; Lee, J.; Kim, Y. Unmanned Aerial Vehicle Swarm Control using Potential Functions and Sliding Mode Control. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2008, 222, 721–730. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Y.; Mei, J.; Gong, Y.; Ma, G. Nonlinear Model Predictive Control for Leaderless UAV Formation Flying with Collision Avoidance under Directed Graphs. arXiv 2025, arXiv:2505.06895. [Google Scholar] [CrossRef]
- Pang, Q.; Zhu, Y.; Chen, Y.; Wang, D.; Suo, W. UAV Formation Control Based on Distributed Kalman Model Predictive Control Algorithm. AIP Adv. 2022, 12, 085304. [Google Scholar] [CrossRef]
- Yahia, O.B.; Erdogan, E.; Kurt, G.K.; Altunbas, I.; Yanikomeroglu, H. A Weather-Dependent Hybrid RF/FSO Satellite Communication for Improved Power Efficiency. IEEE Wirel. Commun. Lett. 2022, 11, 573–577. [Google Scholar] [CrossRef]
- Ciaramella, E.; Arimoto, Y.; Contestabile, G.; Presi, M.; D’Errico, A.; Guarino, V.; Matsumoto, M. 1.28 Terabit/s (32x40 Gbit/s) WDM Transmission System for Free Space Optical Communications. IEEE J. Sel. Areas Commun. 2009, 27, 1639–1645. [Google Scholar] [CrossRef]


| Reference | Study Type | Link Distance | Turbulence Considered | Other Key Parameters |
|---|---|---|---|---|
| [9] | Lab experiment + Simulation | 1.77 m lab test; 4 km altitude simulated | Yes (simulated beam divergence and turbulence) | 633 nm He-Ne laser, gimbal repeatability elevation/; tested on vibration-isolated table |
| [10] | Real-world balloon trial | Balloon platform, 50 mm aperture periscope | Limited (cloud outages noted; turbulence not quantified) | Compact FELT payload (18 kg), 2-DoF periscope steering, CMOS camera + Vision tracking |
| [13] | Lab experiment (model train track) | Short range (in meters) | No | Mechanical gimbal + PSD; simple proportional algorithm; angular velocities up to /s |
| [14] | Prototype for UAV (lab tested) | Air-to-Air (targeted km-scale, but not specified) | No | Lightweight (2.3 kg) 2-axis gimbal, piezo servo motors (0.069 arcsec resolution), DGPS/IMU-based tracking. |
| [16] | Ground-to-UAV experiment (lab + concept) | Indoor prototype; scalable to km | No (beacon assumed ideal) | MEMS-based modulating retroreflector (MRR). gimbal + FSM on ground; beacon-based tracking |
| [15] | Lab prototype (UAV gimbal) | Indoor demo | No | Compact carbon-fiber/magnesium gimbal, 3.5 kg, refractive telescope + FSM. |
| [18,19] | Real-world cubesat missions | LEO body pointing (∼500 km) | No explicit turbulence model (space vacuum) | Body pointing using ACS (reaction wheels, star tracker, GPS). Achieved < |
| [20,21] | Simulation (theoretical model) | UAV hovering link; distances not specified | Implicit; UAV fluctuations modeled statistically | QPD-based tracking; ML-based channel estimation. BER + tracking error analyzed with Monte Carlo simulations |
| [22] | Simulation (Channel model) | UAV-to-UAV, variable | Yes; pointing error with Hoyt distribution | Statistical model including UAV jitter; oscillating mirror terminals; anisotropic error distributions |
| [23] | Simulation (RIS-assisted UAV) | UAV–ground; distances not explicit | Yes; atmospheric loss + pointing error modeled | RIS-based optimisation with PSO/PPO; improved capacity and robustness. Energy-efficient passive beamforming |
| [26] | Lab/Simulation (gimbal control loop) | 2-axis gimbal (short range) | No turbulence; focused on control stability | LQG with loop transfer recovery; better margins vs PID. |
| [29,30] | Real-world cubesat missions | LEO–ground (200–1000 km) | Yes; ground telescope AO turbulence | Body pointing with star trackers and RW. TBIRD achieved >150–200 Gbps downlink |
| [27] | Lab experiment | Short-range optical bench | No atmospheric turbulence | MPC-controlled piezo FSM; nonradian precision, high bandwidth |
| [28] | Simulation (UAV model) | UAV–ground (fixed altitude, 3D jitter) | Yes; roll/pitch/yaw jitter modeled statistically | Joint trajectory + pointing optimization; 11.8% energy efficiency gain |
| [31] | Simulation/Lab training | Aircraft ADS-B data; prediction only | Not turbulence, but trajectory errors modeled | Transformer-based long-term trajectory predictor (GPU trained). ADE reduced by 8.2% FDE by 51% |
| [34] | Simulation | UAV swarm; distances not explicit | No | Collaborative pointing via federated learning; dual RF/FSO links |
| [35] | Lab experiment | 1 km simulated | Yes; turbulence chamber + Gaussian probe beam | Deep learning AO correction (MCCA-PNet) |
| [36] | Simulation | LEO–GEO (∼34,593–42,184 km) | No turbulence | Federated reinforcement learning for constellation scheduling; reduce hop count and latency |
| Feature | UAV–Ground Links | HAPS–Ground Links | Satellite–Ground Links | Satellite–HAPS Links | Inter-Satellite Links |
|---|---|---|---|---|---|
| Primary Pointing Challenge | Robust stabilization against high-frequency platform vibrations. | Long duration stability against platform vibrations. | Compensating for intense atmospheric turbulence and accuracy over vast distance. | Asymmetric link with a quasi-stationary aerial platform. | High relative velocity, maintaining lock during fast passes, and extreme absolute accuracy over vast distances. |
| Link Distance | <10 km | 20–50 km | 500–2000 km (LEO) | 500–36,000 km | 1000–8000 km (LEO), minimum 33,786 km (GEO) |
| Turbulence Path | Severe, often with the entire path in the thickest, most turbulent air. | Severe, path traversing from stratospheric layer to densest part of the atmosphere. | Entire atmosphere with severe turbulence near the ground. | Minimal (only thin stratospheric layer). | None (Operates in vacuum). |
| Platform Vibration | High-frequency and -amplitude vibrations from engines/rotors. | Low-frequency, high-altitude HAPS platform sway. | Predictable orbital motion, ground station is stable. | High-frequency satellite jitter and low-frequency HAPS sway. | High-frequency jitter at LEO, low amplitude from reaction wheels. |
| Key Complexity | Rejecting aggressive platform motion in a cluttered, dynamic environment. | Maintaining a continuous link for days/weeks from a drifting platform. | Weather dependency like cloud blockage. | Balancing space-grade precision with atmospheric link adaptability. | Point-ahead calculation at high angular rates, extreme link budget, acquisition time, and pointing loss. |
| Feature | Coarse Pointing | Fine Pointing |
|---|---|---|
| Range | 10– | < |
| Resolution | 0.1–1 mrad | <0.01 mrad |
| Bandwidth | 1–50 Hz | 1–10 kHz |
| Actuation | Gimbals, Pan-Tilt Units | FSMs, MEMS Mirrors, LCBDs |
| Response to | Platform motion, link acquistion | Jitter, turbulence, fine correction |
| Sensors | GPS, IMU, Camera, Star Trackers | QPD, PSD, Beam Position Detectors |
| Control | PID, Kalman, Model-Predictive | Adaptive, LQG, Fast PID |
| Type | DoF | Motion Axes | Application | Power Consumption | Pointing Accuracy | Pros | Cons |
|---|---|---|---|---|---|---|---|
| 1-axis Gimbal | 1 DoF | Pitch or Yaw | Fixed-wing UAVs with constrained payload, small high-altitude balloons | Low | Moderate | Simple, low-cost | Limited motion, less precise |
| 2-axis Gimbal | 2 DoFs | Pitch + Yaw | Multirotors, high-speed beam alignment, airships, stratospheric UAVs | Medium | High | Better Alignment | Medium complexity |
| 3-axis Gimbal | 2 DoFs | Pitch+Yaw+ Roll | Advanced UAVs needing roll compensation, satellites, spacecraft, payloads, high-altitude reconnaissance platforms | High | Very High | Full compensation precise | High copmplexity, heavy |
| CubeSat ADCS | Reaction wheels + 2-DoF micro gimbal | Full-body attitude control + fine az/el stage | Cubesats, small satellites (OCSD, AeroCube-7, TBIRD) | Medium | High (sub-mrad) | Low-SWaP integration with ADCS; compact | Limited torque, relies on ADCS stability |
| OPA | Electronics fine steering | Beam steering without mechanics | CubeSats, future smallsat terminals | Low | Very high (micro radian level) | No moving parts, fast response | Limited angular range, optical loss, emerging tech |
| Hexapod | 6 DoFs | Translational + Rotational | HAPs, stratospheric airships, vibration isolation platforms | High | High (sub-mrad) | 6-DoF correction, robust to turbulence | Bulky, heavy, high power demand |
| Feature | Mechanically Decoupled | Nested Gimbal |
|---|---|---|
| Axis Interference | Minimal | High |
| Size | Large | Compact |
| Complexity of Control | Simple | Complex (due to coupling) |
| Cable Routing | Complicated | Easy |
| Scalability | High | Limited by nesting constraints |
| Suitability for UAV | Low to Medium | High |
| Rotation Range | Wide (independent) | Limited by internal structure |
| Actuation Type | Principle | Use Case | Pros | Cons | Applications |
|---|---|---|---|---|---|
| Brushed DC Motors | Electro-mechanical torque via brushes | Legacy or cost-sensitive | Simple, low cost | Wear and tear, “EMI”, less precise | Low-cost UAV gimbals, legacy payloads |
| Brushless DC Motors (BLDC) | Electronic commutation, magnetic torque | UAV gimbals, fine pointing | Compact, efficient, long life | Requires ESC/FOC drivers | UAV lasercom terminals, small-satellite gimbals |
| Stepper Motors | Electromagnetic discrete steps | Coarse pointing systems | Open-loop control possible, precise steps | Can miss steps under high load | Coarse alignment in satellite optical terminals |
| Voice Coil Actuators | Linear magnetic field interaction | Fast stabilization (fine) | Fast response, frictionless | Small travel range, needs feedback | Fine beam steering for FSO ATP subsystems |
| Piezo-electric Actuators | Crystal deformation via voltage | Sub-microradian fine tracking | Ultra-precision | Very small range, expensive | Fine beam steering mirrors in optical communication |
| Harmonic Drive (w/Servo Motor) | Flex-spline torque gear system | Nested gimbal needing precision | Zero backlash, high torque density | Complex control, cost | High-precision satellite gimbals for GEO/LEO optical links |
| Magnetic Torquers | Magnetic interaction with Earth’s field | Space-based altitude control | No moving parts | Very low torque, slow | Satellite coarse atitude control before gimbal pointing |
| Reaction Wheels | Conservation of angular momentum | Satellite gimbal platforms | Precise torque control | Large, slow, high power consumption | Satellite fine pointing and stabilization for optical links |
| Gyroscopes (Control Moment Gyros-CMG) | Rotating mass generating torque | Spacecraft fine attitude control | High torque, precise attitude control | Complex, heavy, high power demand | High-capacity satellites needing agile optical beam poiniting |
| MEMS Actuators (Micro-mirrors, scanners) | Electrostatic/thermal deformation at micro-scale | Beam steering, fine pointing | Compact, low power, high speed | Limited angular range, fragile | CubeSat FSO ATP systems, miniature terminals |
| Shape Memory Alloys (SMAs) | Phase change deformation via heating | Deployable or low-power actuation | Simple, lightweight, low power | Slow response, hyteresis | CubeSat deployable optics, secondary pointing |
| Electrostatic Actuators | Coulomb force-based actuation | MEMS-level fine actuation | Ultra-low power, fast response | Tiny forces, limited travel | MEMS micomirrors for optical communication beam steering |
| Magnetostrictive Actuators | Strain from magnetic domain alignment | Ultra-fine motion systems | Precise, high bandwidth | Expensive, limited adoption | Niche optical ATP systems requiring ultra-stability |
| Actuation Type | Pointing Accuracy/Repeatability | Slew Rate/Bandwidht/ Response Time | Angular Range | SWaP | Lifetime | Environmental Tolerance |
|---|---|---|---|---|---|---|
| Brushed DC Motor | Low–Medium; for coarse positions, arc minutes/degrees, brushes create micro noise, limited repeatablity | Low–Medium; moderate response, limited high bandwidth control due to commutation and brush dynamics | Large (full turn via gearing) | Medium (cheap, moderate mass, brushes consume power) | Lower; brush wear limits life, maintenance required | Moderate; ok in benign air; poor for vacuum (brush outgassing/wear) and long-duration space use |
| BLDC | Medium–High; sub-arc-sec to arc-sec achievable with precision encoders/direct-drive designs, smooth torque reduces jitter | Medium–High; good dynamic response, high continuous torque; may have cogging/torque ripple if not optimized | Large (with bearing/gimbal) | Medium; good torque density, favorable SWaP for UAVs/space when optimized | High; no brushes so long life, reliability depends on bearings/ electronics | Good; can be used in airborne systems, space-qualified BLDC variants exist but require radiation/ thermal design |
| Stepper Motor | Medium; step resolution, therefore precise open-loop positioning but risk of missed steps under load, closed-loop microstepping improves repeatability | Low–Medium; strong at low speeds, poorer at high speeds (resonance/noise) | Large (full-turn with steps) | Medium; simple electronics but power drawn can be high (holding current) | Medium; robust mechanically but step loss under overload, heating issues | Moderate; commonly used in ground/air, space use requires careful de-energized holding strategies |
| Voice-Coil Actuator (VCA) | High for fine stages (sub-microradian to microradian when used on small mirrors/FSMs), very low hysteresis | Very High; excellent bandwidth (hundreds Hz to kHz) and smooth continuous force, ideal for jitter suppression | Small to Medium typically limited stroke (mm), small angular deflection when driving mirror | Low–Medium; compact and relatively lightweight for fine optics, power depends on duty | High; no mechanical contact wear (magnetic drive) but heating can limit continuous use | Good in atmosphere; for space must consider magnetics and thermal design, many FSMs with VCAs are space-qualified (with care) |
| Piezoelectric Actuators | Very High; sub-microradians to sub arc sec or micro stages, excellent for nanoradian-level fine pointing in short ranges | Very High; bandwidth upto kHz or higher (fast small motion response) | Very Small; limited stroke (micrometer to sub-milimeter) so angular deflection is tiny, fine corrections only | Very Low; but medium for power (drive electronics require high power) | High for many cycles but can suffer from creep, hysteresis and depoling over long time/high temp if not managed | Good for vacuum but temperature sensitivity and long term stability must be managed; space MEMS/piezo use exists |
| Harmonic Drive | High near zero-backlash, excellent repeatability (used in precision gimbals and space actuators) | Low–Medium; gear reduction reduces bandwidth; good for precise slow moves, not high bandwidth | Large (full motion depending on motor) | Medium–High adds mass/volume but provides high torque in compact package | High; robust gear life but lubrication/wear is a consideration in long missions | Good for atmosphere, space gears require vacuum-compatible lubrication and careful qualification |
| Magnetic Troquers | Very Low for fine pointing (used fpr coarse attitude control only; torque small relative to reaction wheels) | Low; slow actuation in seconds and low bandwidth | N/A actuates body attitude not local gimbal | Very Low SWaP; lightweight, low power for coarse control | High simple solid state coils, long life | Excellent for LEO momentum management, but ineffective far from Earth (weak field) |
| Reaction Wheels | High (used for spacecraft coarse and fine attitude control; can support arc-sec or better LoS when coupled with control filters) | Low–Medium; wheel spin control has limited bandwidth, but can be used with FSMs for high-bandwidth corrections | N/A (body control) | Medium–High; substantial mass and power depending on required angular momentum | Medium bearing and motors wears; micro-vibration from RWAs can degrade pointing unless mitigated | Very good in space, but reaction wheel induces jitter must be mitigated for microradians pointing |
| Control Moment Gyroscopes | High for large torque agile pointing (used for fast slewing/precise reorientation), not used for tiny local beam steering but for body maneuvers | Medium–High; can produce large torques quickly (but control singularities exist) | N/A (body control) | High; heavy and power hungry for significant torque | High but mechanical complexity and singularity management are issues; maintenance is impossible in space | Space Grade; widely used in large spacecraft but not suited for small SWaP platforms |
| MEMS Actuators | Very high for small angles (microradians to sub micro-radians) | Very High bandwidth often in kHz; excellent for fine jitter suppression | Very Small typical angular ranges to depending on design | Very Low; tiny size, and power, suitable for cubesats. | Variable many cycles possible but fatigue, dielectric charging, or radiation effects can limit life, qualification needed for space | Good in vacuum if space-qualified; radiation and thermal cycling can affect some MEMS types needs qualification |
| Shape Memory Alloys | Low slow, coarse motion, low precision | Very Low, slow thermal actuation (seconds to minutes) | Medium (depends on linkage) | Very low weight, but low efficiency too (heating required) | Medium–Low; fatigue from cycles, hysteresis and drift are common | Moderate; thermal and repeated cycling impact life; not ideal for continuous pointing |
| Electrostatic Actuators | High at MEMS scale but limited force/travel | Very High, but at micro scale (microseconds to milliseconds) | Very Small (micrometer displacements, small angular ranges) | Very Low (excellent for micro terminals) | Variable; dielectric charging and stiction can be failure modes; vacuum performance good if designed properly | Good for vacuum if space qualified, careful design to avoid charging and stiction |
| Magneto strictive Actuators | Very High (ultra fine motion possible in niche systems) high bandwidth and precision | High; good bandwidth for small strokes | Small (limited stroke) | Medium can be compact but require magnetic materials and drive currents | High; solid state, few moving parts, but specialized materials may fatigue under extremes | Good if engineered for environment, limited adoption in mainstream FSO due to cost/complexity |
| Platform | Requirements (SWaP, Vibration, Environment, Lifetime) | Suitable Motor/Gimbal Types |
|---|---|---|
| Small UAVs/Multirotor | Very tight constraints on weight, power, size; high vibration; need for moderate pointing accuracy; fast slewing; possibly intermittent operations. | Lightweight BLDC + small direct-drive motors; possibly voice coil/arc-segment for fine axes; minimal gear reduction. |
| HAPSs | Somewhat more forgiving on weight; but still constrained; environmental temperature extremes; long duration; potential atmospheric turbulence partly mitigated by altitude. | Medium-torque BLDC or servo motors; possibly gear assisted for large optics; voice coil for fine pointing; redundancy for reliability. |
| CubeSats/Small Satellites | Very strict SWaP; vacuum, radiation; long lifetime; limited thermal dissipation; orbital perturbations (nutation, jitter) from reaction wheels, internal mechanisms. | Micro gimbals or MEMS actuators for fine pointing; perhaps small brushless servos for coarse pointing; minimal gear to reduce backlash; use of high-precision encoders. |
| Large Satellites/GEO Telescopes/Ground Station Tracking | Large payloads; high angular resolution; need for high stability; environmental conditions vary; long missions. | High-torque servos/BLDC with gear reductions; voice coil fine steer mirrors/tip-tilt stages for jitter; large, robust gimbals. |
| Inter-Satellite/Deep Space FSO Links | Very long missions; high pointing accuracy; large distances therefore small pointing errors magnified; extreme environmental conditions (radiation, thermal swings). | High-precision BLDC/servo with fine steering mirrors (possibly MEMS or piezoelectric); perhaps redundant systems; minimal moving mass; low power consumption; high durability. |
| Algorithm | Typical Use | Bandwidth | Accuracy | Complexity | Hardware/Software Needs | Energy Efficiency | Resistance to Noise | Adaptability Across Platforms |
|---|---|---|---|---|---|---|---|---|
| PID | Coarse and fine (fast PID variants used for FSMs) | Medium–High (inner loops up to ∼1 kHz possible) | Medium (good for well behaved linear regions; sensitive to noise and nonlinearities) | Low (simple to design; manual/heuristic tuning) | Low-end MCU (STM32) + sensors/encoders; filtering recommended | High (low compute) | Low–Medium (derivative term is noise sensitive; needs filtering) | Good for UAVs and HAPSs after tuning; less ideal for sub-arcsecond satellite needs |
| LQR | Coarse (outer loop), reaction wheel attitude control | Low–Medium (10–100 Hz) | Medium for well modeled linear systems | Medium (requires linear model, Riccati solve) | MCU/small embedded CPU with linear algebra | Medium (optimal control reduces excessive actuation) | Medium (model mismatch reduces robustness unless combined with estimators) | Good for HAPSs, UAVs; cubesats benefit with careful modeling |
| LQG | Fine and coarse (noisy sensors; requires estimator) | Medium | Medium–High (estimation + optimal control) | High (state model + observer + gains) | MCU/embedded CPU + sensor fusion (IMU, encoders) | Medium | Medium (kalman helps with noisy measurements) | Good across platform if models available |
| EKF | Supporting role for coarse/fine (sensor fusion) | Medium (100–500 Hz) | High (fuses IMU/GPS/vision; reduces drift) | High (nonlinear models, tuning) | MCU + IMU/GPS/camera | Medium | Medium (robust to sensor noise if modeled) | Essential for GNSS - denied/ vision-assisted modes |
| MPC | Fine/predictive pointing (jitter supression, trajectory foresight) | Medium–Low (depends on horizon; heavier compute) | High (handles constraints, multivariate coupling) | High (online optimization; horizon tuning) | Embedded CPU/co-processor/ real-time QP solver | Low–Medium (compute intensive) | Medium (explicit constraint handling; can mitigate disturbances if predicted) | High potential for UAV/HAPSs; satellites require lighter-weight or offline MPC |
| Adaptive PID | Coarse & fine where dynamics vary | Medium–High | Medium (adapts to changing dynamics) | Medium–High (adaptive law or fuzzy rules) | MCU with modest compute; adaptive routines | Medium (some copmute, but less than MPC) | Medium (adapts to changing noise/disturbance statistics) | Very good for UAVs and HAPSs; useful when payload or environment changes |
| SMC | Fine/coarse when robustness is required (disturbances) | High (can be implemented high-rate) | High (robust to matched uncertainties) | Medium–High (chattering mitigation needed) | MCU; may require filters/observers | Medium | High (robust to disturbances, model errors) | Good for turbulent UAV/HAPS scenarios; needs careful design for sensitive optics |
| AI/ML predictive controllers | Predictive fine/coarse pointing (trajectory prediction, pre-steer) | Depends (inference fast; training costly) | Potentially high (if trained on representative data) | High (data collection, training, validation) | MCU + lightweight NN runtime (or onboard CPU on larger platforms) | Medium–Low (inference efficient; training offline) | Varies (can be brittle to data; requires robust training) | High potential for UAV swarms and HAPSs; for satellites, needs rigorous validation |
| Hybrid Schemes | Integrated coarse; fine stacks | Medium–High (combined strengths) | High (best disturbance rejection and estimation) | High (integrates estimators + controller) | Multi-core MCU/embedded CPU + sensors | Medium | High (combines estimation + control robustness) | Flexible across UAV/HAPSs/ satellites with appropriate partitioning |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhruv; Kaushal, H. A Review of Pointing Modules and Gimbal Systems for Free-Space Optical Communication in Non-Terrestrial Platforms. Photonics 2025, 12, 1001. https://doi.org/10.3390/photonics12101001
Dhruv, Kaushal H. A Review of Pointing Modules and Gimbal Systems for Free-Space Optical Communication in Non-Terrestrial Platforms. Photonics. 2025; 12(10):1001. https://doi.org/10.3390/photonics12101001
Chicago/Turabian StyleDhruv, and Hemani Kaushal. 2025. "A Review of Pointing Modules and Gimbal Systems for Free-Space Optical Communication in Non-Terrestrial Platforms" Photonics 12, no. 10: 1001. https://doi.org/10.3390/photonics12101001
APA StyleDhruv, & Kaushal, H. (2025). A Review of Pointing Modules and Gimbal Systems for Free-Space Optical Communication in Non-Terrestrial Platforms. Photonics, 12(10), 1001. https://doi.org/10.3390/photonics12101001






