Secure Downlink Transmission with NOMA-Based Mixed FSO/RF Communications in Space–Air–Ground Integrated Networks

Abstract

Security is paramount in space–air–ground integrated networks (SAGINs) due to their inherent openness and the broadcast characteristics of wireless transmission. In this paper, we propose a secure downlink transmission scheme with NOMA-based mixed FSO/RF communications for SAGINs. Specifically, the satellite communicates with two ground users through an unmanned aerial vehicle (UAV) relay, where FSO and RF transmissions are adopted for the satellite–relay and relay–user links, respectively. Furthermore, the NOMA technique is integrated to further enhance secrecy performance. Subsequently, exact closed-form expressions for the secrecy outage probability of the downlink transmission link in SAGINs are derived. Finally, Monte Carlo simulations are performed to validate the effectiveness of the proposed secure downlink transmission scheme and the accuracy of the analytical expressions.

1. Introduction

1.1. Background

The space–air–ground integrated network (SAGIN) has emerged as a critical architecture for future wireless communications, envisioned to deliver seamless, high-capacity, and ubiquitous connectivity on the global scale [1,2]. By integrating satellite networks, aerial networks, and terrestrial communications, SAGINs significantly extend the communication coverage, particularly in remote rural regions, oceans and mountainous areas where traditional terrestrial networks are unavailable [3]. The extensive coverage and broadcast nature of wireless transmission also make SAGINs vulnerable to security risks, including malicious eavesdropping. However, ensuring secure transmission in SAGINs has garnered substantial research attention.

Free-space optical (FSO) communication is regarded as a highly promising technology for SAGINs, especially in satellite-to-ground scenarios. It offers a compelling combination of exceptionally high data rates, license-free spectrum, and inherent security advantages [4,5,6]. Despite these benefits, FSO links are highly susceptible to atmospheric conditions in practical deployment. Adverse weather and atmospheric turbulence can induce intense signal fading and scintillation, which in turn lead to degraded link reliability and frequent outages [7]. These limitations can be effectively mitigated through the adoption of a mixed FSO and RF communication architecture [8].

Extensive recent research has focused on improving transmission stability of communication systems by integrating UAV-based relaying with mixed FSO-RF technology. The UAV relay acts as an intermediate node, establishing a stable FSO link to the Low Earth Orbit (LEO) satellite and subsequently forwarding the data to the ground station [9]. Owing to the scarcity of licensed RF spectrum coupled with exponential growth in wireless traffic, non-orthogonal multiple access (NOMA) has the potential to further increase spectral efficiency [10,11,12]. However, in NOMA systems, the same spectrum resources are shared among multiple users. Once the system is eavesdropped on, the information of multiple users will be leaked simultaneously. Moreover, due to the open medium and long-distance communication, security is a critical issue in the wireless communication. Recently, information-theoretic physical layer security (PLS) has emerged as a prevalent technique for addressing secrecy issues at the physical layer [13,14]. PLS enables secure wireless communication by leveraging the inherent randomness of the communication medium. This approach has been successfully incorporated into both NOMA and mixed FSO-RF systems, offering innovative pathways to address critical security challenges [15,16].

1.2. Related Works

We investigated various mixed FSO-RF relaying communication systems and presented a comprehensive in

Table 1. Literature review on some related FSO-RF systems.

Ref.	FSO	RF	NOMA	Relay	Metrics
[17]	Gamma-Gamma	Nakagami-m	✗	DF	SOP, SPSC
[18]	$\mathrm{Málaga} (\mathcal{M}$)	Nakagami-m	✗	DF	SOP, EST
[19]	$\mathrm{Málaga} (\mathcal{M}$)	Nakagami-m	✗	DF	SOP, EST
[20]	Gamma-Gamma	Nakagami-m	✓	DF	SOP
[21]	$\mathrm{Málaga} (\mathcal{M}$)	Nakagami-m	✗	DF	SOP, ASC
[22]	$\mathrm{Málaga} (\mathcal{M}$)	Shadowed-Rician	✓	DF	SOP
[23]	Fisher-Snedecor	Nakagami-m	✗	DF	SOP
[24]	$\mathrm{Málaga} (\mathcal{M}$)	Shadowed-Rician	✗	AF	SOP, EST, SPSC
[25]	Gamma-Gamma	Shadowed-Rician	✗	AF	SOP, COP
[26]	Gamma-Gamma	Nakagami-m	✓	AF	SOP, ASC
[27]	$\mathrm{Málaga} (\mathcal{M}$)	Rayleigh	✗	DF	ASC, SOP, EST

. According to Table 1, it is evident that the majority of studies on this system focus on decode-and forward (DF) relaying protocols [17,18,19,20,21,22,23,24], and amplify-and-forward (AF) relays which encompass fixed-gain [24,25,26]. In FSO-RF systems, signal fading is predominantly induced by atmospheric turbulence and pointing errors. The Gamma-Gamma distribution [17,20,25,26] is considered as the most typical distribution for the irradiance, and the Málaga ($\mathcal{M}$) distribution [18,19,21,22,24,27] is presented in [28] to model the variability in irradiance of an infinite optical wavefront as it propagates through turbulent media across all levels of irradiance. Heterodyne detection (HD) and indirect modulation/direct detection (IM/DD) are widely adopted in FSO systems, with HD offering higher sensitivity at the cost of increased complexity compared to IM/DD. For the RF links, the Nakagami-m distribution and the Shadowed-Rician distribution are the most commonly used models [17,18,19,20,21,22,23,24,25,26], as well as Rayleigh [27]. In the existing literature, only a limited number of studies have considered the application of NOMA technology [20,22,26]. Liu et al. [20] propose the use of a Reconfigurable Intelligent Surface (RIS) as a passive means to enhance secrecy performance. While the study in [22] considers the impact of fog absorption on FSO links and the random spatial distribution of terrestrial users, Osman et al. [26] explore MIMO and Artificial Noise (AN) as active countermeasures for colluding eavesdroppers.

1.3. Motivations and Contributions

The existing literature reveals that the investigation of physical layer security (PLS) for NOMA-based mixed FSO-RF systems in SAGIN remains largely unexplored, yet this area represents a pressing and critical research need. To address this gap, we propose a novel framework integrating NOMA with mixed FSO-RF transmission in the presence of an eavesdropper (E). The PLS performance is rigorously analyzed, with key contributions summarized as follows:

• We propose a novel secure transmission scheme for the SAGIN downlinks, which is a NOMA-based mixed FSO-RF communication system. Additionally, we analyze the secure transmission performance of this system.
• An analytical expression for the secrecy outage probability (SOP) in the presence of an eavesdropper was derived. Furthermore, extensive experiments were conducted to validate the advantages of the proposed NOMA-based mixed FSO-RF communication system and the accuracy of the derived SOP analytical expression.
• We investigated the impact of both amplify-and-forward (AF) and decode-and-forward (DF) relay protocols on the secure transmission performance within SAGIN. Experimental results demonstrate that the DF relay protocol achieves superior secrecy performance compared to the AF scheme.

The remainder of this paper is organized as follows. The system and channel models of the proposed are discussed in Section 2. In Section 3, the security performance of proposed system is analyzed. Afterwards, Section 4 discusses the results of numerical analysis and simulation. Finally, Section 5 summarizes the paper.

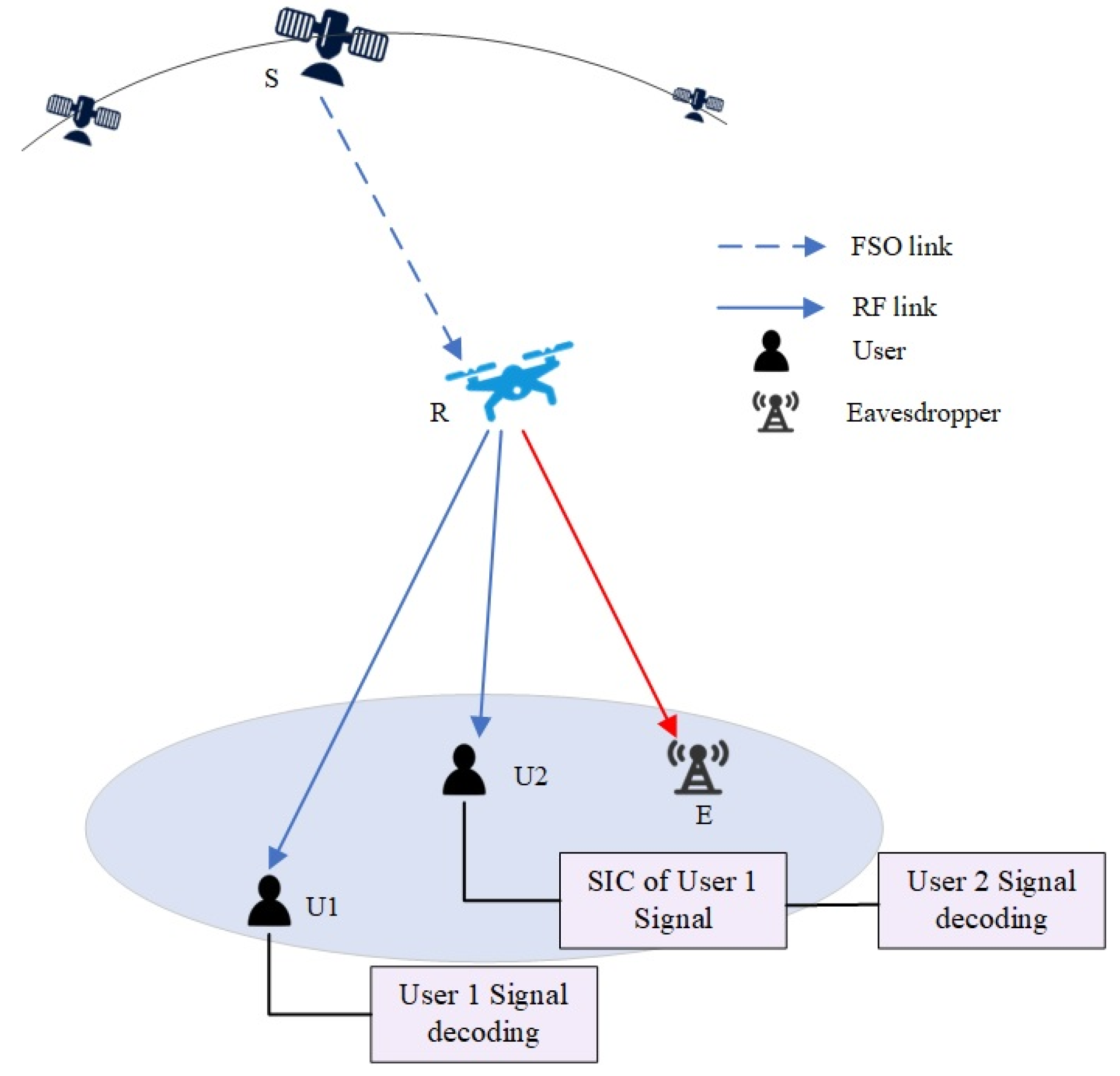
2. System and Channel Models

Traditional satellite-terrestrial communication systems suffer from significant security issues due to the open nature of their channels and the broadcast characteristics of their signals. In contrast, satellite–terrestrial laser communication links, benefiting from the characteristics of free-space optical (FSO) communication, hold promise for addressing this security issue. However, laser communication is highly susceptible to channel influences. Atmospheric turbulence and pointing errors can severely degrade transmission performance. Moreover, laser communication is limited to line-of-sight (LOS) transmission, resulting in poor channel resistance to obstruction [28]. Therefore, the introduction of UAV relays can effectively mitigate this issue.

Based on the above analysis, we propose a secure transmission scheme for a NOMA-based mixed FSO-RF system in SAGIN. The FSO link is employed between the LEO satellite and the UAV relay, with the UAV establishing connections to multiple users via RF links. Moreover, NOMA technology is utilized to further improve spectral efficiency. The specific scheme is illustrated in Figure 1. The source (S) transmits mutually independent information to the two ground users (U₁ and U₂) simultaneously via an UAV relay (R). The communication system is designed as a two-hop transmission process. In the first phase transmission, S transmits a non-orthogonal multiple access (NOMA) signal to the relay (R) via the FSO link. In the second phase transmission, an optical-to-electrical (O/E) conversion is first performed at R, and the resulting electrical signal is then forwarded to multiusers over RF links using either an amplify-and-forward (AF) or decode-and-forward (DF) protocol, in the presence of an eavesdropper (E). The NOMA technique is utilized in this RF link. We assume that the source node has a single aperture, and the relay node has an optical receiving aperture and an RF transmitting antenna. The ground user employs a single antenna. All devices operate in half-duplex mode to avoid self-interference.

2.1. S-R FSO Link

In the first hop, the FSO link is assumed to follow Gamma-Gamma fading channels with atmospheric attenuation and pointing errors. The signal received at the UAV relay (R) is expressed as

$$y_R=\sqrt{P_s}{I}_{SR}{\eta }_{SR}{x}_s+n_R$$

(1)

and instantaneous signal-to-noise ratio (SNR) at node R can be given as

$${\gamma }_{SR}={\displaystyle \frac{P_s{\left|I_{SR}{\eta }_{SR}\right|}^2}{{\sigma }_R^2}}$$

(2)

where $P_S$ is the transmit power of LEO satellite S, nR is the additive white Gaussian noise (AWGN) variable at the relay with mean zero and variance ${\sigma }_R^2$. And the channel coefficient of the overall FSO link can be expressed as $I_{SR}=I_{SR}^l{I}_{SR}^a{I}_{SR}^p$, where $I_{SR}^p$ indicates geometric spreading and pointing errors; $I_{SR}^a$ denotes the impact of atmospheric turbulence; $I_{SR}^l$ represents the atmospheric attenuation due to path loss. ${\eta }_{SR}$ is the optical-to-electrical conversion coefficient. Furthermore, $x_s$ represents the superimposed signal denoted as

$$x_s=a_1{x}_1+a_2{x}_2$$

(3)

where $x_1$ and $x_2$ denote the transmitting signals of U₁ and U₂, $a_1$ and $a_2$ are the power allocation coefficients of $x_1$ and $x_2$, respectively. Based on the NOMA approach, we assumed that U₁ is a far-user requiring a higher transmission power, while U₂ is a near-user requiring a lower transmission power. Then, it has $a_1>a_2$ with $a_1^2+a_2^2=1$.

The probability density function (PDF) of instantaneous SNR can be written in terms of Meijer G-function $G_{p,q}^{m,n}(\cdot )$ which is defined in (Ref. [29], Equation (9.301)), and (Ref. [30], Equation (07.34.02.0001.01)), and given as (Ref. [31], Equation (4))

$$f_{{\gamma }_{SR}}\left({\gamma }_{SR}\right)={\displaystyle \frac{{\xi }^2}{r{\gamma }_{SR}\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\beta \right)}}{G}_{\mathrm{1,3}}^{\mathrm{3,0}}\left[h\alpha \beta {\left({\displaystyle \frac{{\gamma }_{SR}}{{\mu }_r}}\right)}^{{\displaystyle \frac{1}{r}}}\left|\begin{array}{c}{\xi }^2+1\\ {\xi }^2,\alpha ,\beta \end{array}\right.\right]$$

(4)

where $\xi$ is the pointing error coefficient, which is used to quantify the severity of beam misalignment. $h={\xi }^2/\left({\xi }^2+1\right)$, and ${\mu }_r$ indicates the average electrical SNR of pertinent link. $\alpha$ and $\beta$ are parameters that indicate large-scale and small-scale irradiance fluctuations, parameter $r$ signifies the detection method used at the UAV relay node (i.e., $r=1$ is associated with heterodyne detection (HD), and $r=2$ is associated with IM/DD). Specifically, ${\mu }_1={\bar{\gamma }}_{SR}$ for HD and ${\mu }_2={\displaystyle \frac{h\alpha \beta \left({\xi }^2+2\right)}{\left({\xi }^2+1\right)\left(\alpha +1\right)\left(\beta +1\right)}}{\bar{\gamma }}_{SR}$ for IM/DD technology. Moreover, $\mathsf{\Gamma }(\cdot )$ represents the Gamma function defined in (Ref. [29], Equation. (8.310)). The cumulative distribution function (CDF) of ${\gamma }_{SR}$ can be deduced by using (Ref. [30], Equation (07.34.21.0084.01)) as follow:

$$F_{{\gamma }_{SR}}\left({\gamma }_{SR}\right)={\displaystyle \frac{{\xi }^2{r}^{\alpha +\beta -2}}{{\left(2\pi \right)}^{r-1}\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\beta \right)}}{G}_{r+\mathrm{1,3}r+1}^{3r,1}\left(\left.{\displaystyle \frac{{\left(h\alpha \beta \right)}^r}{r^{2r}{\mu }_r}}{\gamma }_{SR}\right|\begin{array}{cc}1& E_1\\ E_2& 0\end{array}\right)$$

(5)

In addition, $E_1=\left\{{\displaystyle \frac{{\xi }^2+1}{r}},\dots ,{\displaystyle \frac{{\xi }^2+r}{r}}\right\}$, and $E_2=\left\{{\displaystyle \frac{{\xi }^2}{r}},\dots ,{\displaystyle \frac{{\xi }^2+r-1}{r}},{\displaystyle \frac{\alpha }{r}},\dots ,{\displaystyle \frac{\alpha +r-1}{r}},{\displaystyle \frac{\beta }{r}}\dots ,{\displaystyle \frac{\beta +r-1}{r}}\right\}$.

2.2. R-U RF Link

For the R-U RF link, optical-to-electrical conversion is performed at node R, and the resulting electrical signals are transmitted to U₁ and U₂ via RF links in the presence of an eavesdropper E. At node R, both amplify-and-forward (AF) and decode-and-forward (DF) relaying protocols are employed.

1.

AF Relaying

The AF relaying protocol works by simply amplifying the received mixed signal, which includes both Gaussian noise and the transmitted signal. It then forwards the amplified signal to the receiver. This approach offers simple operation and low complexity. However, it has a drawback: noise is also amplified in the process. This makes it harder for the receiver to correctly decode the desired signal.

R first processes an optical-to-electrical conversion and then amplifies and broadcasts the multiplexed signal to U_k. The signals received at node Z, $Z\in \left\{U_1,U_2,E\right\}$ can be given

$$y_Z=\sqrt{P_S}G{I}_{SR}{I}_{RZ}{\eta }_{SR}{x}_s+G{I}_{RZ}{n}_R+n_Z$$

(6)

where $G=\sqrt{P_R/\left(P_S{\left|I_{SR}\right|}^2+{\sigma }_R^2\right)}$ is the amplifying coefficient defined in [32], and $P_R$ indicates the transmission power of R. $I_{{RU}_k}$ and $I_{RE}$ are the channel gains between R and U_k as well as E, $n_{U_k}$ and $n_E$ are the AWGN at U_k and E with zero mean and variances of ${\sigma }_{U_k}^2$ and ${\sigma }_E^2$, respectively. The RF channels are modeled as Nakagami-m distribution with a shape parameter $m_{RZ}$ that determines the fading severity.

The probability density function (PDF) and the CDF expressions of ${\gamma }_{RZ}$ can be denoted, respectively, as

$$f_{{\gamma }_{RZ}}\left(\gamma \right)={\Omega }_{RZ}^{m_{RZ}}{\displaystyle \frac{{\gamma }^{m_{RZ}-1}}{\mathsf{\Gamma }\left(m_{RZ}\right)}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\Omega }_{RZ}\gamma \right)$$

(7)

and

$$F_{{\gamma }_{RZ}}\left(\gamma \right)=1-{\displaystyle \sum _{l=1}^{m_{RZ}-1}}{\displaystyle \frac{{\left({\Omega }_{RZ}\gamma \right)}^l}{l!}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\Omega }_{RZ}\gamma \right)$$

(8)

where ${\Omega }_{RZ}=m_{RZ}/{\overline{\gamma }}_{RZ}$, and ${\overline{\gamma }}_{RZ}$ represents the average SNR.

In the NOMA networks, successive interference cancelation (SIC) is adopted at each ground user to mitigate the interference of the others. The decoding order is the increasing order of the channel gain. For the remote user U₁, it decodes its own information while considering $x_2$ as interference. Hence, the end-to-end signal-to-interference-plus-noise ratio (SINR) for U₁ to decode $x_1$ can be written as

$${\gamma }_{U_1,x_1}={\displaystyle \frac{{\gamma }_{SR}{\gamma }_{R{U}_1}{a}_1^2}{a_2^2{\gamma }_{SR}{\gamma }_{R{U}_1}+{\gamma }_{SR}+{\gamma }_{R{U}_1}+1}}$$

(9)

For the near user U₂, successive interference cancelation (SIC) is employes to eliminate $x_1$ from the superimposed signal, and then decodes its own information $x_2$. Therefore, the end-to-end SINR received at U₂ is

$${\gamma }_{U_2,x_2}={\displaystyle \frac{{\gamma }_{SR}{\gamma }_{R{U}_2}{a}_2^2}{{\gamma }_{SR}+{\gamma }_{R{U}_2}+1}}$$

(10)

Besides, the end-to-end instantaneous SNR for E to decode $x_k$ is given by

$${\gamma }_{E,x_k}={\displaystyle \frac{{\gamma }_{SR}{\gamma }_{RE}{a}_k^2}{{\gamma }_{SR}+{\gamma }_{RE}+1}}$$

(11)

2.

DF Relaying

For the DF relay protocol, the relay decodes the received signal, which contains Gaussian noise. It then encodes the decoded signal and forwards it to the receiver. While decoding noisy signals increases computational complexity, DF relaying mitigates noise accumulation, thus achieving higher reliability.

R decodes the received signal by utilizing SIC. In particular, R first decodes $x_1$, which is transmitted at a higher power, while treating $x_2$ as noise. Next, the end-to-end SINR for R to decode $x_1$ is

$${\gamma }_{R,x_1}={\displaystyle \frac{{\gamma }_{SR}{a}_1^2}{{\gamma }_{SR}{a}_2^2+1}}$$

(12)

Following this, R removes $x_1$ from the received signal and then decodes $x_2$ with the SINR illustrated as

$${\gamma }_{R,x_2}={\gamma }_{SR}{a}_2^2$$

(13)

Therefore, the decoded signals are electrically converted by relay node R, re-encoded, and transmitted to U₁ and U₂ via radio frequency (RF) links. Moreover, the signal received at Z can be deduced as

$$y_Z=\sqrt{P_R}{I}_{RZ}{x}_s+n_Z$$

(14)

Next, SIC is utilized to decode the received signals, and the end-to-end SINR at U₁ and U₂ for detecting their independent signals are respectively

$${\gamma }_{U_1,x_1}={\displaystyle \frac{{\gamma }_{R{U}_1}{a}_1^2}{a_2^2{\gamma }_{R{U}_1}+1}}$$

(15)

and

$${\gamma }_{U_2,x_2}={\gamma }_{R{U}_2}{a}_2^2$$

(16)

Following the approach in reference [33], we consider the worst-case scenario where E can completely eliminate the interference between the signals, thus decoding both $x_1$ and $x_2$. However, in practical scenarios, this case overestimates the eavesdropper’s capabilities. Consequently, it can also be regarded as the lower bound of the system’s PLS performance. And the SINR for E to decode $x_k$ can be written as

$${\gamma }_{E,x_k}={\gamma }_{RE}{a}_k^2$$

(17)

3. Security Performance Analysis

To conduct an in-depth analysis of the system, we have to investigate the secrecy performance, which includes the instantaneous channel capacity. Subsequently, we present new analytical expressions for PLS performance metrics, which include the secrecy capacity (SC) and secrecy outage probability (SOP).

3.1. Secrecy Capacity

The secrecy capacity (SC) is the difference between the main channel capacity and the wiretap channel capacity. The secrecy capacity C_S represents the maximum secure communication rate that the transmission channel can achieve, and is formally defined as

$$C_S={\left[C_D-C_E\right]}^{+}={\left[{\displaystyle \frac{1}{2}}{\log }_2\left(1+{\gamma }_D\right)-{\displaystyle \frac{1}{2}}{\log }_2\left(1+{\gamma }_E\right)\right]}^{+}$$

(18)

where $C_D$ and $C_E$ are the instantaneous capacities of the legitimate link and the eavesdropping link, respectively, and ${\left[x\right]}^{+}\triangleq \mathrm{m}\mathrm{a}\mathrm{x}\left(x,0\right)$, the system secrecy capacity C_S is non–negative.

3.

AF Relaying

The instantaneous secrecy capacity of the ground user U_k can be expressed as

$$\begin{array}{rr}{C}_{U_k}^{AF}& ={\displaystyle \frac{1}{2}}{\log }_2\left({\displaystyle \frac{1+{\gamma }_{U_k}}{1+{\gamma }_{E,x_k}}}\right)\end{array}$$

(19)

4.

DF Relaying

For DF relaying systems, the end-to-end capacity of U_k is determined as the minimum of the S-R link and the R-U link capacities, represented by

$$\begin{array}{ll}{C}_{U_k}& =\mathrm{m}\mathrm{i}\mathrm{n}\left\{C_{R,x_k }, C_{U_k,x_k}\right\}\\ & =\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\displaystyle \frac{1}{2}}{\log }_2\left(1+{\gamma }_{R,x_k}\right), {\displaystyle \frac{1}{2}}{\log }_2\left(1+{\gamma }_{U_k,x_k}\right)\right\}\end{array}$$

(20)

And the channel capacity for E to detect $x_k$ is $C_{E,x_k}={\displaystyle \frac{1}{2}}{\mathrm{l}\mathrm{o}\mathrm{g}}_2\left(1+{\gamma }_{E,x_k}\right)$. Therefore, the instantaneous SC of each other can be written as

$$\begin{array}{ll}{C}_{U_k}^{DF}& ={\left[C_{U_k}-C_{E,x_k}\right]}^{+}\\ & ={\left[\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\displaystyle \frac{1}{2}}{\log }_2\left(1+{\gamma }_{R,x_k}\right),{\displaystyle \frac{1}{2}}{\log }_2\left({\displaystyle \frac{1+{\gamma }_{U_k,x_k}}{1+{\gamma }_{E,x_k}}}\right)\right\}\right]}^{+}\end{array}$$

(21)

3.2. Security Outage Probability

The SOP is a key metric for evaluating the security performance of communication systems and is widely used in the field of wireless communications. The security outage occurs when the system’s secrecy capacity drops below a predefined target secrecy rate Rs.

5.

AF Relaying

In NOMA networks, Secrecy outage occurs once the secrecy capacity of either $C_{U_1}$ or $C_{U_2}$ is under its target threshold $C_{th}$. Therefore, the SOP of the system is

$$\begin{array}{ll}{P}_{SOP}^{AF}& =\mathrm{P}\mathrm{r}\left[C_{U_1}^{AF}<C_{th1}\right]+\mathrm{P}\mathrm{r}\left[C_{U_2}^{AF}<C_{th2}\right]\\ & =1-\mathrm{P}\mathrm{r}\left({\displaystyle \frac{1+{\gamma }_{U_1,x_1}}{1+{\gamma }_{E,x_1}}}\ge {\psi }_1\right)\mathrm{P}\mathrm{r}\left({\displaystyle \frac{1+{\gamma }_{U_2,x_2}}{1+{\gamma }_{E,x_2}}}\ge {\psi }_2\right)\end{array}$$

(22)

where ${\psi }_1=2^{2C_{th1}}$ and ${\psi }_2=2^{2C_{th2}}$. Owing to the correlation among ${\gamma }_{U_1,x_1}$, ${\gamma }_{E,x_1}$, ${\gamma }_{U_{2,x_2}}$ and ${\gamma }_{E,x_2}$, an exact closed-form solution for Equation (22) remains analytically intractable. Therefore, in the high-SNR regimes, using the tight approximation ${\displaystyle \frac{1+x}{1+y}}\approx {\displaystyle \frac{x}{y}}$ (Ref. [33], 37 (12)), Equation (22) can be further approximated as

$$\begin{array}{rr}{P}_{SOP}^{AF}& \approx 1-\left[\underset{P_1}{\underbrace{\mathrm{P}\mathrm{r}\left({\displaystyle \frac{{\gamma }_{SR}{\gamma }_{R{U}_2}}{{\gamma }_{SR}+{\gamma }_{R{U}_2}}}>{\psi }_2{\displaystyle \frac{{\gamma }_{SR}{\gamma }_{RE}}{{\gamma }_{SR}+{\gamma }_{RE}}}\right)}}-\underset{P_2}{\underbrace{\mathrm{P}\mathrm{r}\left({\displaystyle \frac{{\gamma }_{SR}{\gamma }_{R{U}_2}}{{\gamma }_{SR}+{\gamma }_{R{U}_2}}}>{\psi }_2{\displaystyle \frac{{\gamma }_{SR}{\gamma }_{RE}}{{\gamma }_{SR}+{\gamma }_{RE}}},{\displaystyle \frac{{\gamma }_{SR}{\gamma }_{RE}}{{\gamma }_{SR}+{\gamma }_{RE}}}>{\eta }_1\right)}}\right]\end{array}$$

(23)

where ${\eta }_1=1/\left(a_2^2{\psi }_1\right)$. Making use of the inequality ${\displaystyle \frac{xy}{x+y}}\le \mathrm{m}\mathrm{i}\mathrm{n}\left(x,y\right)$, which is adopted in many papers, e.g., (Ref. [34], Equation (15)), (Ref. [35], Equation (6)), $P_1$ and $P_2$ can be further approximated as

$$P_1=\mathrm{P}\mathrm{r}\left(\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\gamma }_{SR},{\gamma }_{R{U}_2}\right\}>{\psi }_2\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\gamma }_{SR},{\gamma }_{RE}\right\}\right)$$

(24)

and

$$P_2=\mathrm{P}\mathrm{r}\left(\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\gamma }_{SR},{\gamma }_{R{U}_2}\right\}>{\psi }_2\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\gamma }_{SR},{\gamma }_{RE}\right\},\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\gamma }_{SR},{\gamma }_{RE}\right\}>{\eta }_1\right)$$

(25)

Note that ${\gamma }_{SR}<{\psi }_2{\gamma }_{SR}$ always holds as ${\psi }_2>1,{\gamma }_{SR}>0$. Hence, we can rewrite $\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\gamma }_{SR},{\gamma }_{R{U}_2}\right\}>{\psi }_2\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\gamma }_{SR},{\gamma }_{RE}\right\}$ as $\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\gamma }_{SR},{\gamma }_{R{U}_2}\right\}>{\psi }_2{\gamma }_{RE}$. Thus, we have

$$\begin{array}{ll}{P}_1& \approx \mathrm{P}\mathrm{r}\left(\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\gamma }_{SR},{\gamma }_{R{U}_2}\right\}>{\psi }_2{\gamma }_{RE}\right)\\ & ={\int }_0^{\infty }\left(1-F_{{\gamma }_{SR}}\left({\psi }_{2}x\right)\right)\left(1-F_{{\gamma }_{R{U}_2}}\left({\psi }_{2}x\right)\right)f_{{\gamma }_{RE}}\left(x\right)dx\end{array}$$

(26)

and

$$\begin{array}{ll}{P}_2& \approx \mathrm{P}\mathrm{r}\left(\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\gamma }_{SR},{\gamma }_{R{U}_2}\right\}>{\psi }_2{\gamma }_{RE}+{\eta }_2,{\gamma }_{SR}>{\eta }_1,{\gamma }_{RE}>{\eta }_1\right)\\ & ={\int }_{{\eta }_1}^{\infty }\left(1-F_{{\gamma }_{SR}}\left({\psi }_{2}x\right)\right)\left(1-F_{{\gamma }_{R{U}_2}}\left({\psi }_{2}x\right)\right)f_{{\gamma }_{RE}}\left(x\right)dx\end{array}$$

(27)

Furthermore, substituting (26) and (27) into (23), the SOP for the proposed system under AF relaying is mathematically deduced as

$$\begin{array}{ll}{P}_{SOP}^{AF}& =1-{\int }_0^{{\eta }_1} \left[1-F_{{\gamma }_{SR}}\left({\psi }_{2}x\right)\right]\left[1-F_{{\gamma }_{R{U}_2}}\left({\psi }_{2}x\right)\right]f_{{\gamma }_{RE}}\left(x\right)dx\\ & =1-{\left({\Omega }_{RE}\right)}^{m_{RE}}{\displaystyle \frac{e^{-{\Omega }_{R{U}_2}}}{\mathsf{\Gamma }\left(m_{RE}\right)}}{\displaystyle \sum _{l=0}^{m_{R{U}_2}-1}} {\displaystyle \frac{{\left({\Omega }_{R{U}_2}\right)}^l}{l!}}{\int }_0^{{\eta }_1} {\left({\psi }_{2}x\right)}^l{x}^{m_{RE}-1}{e}^{-\left({\Omega }_{RE}+{\psi }_2{\Omega }_{R{U}_2}\right)x}\\ & \times \left[1-{\displaystyle \frac{{\xi }^2{r}^{\alpha +\beta -2}}{{\left(2\pi \right)}^{r-1}\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\beta \right)}}{G}_{r+\mathrm{1,3}r+1}^{3r,1}\left({\displaystyle \frac{{\left(h\alpha \beta \right)}^r}{{\mu }_r{r}^{2r}}}\left({\psi }_{2}x\right)|\begin{array}{c}1,E_1\\ E_2,0\end{array}\right)\right]dx\end{array}$$

(28)

The Gauss-Chebyshev quadrature provides an efficient numerical integration method for functions with singularities at the interval endpoints (Ref. [34], Equation (34)). Then, (28) can be approximated as

$$\begin{array}{ll}& P_{SOP}^{AF}=1-{\displaystyle \frac{{\eta }_1\pi e^{-{\Omega }_{R{U}_2}}}{2N\mathsf{\Gamma }\left(m_{RE}\right)}}{\Omega }_{RE}^{m_{RE}}{\displaystyle \sum _{l=0}^{m_{R{U}_2}-1}} {\displaystyle \sum _{k=1}^N}{\displaystyle \frac{{\left({\Omega }_{R{U}_2}\right)}^l}{l!}}\sqrt{1-{\varphi }_n^2}{\omega }_n^{m_{RE}-1}{e}^{-\left({\Omega }_{RE}+{\psi }_2{\Omega }_{R{U}_2}\right){\omega }_n}\\ & \times {\left({\psi }_2{\omega }_n\right)}^l\left[1-{\displaystyle \frac{{\xi }^2{r}^{\alpha +\beta -2}}{{\left(2\pi \right)}^{r-1}\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\beta \right)}}{G}_{r+\mathrm{1,3}r+1}^{3r,1}\left({\displaystyle \frac{{\left(h\alpha \beta \right)}^r}{{\mu }_r{r}^{2r}}}\left({\psi }_2{\omega }_n\right)|\begin{array}{c}1,E_1\\ E_2,0\end{array}\right)\right]\end{array}$$

(29)

where ${\varphi }_n=\cos \left(\left(2N-1\right)/2N\right)$, ${\omega }_n={\eta }_1\left({\varphi }_n+1\right)/2$.

6.

DF Relaying

The SOP for the DF protocol is given as

$$\begin{array}{ll}{P}_{SOP}^{DF}& =\mathrm{P}\mathrm{r}\left[\left(C_{U_1}^{DF}\le C_{th1}\right)\cup \left( C_{U_2}^{DF}\le C_{th2}\right)\right]\\ & =1-\mathrm{P}\mathrm{r}\left(C_{U_1}^{DF}>C_{th1}\right)\mathrm{P}\mathrm{r}\left( C_{U_2}^{DF}>C_{th2}\right)\end{array}$$

(30)

Substituting (21) into (30), it has

$$\begin{array}{ll}{P}_{SOP}^{DF}& =1-\mathrm{P}\mathrm{r}\left(\mathrm{m}\mathrm{i}\mathrm{n}\left\{1+{\gamma }_{R,x_1},{\displaystyle \frac{1+{\gamma }_{U_1,x_1}}{1+{\gamma }_{E,x_1}}}\right\}>{\psi }_1,\mathrm{m}\mathrm{i}\mathrm{n}\left\{1+{\gamma }_{R,x_2},{\displaystyle \frac{1+{\gamma }_{U_2,x_2}}{1+{\gamma }_{E,x_2}}}\right\}>{\psi }_2\right)\\ & =1-\underset{P_3}{\underbrace{\mathrm{P}\mathrm{r}\left({\gamma }_{R,x_1}>{\psi }_1-1,{\gamma }_{R,x_2}>{\psi }_2-1\right)}}\underset{P_4}{\underbrace{\mathrm{P}\mathrm{r}\left({\displaystyle \frac{1+{\gamma }_{U_1,x_1}}{1+{\gamma }_{E,x_1}}}>{\psi }_1,{\displaystyle \frac{1+{\gamma }_{U_2,x_2}}{1+{\gamma }_{E,x_2}}}>{\psi }_2\right)}}\end{array}$$

(31)

Owing to the complexity of statistical analysis, deriving an exact closed-form expression for the aforementioned SOP proves challenging. Thus, in high-SNR regimes, an approximate method should be adopted, namely

$$\begin{array}{ll}{P}_3& \approx \mathrm{P}\mathrm{r}\left({\gamma }_{SR}>\mathrm{m}\mathrm{a}\mathrm{x}\left\{{\eta }_2,{\eta }_3\right\}\right)\\ & =1-{\displaystyle \frac{{\xi }^2{r}^{\alpha +\beta -2}}{{\left(2\pi \right)}^{r-1}\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\beta \right)}}{G}_{r+\mathrm{1,3}r+1}^{3r,1}\left[\left.{\displaystyle \frac{{\left(h\alpha \beta \right)}^r}{r^{2r}{\mu }_r}}\mathrm{m}\mathrm{a}\mathrm{x}\left\{{\eta }_2,{\eta }_3\right\}\right|\begin{array}{cc}1& E_1\\ E_2& 0\end{array}\right]\end{array}$$

(32)

where we have used ${\displaystyle \frac{xy}{x+y}}\le \mathrm{m}\mathrm{i}\mathrm{n}\left(x,y\right)$(Ref. [34], Equation (15)), (Ref. [35], Equation (6)), ${\eta }_2=\left({\psi }_1-1\right)/\left({1-a}_2^2{\psi }_1\right)$, ${\eta }_3=\left({\psi }_2-1\right)/a_2^2$. And $P_3$ in (31) can be approximated as

$$\begin{array}{ll}{P}_4& \approx \mathrm{P}\mathrm{r}\left({\displaystyle \frac{{\gamma }_{U_1,x_1}}{{\gamma }_{E,x_1}}}>{\psi }_1, {\displaystyle \frac{{\gamma }_{U_2,x_2}}{{\gamma }_{E,x_2}}}>{\psi }_2\right)\\ & ={\displaystyle \frac{{{\Omega }_{RE}^{m_{RE}}\gamma }^{m_{RE}-1}}{\mathsf{\Gamma }\left(m_{RE}\right)}}{\displaystyle \sum _{l=0}^{m_{R{U}_2}-1}} {\displaystyle \frac{{\left({\Omega }_{R{U}_2}\right)}^l}{l!}}{\int }_0^{{\eta }_1} {\left({\psi }_{2}x\right)}^l e^{-\left({\Omega }_{RE}+{\psi }_2{\Omega }_{R{U}_2}\right)x}dx\end{array}$$

(33)

Thus, the integral can be solved using Gaussian-Chebyshev quadrature formula (Ref. [29], Equation (3.351.18)), as follows

$$\begin{array}{cc}& P_4={\displaystyle \frac{{{\Omega }_{RE}^{m_{RE}}\gamma }^{m_{RE}-1}}{\mathsf{\Gamma }\left(m_{RE}\right)}}{\displaystyle \sum _{l=0}^{m_{R{U}_2}-1}} {\displaystyle \sum _{v=0}^l}\left({\displaystyle \genfrac{}{}{0pt}{}{l}{v}}\right){\displaystyle \frac{{\left({\Omega }_{R{U}_2}\right)}^l}{l!}}{\left({\displaystyle \frac{{\psi }_2}{{\Omega }_{RE}+{\psi }_2{\Omega }_{R{U}_2}}}\right)}^v\left(v-1\right)!\\ & \times \left(1-e^{{\eta }_1\left({\Omega }_{RE}+{\psi }_2{\Omega }_{R{U}_2}\right)}{\displaystyle \sum _{p=0}^{v-1}}{\displaystyle \frac{{\left({\eta }_1\right)}^l}{p!{\left({\Omega }_{RE}+{\psi }_2{\Omega }_{R{U}_2}\right)}^{-p}}}\right)\end{array}$$

(34)

Finally, Substituting (32) and (34) into Equation (31) as

$$\begin{array}{ll}{P}_{SOP}^{DF}& =1-{\displaystyle \frac{{{\Omega }_{RE}^{m_{RE}}\gamma }^{m_{RE}-1}}{\mathsf{\Gamma }\left(m_{RE}\right)}}{\displaystyle \sum _{l=0}^{m_{R{U}_2}-1}} {\displaystyle \sum _{v=0}^l}\left({\displaystyle \genfrac{}{}{0pt}{}{l}{v}}\right){\displaystyle \frac{{\left({\Omega }_{R{U}_2}\right)}^l}{l!}}{\left({\displaystyle \frac{{\psi }_2}{{\Omega }_{RE}+{\psi }_2{\Omega }_{R{U}_2}}}\right)}^v\left(v-1\right)!\\ & \times \left[1-{\displaystyle \frac{{\xi }^2{r}^{\alpha +\beta -2}}{{\left(2\pi \right)}^{r-1}\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }\left(\beta \right)}}{G}_{r+\mathrm{1,3}r+1}^{3r,1}\left({\displaystyle \frac{{\left(h\alpha \beta \right)}^r}{{\mu }_r{r}^{2r}}}\mathrm{m}\mathrm{a}\mathrm{x}\left\{{\eta }_2,{\eta }_3\right\}|\begin{array}{c}1,E_1\\ E_2,0\end{array}\right)\right]\\ & \times \left(1-e^{{\eta }_1\left({\Omega }_{RE}+{\psi }_2{\Omega }_{R{U}_2}\right)}{\displaystyle \sum _{p=0}^{v-1}}{\displaystyle \frac{{\left({\eta }_1\right)}^l}{p!{\left({\Omega }_{RE}+{\psi }_2{\Omega }_{R{U}_2}\right)}^{-p}}}\right)\end{array}$$

(35)

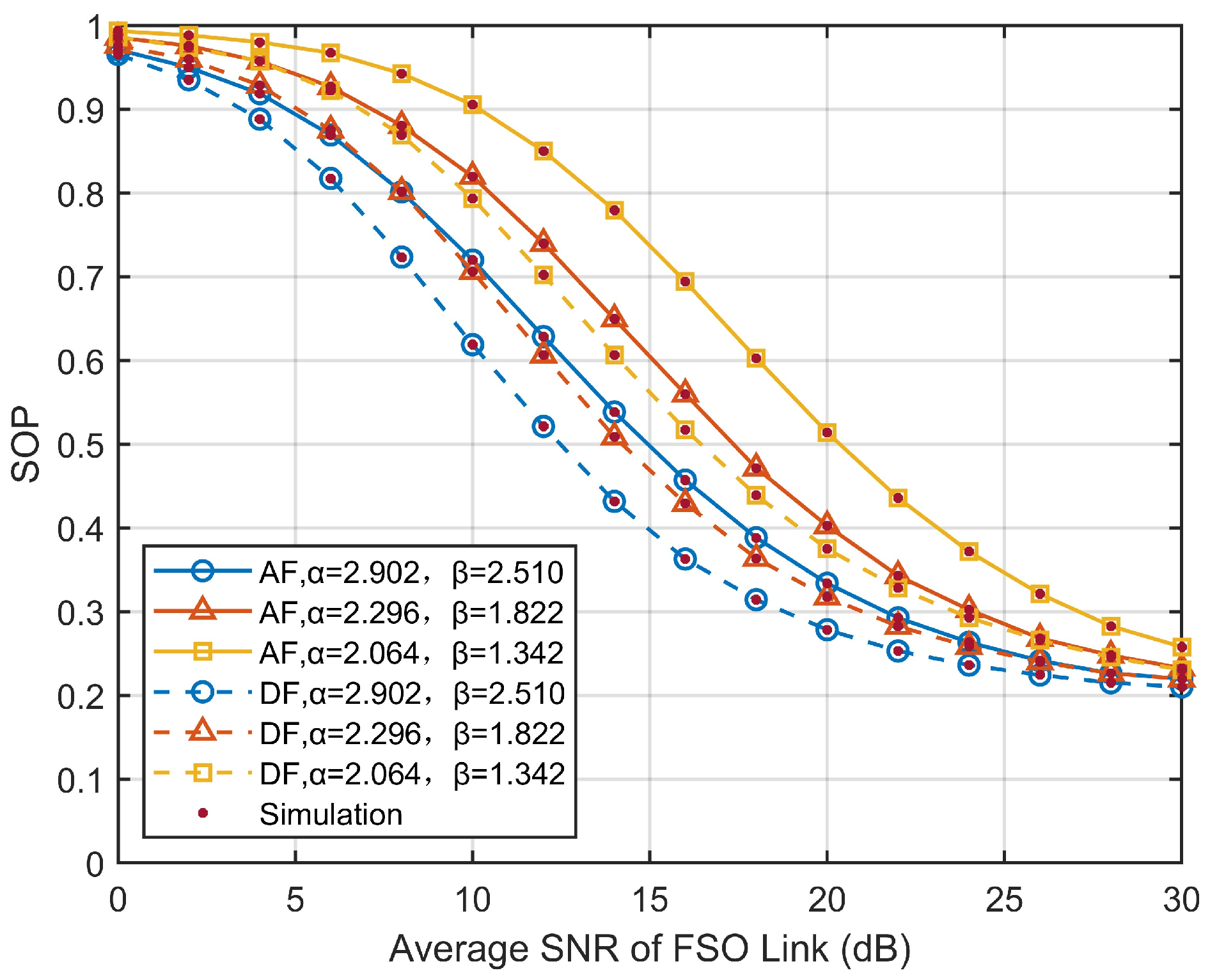
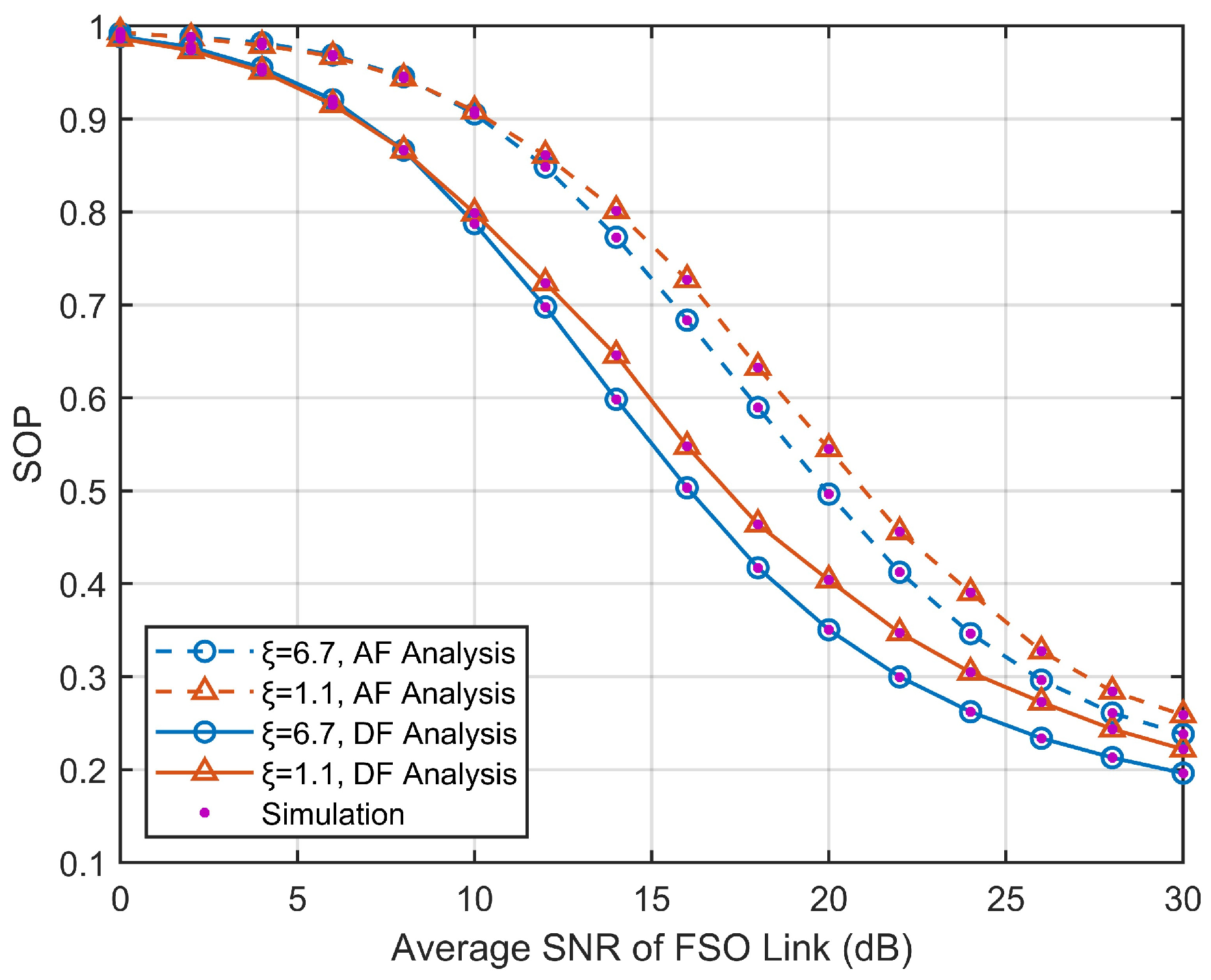
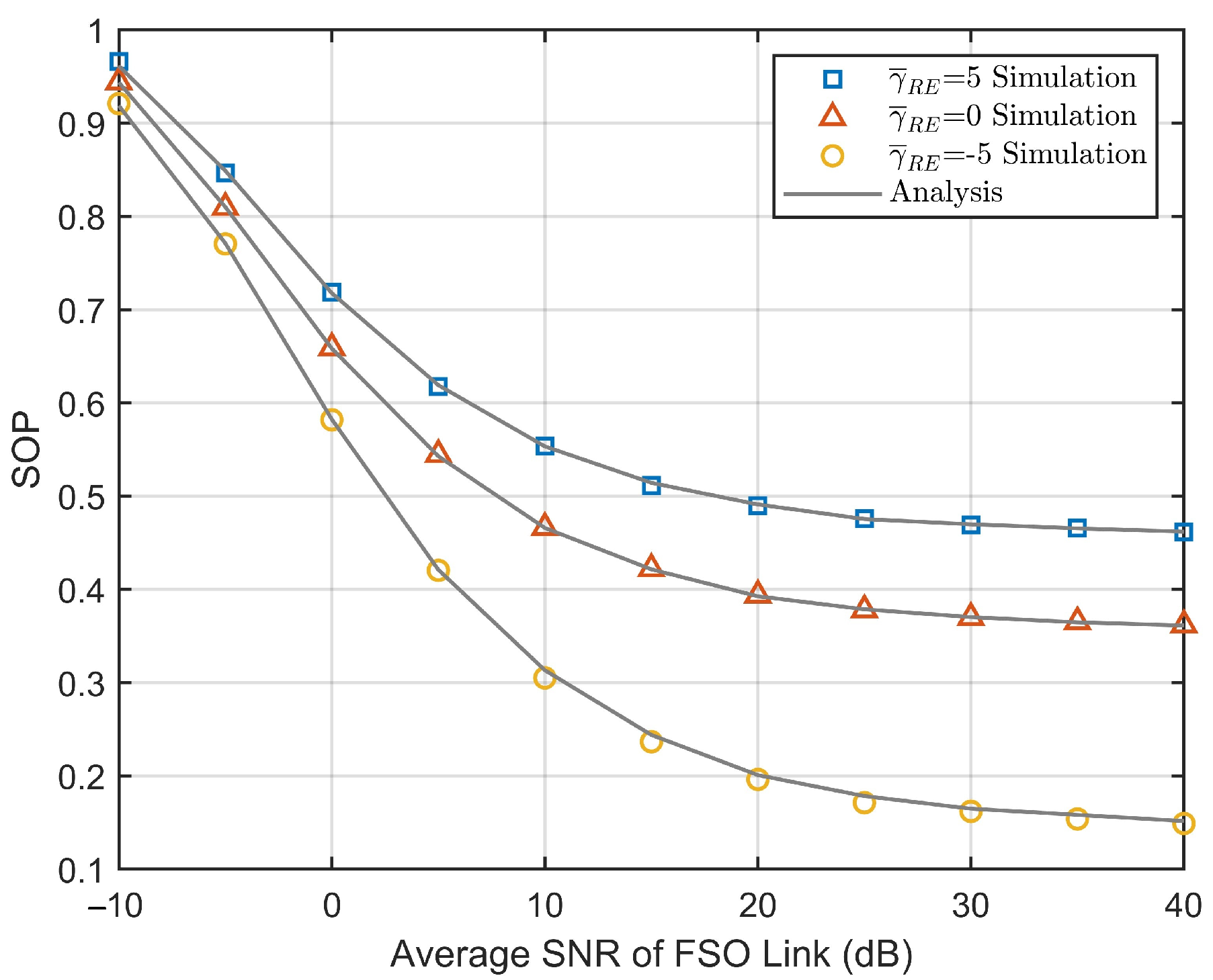
4. Numerical Results and Discussion

This section presents numerical results to validate the impact of key system parameters on the PLS performance of the proposed system. Specifically, the relevant theoretical analysis is validated through Monte Carlo simulations. The relevant system parameters are listed in

Table 2. List of system parameters.

Parameter	Symbol	Value
Altitude of satellite	$H_S$	600 km
Altitude of UAV	$H_R$	20 km
Altitude of ground user	$H_U$	5 m
Wavelength	$\lambda$	1550 nm
Conversion coefficients	${\eta }_S, {\eta }_R$	0.85
Pointing error coefficient	${\xi }_1, {\xi }_2$	1.1, 6.7
Diameter of aperture at receiver	$D$	1 m

. The FSO link model corresponding to weak, moderate, and strong turbulence parameters [36,37,38] in

Table 3. Atmospheric turbulence conditions.

Atmospheric Turbulence	Parameter Values
Weak turbulence	$\alpha =2.902,\beta =2.510$
Moderate turbulence	$\alpha =2.296,\beta =1.822$
Strong turbulence	$\alpha =2.064,\beta =1.342$

. All results are derived through 1 × 10⁶ Monte Carlo simulations. Despite approximations necessitated by mathematical complexity during analytical derivation, the strong agreement between simulation and theoretical results verifies that the introduced errors are negligible. Furthermore, path loss, atmospheric turbulence, and pointing errors are accounted for in the analysis. Besides, the parameters for R-U RF link are considered as $m_1=5,b_1=0.251,{\Omega }_1=0.279$ under moderate shadowing scenarios [39].

This study is based on the assumption of quasi-static channels, where turbulence correlation remains stable over the symbol duration. While time-varying turbulence effects are of practical significance, their analytical incorporation remains a research challenge that necessitates fundamental advancements in channel modeling.

Figure 2 plots the system SOP curves for the two relaying protocols versus different values of ${\overline{\gamma }}_{SR}$, under three turbulence conditions. The simulation parameters are set as follows: $\xi =6.7$, ${\overline{\gamma }}_{R{U}_1}=15 \mathrm{d}\mathrm{B}$, ${\overline{\gamma }}_{R{U}_2}=20 \mathrm{d}\mathrm{B}$, ${\overline{\gamma }}_{RE}=-5 \mathrm{d}\mathrm{B}$, $C_{th1}=0.1 \mathrm{b}\mathrm{i}\mathrm{t}/\mathrm{s}/\mathrm{H}\mathrm{z}$, and $C_{th2}=0.4 \mathrm{b}\mathrm{i}\mathrm{t}/\mathrm{s}/\mathrm{H}\mathrm{z}$. We can clearly observe that secrecy performance decreases as ${\overline{\gamma }}_{SR}$ increases, and the mixed system employing the DF relay protocol generally demonstrates superior secrecy performance compared to that using the AF one. However, the trends of performance degradation slow down at higher values of ${\overline{\gamma }}_{SR}$. Additionally, the system SOP is almost the same for two relaying protocols, because the impact of noise on SOP at high SNR can be ignored. And the SOP values exhibit a decreasing trend with increasing $\left(\alpha ,\beta \right)$ values, which is attributed to the improved secrecy performance under weaker turbulence conditions.

Figure 3 illustrates the SOP for AF and DF relaying versus ${\overline{\gamma }}_{SR}$ under different pointing error values Herein, the system is assumed to adopt HD technology (r = 1). The parameters are set as (α, β) = (2.296, 1.822), ξ = 6.7, r = 2, $C_{th1}=0.1 \mathrm{b}\mathrm{i}\mathrm{t}/\mathrm{s}/\mathrm{H}\mathrm{z}$, and $C_{th2}=0.4 \mathrm{b}\mathrm{i}\mathrm{t}/\mathrm{s}/\mathrm{H}\mathrm{z}$. It can be observed that, as the average SNR ${\overline{\gamma }}_{SR}$ increases, the system SOP decreases. The analysis further demonstrates that system SOP with HD technique is superior to that the IM/DD one. Under the condition of unchanged parameters, the secrecy performance improves significantly when the pointing error parameter decreases from ξ = 1.1 (strong pointing error) to ξ = 6.7 (weak pointing error).

Figure 4 plots the SOP versus ${\overline{\gamma }}_{SR}$ with the different values of ${\overline{\gamma }}_{RE}$, with parameters set as $\left(\alpha , \beta \right)=(2.296,1.822)$, $\xi =6.7$, $\mathrm{r}=2$, $C_{th1}=0.1 \mathrm{b}\mathrm{i}\mathrm{t}/\mathrm{s}/\mathrm{H}\mathrm{z}$, and $C_{th1}=0.4 \mathrm{b}\mathrm{i}\mathrm{t}/\mathrm{s}/\mathrm{H}\mathrm{z}$. It can be clearly observed that high values of ${\overline{\gamma }}_{RE}$ significantly degrade the system secrecy performance. This phenomenon stems from the inherent channel quality advantages of the legitimate links compared to the eavesdropping links. Moreover, in the high-SNR regime, the system SOP remains nearly constant as ${\overline{\gamma }}_{SR}$ increasing, and has little impact on the system’s security performance. This is mainly because the SOP is predominantly determined by the S-R FSO link.

Figure 5 depicts the system SOP versus $a_1$ for both AF and DF relaying techniques, with parameters set as $\left(\alpha , \beta \right)=(2.296,1.822)$, $\xi =6.7$, $\mathrm{r}=2$, $C_{th1}=0.2 \mathrm{b}\mathrm{i}\mathrm{t}/\mathrm{s}/\mathrm{H}\mathrm{z}$, and $C_{th1}=0.4 \mathrm{b}\mathrm{i}\mathrm{t}/\mathrm{s}/\mathrm{H}\mathrm{z}$. It can be clearly seen that system SOP first decreases and then increases as a function of increasing $a_1$ values. Since an optimal power allocation coefficient exists in NOMA networks, the system can reach the best PLS performance. Furthermore, we can also find that the system employing HD ($r=1$) technique can achieve better security performance compared with the IM/DD ($r=2$) one.

As can be observed from the figures, the analytical results exhibit a strong consistency with the corresponding simulation outcomes, thereby validating the accuracy of the proposed analytical expressions.

5. Conclusions

In this article, we propose a novel secure transmission scheme for the SAGIN downlinks. Additionally, a comprehensive analysis is conducted on the security performance of the proposed NOMA-based mixed FSO-RF communication system. Assuming an eavesdropper attacks the RF link, we have derived the closed-form expression for the SOP. Furthermore, considering the effects of atmospheric turbulence and pointing errors, extensive experiments were conducted to validate the advantages of the proposed system and the accuracy of the derived SOP analytical expression. We also compare the influence of two different relaying schemes on the secure transmission performance within SAGIN. The results demonstrate that the DF relaying exhibits superior SOP performance compared to the AF relaying, while also achieving enhanced security performance through the improvement of legitimate link channel conditions. To further enhance the security and capacity of the mixed SAGIN, future research will extend to multi-antenna and massive connectivity scenarios and incorporate MIMO techniques.