Time-Averaged Energy Flow and Momentum of Electromagnetic Waves in Homogeneous Isotropic Linear Media

Abstract

There exist multiple different even non-equivalent expressions describing characteristics of electromagnetic wave energy flow and momentum in media, which makes the issue confusing. For simplicity (without loss of generality), we shall consider a case where a harmonic homogeneous plane wave (HHPW) travels in a homogeneous isotropic linear medium (HILM); thus, both time-dependent Poynting’s vector $\stackrel{⃑}{S}\left(t\right)$ and time-dependent momentum density $\stackrel{⃑}{G}\left(t\right)$ are rigorously derived from continuity equations. Then, referring to recent studies of stored and dissipated energies of electromagnetic waves in lossy media, time-averaged Poynting’s vector <$\stackrel{⃑}{S}$> and time-averaged momentum density <$\stackrel{⃑}{G}$> are obtained according to the time dependence of the terms arising in the expressions of $\stackrel{⃑}{S}\left(t\right)$ and $\stackrel{⃑}{G}\left(t\right)$, respectively. On this basis, a new way is proposed to determine the direction relation between <$\stackrel{⃑}{S}$> and <$\stackrel{⃑}{G}$> of HHPWs in an HILM, and it is demonstrated that, in an HILM, the propagation direction of <$\stackrel{⃑}{S}$> is always consistent with that of <$\stackrel{⃑}{G}$>, which may be applied to explain why the predicted reversal of electromagnetic wave momentum in a left-handed material has not been observed up to now. This work may be helpful to further discuss, and even eliminate, the confusion arising in related issues, and deepen the understanding of the energy flow and momentum of electromagnetic waves in media.

1. Introduction

Electromagnetic wave energy, energy flow, momentum, and their characteristics are important contents of both electromagnetic field theory and electrodynamics, which have been investigated extensively and applied widely [1,2,3,4,5]. However, it is known that there exist multiple different even non-equivalent expressions describing the characteristics of energy, energy flow, and momentum of an electromagnetic wave traveling in a medium, which makes the related issues confusing [6,7,8,9,10,11,12,13,14,15,16,17]. As a typical instance, the Abraham–Minkowski controversy (A-MC) has not been fully resolved yet, which has lasted for more than 100 years [6,7].

In the 1960s, Veselago predicted the existence of left-handed materials (LHMs) and proposed a lot of novel phenomena associated with LHMs, such as negative refraction, reversal of the Cerenkov effect, and reversal of the Doppler effect [18], which have been verified experimentally [19,20,21] and provided opportunities to further study both electromagnetic theory and electromagnetic phenomena [22,23,24,25,26,27,28,29,30,31,32]. Typically, mainly due to unreasonable predictions of negative stored energy for an electromagnetic wave traveling in an LHM [22], how to correctly describe stored and dissipated energies of electromagnetic waves in lossy media has been re-investigated [22,23,24,25,26]. It has been demonstrated that, to properly describe stored and dissipated energy, it is important to reasonably divide the total energy into a stored part and a dissipated one [23,24,25,26]. Noting that different expressions of electromagnetic wave momentum are usually related to the diversion of total momentum into an electromagnetic part and a material one [6,7,8,9,10,11,12,13,14,15,16,17,27,28], it is clear that recent studies of stored and dissipated energies of electromagnetic waves in lossy media may provide useful references to further study the momentum of electromagnetic waves in media. On the other hand, it is noted that the predicted reversal of electromagnetic wave momentum, i.e., time-averaged momentum density (TAMD) anti-parallel to the time-averaged Poynting’s vector (TAPV) of an electromagnetic wave in an LHM [18], has not been observed experimentally up to now, and thus becomes an interesting topic [27,28].

In this work, we shall attempt to propose a rigorous way to address the energy, energy flow, and momentum of electromagnetic waves in media. For simplicity, we shall consider a case of a harmonic homogeneous plane wave (HHPW) traveling in a homogeneous isotropic linear medium (HILM), and rigorously derive expressions of energy flow density, momentum density, and the time-averaged values of TAPV $<\stackrel{⃑}{S}>$ and TAMD $<\stackrel{⃑}{G}$>. It is well known that, in anisotropic media, direction of energy flow is usually non-consistent with that of momentum. However, it is not easy to strictly determine direction relation between energy flow and momentum of an electromagnetic wave in the (lossy) anisotropic media. In addition, the complex induced by anisotropy may hinder to deepen the understanding of direction relation between energy flow and momentum of an electromagnetic wave traveling in a left-handed material, which has not been fully understood yet. Therefore, we shall pay our attention on direction relation between energy flow and momentum of an electromagnetic wave in the isotropic media Upon this basis, the inner product of $<\stackrel{⃑}{S}>·Re(\widetilde{\stackrel{⃑}{k}})$($\tilde{k}$ is the complex wave number) is adopted to determine the direction relationship between $<\stackrel{⃑}{S}>$ and $Re(\widetilde{\stackrel{⃑}{k}})$ [33,34]; similarly, $<\stackrel{⃑}{G}>·Re(\widetilde{\stackrel{⃑}{k}})$ is obtained to determine the direction relationship between $<\stackrel{⃑}{G}$> and $Re(\widetilde{\stackrel{⃑}{k}})$; thus, a new way to determine the direction relation between $<\stackrel{⃑}{S}>$ and $<\stackrel{⃑}{G}$> in HILMs is proposed. The remainder of this paper is organized as follows: In Section 2, expressions of energy flow density, momentum density, and the time-averaged values of an HHPW in an HILM are derived rigorously. In Section 3, the propagation direction relation between the time-averaged energy flow and time-averaged momentum of electromagnetic waves in HILMs is addressed. In Section 4, several discussions are presented. Finally, some conclusions are drawn in Section 5.

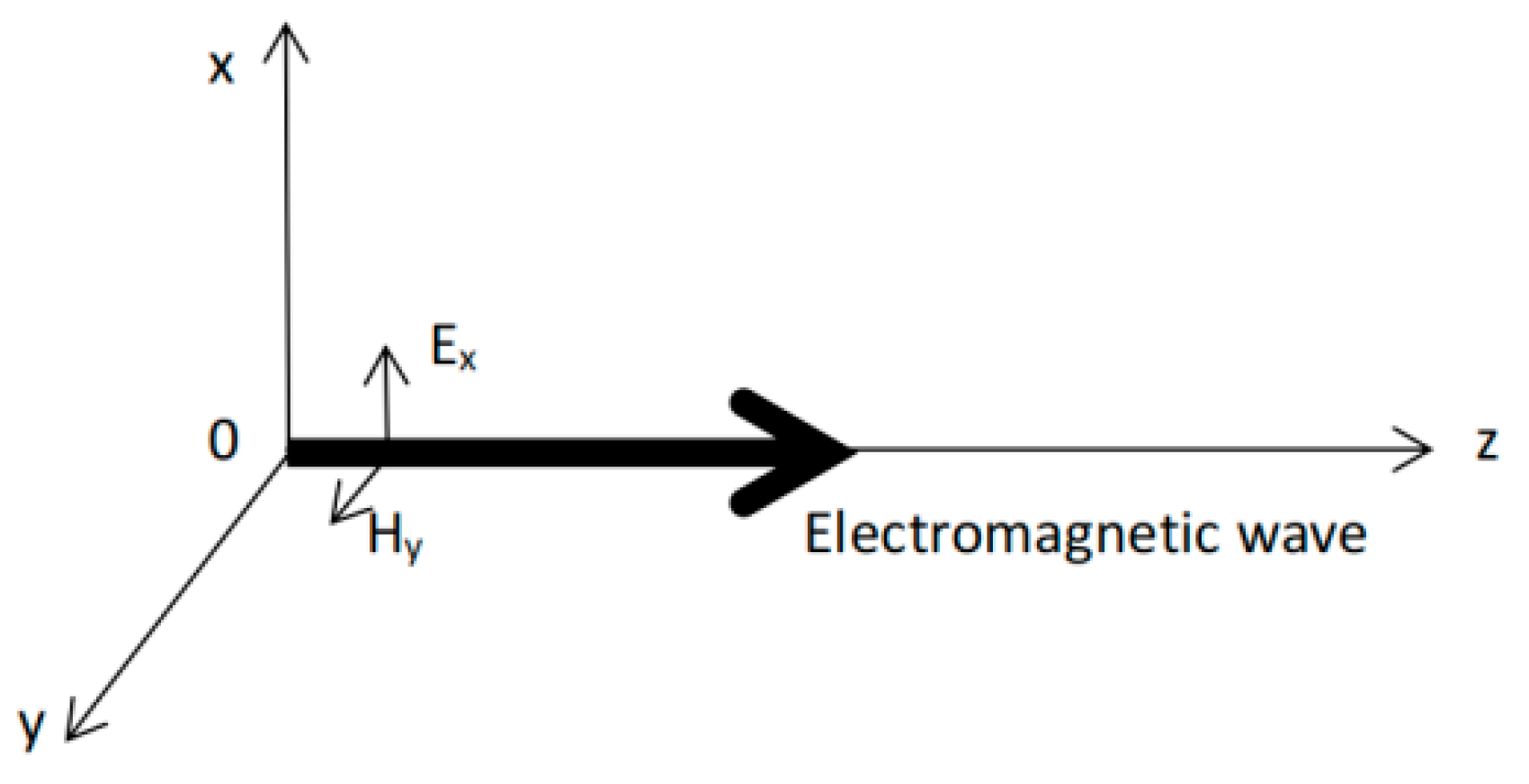
2. Energy Flow and Momentum for an HHPW Traveling in an HILM

Generally, Poynting’s theorem may be derived from the time rate of work done by Lorentz force density $\stackrel{\rightharpoonup }{f}$ as [3]

$$\stackrel{\rightharpoonup }{f}\cdot \stackrel{\rightharpoonup }{v}=\rho (\stackrel{\rightharpoonup }{E}+\stackrel{\rightharpoonup }{v}\times \stackrel{\rightharpoonup }{B})\cdot \stackrel{\rightharpoonup }{v}=\stackrel{\rightharpoonup }{J}\cdot \stackrel{\rightharpoonup }{E}=-\nabla \cdot (\stackrel{\rightharpoonup }{E}\times \stackrel{\rightharpoonup }{H})-(\stackrel{\rightharpoonup }{E}\cdot {\displaystyle \frac{\partial \stackrel{\rightharpoonup }{D}}{\partial t}}+\stackrel{\rightharpoonup }{H}\cdot {\displaystyle \frac{\partial \stackrel{\rightharpoonup }{B}}{\partial t}}).$$

(1)

where $\rho$ is the charge density, $\stackrel{\rightharpoonup }{v}$ is the speed of the charge, and $\stackrel{\rightharpoonup }{J}$, $\stackrel{\rightharpoonup }{E}$, $\stackrel{\rightharpoonup }{B}$, $\stackrel{\rightharpoonup }{H}$ and $\stackrel{\rightharpoonup }{D}$ are the electric current density, electric field intensity, magnetic flux density, magnetic field intensity, and electric flux density, respectively. For simplicity, we assume $\stackrel{\rightharpoonup }{J}\cdot \stackrel{\rightharpoonup }{E}=0$, i.e., energy losses induced by electric current are neglected; thus, there is

$$0=-\nabla \cdot (\stackrel{\rightharpoonup }{E}\times \stackrel{\rightharpoonup }{H})-(\stackrel{\rightharpoonup }{E}\cdot {\displaystyle \frac{\partial \stackrel{\rightharpoonup }{D}}{\partial t}}+\stackrel{\rightharpoonup }{H}\cdot {\displaystyle \frac{\partial \stackrel{\rightharpoonup }{B}}{\partial t}}).$$

(2)

where $\stackrel{\rightharpoonup }{S}\equiv \stackrel{\rightharpoonup }{E}\times \stackrel{\rightharpoonup }{H}$ is the time-dependent Poynting’s vector (TDPV), and $P\equiv -(\stackrel{\rightharpoonup }{E}\cdot {\displaystyle \frac{\partial \stackrel{\rightharpoonup }{D}}{\partial t}}+\stackrel{\rightharpoonup }{H}\cdot {\displaystyle \frac{\partial \stackrel{\rightharpoonup }{B}}{\partial t}})$ can be taken as part of the time rate of work done by Lorentz force density, which relates to stored and dissipated energy density u; thus, we have

$${\displaystyle \frac{\partial u}{\partial t}}=\stackrel{⃑}{E}\cdot {\displaystyle \frac{\partial \stackrel{⃑}{D}}{\partial t}}+\stackrel{⃑}{H}\cdot {\displaystyle \frac{\partial \stackrel{⃑}{B}}{\partial t}}.$$

(3)

On the other hand, based on differential Maxwell’s equations, Lorentz force density may be given as [3]

$$\stackrel{⃑}{f}=(\nabla \cdot \stackrel{⃑}{D})\stackrel{⃑}{E}+(\nabla \times \stackrel{⃑}{H}-{\displaystyle \frac{\partial \stackrel{⃑}{D}}{\partial t}})\times \stackrel{⃑}{B}+(\nabla \cdot \stackrel{⃑}{B})\stackrel{⃑}{H}+(\nabla \times \stackrel{⃑}{E}+{\displaystyle \frac{\partial \stackrel{⃑}{B}}{\partial t}})\times \stackrel{⃑}{D}.$$

(4)

There exist the following relations [3]:

$$\nabla \cdot \left(\stackrel{⃑}{D}\stackrel{⃑}{E}\right)=(\nabla \cdot \stackrel{⃑}{D})\stackrel{⃑}{E}+(\stackrel{⃑}{D}\cdot \nabla )\stackrel{⃑}{E} ,$$

(5)

$$\nabla \cdot \left(\stackrel{⃑}{B}\stackrel{⃑}{H}\right)=(\nabla \cdot \stackrel{⃑}{B})\stackrel{⃑}{H}+(\stackrel{⃑}{B}\cdot \nabla )\stackrel{⃑}{H} ,$$

(6)

$$(\nabla \times \stackrel{⃑}{E})\times \stackrel{⃑}{D}=(\stackrel{⃑}{D}\cdot \nabla )\stackrel{⃑}{E}-{\sum }_{\zeta =x,y,z}{\sum }_{\xi =x,y,z}{\displaystyle \frac{\partial E_{\xi }}{\partial \zeta }}{D}_{\xi }{\widehat{e}}_{\zeta } ,$$

(7)

$$(\nabla \times \stackrel{⃑}{H})\times \stackrel{⃑}{B}=(\stackrel{⃑}{B}\cdot \nabla )\stackrel{⃑}{H}-{\sum }_{\zeta =x,y,z}{\sum }_{\xi =x,y,z}{\displaystyle \frac{\partial H_{\xi }}{\partial \zeta }}{B}_{\xi }{\widehat{e}}_{\zeta .}$$

(8)

where $\xi =x,y,z$, $\zeta =x,y,z$, and ${\widehat{e}}_{\zeta }$ is the unit vector along the direction of $\zeta$. Applying Equations (4)–(8), we have

$$\stackrel{⃑}{f}=-[{\sum }_{\zeta =x,y,z;}{\sum }_{\xi =x,y,z}\left({\displaystyle \frac{\partial E_{\xi }}{\partial \zeta }}{D}_{\xi }+{\displaystyle \frac{\partial H_{\xi }}{\partial \zeta }}{B}_{\xi }\right){\widehat{e}}_{\zeta }-\nabla \cdot (\stackrel{⃑}{D}\stackrel{⃑}{E}+\stackrel{⃑}{B}\stackrel{⃑}{H}\left)\right]-{\displaystyle \frac{\partial }{\partial t}}(\stackrel{⃑}{D}\times \stackrel{⃑}{B})$$

(9)

Usually, Equation (9) is applied to address the momentum properties of electromagnetic waves.

However, it is known that for the where that an electromagnetic wave travels in a medium, both Equations (2) and (9) cannot always be rewritten in the usual standard form of continuous equations [9,10,17,26].

2.1. Rigorous Derivations Based on Continuity Equations

For simplicity, we consider a case where an HHPW travels in an HILM as shown in Figure 1. Noting that an arbitrary electromagnetic wave usually may be composed of HHPWs, this simple example does not lose any generalizability. Choosing time dependence $e^{i\omega t}$, an HILM can be generally represented by a complex scalar permittivity $\tilde{\epsilon }=\left|\tilde{\epsilon }\right|\mathit{exp}(-i{\alpha }_{\epsilon })={\epsilon }^{\prime }-i{\epsilon }^{″}$ and permeability $\tilde{\mu }=\left|\tilde{\mu }\right|\mathit{exp}(-i{\alpha }_{\mu })={\mu }^{\prime }-i{\mu }^{″}$. ${\alpha }_{\epsilon \left(\mu \right)}$ is the electric (magnetic) damping angle (in this paper, complex-valued parameters are marked with ‘‘~’’) [3,4]. The field quantities of electric field intensity $\stackrel{\rightharpoonup }{E}$, electric flux density $\stackrel{\rightharpoonup }{D}$, magnetic field intensity $\stackrel{\rightharpoonup }{H}$, and magnetic flux density $\stackrel{\rightharpoonup }{B}$ of the HHPW can be, respectively, given as follows [4]:

$$\stackrel{⃑}{E}=\mathit{Re}(\widetilde{\stackrel{⃑}{E}})=\mathit{Re}(E_{x0}{e}^{i\omega t-i{k}^{\prime }z-k^{″}z}){\widehat{e}}_x,$$

(10)

$$\stackrel{⃑}{D}=\mathit{Re}(\widetilde{\stackrel{⃑}{D}})=\mathit{Re}\left(\right|\tilde{\epsilon }|E_{x0}{e}^{i\omega t-i{k}^{\prime }z-k^{″}z-i{\alpha }_{\epsilon }}){\widehat{e}}_x,$$

(11)

$$\stackrel{⃑}{H}=\mathit{Re}(\widetilde{\stackrel{⃑}{H}})=\mathit{Re}({\displaystyle \frac{1}{\widetilde{|\eta }|}}{E}_{x0}{e}^{i\omega t-i{k}^{\prime }z-k^{″}z+i{\alpha }_{\eta }}){\widehat{e}}_y,$$

(12)

$$\stackrel{⃑}{B}=\mathit{Re}(\widetilde{\stackrel{⃑}{B}})=\mathit{Re}({\displaystyle \frac{\left|\tilde{\mu }\right|}{|\widetilde{\eta |}}}{E}_{x0}{e}^{i\omega t-i{k}^{\prime }z-k^{″}z+i({\alpha }_{\eta }-{\alpha }_{\mu })}){\widehat{e}}_y,$$

(13)

where $\tilde{k}=k^{\prime }-j{k}^{″}=\omega \sqrt{\left|\tilde{\epsilon }\right|\left|\tilde{\mu }\right|}{e}^{-i{\alpha }_k}$ (${\alpha }_k={\displaystyle \frac{{\alpha }_{\mu }+{\alpha }_{\epsilon }}{2}}$) is the complex wave number, $\tilde{\eta }=\sqrt{\left|\tilde{\mu }\right|/\left|\tilde{\epsilon }\right|}{e}^{-i{\alpha }_{\eta }}$ (${\alpha }_{\eta }={\displaystyle \frac{{\alpha }_{\mu }-{\alpha }_{\epsilon }}{2}}$) is the complex impedance of the medium, and ${\widehat{e}}_{x(y,z)}$ is the unit vector along the x(y,z) direction. On the other hand, we shall point out that, for a general complex parameter $\tilde{A}$, there is

$$\mathit{Re}(\tilde{A})={\displaystyle \frac{1}{2}}(\tilde{A}+{\tilde{A}}^{*}).$$

(14)

It is known from Equations (2) and (3) that, in a lossless HILM, Equation (3) may be rewritten as ${\displaystyle \frac{\partial u}{\partial t}}={\displaystyle \frac{\partial }{\partial t}}(\stackrel{⃑}{E}\cdot \stackrel{⃑}{D}+\stackrel{⃑}{H}\cdot \stackrel{⃑}{B})$; thus, a standard form of a continuous equation is obtained as $\nabla \cdot (\stackrel{⃑}{E}\times \stackrel{⃑}{H})+{\displaystyle \frac{\partial }{\partial t}}(\stackrel{⃑}{E}\cdot \stackrel{⃑}{D}+\stackrel{⃑}{H}\cdot \stackrel{⃑}{B})=0$ [3,4]. To obtain a standard form of a continuous equation in a general HILM (including a lossy HILM), it is clear that it is necessary to properly treat Equation (3). Adopting Equations (3) and (10)–(14), we have

$$\begin{gathered} {\displaystyle \frac{\partial u}{\partial t}}={\displaystyle \frac{1}{4}}[(\widetilde{\stackrel{⃑}{E}}+{\widetilde{\stackrel{⃑}{E}}}^{*})\cdot {\displaystyle \frac{\partial }{\partial t}}(\widetilde{\stackrel{⃑}{D}}+{\widetilde{\stackrel{⃑}{D}}}^{*})+(\widetilde{\stackrel{⃑}{H}}+{\widetilde{\stackrel{⃑}{H}}}^{*})\cdot {\displaystyle \frac{\partial }{\partial t}}(\widetilde{\stackrel{⃑}{B}}+{\widetilde{\stackrel{⃑}{B}}}^{*})] \\ ={\displaystyle \frac{1}{8}}{\displaystyle \frac{\partial }{\partial t}}(\widetilde{\stackrel{⃑}{E}}\cdot \widetilde{\stackrel{⃑}{D}}+{\widetilde{\stackrel{⃑}{E}}}^{*}\cdot {\widetilde{\stackrel{⃑}{D}}}^{*}+\widetilde{\stackrel{⃑}{H}}\cdot \widetilde{\stackrel{⃑}{B}}+{\widetilde{\stackrel{⃑}{H}}}^{ *}\cdot {\widetilde{\stackrel{⃑}{B}}}^{*})+{\displaystyle \frac{1}{4}}[\widetilde{\stackrel{⃑}{E}}\cdot {\displaystyle \frac{\partial {\widetilde{\stackrel{⃑}{D}}}^{*}}{\partial t}}+{\widetilde{\stackrel{⃑}{E}}}^{*}\cdot {\displaystyle \frac{\partial \widetilde{\stackrel{⃑}{D}}}{\partial t}}+\widetilde{\stackrel{⃑}{H}}\cdot {\displaystyle \frac{\partial {\widetilde{\stackrel{⃑}{B}}}^{*}}{\partial t}}+{\widetilde{\stackrel{⃑}{H}}}^{*}\cdot {\displaystyle \frac{\partial \widetilde{\stackrel{⃑}{B}}}{\partial t}}] \\ ={\displaystyle \frac{\partial }{\partial t}}\{{\displaystyle \frac{1}{4}}Re(\widetilde{\stackrel{⃑}{E}}\cdot \widetilde{\stackrel{⃑}{D}}+\widetilde{\stackrel{⃑}{H}}\cdot \widetilde{\stackrel{⃑}{B}})+{\displaystyle \frac{1}{2}}\omega [|\widetilde{\stackrel{⃑}{E}}||\widetilde{\stackrel{⃑}{D}}|\mathit{sin}{\alpha }_{\epsilon }+|\widetilde{\stackrel{⃑}{H}}||\widetilde{\stackrel{⃑}{B}}|\mathit{sin}{\alpha }_{\mu }]t\} \end{gathered}$$

(15)

Following Poynting’s theorem given by Equation (2), and combining it with Equation (15), a standard form of continuous equation is obtained as

$$\nabla \cdot (\stackrel{⃑}{E}\times \stackrel{⃑}{H})+{\displaystyle \frac{\partial }{\partial t}}\{{\displaystyle \frac{1}{4}}Re(\widetilde{\stackrel{⃑}{E}}\cdot \widetilde{\stackrel{⃑}{D}}+\widetilde{\stackrel{⃑}{H}}\cdot \widetilde{\stackrel{⃑}{B}})+{\displaystyle \frac{1}{2}}\omega [|\widetilde{\stackrel{⃑}{E}}||\widetilde{\stackrel{⃑}{D}}|\mathit{sin}{\alpha }_{\epsilon }+|\widetilde{\stackrel{⃑}{H}}||\widetilde{\stackrel{⃑}{B}}|\mathit{sin}{\alpha }_{\mu }]t\}=0.$$

(16)

Following Equation (16), TDPV $\stackrel{⃑}{S}$ and energy density $u$ may be, respectively, given as

$$\stackrel{⃑}{S}=\stackrel{⃑}{E}\times \stackrel{⃑}{H},$$

(17)

$$u={\displaystyle \frac{1}{4}}Re(\widetilde{\stackrel{⃑}{E}}\cdot \widetilde{\stackrel{⃑}{D}}+\widetilde{\stackrel{⃑}{H}}\cdot \widetilde{\stackrel{⃑}{B}})+{\displaystyle \frac{1}{2}}\omega [|\widetilde{\stackrel{⃑}{E}}||\widetilde{\stackrel{⃑}{D}}|\mathit{sin}{\alpha }_{\epsilon }+|\widetilde{\stackrel{⃑}{H}}||\widetilde{\stackrel{⃑}{B}}|\mathit{sin}{\alpha }_{\mu }]t.$$

(18)

On the other hand, by adopting Equation (14), we shall rewrite Equation (9) as

$$\begin{gathered} \stackrel{⃑}{f}=-\{{\displaystyle \frac{1}{8}}\sum _{\zeta =x,y,z;}\sum _{\xi =x,y,z}{\displaystyle \frac{\partial }{\partial \zeta }}({\tilde{E}}_{\xi }\cdot {\tilde{D}}_{\xi }+{\tilde{E}}_{\xi }^{*}\cdot {\tilde{D}}_{\xi }^{*})+{\displaystyle \frac{1}{4}}\sum _{\zeta =x,y,z;}\sum _{\xi =x,y,z}({\displaystyle \frac{\partial {\tilde{E}}_{\xi }}{\partial \zeta }}\cdot {\tilde{D}}_{\xi }^{*}+{\displaystyle \frac{\partial {\tilde{E}}_{\xi }^{*}}{\partial \zeta }}\cdot {\tilde{D}}_{\xi }) \\ +{\displaystyle \frac{1}{8}}\sum _{\zeta =x,y,z;}\sum _{\xi =x,y,z}({\displaystyle \frac{\partial }{\partial \zeta }}({\tilde{H}}_{\xi }\cdot {\tilde{B}}_{\xi }+{\tilde{H}}_{\xi }^{*}\cdot {\tilde{B}}_{\xi }^{*})+{\displaystyle \frac{1}{4}}\sum _{\zeta =x,y,z;}\sum _{\xi =x,y,z}({\displaystyle \frac{\partial {\tilde{H}}_{\xi }}{\partial \zeta }}\cdot {\tilde{B}}_{\xi }^{*}+{\displaystyle \frac{\partial {\tilde{H}}_{\xi }^{*}}{\partial \zeta }}\cdot {\tilde{B}}_{\xi }) \\ -{\displaystyle \frac{1}{4}}\nabla \cdot [(\widetilde{\stackrel{⃑}{D}}+{\widetilde{\stackrel{⃑}{D}}}^{*})(\widetilde{\stackrel{⃑}{E}}+{\widetilde{\stackrel{⃑}{E}}}^{*})+(\widetilde{\stackrel{⃑}{B}}+{\widetilde{\stackrel{⃑}{B}}}^{*})(\widetilde{\stackrel{⃑}{H}}+{\widetilde{\stackrel{⃑}{H}}}^{*})]\} \\ -{\displaystyle \frac{1}{4}}{\displaystyle \frac{\partial }{\partial t}}[(\widetilde{\stackrel{⃑}{D}}+{\widetilde{\stackrel{⃑}{D}}}^{*})\times (\widetilde{\stackrel{⃑}{B}}+{\widetilde{\stackrel{⃑}{B}}}^{*})]. \end{gathered}$$

(19)

Referring to the derivation process of Equation (16) from Equations (2) and (3), it is clear that, to obtain a standard form of a continuous equation from Equation (19), it is necessary to properly treat the terms of ${\sum }_{\zeta =x,y,z}{\sum }_{\xi =x,y,z}({\displaystyle \frac{\partial {\tilde{E}}_{\xi }}{\partial \zeta }}\cdot {\tilde{D}}_{\xi }^{*}+{\displaystyle \frac{\partial {\tilde{E}}_{\xi }^{*}}{\partial \zeta }}\cdot {\tilde{D}}_{\xi })$ and ${\sum }_{\zeta =x,y,z}{\sum }_{\xi =x,y,z}({\displaystyle \frac{\partial {\tilde{H}}_{\xi }}{\partial \zeta }}\cdot {\tilde{B}}_{\xi }^{*}+{\displaystyle \frac{\partial {\tilde{H}}_{\xi }^{*}}{\partial \zeta }}\cdot {\tilde{B}}_{\xi })$. Following Equations (10)–(13), it is interestingly found that the following holds:

$$\begin{gathered} \sum _{\zeta =x,y,z}\sum _{\xi =x,y,z}({\displaystyle \frac{\partial {\tilde{E}}_{\xi }}{\partial \zeta }}\cdot {\tilde{D}}_{\xi }^{*}+{\displaystyle \frac{\partial {\tilde{E}}_{\xi }^{*}}{\partial \zeta }}\cdot {\tilde{D}}_{\xi })+\sum _{\zeta =x,y,z}\sum _{\xi =x,y,z}({\displaystyle \frac{\partial {\tilde{H}}_{\xi }}{\partial \zeta }}\cdot {\tilde{B}}_{\xi }^{*}+{\displaystyle \frac{\partial {\tilde{H}}_{\xi }^{*}}{\partial \zeta }}\cdot {\tilde{B}}_{\xi }) \\ =|\tilde{\epsilon }|E_{x0}^2{e}^{-2k^{″}z}\{[(-i{k}^{\prime }-k^{″})e^{i{\alpha }_{\epsilon }}+\left(i{k}^{\prime }-k^{″}\right)e^{-i{\alpha }_{\epsilon }}] \\ +[(-i{k}^{\prime }-k^{″})e^{i{\alpha }_{\mu }}+\left(i{k}^{\prime }-k^{″}\right)e^{-i{\alpha }_{\mu }}]\} \\ =|\tilde{\epsilon }|E_{x0}^2{e}^{-2k^{″}z}k\{[\mathit{sin}{\alpha }_{\epsilon }\mathit{cos}{\alpha }_k-\mathit{cos}{\alpha }_{\epsilon }\mathit{sin}{\alpha }_k] \\ +[\mathit{sin}{\alpha }_{\mu }\mathit{cos}{\alpha }_k-\mathit{cos}{\alpha }_{\mu }\mathit{sin}{\alpha }_k]\} \\ =|\tilde{\epsilon }|E_{x0}^2{e}^{-2k^{″}z}k(-\mathit{sin}{\alpha }_{\eta }+\mathit{sin}{\alpha }_{\eta })=0. \end{gathered}$$

(20)

Setting the condition of $\stackrel{⃑}{f}=0$, a standard form of continuity equation may be obtained as

$$\nabla \cdot [{\displaystyle \frac{1}{4}}\stackrel{⃡}{I}Re(\widetilde{\stackrel{⃑}{E}}\cdot \widetilde{\stackrel{⃑}{D}}+\widetilde{\stackrel{⃑}{H}}\cdot \widetilde{\stackrel{⃑}{B}})-(\stackrel{⃑}{D} \stackrel{⃑}{E}+\stackrel{⃑}{B} \stackrel{⃑}{H})]+{\displaystyle \frac{\partial }{\partial t}}(\stackrel{⃑}{D}\times \stackrel{⃑}{B})=0.$$

(21)

Based on Equation (21), the stress tensor density $\stackrel{⃡}{T}$ and momentum density $\stackrel{⃑}{G}$ are, respectively, given as [17]

$$\stackrel{⃡}{T}={\displaystyle \frac{1}{4}}\stackrel{⃡}{I}Re(\widetilde{\stackrel{⃑}{E}}\cdot \widetilde{\stackrel{⃑}{D}}+\widetilde{\stackrel{⃑}{H}}\cdot \widetilde{\stackrel{⃑}{B}})+(\stackrel{⃑}{D} \stackrel{⃑}{E}+\stackrel{⃑}{B} \stackrel{⃑}{H}),$$

(22)

$$\stackrel{⃑}{G}=\stackrel{⃑}{D}\times \stackrel{⃑}{B}.$$

(23)

We shall stress that both Equations (17) and (23) are derived strictly from continuity equations, in principle, which are appropriate to be applied to properly describe the energy flow and momentum properties of an HHPW in an HILM.

2.2. On Time-Averaged Quantities

It is known that a number of electromagnetic properties and/or phenomena are described by using time-averaged quantities, such as time-averaged stored energy density (TASED) $<u_{sto}>$, time-averaged dissipated energy density (TADED) $<u_{dis}>$, time-averaged energy flow density (i.e., TAPV) $<\stackrel{⃑}{S}>$, and TAMD $<\stackrel{⃑}{G}$>. However, it is noted that there exist different and even non-equivalent expressions of $<u_{sto}>$ and $<u_{dis}>$, which may be mainly due to the application of different divisions of the total energy into a stored part and a dissipated one [23,24,25,26]. Correspondingly, different expressions of $<\stackrel{⃑}{S}>$ are adopted [10,27]. On the other hand, mainly due to different divisions of total momentum into the electromagnetic part and the material one, different expressions of $<\stackrel{⃑}{G}>$ may also be obtained [4,5,6,7,8,9,10,11,12,27,28]. Unfortunately, non-equivalent predictions may be proposed by using different expressions, which cause confusion in understanding the properties of electromagnetic wave energy, energy flow, and momentum [6,7,8,9,10,11,12,13,14,15,16,17,22,23,24,25,26,27,28,29,30,31,32].

Recently, it has been noted that the terms arising in the expression of ${\displaystyle \frac{\partial u}{\partial t}}$ given by Equation (15) may generally be divided into time-periodic terms of ${\displaystyle \frac{\partial }{\partial t}}[{\displaystyle \frac{1}{4}}Re(\widetilde{\stackrel{⃑}{E}}\cdot \widetilde{\stackrel{⃑}{D}}+\widetilde{\stackrel{⃑}{H}}\cdot \widetilde{\stackrel{⃑}{B}})]$ and time-independent ones of ${\displaystyle \frac{1}{2}}\omega [|\widetilde{\stackrel{⃑}{E}}||\widetilde{\stackrel{⃑}{D}}|\mathit{sin}{\alpha }_{\epsilon }+|\widetilde{\stackrel{⃑}{H}}||\widetilde{\stackrel{⃑}{B}}|\mathit{sin}{\alpha }_{\mu }]$ [25,26]. The time-periodic terms mean that the electromagnetic energy is stored and then released by turns, i.e., the periodic terms relate to stored energy; the time-independent terms mean that the electromagnetic energy is converted into non-electromagnetic energy monotonously, i.e., the time-independent terms relate to dissipated energy. Thus, expressions of both $<u_{dis}>$ and $<u_{sto}>$ with intuitive physical images and clear physical meanings may be obtained. The obtained $<u_{sto}>$ is positive definite, and the $<u_{dis}>$ is verified to be applicable experimentally [25,26].

Referring to recent studies of the energy characteristics of electromagnetic waves in lossy media [25,26], we apply the following relation [5]:

$$\mathit{Re}({\widetilde{\stackrel{⃑}{A}}}_1)\times \mathit{Re}({\widetilde{\stackrel{⃑}{A}}}_2)={\displaystyle \frac{1}{2}}Re({\widetilde{\stackrel{⃑}{A}}}_1\times {\widetilde{\stackrel{⃑}{A}}}_2),$$

(24)

It is clear that, for the case of an HHPW traveling in an HILM, TDPV $\stackrel{⃑}{S}$ given by Equation (17) may be generally divided into a time-periodic term of ${\displaystyle \frac{1}{2}}Re(\widetilde{\stackrel{⃑}{E}}\times \widetilde{\stackrel{⃑}{H}})$ and a time-independent one of ${\displaystyle \frac{1}{2}}Re(\widetilde{\stackrel{⃑}{E}}\times {\widetilde{\stackrel{⃑}{H}}}^{*})$. The time-periodic term of ${\displaystyle \frac{1}{2}}Re(\widetilde{\stackrel{⃑}{E}}\times \widetilde{\stackrel{⃑}{H}})$ means that the electromagnetic energy is transported forward and then backward by turns, and its time-averaged value is equal to zero; the time-independent term of ${\displaystyle \frac{1}{2}}Re(\widetilde{\stackrel{⃑}{E}}\times {\widetilde{\stackrel{⃑}{H}}}^{*})$ means that the electromagnetic energy is transported forward monotonously. Thus, TAPV $<\stackrel{⃑}{S}>$ is obtained as

$$<\stackrel{⃑}{S}(z)>={\displaystyle \frac{1}{2}}Re(\widetilde{\stackrel{⃑}{E}}\times {\widetilde{\stackrel{⃑}{H}}}^{*})={\displaystyle \frac{1}{2{|\widetilde{\eta |}}^2}}{E}_{x0}^2{e}^{-2k^{″}z}Re(\tilde{\eta }){\widehat{e}}_z.$$

(25)

Similarly, for the case of an HHPW traveling in an HILM, the electromagnetic momentum density $\stackrel{⃑}{G}$ given by Equation (23) may be generally divided into a time-periodic term of ${\displaystyle \frac{1}{2}}Re(\widetilde{\stackrel{⃑}{D}}\times \widetilde{\stackrel{⃑}{B}})$ and a time-independent one of ${\displaystyle \frac{1}{2}}Re(\widetilde{\stackrel{⃑}{D}}\times {\widetilde{\stackrel{⃑}{B}}}^{*})$. The time-periodic term of ${\displaystyle \frac{1}{2}}Re(\widetilde{\stackrel{⃑}{D}}\times \widetilde{\stackrel{⃑}{B}})$ means that the electromagnetic momentum is transported forward and then backward by turns, and its time-averaged value is equal to zero; the time-independent term of ${\displaystyle \frac{1}{2}}Re(\widetilde{\stackrel{⃑}{D}}\times {\widetilde{\stackrel{⃑}{B}}}^{*})$ means that the electromagnetic momentum is transported forward monotonously. Thus, TAMD $<\stackrel{⃑}{G}>$ is obtained as

$$<\stackrel{⃑}{G}(z)>={\displaystyle \frac{1}{2}}Re(\widetilde{\stackrel{⃑}{D}}\times {\widetilde{\stackrel{⃑}{B}}}^{*})={\displaystyle \frac{1}{2{|\widetilde{\eta |}}^2}}|\tilde{\epsilon }\tilde{\mu }|E_{x0}^2{e}^{-2k^{″}z}Re(\tilde{\eta }){\widehat{e}}_z.$$

(26)

Following the derivation processes of both TAPV and TAMD mentioned above, it is clear that TAPV $<\stackrel{⃑}{S}>$ given by Equation (25) and TAMD $<\stackrel{⃑}{G}>$ given by Equation (26) have intuitive physical images and clear physical meanings. In addition, we shall point out that, compared with the usual treatment of dividing total momentum into electromagnetic and material components, here, the electromagnetic wave arising in media is taken as a natural whole, i.e., both energy flow and momentum are no longer divided into electromagnetic and material components, which is useful to self-consistently describe the properties of both electromagnetic energy and momentum [17]. Below, based on Equations (25) and (26), we shall propose a new way to determine the direction relation between TAPV and TAMD in HILMs, which may be helpful to deepen the understanding of electromagnetic properties of metamaterials, and explore proper experiments to test the applicability of the existed expressions of TAPV and TAMD.

3. Direction Relationship Between $<\stackrel{⃑}{\mathit{S}}>$ and $<\stackrel{⃑}{\mathit{G}}>$ in HILMs

Direction relationships among $<\stackrel{⃑}{S}>$, $<\stackrel{⃑}{G}>$, and wave vector $Re(\widetilde{\stackrel{⃑}{k}})$ may be applied as useful indicators to reveal novel properties of electromagnetic waves in metamaterials [18,27,28]. Here, we shall recall an approach to determine the direction relationship between $<\stackrel{⃑}{S}>$ and wave vector $Re(\widetilde{\stackrel{⃑}{k}})$ [33,34], and provide a similar approach to determine the direction relationship between $<\stackrel{⃑}{G}>$ and wave vector $Re(\widetilde{\stackrel{⃑}{k}})$.

Generally, the direction relationship between $<\stackrel{⃑}{S}(z)>$ and $Re(\widetilde{\stackrel{⃑}{k}})$ can be well described by using the inner product of $<\stackrel{⃑}{S}>\cdot Re(\widetilde{\stackrel{⃑}{k}})$[33,34]. In an HILM, $<\stackrel{⃑}{S}>\cdot Re(\widetilde{\stackrel{⃑}{k}})$ may be rigorously derived as [34]

$$<\stackrel{⃑}{S}>\cdot Re(\widetilde{\stackrel{⃑}{k}})=Re(\tilde{\eta })Re(\tilde{k})H^2/2.$$

(27)

Following Equation (27), the direction relation between $<\stackrel{⃑}{S}>$ and $Re(\widetilde{\stackrel{⃑}{k}})$ may be fully determined according to the sign of $\cos [({\alpha }_{\mu }+{\alpha }_{\epsilon })/2]\cos [({\alpha }_{\mu }-{\alpha }_{\epsilon })/2]$. As an instance, the condition for left-handedness is given as [33,34]

$$\cos [({\alpha }_{\mu }+{\alpha }_{\epsilon })/2]\cos [({\alpha }_{\mu }-{\alpha }_{\epsilon })/2]<0.$$

(28)

Similarly, the direction relationship between $<\stackrel{⃑}{G}>$ and $Re(\widetilde{\stackrel{⃑}{k}})$ may be addressed by using the inner product of $<\stackrel{⃑}{G}>\cdot Re(\widetilde{\stackrel{⃑}{k}})$. Applying Equations (14) and (26), there is

$$\langle \stackrel{⃑}{G}\rangle \cdot Re(\widetilde{\stackrel{⃑}{k}})=(\widetilde{\stackrel{⃑}{D}}\times {\widetilde{\stackrel{⃑}{B}}}^{*}+{\widetilde{\stackrel{⃑}{D}}}^{*}\times \widetilde{\stackrel{⃑}{B}})\cdot (\widetilde{\stackrel{⃑}{k}}+{\widetilde{\stackrel{⃑}{k}}}^{*})/8.$$

(29)

Noting the following relation

$$(\stackrel{⃑}{a}\times b)\cdot \stackrel{⃑}{c}=(\stackrel{⃑}{c}\times \stackrel{⃑}{a})\cdot \stackrel{⃑}{b}=-(\stackrel{⃑}{c}\times \stackrel{⃑}{b})\cdot \stackrel{⃑}{a},$$

(30)

Equation (29) becomes

$$\langle \stackrel{⃑}{G}\rangle \cdot Re(\widetilde{\stackrel{⃑}{k}})=(\widetilde{\stackrel{⃑}{k}}\times \widetilde{\stackrel{⃑}{D}}\cdot {\widetilde{\stackrel{⃑}{B}}}^{*}-\widetilde{\stackrel{⃑}{k}}\times \widetilde{\stackrel{⃑}{B}}\cdot {\widetilde{\stackrel{⃑}{D}}}^{*}-{\widetilde{\stackrel{⃑}{k}}}^{*}\times {\widetilde{\stackrel{⃑}{B}}}^{*}\cdot \widetilde{\stackrel{⃑}{D}}+{\widetilde{\stackrel{⃑}{k}}}^{*}\times {\widetilde{\stackrel{⃑}{D}}}^{*}\cdot \widetilde{\stackrel{⃑}{B}})/8.$$

(31)

According to Maxwell’s curl equations, there are

$$\widetilde{\stackrel{⃑}{k}}\times \widetilde{\stackrel{⃑}{E}}=\widetilde{\stackrel{⃑}{k}}\times \widetilde{\stackrel{⃑}{D}}/\tilde{\epsilon }=\omega \widetilde{\stackrel{⃑}{B}},$$

(32)

$$\widetilde{\stackrel{⃑}{k}}\times \widetilde{\stackrel{⃑}{H}}=\widetilde{\stackrel{⃑}{k}}\times \widetilde{\stackrel{⃑}{B}}/\tilde{\mu }=-\omega \widetilde{\stackrel{⃑}{D}}.$$

(33)

Substituting Equations (32) and (33) into Equation (31), it is obtained that

$$\langle \stackrel{⃑}{G}\rangle \cdot Re(\widetilde{\stackrel{⃑}{k}})=[\omega \tilde{\epsilon }\widetilde{\stackrel{⃑}{B}}\cdot {\widetilde{\stackrel{⃑}{B}}}^{*}+\omega \tilde{\mu }\widetilde{\stackrel{⃑}{D}}\cdot {\widetilde{\stackrel{⃑}{D}}}^{*}+\omega {(\tilde{\mu }\widetilde{\stackrel{⃑}{D}})}^{*}\cdot \widetilde{\stackrel{⃑}{D}}+\omega {(\tilde{\epsilon }\widetilde{\stackrel{⃑}{B}})}^{*}\cdot \widetilde{\stackrel{⃑}{B}}]/8.$$

(34)

Further considering the relations of $\widetilde{\stackrel{⃑}{B}}=\tilde{\mu }\widetilde{\stackrel{⃑}{H}}$ and $\widetilde{\stackrel{⃑}{D}}=\tilde{\epsilon }\widetilde{\stackrel{⃑}{E}}$, we have

$$\begin{array}{l}<\stackrel{⃑}{G}>\cdot Re(\widetilde{\stackrel{⃑}{k}})=\omega [\tilde{\epsilon }\tilde{\mu }{\tilde{\mu }}^{*}+\tilde{\mu }(\tilde{k}/\omega )(\tilde{k}/\omega {)}^{*}+{\tilde{\mu }}^{*}(\tilde{k}/\omega {)}^{*}(\tilde{k}/\omega )+{\tilde{\epsilon }}^{*}{\tilde{\mu }}^{*}\tilde{\mu }]\widetilde{\stackrel{⃑}{H}}\cdot {\widetilde{\stackrel{⃑}{H}}}^{*}/8\\ \begin{array}{ccc} & & \end{array}=[(\tilde{\epsilon }{\tilde{\mu }}^{*}\tilde{\eta })\tilde{k}+(\tilde{\epsilon }{\tilde{\mu }}^{*}\tilde{\eta }{)}^{*}\tilde{k}+(\tilde{\epsilon }{\tilde{\mu }}^{*}\tilde{\eta }){\tilde{k}}^{*}+(\tilde{\epsilon }{\tilde{\mu }}^{*}\tilde{\eta }{)}^{*}{\tilde{k}}^{*}]\widetilde{\stackrel{⃑}{H}}\cdot {\widetilde{\stackrel{⃑}{H}}}^{*}/8\\ \begin{array}{ccc} & & \end{array}=Re(\tilde{\epsilon }{\tilde{\mu }}^{*}\tilde{\eta })Re(\tilde{k})H^2/2\\ \begin{array}{ccc} & & \end{array}=|\tilde{\epsilon }\tilde{\mu }|Re(\tilde{\eta })Re(\tilde{k})H^2/2\end{array}.$$

(35)

Following Equation (35), the direction relation between $<\stackrel{⃑}{G}>$ and $Re(\widetilde{\stackrel{⃑}{k}})$ may be fully determined according to the sign of $\cos [({\alpha }_{\mu }+{\alpha }_{\epsilon })/2]\cos [({\alpha }_{\mu }-{\alpha }_{\epsilon })/2]$.

It is clear from Equations (27) and (35) that, for the case of an HHPW traveling in an HILM, the propagation direction of <$\stackrel{⃑}{S}$> is always consistent with that of <$\stackrel{⃑}{G}$>, and even the HILM is an LHM, which may be applied to explain why the predicted reversal of electromagnetic wave momentum has not been observed experimentally [18,27,28]. Meanwhile, we shall point out that both HHPW and HILM are ideal models. In real-world physical systems, on the one hand, the electromagnetic wave may be either non-plane or inhomogeneous; on the other hand, the media encountered usually hold finite sizes, and may be inhomogeneous, anisotropic, or non-linear. The possible effects of these factors have not been considered in the derivation process of both Equations (27) and (35). Therefore, in practice, Equations (27) and (35) should be used with caution.

4. Discussion

4.1. Comparison with Previous Theoretical Research

It is known that electromagnetic momentum in media continues to be a controversial subject; various definitions and interpretations have been proposed [6,7,8,9,10,11,12,13,14,15,16,17]. Correspondingly, different results may be obtained for the same issue. Veselago first predicted that, in an LHM, the TAMD of an electromagnetic wave

$$<\stackrel{⃑}{G}>={\displaystyle \frac{1}{2}}Re[\epsilon \mu \stackrel{⃑}{E}\times {\stackrel{⃑}{H}}^{*}+{\displaystyle \frac{\stackrel{⃑}{k}}{2}}({\displaystyle \frac{\partial \epsilon }{\partial \omega }}{|\stackrel{⃑}{E}|}^2+{\displaystyle \frac{\partial \mu }{\partial \omega }}{|\stackrel{⃑}{H}|}^2)]$$

(36)

is anti-parallel to the TAPV [18]. Secondly, Kemp et al. demonstrated that the TAMD of an electromagnetic wave in an isotropic medium may be given as

$$<\stackrel{⃑}{G}>={\displaystyle \frac{1}{2}}Re[\stackrel{⃑}{D}\times {\stackrel{⃑}{B}}^{*}+\stackrel{⃑}{k}{\displaystyle \frac{{\epsilon }_0\omega {\omega }_{ep}^2}{{({\omega }^2-{\omega }_{e0}^2)}^2+{\gamma }_e^2{\omega }^2}}{|\stackrel{⃑}{E}|}^2+\stackrel{⃑}{k}{\displaystyle \frac{{\epsilon }_0\omega F{\omega }_{mp}^2}{{({\omega }^2-{\omega }_{m0}^2)}^2+{\gamma }_m^2{\omega }^2}}{|\stackrel{⃑}{H}|}^2)].$$

(37)

where ${\omega }_{e0} ({\omega }_{m0})$ is the resonance frequency of the electric (magnetic) dipole oscillators, ${\gamma }_e$ (${\gamma }_m$) is the damping frequency, and ${\omega }_{ep}^2$ ($F{\omega }_{mp}^2$) is a measure of the strength of the interaction between the oscillators and the electricity (magnet). Furthermore, it is predicted that the momentum flux of a monochromatic wave in an isotropic LHM is opposite to the power flow direction. However, the momentum density in a lossy medium with a negative index of refraction may be parallel or anti-parallel to the power flow [27]. Thirdly, based on mass-polariton theory, Partanen et al. suggest that the momentum density of an electromagnetic wave in an isotropic medium may be given as the sum of the electromagnetic momentum density ${\stackrel{⃑}{G}}_{EM}$ and the momentum density of the mass density wave ${\stackrel{⃑}{G}}_{MDW}$, i.e.,

$$\stackrel{⃑}{G}={\stackrel{⃑}{G}}_{EM}+{\stackrel{⃑}{G}}_{MDW}.$$

(38)

It is further predicted that the momentum of light in LHM can be either positive or negative depending on the sub-wavelength structure [28].

On the other hand, it is noted that TAMD given by Equation (36) relates to a non-positive-definite expression of TASED $<u_{sto}>$, which is usually written as [4,22]

$$<u_{sto}>={\displaystyle \frac{1}{4}}{\displaystyle \frac{\partial (\omega \epsilon )}{\partial \omega }}{|\stackrel{⃑}{E}|}^2+{\displaystyle \frac{1}{4}}{\displaystyle \frac{\partial (\omega \mu )}{\partial \omega }}{|\stackrel{⃑}{H}|}^2).$$

(39)

Referring to one type of positive-definite expression of TASED [23,27], TAMD given by Equation (37) is proposed. In addition, the momentum density given by Equation (38) is associated with the unresolved A-MC [6,7,8,9,10,11,12,13,14,15,16,17,28]. Therefore, the expressions of TAMD (or momentum density) and their related theories still need to be further investigated.

Apparently, our work provides a new perspective to re-investigate the properties of energy flow and momentum of electromagnetic waves in metamaterials, which may be helpful to understand the previous observation and further explore proper experiments to test the applicability of the related theories.

4.2. On Experiment Examination

As an instance, the recoil momentum of a photon in a dilute gas was determined with a two-pulse light grating interferometer using near-resonant laser light; it was found that the optical momentum transfer to dielectric media was in direct proportion to the macroscopic index of refraction [35]. It is further pointed out that observations have not revealed a dependence on the slope of the dielectric function as in Equation (36), which has been taken as indirect rather than direct experimental evidence demonstrating that the predicted reversal of electromagnetic wave momentum has not been observed experimentally [27].

Furthermore, it is well known that A-MC has lasted for more than 100 years [6,7], which may be partly attributed to the difficulties of experimental examination of the related theories [9,13]. Similar difficulties may also be encountered in experimental examinations of the direction relationship between $<\stackrel{⃑}{S}>$ and $<\stackrel{⃑}{G}>$ in various media, which is necessary to be further studied.

5. Conclusions

In summary, we have proposed a rigorous way to address the energy flow and momentum of an HHPW traveling in HILMs. TDPV $\stackrel{⃑}{S}(t)$, TDMD $\stackrel{⃑}{G}(t)$, TAPV $<\stackrel{⃑}{S}>$ and TAMD $<\stackrel{⃑}{G}>$ have been rigorously derived. Furthermore, the inner products of $<\stackrel{⃑}{S}>\cdot Re(\widetilde{\stackrel{⃑}{k}})$ and $<\stackrel{⃑}{G}>\cdot Re(\widetilde{\stackrel{⃑}{k}})$ have been applied to determine the direction relations among $<\stackrel{⃑}{S}>$, $<\stackrel{⃑}{G}>$ and $Re(\widetilde{\stackrel{⃑}{k}})$; it has been demonstrated that, in an HILM, the propagation direction of <$\stackrel{⃑}{S}$> of an HHPW is always consistent with that of <$\stackrel{⃑}{G}$>, which may be applied to explain why the predicted reversal of electromagnetic wave momentum has not been observed up to now, provide a new perspective to address the unsolved A-MC, and offer the possibility to weaken, and even eliminate, the confusion that has arisen in the related issues.

Finally, we shall point out that, in this work, to propose a rigorous way to address the energy, energy flow, and momentum of electromagnetic waves in media, for simplicity, ideal models of both HHPW and HILM are applied. It would be interesting to further consider the effects of several other factors, such as anisotropy, non-linearity, dispersion, and non-uniformity of media, on the direction relationships among $<\stackrel{⃑}{S}>$, $<\stackrel{⃑}{G}>$ and $Re(\widetilde{\stackrel{⃑}{k}})$, which may be helpful to further explore the direction relationship between $<\stackrel{⃑}{S}>$ and $<\stackrel{⃑}{G}>$ in metamaterials, experimentally test the related theories, and deepen the understanding of the energy flow and momentum of electromagnetic waves in media.