Singularities in Computational Optics
Abstract
:1. Introduction
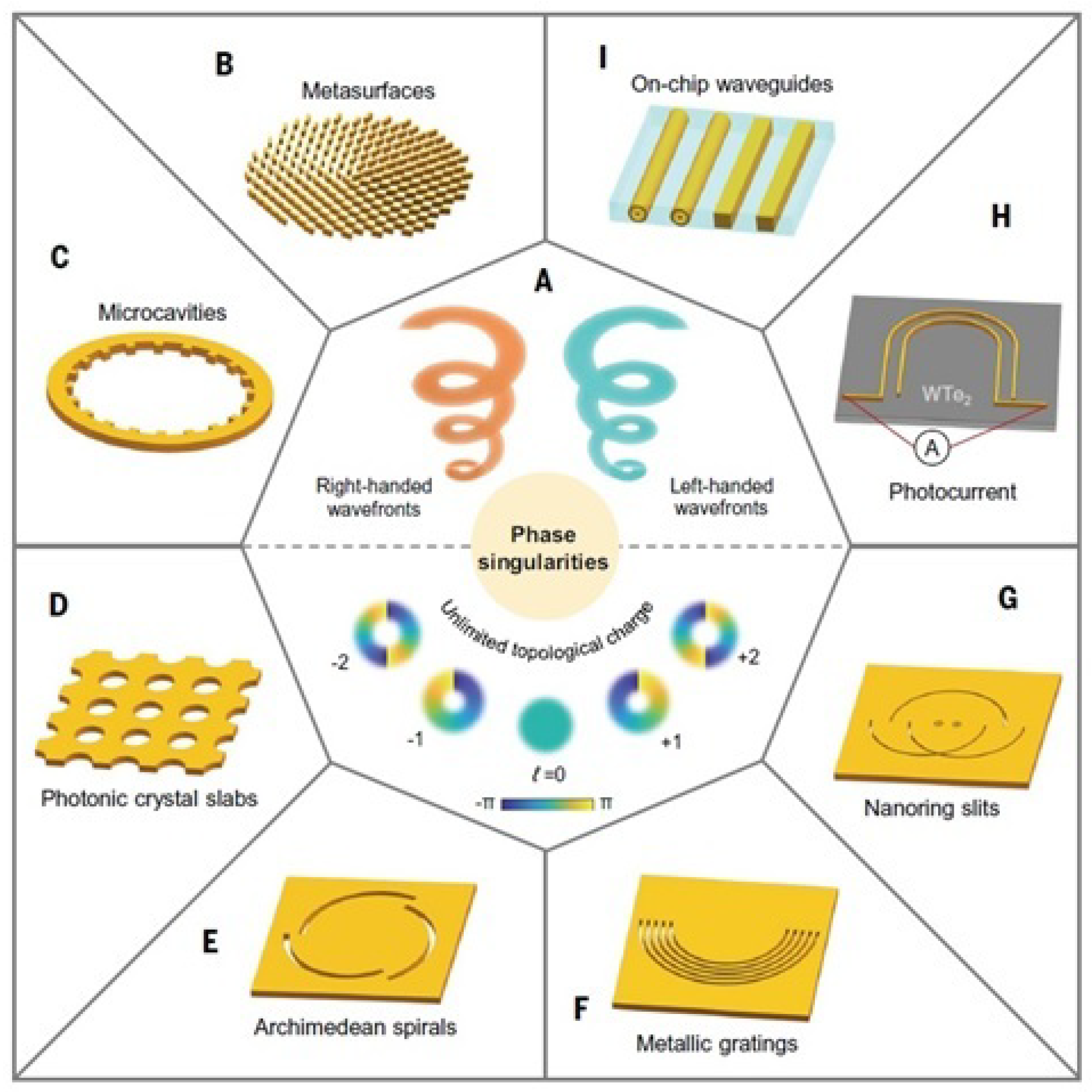
1.1. Singularities
1.2. Computation Optics
1.3. Organization of This Article
2. Singularities in Computational Optics
2.1. Diffusers
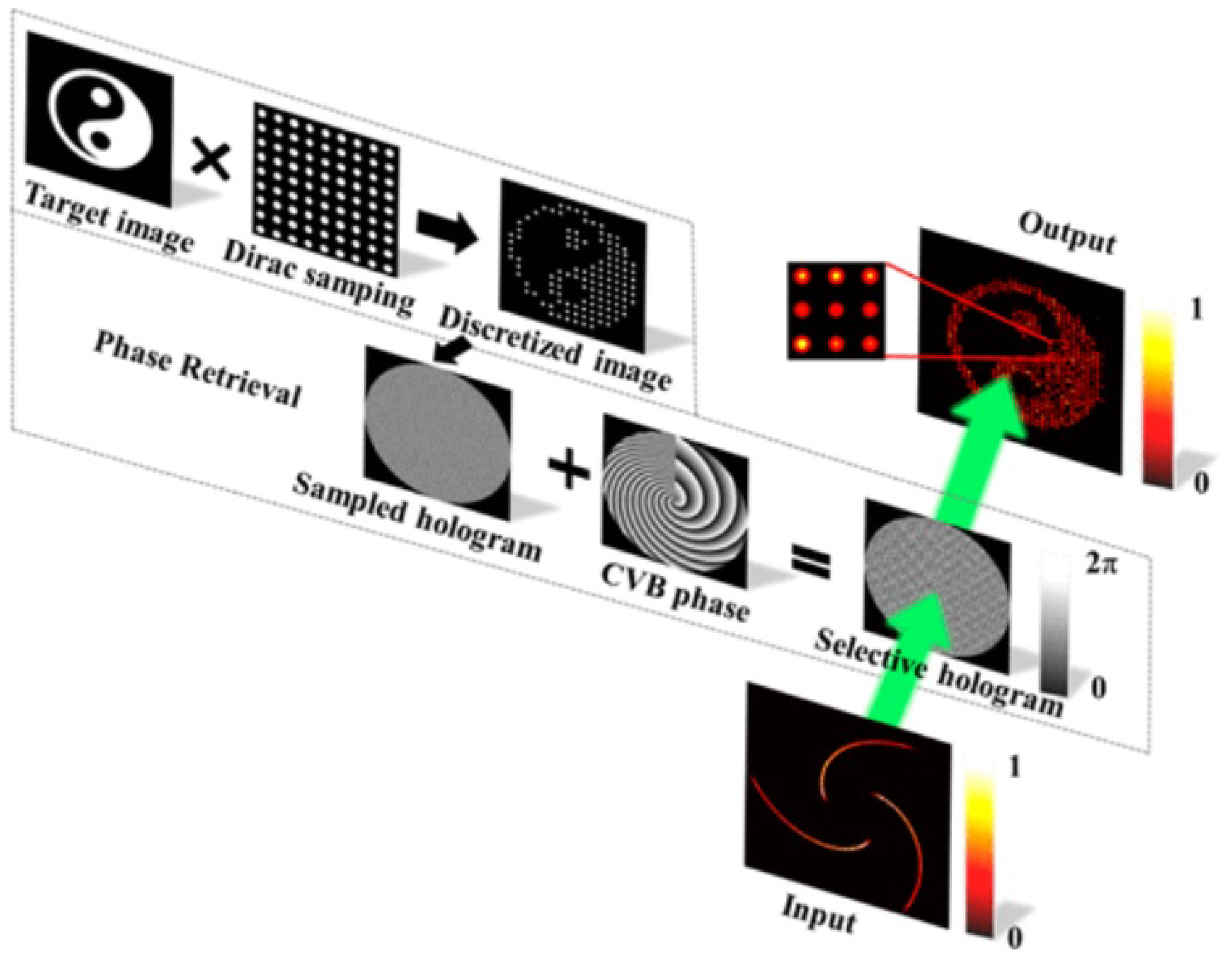
2.2. Computer-Generated Hologram and Phase Retrieval
2.3. Vortex Stagnation Problem in Computer-Generated Hologram (CGH) Design
2.4. Phase Unwrapping in the Presence of Vortices
2.5. Diversity Mechanism Provided by Vortex Phase
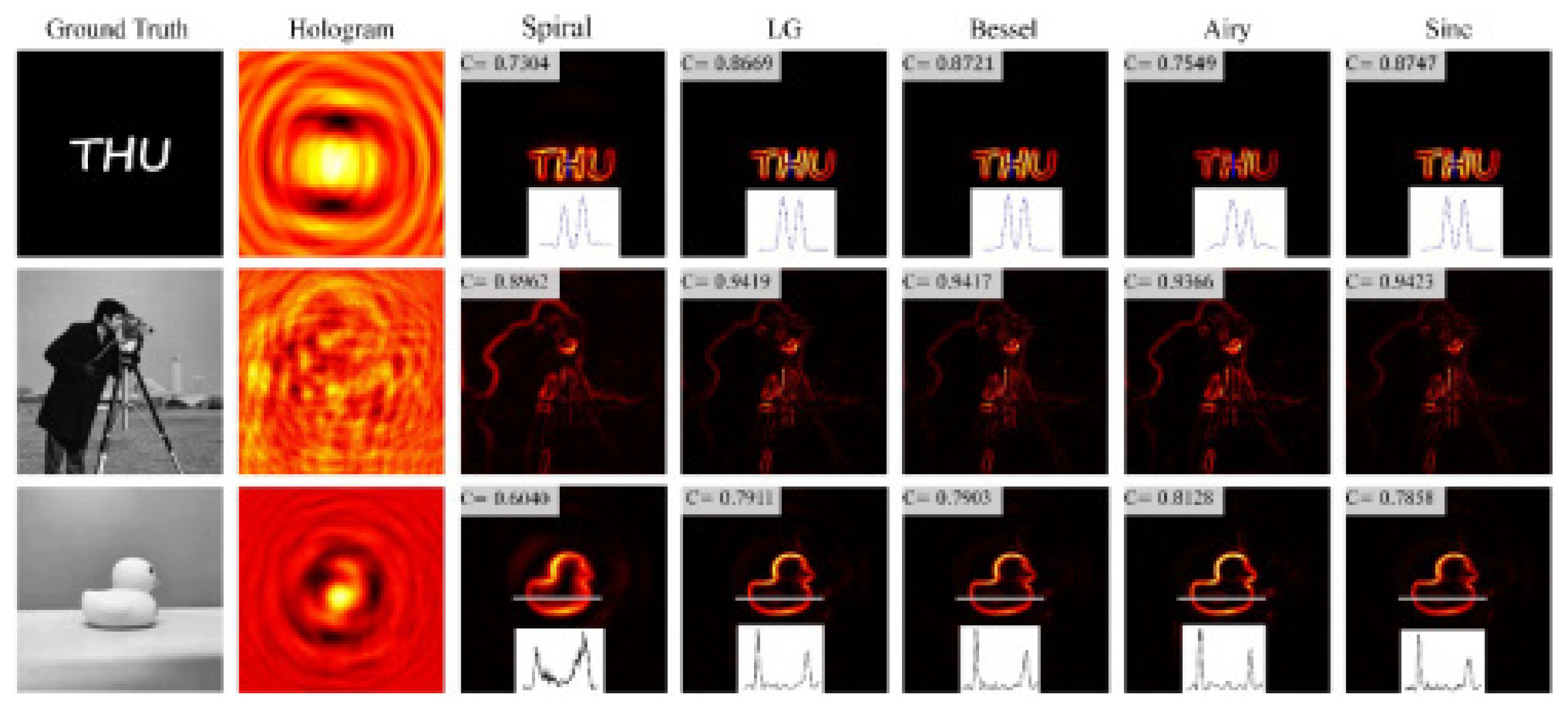
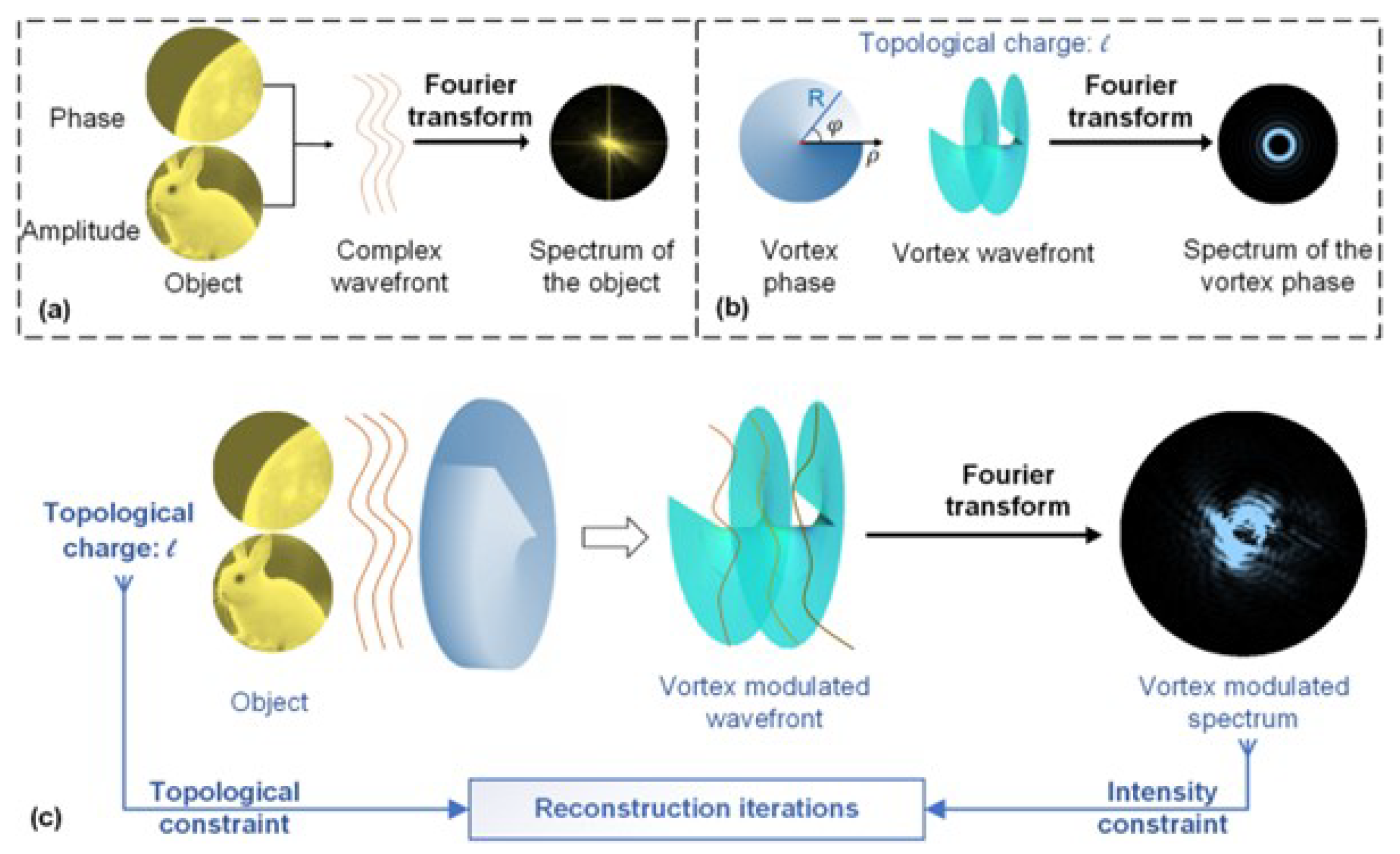
2.6. Phase Retrieval by Spiral Phase Diversity
2.7. Twin Stagnation Free Phase Retrieval
2.8. Underwater Communication
2.9. Focusing of Singular Beam
2.10. Helmholtz–Hodge Decomposition
2.11. Edge Enhancement
Scalar and Vector Vortex Filtering
2.12. Nanoscale Imaging
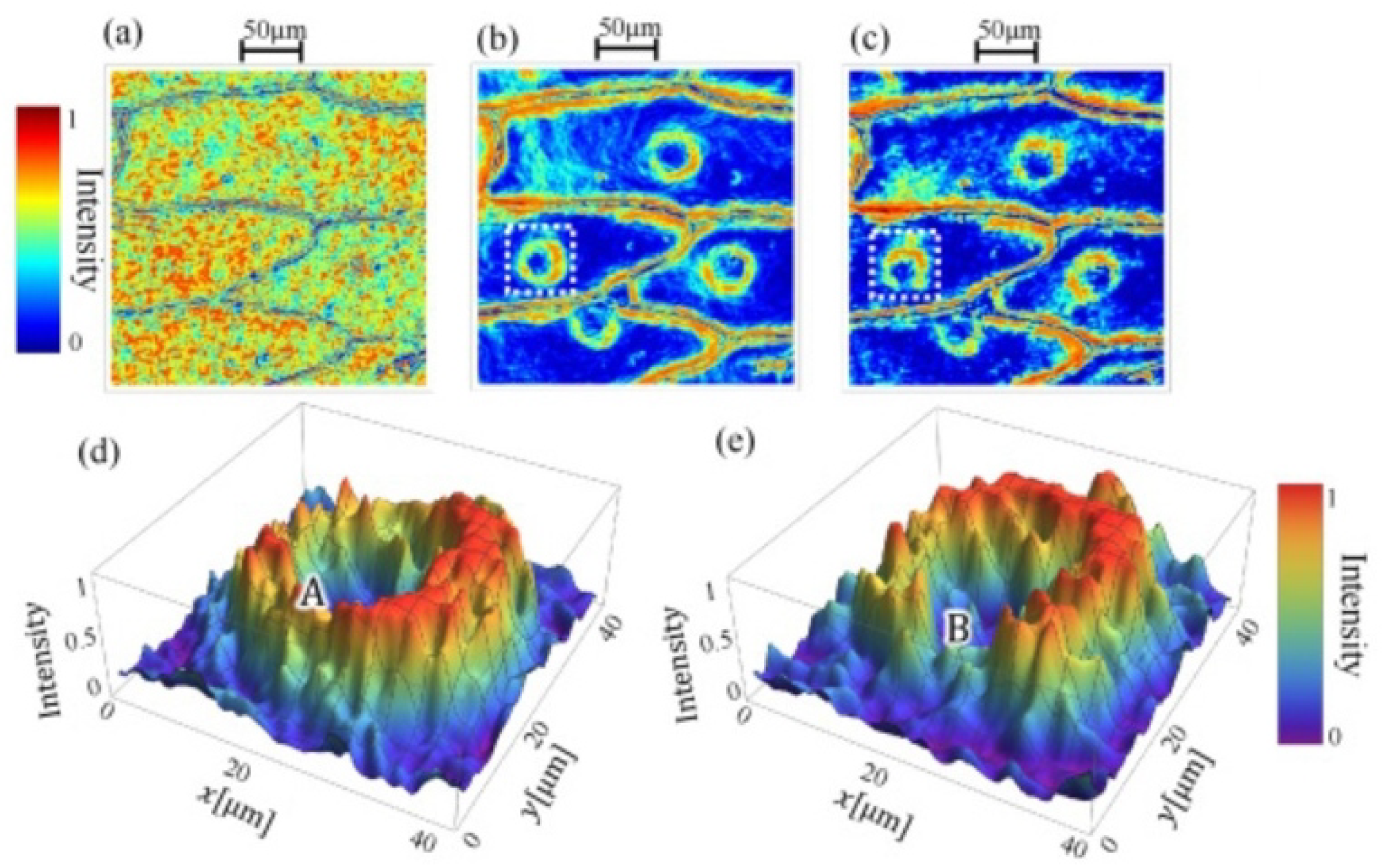
2.13. Optical Vortex Metrology
2.14. Metasurfaces
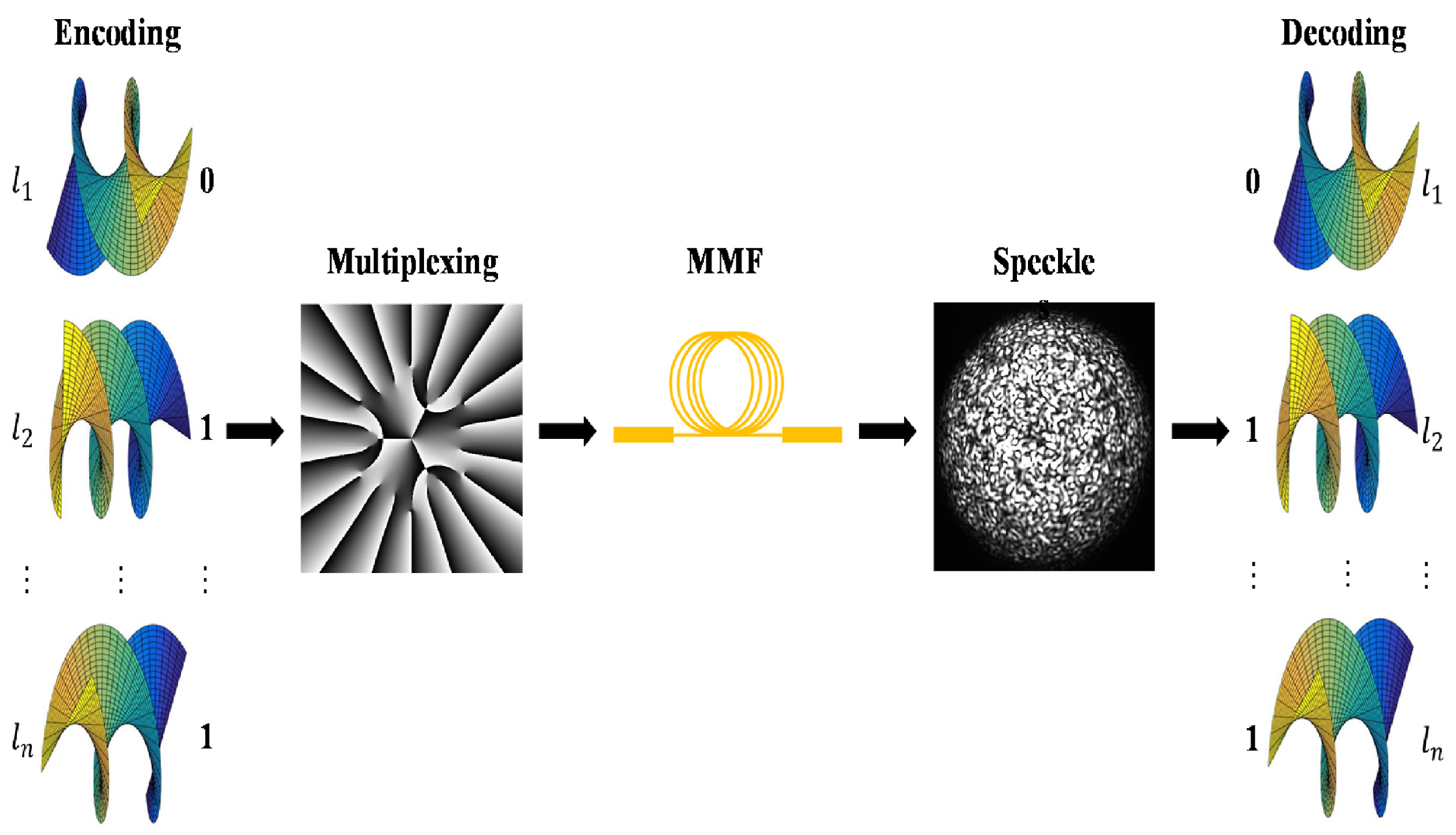
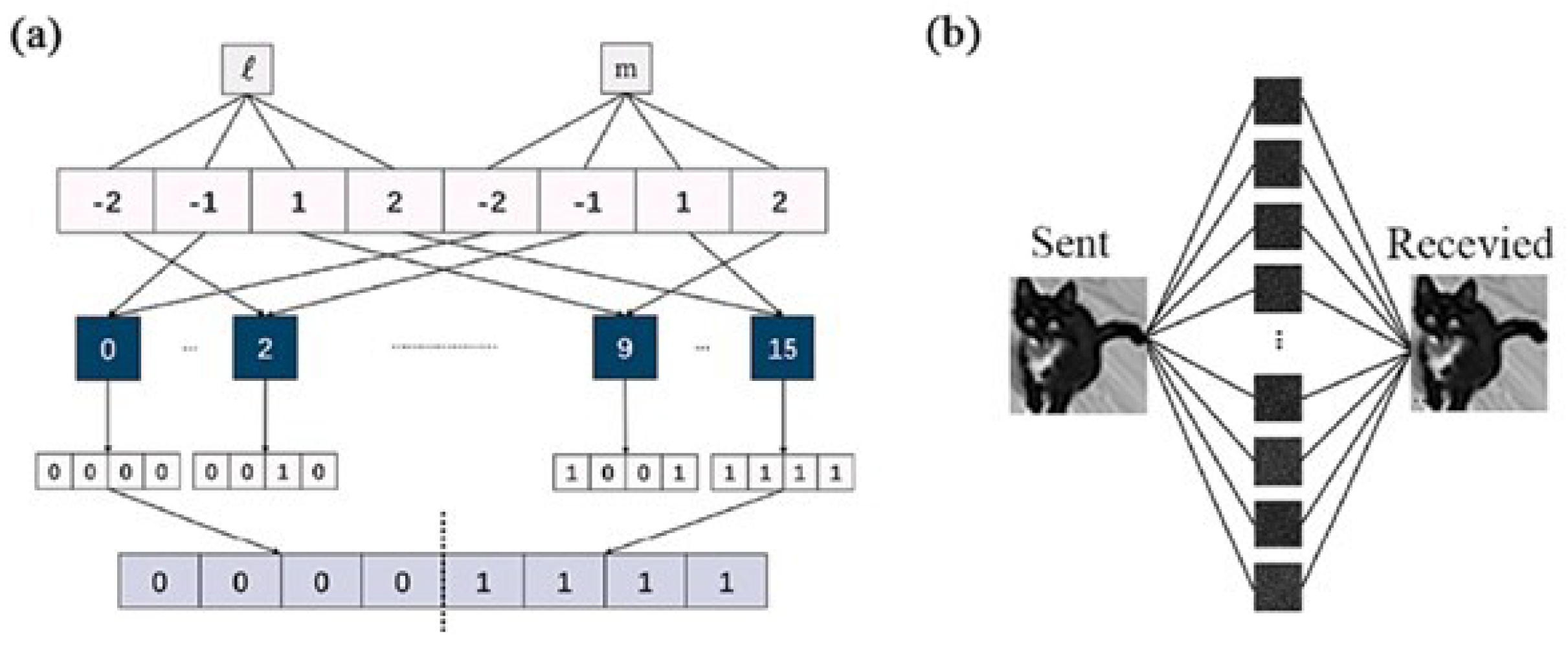
2.15. OAM Multiplexing and Communication
2.16. EM Vortex Imaging
2.17. Coherent Diffraction Imaging
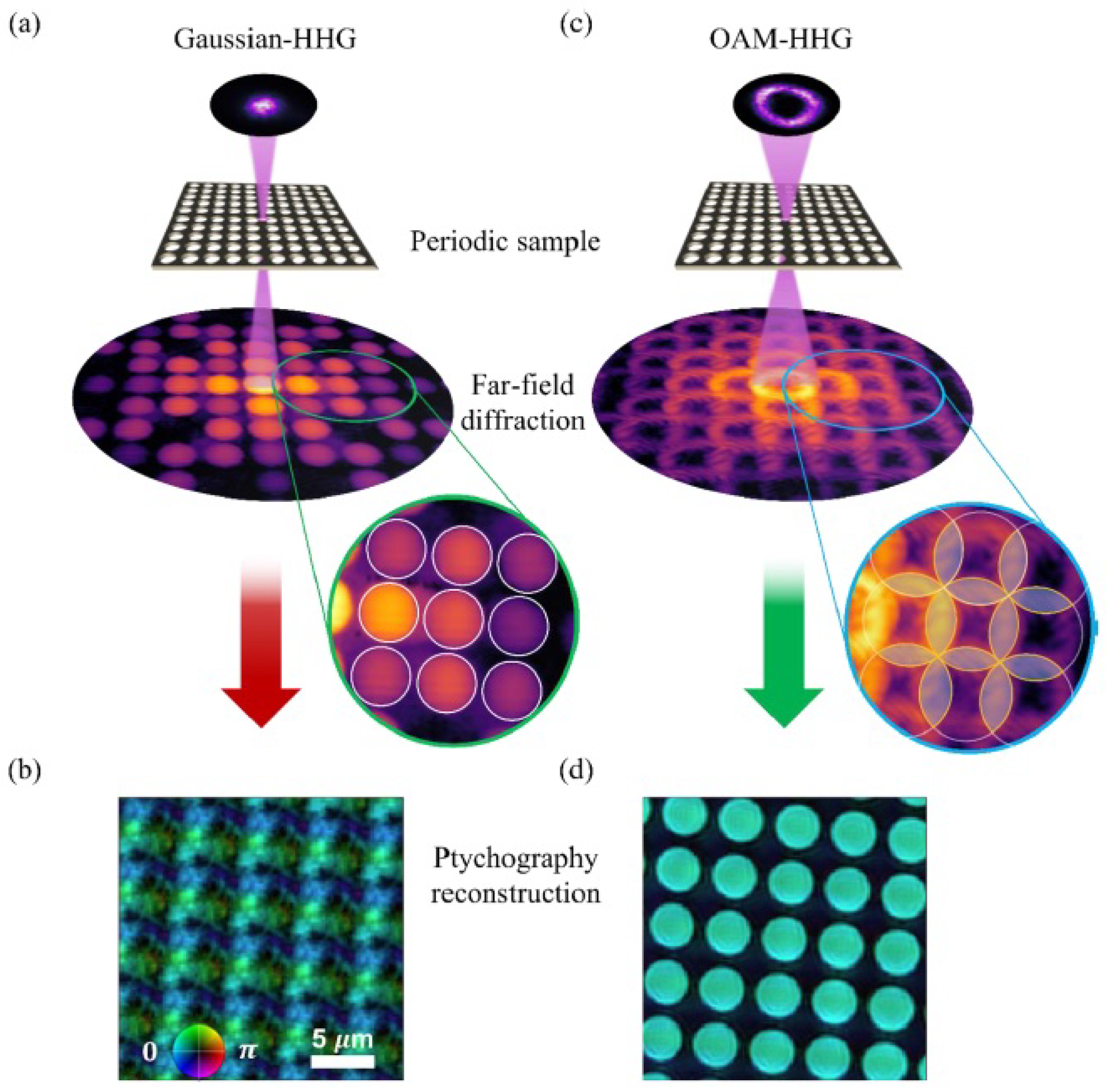
2.18. Ptychography
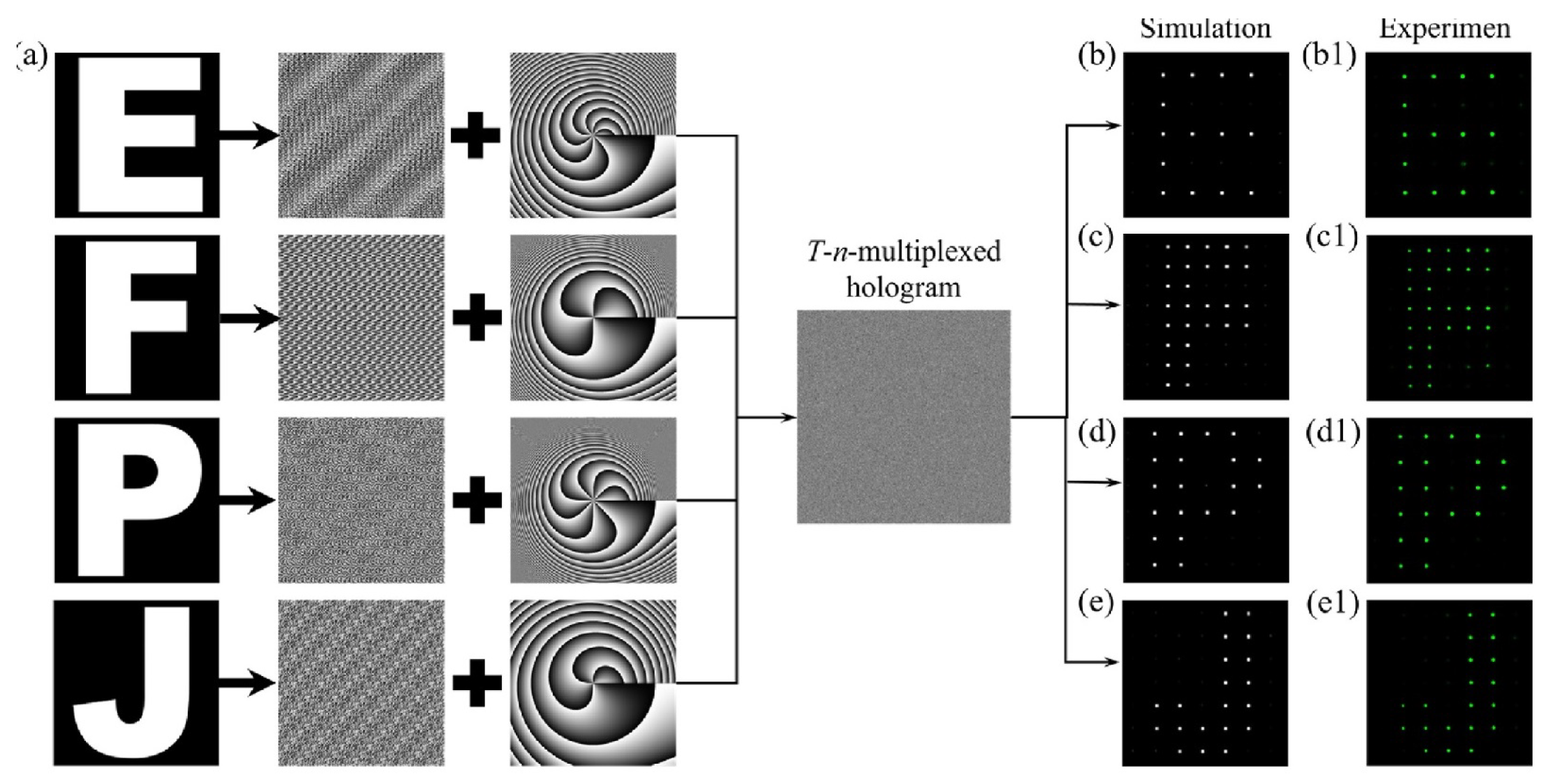
2.19. Encryption
2.20. Deep Learning
3. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Senthilkumaran, P. Singularities in Physics and Engineering; IOP Publishing: Bristol, UK, 2024. [Google Scholar]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.; Woerdman, J. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef] [PubMed]
- Coullet, P.; Gil, L.; Rocca, F. Optical vortices. Opt. Commun. 1989, 73, 403–408. [Google Scholar] [CrossRef]
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photonics 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Ruchi; Senthilkumaran, P.; Pal, S.K. Phase singularities to polarization singularities. Int. J. Opt. 2020, 2020, 2812803. [Google Scholar] [CrossRef]
- Senthilkumaran, P.; Masajada, J.; Sato, S. Interferometry with vortices. Int. J. Opt. 2012, 2012, 517591. [Google Scholar] [CrossRef]
- Pachava, S.; Dharmavarapu, R.; Vijayakumar, A.; Jayakumar, S.; Manthalkar, A.; Dixit, A.; Viswanathan, N.K.; Srinivasan, B.; Bhattacharya, S. Generation and decomposition of scalar and vector modes carrying orbital angular momentum: A review. Opt. Eng. 2020, 59, 041205. [Google Scholar] [CrossRef]
- Porfirev, A.P.; Kuchmizhak, A.A.; Gurbatov, S.O.; Juodkazis, S.; Khonina, S.N.; Kulchin, Y.N. Phase singularities and optical vortices in photonics. Phys. Usp 2022, 192, 841–866. [Google Scholar] [CrossRef]
- Angelsky, O.; Bekshaev, A.Y.; Vasnetsov, M.; Zenkova, C.Y.; Maksimyak, P.; Zheng, J. Optical phase singularities: Physical nature, manifestations and applications. Front. Phys. 2022, 10, 1060787. [Google Scholar] [CrossRef]
- Khare, K.; Butola, M.; Rajora, S. Fourier Optics and Computational Imaging; Springer Nature: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Lohmann, A.W.; Paris, D. Binary Fraunhofer holograms, generated by computer. Appl. Opt. 1967, 6, 1739–1748. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.K. Principles and techniques of digital holographic microscopy. SPIE Rev. 2010, 1, 018005. [Google Scholar] [CrossRef]
- Gerchberg, R.W. A practical algorithm for the determination of plane from image and diffraction pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Gu, B.; Yang, G. On the phase retrieval problem in optical and electronic microscopy. Acta Opt. Sin. 1981, 1, 517–522. [Google Scholar]
- Yang, G.Z.; Gu, B.Y. On the amplitude-phase retrieval problem in optical systems. Acta Opt. Sin. 1981, 30, 410–413. [Google Scholar] [CrossRef]
- Fienup, J.R. Reconstruction of an object from the modulus of its Fourier transform. Opt. Lett. 1978, 3, 27–29. [Google Scholar] [CrossRef] [PubMed]
- Collaro, A.; Franceschetti, G.; Palmieri, F.; Ferreiro, M.S. Phase unwrapping by means of genetic algorithms. J. Opt. Soc. Am. A 1998, 15, 407–418. [Google Scholar] [CrossRef]
- Quatieri, T.; Oppenheim, A. Iterative techniques for minimum phase signal reconstruction from phase or magnitude. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1187–1193. [Google Scholar] [CrossRef]
- Butola, M.; Rajora, S.; Khare, K. Phase retrieval with complexity guidance. J. Opt. Soc. Am. A 2019, 36, 202–211. [Google Scholar] [CrossRef]
- Rai, M.R.; Vijayakumar, A.; Rosen, J. Non-linear adaptive three-dimensional imaging with interferenceless coded aperture correlation holography (I-COACH). Opt. Express 2018, 26, 18143–18154. [Google Scholar] [CrossRef]
- Fienup, J.R. Phase retrieval algorithms: A personal tour. Appl. Opt. 2012, 52, 45–56. [Google Scholar] [CrossRef] [PubMed]
- Guo, C.; Liu, S.; Sheridan, J.T. Iterative phase retrieval algorithms. I: Optimization. Appl. Opt. 2015, 54, 4698–4708. [Google Scholar] [CrossRef]
- Shechtman, Y.; Eldar, Y.C.; Cohen, O.; Chapman, H.N.; Miao, J.; Segev, M. Phase retrieval with application to optical imaging: A contemporary overview. IEEE Signal Process. Mag. 2015, 32, 87–109. [Google Scholar] [CrossRef]
- Guo, C.; Wei, C.; Tan, J.; Chen, K.; Liu, S.; Wu, Q.; Liu, Z. A review of iterative phase retrieval for measurement and encryption. Opt. Lasers Eng. 2017, 89, 2–12. [Google Scholar] [CrossRef]
- Himanshu, S.B.G.; Yadav, R.K.; Poply, V. Different Phase Retrieval Algorithms: A Review. Int. J. Future Gener. Commun. Netw. 2020, 13, 1978–1989. [Google Scholar]
- Leith, E.N.; Upatnieks, J. Wavefront reconstruction with diffused illumination and three-dimensional objects. J. Opt. Soc. Am. 1964, 54, 1295–1301. [Google Scholar] [CrossRef]
- Baranova, N.; Zel’dovich, B.Y.; Mamaev, A.; Pilipetski, N.; Shkunov, V. Speckle-inhomogeneous field wavefront dislocations. Pis’ ma Zh. Eks. Teor. Fiz 1981, 33, 206–210. [Google Scholar]
- Freund, I.; Shvartsman, N.; Freilikher, V. Optical dislocation networks in highly random media. Opt. Commun. 1993, 101, 247–264. [Google Scholar] [CrossRef]
- Shvartsman, N.; Freund, I. Vortices in random wave fields: Nearest neighbor anticorrelations. Phys. Rev. Lett. 1994, 72, 1008. [Google Scholar] [CrossRef] [PubMed]
- May, M.; Françon, M. Correlation and information processing using speckles. J. Opt. Soc. Am. 1976, 66, 1275–1282. [Google Scholar] [CrossRef]
- Takai, N.; Iwai, T.; Asakura, T. Correlation distance of dynamic speckles. Appl. Opt. 1983, 22, 170–177. [Google Scholar] [CrossRef] [PubMed]
- Lecompte, D.; Smits, A.; Bossuyt, S.; Sol, H.; Vantomme, J.; Van Hemelrijck, D.; Habraken, A. Quality assessment of speckle patterns for digital image correlation. Opt. Lasers Eng. 2006, 44, 1132–1145. [Google Scholar] [CrossRef]
- Dogariu, A.; Carminati, R. Electromagnetic field correlations in three-dimensional speckles. Phys. Rep. 2015, 559, 1–29. [Google Scholar] [CrossRef]
- Bräuer, R.; Wojak, U.; Wyrowski, F.; Bryngdahl, O. Digital diffusers for optical holography. Opt. Lett. 1991, 16, 1427–1429. [Google Scholar] [CrossRef]
- Bräuer, R.; Wyrowski, F.; Bryngdahl, O. Diffusers in digital holography. J. Opt. Soc. Am. A 1991, 8, 572–578. [Google Scholar] [CrossRef]
- Nakayama, Y.; Kato, M. Diffuser with pseudorandom phase sequence. J. Opt. Soc. Am. 1979, 69, 1367–1372. [Google Scholar] [CrossRef]
- Dallas, W. Deterministic diffusers for holography. Appl. Opt. 1973, 12, 1179–1187. [Google Scholar] [CrossRef] [PubMed]
- Hirsch, P.M.; Jordan, J.A., Jr.; Lesem, L.B. Method of Making an Object Dependent Diffuser. U.S. Patent 3,619,022, 9 November 1971. [Google Scholar]
- Wyrowski, F.; Bryngdahl, O. Iterative Fourier-transform algorithm applied to computer holography. J. Opt. Soc. Am. A 1988, 5, 1058–1065. [Google Scholar] [CrossRef]
- Fienup, J.; Wackerman, C. Phase-retrieval stagnation problems and solutions. J. Opt. Soc. Am. A 1986, 3, 1897–1907. [Google Scholar] [CrossRef]
- Aagedal, H.; Schmid, M.; Beth, T.; Teiwes, S.; Wyrowski, F. Theory of speckles in diffractive optics and its application to beam shaping. J. Mod. Opt. 1996, 43, 1409–1421. [Google Scholar] [CrossRef]
- Senthilkumaran, P.; Wyrowski, F. Phase synthesis in wave-optical engineering: Mapping-and diffuser-type approaches. J. Mod. Opt. 2002, 49, 1831–1850. [Google Scholar] [CrossRef]
- Senthilkumaran, P.; Wyrowski, F.; Schimmel, H. Vortex stagnation problem in iterative Fourier transform algorithms. Opt. Lasers Eng. 2005, 43, 43–56. [Google Scholar] [CrossRef]
- Ghiglia, D.C.; Mastin, G.A.; Romero, L.A. Cellular-automata method for phase unwrapping. J. Opt. Soc. Am. A 1987, 4, 267–280. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Zebker, H.A.; Werner, C.L. Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef]
- Huntley, J.; Buckland, J. Characterization of sources of 2π phase discontinuity in speckle interferograms. J. Opt. Soc. Am. A 1995, 12, 1990–1996. [Google Scholar] [CrossRef]
- Ghiglia, D.C.; Pritt, M.D. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Aoki, T.; Sotomaru, T.; Ozawa, T.; Komiyama, T.; Miyamoto, Y.; Takeda, M. Two-dimensional phase unwrapping by direct elimination of rotational vector fields from phase gradients obtained by heterodyne techniques. Opt. Rev. 1998, 5, 374–379. [Google Scholar] [CrossRef]
- Bahl, M.; Senthilkumaran, P. Helmholtz Hodge decomposition of scalar optical fields. J. Opt. Soc. Am. A 2012, 29, 2421–2427. [Google Scholar] [CrossRef]
- Khare, K. Complex signal representation, Mandel’s theorem, and spiral phase quadrature transform. Appl. Opt. 2008, 47, E8–E12. [Google Scholar] [CrossRef]
- Mandel, L. Complex representation of optical fields in coherence theory. J. Opt. Soc. Am. A 1967, 57, 613–617. [Google Scholar] [CrossRef]
- Fienup, J.R. Phase retrieval algorithms: A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef]
- Paganin, D.; Nugent, K.A. Noninterferometric phase imaging with partially coherent light. Phys. Rev. Lett. 1998, 80, 2586. [Google Scholar] [CrossRef]
- Dorrer, C.; Zuegel, J. Optical testing using the transport-of-intensity equation. Opt. Express 2007, 15, 7165–7175. [Google Scholar] [CrossRef]
- Anand, A.; Pedrini, G.; Osten, W.; Almoro, P. Wavefront sensing with random amplitude mask and phase retrieval. Opt. Lett. 2007, 32, 1584–1586. [Google Scholar] [CrossRef] [PubMed]
- Almoro, P.; Pedrini, G.; Osten, W. Complete wavefront reconstruction using sequential intensity measurements of a volume speckle field. Appl. Opt. 2006, 45, 8596–8605. [Google Scholar] [CrossRef]
- Díaz-Doutón, F.; Pujol, J.; Arjona, M.; Luque, S.O. Curvature sensor for ocular wavefront measurement. Opt. Lett. 2006, 31, 2245–2247. [Google Scholar] [CrossRef]
- Sharma, M.K.; Gaur, C.; Senthilkumaran, P.; Khare, K. Phase imaging using spiral-phase diversity. Appl. Opt. 2015, 54, 3979–3985. [Google Scholar] [CrossRef]
- Echeverri-Chacón, S.; Restrepo, R.; Cuartas-Vélez, C.; Uribe-Patarroyo, N. Vortex-enhanced coherent-illumination phase diversity for phase retrieval in coherent imaging systems. Opt. Lett. 2016, 41, 1817–1820. [Google Scholar] [CrossRef]
- Scivier, M.; Fiddy, M. Phase ambiguities and the zeros of multidimensional band-limited functions. J. Opt. Soc. Am. A 1985, 2, 693–697. [Google Scholar] [CrossRef]
- Wackerman, C.; Yagle, A. Use of Fourier domain real-plane zeros to overcome a phase retrieval stagnation. J. Opt. Soc. Am. A 1991, 8, 1898–1904. [Google Scholar] [CrossRef]
- Wackerman, C.C.; Yagle, A.E. Phase retrieval and estimation with use of real-plane zeros. J. Opt. Soc. Am. A 1994, 11, 2016–2026. [Google Scholar] [CrossRef]
- Kularia, M.; Banerjee, M.; Khare, K. Twin-stagnation free phase retrieval with vortex phase illumination. J. Opt. Soc. Am. A 2024, 41, 2016–2026. [Google Scholar] [CrossRef] [PubMed]
- Cheng, M.; Guo, L.; Li, J.; Zhang, Y. Channel capacity of the OAM-based free-space optical communication links with Bessel–Gauss beams in turbulent ocean. IEEE Photonics J. 2016, 8, 7901411. [Google Scholar] [CrossRef]
- Zhang, Y.; Shan, L.; Li, Y.; Yu, L. Effects of moderate to strong turbulence on the Hankel-Bessel-Gaussian pulse beam with orbital angular momentum in the marine-atmosphere. Opt. Express 2017, 25, 33469–33479. [Google Scholar] [CrossRef]
- Li, Y.; Yu, L.; Zhang, Y. Influence of anisotropic turbulence on the orbital angular momentum modes of Hermite-Gaussian vortex beam in the ocean. Opt. Express 2017, 25, 12203–12215. [Google Scholar] [CrossRef] [PubMed]
- Rusch, L.A.; Rad, M.; Allahverdyan, K.; Fazal, I.; Bernier, E. Carrying data on the orbital angular momentum of light. IEEE Commun. Mag. 2018, 56, 219–224. [Google Scholar] [CrossRef]
- Willner, A.E.; Zhao, Z.; Ren, Y.; Li, L.; Xie, G.; Song, H.; Liu, C.; Zhang, R.; Bao, C.; Pang, K. Underwater optical communications using orbital angular momentum-based spatial division multiplexing. Opt. Commun. 2018, 408, 21–25. [Google Scholar] [CrossRef]
- Amhoud, E.M.; Ooi, B.S.; Alouini, M.S. A unified statistical model for atmospheric turbulence-induced fading in orbital angular momentum multiplexed FSO systems. IEEE Trans. Wirel. Commun. 2019, 19, 888–900. [Google Scholar] [CrossRef]
- Sawant, A.; Lee, I.; Jung, B.C.; Choi, E. Ultimate capacity analysis of orbital angular momentum channels. IEEE Wirel. Commun. 2020, 28, 90–96. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, B.; Gao, Z.; Zhao, G.; Duan, Z. Evolution behavior of Gaussian Schell-model vortex beams propagating through oceanic turbulence. Opt. Express 2014, 22, 17723–17734. [Google Scholar] [CrossRef]
- Yan, B.; Lu, Z.; Hu, J.; Xu, T.; Zhang, H.; Lin, W.; Yue, Y.; Liu, H.; Liu, B. Orbital angular momentum (OAM) carried by asymmetric vortex beams for wireless communications: Theory, experiment and current challenges. IEEE J. Sel. Top. Quantum Electron. 2020, 27, 7600310. [Google Scholar] [CrossRef]
- Köse, U.; Güraksin, G.E.; Deperlioğlu, Ö. Improving underwater image quality via vortex optimization algorithm. In Proceedings of the International Multidisciplinary Conference (IMUCO 2016), Antalya, Turkey, 10–13 October 2016; p. 327. [Google Scholar]
- Chang, H.; Yin, X.; Cui, X.; Chen, X.Z.; Su, Y.Z.; Ma, J.X.; Wang, Y.J.; Zhang, L.; Xin, X. Performance analysis of adaptive optics with a phase retrieval algorithm in orbital-angular-momentum-based oceanic turbulence links. Appl. Opt. 2019, 58, 6085–6090. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Yan, Q.; Zhang, Y.; Hu, L. Received probability of perfect optical vortex in absorbent and weak turbulent seawater links. Appl. Opt. 2021, 60, 10772–10779. [Google Scholar] [CrossRef] [PubMed]
- Yan, Q.; Zhang, Y.; Yu, L.; Zhu, Y. Absorptive turbulent seawater and parameter optimization of perfect optical vortex for optical communication. J. Mar. Sci. Eng. 2022, 10, 1256. [Google Scholar] [CrossRef]
- Hefner, B.T.; Marston, P.L. An acoustical helicoidal wave transducer with applications for the alignment of ultrasonic and underwater systems. J. Acoust. Soc. Am. 1999, 106, 3313–3316. [Google Scholar] [CrossRef]
- Kelly, M.E.; Shi, C. Design and simulation of acoustic vortex wave arrays for long-range underwater communication. JASA Express Lett. 2023, 3, 076001. [Google Scholar] [CrossRef] [PubMed]
- Volke-Sepúlveda, K.; Santillán, A.O.; Boullosa, R.R. Transfer of angular momentum to matter from acoustical vortices in free space. Phys. Rev. Lett. 2008, 100, 024302. [Google Scholar] [CrossRef]
- Thidé, B.; Then, H.; Sjöholm, J.; Palmer, K.; Bergman, J.; Carozzi, T.; Istomin, Y.N.; Ibragimov, F.N.; Khamitova, R. Utilization of photon orbital angular momentum in the low-frequency radio domain. Phys. Rev. Lett. 2007, 99, 087701. [Google Scholar] [CrossRef]
- Edfors, O.; Johansson, A.J. Is orbital angular momentum (OAM) based radio communication an unexploited area? IEEE Trans. Antennas Propag. 2011, 60, 1126–1131. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Q.; Qu, F.; Wei, Y.; Tu, X.; Xu, J.; Xu, W.; Yang, L. High-Speed Underwater Acoustic Orbital Angular Momentum Communications. IEEE J. Ocean. Eng. 2024, 49, 1588–1604. [Google Scholar] [CrossRef]
- Das, A.T.; Rajesh, R.; Gopinath, P. Performance analysis of Sinh and Cosh Gaussian vortex beam in vertical underwater optical communication. Waves Random Complex Media 2024, 1–28. [Google Scholar] [CrossRef]
- Dorn, R.; Quabis, S.; Leuchs, G. Sharper focus for a radially polarized light beam. Phys. Rev. Lett. 2003, 91, 233901. [Google Scholar] [CrossRef]
- Vicidomini, G.; Bianchini, P.; Diaspro, A. STED super-resolved microscopy. Nat. Methods 2018, 15, 173–182. [Google Scholar] [CrossRef] [PubMed]
- Hecht, E. Optics; Pearson Education India: New Delhi, India, 2012. [Google Scholar]
- Fatemi, F.K.; Bashkansky, M. Focusing properties of high charge number vortex laser beams. Appl. Opt. 2007, 46, 7573–7578. [Google Scholar] [CrossRef] [PubMed]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Mahajan, V.N. Optical Imaging and Aberrations: Ray Geometrical Optics; SPIE Press: Bellingham, WA, USA, 1998. [Google Scholar]
- Sheppard, C.; Matthews, H. Imaging in high-aperture optical systems. J. Opt. Soc. Am. A 1987, 4, 1354–1360. [Google Scholar] [CrossRef]
- Sheppard, C.J. Validity of the Debye approximation. Opt. Lett. 2000, 25, 1660–1662. [Google Scholar] [CrossRef]
- Stamnes, J.J. Waves in Focal Regions: Propagation, Diffraction and Focusing of Light, Sound and Water Waves; Routledge: London, UK, 2017. [Google Scholar]
- Wolf, E.; Li, Y. Conditions for the validity of the Debye integral representation of focused fields. Opt. Commun. 1981, 39, 205–210. [Google Scholar] [CrossRef]
- Richards, B.; Wolf, E. Electromagnetic diffraction in optical systems, II. Structure of the image field in an aplanatic system. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1959, 253, 358–379. [Google Scholar]
- Helseth, L. Optical vortices in focal regions. Opt. Commun. 2004, 229, 85–91. [Google Scholar] [CrossRef]
- Bokor, N.; Iketaki, Y.; Watanabe, T.; Fujii, M. Investigation of polarization effects for high-numerical-aperture first-order Laguerre-Gaussian beams by 2D scanning with a single fluorescent microbead. Opt. Express 2005, 13, 10440–10447. [Google Scholar] [CrossRef]
- Kant, R. An analytical solution of vector diffraction for focusing optical systems with Seidel aberrations: I. spherical aberration, curvature of field, and distortion. J. Mod. Opt. 1993, 40, 2293–2310. [Google Scholar] [CrossRef]
- Kant, R. An analytical method of vector diffraction for focusing optical systems with Seidel aberrations II: Astigmatism and coma. J. Mod. Opt. 1995, 42, 299–320. [Google Scholar] [CrossRef]
- Singh, R.K.; Senthilkumaran, P.; Singh, K. Focusing of a vortex carrying beam with Gaussian background by a lens in the presence of spherical aberration and defocusing. Opt. Lasers Eng. 2007, 45, 773–782. [Google Scholar] [CrossRef]
- Singh, R.K.; Senthilkumaran, P.; Singh, K. Influence of astigmatism and defocusing on the focusing of a singular beam. Opt. Commun. 2007, 270, 128–138. [Google Scholar] [CrossRef]
- Singh, R.K.; Senthilkumaran, P.; Singh, K. Effect of coma on the focusing of an apertured singular beam. Opt. Lasers Eng. 2007, 45, 488–494. [Google Scholar] [CrossRef]
- Singh, R.K.; Senthilkumaran, P.; Singh, K. Effect of primary spherical aberration on high-numerical-aperture focusing of a Laguerre-Gaussian beam. J. Opt. Soc. Am. A 2008, 25, 1307–1318. [Google Scholar] [CrossRef]
- Singh, R.K.; Senthilkumaran, P.; Singh, K. Focusing of linearly-, and circularly polarized Gaussian background vortex beams by a high numerical aperture system afflicted with third-order astigmatism. Opt. Commun. 2008, 281, 5939–5948. [Google Scholar] [CrossRef]
- Pal, S.K.; Singh, R.K.; Senthilkumaran, P. Effect of primary astigmatism on the tight focusing of ellipse field singularities. Opt. Laser Technol. 2024, 169, 110078. [Google Scholar] [CrossRef]
- Pal, S.K.; Singh, R.K.; Senthilkumaran, P. Influence of Primary Coma on the Tightly Focusing Characteristics of Circular Basis Hybrid Order Poincaré Sphere Beams. Photonics 2024, 11, 98. [Google Scholar] [CrossRef]
- Pal, S.K.; Somers, L.; Singh, R.K.; Senthilkumaran, P.; Arie, A. Focused polarization ellipse field singularities: Interaction of spin-orbital angular momentum and the formation of optical Möbius strips. Phys. Scr. 2023, 98, 055507. [Google Scholar] [CrossRef]
- Freund, I. Cones, spirals, and Möbius strips, in elliptically polarized light. Opt. Commun. 2005, 249, 7–22. [Google Scholar] [CrossRef]
- Bauer, T.; Banzer, P.; Karimi, E.; Orlov, S.; Rubano, A.; Marrucci, L.; Santamato, E.; Boyd, R.W.; Leuchs, G. Observation of optical polarization Möbius strips. Science 2015, 347, 964–966. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Edgar, J.S.; Jeffries, G.D.; McGloin, D.; Chiu, D.T. Spin-to-orbital angular momentum conversion in a strongly focused optical beam. Phys. Rev. Lett. 2007, 99, 073901. [Google Scholar] [CrossRef] [PubMed]
- Bahl, M.; Senthilkumaran, P. Focal plane internal energy flows of singular beams in astigmatically aberrated low numerical aperture systems. J. Opt. Soc. Am. A 2014, 31, 2046–2054. [Google Scholar] [CrossRef]
- Bahl, M.; Singh, B.K.; Kumar, R.; Senthilkumaran, P. Internal energy flows of coma-affected singular beams in low-numerical-aperture systems. J. Opt. Soc. Am. A 2015, 32, 514–521. [Google Scholar] [CrossRef] [PubMed]
- Bahl, M.; Senthilkumaran, P. Energy circulations in singular beams diffracted through an isosceles right triangular aperture. Phys. Rev. A 2015, 92, 013831. [Google Scholar] [CrossRef]
- Sharma, M.K.; Joseph, J.; Senthilkumaran, P. Selective edge enhancement using anisotropic vortex filter. Appl. Opt. 2011, 50, 5279–5286. [Google Scholar] [CrossRef]
- Khonina, S.; Kotlyar, V.; Shinkaryev, M.; Soifer, V.; Uspleniev, G. The phase rotor filter. J. Mod. Opt. 1992, 39, 1147–1154. [Google Scholar] [CrossRef]
- Lohmann, A.W.; Mendlovic, D.; Zalevsky, Z. Fractional hilbert transform. Opt. Lett. 1996, 21, 281–283. [Google Scholar] [CrossRef]
- Davis, J.A.; McNamara, D.E.; Cottrell, D.M. Analysis of the fractional Hilbert transform. Appl. Opt. 1998, 37, 6911–6913. [Google Scholar] [CrossRef]
- Davis, J.A.; McNamara, D.E.; Cottrell, D.M.; Campos, J. Image processing with the radial Hilbert transform: Theory and experiments. Opt. Lett. 2000, 25, 99–101. [Google Scholar] [CrossRef]
- Pan, Y.; Jia, W.; Yu, J.; Dobson, K.; Zhou, C.; Wang, Y.; Poon, T.C. Edge extraction using a time-varying vortex beam in incoherent digital holography. Opt. Lett. 2014, 39, 4176–4179. [Google Scholar] [CrossRef]
- Sharma, M.K.; Joseph, J.; Senthilkumaran, P. Selective edge enhancement using shifted anisotropic vortex filter. J. Opt. 2013, 42, 1–7. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, Z.; Sun, H.; Xia, J.; Ding, J. Vectorial optical vortex filtering for edge enhancement. J. Opt. 2016, 18, 035703. [Google Scholar] [CrossRef]
- Bhargava Ram, B.; Senthilkumaran, P.; Sharma, A. Polarization-based spatial filtering for directional and nondirectional edge enhancement using an S-waveplate. Appl. Opt. 2017, 56, 3171–3178. [Google Scholar] [CrossRef]
- Gu, Z.; Yin, D.; Nie, S.; Feng, S.; Xing, F.; Ma, J.; Yuan, C. Advances of image edge enhancement based on vortex filtering. Infrared Laser Eng. 2019, 48, 603015. [Google Scholar]
- Gao, Z.; Wang, Y.; Han, L.; Li, C.; Xin, X. Image edge enhancement technique using a novel optical vortex filtering. In Proceedings of the 2021 19th International Conference on Optical Communications and Networks (ICOCN), Qufu, China, 23–27 August 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–3. [Google Scholar]
- Tan, W.; Bai, Y.; Huang, X.; Jiang, T.; Nan, S.; Fu, Q.; Zou, X.; Fu, X. Enhancing critical resolution of a ghost imaging system by using a vortex beam. Opt. Express 2022, 30, 14061–14072. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Ma, J.; Sun, D.; Tian, Z.; Cao, L.; Su, P. Amp-vortex edge-camera: A lensless multi-modality imaging system with edge enhancement. Opt. Express 2023, 31, 22519–22531. [Google Scholar] [CrossRef]
- Yu, X.; Wang, Z.; Cheng, X.; Zhao, L.; Li, X.; Sun, Y. Nonlinear edge enhancement imaging based on Laguerre–Gaussian superimposed vortex filters. Opt. Lett. 2024, 49, 482–485. [Google Scholar] [CrossRef]
- Rosen, J.; Brooker, G. Digital spatially incoherent Fresnel holography. Opt. Lett. 2007, 32, 912–914. [Google Scholar] [CrossRef] [PubMed]
- Rosen, J.; Brooker, G. Non-scanning motionless fluorescence three-dimensional holographic microscopy. Nat. Photonics 2008, 2, 190–195. [Google Scholar] [CrossRef]
- He, J.; Zhang, P.; Su, J.; Wang, J.; Tian, Y.; Hu, Y.; Ma, F. Edge enhancement in three-dimensional vortex imaging based on FINCH by Bessel-like spiral phase modulation. Opt. Express 2024, 32, 1438–1450. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, Y.; He, Y.; Zhou, L.; Li, Y.; He, W.; Gu, G.; Chen, Q. Short-wavelength-infrared upconversion edge enhancement imaging based on a Laguerre-Gaussian composite vortex filter. Opt. Express 2024, 32, 21696–21707. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.; Tao, S. Generation of auto-focusing vortex beam via segment vortex phase for imaging edge-enhancement. Phys. Scr. 2024, 99, 055517. [Google Scholar] [CrossRef]
- Zangpo, J.; Kobayashi, H. Single-pixel edge enhancement of object via convolutional filtering with localized vortex phase. arXiv 2024, arXiv:2403.15014. [Google Scholar]
- Xu, D.; Zhang, W. Implementing the edge enhancement with vortex filter in both linear and nonlinear optics. Front. Phys. 2023, 11, 1276830. [Google Scholar] [CrossRef]
- Beresna, M.; Gecevičius, M.; Kazansky, P.G. Polarization sensitive elements fabricated by femtosecond laser nanostructuring of glass. Opt. Mater. Express 2011, 1, 783–795. [Google Scholar] [CrossRef]
- Slussarenko, S.; Murauski, A.; Du, T.; Chigrinov, V.; Marrucci, L.; Santamato, E. Tunable liquid crystal q-plates with arbitrary topological charge. Opt. Express 2011, 19, 4085–4090. [Google Scholar] [CrossRef]
- Marrucci, L. The q-plate and its future. J. Nanophotonics 2013, 7, 078598. [Google Scholar] [CrossRef]
- Khonina, S.; Porfirev, A.; Ustinov, A. Sudden autofocusing of superlinear chirp beams. J. Opt. 2018, 20, 025605. [Google Scholar] [CrossRef]
- Li, D.; Feng, S.; Nie, S.; Ma, J.; Yuan, C. Scalar and vectorial vortex filtering based on geometric phase modulation with a q-plate. J. Opt. 2019, 21, 065702. [Google Scholar] [CrossRef]
- Zangpo, J.; Kawabe, T.; Kobayashi, H. Edge-enhanced microscopy of complex objects using scalar and vectorial vortex filtering. Opt. Express 2023, 31, 38388–38399. [Google Scholar] [CrossRef] [PubMed]
- Segawa, S.; Kozawa, Y.; Sato, S. Demonstration of subtraction imaging in confocal microscopy with vector beams. Opt. Lett. 2014, 39, 4529–4532. [Google Scholar] [CrossRef] [PubMed]
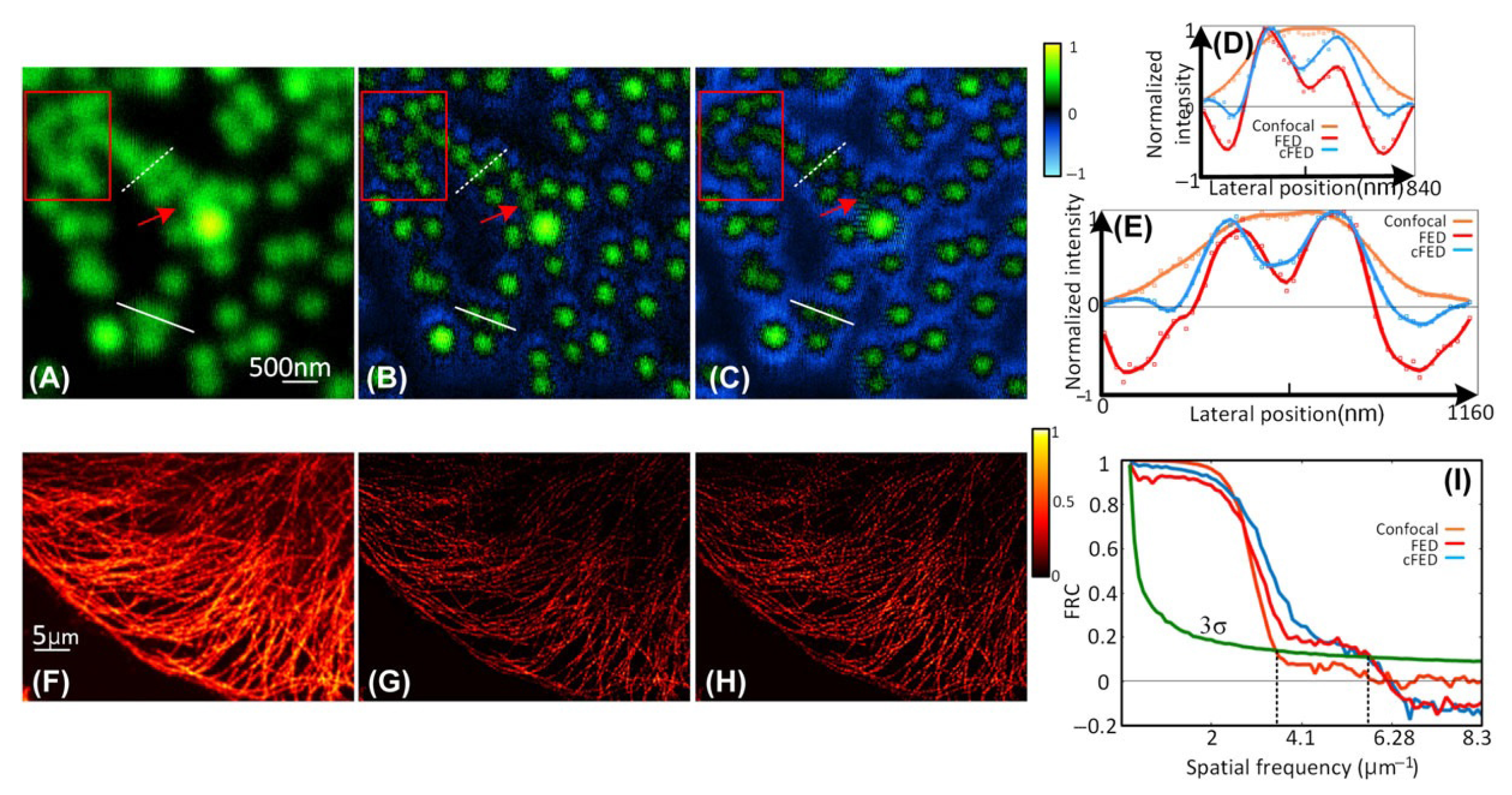
- Rong, Z.; Kuang, C.; Fang, Y.; Zhao, G.; Xu, Y.; Liu, X. Super-resolution microscopy based on fluorescence emission difference of cylindrical vector beams. Opt. Commun. 2015, 354, 71–78. [Google Scholar] [CrossRef]
- Zhu, D.; Liu, W.; Zhang, Z.; Zheng, C.; Chen, Y.; Li, C.; Kuang, C.; Fan, J.; Xu, Y.; Liu, X.; et al. Enhancement of fluorescence emission difference microscopy using conjugated vortex phase modulation. J. Microsc. 2018, 272, 151–159. [Google Scholar] [CrossRef] [PubMed]
- Masajada, J.; Leniec, M.; Jankowska, E.; Thienpont, H.; Ottevaere, H.; Gomez, V. Deep microstructure topography characterization with optical vortex interferometer. Opt. Express 2008, 16, 19179–19191. [Google Scholar] [CrossRef] [PubMed]
- Masajada, J.; Leniec, M.; Augustyniak, I. Optical vortex scanning inside the Gaussian beam. J. Opt. 2011, 13, 035714. [Google Scholar] [CrossRef]
- Augustyniak, I.; Popiołek-Masajada, A.; Masajada, J.; Drobczyński, S. New scanning technique for the optical vortex microscope. Appl. Opt. 2012, 51, C117–C124. [Google Scholar] [CrossRef] [PubMed]
- Popiołek-Masajada, A.; Masajada, J.; Kurzynowski, P. Analytical model of the optical vortex scanning microscope with a simple phase object. Photonics 2017, 4, 38. [Google Scholar] [CrossRef]
- Sokolenko, B.; Shostka, N.; Karakchieva, O.; Poletaev, D.; Voytitsky, V.; Halilov, S.; Prisyazhniuk, A.; Ilyasova, A.; Kolosenko, E. Optical vortex phase determination for nanoscale imaging. J. Phys. Conf. Ser. 2018, 1062, 012004. [Google Scholar] [CrossRef]
- Ni, J.; Huang, C.; Zhou, L.M.; Gu, M.; Song, Q.; Kivshar, Y.; Qiu, C.W. Multidimensional phase singularities in nanophotonics. Science 2021, 374, eabj0039. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.P.; Pandey, N.; Khare, K. High contrast computational imaging with vortex phase diversity. J. Phys. B At. Mol. Opt. Phys. 2024, 57, 225402. [Google Scholar] [CrossRef]
- Lee, H.; Kim, J.; Kim, H.H.; Kim, C.S.; Kim, J. Review on optical imaging techniques for multispectral analysis of nanomaterials. Nanotheranostics 2022, 6, 50. [Google Scholar] [CrossRef]
- Wang, W.; Qiao, Y.; Ishijima, R.; Yokozeki, T.; Honda, D.; Matsuda, A.; Hanson, S.G.; Takeda, M. Constellation of phase singularities in a specklelike pattern for optical vortex metrology applied to biological kinematic analysis. Opt. Express 2008, 16, 13908–13917. [Google Scholar] [CrossRef]
- Wang, W.; Yokozeki, T.; Ishijima, R.; Wada, A.; Miyamoto, Y.; Takeda, M.; Hanson, S.G. Optical vortex metrology for nanometric speckle displacement measurement. Opt. Express 2006, 14, 120–127. [Google Scholar] [CrossRef]
- Wang, W.; Dennis, M.R.; Ishijima, R.; Yokozeki, T.; Matsuda, A.; Hanson, S.G.; Takeda, M. Poincaré sphere representation for the anisotropy of phase singularities and its applications to optical vortex metrology for fluid mechanical analysis. Opt. Express 2007, 15, 11008–11019. [Google Scholar] [CrossRef]
- Takeda, M.; Wang, W.; Hanson, S.G.; Miyamoto, Y. Optical vortex metrology: Are phase singularities foes or friends in optical metrology? In Proceedings of the Eighth International Conference on Correlation Optics, Chernivsti, Ukraine, 11–14 September 2007; SPIE: Bellingham, WA, USA, 2008; Volume 7008, pp. 410–417. [Google Scholar]
- Wang, W.; Yokozeki, T.; Ishijima, R.; Takeda, M.; Hanson, S.G. Optical vortex metrology based on the core structures of phase singularities in Laguerre-Gauss transform of a speckle pattern. Opt. Express 2006, 14, 10195–10206. [Google Scholar] [CrossRef] [PubMed]
- Umapathy, K.; Nair, K.; Masse, S.; Krishnan, S.; Rogers, J.; Nash, M.P.; Nanthakumar, K. Phase mapping of cardiac fibrillation. Circ. Arrhythmia Electrophysiol. 2010, 3, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Kuklik, P.; Zeemering, S.; Maesen, B.; Maessen, J.; Crijns, H.J.; Verheule, S.; Ganesan, A.N.; Schotten, U. Reconstruction of instantaneous phase of unipolar atrial contact electrogram using a concept of sinusoidal recomposition and Hilbert transform. IEEE Trans. Biomed. Eng. 2014, 62, 296–302. [Google Scholar] [CrossRef] [PubMed]
- Kuklik, P.; Zeemering, S.; van Hunnik, A.; Maesen, B.; Pison, L.; Lau, D.H.; Maessen, J.; Podziemski, P.; Meyer, C.; Schäffer, B.; et al. Identification of rotors during human atrial fibrillation using contact mapping and phase singularity detection: Technical considerations. IEEE Trans. Biomed. Eng. 2016, 64, 310–318. [Google Scholar]
- Roney, C.H.; Cantwell, C.D.; Bayer, J.D.; Qureshi, N.A.; Lim, P.B.; Tweedy, J.H.; Kanagaratnam, P.; Peters, N.S.; Vigmond, E.J.; Ng, F.S. Spatial resolution requirements for accurate identification of drivers of atrial fibrillation. Circ. Arrhythmia Electrophysiol. 2017, 10, e004899. [Google Scholar] [CrossRef] [PubMed]
- Bray, M.A.; Lin, S.F.; Aliev, R.R.; Roth, B.J.; Wikswo, J.P., Jr. Experimental and theoretical analysis of phase singularity dynamics in cardiac tissue. J. Cardiovasc. Electrophysiol. 2001, 12, 716–722. [Google Scholar] [CrossRef] [PubMed]
- Rantner, L.; Wieser, L.; Stühlinger, M.; Hintringer, F.; Tilg, B.; Fischer, G. Detection of phase singularities in triangular meshes. Methods Inf. Med. 2007, 46, 646–654. [Google Scholar] [PubMed]
- Tomii, N.; Yamazaki, M.; Arafune, T.; Honjo, H.; Shibata, N.; Sakuma, I. Detection algorithm of phase singularity using phase variance analysis for epicardial optical mapping data. IEEE Trans. Biomed. Eng. 2015, 63, 1795–1803. [Google Scholar] [CrossRef]
- Li, X.; Almeida, T.P.; Dastagir, N.; Guillem, M.S.; Salinet, J.; Chu, G.S.; Stafford, P.J.; Schlindwein, F.S.; Ng, G.A. Standardizing Single-Frame Phase Singularity Identification Algorithms and Parameters in Phase Mapping During Human Atrial Fibrillation. Front. Physiol. 2020, 11, 869. [Google Scholar] [CrossRef] [PubMed]
- Molavi Tabrizi, A.; Mesgarnejad, A.; Bazzi, M.; Luther, S.; Christoph, J.; Karma, A. Spatiotemporal organization of electromechanical phase singularities during high-frequency cardiac arrhythmias. Phys. Rev. X 2022, 12, 021052. [Google Scholar] [CrossRef]
- Masajada, J.; Dubik, B. Optical vortex generation by three plane wave interference. Opt. Commun. 2001, 198, 21–27. [Google Scholar] [CrossRef]
- Vyas, S.; Senthilkumaran, P. Interferometric optical vortex array generator. Appl. Opt. 2007, 46, 2893–2898. [Google Scholar] [CrossRef]
- Vyas, S.; Senthilkumaran, P. Vortex array generation by interference of spherical waves. Appl. Opt. 2007, 46, 7862–7867. [Google Scholar] [CrossRef] [PubMed]
- Masajada, J.; Popiołek-Masajada, A.; Wieliczka, D.M. The interferometric system using optical vortices as phase markers. Opt. Commun. 2002, 207, 85–93. [Google Scholar] [CrossRef]
- Popiołek-Masajada, A.; Borwińska, M. High sensitivity wave tilt measurements with optical vortex interferometer. In Proceedings of the Optical Sensing II, Strasbourg, France, 3–7 April 2006; SPIE: Bellingham, WA, USA, 2006; Volume 6189, pp. 53–59. [Google Scholar]
- Popiołek-Masajada, A.; Borwińska, M.; Dubik, B. Reconstruction of a plane wave’s tilt and orientation using an optical vortex interferometer. Opt. Eng. 2007, 46, 073604. [Google Scholar] [CrossRef]
- Frączek, W.; Mroczka, J. Optical vortices as phase markers to wave-front deformation measurement. Metrol. Meas. Syst. 2008, 15, 433–440. [Google Scholar]
- Woźniak, W.; Banach, M. Measurements of linearly birefringent media parameters using the optical vortex interferometer with the Wollaston compensator. J. Opt. Pure Appl. Opt. 2009, 11, 094024. [Google Scholar] [CrossRef]
- Shuang, Y.; Zhao, H.; Ji, W.; Cui, T.J.; Li, L. Programmable High-Order OAM-Carrying Beams for Direct-Modulation Wireless Communications. IEEE J. Emerg. Sel. Top. Circuits Syst. 2020, 10, 29–37. [Google Scholar] [CrossRef]
- Zhou, H.; Li, X.; Ullah, N.; Geng, G.; Li, J.; Li, X.; Wang, Y.; Huang, L. Single-shot phase retrieval based on anisotropic metasurface. Appl. Phys. Lett. 2022, 120, 161702. [Google Scholar] [CrossRef]
- Khare, K.; Lochab, P.; Senthilkumaran, P. Orbital Angular Momentum States of Light; IOP Publishing: Bristol, UK, 2020; pp. 2053–2563. [Google Scholar] [CrossRef]
- Lochab, P.; Senthilkumaran, P.; Khare, K. Robust laser beam engineering using polarization and angular momentum diversity. Opt. Express 2017, 25, 17524–17529. [Google Scholar] [CrossRef]
- Lochab, P.; Senthilkumaran, P.; Khare, K. Designer vector beams maintaining a robust intensity profile on propagation through turbulence. Phys. Rev. A 2018, 98, 023831. [Google Scholar] [CrossRef]
- Willner, A.E.; Song, H.; Zou, K.; Zhou, H.; Su, X. Orbital angular momentum beams for high-capacity communications. J. Light. Technol. 2022, 41, 1918–1933. [Google Scholar] [CrossRef]
- Sachdeva, S.; Kaur, S.; Arora, R.; Sindhwani, M.; Arora, K.; Cho, W.; Joshi, G.P.; Doo, I.C. Ultra-high capacity optical satellite communication system using PDM-256-QAM and optical angular momentum beams. Sensors 2023, 23, 786. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Zhang, L.; Yang, H.; Sun, Q.; Zhang, D. Identification of multimodal vortex optical orbital angular momentum in multimode fiber speckle patterns. Opt. Commun. 2024, 573, 131009. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, J.; Lu, X.; Hu, Z.; Gao, J.; Liu, K.; Zhan, Q.; Cai, Y.; Zhao, C. Single-shot phase retrieval for randomly fluctuated and obstructed vortex beams. Sci. China Phys. Mech. Astron. 2024, 67, 244211. [Google Scholar] [CrossRef]
- Eshaghi, M.; Acevedo, C.H.; Batarseh, M.; Guzman-Sepulveda, J.R.; Dogariu, A. Phase memory of optical vortex beams. Sci. Rep. 2022, 12, 10428. [Google Scholar] [CrossRef]
- Liu, K.; Cheng, Y.; Yang, Z.; Wang, H.; Qin, Y.; Li, X. Orbital-angular-momentum-based electromagnetic vortex imaging. IEEE Antennas Wirel. Propag. Lett. 2014, 14, 711–714. [Google Scholar] [CrossRef]
- Liu, K.; Cheng, Y.; Li, X.; Gao, Y. Microwave-sensing technology using orbital angular momentum: Overview of its advantages. IEEE Veh. Technol. Mag. 2019, 14, 112–118. [Google Scholar] [CrossRef]
- Bu, X.; Zhang, Z.; Chen, L.; Liang, X.; Tang, H.; Wang, X. Implementation of vortex electromagnetic waves high-resolution synthetic aperture radar imaging. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 764–767. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y.; Wang, J.; Liu, K.; Wang, H. Electromagnetic vortex enhanced imaging using fractional OAM beams. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 948–952. [Google Scholar] [CrossRef]
- Liu, D.; Shi, H.; Yang, T.; Zhang, L. Autofocusing and imaging algorithm for moving target by vortex electromagnetic wave radar. Digit. Signal Process. 2023, 134, 103903. [Google Scholar] [CrossRef]
- Li, R.; Cao, L. Complex wavefront sensing based on alternative structured phase modulation. Appl. Opt. 2021, 60, A48–A53. [Google Scholar] [CrossRef]
- Li, R.; Cao, L. Complex wavefront sensing based on coherent diffraction imaging using vortex modulation. Sci. Rep. 2021, 11, 9019. [Google Scholar] [CrossRef]
- Rodenburg, J.M.; Faulkner, H.M. A phase retrieval algorithm for shifting illumination. Appl. Phys. Lett. 2004, 85, 4795–4797. [Google Scholar] [CrossRef]
- Li, P.; Maiden, A.M. Ten implementations of ptychography. J. Microsc. 2018, 269, 187–194. [Google Scholar] [CrossRef]
- Rodenburg, J.M. Ptychography and related diffractive imaging methods. Adv. Imaging Electron Phys. 2008, 150, 87–184. [Google Scholar]
- McMorran, B.J.; Agrawal, A.; Anderson, I.M.; Herzing, A.A.; Lezec, H.J.; McClelland, J.J.; Unguris, J. Electron vortex beams with high quanta of orbital angular momentum. Science 2011, 331, 192–195. [Google Scholar] [PubMed]
- Clark, C.W.; Barankov, R.; Huber, M.G.; Arif, M.; Cory, D.G.; Pushin, D.A. Controlling neutron orbital angular momentum. Nature 2015, 525, 504–506. [Google Scholar] [CrossRef] [PubMed]
- Esashi, Y.; Liao, C.T.; Wang, B.; Brooks, N.; Dorney, K.M.; Hernández-García, C.; Kapteyn, H.; Adams, D.; Murnane, M. Ptychographic amplitude and phase reconstruction of bichromatic vortex beams. Opt. Express 2018, 26, 34007–34015. [Google Scholar] [CrossRef] [PubMed]
- Chen, J. Research on the Application of Vortex Beam in Ptychography. Ph.D. Thesis, University of York, York, UK, 2020. [Google Scholar]
- Faulkner, H.M.L.; Rodenburg, J. Movable aperture lensless transmission microscopy: A novel phase retrieval algorithm. Phys. Rev. Lett. 2004, 93, 023903. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Brooks, N.J.; Johnsen, P.; Jenkins, N.W.; Esashi, Y.; Binnie, I.; Tanksalvala, M.; Kapteyn, H.C.; Murnane, M.M. High-fidelity ptychographic imaging of highly periodic structures enabled by vortex high harmonic beams. Optica 2023, 10, 1245–1252. [Google Scholar] [CrossRef]
- Pancaldi, M.; Guzzi, F.; Bevis, C.S.; Manfredda, M.; Barolak, J.; Bonetti, S.; Bykova, I.; De Angelis, D.; De Ninno, G.; Fanciulli, M.; et al. High-resolution ptychographic imaging at a seeded free-electron laser source using OAM beams. Optica 2024, 11, 403–411. [Google Scholar] [CrossRef]
- Thibault, P.; Menzel, A. Reconstructing state mixtures from diffraction measurements. Nature 2013, 494, 68–71. [Google Scholar] [CrossRef] [PubMed]
- Guzzi, F.; Kourousias, G.; Billè, F.; Pugliese, R.; Gianoncelli, A.; Carrato, S. A modular software framework for the design and implementation of ptychography algorithms. PeerJ Comput. Sci. 2022, 8, e1036. [Google Scholar] [CrossRef]
- Guzzi, F.; Kourousias, G.; Gianoncelli, A.; Billè, F.; Carrato, S. A parameter refinement method for ptychography based on deep learning concepts. Condens. Matter 2021, 6, 36. [Google Scholar] [CrossRef]
- Lee, S.Y.; Park, E.; Kim, S.; Jo, E.; Lee, S.Y.; Choi, J.W.; Song, C. Off-Axis X-Ray Vortex Beam Ptychography. ACS Photonics 2024, 11, 3804–3810. [Google Scholar] [CrossRef]
- Nishchal, N.K. Optical Cryptosystems; IOP Publishing: Bristol, UK, 2019; pp. 2053–2563. [Google Scholar] [CrossRef]
- Wang, X.; Chen, W.; Chen, X. Optical image hiding using double-phase retrieval algorithm based on nonlinear cryptosystem under vortex beam illumination. J. Opt. 2015, 17, 035704. [Google Scholar] [CrossRef]
- Liansheng, S.; Bei, Z.; Xiaojuan, N.; Ailing, T. Optical multiple-image encryption based on the chaotic structured phase masks under the illumination of a vortex beam in the gyrator domain. Opt. Express 2016, 24, 499–515. [Google Scholar] [CrossRef]
- Singh, H.; Tirth, V.; Singh, R.K.; Algahtani, A.; Islam, S. Designing of an optical vortices phase mask and used in the frequency domain of linear canonical transform for double image encryption. Imaging Sci. J. 2020, 68, 288–304. [Google Scholar] [CrossRef]
- Kumar, P.; Nishchal, N.K.; Omatsu, T.; Rao, A.S. Optical vortex array for two-dimensional exclusive-OR operation. Appl. Phys. B 2022, 128, 98. [Google Scholar] [CrossRef]
- Yang, Q.; Xie, Z.; Zhang, M.; Ouyang, X.; Xu, Y.; Cao, Y.; Wang, S.; Zhu, L.; Li, X. Ultra-secure optical encryption based on tightly focused perfect optical vortex beams. Nanophotonics 2022, 11, 1063–1070. [Google Scholar] [CrossRef]
- Mandapati, V.C.; Vardhan, H.; Prabhakar, S.; Sakshi; Kumar, R.; Reddy, S.G.; Singh, R.P.; Singh, K. Multi-user nonlinear optical cryptosystem based on polar decomposition and fractional vortex speckle patterns. Photonics 2023, 10, 561. [Google Scholar] [CrossRef]
- Shikder, A.; Kumar, P.; Nishchal, N.K. Image Encryption by Structured Phase Encoding and Its Effectiveness in Turbulent Medium. IEEE Photonics Technol. Lett. 2023, 35, 128–131. [Google Scholar] [CrossRef]
- Shikder, A.; Rao, S.K.; Kumar, P.; Nishchal, N.K. Binary image encryption with a QR code-encoded optical beam having an array of vortices. J. Opt. Soc. Am. A 2024, 41, A73–A82. [Google Scholar] [CrossRef] [PubMed]
- Shikder, A.; Nishchal, N.K. Generation of optical vortex lattices by in-line phase modulation with partially coherent light. J. Opt. Soc. Am. A 2023, 40, 1231–1236. [Google Scholar] [CrossRef] [PubMed]
- Rao, S.K.; Nishchal, N.K.; AlFalou, A. Optical asymmetric image encryption using vectorial light field encoding. Opt. Commun. 2024, 554, 130097. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Z.; Zhou, Q.; Zhang, L.; Xu, B.; Wang, X. Holographic encryption with power-exponent helicon-conical optical vortices. Opt. Commun. 2024, 573, 131020. [Google Scholar] [CrossRef]
- Liu, R.; Li, Y.; Liu, Y.; Deng, D.; Wang, D.; Ding, S.; Wu, J. Multichiral Vortex Beam for High-Quality Information Encryption. ACS Photonics 2024, 11, 3105–3111. [Google Scholar] [CrossRef]
- Quesnel, M.; de Xivry, G.O.; Louppe, G.; Absil, O. A deep learning approach for focal-plane wavefront sensing using vortex phase diversity. Astron. Astrophys. 2022, 668, A36. [Google Scholar] [CrossRef]
- Balasubramaniam, G.M.; Biton, N.; Arnon, S. Imaging through diffuse media using multi-mode vortex beams and deep learning. Sci. Rep. 2022, 12, 1561. [Google Scholar]
- Ding, G.; Xiong, W.; Wang, P.; Huang, Z.; He, Y.; Liu, J.; Li, Y.; Fan, D.; Chen, S. Spatial phase retrieval of vortex beam using convolutional neural network. J. Opt. 2022, 24, 025701. [Google Scholar] [CrossRef]
- Feng, F.; Hu, J.; Wang, Y.; Guo, Z.; Li, N.; Zhao, B.; Yuan, X.; Somekh, M. Deep-learning enabled simultaneous detection of phase and polarization singularities of CVVBs and its application to image transmission. Opt. Laser Technol. 2024, 168, 109890. [Google Scholar] [CrossRef]
- Arora, G.; Butola, A.; Rajput, R.; Agarwal, R.; Agarwal, K.; Horsch, A.; Prasad, D.K.; Senthilkumaran, P. Taxonomy of hybridly polarized Stokes vortex beams. Opt. Express 2024, 32, 7404–7416. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Wei, H.; Du, Q.; Fu, Y.; Zhou, H. Degraded image restoration of vortex beam array based on deep learning. Phys. Scr. 2024, 99, 065537. [Google Scholar] [CrossRef]















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deepa, S.; Khare, K.; Paramasivam, S. Singularities in Computational Optics. Photonics 2025, 12, 96. https://doi.org/10.3390/photonics12020096
Deepa S, Khare K, Paramasivam S. Singularities in Computational Optics. Photonics. 2025; 12(2):96. https://doi.org/10.3390/photonics12020096
Chicago/Turabian StyleDeepa, S., Kedar Khare, and Senthilkumaran Paramasivam. 2025. "Singularities in Computational Optics" Photonics 12, no. 2: 96. https://doi.org/10.3390/photonics12020096
APA StyleDeepa, S., Khare, K., & Paramasivam, S. (2025). Singularities in Computational Optics. Photonics, 12(2), 96. https://doi.org/10.3390/photonics12020096





