Realization of the Compact Magneto-Optical Trap Based on Single Laser with Frequency Modulation
Abstract
:1. Introduction
2. Experimentation
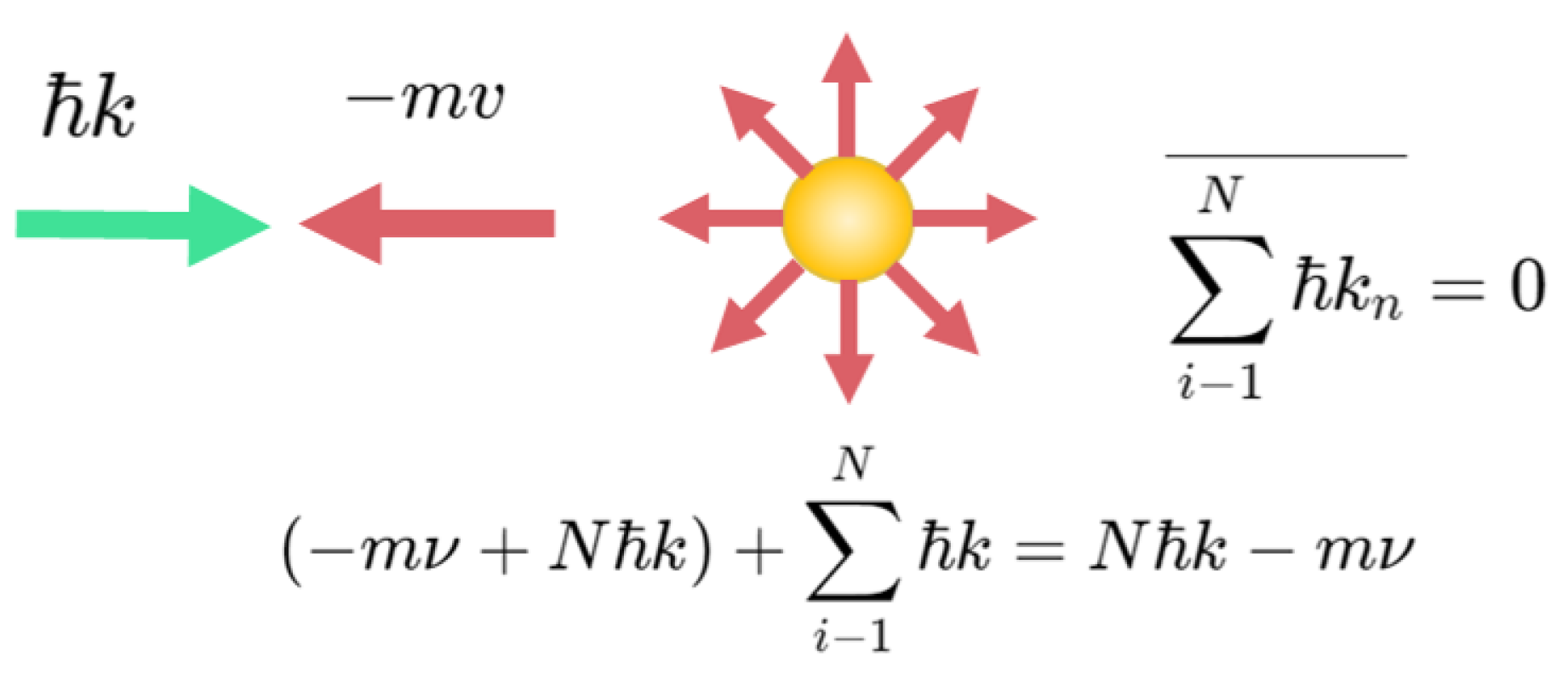
2.1. Experimental Principle
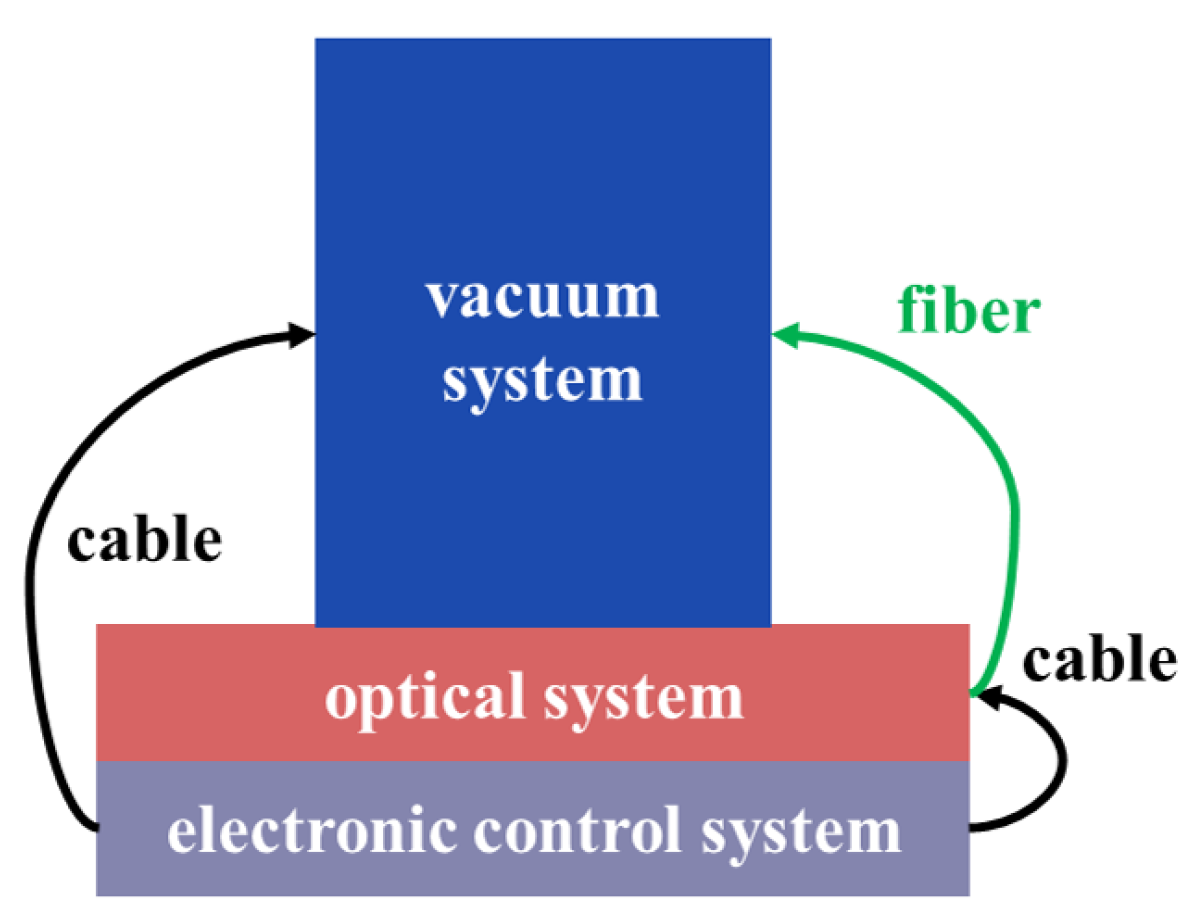
2.2. Experimental Apparatus
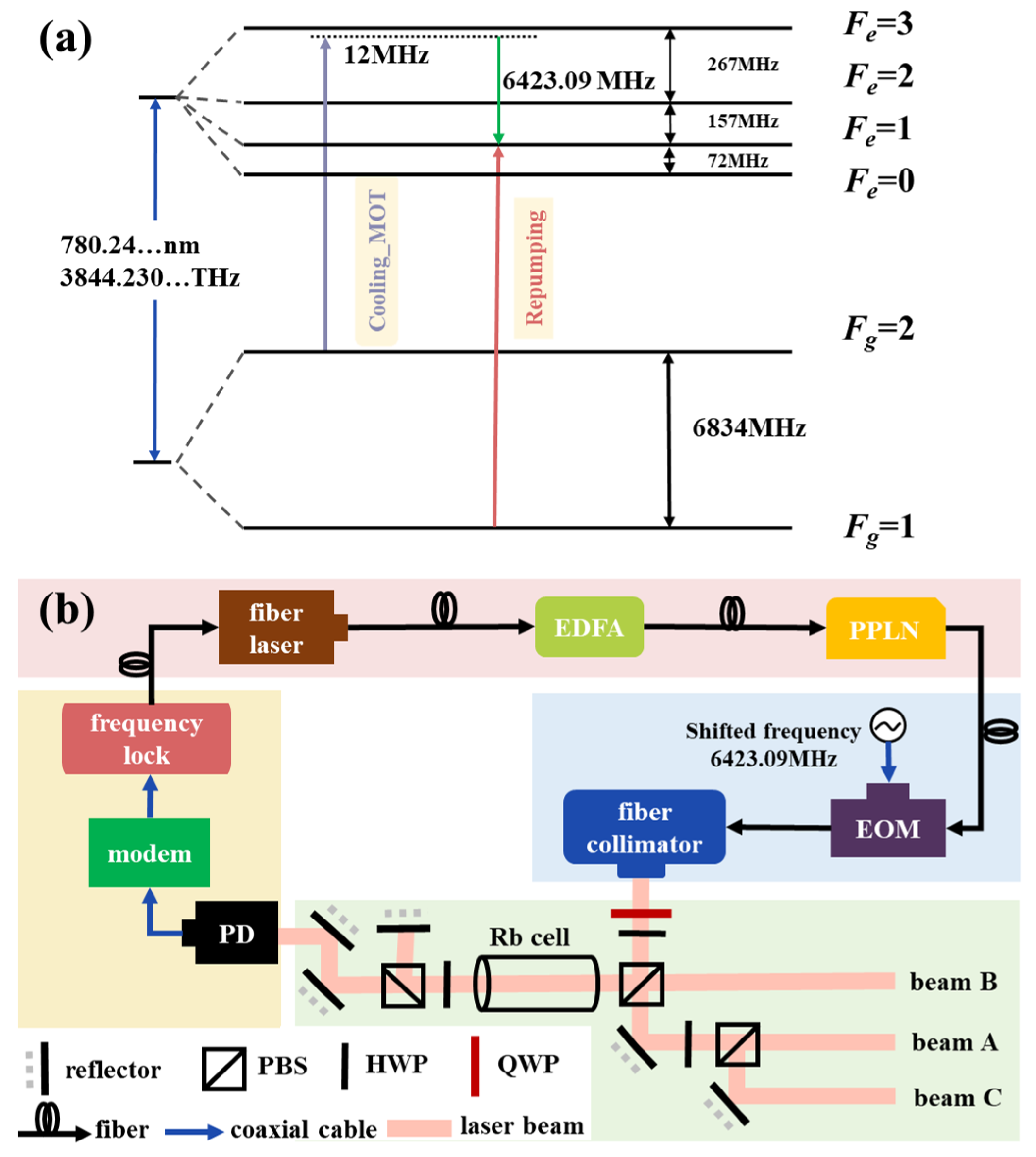
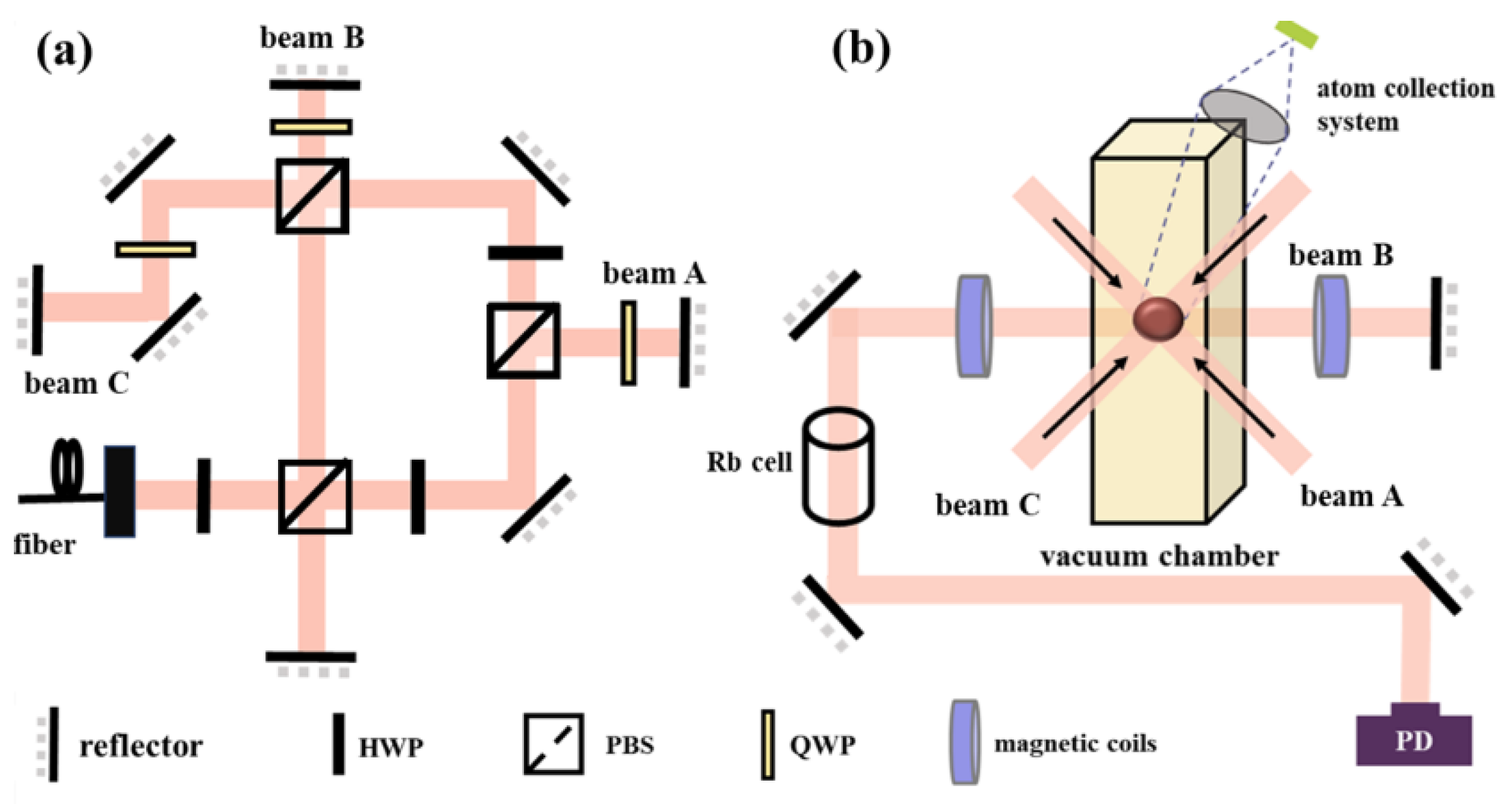
2.2.1. Optical System
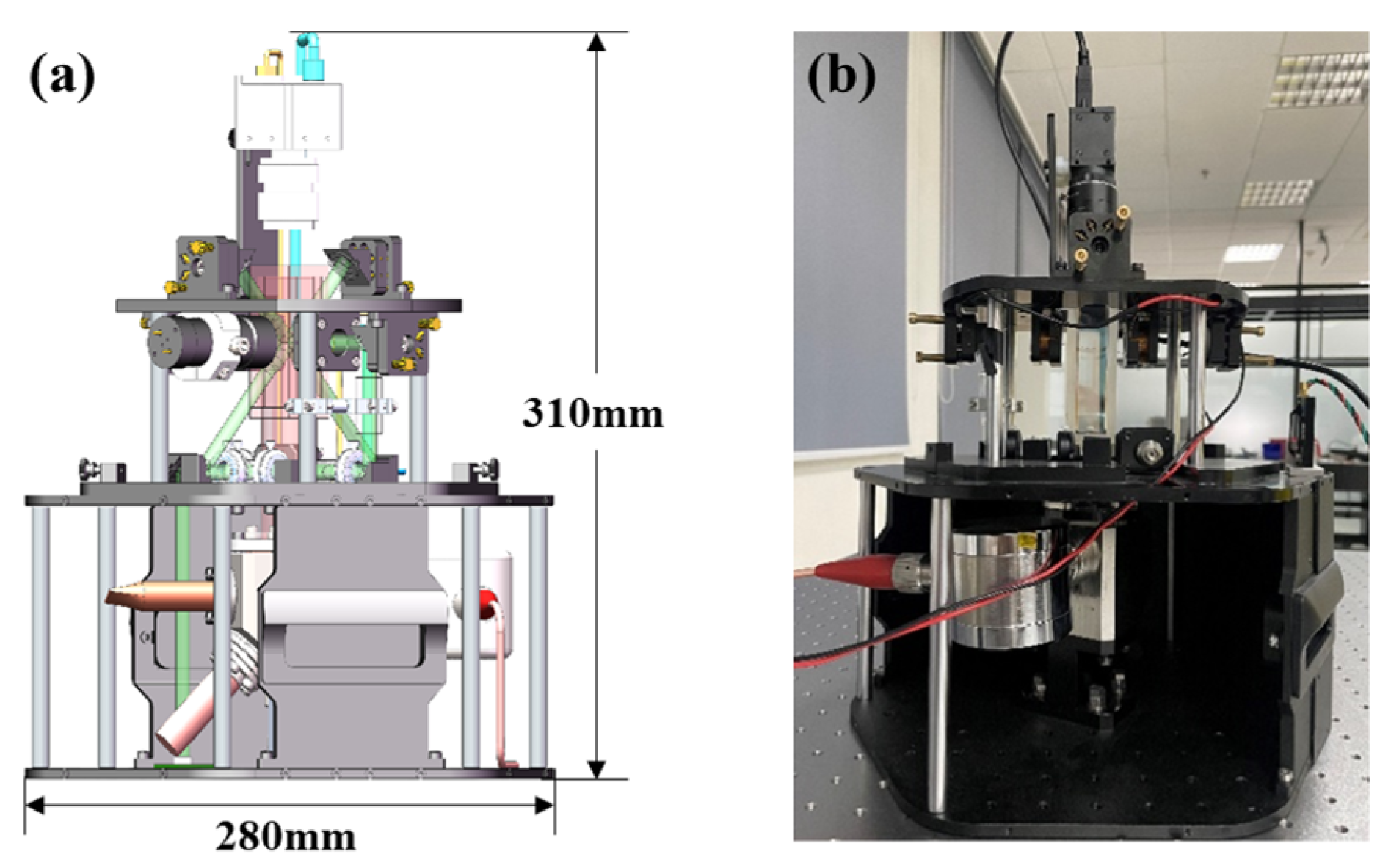
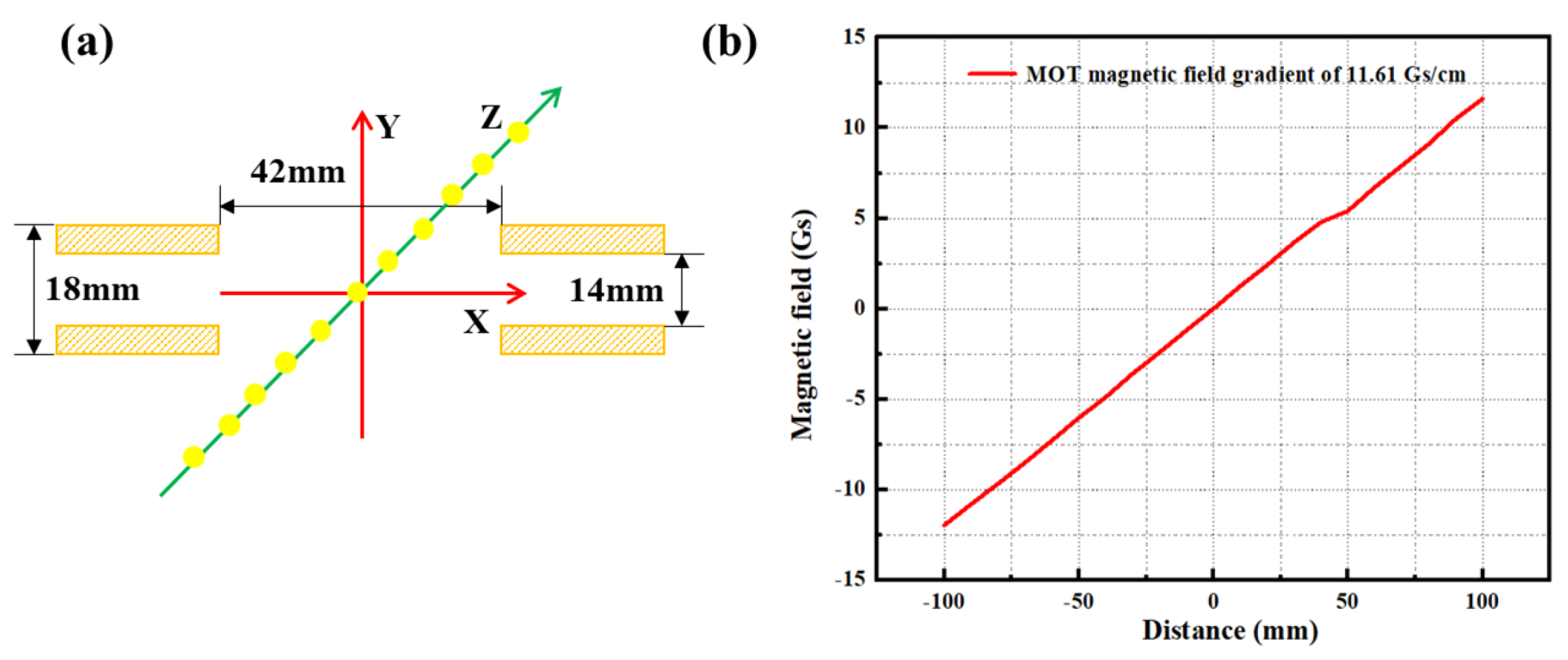
2.2.2. Vacuum System
2.2.3. Electronic Control System
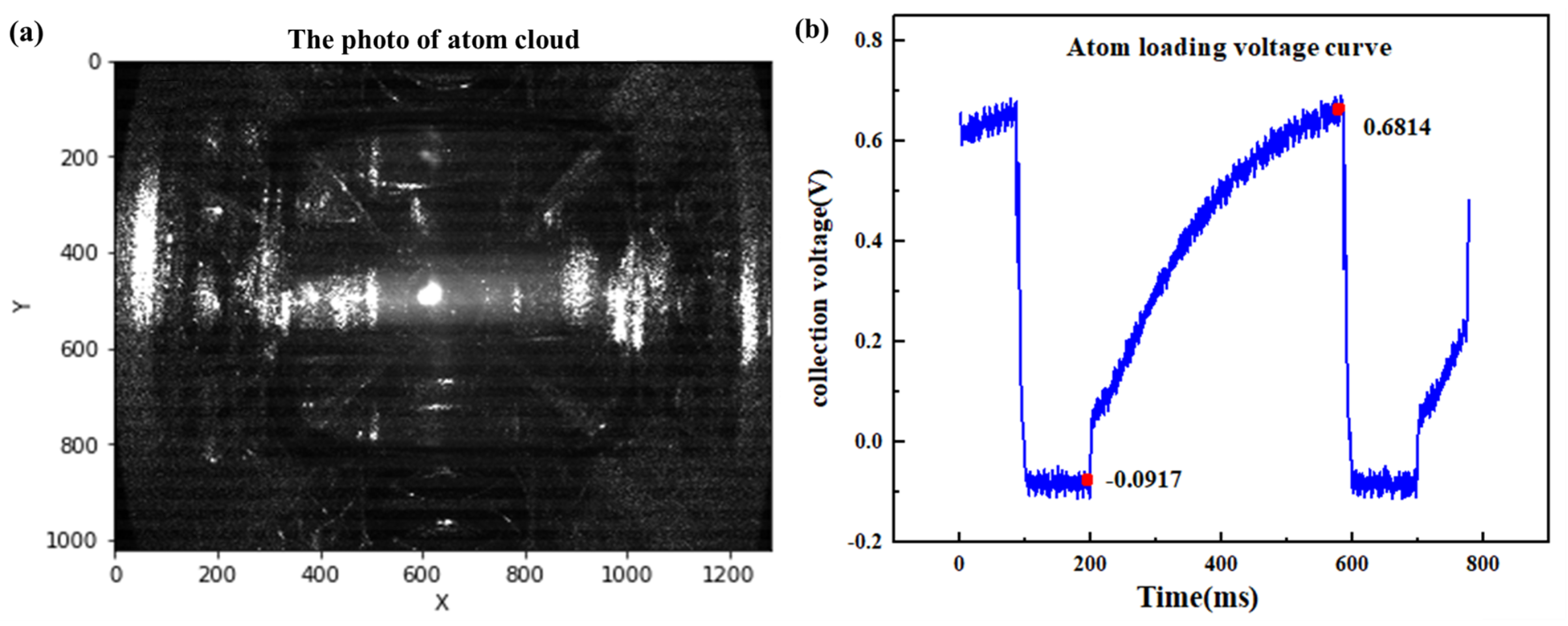
3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Phillips, W.D. Nobel Lecture: Laser cooling and trapping of neutral atoms. Rev. Mod. Phys. 1998, 70, 721. [Google Scholar] [CrossRef]
- Slusher, R.; Hollberg, L.; Yurke, B.; Mertz, J.; Valley, J. Observation of squeezed states generated by four-wave mixing in an optical cavity. Phys. Rev. Lett. 1985, 55, 2409. [Google Scholar] [CrossRef] [PubMed]
- Phillips, W.D.; Metcalf, H. Laser deceleration of an atomic beam. Phys. Rev. Lett. 1982, 48, 596. [Google Scholar] [CrossRef]
- Aspect, A.; Arimondo, E.; Kaiser, R.E.A.; Vansteenkiste, N.; Cohen-Tannoudji, C. Laser cooling below the one-photon recoil energy by velocity-selective coherent population trapping. Phys. Rev. Lett. 1988, 61, 826. [Google Scholar] [CrossRef]
- Gerginov, V.; Nemitz, N.; Weyers, S.; Schröder, R.; Griebsch, D.; Wynands, R. Uncertainty evaluation of the caesium fountain clock PTB-CSF2. Metrologia 2009, 47, 65. [Google Scholar] [CrossRef]
- Elgin, J.D.; Heavner, T.P.; Kitching, J.; Donley, E.A.; Denney, J.; Salim, E.A. A cold-atom beam clock based on coherent population trapping. Appl. Phys. Lett. 2019, 115, 033503. [Google Scholar] [CrossRef]
- Levi, F.; Calonico, D.; Calosso, C.E.; Godone, A.; Micalizio, S.; Costanzo, G.A. Accuracy evaluation of ITCsF2: A nitrogen cooled caesium fountain. Metrologia 2014, 51, 270. [Google Scholar] [CrossRef]
- Heavner, T.P.; Donley, E.A.; Levi, F.; Costanzo, G.; Parker, T.E.; Shirley, J.H.; Ashby, N.; Barlow, S.; Jefferts, S. First accuracy evaluation of NIST-F2. Metrologia 2014, 51, 174. [Google Scholar] [CrossRef]
- Fang, F.; Chen, W.; Liu, K.; Liu, N.; Suo, R.; Li, T. Design of the new NIM6 fountain with collecting atoms from a 3D MOT loading optical molasses. In Proceedings of the 2015 Joint Conference of the IEEE International Frequency Control Symposium & the European Frequency and Time Forum, Denver, CO, USA, 12–16 April 2015; IEEE: New York, NY, USA, 2015; pp. 492–494. [Google Scholar]
- Fang, F.; Li, M.; Lin, P.; Chen, W.; Liu, N.; Lin, Y.; Wang, P.; Liu, K.; Suo, R.; Li, T. NIM5 Cs fountain clock and its evaluation. Metrologia 2015, 52, 454. [Google Scholar] [CrossRef]
- Kasevich, M.; Chu, S. Measurement of the gravitational acceleration of an atom with a light-pulse atom interferometer. Appl. Phys. B 1992, 54, 321–332. [Google Scholar] [CrossRef]
- Poli, N.; Wang, F.Y.; Tarallo, M.; Alberti, A.; Prevedelli, M.; Tino, G. Precision Measurement of Gravity with Cold Atoms in an Optical Lattice and Comparison with a Classical Gravimeter. Phys. Rev. Lett. 2011, 106, 038501. [Google Scholar] [CrossRef] [PubMed]
- Merlet, S.; Bodart, Q.; Malossi, N.; Landragin, A.; Dos Santos, F.P.; Gitlein, O.; Timmen, L. Comparison between two mobile absolute gravimeters: Optical versus atomic interferometers. Metrologia 2010, 47, L9. [Google Scholar] [CrossRef]
- Schmidt, M.; Senger, A.; Hauth, M.; Freier, C.; Schkolnik, V.; Peters, A. A mobile high-precision absolute gravimeter based on atom interferometry. Gyroscopy Navig. 2011, 2, 170–177. [Google Scholar] [CrossRef]
- Vitushkin, L.F. Absolute gravity measurements. In Encyclopedia of Geodesy; Springer: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Altin, P.; Johnsson, M.; Negnevitsky, V.; Dennis, G.; Anderson, R.P.; Debs, J.; Szigeti, S.; Hardman, K.; Bennetts, S.; McDonald, G.; et al. Precision atomic gravimeter based on Bragg diffraction. N. J. Phys. 2013, 15, 023009. [Google Scholar] [CrossRef]
- DiFrancesco, D.; Grierson, A.; Kaputa, D.; Meyer, T. Gravity gradiometer systems–Advances and challenges. Geophys. Prospect. 2009, 57, 615–623. [Google Scholar] [CrossRef]
- Moody, M.V.; Paik, H.J.; Canavan, E.R. Three-axis superconducting gravity gradiometer for sensitive gravity experiments. Rev. Sci. Instrum. 2002, 73, 3957–3974. [Google Scholar] [CrossRef]
- Gustavson, T.; Bouyer, P.; Kasevich, M. Precision rotation measurements with an atom interferometer gyroscope. Phys. Rev. Lett. 1997, 78, 2046. [Google Scholar] [CrossRef]
- Gustavson, T.; Landragin, A.; Kasevich, M. Rotation sensing with a dual atom-interferometer Sagnac gyroscope. Class. Quantum Gravity 2000, 17, 2385. [Google Scholar] [CrossRef]
- Fang, J.; Qin, J. Advances in atomic gyroscopes: A view from inertial navigation applications. Sensors 2012, 12, 6331–6346. [Google Scholar] [CrossRef]
- Monroe, C.; Robinson, H.; Wieman, C. Observation of the cesium clock transition using laser-cooled atoms in a vapor cell. Opt. Lett. 1991, 16, 50–52. [Google Scholar] [CrossRef]
- Haus, H.A.; Huang, W. Coupled-mode theory. Proc. IEEE 1991, 79, 1505–1518. [Google Scholar] [CrossRef]
- Gallagher, A.; Pritchard, D.E. Exoergic collisions of cold Na-Na. Phys. Rev. Lett. 1989, 63, 957. [Google Scholar] [CrossRef] [PubMed]
- Sesko, D.; Walker, T.; Monroe, C.; Gallagher, A.; Wieman, C. Collisional losses from a light-force atom trap. Phys. Rev. Lett. 1989, 63, 961. [Google Scholar] [CrossRef] [PubMed]
- Jessen, P.S.; Gerz, C.; Lett, P.D.; Phillips, W.D.; Rolston, S.; Spreeuw, R.; Westbrook, C. Observation of quantized motion of Rb atoms in an optical field. Phys. Rev. Lett. 1992, 69, 49. [Google Scholar] [CrossRef]
- Julienne, P.S.; Vigué, J. Cold collisions of ground-and excited-state alkali-metal atoms. Phys. Rev. A 1991, 44, 4464. [Google Scholar] [CrossRef]
- Zhang, S. Acta Physica Sinica. Acta Phys. Sin. 2005. [Google Scholar]
- Doherty, A.; Parkins, A.; Tan, S.; Walls, D. Motion of a two-level atom in an optical cavity. Phys. Rev. A 1997, 56, 833. [Google Scholar] [CrossRef]
- Lett, P.D.; Watts, R.N.; Westbrook, C.I.; Phillips, W.D.; Gould, P.L.; Metcalf, H.J. Observation of atoms laser cooled below the Doppler limit. Phys. Rev. Lett. 1988, 61, 169. [Google Scholar] [CrossRef]
- Yuntao, C.; Xiangxiang, L.; Delong, K.; Luyan, N. Design of Ultra-High Vacuum System for Magneto-Optical Trap of Rb Atom. Navig. Position. Timing 2018, 5, 82–86. [Google Scholar] [CrossRef]
- Vovrosh, J.; Wilkinson, K.; Hedges, S.; McGovern, K.; Hayati, F.; Carson, C.; Selyem, A.; Winch, J.; Stray, B.; Earl, L.; et al. Magneto-optical trapping in a near-suface borehole. PLoS ONE 2023, 18, e0288353. [Google Scholar] [CrossRef]
- Hui, D.; Bei, G.; Dianqiang, S.; Zhonghua, J.; Yuan, J.; Yifei, M.; Yanting, Z. Portable Miniaturized Magneto-Optical Trap System. Laser Technol. 2023, 1–10. Available online: https://www.scholarmate.com/S/12n35t (accessed on 18 January 2025).
- Shimizu, F.; Shimizu, K.; Takuma, H. Four-beam laser trap of neutral atoms. Opt. Lett. 1991, 16, 339–341. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.; Kim, J.; Noh, H.; Jhe, W. Single-beam atom trap in a pyramidal and conical hollow mirror. Opt. Lett. 1996, 21, 1177–1179. [Google Scholar] [CrossRef] [PubMed]
- Pollock, S.; Cotter, J.; Laliotis, A.; Hinds, E. Integrated magneto-optical traps on a chip using silicon pyramid structures. Opt. Express 2009, 17, 14109–14114. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Grover, J.; Orozco, L.; Rolston, S. Sub-Doppler cooling of neutral atoms in a grating magneto-optical trap. JOSA B 2013, 30, 2869–2874. [Google Scholar] [CrossRef]
- Hyodo, M.; Nakayama, K.; Watanabe, M.; Ohmukai, R. Mirror magneto-optical trap exploiting hexapole-compensated magnetic field. Phys. Rev. A—At. Mol. Opt. Phys. 2007, 76, 013419. [Google Scholar] [CrossRef]
- Isichenko, A.; Chauhan, N.; Bose, D.; Wang, J.; Kunz, P.D.; Blumenthal, D.J. Photonic integrated beam delivery for a rubidium 3D magneto-optical trap. Nat. Commun. 2023, 14, 3080. [Google Scholar] [CrossRef]
- Debye, P. Einige bemerkungen zur magnetisierung bei tiefer temperatur. Ann. Phys. 1926, 386, 1154–1160. [Google Scholar] [CrossRef]
- Giauque, W. A thermodynamic treatment of certain magnetic effects. A proposed method of producing temperatures considerably below 1 absolute. J. Am. Chem. Soc. 1927, 49, 1864–1870. [Google Scholar] [CrossRef]
- Chu, S. Nobel Lecture: The manipulation of neutral particles. Rev. Mod. Phys. 1998, 70, 685. [Google Scholar] [CrossRef]
- Cohen-Tannoudji, C.N. Nobel Lecture: Manipulating atoms with photons. Rev. Mod. Phys. 1998, 70, 707. [Google Scholar] [CrossRef]
- Metcalf, H.J.; Van der Straten, P. Laser Cooling and Trapping; Springer Science & Business Media: New York, NY, USA, 1999; Available online: https://api.semanticscholar.org/CorpusID:14942756 (accessed on 18 January 2025).
- McCarron, D. Laser cooling and trapping molecules. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 212001. [Google Scholar] [CrossRef]
- Kox, A.J. The discovery of the electron: II. The Zeeman effect. Eur. J. Phys. 1997, 18, 139. [Google Scholar] [CrossRef]
- Harmin, D.A. Theory of the Stark effect. Phys. Rev. A 1982, 26, 2656. [Google Scholar] [CrossRef]
- Pipkin, F.M. 1966 Nobel Laureate in Physics: Alfred Kastler. Science 1966, 154, 747–749. [Google Scholar] [CrossRef]
- Raab, E.L.; Prentiss, M.; Cable, A.; Chu, S.; Pritchard, D.E. Trapping of neutral sodium atoms with radiation pressure. Phys. Rev. Lett. 1987, 59, 2631. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, Y.; Jiang, K.; Zhan, M. Bichromatic electromagnetically induced transparency in cold rubidium atoms. Phys. Rev. A 2003, 68, 063810. [Google Scholar] [CrossRef]
- Wenwen, L.; Qian, L.; Angang, L.; Yu, X.; Lin, L.; Rui, L.; Jie, M.; Taijun, P.; Bin, W.; Xinping, X.; et al. Integrated Design and Realization of Two-Dimensional Magneto-Optical Trap for Ultra-Cold Atomic Physics Rack in Space. China Laser 2022, 49, 193–202. [Google Scholar]
- Daji, Z.; Min, H.; Xian, Z.; Kaikai, H.; Xuanhui, L. 2D cold atomic beam system for increasing the loading rate of 3D MOT. Infrared Laser Eng. 2019, 48, 0506003. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, S.; Wu, B.; Cao, P.; Guo, X.; Zhao, Y.; Li, D.; Niu, J.; Zhang, C.; Cheng, B.; Weng, K.; et al. Realization of the Compact Magneto-Optical Trap Based on Single Laser with Frequency Modulation. Photonics 2025, 12, 98. https://doi.org/10.3390/photonics12020098
Bao S, Wu B, Cao P, Guo X, Zhao Y, Li D, Niu J, Zhang C, Cheng B, Weng K, et al. Realization of the Compact Magneto-Optical Trap Based on Single Laser with Frequency Modulation. Photonics. 2025; 12(2):98. https://doi.org/10.3390/photonics12020098
Chicago/Turabian StyleBao, Shuning, Bin Wu, Pengfei Cao, Xiaochun Guo, Yingpeng Zhao, Dianrong Li, Jingyu Niu, Cheng Zhang, Bing Cheng, Kanxing Weng, and et al. 2025. "Realization of the Compact Magneto-Optical Trap Based on Single Laser with Frequency Modulation" Photonics 12, no. 2: 98. https://doi.org/10.3390/photonics12020098
APA StyleBao, S., Wu, B., Cao, P., Guo, X., Zhao, Y., Li, D., Niu, J., Zhang, C., Cheng, B., Weng, K., Wang, X., & Lin, Q. (2025). Realization of the Compact Magneto-Optical Trap Based on Single Laser with Frequency Modulation. Photonics, 12(2), 98. https://doi.org/10.3390/photonics12020098




