Exciton-Resonance-Enhanced Two-Photon Absorption in Three-Dimensional Hybrid Organic–Inorganic Perovskites
Abstract
1. Introduction
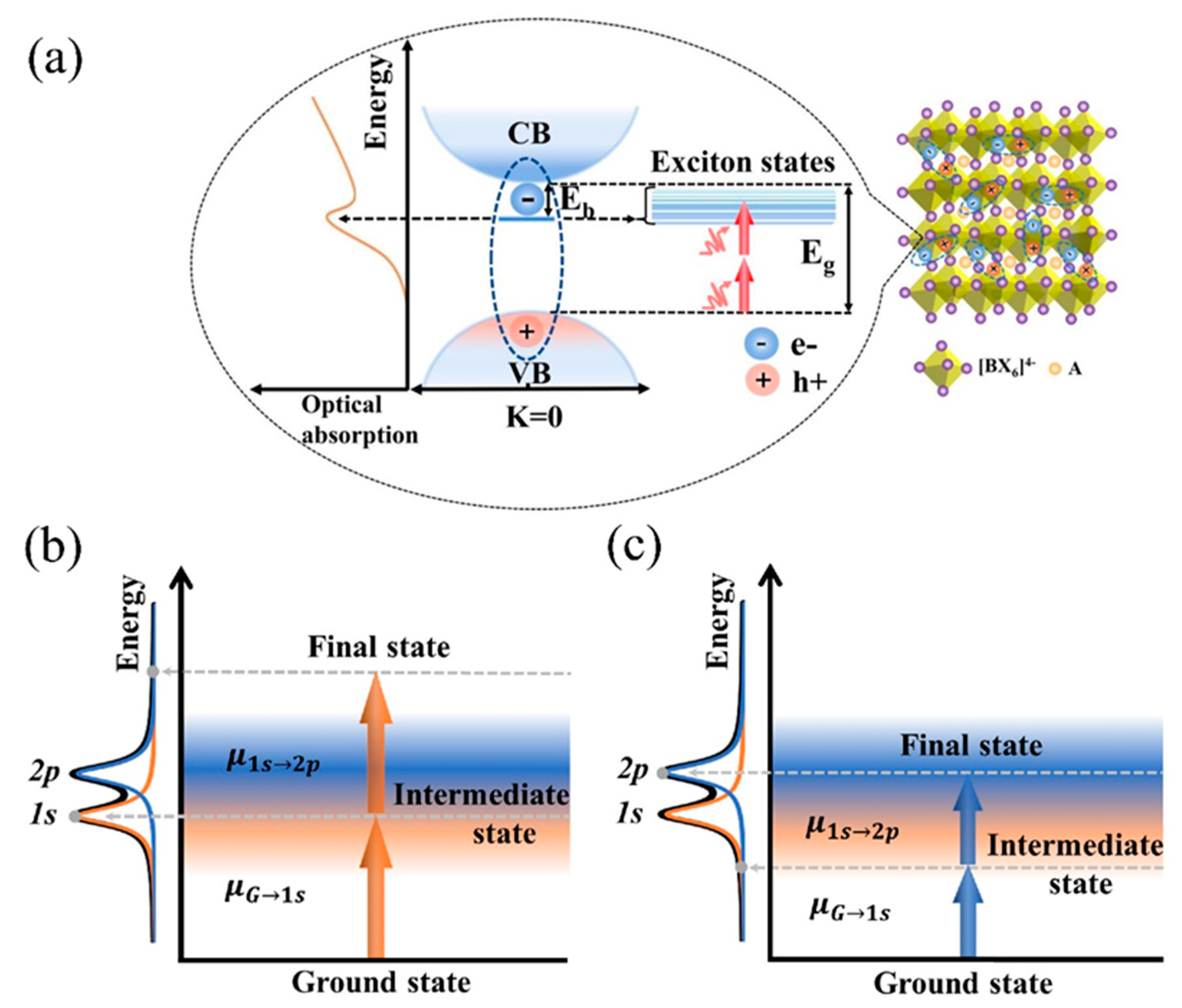
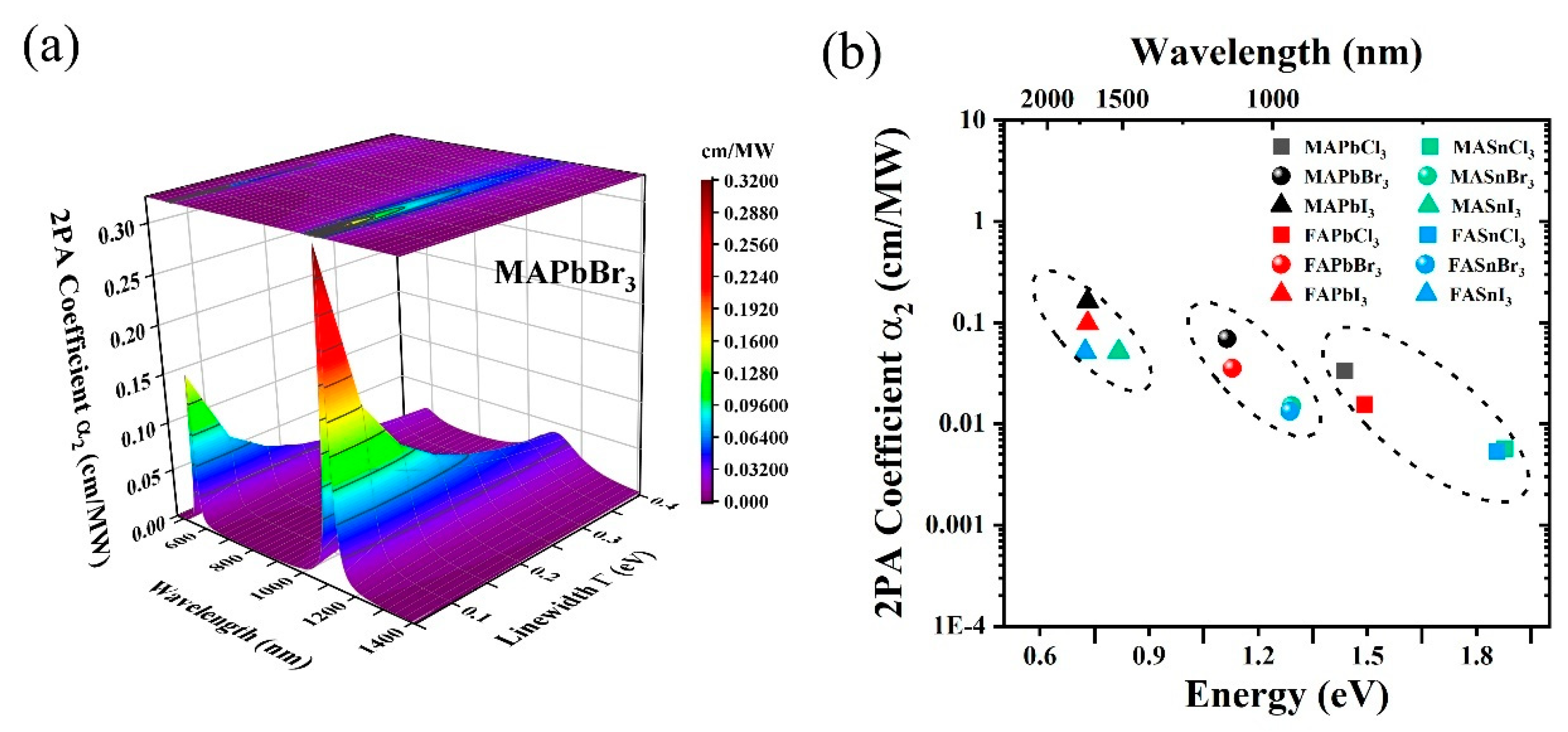
2. Principles and Simulations
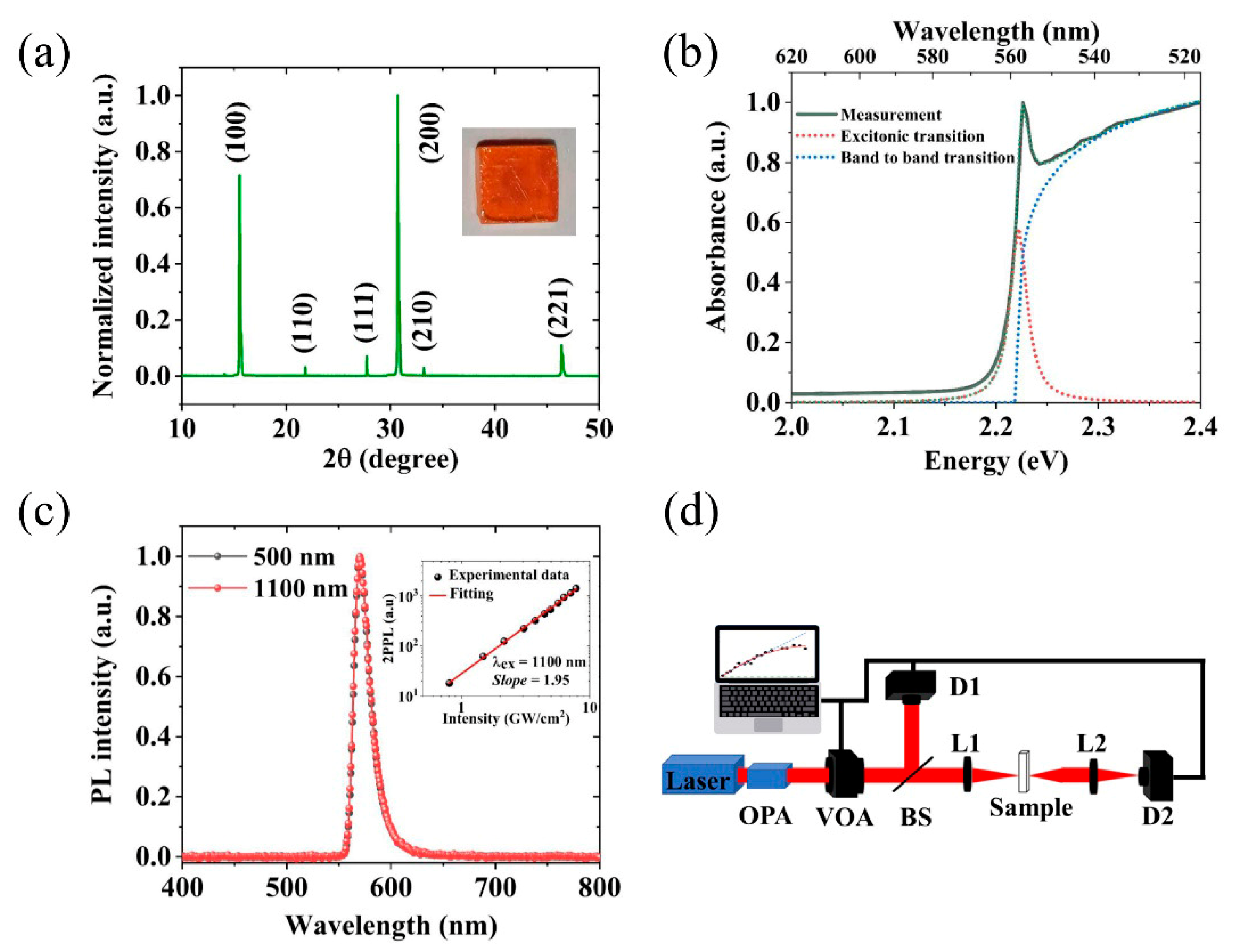
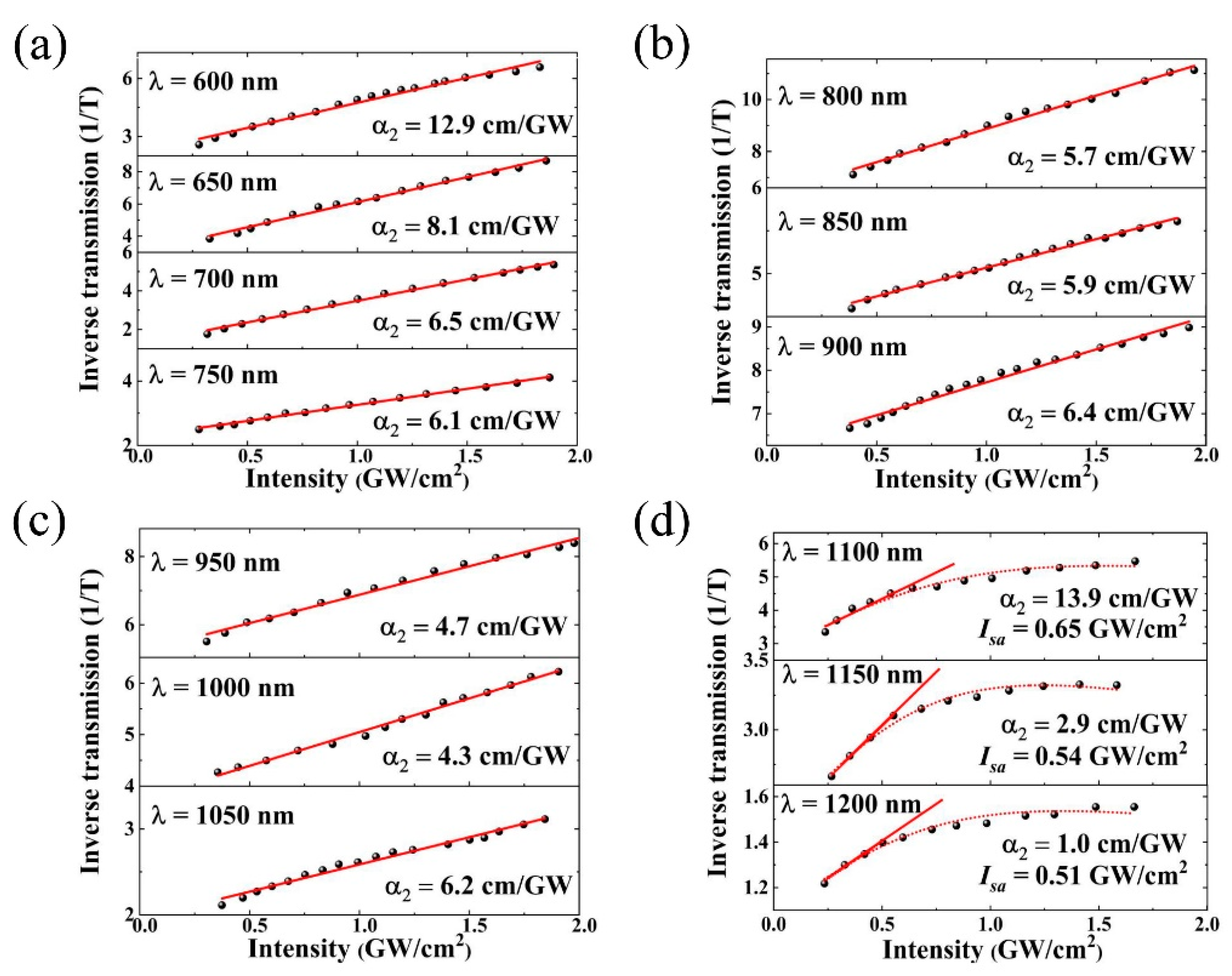
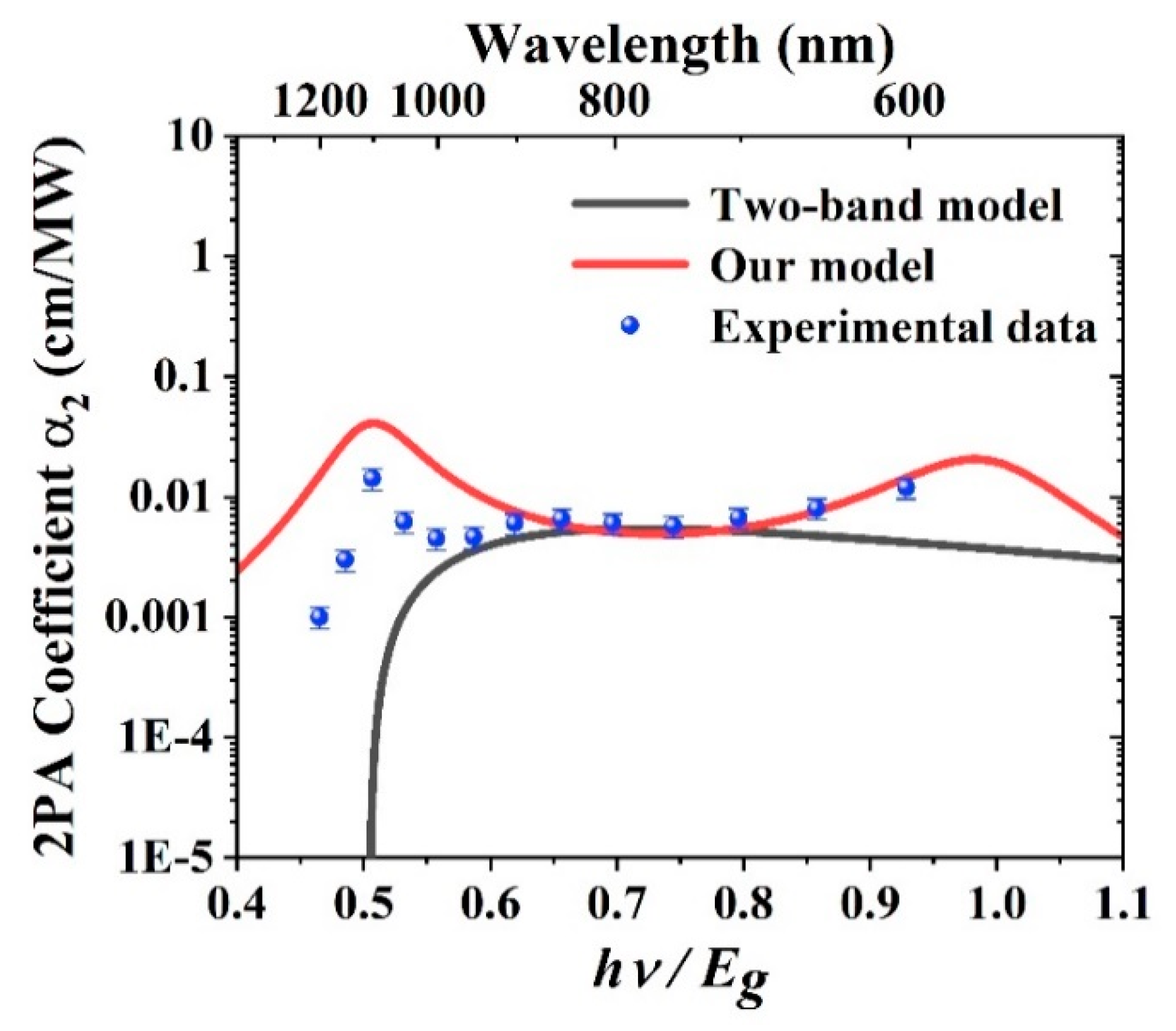
3. Experimental Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
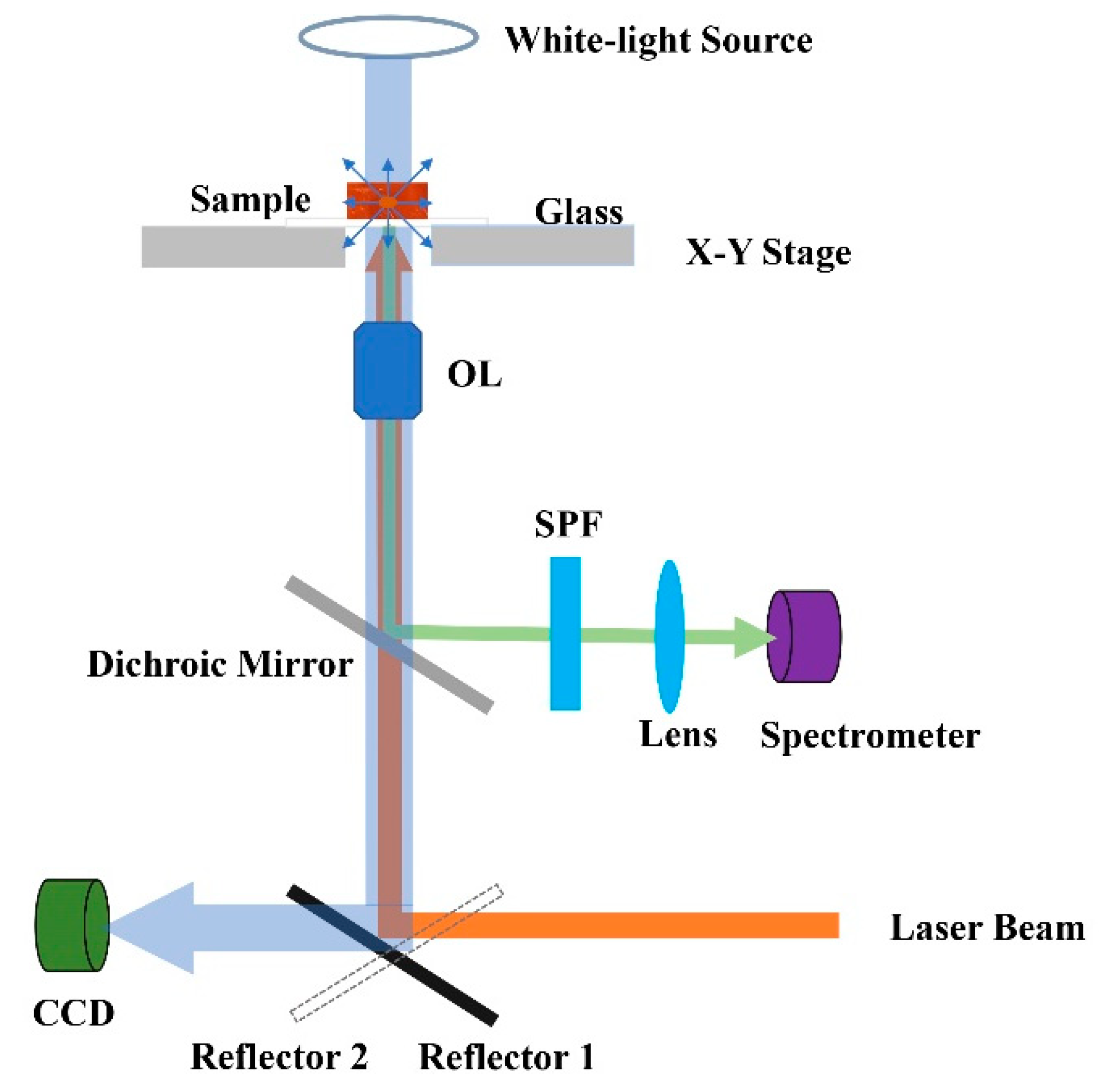
Appendix A. Experimental Section
Appendix A.1. Synthesis of MAPbBr3 Single Crystals
Appendix A.2. X-Ray Diffraction Characterization
Appendix A.3. The Linear Absorption
Appendix A.4. 1PPL and 2PPL
References
- Boyd, R.W. Nonlinear Optics; Academic Press: Burlington, ON, Canada, 2008. [Google Scholar]
- Baranowski, M.; Plochocka, P. Excitons in Metal-Halide Perovskites. Adv. Energy Mater. 2020, 10, 1903659. [Google Scholar] [CrossRef]
- Green, M.A.; Ho-Baillie, A.; Snaith, H.J. The emergence of perovskite solar cells. Nat. Photonics 2014, 8, 506–514. [Google Scholar] [CrossRef]
- Xiao, Z.; Kerner, R.A.; Zhao, L.; Tran, N.L.; Lee, K.M.; Koh, T.W.; Scholes, G.D.; Rand, B.P. Efficient perovskite light-emitting diodes featuring nanometre-sized crystallites. Nat. Photonics 2017, 11, 108–115. [Google Scholar] [CrossRef]
- Bi, Y.; Hutter, E.M.; Fang, Y.; Dong, Q.; Huang, J.; Savenije, T.J. Charge Carrier Lifetimes Exceeding 15 μs in Methylammonium Lead Iodide Single Crystals. J. Phys. Chem. Lett. 2016, 7, 923–928. [Google Scholar] [CrossRef]
- Cui, Y.; Fang, Q.; Huang, Z.; Xue, G.; Xu, G.; Yu, W. Frequency up-conversion of s-triazine derivatives via two photon absorption and second-harmonic generation. J. Mater. Chem. 2004, 15, 2443–2449. [Google Scholar] [CrossRef]
- Bharali, D.J.; Lucey, D.W.; Jayakumar, H.; Pudavar, H.E.; Prasad, P.N. Folate-Receptor-Mediated Delivery of InP Quantum Dots for Bioimaging Using Confocal and Two-Photon Microscopy. J. Am. Chem. Soc. 2005, 127, 11364–11371. [Google Scholar] [CrossRef] [PubMed]
- Kawata, S.; Sun, H.; Tanaka, T.; Takada, K. Finer features for functional microdevices. Nature 2001, 412, 697–698. [Google Scholar] [CrossRef]
- Zhou, F.; Ji, W. Two-photon absorption and subband photodetection in monolayer MoS2. Opt. Lett. 2017, 42, 3113–3116. [Google Scholar] [CrossRef]
- Lott, J.; Ryan, C.; Valle, B.; Johnson, J.R.; Schiraldi, D.A.; Shan, J.; Singer, K.D.; Weder, C. Two-Photon 3D Optical Data Storage via Aggregate Switching of Excimer-Forming Dyes. Adv. Mater. 2011, 23, 2425–2429. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, Q.; Zhang, C.; Wang, R.; Wu, H.; Zhang, X.; Xing, G.; Yu, W.W.; Wang, X.; Zhang, Y.; et al. Two-Photon-Pumped Perovskite Semiconductor Nanocrystal Lasers. J. Am. Chem. Soc. 2016, 138, 3761–3768. [Google Scholar] [CrossRef]
- Chouhan, L.; Ghimire, S.; Subrahmanyam, C.; Miyasaka, T.; Biju, V. Synthesis, optoelectronic properties and applications of halide perovskites. Chem. Soc. Rev. 2020, 49, 2869–2885. [Google Scholar] [CrossRef] [PubMed]
- Gratzel, M. The light and shade of perovskite solar cells. Nat. Mater. 2014, 13, 838–841. [Google Scholar] [CrossRef]
- Manser, J.S.; Christians, J.A.; Kamat, P.V. Intriguing Optoelectronic Properties of Metal Halide Perovskites. Chem. Rev. 2016, 116, 12956–13008. [Google Scholar] [CrossRef]
- Fakharuddin, A.; Shabbir, U.; Qiu, W.; Iqbal, T.; Sultan, M.; Heremans, P.; Schmidt-Mende, L. Inorganic and Layered Perovskites for Optoelectronic Devices. Adv. Mat. 2019, 31, 1807095. [Google Scholar] [CrossRef]
- Srimath Kandada, A.R.; Silva, C. Exciton Polarons in Two-Dimensional Hybrid Metal-Halide Perovskites. J. Phys. Chem. Lett. 2020, 11, 3173–3184. [Google Scholar] [CrossRef] [PubMed]
- Mauck, C.M.; Tisdale, W.A. Excitons in 2D Organic–Inorganic Halide Perovskites. Trends Chem. 2019, 1, 380–392. [Google Scholar] [CrossRef]
- Marongiu, D.; Saba, M.; Quochi, F.; Mura, A.; Bongiovanni, G. The role of excitons in 3D and 2D lead halide perovskites. J. Mater. Chem. C 2019, 7, 12006–12018. [Google Scholar] [CrossRef]
- Ghimire, S.; Klinke, C. Two-dimensional halide perovskites: Synthesis, optoelectronic properties, stability, and applications. Nanoscale 2021, 13, 12394–12422. [Google Scholar] [CrossRef] [PubMed]
- Sercel, P.C.; Lyons, J.L.; Bernstein, N.; Efros, A.L. Quasicubic model for metal halide perovskite nanocrystals. J. Chem. Phys. 2019, 151, 234106. [Google Scholar] [CrossRef]
- Liu, Y.; Lorenz, M.; Ievlev, A.V.; Ovchinnikova, O.S. Secondary Ion Mass Spectrometry (SIMS) for Chemical Characterization of Metal Halide Perovskites. Adv. Funct. Mater. 2020, 30, 2002201. [Google Scholar] [CrossRef]
- Zhou, F.; Ran, X.; Fan, D.; Lu, S.; Ji, W. Perovskites: Multiphoton Absorption and Applications Adv. Opt. Mater. 2021, 9, 202100292. [Google Scholar] [CrossRef]
- Lu, W.G.; Chen, C.; Han, D.; Yao, L.; Han, J.; Zhong, H.; Wang, Y. Nonlinear Optical Properties of Colloidal CH3NH3PbBr3 and CsPbBr3 Quantum Dots: A Comparison Study Using Z-Scan Technique. Adv. Opt. Mater. 2016, 4, 1732–1737. [Google Scholar] [CrossRef]
- Wei, Q.; Du, B.; Wu, B.; Guo, J.; Li, M.J.; Fu, J.; Zhang, Z.; Yu, J.; Hou, T.; Xing, G.; et al. Two-Photon Optical Properties in Individual Organic Inorganic Perovskite Microplates. Adv. Opt. Mater. 2017, 5, 1700809. [Google Scholar] [CrossRef]
- Abdelwahab, I.; Grinblat, G.; Leng, K.; Li, Y.; Chi, X.; Rusydi, A.; Maier, S.A.; Loh, K.P. Highly Enhanced Third-Harmonic Generation in 2D Perovskites at Excitonic Resonances. ACS Nano 2018, 12, 644–650. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Zhou, F.; Zhang, Q.; Eda, G.; Ji, W. Layered Hybrid Perovskites for Highly Efficient Three-Photon Absorbers: Theory and Experimental Observation. Adv. Sci. 2019, 6, 1801626. [Google Scholar] [CrossRef]
- Zhou, F.; Abdelwahab, I.; Leng, K.; Loh, K.P.; Ji, W. 2D Perovskites with Giant Excitonic Optical Nonlinearities for High-Performance Sub-Bandgap Photodetection. Adv. Mater. 2019, 31, 1904155. [Google Scholar] [CrossRef]
- Wang, W.; Liu, R.; Zhu, S.; Zhou, M.; Jin, B.; Lu, S.; Liu, M.; Su, X.; Ji, W. Enhanced three-photon absorption excited at near-infrared laser pulses and stability of MAPbBr3 quantum dots encapsulated in mesoporous single MOF-5 crystals. J. Mater. Chem. C. 2025. [Google Scholar] [CrossRef]
- Zhou, F.; Nieva, C.J.; Fan, D.; Lu, S.; Ji, W. Superior optics Kerr effects induced by two-dimensional excitons. Photonics Res. 2022, 10, 834–842. [Google Scholar] [CrossRef]
- Lin, J.H.; Hsu, J.F.; Yang, Y.C.; Lin, C.; Huang, C.C.; Ge, Y. Nonlinear Absorption in 2D Ruddlesden–Popper Perovskites: Pathways to Ultrafast Optical Applications. J. Phys. Chem. Lett. 2024, 15, 9644–9651. [Google Scholar] [CrossRef]
- Yu, W.; Lee, K.J.; Li, Y.; Huang, Z.; Zhou, R.; Chen, A.; Guo, C. Advancements in halide perovskite photonics. Adv. Opt. Photonics 2024, 16, 868–957. [Google Scholar] [CrossRef]
- Shen, W.; Chen, J.; Wu, J.; Li, X.; Zeng, H. Nonlinear Optics in Lead Halide Perovskites: Mechanisms and Applications. ACS Photonics 2021, 8, 113–124. [Google Scholar] [CrossRef]
- Qiu, D.Y.; Da Jornada, F.H.; Louie, S.G. Optical Spectrum of MoS2: Many-Body Effects and Diversity of Exciton States. Phys. Rev. Lett. 2013, 111, 216805. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, D.J. Introduction to Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Saouma, F.O.; Park, D.Y.; Kim, S.H.; Jeong, M.S.; Jang, J.I. Multiphoton Absorption Coefficients of Organic−Inorganic Lead Halide Perovskites CH3NH3PbX3 (X = Cl, Br, I) Single Crystals. Chem. Mater. 2017, 29, 6876–6882. [Google Scholar] [CrossRef]
- Walters, G.; Sutherland, B.R.; Hoogland, S.; Shi, D.; Comin, R.; Sellan, D.P.; Bakr, O.M.; Sargent, E.H. Two-Photon Absorption in Organometallic Bromide Perovskites. ACS Nano 2015, 9, 9340–9346. [Google Scholar] [CrossRef]
- Faghihnasiri, M.; Izadifard, M.; Ghazi, M.E. Study of strain effects on electronic and optical properties of CH3NH3PbX3 (X¼Cl, Br, I) perovskites. Phys. B 2020, 582, 412024. [Google Scholar] [CrossRef]
- Wei, T.C.; Mokkapati, S.; Li, T.Y.; Lin, C.H.; Lin, G.R.; Jagadish, C.; He, J.H. Nonlinear Absorption Applications of CH3NH3PbBr3 Perovskite Crystals. Adv. Funct. Mater. 2018, 28, 1707175. [Google Scholar] [CrossRef]
- Van Stryland, E.W.; Woodall, M.A.; Vanherzeele, H.; Soileau, M.J. Energy band-gap dependence of two-photon absorption. Opt. Lett. 1985, 10, 490–492. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ran, X.; Xiang, X.; Zhou, F.; Lu, S. Exciton-Resonance-Enhanced Two-Photon Absorption in Three-Dimensional Hybrid Organic–Inorganic Perovskites. Photonics 2025, 12, 261. https://doi.org/10.3390/photonics12030261
Ran X, Xiang X, Zhou F, Lu S. Exciton-Resonance-Enhanced Two-Photon Absorption in Three-Dimensional Hybrid Organic–Inorganic Perovskites. Photonics. 2025; 12(3):261. https://doi.org/10.3390/photonics12030261
Chicago/Turabian StyleRan, Xing, Xin Xiang, Feng Zhou, and Shunbin Lu. 2025. "Exciton-Resonance-Enhanced Two-Photon Absorption in Three-Dimensional Hybrid Organic–Inorganic Perovskites" Photonics 12, no. 3: 261. https://doi.org/10.3390/photonics12030261
APA StyleRan, X., Xiang, X., Zhou, F., & Lu, S. (2025). Exciton-Resonance-Enhanced Two-Photon Absorption in Three-Dimensional Hybrid Organic–Inorganic Perovskites. Photonics, 12(3), 261. https://doi.org/10.3390/photonics12030261



