Machine Learning-Assisted Mitigation of Optical Multipath Interference in PAM4 IM-DD Transmission Systems
Abstract
:1. Introduction
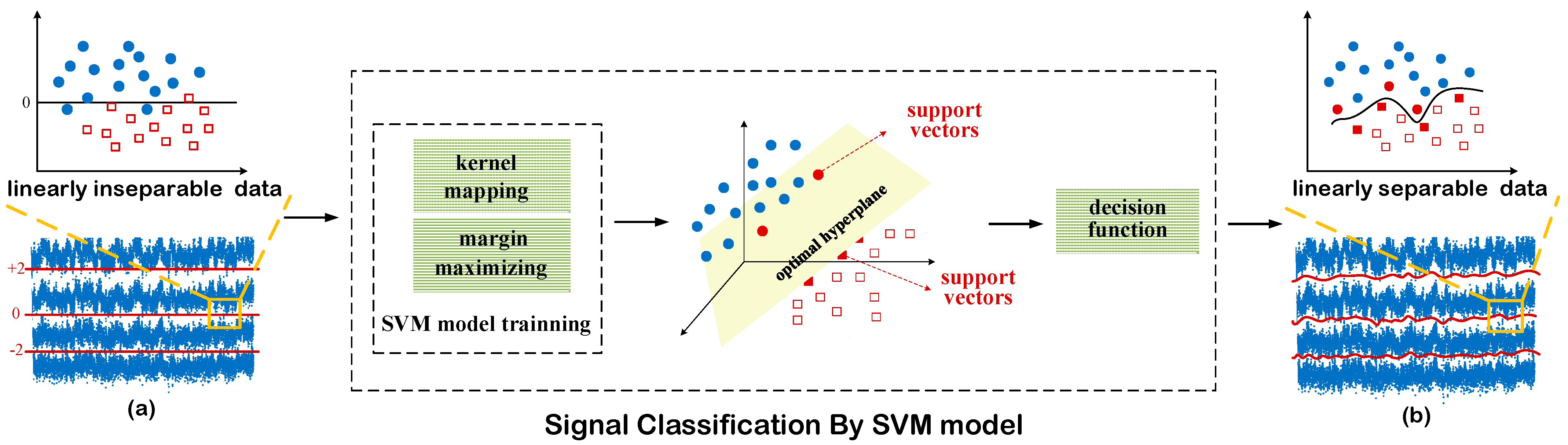
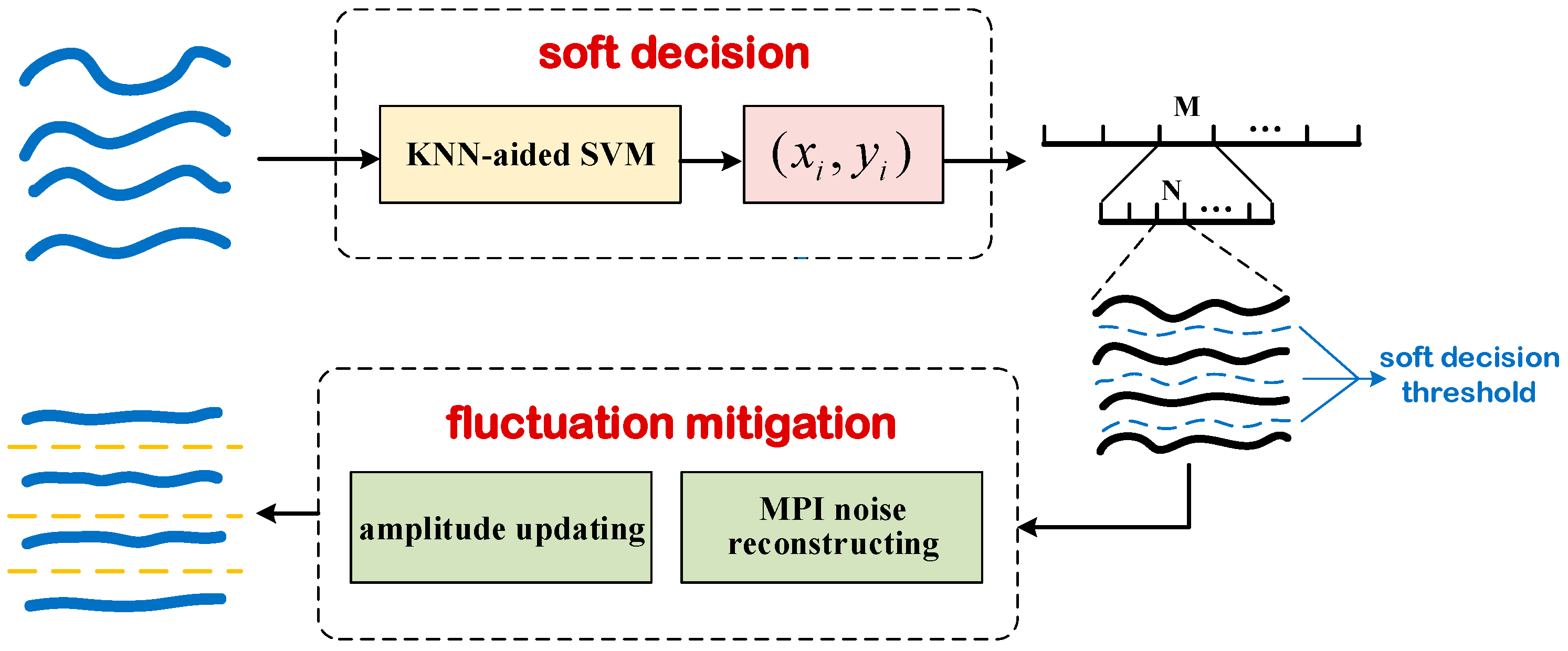
2. Principle of the KNN-Aided SVM+RF-M Scheme
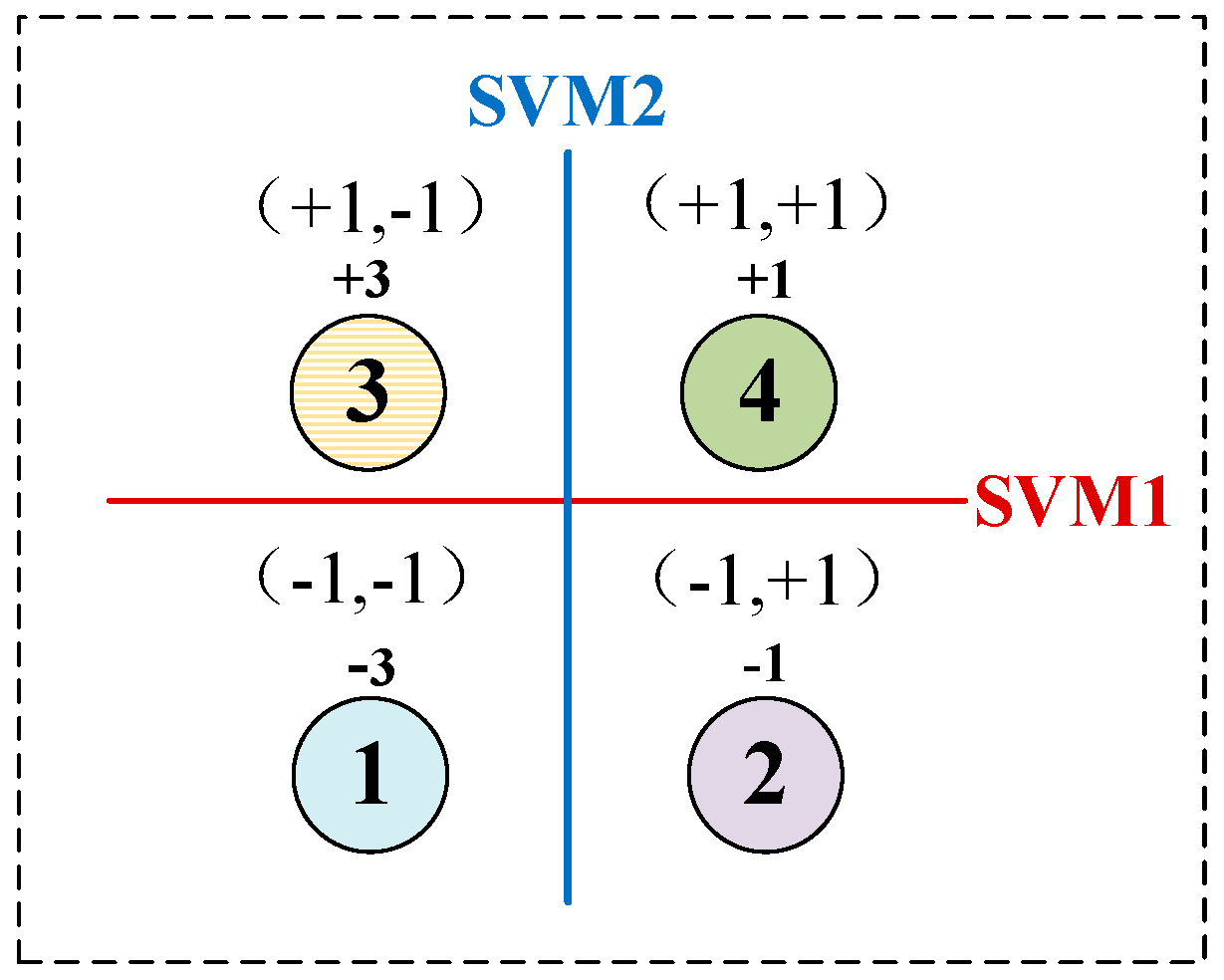
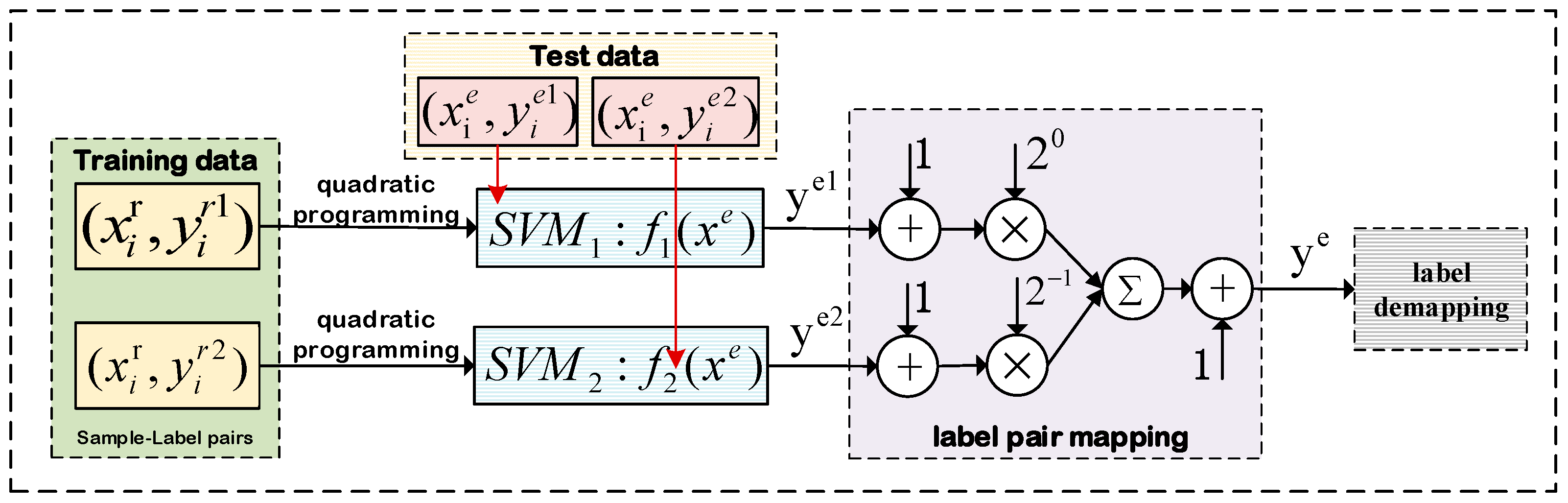
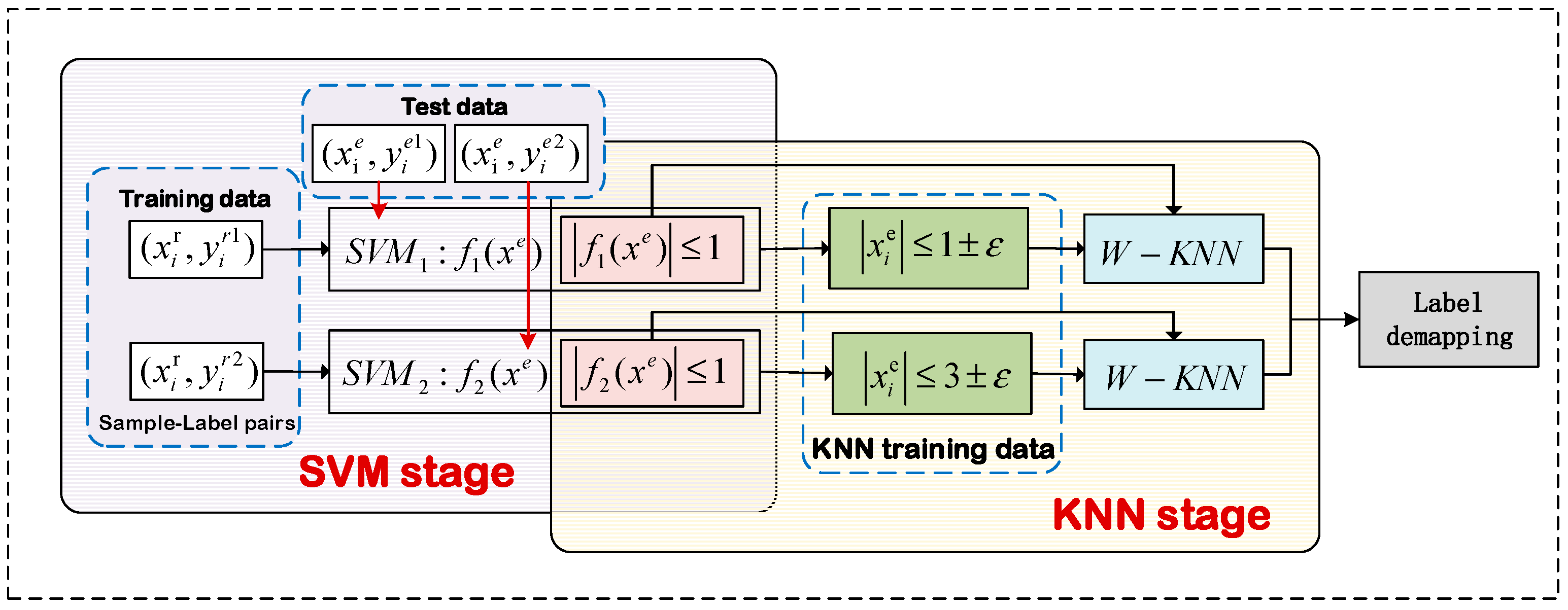
2.1. KNN-Aided SVM Algorithm
2.2. Fluctuation Mitigation Based on RF-M
3. Results and Discussion
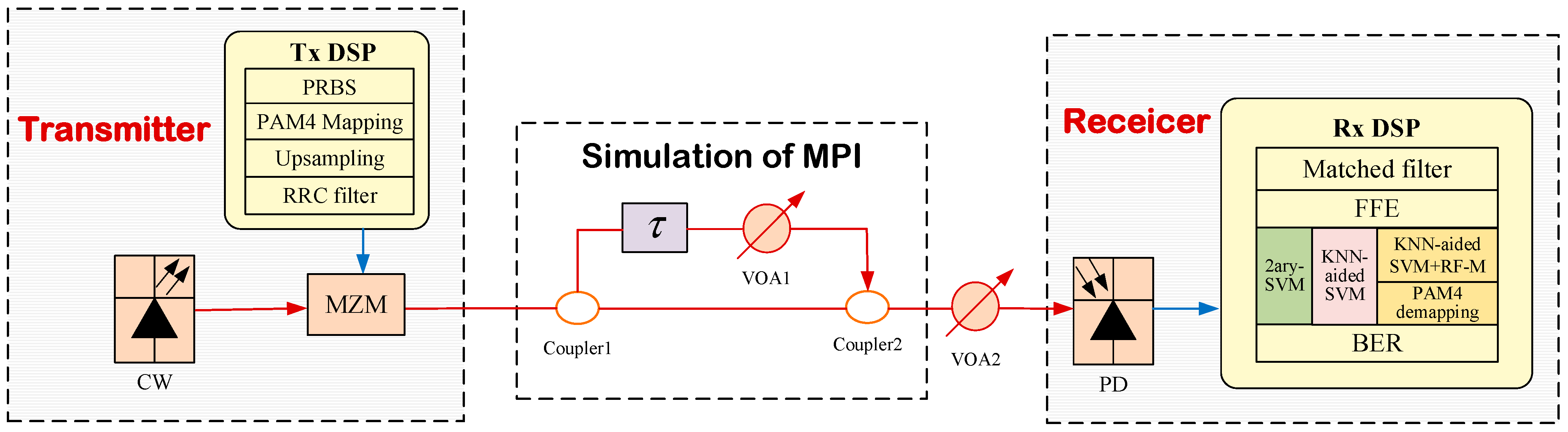
3.1. Simulation Setup
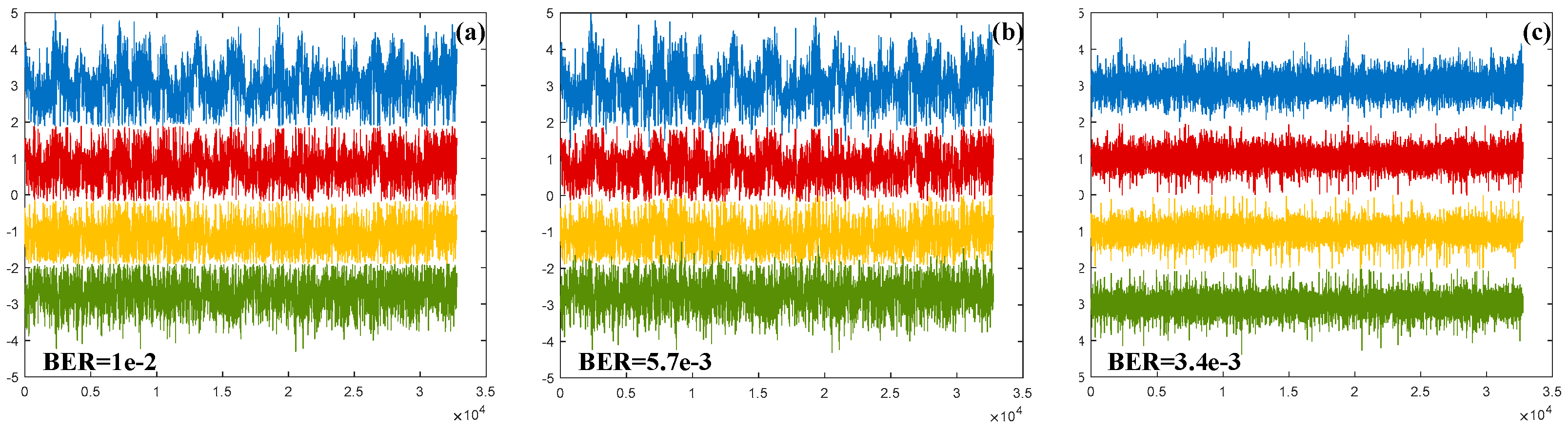
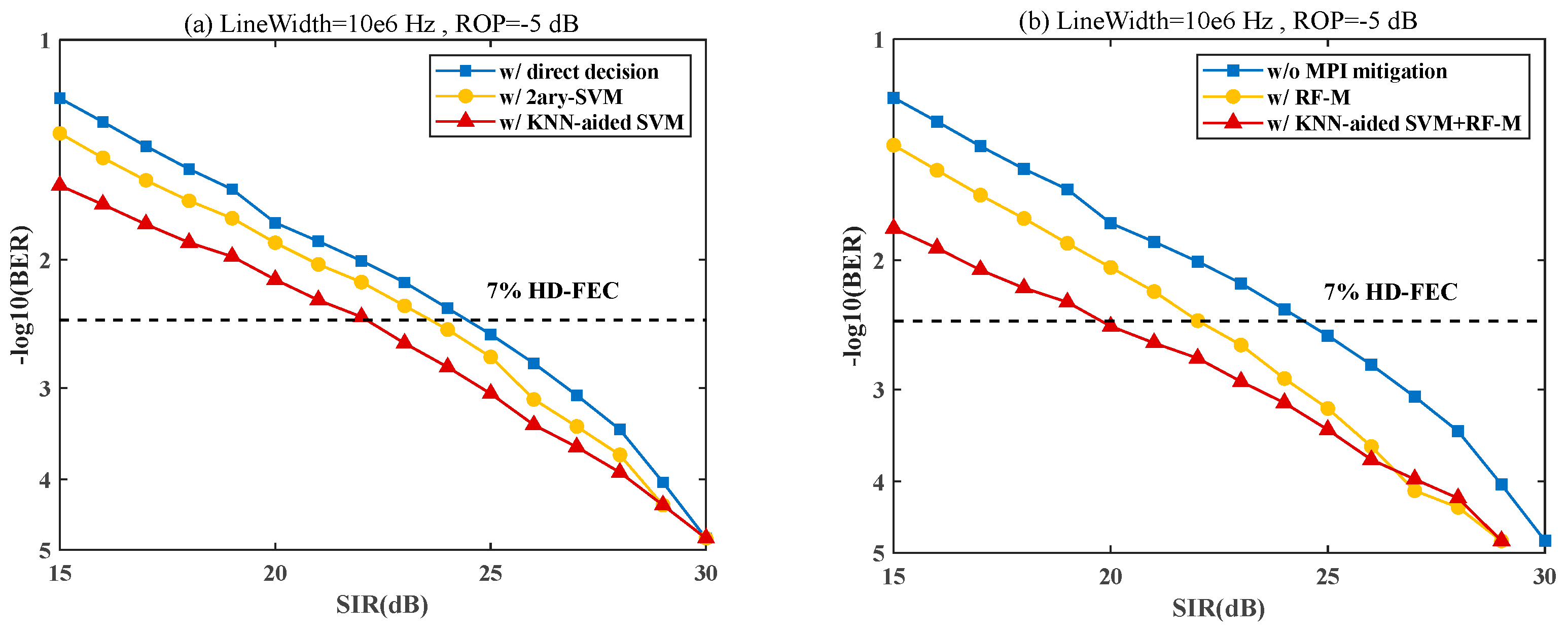
3.2. Simulation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kachris, C.; Tomkos, I. A survey on optical interconnects for data centers. IEEE Commun. Surv. Tutor. 2012, 14, 1021–1036. [Google Scholar] [CrossRef]
- Pang, X.; Ozolins, O.; Lin, R.; Zhang, L.; Udalcovs, A.; Xue, L.; Schatz, R.; Westergren, U.; Xiao, S.; Hu, W.; et al. 200 Gbps/lane IM/DD technologies for short reach optical interconnects. J. Light. Technol. 2020, 38, 492–503. [Google Scholar] [CrossRef]
- Wei, J.; Stojanovic, N.; Zhang, L.; Calabrò, S.; Rahman, T.; Xie, C.; Charlet, G. Experimental comparison of modulation formats for 200 G/λ IMDD data centre networks. In Proceedings of the 45th European Conference on Optical Communication (ECOC 2019), Dublin, Ireland, 22–26 September 2019; pp. 1–4. [Google Scholar]
- Zhong, K.; Zhou, X.; Wang, Y.; Gui, T.; Yang, Y.; Yuan, J.; Wang, L.; Chen, W.; Zhang, H.; Man, J.; et al. Recent advances in short reach transmission systems. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 19–23 March 2017. Paper Tu2D.7. [Google Scholar]
- 400G-FR4 Technical Specification Rev 2.0, 100G Lambda MSA Group. 2018. Available online: http://100glambda.com/specifications/download/2-specifications/7-400g-fr4-technical-spec-d2p0-2 (accessed on 18 September 2018).
- P802.3df/D3.1; IEEE Draft Standard for Ethernet Amendment: Media Access Control Parameters for 800 Gb/s and Physical Layers and Management Parameters for 400 Gb/s and 800 Gb/s Operation. IEEE: Piscataway, NJ, USA, 2023.
- The Path to 800g—New Ethernet Standards for Higher Speeds. 2022. Available online: https://osi.rosenberger.com/news-media/800g-ethernet-standards (accessed on 1 January 2022).
- Wettlin, T.; Calabrò, S.; Rahman, T.; Wei, J.; Stojanovic, N.; Pachnicke, S. DSP for high-speed short-reach IM/DD systems using PAM. J. Light. Technol. 2020, 38, 6771–6778. [Google Scholar] [CrossRef]
- Wen, Y.J.; Cui, Y.; Bai, Y. Mitigation of optical multipath interference impact for directly detected PAMn system. Opt. Express 2020, 28, 38317–38333. [Google Scholar] [CrossRef] [PubMed]
- Cheng, N.; Zhang, D.; Ge, D.; Song, Y.; Lv, M.; Li, S.; Lv, B.; Zheng, X. Optical Multipath Interference Mitigation for PAM4 Transmission Using Line Coding and High-pass Filtering. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 5–9 March 2023; Optica Publishing Group: Washington, DC, USA, 2023; p. W2A-24. [Google Scholar]
- Li, Y.; Wei, Z.; Fu, H.Y. Adaptive Decision Threshold for Multipath Interference Impaired 40-Gb/s PAM4 IM/DD Optical Transmission. In Proceedings of the 2023 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 7–12 May 2023; pp. 1–2. [Google Scholar]
- Huo, J.; Zhu, J.; Zhu, Z.; Zhang, X.; Liu, S.; Tao, J. Mitigation of optical multipath interference algorithms in IM-DD transmission system. China Commun. 2024, 21, 1–9. [Google Scholar]
- Xie, Y.; Wang, Y.; Kandeepan, S.; Wang, K. Machine learning applications for short reach optical communication. Photonics 2022, 9, 30. [Google Scholar] [CrossRef]
- Karanov, B.; Chagnon, M.; Aref, V.; Ferreira, F.; Lavery, D.; Bayvel, P.; Schmalen, L. Experimental Investigation of Deep Learning for Digital Signal Processing in Short Reach Optical Fiber Communications. In Proceedings of the 2020 IEEE Workshop on Signal Processing Systems (SiPS), Coimbra, Portugal, 20–22 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Argyris, A.; Bueno, J.; Fischer, I. Photonic machine learning implementation for signal recovery in optical communications. Sci. Rep. 2018, 8, 8487. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Du, J.; Sun, L.; Zhang, W.; Xu, K.; Chen, X.; Reed, G.T.; He, Z. Nonlinear distortion mitigation by machine learning of SVM classification for PAM-4 and PAM-8 modulated optical interconnection. J. Light. Technol. 2018, 36, 650–657. [Google Scholar] [CrossRef]
- Zheng, X.; Liu, J.; Liu, J. An Equalization Method based on W-KNN for PON with PAM4. In Proceedings of the 2019 18th International Conference on Optical Communications and Networks (ICOCN), Huangshan, China, 5–8 August 2019; pp. 1–3. [Google Scholar]
- Huo, J.; Wang, M.; He, M.; Zhou, X.; Long, K. Joint SVM and KNN module algorithm for 16-QAM signal decision. Opt. Eng. 2020, 59, 126105. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, W.; Huo, J.; Zhu, J.; Tao, J.; Qin, P.; Zhang, X.; Bai, H. Machine Learning-Assisted Mitigation of Optical Multipath Interference in PAM4 IM-DD Transmission Systems. Photonics 2025, 12, 310. https://doi.org/10.3390/photonics12040310
Cui W, Huo J, Zhu J, Tao J, Qin P, Zhang X, Bai H. Machine Learning-Assisted Mitigation of Optical Multipath Interference in PAM4 IM-DD Transmission Systems. Photonics. 2025; 12(4):310. https://doi.org/10.3390/photonics12040310
Chicago/Turabian StyleCui, Wenxin, Jiahao Huo, Jin Zhu, Jianlong Tao, Peng Qin, Xiaoying Zhang, and Haolin Bai. 2025. "Machine Learning-Assisted Mitigation of Optical Multipath Interference in PAM4 IM-DD Transmission Systems" Photonics 12, no. 4: 310. https://doi.org/10.3390/photonics12040310
APA StyleCui, W., Huo, J., Zhu, J., Tao, J., Qin, P., Zhang, X., & Bai, H. (2025). Machine Learning-Assisted Mitigation of Optical Multipath Interference in PAM4 IM-DD Transmission Systems. Photonics, 12(4), 310. https://doi.org/10.3390/photonics12040310




