Multi-Channel Sparse-Frequency-Scanning White-Light Interferometry with Adaptive Mode Locking for Pulse Wave Velocity Measurement
Abstract
:1. Introduction
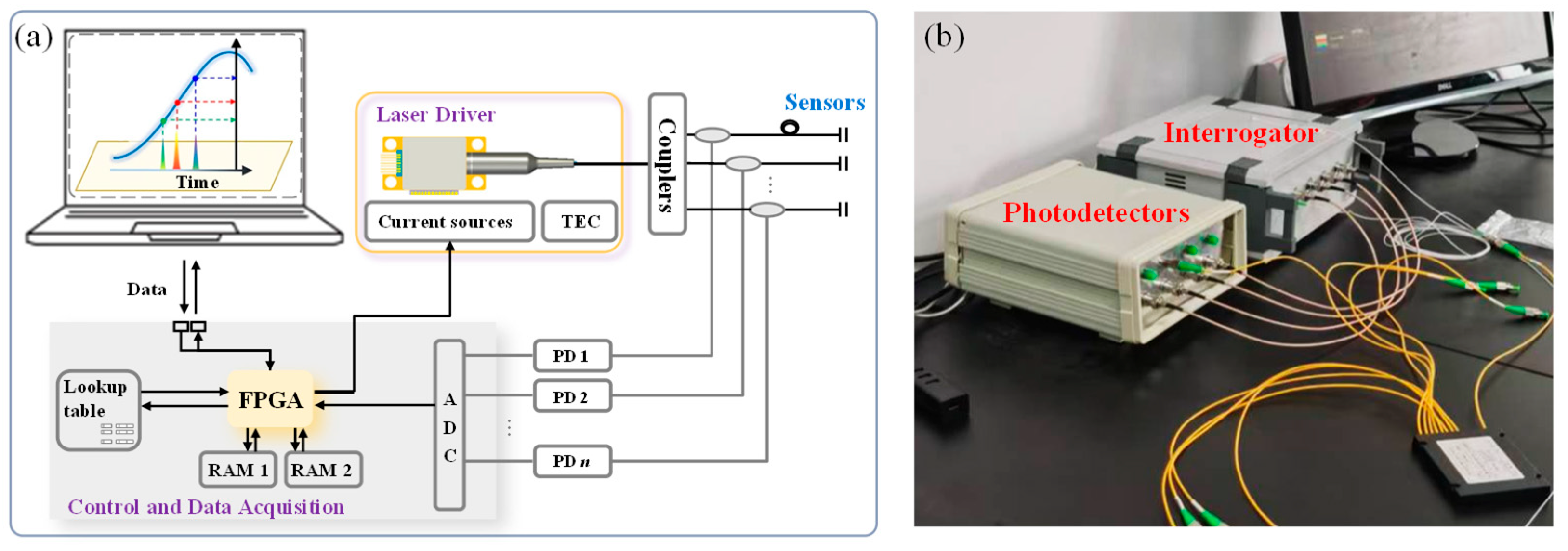
2. Sensors and Interrogators
2.1. Sparse-Frequency-Scanning White-Light Interferometry System
2.2. Diaphragm-Based Fabry–Pérot Pulse Wave Sensor
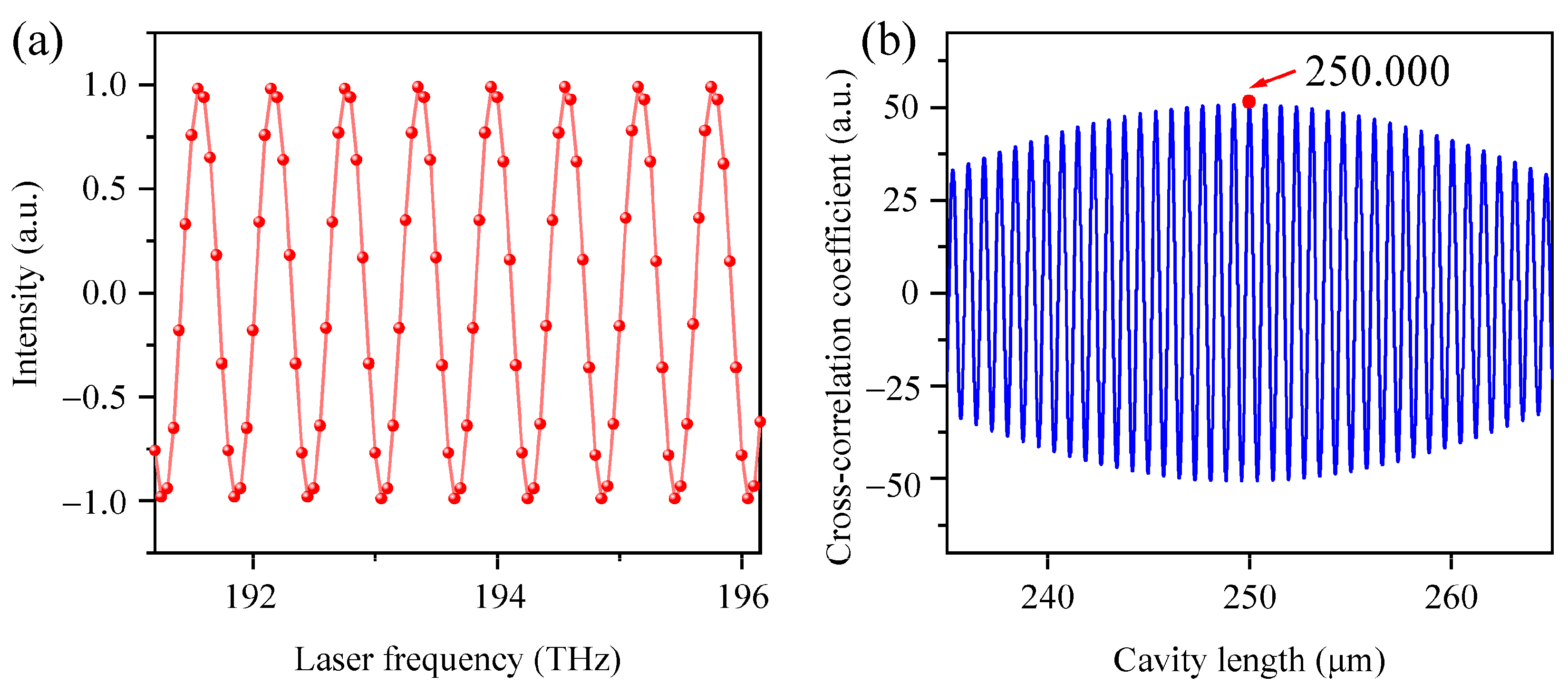
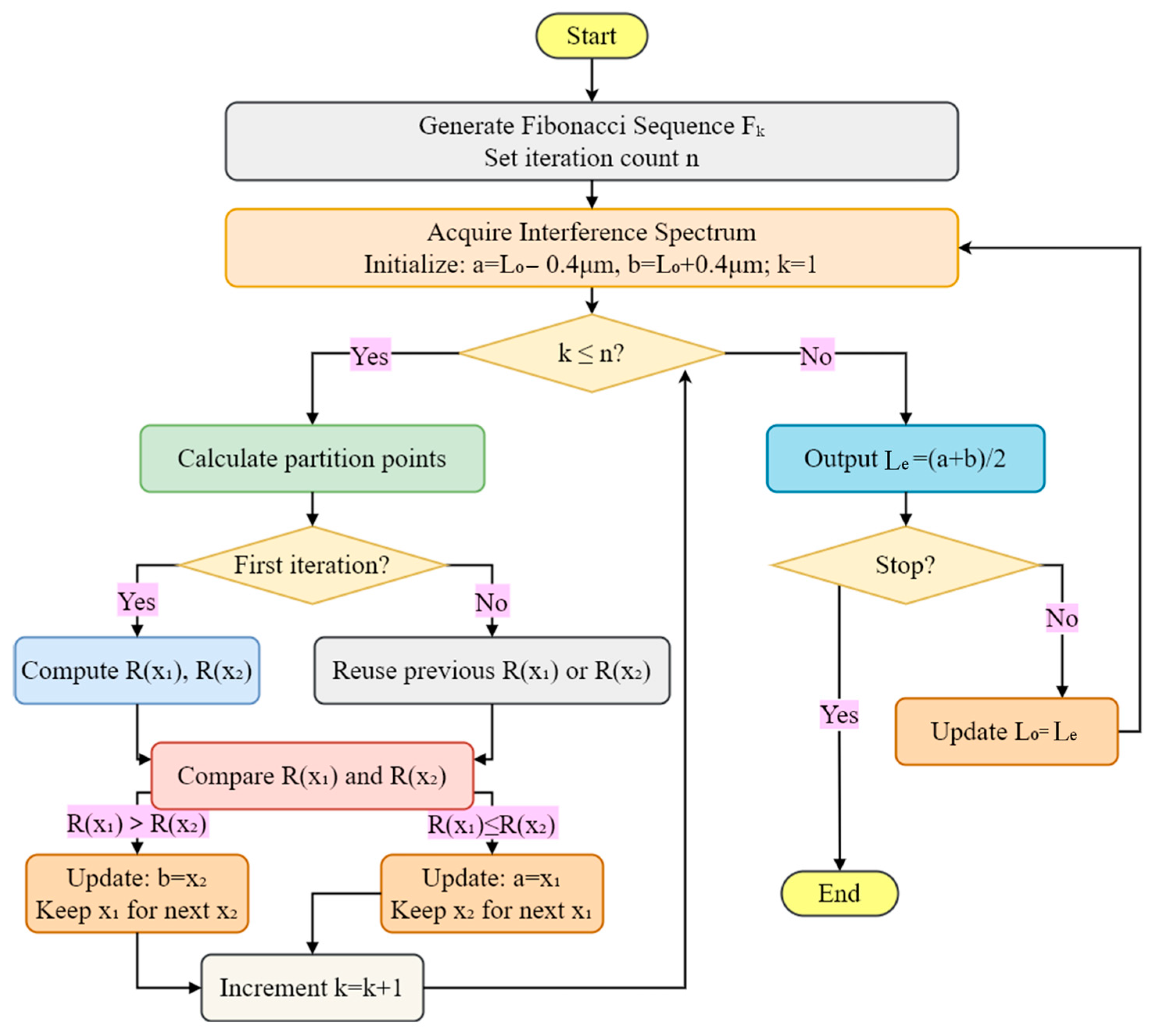
3. Fibonacci-Optimized Adaptive Mode-Locking Algorithm
- Search range confinement: restrict template matching to a ±0.4 μm neighborhood around the initial cavity length L0;
- Computational optimization: implement a Fibonacci search strategy to reduce algorithmic complexity.
- (1)
- Initialization:
- (2)
- Calculate the partition points:
- (3)
- Narrow the search interval. Calculate the cross-correlation coefficient based on Equation (3):
- (4)
- Output the estimated cavity length Le:
- (5)
- Adaptive mode locking:
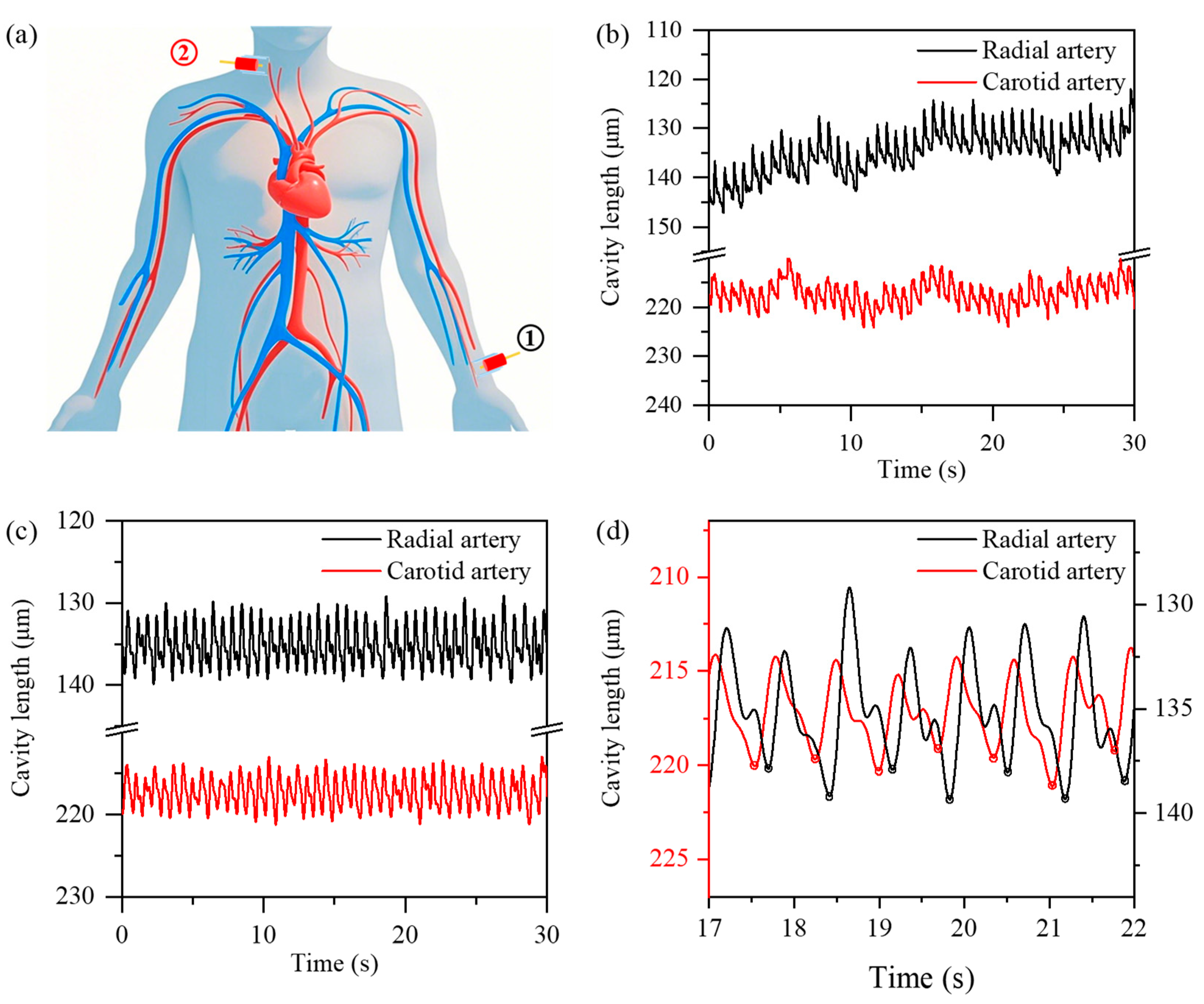
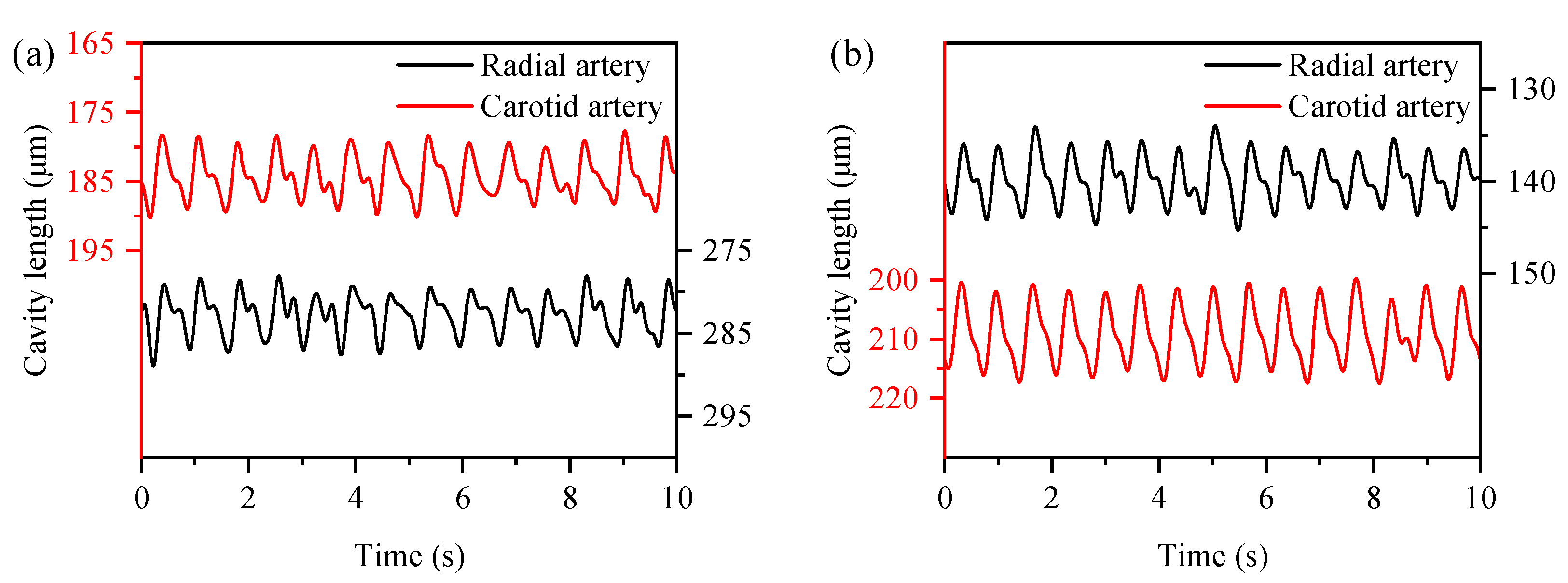
4. Pulse Wave Velocity Measurement
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sarabi, M.R.; Jiang, N.; Ozturk, E.; Yetisen, A.K.; Tasoglu, S. Biomedical optical fibers. Lab Chip 2021, 21, 627–640. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.; Zheng, T.; Wu, H.; Wu, Q.; Wang, Y. Wearable optical fiber sensors in medical monitoring applications: A review. Sensors 2023, 23, 6671. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Li, Y.; Fang, F.; Li, L.; Yan, Z.; Zhang, L.; Sun, Q. Highly sensitive and miniature microfiber-based ultrasound sensor for photoacoustic tomography. Opto-Electron. Adv. 2022, 5, 200076-1–200076-8. [Google Scholar] [CrossRef]
- Jha, R.; Mishra, P.; Kumar, S. Advancements in optical fiber-based wearable sensors for smart health monitoring. Biosens. Bioelectron. 2024, 254, 116232. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Liu, D.; Cai, Z.; Du, B.; Zou, M.; Tang, S.; Li, B.; Xiong, C.; Ji, P.; Zhang, L. A wearable breath sensor based on fiber-tip microcantilever. Biosensors 2022, 12, 168. [Google Scholar] [CrossRef] [PubMed]
- Shao, M.; Yuan, Y.; Wang, M.; Liu, Y.; Qiao, X. Optical fiber sensor for wearable and accurate human respiratory monitoring. Biomed. Opt. Express 2024, 15, 4132–4146. [Google Scholar] [CrossRef]
- Xiong, L.; Zhong, H.; Wan, S.; Yu, J. Single-point curved fiber optic pulse sensor for physiological signal prediction based on the genetic algorithm-support vector regression model. Opt. Fiber Technol. 2024, 82, 103583. [Google Scholar] [CrossRef]
- Martinek, R.; Nedoma, J.; Fajkus, M.; Kahankova, R.; Konecny, J.; Janku, P.; Kepak, S.; Bilik, P.; Nazeran, H. A phonocardiographic-based fiber-optic sensor and adaptive filtering system for noninvasive continuous fetal heart rate monitoring. Sensors 2017, 17, 890. [Google Scholar] [CrossRef]
- Shin, J.; Liu, Z.; Bai, W.; Liu, Y.; Yan, Y.; Xue, Y.; Kandela, I.; Pezhouh, M.; MacEwan, M.R.; Huang, Y.; et al. Bioresorbable optical sensor systems for monitoring of intracranial pressure and temperature. Sci. Adv. 2019, 5, eaaw1899. [Google Scholar] [CrossRef]
- Najafzadeh, A.; Serandi Gunawardena, D.; Liu, Z.; Tran, T.; Tam, H.-Y.; Fu, J.; Chen, B.K. Application of fibre bragg grating sensors in strain monitoring and fracture recovery of human femur bone. Bioengineering 2020, 7, 98. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; Yang, L.; Fang, F.; Yan, Z.; Sun, Q. Continuous and Accurate Blood Pressure Monitoring Based on Wearable Optical Fiber Wristband. IEEE Sens. J. 2021, 21, 3049–3057. [Google Scholar]
- Peltokangas, M.; Telembeci, A.A.; Verho, J.; Mattila, V.M.; Romsi, P.; Vehkaoja, A.; Lekkala, J.; Oksala, N. Parameters Extracted From Arterial Pulse Waves as Markers of Atherosclerotic Changes: Performance and Repeatability. IEEE J. Biomed. Health Inform. 2018, 22, 750–757. [Google Scholar] [PubMed]
- Li, C.; Guo, M.; Wang, Z.; Zhao, X.; Qi, H.; Han, X.; Cui, D.; Zhao, J.; Peng, W.; Chen, K. Fiber-Optic Photoacoustic Gas Sensor with Multiplexed Fabry–Pérot Interferometric Cantilevers. Anal. Chem. 2023, 95, 17477–17485. [Google Scholar]
- Qi, X.; Binghe, M.; Zhiyong, T.; Ruofei, L.; Zhibo, M. Dynamic Demodulation Technique for Tandem Dual-Cavity EFPI Sensors Enabling Simultaneous Temperature Measurement in Harsh Environment. IEEE Sens. J. 2024, 24, 28844–28851. [Google Scholar] [CrossRef]
- Lee, C.-L.; Ma, C.-T.; Yeh, K.-C.; Chen, Y.-M. A Dual-Cavity Fiber Fabry–Pérot Interferometer for Simultaneous Measurement of Thermo-Optic and Thermal Expansion Coefficients of a Polymer. Polymers 2022, 14, 4966. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Yang, Y.; Zheng, Y.; Yi, S.; Chen, S.; Duan, C.; Tian, Y.; Zhang, J. Vector magnetic field characteristics of magneto-shape effect with high figure of merit based on fiber optic vernier effect. Opt. Laser Technol. 2025, 181, 111670. [Google Scholar] [CrossRef]
- Chen, Y.; Lei, X.; Zhang, P.; Liu, X.; Zhang, W.; Shao, B.; Liu, H. Dynamic demodulation of low-finesse fabry-perot sensors based on instantaneous frequency analysis. J. Light. Technol. 2022, 40, 2996–3002. [Google Scholar]
- Ren, Y.; Zhang, P.; Shao, B.; Han, G.; Chang, X.; Liu, X.; Lei, X. Adaptive active reconstruction algorithm for dynamic clearance frequency-sweep interference signals. Measurement 2025, 245, 116562. [Google Scholar]
- Jiang, Y. High-resolution interrogation technique for fiber optic extrinsic Fabry–Perot interferometric sensors by the peak-to-peak method. Appl. Opt. 2008, 47, 925–932. [Google Scholar]
- Zheng, H.; Ma, L.; Li, C.; Jie, R.; Zhuang, Y.; Zhu, C.; Rao, Y. Detection of large dynamic range acoustic signal using OPD-based fiber-optic interferometric demodulation with SNR enhancement. J. Light. Technol. 2024, 42, 4689–4697. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, A. Fast white light interferometry demodulation algorithm for low-finesse Fabry–Pérot sensors. IEEE Photonics Technol. Lett. 2015, 27, 817–820. [Google Scholar] [CrossRef]
- Zhou, X.; Yu, Q. Wide-range displacement sensor based on fiber-optic Fabry–Perot interferometer for subnanometer measurement. IEEE Sens. J. 2010, 11, 1602–1606. [Google Scholar] [CrossRef]
- Xie, J.; Wang, F.; Pan, Y.; Wang, J.; Hu, Z.; Hu, Y. High resolution signal-processing method for extrinsic Fabry–Perot interferometric sensors. Opt. Fiber Technol. 2015, 22, 1–6. [Google Scholar] [CrossRef]
- Jain, S.; Nehra, M.; Kumar, R.; Dilbaghi, N.; Hu, T.; Kumar, S.; Kaushik, A.; Li, C.-z. Internet of medical things (IoMT)-integrated biosensors for point-of-care testing of infectious diseases. Biosens. Bioelectron. 2021, 179, 113074. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Jing, Z.; Li, A.; Liu, Y.; Huang, Z.; Zhang, Y.; Peng, W. Common-path dual-wavelength quadrature phase demodulation of EFPI sensors using a broadly tunable MG-Y laser. Opt. Express 2019, 27, 27873–27881. [Google Scholar] [CrossRef]
- Liu, Q.; Jing, Z.; Xia, Z.; Huang, Z.; Peng, W. Fiber-Optic Ultrasonic Sensing via Quasi-Continuous Quadrature Frequency Modulation. IEEE Photonics Technol. Lett. 2020, 32, 1385–1388. [Google Scholar] [CrossRef]
- Chen, H.; Liu, J.; Zhang, X.; Wang, W.; Ma, Z.; Lv, W.; Guo, Z. High-Order Harmonic-Frequency Cross-Correlation Algorithm for Absolute Cavity Length Interrogation of White-Light Fiber-Optic Fabry-Perot Sensors. J. Light. Technol. 2020, 38, 953–960. [Google Scholar] [CrossRef]
- Ushakov, N.A.; Liokumovich, L.B. Abrupt λ/2 demodulation errors in spectral interferometry: Origins and suppression. IEEE Photonics Technol. Lett. 2020, 32, 1159–1162. [Google Scholar] [CrossRef]
- Shao, B.; Zhang, W.; Zhang, P.; Chen, W. Dynamic Clearance Measurement Using Fiber-Optic Frequency-Swept and Frequency-Fixed Interferometry. IEEE Photonics Technol. Lett. 2020, 32, 1331–1334. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, W.; Shao, B.; Zhang, P.; Chen, W. Algorithm of Doppler error suppression in frequency-swept interferometry for the dynamic axial clearance measurement of high-speed rotating machinery. Opt. Express 2021, 29, 42471–42484. [Google Scholar] [CrossRef]
- Ushakov, N.A.; Markvart, A.A.; Liokumovich, L.B. Pulse Wave Velocity Measurement With Multiplexed Fiber Optic Fabry–Perot Interferometric Sensors. IEEE Sens. J. 2020, 20, 11302–11312. [Google Scholar] [CrossRef]
- Hsu, Y.P.; Young, D.J. Skin-Coupled Personal Wearable Ambulatory Pulse Wave Velocity Monitoring System Using Microelectromechanical Sensors. IEEE Sens. J. 2014, 14, 3490–3497. [Google Scholar]



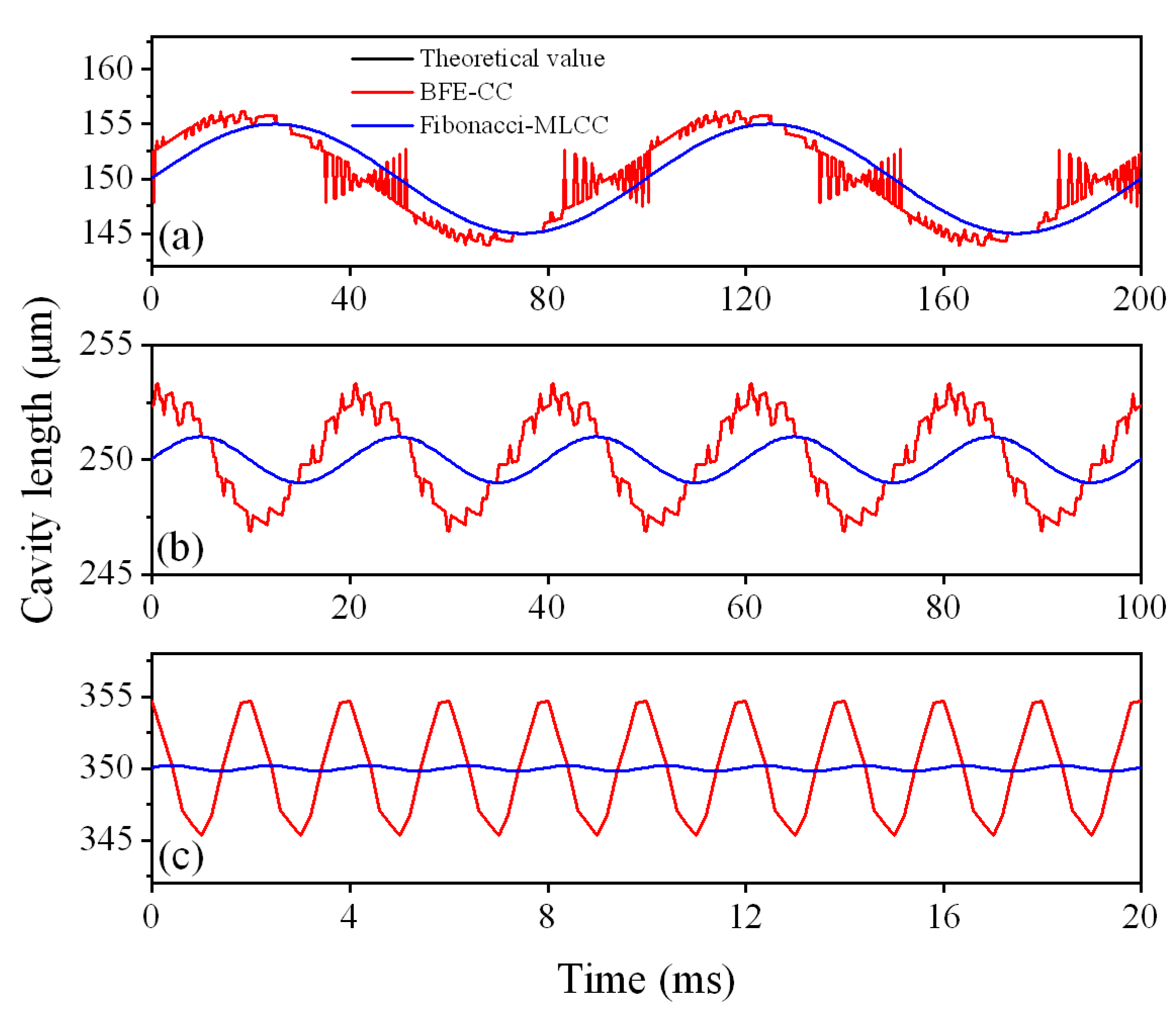
| Applied Vibration | Theoretical Value | BFE | CC | BFE-CC | MLCC | Fibonacci–MLCC |
|---|---|---|---|---|---|---|
| 0 Hz, 0 nm | 250.000 | 249.593 | 250.000 | 250.000 | 250.000 | 205.0007 |
| 2 Hz, 20 μm | 250.025 | 251.604 | 251.572 | 251.572 | 250.024 | 250.0243 |
| 50 Hz, 1000 nm | 250.031 | 252.119 | 252.352 | 252.352 | 250.030 | 250.0308 |
| 100 Hz, 1000 nm | 250.062 | 254.753 | 254.706 | 254.706 | 250.062 | 250.0623 |
| 500 Hz, 200 nm | 250.060 | 254.466 | 254.704 | 254.704 | 250.060 | 250.0610 |
| 500 Hz, 500 nm | 250.151 | 261.953 | 261.762 | 261.762 | 250.153 | 250.1528 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Gao, L.; Qian, C.; Wang, Y.; Liu, W.; Cai, X.; Liu, Q. Multi-Channel Sparse-Frequency-Scanning White-Light Interferometry with Adaptive Mode Locking for Pulse Wave Velocity Measurement. Photonics 2025, 12, 316. https://doi.org/10.3390/photonics12040316
Xu Y, Gao L, Qian C, Wang Y, Liu W, Cai X, Liu Q. Multi-Channel Sparse-Frequency-Scanning White-Light Interferometry with Adaptive Mode Locking for Pulse Wave Velocity Measurement. Photonics. 2025; 12(4):316. https://doi.org/10.3390/photonics12040316
Chicago/Turabian StyleXu, Yifei, Laiben Gao, Cheng Qian, Yiping Wang, Wenyan Liu, Xiaoyan Cai, and Qiang Liu. 2025. "Multi-Channel Sparse-Frequency-Scanning White-Light Interferometry with Adaptive Mode Locking for Pulse Wave Velocity Measurement" Photonics 12, no. 4: 316. https://doi.org/10.3390/photonics12040316
APA StyleXu, Y., Gao, L., Qian, C., Wang, Y., Liu, W., Cai, X., & Liu, Q. (2025). Multi-Channel Sparse-Frequency-Scanning White-Light Interferometry with Adaptive Mode Locking for Pulse Wave Velocity Measurement. Photonics, 12(4), 316. https://doi.org/10.3390/photonics12040316






