Far-Zone Spectral Density of Light Waves Scattered by Random Anisotropic Hollow Medium

Abstract

A random anisotropic hollow scatterer is discussed and the far-zone characteristics of scalar light waves scattered by this type of medium are theoretically analyzed. The results show that the scattered far-zone spectral density distributions have interesting patterns of “central ellipses and peripheral circles” or “central circles and peripheral ellipses”, which are decided by the outer and inner correlation lengths of the scatterer. This phenomenon provides some new insights into the generation and manipulation of the scattered far field, and can be applied in the reconstruction of the scattering medium’s structure.

1. Introduction

The statistical optical properties of the scattered field vary significantly as the light wave is scattered through different types of media. These variations are closely related to the structural characteristics of the medium, implying that the statistical optical properties of scattered light waves reflect the structural information of the medium. Therefore, it is possible to deduce the structural characteristics of an unknown medium from the light field scattered by it. The study of light waves being scattered by different types of scattering media has always been a hot topic in the field of scattering research [1,2], especially by the traditional media such as deterministic media and quasi-homogeneous media [3,4,5,6,7]. A review of this work has been made by Wolf and his collaborator [8,9]. Meanwhile, researchers have also extended their studies from traditional media to various new media, such as anisotropic quasi-homogeneous media [10,11,12], anisotropic particles [13,14,15], semi-soft boundary media [16,17], hollow media [18,19], and media with PT symmetry [20,21,22]. In applications such as target detection, remote sensing, and medical diagnostics, these studies have shown significant potential and value [23,24,25,26].

Currently, most of the studies on scattering media focus on solid media, and few studies have been conducted on hollow media. In addition, studies on hollow media have focused almost exclusively on isotropic hollow media [18,19]. However, one may encounter anisotropic media in practice, for example, an elliptocyte [27]. Moreover, the anisotropic medium is a more general model and the often mentioned isotropic scatterer is a special case of this model.

In this paper, we considered the scattering behaviors of random anisotropic hollow media, i.e., the effective lengths of the scattering medium in each direction are different and the structure of the scattering medium is hollow-profile. The far-zone spectral density distribution of light waves scattered by a random anisotropic hollow medium is analyzed theoretically and the effects of the outer and inner correlation lengths of the anisotropic hollow medium on the spectral density distribution of the scattered field are discussed.

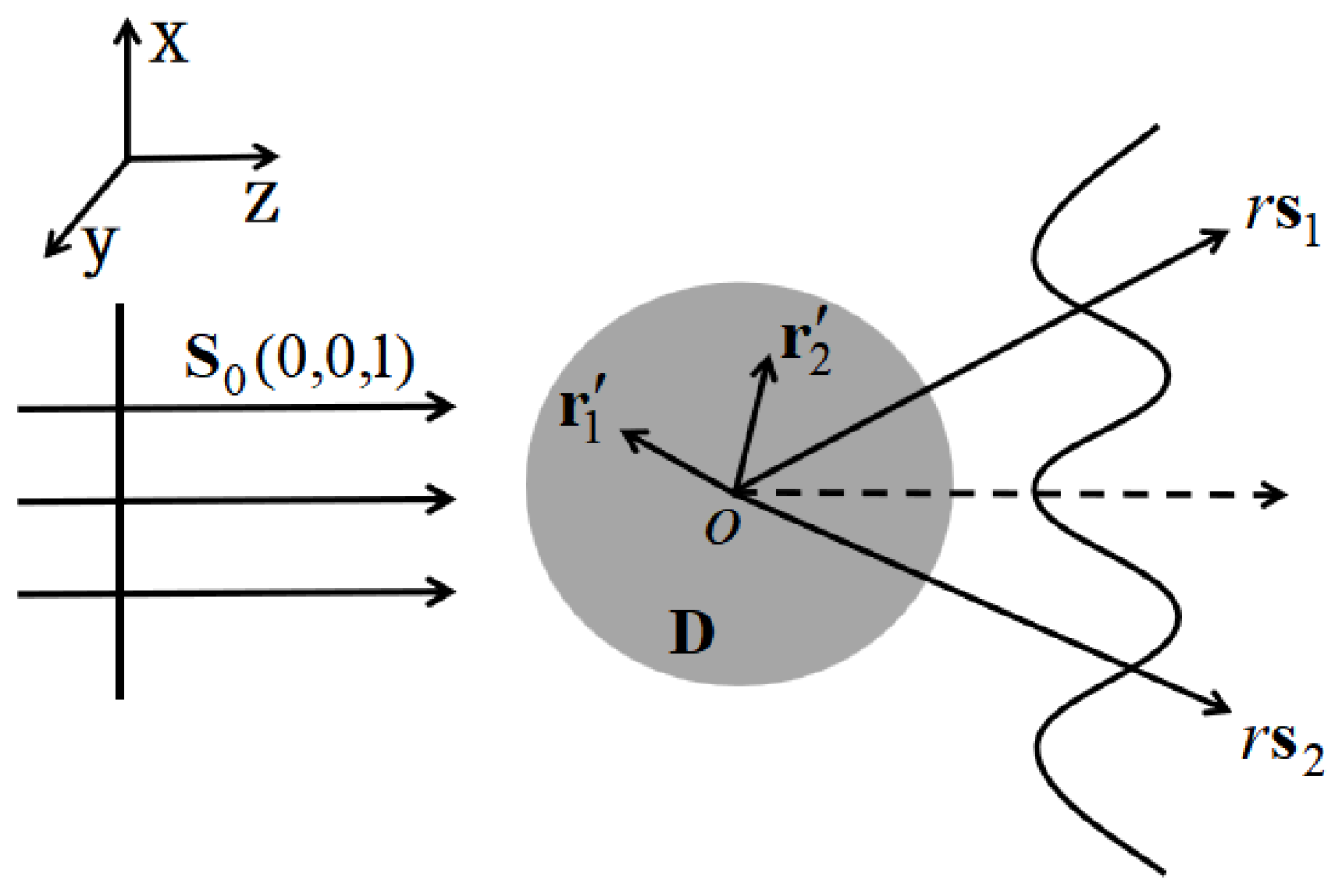
2. Theoretical Foundations

As shown in Figure 1, suppose that a polychromatic plane light wave, propagating in a direction denoted by a unit vector ${\mathrm{S}}_0\left(0,0,1\right)$, hits a scatterer occupying a finite domain D. The cross-spectral density function should be used to describe the optical properties of the incident light, which is defined by [9]

$$W^{(i)}\left({\mathbf{r}}_1^{\prime },{\mathbf{r}}_2^{\prime },s_0,\omega \right)=〈U^{(i)\ast }\left({\mathbf{r}}_1^{\prime },s_0,\omega \right)U^{(i)}\left({\mathbf{r}}_2^{\prime },s_0,\omega \right)〉,$$

(1)

where the asterisk “$\ast$” represents complex conjugation, the corner brackets “$〈\dots 〉$” represent the ensemble averaging of the incident light field, and $U^{(i)}\left(r^{\prime },s_0,\omega \right)$ represents the field of the incident wave at spatial position $r^{\prime }$ and can be expressed as:

$$U^{(i)}\left(r^{\prime },s_0,\omega \right)=a\left(\omega \right)\exp \left(ik{s}_0\cdot r^{\prime }\right),$$

(2)

where $a\left(\omega \right)$ is a random function, and $k=\omega /c$ is the free-space wave number with $c$ being the light speed in vacuum.

Substituting Equation (2) into Equation (1), we obtain the cross-spectral density function of the incident wave as

$$W^{(i)}\left({\mathbf{r}}_1^{\prime },{\mathbf{r}}_2^{\prime },s_0,\omega \right)=S^{(i)}\left(\omega \right)\exp \left[ik{s}_0\cdot ({\mathbf{r}}_2^{\prime }-{\mathbf{r}}_1^{\prime })\right],$$

(3)

and

$$S^{\left(i\right)}\left(\omega \right)=〈a^{\ast }\left(\omega \right)a\left(\omega \right)〉,$$

(4)

which is the spectrum of the incident field, independent of position.

For a random medium, the scattering potential is a random function of position and can be described by its two-point correlation function $C_F\left({\mathbf{r}}_1^{\prime },{\mathbf{r}}_2^{\prime },\omega \right)$, and

$$C_F\left({\mathbf{r}}_1^{\prime },{\mathbf{r}}_2^{\prime },\omega \right)=〈F^{\ast }\left({\mathbf{r}}_1^{\prime },\omega \right)F\left({\mathbf{r}}_2^{\prime },\omega \right)〉,$$

(5)

where $F\left(r^{\prime },\omega \right)=k^2/4\pi \left[n^2\left(r^{\prime },\omega \right)-1\right]$ is the scattering potential function of the medium. For an anisotropic random medium, the cross-spectral density function of the scattered far field is given by [8,9]

$$W^{(s)}\left(r{s}_1,r{s}_2,s_0,\omega \right)={\displaystyle \frac{S^{(i)}\left(\omega \right)}{r^2}}{\tilde{C}}_F\left[-K_1,K_2,\omega \right],$$

(6)

where

$$K_1=k\left(s_1-s_0\right),K_2=k\left(s_2-s_0\right),$$

(7)

$s_1$ and $s_2$ are the unit vector of scattering direction, and

$${\tilde{C}}_F\left[K_1,K_2,\omega \right]={\displaystyle {\iint }_D{C}_F\left({\mathbf{r}}_1^{\prime },{\mathbf{r}}_2^{\prime },\omega \right)}\exp \left[-i(K_1\cdot {\mathbf{r}}_1^{\prime }+K_2\cdot {\mathbf{r}}_2^{\prime })\right]d^3{r}_1^{\prime }{d}^3{r}_2^{\prime },$$

(8)

is the six-dimensional spatial Fourier transform of $C_F\left({\mathbf{r}}_1^{\prime },{\mathbf{r}}_2^{\prime },\omega \right)$.

When the two scattering directions coincide (i.e., $s_1=s_2=s$), the cross-spectral density function reduces to the spectral density of the far-zone scattered field, in the form of [9]

$$S^{\left(s\right)}\left(rs,s_0,\omega \right)={\displaystyle \frac{S^{(i)}\left(\omega \right)}{r^2}}{\tilde{C}}_F\left[-k\left(s-s_0\right),k\left(s-s_0\right),\omega \right].$$

(9)

In practical application, the scattering medium may be anisotropy, for example, the elliptocyte [27]. In such case, the Fourier transform of the correlation function for an anisotropic scatterer is

$${\tilde{C}}_F\left[-k\left(s-s_0\right),k\left(s-s_0\right),\omega \right]={\displaystyle \prod _{i=x}^z{\tilde{C}}_{Fi}\left[-k\left(s_i-s_{0i}\right),k\left(s_i-s_{0i}\right),\omega \right]},$$

(10)

where ${\tilde{C}}_{Fi}\left[-k\left(s_i-s_{0i}\right),k\left(s_i-s_{0i}\right),\omega \right]$ is the Fourier transform of the correlation function component along the i-direction, expressed as

$${\tilde{C}}_{Fi}\left[-k\left(s_i-s_{0i}\right),k\left(s_i-s_{0i}\right),\omega \right]={\displaystyle \iint C_{Fi}\left(r_{1i}^{\prime },r_{2i}^{\prime },\omega \right)}\exp \left[-ik\left(s_i-s_{0i}\right)\left(r_{2i}^{\prime }-r_{1i}^{\prime }\right)\right]d{r}_{1i}^{\prime }d{r}_{2i}^{\prime }.$$

(11)

It should be indicated that for anisotropic media, the scattering potential correlation function is different in each direction.

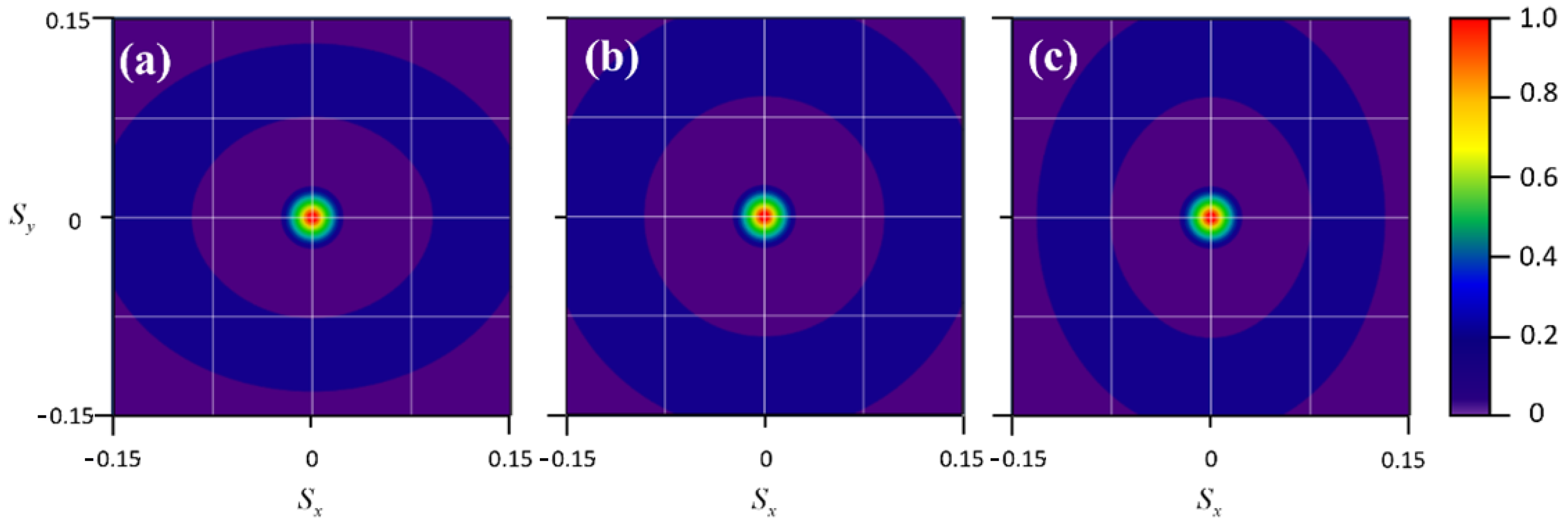
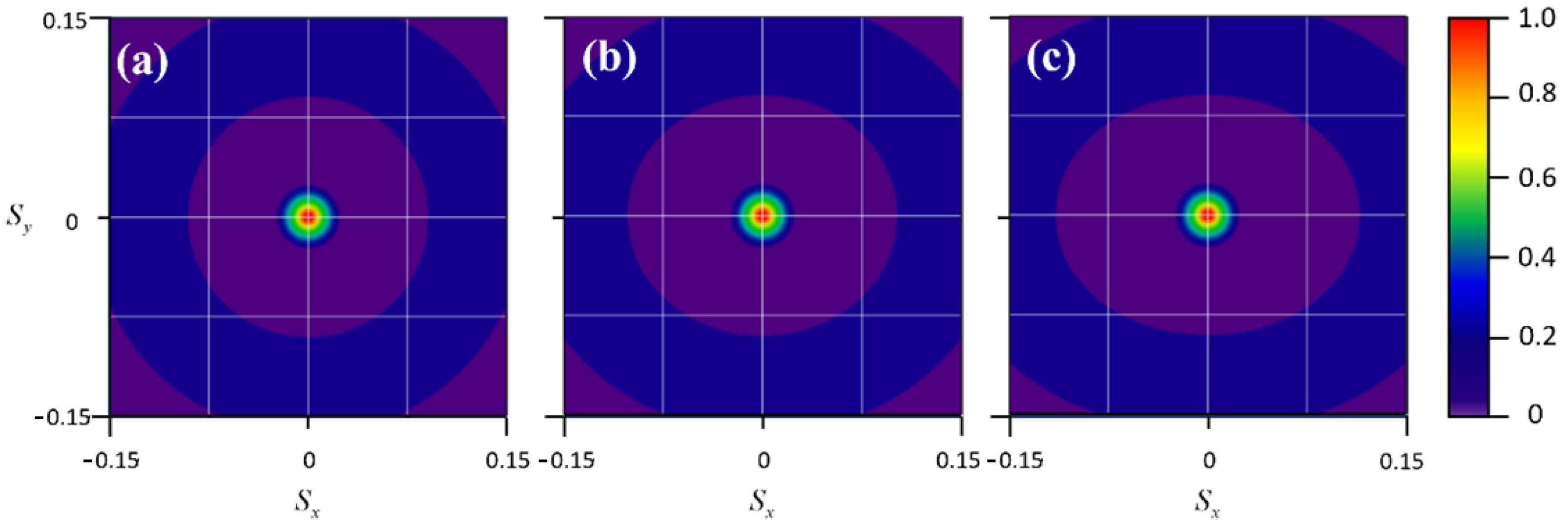
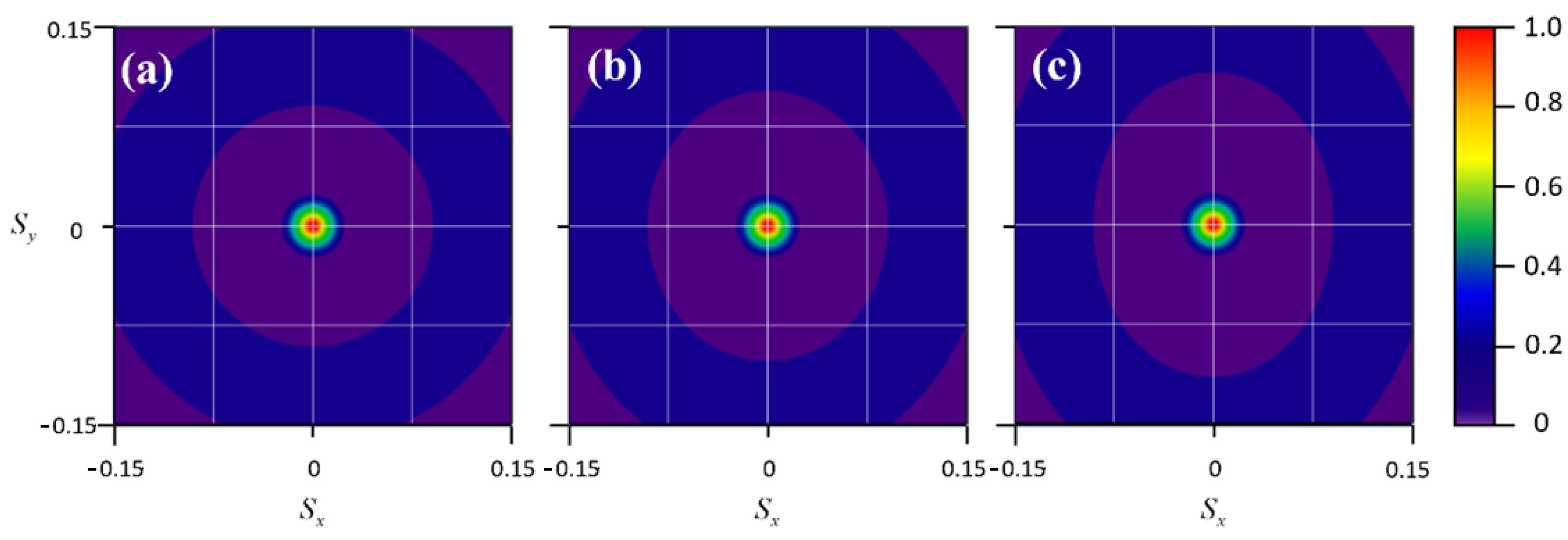
3. Numerical Results and Discussion

As the research object of the random hollow medium is extended from an isotropic one to an anisotropic one, its scattering potential correlation function can be expressed as [10,19].

$$\begin{array}{cc}\hfill C_F\left({\mathbf{r}}_1^{\prime },{\mathbf{r}}_2^{\prime },\omega \right)& ={\displaystyle \frac{1}{C_0}}\exp \left[-{\displaystyle \frac{{\left(x_1+x_2\right)}^2}{8{\sigma }_{Ix}^2}}\right]\exp \left[-{\displaystyle \frac{{\left(y_1+y_2\right)}^2}{8{\sigma }_{Iy}^2}}\right]\exp \left[-{\displaystyle \frac{{\left(z_1+z_2\right)}^2}{8{\sigma }_{Iz}^2}}\right]\hfill \\ \hfill & {\displaystyle \sum _{m=1}^M\frac{{\left(-1\right)}^{m-1}}{M}\left(\begin{array}{c}M\\ m\end{array}\right)}\left\{\exp \left[-m{\displaystyle \frac{{\left(x_2-x_1\right)}^2}{2{\sigma }_{\mu ox}^2}}\right]\right.\exp \left[-m{\displaystyle \frac{{\left(y_2-y_1\right)}^2}{2{\sigma }_{\mu oy}^2}}\right]\exp \left[-m{\displaystyle \frac{{\left(z_2-z_1\right)}^2}{2{\sigma }_{\mu oz}^2}}\right]\hfill \\ \hfill & -\left.\exp \left[-m{\displaystyle \frac{{\left(x_2-x_1\right)}^2}{2{\sigma }_{\mu px}^2}}\right]\exp \left[-m{\displaystyle \frac{{\left(y_2-y_1\right)}^2}{2{\sigma }_{\mu py}^2}}\right]\exp \left[-m{\displaystyle \frac{{\left(z_2-z_1\right)}^2}{2{\sigma }_{\mu pz}^2}}\right]\right\},\hfill \end{array}$$

(12)

where

$$C_0={\displaystyle \sum _{m=1}^M\frac{{\left(-1\right)}^{m-1}}{M}}\left(\begin{array}{c}M\\ m\end{array}\right),$$

(13)

is the normalization factor, $\left(\begin{array}{c}M\\ m\end{array}\right)$ is the binomial coefficients with $M$ representing the shell thickness of the scatterer, ${\sigma }_{Ii}\left(i=x,y,z\right)$ is the effective radius of the scatterer, and ${\sigma }_{\mu oi}\left(x,y,z\right)$ and ${\sigma }_{\mu pi}\left(i=x,y,z\right)$ denote the outer and inner correlation lengths of the random anisotropic hollow medium, respectively. To ensure that the medium satisfies the non-negativity condition, the outer and inner correlation lengths of the scatterer must satisfy the inequality ${\sigma }_{\mu oi}\left(x,y,z\right)>{\sigma }_{\mu pi}\left(x,y,z\right)$.

For the convenience of calculation, we make the following variable transformation:

$$R_S=\left(R_{Sx},R_{Sy},R_{Sz}\right),R_{Sx}=x_2+x_1,R_{Sy}=y_2+y_1,R_{Sz}=z_2+z_1,$$

(14a)

$$R_D=\left(R_{Dx},R_{Dy},R_{Dz}\right),R_{Dx}=x_2-x_1,R_{Dy}=y_2-y_1,R_{Dz}=z_2-z_1.$$

(14b)

Substituting Equation (12) into Equation (8) and combining with Equation (14), we can obtain that

$$\begin{array}{cc}\hfill {\tilde{C}}_F\left(K_1,K_2,\omega \right)& ={\displaystyle \frac{1}{2C_0}}{\displaystyle \int \exp \left[-\frac{R_{Sx}^2+R_{Dx}^2}{16{\sigma }_{Ix}^2}\right]}\exp \left[-{\displaystyle \frac{R_{Sy}^2+R_{Dy}^2}{16{\sigma }_{Iy}^2}}\right]\exp \left[-{\displaystyle \frac{R_{Sz}^2+R_{Dz}^2}{16{\sigma }_{Iz}^2}}\right]\hfill \\ & {\displaystyle \sum _{m=1}^M\frac{{\left(-1\right)}^{m-1}}{M}\left(\begin{array}{c}M\\ m\end{array}\right)}\left\{\exp \left[-m{\displaystyle \frac{R_{Dx}^2}{2{\sigma }_{\mu ox}^2}}\right]\exp \left[-m{\displaystyle \frac{R_{Dy}^2}{2{\sigma }_{\mu oy}^2}}\right]\exp \left[-m{\displaystyle \frac{R_{Dz}^2}{2{\sigma }_{\mu oz}^2}}\right]\right.\hfill \\ & -\left.\exp \left[-m{\displaystyle \frac{R_{Dx}^2}{2{\sigma }_{\mu px}^2}}\right]\exp \left[-m{\displaystyle \frac{R_{Dy}^2}{2{\sigma }_{\mu py}^2}}\right]\exp \left[-m{\displaystyle \frac{R_{Dz}^2}{2{\sigma }_{\mu pz}^2}}\right]\right\}\hfill \\ & \times \exp \left[-{\displaystyle \frac{i}{2}}(K_1+K_2)\cdot R_S\right]\exp \left[{\displaystyle \frac{i}{2}}(K_1-K_2)\cdot R_D\right]d^3{R}_S{d}^3{R}_D,\hfill \end{array}$$

(15)

and then, performing some calculations by using the following integral formula,

$${\displaystyle {\int }_{+\infty }^{+\infty }}\exp \left(-p{x}^2+2qx\right)dx=\left[\exp \left({\displaystyle \frac{q^2}{p}}\right)\right]\sqrt{{\displaystyle \frac{\pi }{p}}},$$

(16)

the six-dimensional Fourier transform expression of the scattering potential correlation function of the random anisotropic hollow medium can be obtained:

$$\begin{array}{cc}\hfill \tilde{C}\left(K_1,K_2,\omega \right)& ={\displaystyle \frac{8^3\sqrt{2}{\pi }^3}{C_0}}{\sigma }_{Ix}^2{\sigma }_{Iy}^2{\sigma }_{Iz}^2\exp \left[-4({\sigma }_{Ix}^2{K}_{Sx}^2+{\sigma }_{Ix}^2{K}_{Sx}^2+{\sigma }_{Ix}^2{K}_{Sx}^2)\right]\hfill \\ \hfill & \times \left\{{\sigma }_{\mu ox}{\sigma }_{\mu oy}{\sigma }_{\mu oz}{\displaystyle \sum _{m=1}^M\frac{{\left(-1\right)}^{m-1}}{M}\left(\begin{array}{c}M\\ m\end{array}\right)}{\left({\displaystyle \frac{1}{{\sigma }_{\mu ox}^2+8m{\sigma }_{Ix}^2}}\right)}^{1/2}{\left({\displaystyle \frac{1}{{\sigma }_{\mu oy}^2+8m{\sigma }_{Iy}^2}}\right)}^{1/2}{\left({\displaystyle \frac{1}{{\sigma }_{\mu oz}^2+8m{\sigma }_{Iz}^2}}\right)}^{1/2}\right.\hfill \\ \hfill & \exp \left[{\displaystyle \frac{-4{\sigma }_{Ix}^2{\sigma }_{\mu ox}^2{(K_{Dx})}^2}{{\sigma }_{\mu ox}^2+8m{\sigma }_{Ix}^2}}-{\displaystyle \frac{4{\sigma }_{Iy}^2{\sigma }_{\mu oy}^2{(K_{Dy})}^2}{{\sigma }_{\mu oy}^2+8m{\sigma }_{Iy}^2}}-{\displaystyle \frac{4{\sigma }_{Iz}^2{\sigma }_{\mu oz}^2{(K_{Dz})}^2}{{\sigma }_{\mu oz}^2+8m{\sigma }_{Iz}^2}}\right]\hfill \\ \hfill & -{\sigma }_{\mu px}{\sigma }_{\mu py}{\sigma }_{\mu pz}{\displaystyle \sum _{m=1}^M\frac{{\left(-1\right)}^{m-1}}{M}\left(\begin{array}{c}M\\ m\end{array}\right)}{\left({\displaystyle \frac{1}{{\sigma }_{\mu px}^2+8m{\sigma }_{Ix}^2}}\right)}^{1/2}{\left({\displaystyle \frac{1}{{\sigma }_{\mu py}^2+8m{\sigma }_{Iy}^2}}\right)}^{1/2}{\left({\displaystyle \frac{1}{{\sigma }_{\mu pz}^2+8m{\sigma }_{Iz}^2}}\right)}^{1/2}\hfill \\ \hfill & \times \left.\exp \left[{\displaystyle \frac{-4{\sigma }_{Ix}^2{\sigma }_{\mu px}^2{(K_{Dx})}^2}{{\sigma }_{\mu px}^2+8m{\sigma }_{Ix}^2}}-{\displaystyle \frac{4{\sigma }_{Iy}^2{\sigma }_{\mu py}^2{(K_{Dy})}^2}{{\sigma }_{\mu py}^2+8m{\sigma }_{Iy}^2}}-{\displaystyle \frac{4{\sigma }_{Iz}^2{\sigma }_{\mu pz}^2{(K_{Dz})}^2}{{\sigma }_{\mu pz}^2+8m{\sigma }_{Iz}^2}}\right]\right\}\hfill \end{array}$$

(17)

where

$$K_S={\displaystyle \frac{K_1+K_2}{2}},K_D={\displaystyle \frac{K_2-K_1}{2}},$$

(18)

$K_{Si}$($i=x,y,z$) and $K_{Di}$($i=x,y,z$) represent the components of $K_S$ and $K_D$, respectively. Based on Equations (17) and (9), the far-zone spectral density of light waves scattered by the random anisotropic hollow medium can be derived as

$$\begin{array}{cc}\hfill S^{\left(s\right)}\left(rs,s_0,\omega \right)& ={\displaystyle \frac{S^{(i)}\left(\omega \right)}{r^2}}{\displaystyle \frac{8^3\sqrt{2}{\pi }^3}{C_0}}{\sigma }_{Ix}^2{\sigma }_{Iy}^2{\sigma }_{Iz}^2\hfill \\ \hfill & \times \left\{{\sigma }_{\mu ox}{\sigma }_{\mu oy}{\sigma }_{\mu oz}{\displaystyle \sum _{m=1}^M\frac{{\left(-1\right)}^{m-1}}{M}\left(\begin{array}{c}M\\ m\end{array}\right)}{\left({\displaystyle \frac{1}{{\sigma }_{\mu ox}^2+8m{\sigma }_{Ix}^2}}\right)}^{1/2}{\left({\displaystyle \frac{1}{{\sigma }_{\mu oy}^2+8m{\sigma }_{Iy}^2}}\right)}^{1/2}{\left({\displaystyle \frac{1}{{\sigma }_{\mu oz}^2+8m{\sigma }_{Iz}^2}}\right)}^{1/2}\right.\hfill \\ \hfill & \exp \left[{\displaystyle \frac{-4{\sigma }_{Ix}^2{\sigma }_{\mu ox}^2{k}^2{(s_x-s_{0x})}^2}{{\sigma }_{\mu ox}^2+8m{\sigma }_{Ix}^2}}-{\displaystyle \frac{4{\sigma }_{Iy}^2{\sigma }_{\mu oy}^2{k}^2{(s_y-s_{0y})}^2}{{\sigma }_{\mu oy}^2+8m{\sigma }_{Iy}^2}}-{\displaystyle \frac{4{\sigma }_{Iz}^2{\sigma }_{\mu oz}^2{k}^2{(s_z-s_{0z})}^2}{{\sigma }_{\mu oz}^2+8m{\sigma }_{Iz}^2}}\right]\hfill \\ \hfill & -{\sigma }_{\mu px}{\sigma }_{\mu py}{\sigma }_{\mu pz}{\displaystyle \sum _{m=1}^M\frac{{\left(-1\right)}^{m-1}}{M}\left(\begin{array}{c}M\\ m\end{array}\right)}{\left({\displaystyle \frac{1}{{\sigma }_{\mu px}^2+8m{\sigma }_{Ix}^2}}\right)}^{1/2}{\left({\displaystyle \frac{1}{{\sigma }_{\mu py}^2+8m{\sigma }_{Iy}^2}}\right)}^{1/2}{\left({\displaystyle \frac{1}{{\sigma }_{\mu pz}^2+8m{\sigma }_{Iz}^2}}\right)}^{1/2}\hfill \\ \hfill & \times \left.\exp \left[{\displaystyle \frac{-4{\sigma }_{Ix}^2{\sigma }_{\mu px}^2{k}^2{(s_x-s_{0x})}^2}{{\sigma }_{\mu px}^2+8m{\sigma }_{Ix}^2}}-{\displaystyle \frac{4{\sigma }_{Iy}^2{\sigma }_{\mu py}^2{k}^2{(s_y-s_{0y})}^2}{{\sigma }_{\mu py}^2+8m{\sigma }_{Iy}^2}}-{\displaystyle \frac{4{\sigma }_{Iz}^2{\sigma }_{\mu pz}^2{k}^2{(s_z-s_{0z})}^2}{{\sigma }_{\mu pz}^2+8m{\sigma }_{Iz}^2}}\right]\right\}.\hfill \end{array}$$

(19)

where $s=\left(s_x,s_y,s_z\right)$ and $s_0=\left(s_{0x},s_{0y},s_{0z}\right)$.

As illustrated in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7, the spectral density of the scattered field is demonstrated under varying inner and outer correlation lengths of scatterers. Figure 2 demonstrates the influence of the outer correlation length of the medium on the scattered spectral density distribution, in which the internal distribution adheres to an elliptical Gaussian distribution, while the external region manifests circular distribution. The overall distribution thus exhibits a configuration that can be described as “central ellipses and peripheral circles”. In (a), (b), and (c) of Figure 2, the lengths of the long and short axes of the internal ellipses change as different computational parameters are chosen.

Figure 3 demonstrates the influence of the inner correlation length of the medium on the scattered spectral density distribution. It can be seen from Figure 3 that the scattered spectral intensities show a circular Gaussian distribution of multiple concentric circles, with the highest value in the center and gradually decreasing outwards, and the shapes of the peripheral circles present as ellipses. Such density distribution can be summarized as “central circles and peripheral ellipses”.

As previously stated, the presence of scatterers exhibiting disparate outer correlation lengths gives rise to the manifestation of scattered spectral density distributions that manifest as the pattern of “central ellipses and peripheral circles”. If the value of the outer correlation length of the medium can be precisely adjusted, it is possible to modulate the shape of the internal elliptical distribution of the scattered spectral density, as illustrated in Figure 4. When $k_{\mu ox}<k_{\mu oy}$, the long axes of the internal ellipses lie on the x-axis. Keeping the value of $k_{\mu oy}$ constant and increasing the value of $k_{\mu ox}$, the lengths of the long axis of the ellipses are shortened. Continuing to increase $k_{\mu ox}$ until $k_{\mu ox}$ equals $k_{\mu oy}$, the internal ellipses turn into circles. When $k_{\mu ox}$ further increases beyond the value of $k_{\mu oy}$, the long axes of the internal ellipses are on the y-axis. Similarly, if we keep the value of $k_{\mu ox}$ constant and gradually increase the value of $k_{\mu oy}$, the lengths of the long axes of the internal ellipses that lie on the y-axis decrease, as shown in Figure 5b,c. When the value of $k_{\mu oy}$ increases to equal $k_{\mu ox}$, the ellipses become circles, as shown in Figure 5a.

When the medium causes the spectral density distribution of the scattered light to show a “central circles and peripheral ellipses” pattern, we can modify the peripheral spectral density distribution of the scattered light field by adjusting the inner correlation length of the medium, as shown in Figure 6 and Figure 7. When $k_{\mu px}<k_{\mu py}$, the long axes of the external ellipses lie on the x-axis. Keeping the value of $k_{\mu py}$ constant and increasing the value of $k_{\mu px}$, the lengths of the long axis of the ellipses are shortened. Continuing to increase $k_{\mu px}$ until $k_{\mu px}$ equals $k_{\mu py}$, the external ellipses turn into circles. When $k_{\mu px}$ further increases beyond the value of $k_{\mu py}$, the long axes of the external ellipses are on the y-axis. As illustrated in Figure 7, if $k_{\mu px}$ is constant and $k_{\mu py}$ is increased, the lengths of the long axes of the external ellipses that lie on the y-axis decrease. When the value of $k_{\mu py}$ increases to equal $k_{\mu px}$, the ellipses become circles.

When $k_{\mu px}<k_{\mu py}$, the focus of the external ellipse lies along the x-axis. Increasing the value of $k_{\mu px}$ until it equals $k_{\mu py}$ gradually shortens the semi-major axis of the external ellipse, ultimately resulting in a circular distribution. When $k_{\mu px}>k_{\mu py}$, the focus of the external ellipse lies along the y-axis. Reducing the value of $k_{\mu px}$ gradually shortens the semi-major axis of the external ellipse, and when $k_{\mu px}=k_{\mu py}$, the ellipse degenerates into a circular distribution.

4. Conclusions

An equation for the far-zone spectral density of light waves scattered by random anisotropic hollow media is derived. Numerical calculations were carried out in this equation to obtain the distributions of the spectral density of light waves scattered by random anisotropic hollow scatterers with different inner and outer correlation lengths, whose effects on the spectral density distributions were also discussed. The results show that the distributions of scattered far-zone spectral densities have interesting patterns of “central ellipses and peripheral circles” or “central circles and peripheral ellipses”. In addition, the far-zone scattered spectral density distribution can be manipulated by the selection of the random anisotropic hollow scatterer of different inner and outer correlation lengths. The outer correlation length of the scatterer determines the central distribution pattern of the scattered spectral density, and the inner correlation length determines the peripheral distribution pattern. These results show that the scattered field is closely related to the structure of the medium, and the anisotropy of the structure of the random anisotropic hollow medium leads to the asymmetry of the spectral intensity distribution of the scattered field. Since the scattered far field is closely related to the structural characteristics of the medium, this result may provide some reference to the inverse problem, i.e., the reconstruction of the structural information of the medium by measuring the optical properties of the scattered field, which has been discussed in previous studies [25,28].