Investigation on the Full-Aperture Diffraction Efficiency of AOTF Based on Tellurium Dioxide Crystals
Abstract
1. Introduction
2. Methods
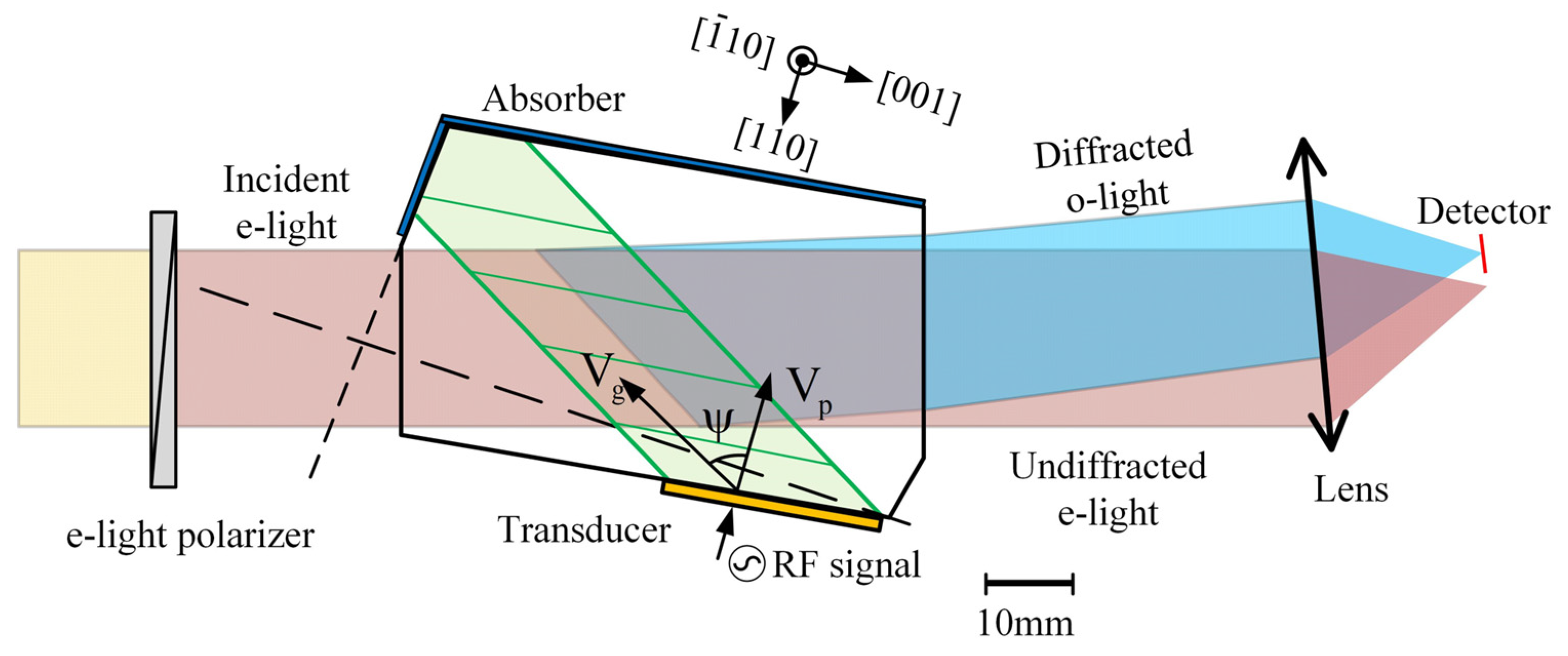
2.1. Configuration of AOTF
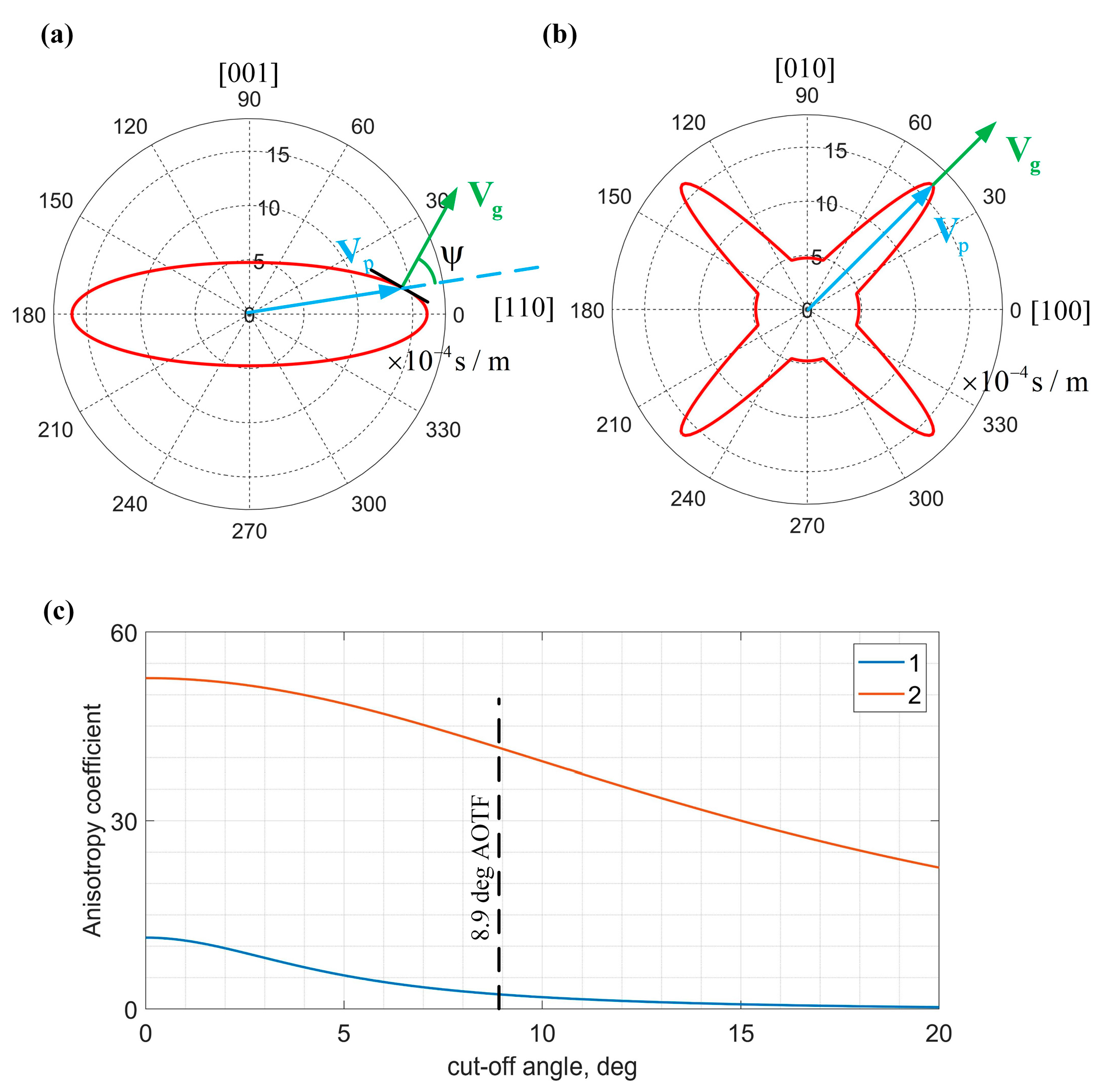
2.2. Simulation of Acoustic Filed
2.3. AO Interation Function
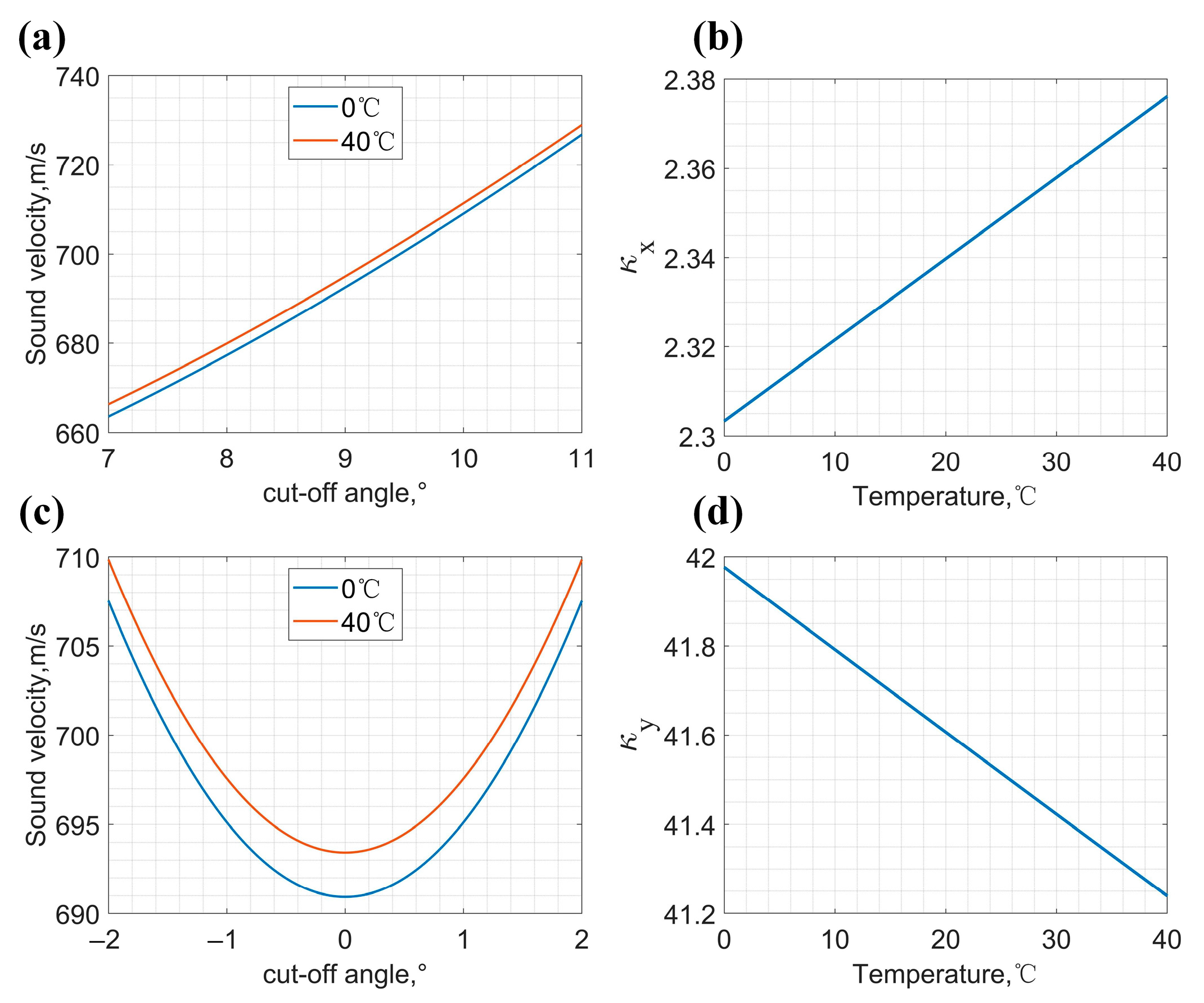
2.4. The Temperature Effect of Acoustic Filed and Diffartion Effiency
3. Experiment and Results
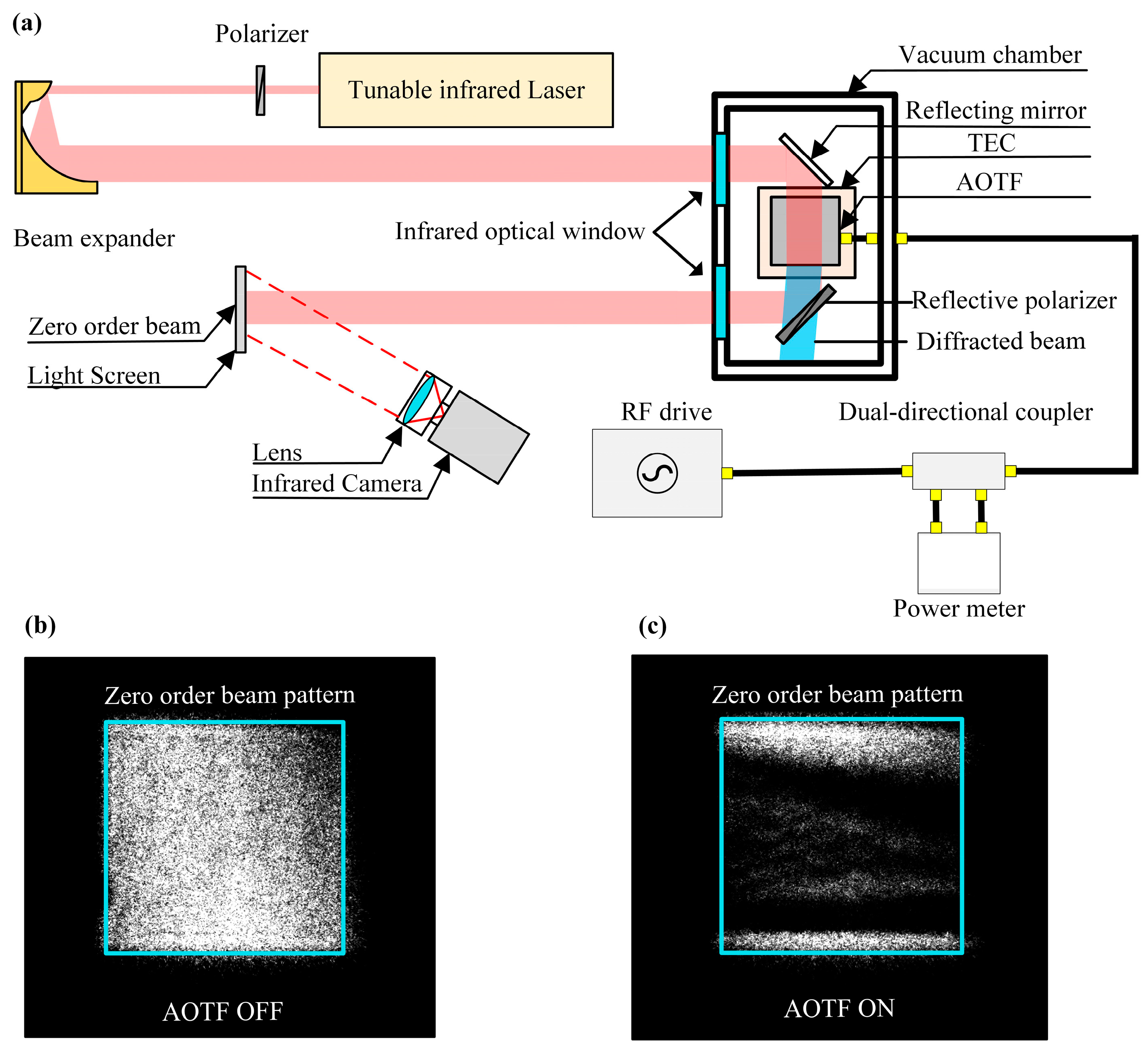
3.1. Experiment Setup
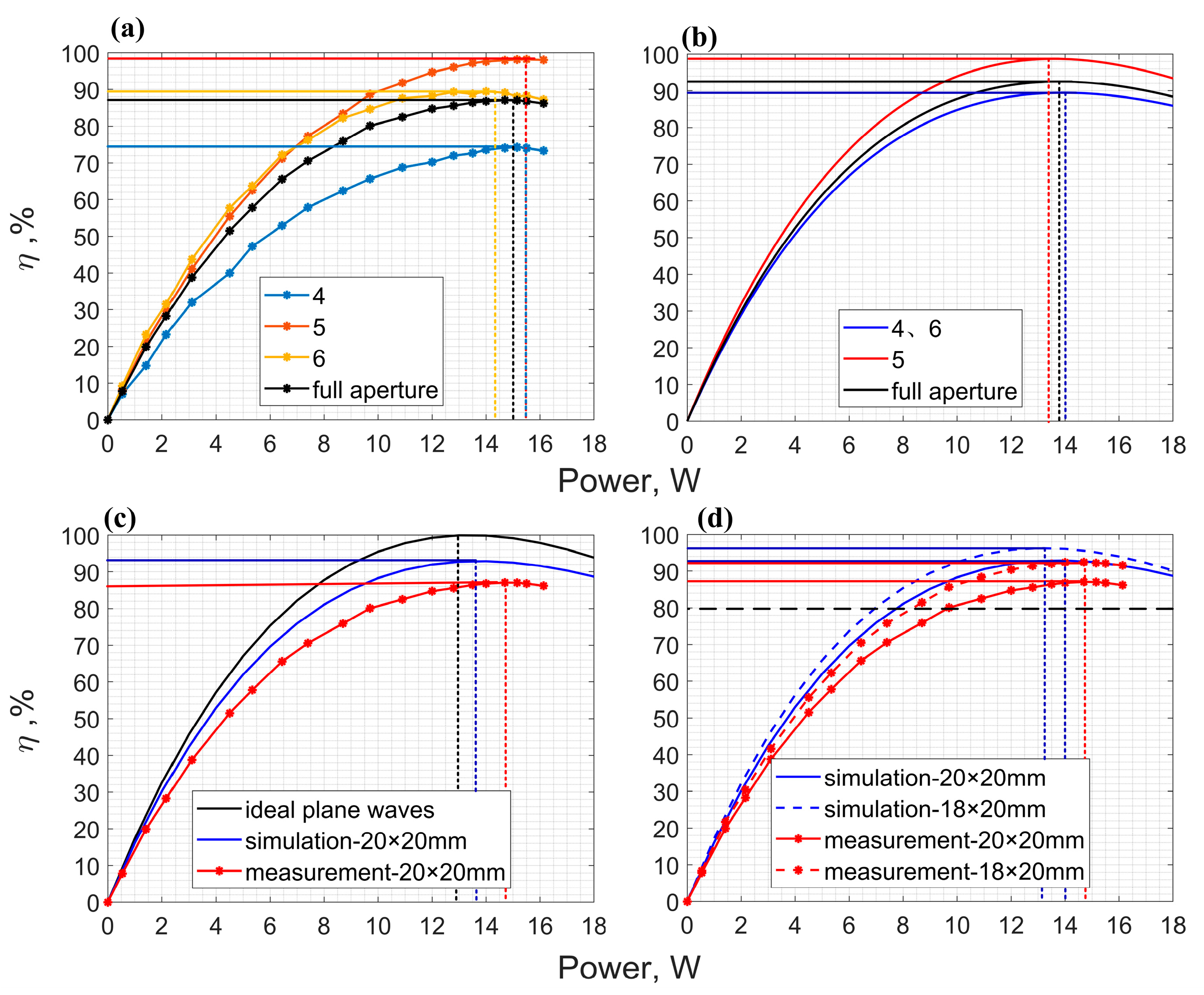
3.1.1. AOTF Consumed Power Test
3.1.2. AOTF Diffraction Efficiency Test
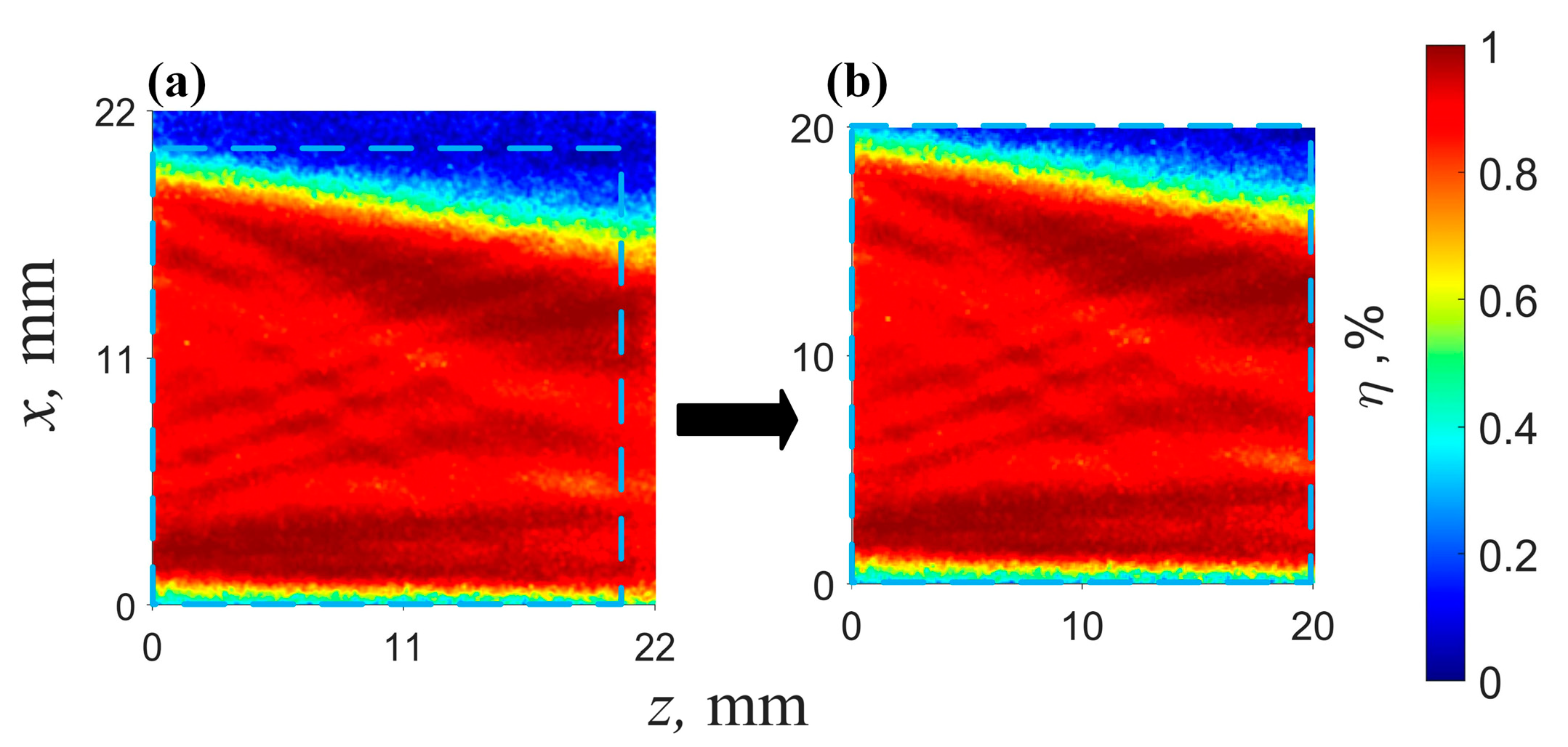
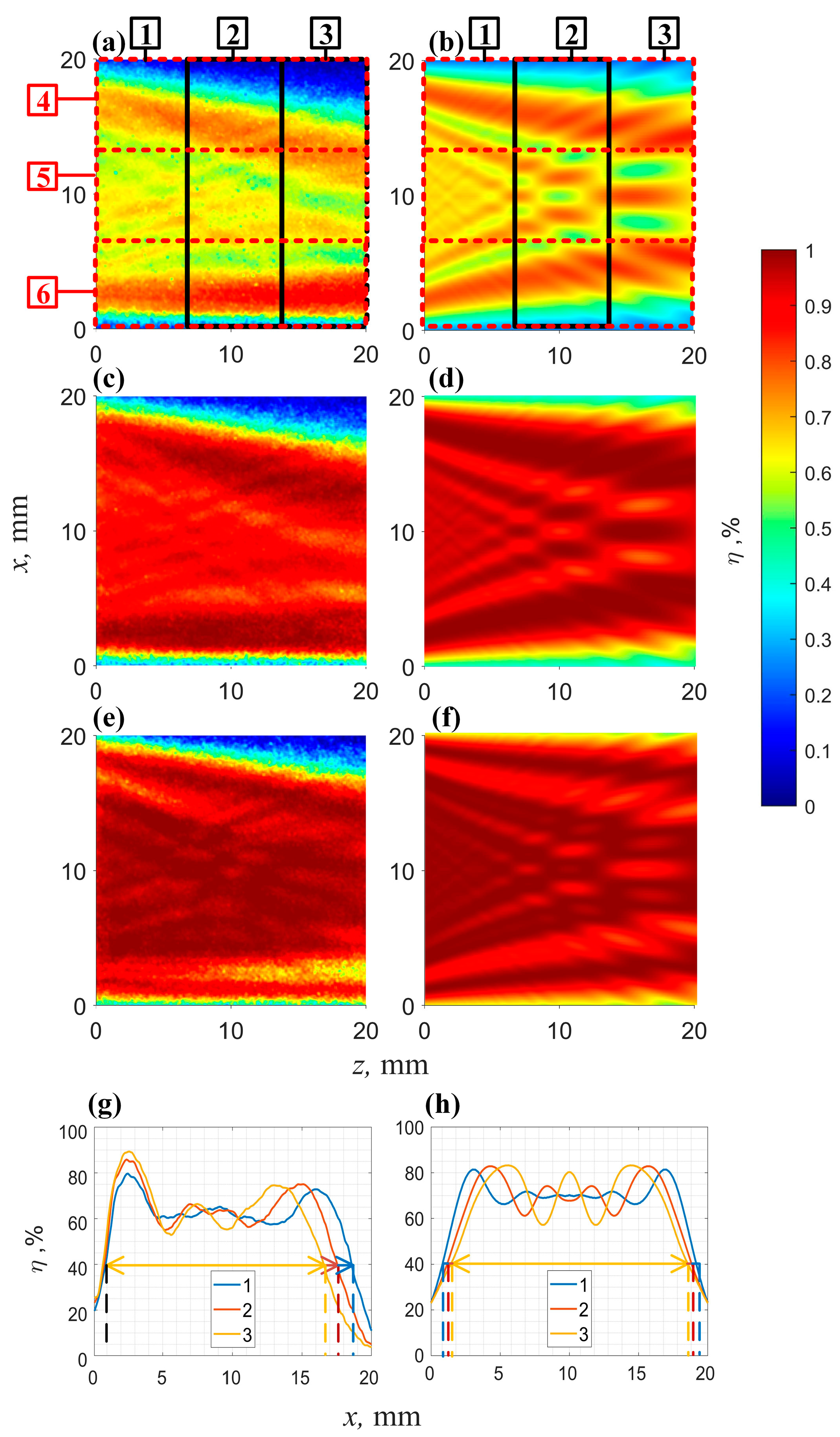
3.2. Experiment of Acoustic Field Influence on the Diffration Effiency
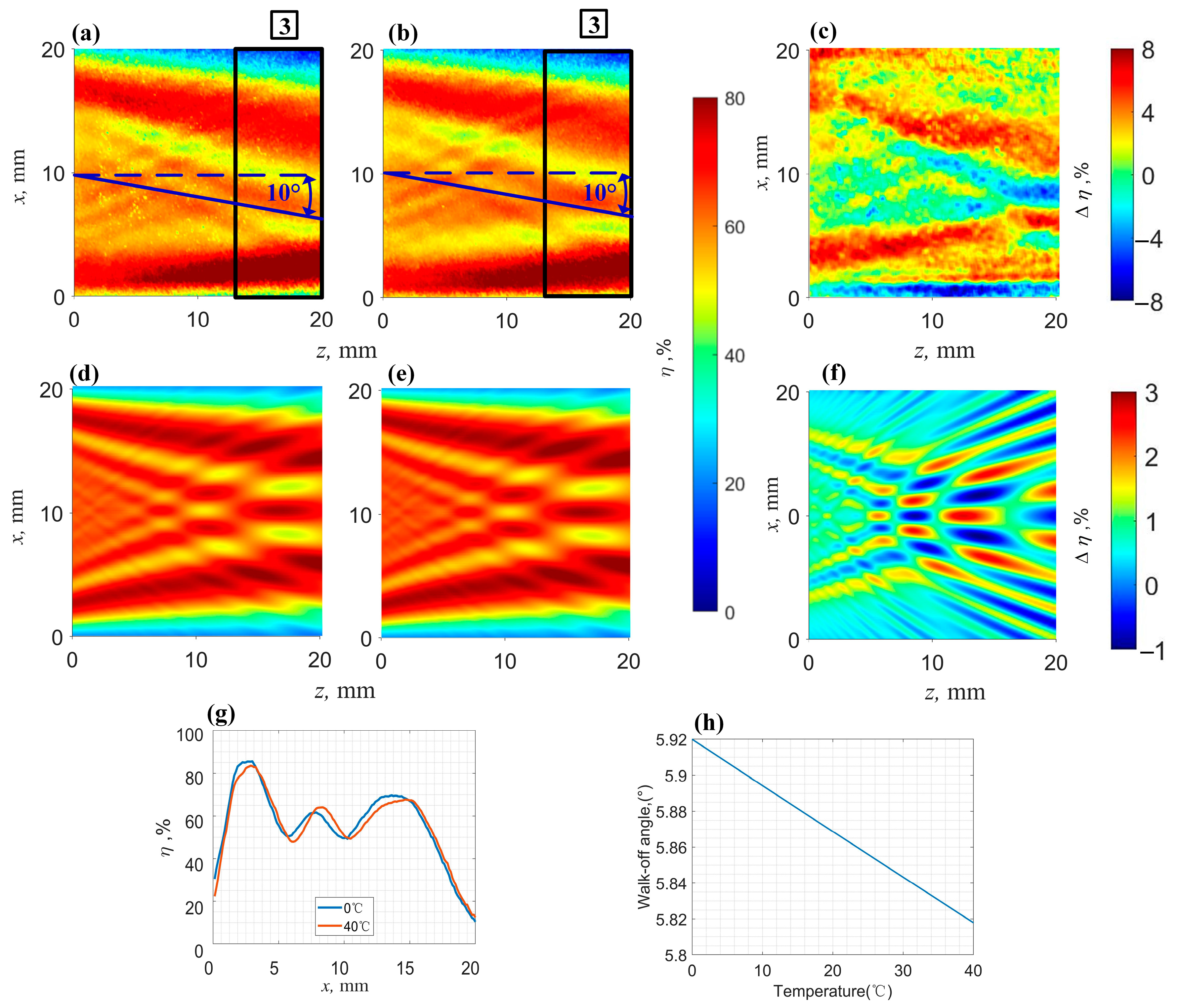
3.3. Temperature Influence on the Diffration Effiency
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bei, L.; Dennis, G.I.; Miller, H.M.; Spaine, T.W.; Carnahan, J.W. Acousto-optic tunable filters: Fundamentals and applications as applied to chemical analysis techniques. Prog. Quantum Electron. 2004, 28, 67–87. [Google Scholar]
- Balakshy, V.; Kupreychik, M.; Mantsevich, S.; Molchanov, V. Acousto-optic cells with phased-array transducers and their application in systems of optical information processing. Materials 2021, 14, 451. [Google Scholar] [CrossRef] [PubMed]
- Machikhin, A.; Batshev, V.; Pozhar, V.; Naumov, A. Single-volume dual-channel acousto-optical tunable filter. Opt. Express 2020, 28, 1150–1157. [Google Scholar]
- Balakshy, V.I. Acousto-optic visualization of optical wavefronts. Appl. Opt. 2018, 57, C56–C63. [Google Scholar]
- Ngoi, B.A.; Venkatakrishnan, K.; Tan, B.; Stanley, P.; Lim, L.E.N. Angular dispersion compensation for acousto-optic devices used for ultrashort-pulsed laser micromachining. Opt. Express 2001, 9, 200–206. [Google Scholar] [CrossRef]
- Mantsevich, S.N.; Voloshin, A.S.; Yushkov, K.B. Optical-frequency-comb generation with collinear acousto-optic diffraction: Theory and simulations. Phys. Rev. A 2019, 100, 013829. [Google Scholar]
- Chang, I.C. Noncollinear acousto-optic filter with large angular aperture. Appl. Phys. Lett. 1974, 25, 370–372. [Google Scholar] [CrossRef]
- Korablev, O.; Montmessin, F.; Trokhimovskiy, A.; Fedorova, A.A.; Shakun, A.V.; Grigoriev, A.V.; Moshkin, B.E.; Ignatiev, N.I.; Forget, F.; Lefèvre, F.; et al. The Atmospheric Chemistry Suite (ACS) of three spectrometers for the ExoMars 2016 trace gas orbiter. Space Sci. Rev. 2018, 214, 7. [Google Scholar]
- Pannell, C. Recent advances in acousto-optic tunable filters for hyper-spectral imaging with real-time spectral unmixing. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 9–14 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–3. [Google Scholar]
- Li, J.; Gui, Y.; Xu, R.; Zhang, Z.; Liu, W.; Lv, G.; Wang, M.; Li, C.; He, Z. Applications of AOTF spectrometers in in situ lunar measurements. Materials 2021, 14, 3454. [Google Scholar] [CrossRef]
- Korablev, O.I.; Belyaev, D.A.; Dobrolenskiy, Y.S.; Trokhimovskiy, A.Y.; Kalinnikov, Y.K. Acousto-optic tunable filter spectrometers in space missions. Appl. Opt. 2018, 57, C103–C119. [Google Scholar]
- Zhe, H.; Li, C.; Xu, R.; Lv, G.; Yuan, L.; Wang, J. Spectrometers based on acousto-optic tunable filters for in-situ lunar surface measurement. J. Appl. Remote Sens. 2019, 13, 027502. [Google Scholar]
- Bellincontro, A.; Taticchi, A.; Servili, M.; Esposto, S.; Farinelli, D.; Mencarelli, F. Feasible application of a portable NIR AOTF tool for on-field prediction of phenolic compounds during the ripening of olives for oil production. J. Agric. Food Chem. 2012, 60, 2665–2673. [Google Scholar] [CrossRef] [PubMed]
- Leitner, R.; Biasio, M.D.; Arnold, T.; Dinh, C.V.; Loog, M.; Duin, R.P. Multi-spectral video endoscopy system for the detection of cancerous tissue. Pattern Recognit. Lett. 2012, 34, 85–93. [Google Scholar]
- Ohmachi, Y.; Uchida, N. Temperature dependence of elastic, dielectric, and piezoelectric constants in TeO2 single crystals. J. Appl. Phys. 1970, 41, 2307–2311. [Google Scholar]
- Uchida, N.; Ohmachi, Y. Elastic and photoelastic properties of TeO2 single crystal. J. Appl. Phys. 1969, 40, 4692–4695. [Google Scholar] [CrossRef]
- Voloshinov, V.B.; Khorkin, V.S.; A Kulakova, L.; Gupta, N. Optic, acoustic and acousto-optic properties of tellurium in close-to-axis regime of diffraction. J. Phys. Commun. 2017, 1, 025006. [Google Scholar] [CrossRef]
- Mantsevich, S.; Kostyleva, E. Shear acoustic wave attenuation influence on acousto-optic diffraction in tellurium dioxide crystal. Appl. Opt. 2020, 59, 6796–6802. [Google Scholar]
- Balakshy, V.I.; Mantsevich, S.N. Propagation of acoustic beams in a paratellurite crystal. Acoust. Phys. 2012, 58, 549–557. [Google Scholar]
- Mantsevich, S.N.; Balakshy, V.I. Acousto-optic interaction in an inhomogeneous acoustic field. Opt. Spectrosc. 2015, 118, 617–622. [Google Scholar]
- Mantsevich, S.N.; Balakshy, V.I.; Molchanov, V.Y.; Yushkov, K.B. Influence of acoustic anisotropy in paratellurite on quasicollinear acousto-optic interaction. Ultrasonics 2015, 63, 39–46. [Google Scholar] [CrossRef]
- Ermakov, A.A.; Balakshy, V.I.; Mantsevich, S.N. Ray spectra and structure of acoustic beams in crystals. Phys. Wave Phenom. 2013, 21, 314–319. [Google Scholar] [CrossRef]
- Mantsevich, S.N.; Kostyleva, E.I. Examination of the temperature influence on phase matching frequency in tunable acousto-optic filters. Ultrasonics 2018, 91, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Mantsevich, S.N.; Korablev, O.; Kalinnikov, Y.; Ivanov, A.; Kiselev, A. Wide-aperture TeO₂ AOTF at low temperatures: Operation and survival. Ultrasonics 2015, 59, 50–58. [Google Scholar] [PubMed]
- Zarubin, V.P.; Yushkov, K.B.; Chizhikov, A.I.; Makarov, O.Y.; Molchanov, V.Y.; Tretiakov, S.A.; Kolesnikov, A.I.; Cherepetskaya, E.B.; Karabutov, A.A. Laser-ultrasonic temperature mapping of an acousto-optic dispersive delay line. NDT E Int. 2018, 98, 171–176. [Google Scholar]
- Schweppe, H. Elastic and piezoelectric properties of paratellurite. Ultrasonics 1970, 8, 84–87. [Google Scholar]
- Mantsevich, S.N.; Kostyleva, E.I. Determination of the paratellurite stiffness constants temperature coefficients by the acousto-optic method. Materialia 2022, 21, 101340. [Google Scholar]
- Balakshy, V.; Voloshinov, V.B.; Karasev, V.A.; Molchanov, V.Y.; Semenkov, V. Compensation of thermal effects in acousto-optic deflector. Proc. SPIE 1996, 2713, 164–171. [Google Scholar]
- Dekemper, E.; Vanhamel, J.; Van Opstal, B.; Fussen, D.; Voloshinov, V.B. Influence of driving power on the performance of UV KDP-based acousto-optical tunable filters. J. Opt. 2015, 17, 075404. [Google Scholar]
- Mi, Z.; Zhao, H.; Guo, Q.; Yu, Y.; Liang, Y. Evaluation of the Tellurium Dioxide Crystal Shear Acoustic Wave Attenuation at 40–140 MHz Frequency. Materials 2024, 17, 4082. [Google Scholar] [CrossRef]
- Fox, A.J. Thermal design for germanium acoustooptic modulators. Appl. Opt. 1987, 26, 872–884. [Google Scholar]
- Jiang, R.; Zhou, Z.; Lv, X.; Zeng, S.; Huang, Z.; Zhou, H. Spatial and temporal thermal analysis of acousto-optic deflectors using finite element analysis model. Ultrasonics 2012, 52, 643–649. [Google Scholar] [CrossRef] [PubMed]
- Lv, G.; Li, J.; Li, C.; Jin, J.; Lin, Y.; Xu, R.; He, Z. Temperature correction and result evaluation of lunar mineralogical spectrometer for Chang’E-5 mission. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5001108. [Google Scholar] [CrossRef]
- Green, R.O.; Pieters, C.; Mouroulis, P.; Eastwood, M.; Boardman, J.; Glavich, T.; Isaacson, P.; Annadurai, M.; Besse, S.; Barr, D.; et al. The Moon Mineralogy Mapper (M3) imaging spectrometer for lunar science: Instrument description, calibration, on-orbit measurements, science data calibration and on-orbit validation. J. Geophys. Res. 2011, 116, E00G19. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mi, Z.; Zhao, H.; Guo, Q.; Zhong, Z.; Zhou, C. Investigation on the Full-Aperture Diffraction Efficiency of AOTF Based on Tellurium Dioxide Crystals. Photonics 2025, 12, 335. https://doi.org/10.3390/photonics12040335
Mi Z, Zhao H, Guo Q, Zhong Z, Zhou C. Investigation on the Full-Aperture Diffraction Efficiency of AOTF Based on Tellurium Dioxide Crystals. Photonics. 2025; 12(4):335. https://doi.org/10.3390/photonics12040335
Chicago/Turabian StyleMi, Zhiyuan, Huijie Zhao, Qi Guo, Zhoujun Zhong, and Chengsheng Zhou. 2025. "Investigation on the Full-Aperture Diffraction Efficiency of AOTF Based on Tellurium Dioxide Crystals" Photonics 12, no. 4: 335. https://doi.org/10.3390/photonics12040335
APA StyleMi, Z., Zhao, H., Guo, Q., Zhong, Z., & Zhou, C. (2025). Investigation on the Full-Aperture Diffraction Efficiency of AOTF Based on Tellurium Dioxide Crystals. Photonics, 12(4), 335. https://doi.org/10.3390/photonics12040335





