Design of High-Efficiency Circularly Polarized Reflection Mirror Based on Chiral Dielectric Metasurface
Abstract
:1. Introduction
2. Materials and Methods
3. Results
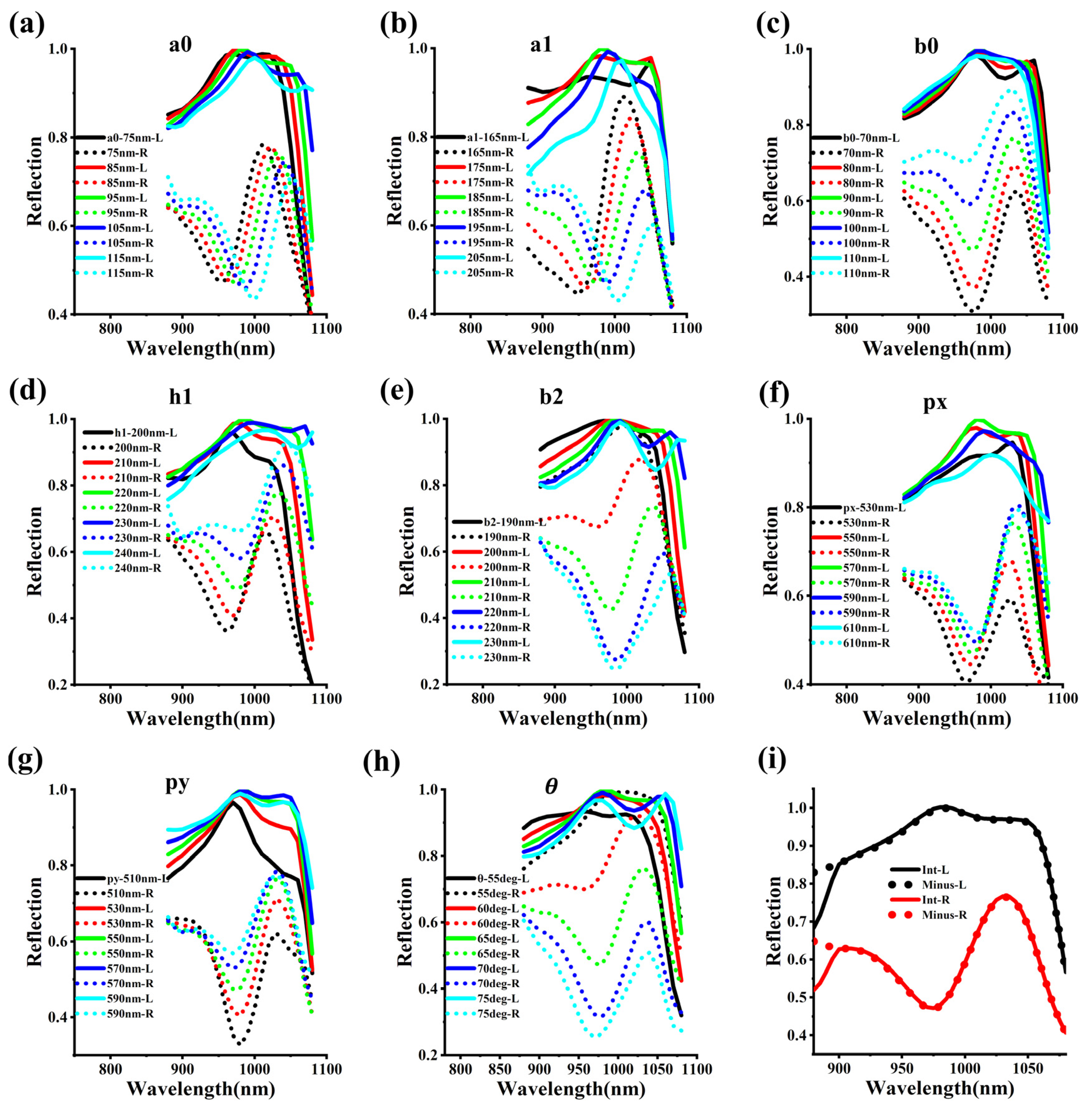
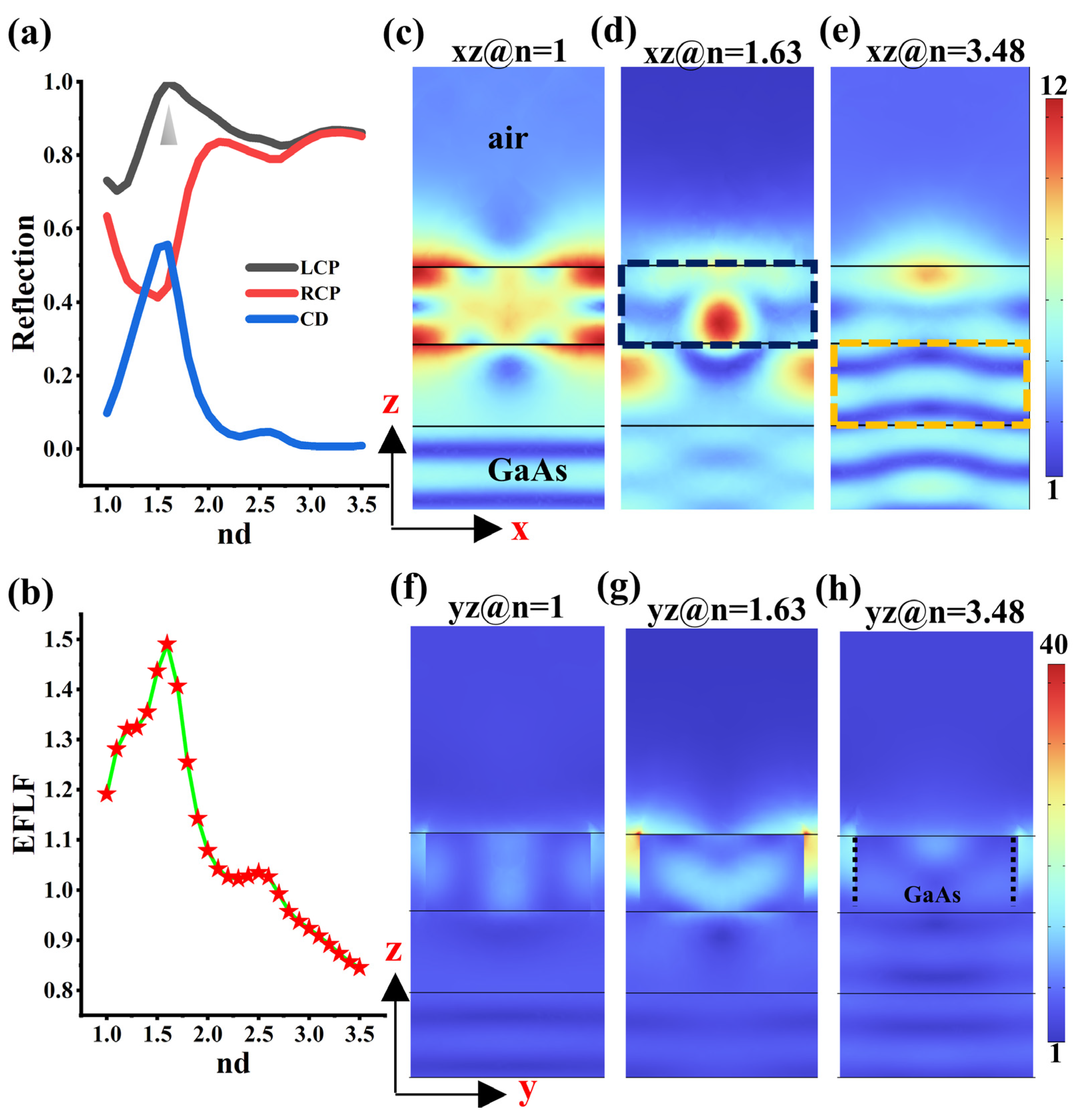
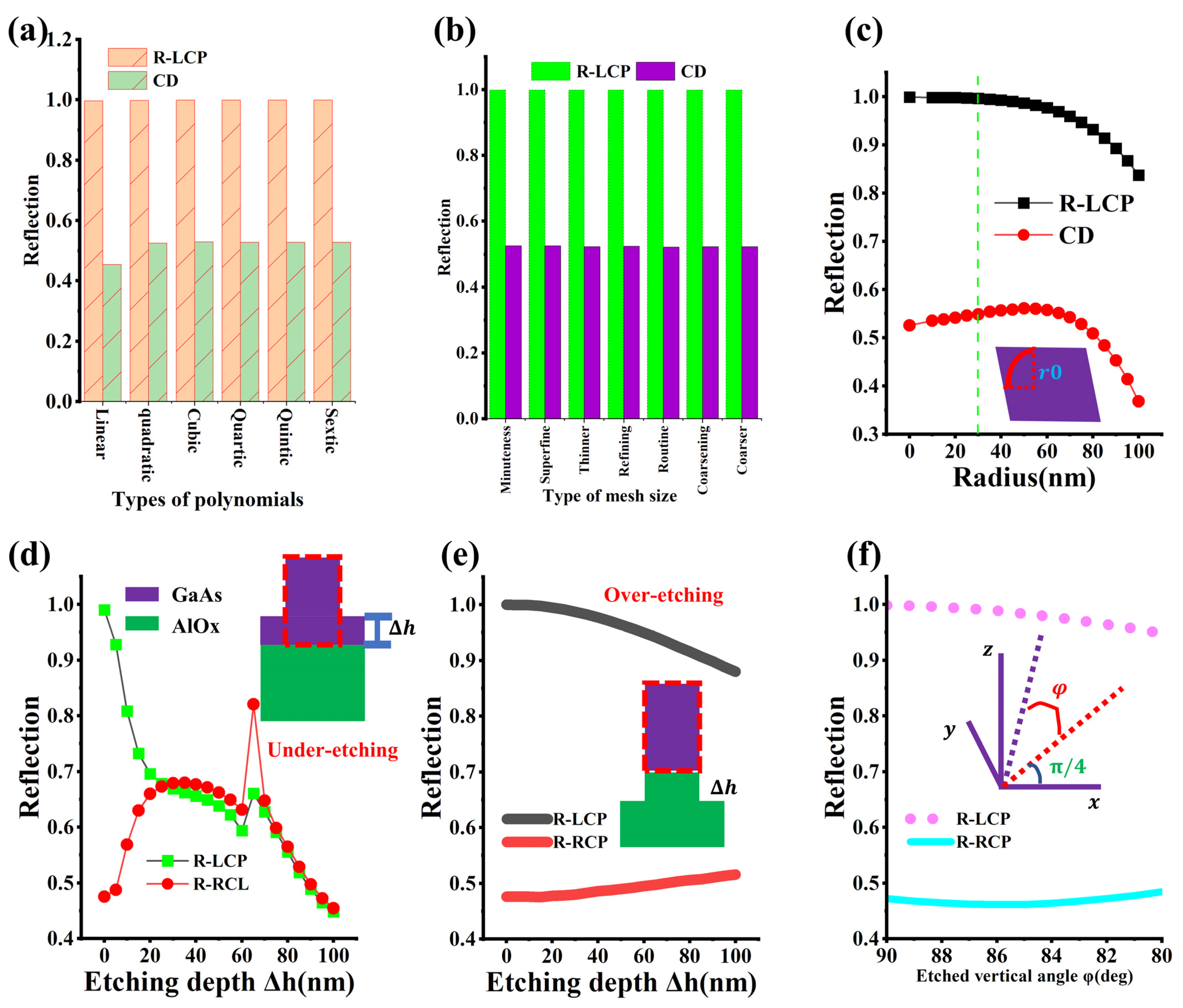
3.1. Scale Factor Analysis
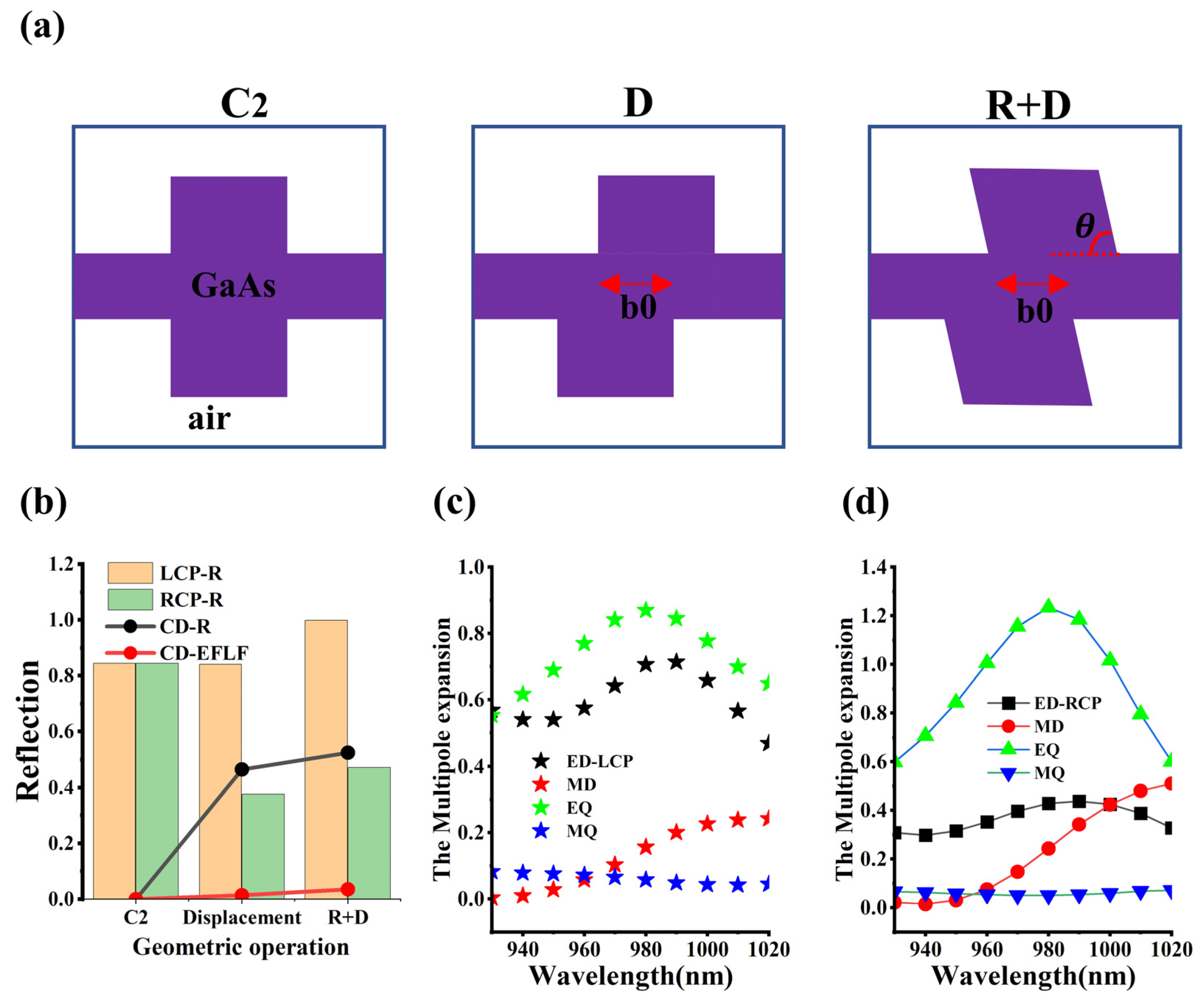
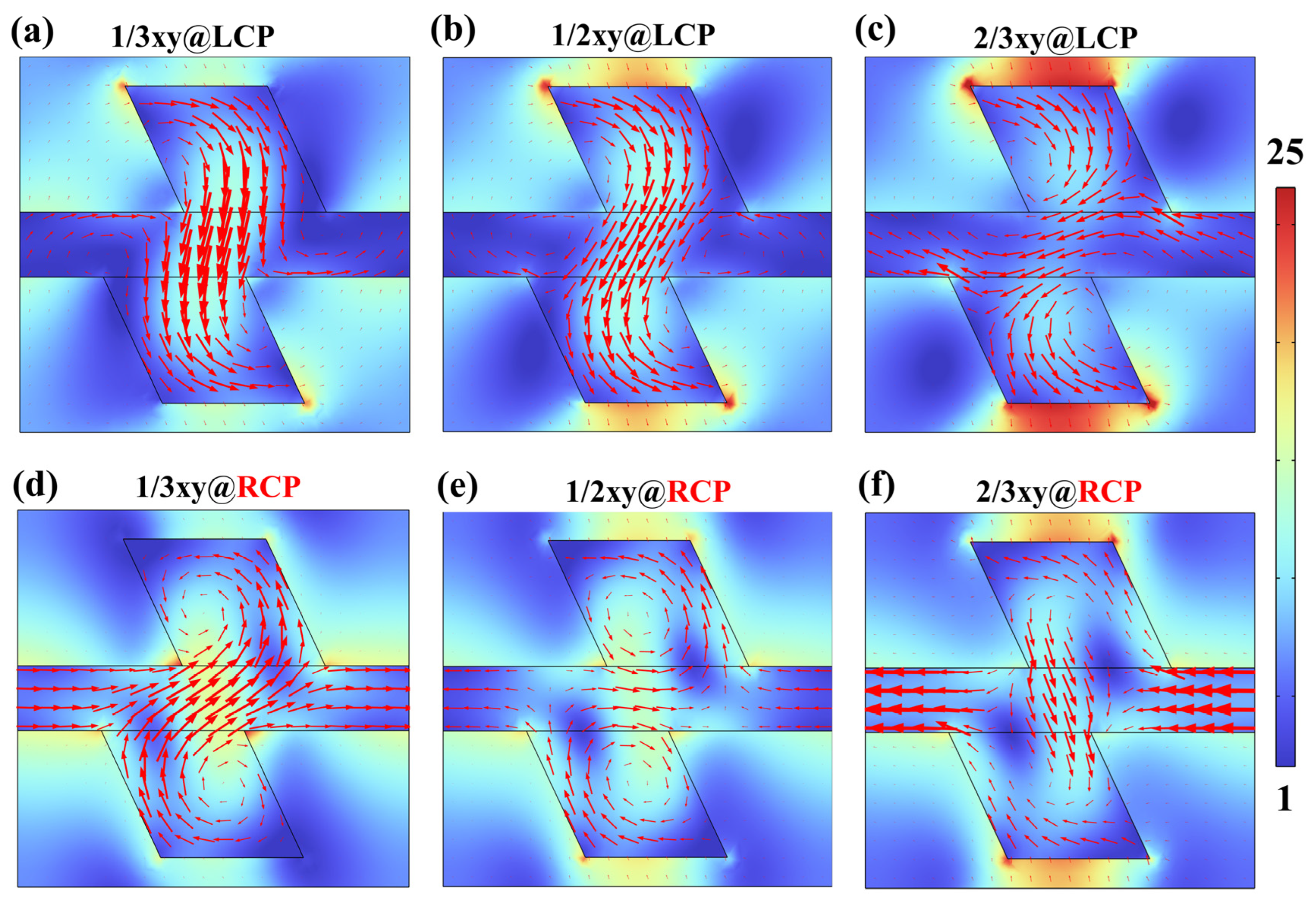
3.2. Chiral Evolution of Metasurfaces
3.3. Error Analysis in Metasurfaces
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hao, C.; Wang, G.; Chen, C.; Xu, J.; Xu, C.; Kuang, H.; Xu, L. Circularly Polarized Light-Enabled Chiral Nanomaterials: From Fabrication to Application. Nano-Micro Lett. 2023, 15, 39. [Google Scholar]
- Yeom, J.; Yeom, B.; Chan, H.; Smith, K.W.; Dominguez-Medina, S.; Bahng, J.H.; Zhao, G.; Chang, W.S.; Chang, S.J.; Chuvilin, A. Chiral Templating of Self-Assembling Nanostructures by Circularly Polarized Light. Nat. Mater. 2015, 14, 66–72. [Google Scholar] [CrossRef] [PubMed]
- Yan, T.; Li, F.; Qi, S.; Tian, J.; Tian, R.; Hou, J.; Luo, Q.; Dong, Z.; Xu, J.; Liu, J. Light-responsive vesicles for enantioselective release of chiral drugs prepared from a supra-amphiphilic M-helix. Chem. Commun. 2019, 56, 149–152. [Google Scholar] [CrossRef] [PubMed]
- Huck, N.P.; Jager, W.F.; De Lange, B.; Feringa, B.L. Dynamic control and amplification of molecular chirality by circular polarized light. Science 1996, 273, 1686–1688. [Google Scholar]
- Sun, M.; Qu, A.; Hao, C.; Wu, X.; Xu, L.; Xu, C.; Kuang, H. Chiral Upconversion Heterodimers for Quantitative Analysis and Bioimaging of Antibiotic-Resistant Bacteria In Vivo. Adv. Mater. 2018, 30, 1804241. [Google Scholar] [CrossRef]
- Wang, W.; Hao, C.; Sun, M.; Xu, L.; Wu, X.; Xu, C.; Kuang, H. Peptide Mediated Chiral Inorganic Nanomaterials for Combating Gram-Negative Bacteria. Adv. Funct. Mater. 2018, 28, 1805112. [Google Scholar]
- Hao, C.; Gao, R.; Li, Y.; Xu, L.; Sun, M.; Xu, C.; Kuang, H. Chiral Semiconductor Nanoparticles for Protein Catalysis and Profiling. Angew. Chem. Int. Ed. 2019, 58, 7371–7374. [Google Scholar]
- Zhao, X.; Xu, L.; Sun, M.; Ma, W.; Kuang, H. Tuning the interactions between chiral plasmonic films and livingcells. Nat. Commun. 2017, 8, 2007. [Google Scholar] [CrossRef]
- Wang, W.; Satyavolu, N.S.R.; Wu, Z.; Zhang, J.R.; Zhu, J.J.; Lu, Y. Near-Infrared Photothermally Activated DNAzyme-Gold Nanoshells for Imaging Metal Ions in Living Cells. Angew. Chem. 2017, 56, 6902–6906. [Google Scholar] [CrossRef]
- Gao, R.; Xu, L.; Hao, C.; Xu, C.; Kuang, H. Circular Polarized Light Activated Chiral Satellite Nanoprobes for the Imaging and Analysis of Multiple Metal Ions in Living Cells. Angew. Chem. 2019, 131, 3953–3957. [Google Scholar]
- Michalzik, R. VCSELs: Fundamentals, Technology and Applications of Vertical-Cavity Surface-Emitting Lasers; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ando, H.; Sogawa, T.; Gotoh, H. Photon-spin controlled lasing oscillation in surface-emitting lasers. Appl. Phys. Lett. 1998, 73, 566–568. [Google Scholar] [CrossRef]
- Iba, S.; Koh, S.; Ikeda, K.; Kawaguchi, H. Room temperature circularly polarized lasing in an optically spin injected vertical-cavity surface-emitting laser with (110) GaAs quantum wells. Appl. Phys. Lett. 2011, 98, 4516. [Google Scholar] [CrossRef]
- Uti, I.; Xu, G.; Lindemann, M.; Junior, P.E.F.; Gerhardt, N.C. Spin-Lasers: Spintronics Beyond Magnetoresistance. Solid State Commun. 2020, 316, 113949. [Google Scholar]
- Tanaka, Y.; Takano, H.; Kurokawa, T. Circular Polarization Resonator based on Cholesteric Liquid Crystal. In Proceedings of the Conference on Lasers & Electro-Optics, San Francisco, CA, USA, 16–21 May 2004; pp. 1062–1067. [Google Scholar]
- Zhou, Y.; Huang, Y.; Wu, S.T. Enhancing cholesteric liquid crystal laser performance using a cholesteric reflector. Opt. Express 2006, 14, 3906–3916. [Google Scholar] [CrossRef]
- Wang, C.T.; Lin, T.H. Polarization-tunable chiral nematic liquid crystal lasing. J. Appl. Phys. 2010, 107, 1707. [Google Scholar] [CrossRef]
- Goldstein, D. Polarized Light; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Kuznetsov, A.I.; Brongersma, M.L.; Yao, J.; Chen, M.K.; Levy, U.; Tsai, D.P.; Zheludev, N.I.; Faraon, A.; Arbabi, A.; Yu, N. Roadmap for Optical Metasurfaces. Appl. Phys. Lett. 2024, 124, 260701. [Google Scholar]
- Kim, J.; Kim, W.; Oh, D.K.; Kang, H.; Kim, H.; Badloe, T.; Kim, S.; Park, C.; Choi, H.; Lee, H. One-step printable platform for high-efficiency metasurfaces down to the deep-ultraviolet region. Light Sci. Appl. 2023, 12, 68. [Google Scholar] [CrossRef]
- Saha, S.; Segal, O.; Fruhling, C.; Lustig, E.; Segev, M.; Boltasseva, A.; Shalaev, V.M. Photonic time crystals: A materials perspective [Invited]. Opt. Express 2023, 31, 8267–8273. [Google Scholar] [CrossRef]
- Vabishchevich, P.; Kivshar, Y. Nonlinear photonics with metasurfaces. Photonics Res. 2023, 11, 122–136. [Google Scholar] [CrossRef]
- Wen, D.; Meng, J.; Cadusch, J.J.; Crozier, K.B. VCSELs with On-Facet Metasurfaces for Polarization State Generation and Detection. Adv. Opt. Mater. 2021, 9, 2001780. [Google Scholar]
- Kulakovskii, V.D.; Lobanov, S.V.; Tikhodeev, S.G.; Hoefling, S.; Weiss, T. Circularly polarized lasing in chiral modulated semiconductor microcavity with GaAs quantum wells. Appl. Phys. Lett. 2016, 109, 171106. [Google Scholar]
- Maksimov, A.A.; Filatov, E.V.; Tartakovskii, I.I.; Kulakovskii, V.D.; Tikhodeev, S.G.; Schneider, C.; Höfling, S. Circularly Polarized Laser Emission from an Electrically Pumped Chiral Microcavity. Phys. Rev. Appl. 2022, 17, L021001. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Han, J.; Kivshar, Y.; Song, Q. Chiral emission from resonant metasurfaces. Science 2022, 377, 1215–1218. [Google Scholar] [PubMed]
- Jia, X.; Kapraun, J.; Wang, J.; Qi, J.; Ji, Y.; Chang-Hasnain, C. Metasurface reflector enables room-temperature circularly polarized emission from VCSEL. Optica 2023, 10, 1093–1099. [Google Scholar]
- Papatryfonos, K.; Angelova, T.; Brimont, A.; Reid, B.; Guldin, S.; Smith, P.R.; Tang, M.; Li, K.; Seeds, A.J.; Liu, H.; et al. Refractive indices of MBE-grown AlxGa(1−x)As ternary alloys in the transparent wavelength region. AIP Adv. 2021, 11, 025327. [Google Scholar] [CrossRef]
- Jensen, F.; Lavrinenko, A.V.; Malureanu, R.; Zhukovsky, S.V.; Andryieuski, A.; Takayama, O.; Shkondin, E. Experimental Demonstration of Effective Medium Approximation Breakdown in Deeply Subwavelength All-Dielectric Multilayers. Phys. Rev. Lett. 2015, 115, 177402. [Google Scholar]
- Yang, B.; Liu, W.; Li, Z.; Cheng, H.; Choi, D.Y.; Chen, S.; Tian, J. Ultrahighly Saturated Structural Colors Enhanced by Multipolar-Modulated Metasurfaces. Nano Lett. 2019, 19, 4221–4228. [Google Scholar]
- Gansel, J.K.; Thiel, M.; Rill, M.S.; Decker, M.; Bade, K.; Saile, V.; von Freymann, G.; Linden, S.; Wegener, M. Gold Helix Photonic Metamaterial as Broadband Circular Polarizer. Science 2009, 325, 1513–1515. [Google Scholar] [CrossRef]
- Cheng, B.; Jiang, B.; Zou, Y.; Song, G. Ultrahigh-Reflectivity Circularly Polarized Mirrors Based on the High-Contrast Subwavelength Chiral Metasurface. Photonics 2024, 11, 923. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, B.; Zou, Y.; Zhai, K.; Song, G. Design of High-Efficiency Circularly Polarized Reflection Mirror Based on Chiral Dielectric Metasurface. Photonics 2025, 12, 341. https://doi.org/10.3390/photonics12040341
Cheng B, Zou Y, Zhai K, Song G. Design of High-Efficiency Circularly Polarized Reflection Mirror Based on Chiral Dielectric Metasurface. Photonics. 2025; 12(4):341. https://doi.org/10.3390/photonics12040341
Chicago/Turabian StyleCheng, Bo, Yuxiao Zou, Kunpeng Zhai, and Guofeng Song. 2025. "Design of High-Efficiency Circularly Polarized Reflection Mirror Based on Chiral Dielectric Metasurface" Photonics 12, no. 4: 341. https://doi.org/10.3390/photonics12040341
APA StyleCheng, B., Zou, Y., Zhai, K., & Song, G. (2025). Design of High-Efficiency Circularly Polarized Reflection Mirror Based on Chiral Dielectric Metasurface. Photonics, 12(4), 341. https://doi.org/10.3390/photonics12040341





