Expansion Dynamics of Rydberg-Dressed Ultracold Fermi Gas
Abstract
1. Introduction
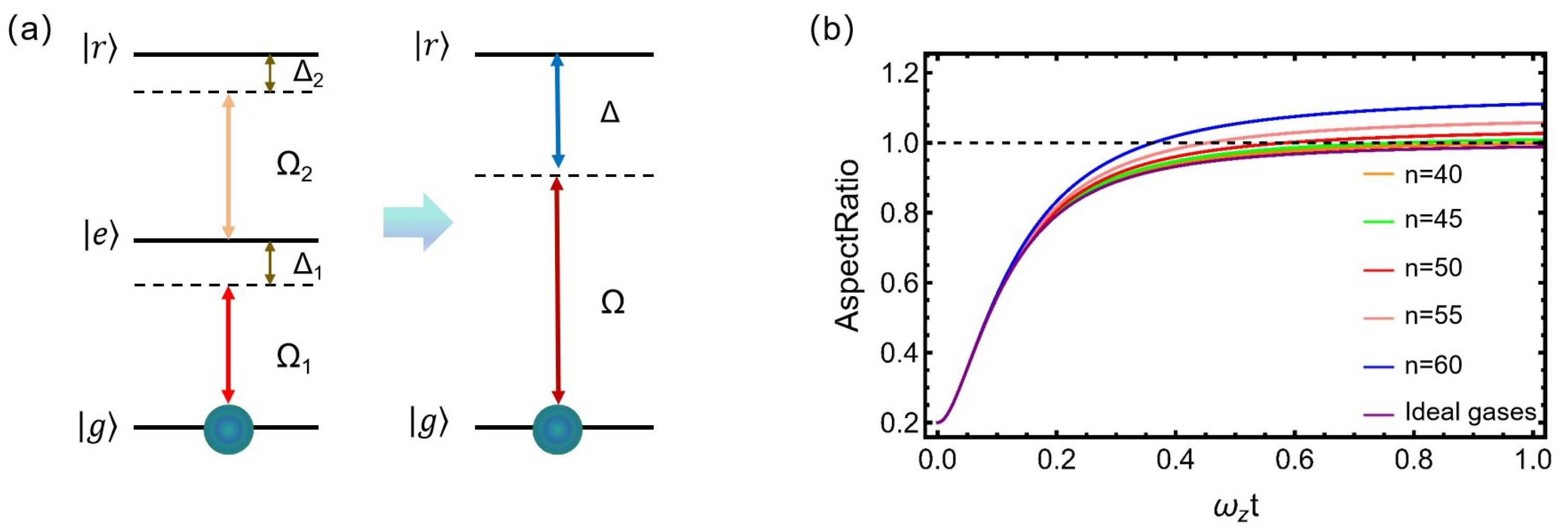
2. Method: Mean-Field Hydrodynamical Description
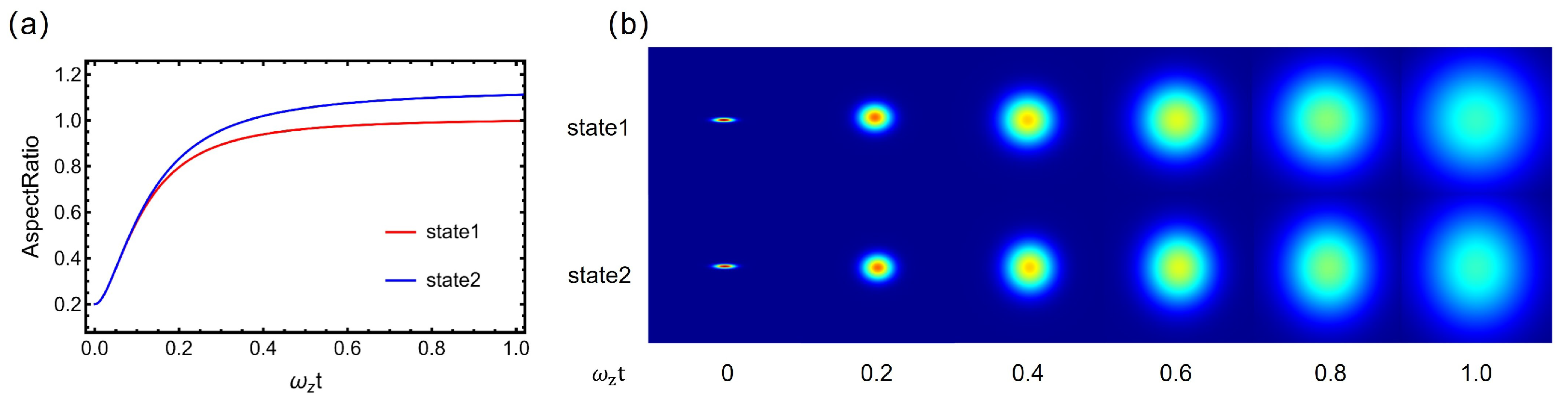
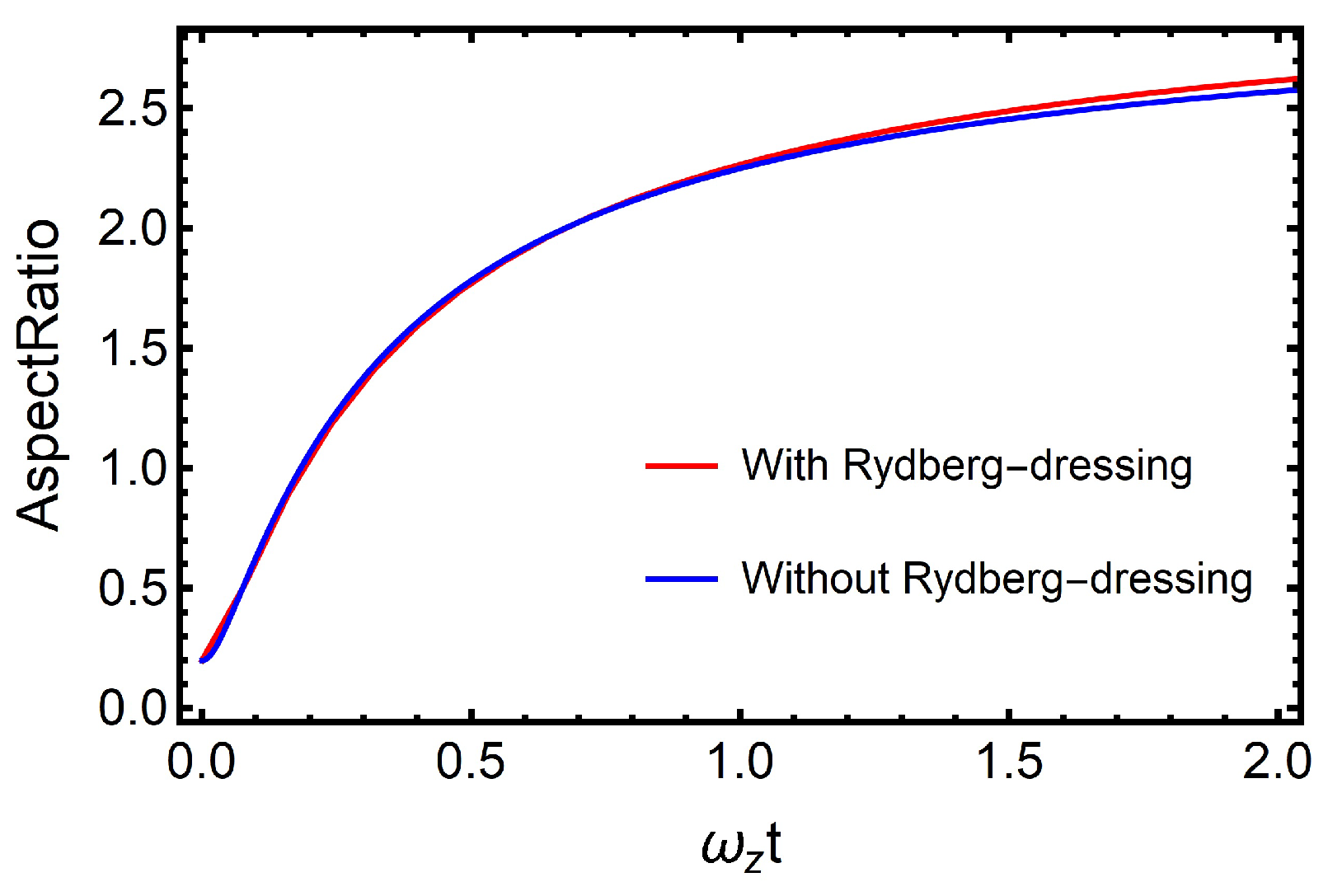
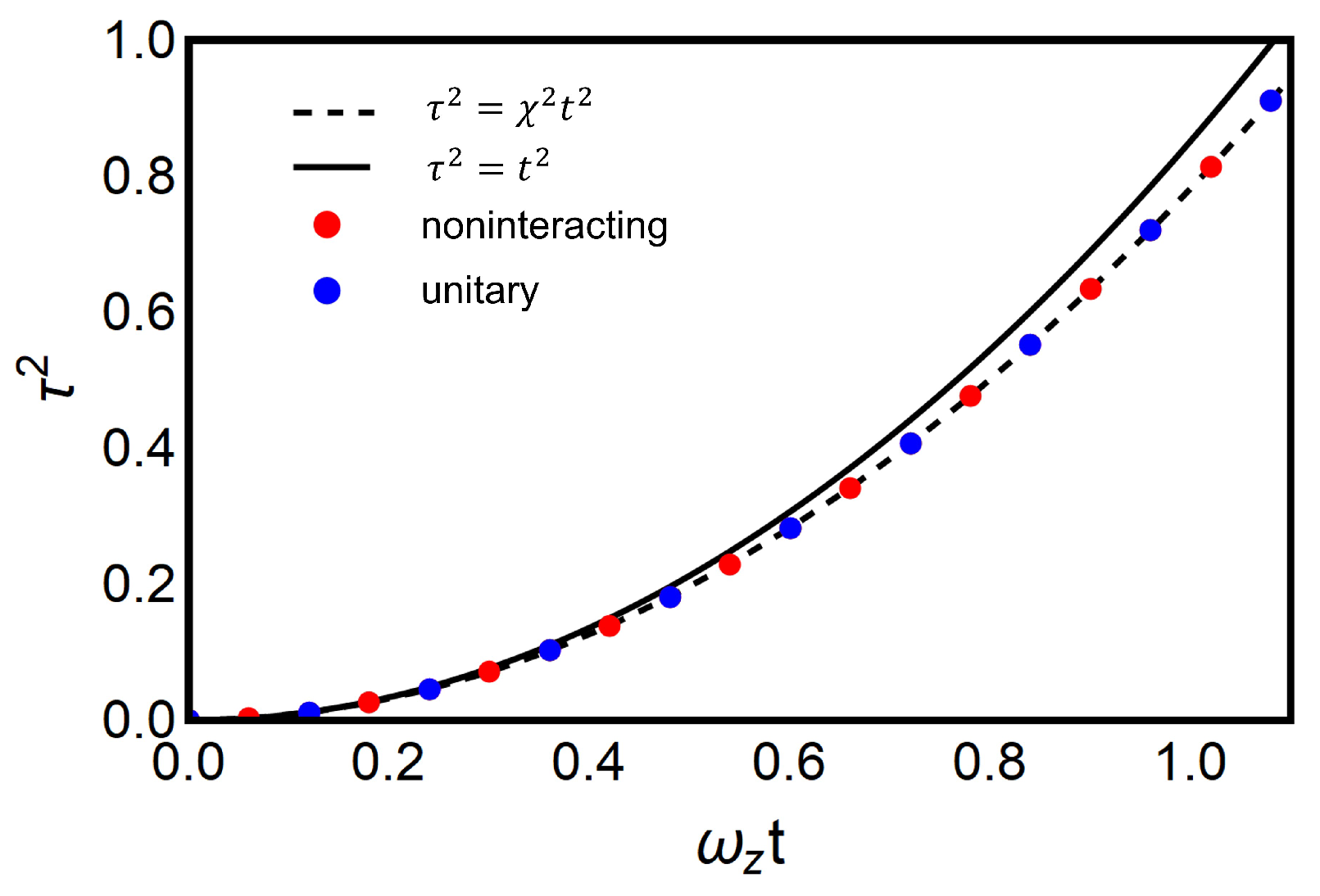
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Description of Energy in Quantum Systems
References
- Gross, C.; Bloch, I. Quantum simulations with ultracold atoms in optical lattices. Science 2017, 357, 995. [Google Scholar] [CrossRef]
- Eigen, C.; Glidden, J.A.P.; Lopes, R.; Cornell, E.A.; Smith, R.P.; Hadzibabic, Z. Universal prethermal dynamics of Bose gases quenched to unitarity. Nature 2018, 563, 221. [Google Scholar] [CrossRef]
- Logan, W.C.; Anita, G.; Lei, F.; Cheng, C. Collective emission of matter-wave jets from driven Bose–Einstein condensates. Nature 2017, 551, 356. [Google Scholar]
- Arunkumar, N.; Jagannathan, A.; Thomas, J.E. Designer Spatial Control of Interactions in Ultracold Gases. Phys. Rev. Lett. 2019, 122, 040405. [Google Scholar]
- Helmrich, S.; Arias, A.; Lochead, G.; Wintermantel, T.M.; Buchhold, M.; Diehl, S.; Whitlock, S. Signatures of self-organized criticality in an ultracold atomic gas. Nature 2020, 577, 481. [Google Scholar]
- Norcia, M.A.; Politi, C.; Klaus, L.; Poli, E.; Sohmen, M.; Mark, M.J.; Bisset, R.N.; Santos, L.; Ferlaino, F. Two-dimensional supersolidity in a dipolar quantum gas. Nature 2021, 596, 357. [Google Scholar]
- Zhang, X.; Chen, Y.; Wu, Z.; Juan; Wang, J.; Fan, J.; Deng, S.; Wu, H. Observation of a superradiant quantum phase transition in an intracavity degenerate Fermi gas. Science 2021, 373, 1359. [Google Scholar] [CrossRef]
- Saffman, M.; Walker, T.G.; Molmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 2010, 82, 2313. [Google Scholar]
- Bouchoule, I.; Mϕlmer, K. Spin squeezing of atoms by the dipole interaction in virtually excited Rydberg states. Phys. Rev. A 2002, 65, 041803. [Google Scholar]
- Henkel, N.; Nath, R.; Pohl, T. Three-Dimensional Roton Excitations and Supersolid Formation in Rydberg-Excited Bose-Einstein Condensates. Phys. Rev. Lett. 2010, 104, 95302. [Google Scholar]
- Madjarov, I.S.; Covey, J.P.; Shaw, A.L.; Choi, J.; Kale, A.; Cooper, A.; Pichler, H.; Schkolnik, V.; Williams, J.R.; Endres, M. High-fidelity entanglement and detection of alkaline-earth Rydberg atoms. Nat. Phys. 2020, 16, 857–861. [Google Scholar]
- Evered, S.J.; Bluvstein, D.; Kalinowski, M.; Ebadi, S.; Manovitz, T.; Zhou, H.; Li, S.H.; Geim, A.A.; Wang, T.T.; Maskara, N.; et al. High-fidelity parallel entangling gates on a neutral-atom quantum computer. Nature 2023, 622, 268–272. [Google Scholar]
- Zhang, Z.H.; Zhang, Z.Y.; Han, S.X.; Zhang, Y.Q.; Zhang, G.Q.; Wu, J.Z.; Sovkov, V.B.; Liu, W.L.; Li, Y.Q.; Zhang, L.J.; et al. Microwave-coupled optical bistability in driven and interacting Rydberg gases. Npj Quantum Inf. 2025, 11, 44. [Google Scholar]
- Liebish, T.C.; Schlagmuller, M.; Engel, F.; Nguyen, H.; Balewski, J.; Lochead, G.; Bottcher, F.; Westphal, K.M.; Kleinbach, K.S.; Schmid, T.; et al. Controlling Rydberg atom excitations in dense background gases. J. Phys. B 2016, 49, 182001. [Google Scholar]
- Sous, J.; Sadeghpour, H.R.; Killian, T.C.; Demler, E.; Schmidt, R. Rydberg impurity in a fermi gas: Quantum statistics and rotational blockade. Rhys. Rev. Res. 2020, 2, 023021. [Google Scholar]
- Balewski, J.B.; Krupp, A.T.; Gaj, A.; Hofferberth, S.; Low, R.; Pfau, T. Rydberg dressing: Understanding of collective many-body effects and implications for experiments. New J. Phys. 2014, 16, 063012. [Google Scholar] [CrossRef]
- Gaul, C.; DeSalvo, B.J.; Aman, J.A.; Dunning, F.B.; Killian, T.C.; Pohl, T. Resonant rydberg dressing of alkaline-earth atoms via electromagnetically induced transparency. Phys. Rev. Lett. 2016, 116, 243001. [Google Scholar] [CrossRef]
- Viteau, M.; Bason, M.; Radogostowicz, J.; Maloss, N.; Morsch, O.; Ciampini, D.; Arimondo, E. Rydberg excitation of a bose-einstein condensate. Laser Phys. 2013, 23, 015502. [Google Scholar]
- Schau, P.; Zeiher, J.; Fukuhara, T.; Hild, S.; Cheneau, M.; Macri, T.; Pohl, T.; Bloch, I.; Gross, C. Crystallization in ising quantum magnets. Science 2015, 347, 14551. [Google Scholar]
- Borish, V.; Markovic, O.; Hines, J.A.; Rajagopal, S.V.; Schleier-Smith, M. Transverse-field ising dynamics in a Rydberg -dressed atomic gas. Phys. Rev. Lett. 2020, 124, 063601. [Google Scholar]
- Xiong, B.; Jen, H.H.; Wang, D.W. Topological superfluid by blockade effects in a Rydberg-dressed fermi gas. Phys. Rev. A 2014, 90, 013631. [Google Scholar] [CrossRef]
- Khasseh, R.; Abedinpour, S.H.; Tanatar, B. Phase diagram and dynamics of Rydberg-dressed fermions in two dimensions. Phys. Rev. A 2017, 96, 053611. [Google Scholar] [CrossRef]
- Li, W.H.; Hsieh, T.C.; Mou, C.Y.; Wang, D.W. Emergence of a metallic quantum solid phase in Rydberg-dressed fermi gas. Phys. Rev. Lett. 2016, 117, 035301. [Google Scholar] [CrossRef]
- Li, X.; Sarma, S.D. Exotic topological density waves in cold atomic Rydberg-dressed fermions. Nat. Commun. 2015, 6, 7137. [Google Scholar] [CrossRef]
- Guardado-Sanchez, E.; Spar, B.M.; Schauss, P.; Belyansky, R.; Young, J.T.; Bienias, P.; Gorshkov, A.V.; Iadecola, T.; Bakr, W.S. Quench Dynamics of a Fermi Gas with Strong Nonlocal Interactions. Phys. Rev. X 2021, 11, 021036. [Google Scholar] [CrossRef]
- Takei, N.; Sommer, C.; Genes, C.; Pupillo, G.; Goto, H.; Koyasu, K.; Chiba, H.; Weidemüller, M.; Ohmori, K. Direct observation of ultrafast many-body electron dynamics in an ultracold Rydberg gas. Nat. Commun. 2016, 7, 13449. [Google Scholar] [CrossRef]
- Thomas, J.E.; Kinast, J.; Turlapov, A. Damping of a Unitary Fermi Gas. Phys. Rev. Lett. 2005, 95, 120402. [Google Scholar] [CrossRef]
- Elliott, E.; Joseph, J.A.; Thomas, J.E. Observation of Conformal Symmetry Breaking and Scale Invariance in Expanding Fermi Gases. Phys. Rev. Lett. 2014, 112, 040405. [Google Scholar] [CrossRef]
- O’Hara, K.M.; Hemmer, S.L.; Gehm, M.E.; Granade, S.R.; Thomas, J.E. Observation of a Strongly Interacting Degenerate Fermi Gas of Atoms. Science 2002, 198, 2179. [Google Scholar] [CrossRef]
- Moroz, S. Scale-invariant Fermi gas in a time-dependent harmonic potential. Phys. Rev. A 2012, 86, 011601. [Google Scholar] [CrossRef]
- Deng, S.; Chenu, A.; Diao, P.; Li, F.; Yu, S.; Coulamy, I.; Campo, A.D.; Wu, H. Superadiabatic quantum friction suppression in finite-time thermodynamics. Sci. Adv. 2018, 4, 4. [Google Scholar] [CrossRef]
- Deng, S.; Diao, P.; Yu, Q.; Campo, A.D.; Wu, H. Shortcuts to adiabaticity in the strongly coupled regime: Nonadiabatic control of a unitary Fermi gas. Phys. Rev. A 2018, 97, 013628. [Google Scholar] [CrossRef]
- Stringari, S. Collective Excitations of a Trapped Bose-Condensed Gas. Phys. Rev. Lett. 1996, 77, 2360. [Google Scholar] [CrossRef]
- Wei, H.; Xiao-Fei, Z.; Deng-Shan, W.; Hai-Feng, J.; Wei, Z.; Shou-Gang, Z. Chiral Supersolid in Spin-Orbit-Coupled Bose Gases with Soft-Core Long-Range Interactions. Phys. Rev. Lett. 2018, 121, 030404. [Google Scholar]
- Pedri, P.; Guéry-Odelin, D.; Stringari, S. Dynamics of a classical gas including dissipative and mean-field effects. Phys. Rev. A 2003, 68, 043608. [Google Scholar] [CrossRef]
- Guéry-Odelin, D. Mean-field effects in a trapped gas. Phys. Rev. A 2002, 66, 033613. [Google Scholar]
- Trenkwalder, A.; Kohstall, C.; Zaccanti, M.; Naik, D.; Sidorov, A.I.; Schreck, F.; Grimm, R. Hydrodynamic Expansion of a Strongly Interacting Fermi-Fermi Mixture. Phys. Rev. Lett. 2011, 106, 115304. [Google Scholar] [CrossRef]
- Wang, L.; Yan, X.; Min, J.; Sun, D.; Xie, X.; Peng, S.; Zhan, M.; Jiang, K. Scale Invariance of a Spherical Unitary Fermi Gas. Phys. Rev. Lett. 2024, 132, 243403. [Google Scholar] [CrossRef]
- Dalfovo, F.; Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of Bose-Einstein condensation in trapped gases. Rev. Mod. Phys. 1999, 71, 463. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, M.; Bao, X.; Yu, S.; Deng, S.; Wu, H. Expansion Dynamics of Rydberg-Dressed Ultracold Fermi Gas. Photonics 2025, 12, 350. https://doi.org/10.3390/photonics12040350
Wu M, Bao X, Yu S, Deng S, Wu H. Expansion Dynamics of Rydberg-Dressed Ultracold Fermi Gas. Photonics. 2025; 12(4):350. https://doi.org/10.3390/photonics12040350
Chicago/Turabian StyleWu, Meimei, Xin Bao, Shuxian Yu, Shujin Deng, and Haibin Wu. 2025. "Expansion Dynamics of Rydberg-Dressed Ultracold Fermi Gas" Photonics 12, no. 4: 350. https://doi.org/10.3390/photonics12040350
APA StyleWu, M., Bao, X., Yu, S., Deng, S., & Wu, H. (2025). Expansion Dynamics of Rydberg-Dressed Ultracold Fermi Gas. Photonics, 12(4), 350. https://doi.org/10.3390/photonics12040350




