Analysis of Pulsed Laser Target Echo Characteristics in Non-Uniform Smoke Environments
Abstract
:1. Introduction
2. Target Echo Signal Model of Pulsed Laser in Non-Uniform Smoke Environments
2.1. Mathematical Model of Pulsed Laser Emission
2.2. Laser Transmission and Scattering Model in Non-Uniform Smoke Environments
2.2.1. Photon Random Walk Model
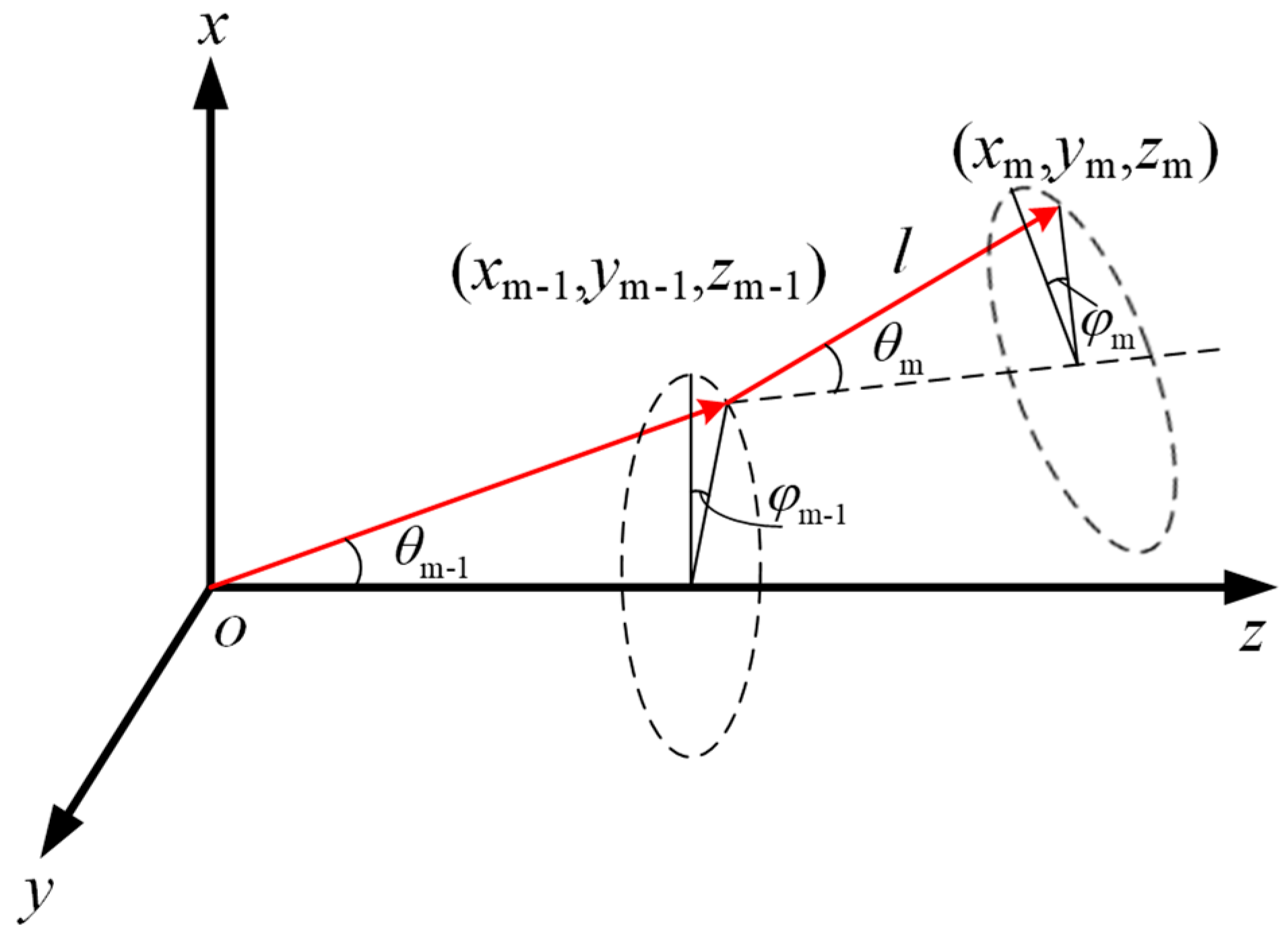
2.2.2. Photon Coordinate Transformation Model
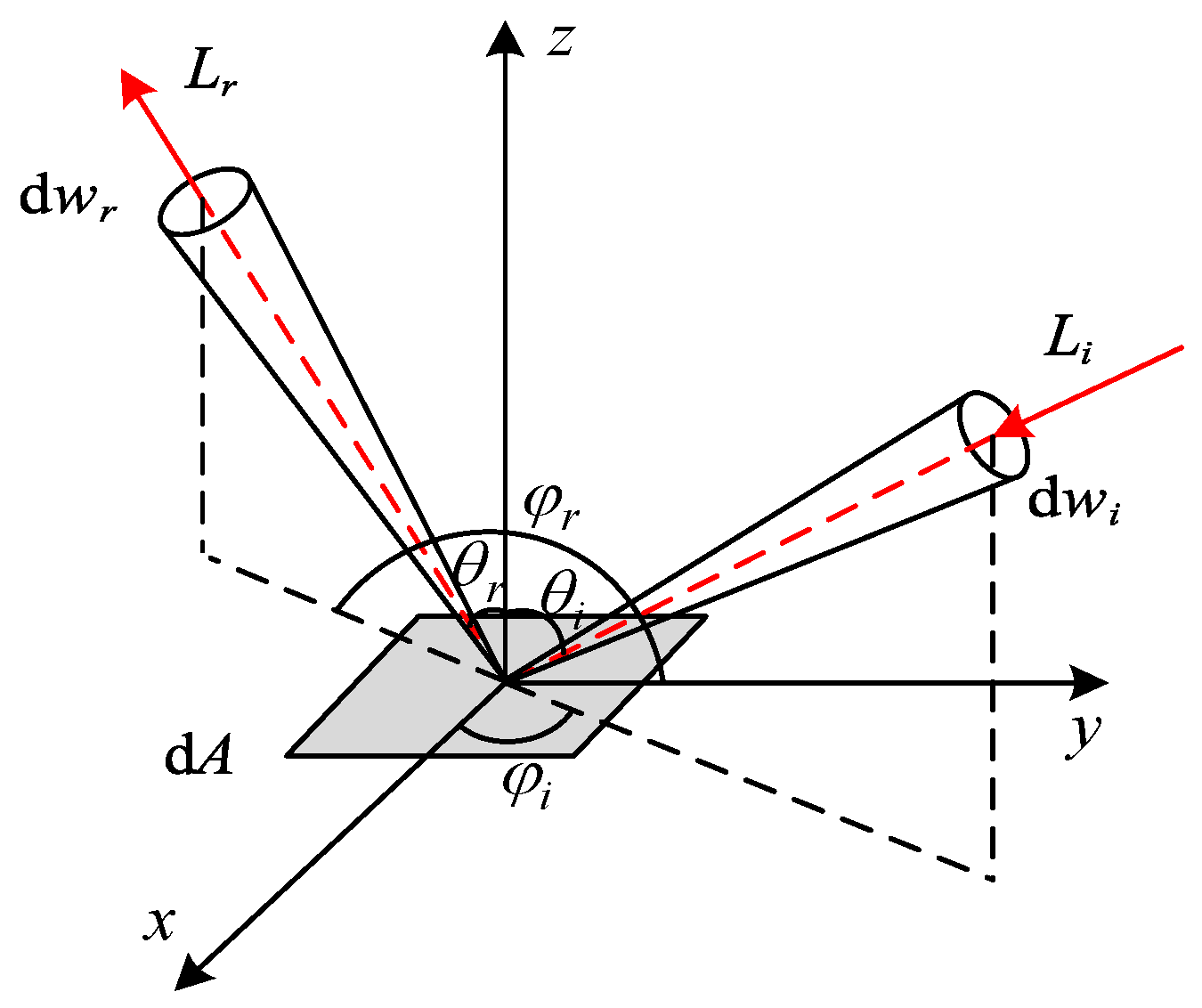
2.3. Target Laser Reflection Mathematical Model
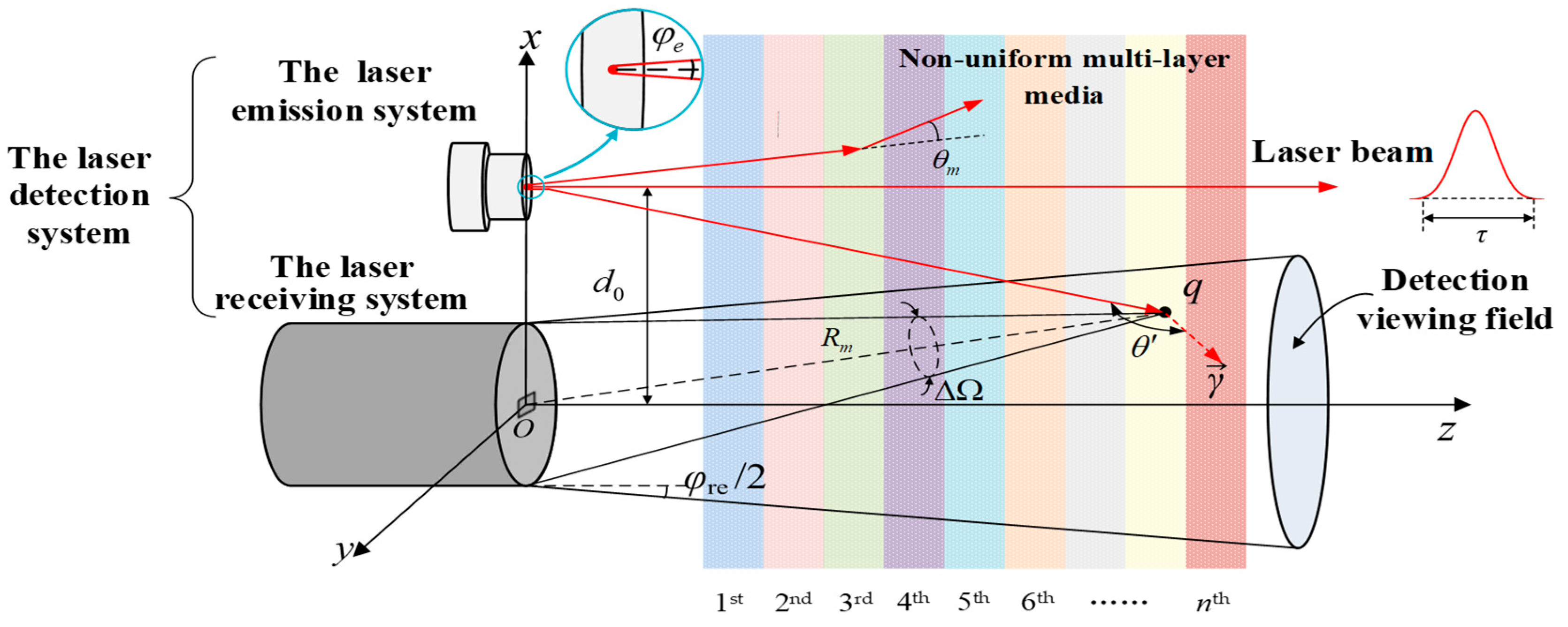
2.4. Semi-Analytical Mathematical Model for Laser Reception
3. Simulations of Laser Echo Signals from Targets in Smoke Environments
3.1. Simulation Conditions and Parameter Settings
3.2. Simulations of Echo Signals Under Different Smoke Concentrations
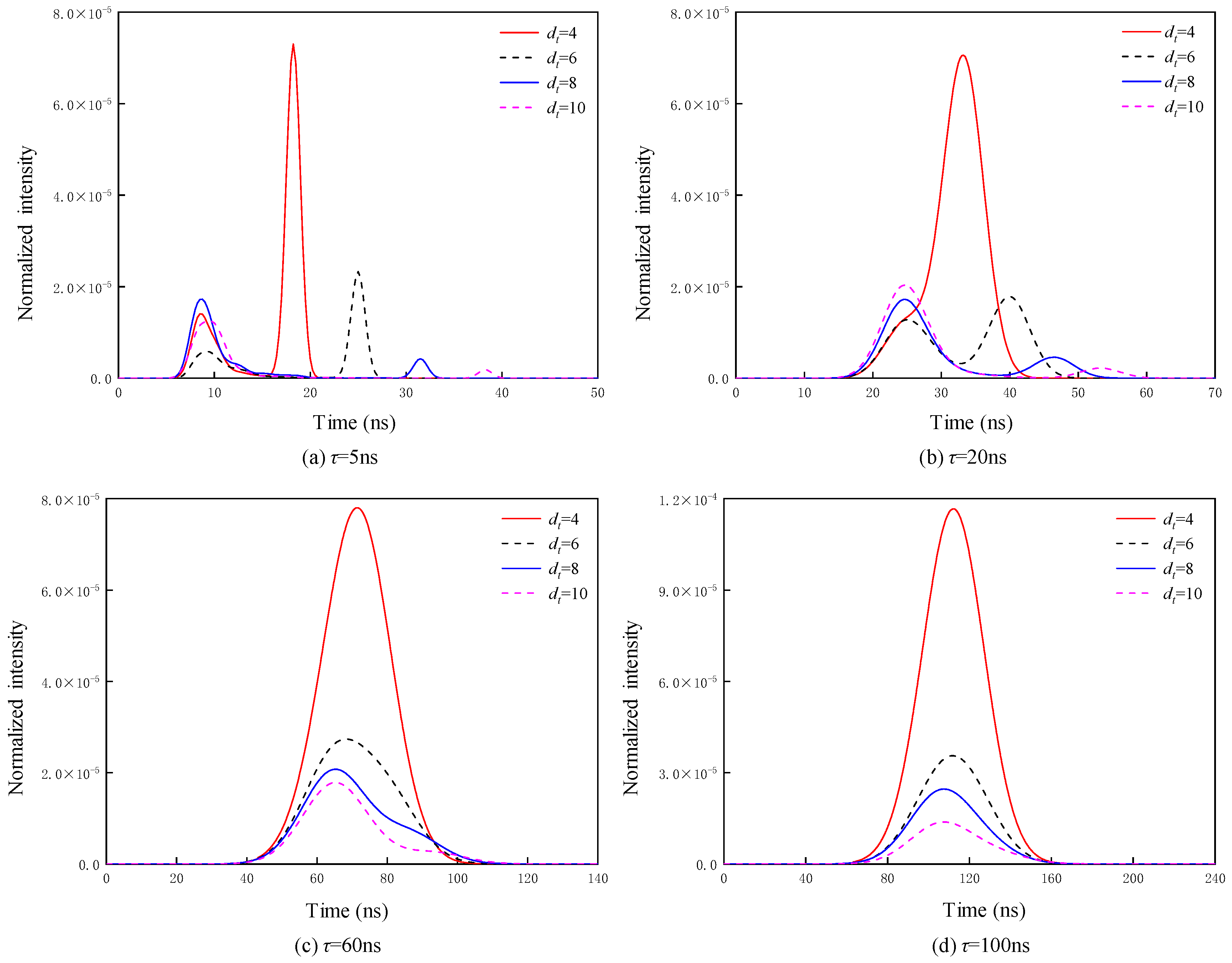
3.3. Simulations of Echo SignaLs Under Different Target Distances
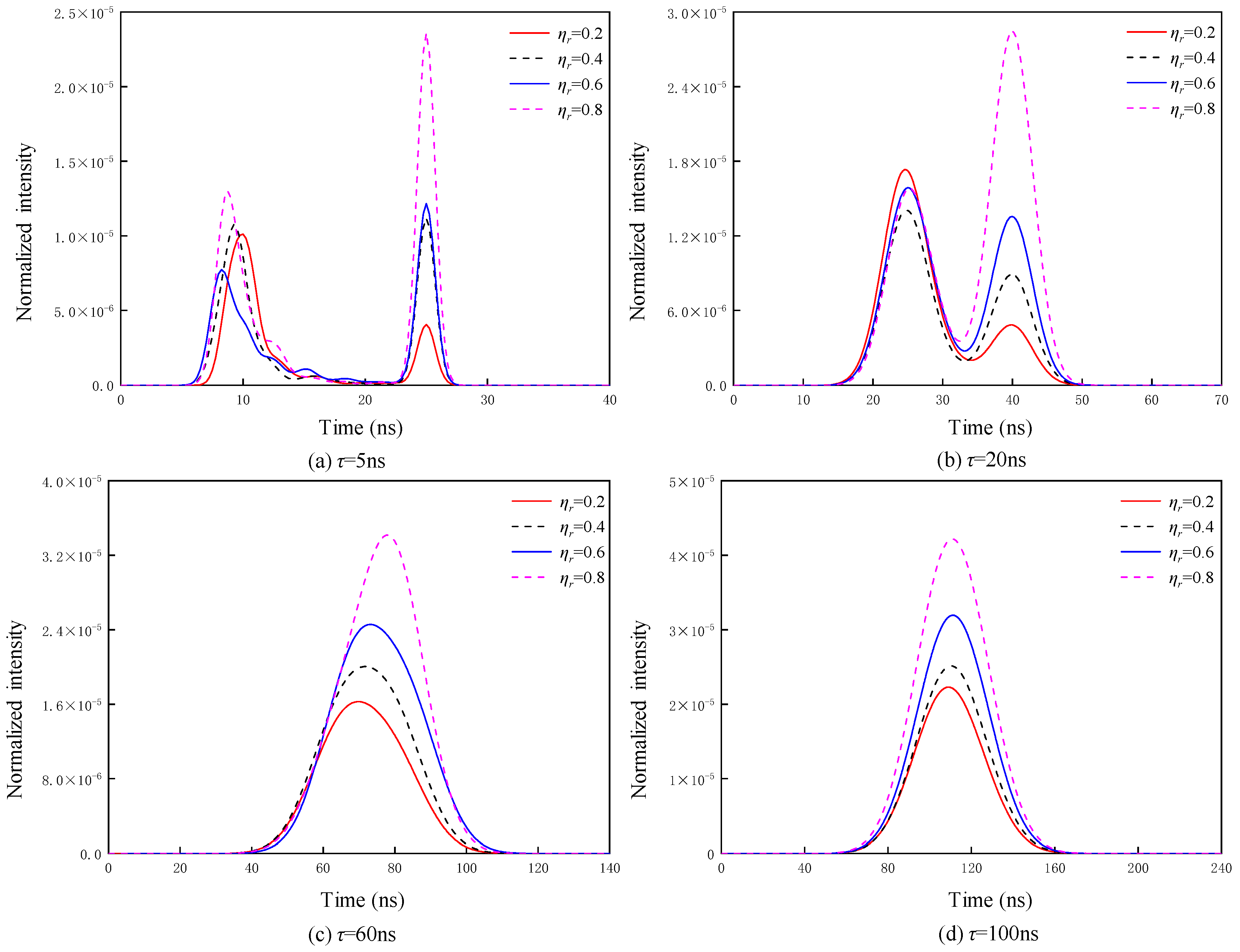
3.4. Simulations of Echo Signals Under Different Target Reflectivities
4. Experimental Validation
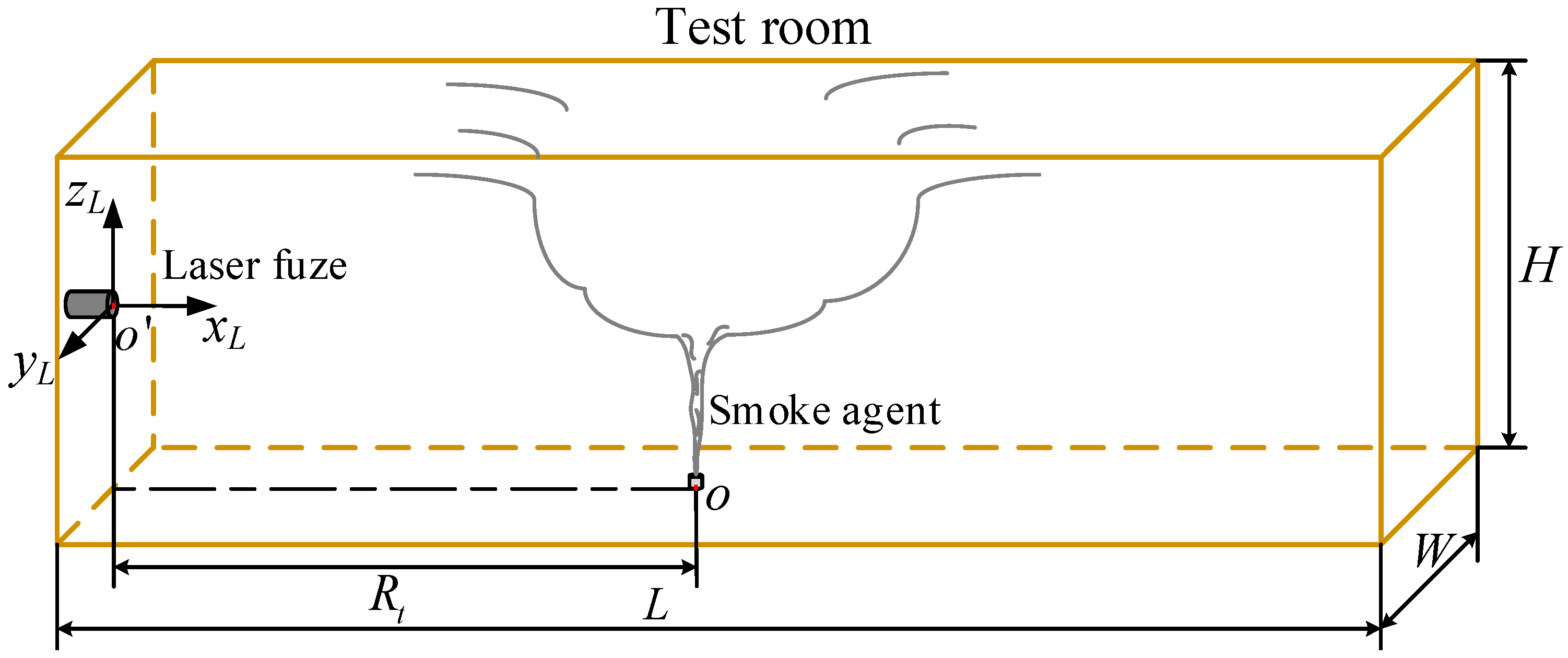
4.1. Experimental Equipment and Environmental Laboratory Setup
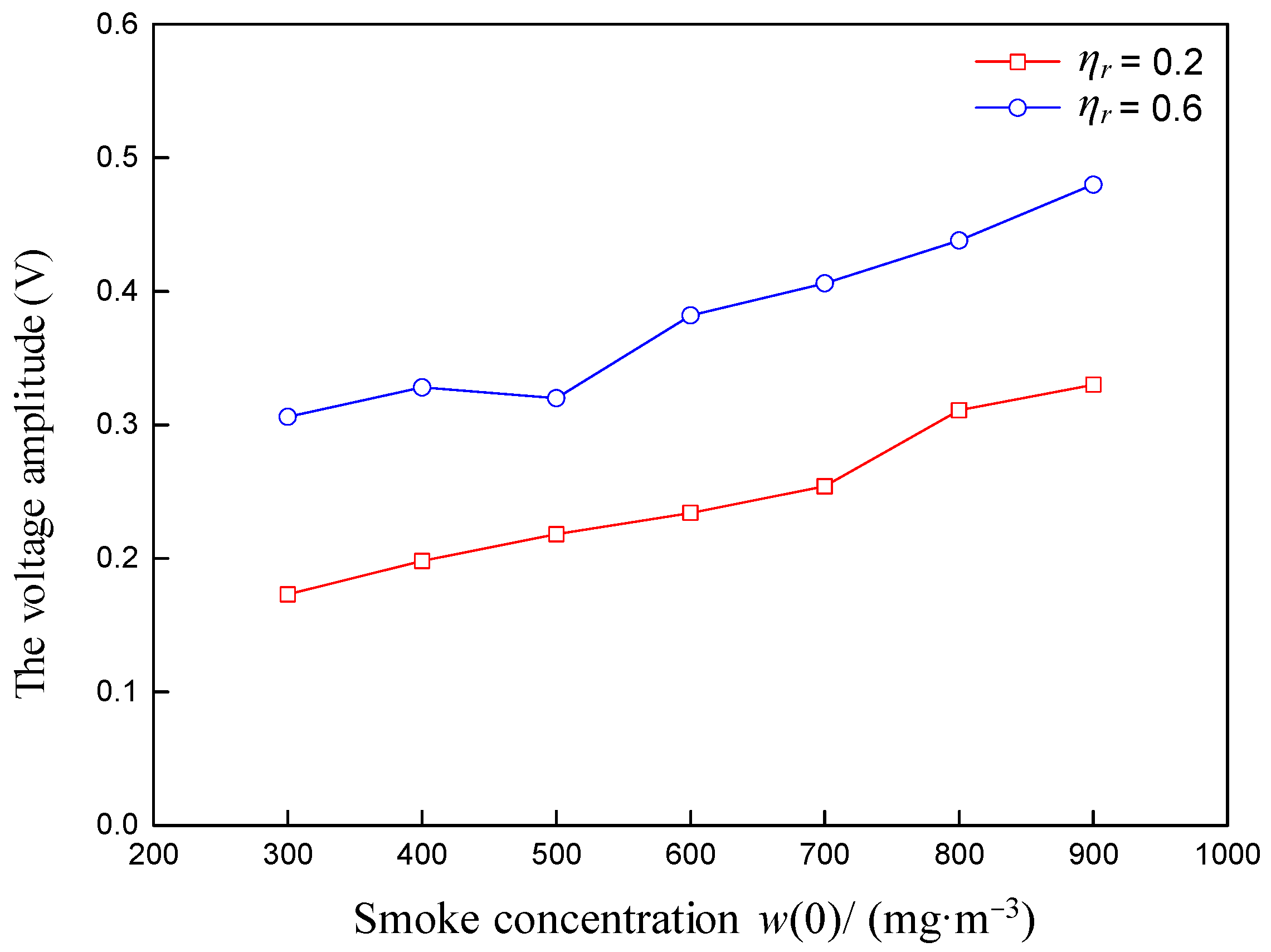
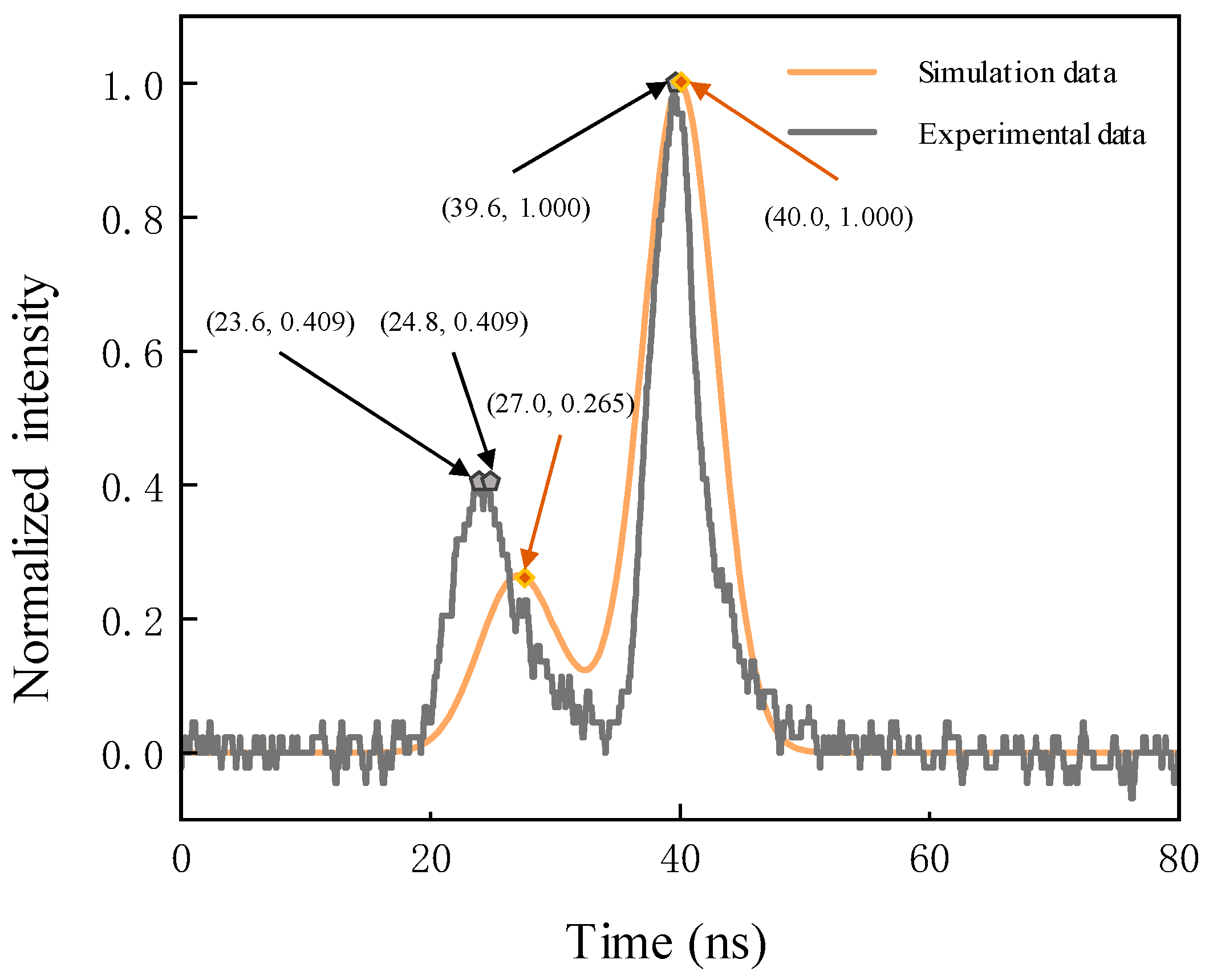
4.2. Experimental Data and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, W.; Li, Y.; Huang, Z. Research on the characteristics of fog backscattering signals for frequency modulated continuous wave laser fuze. Optik 2016, 127, 9046–9055. [Google Scholar] [CrossRef]
- Guo, J.; Liu, X.; Liu, W.; Luo, A.; Si, X. Multi-feature fusion target recognition method based on forward-looking dual linear array scanning laser fuze. Opt. Laser Technol. 2024, 181, 111860. [Google Scholar] [CrossRef]
- Li, H. Spatial-temporal scanning detection model and calculation method of laser fuze. Microw. Opt. Technol. Lett. 2023, 65, 356–364. [Google Scholar] [CrossRef]
- Pan, Z.; Song, C.; Liu, B.; Wang, X.; Deng, M.; Su, H. Accurate ranging of dual wavelength FMCW laser fuze under different types of aerosol interference. IEEE Sens. J. 2022, 22, 18953–18960. [Google Scholar]
- Wang, F.; Chen, H.; Yang, S.; Xu, L. Comparison of detection performance of near-, mid-, and far-infrared laser fuzes in clouds. Appl. Opt. 2018, 57, 8078–8086. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, H.; Zhang, X. Propagating Characteristics of Pulsed Laser in Rain. Int. J. Antennas Propag. 2015, 2015, 292905. [Google Scholar] [CrossRef]
- Grabner, M.; Kvicera, V. Multiple scattering in rain and fog on free-space optical links. J. Light. Technol. 2014, 32, 513–520. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, B.; Wu, K.; Liang, Y.; Hao, S.; Huang, Z. FMCW Laser Fuze Structure with Multi-Channel Beam Based on 3D Particle Collision Scattering Model under Smoke Interference. Sensors 2024, 24, 5395. [Google Scholar] [CrossRef]
- Pang, Z.; Song, C.; Liu, B. A Study on Accurate Ranging Method of a Dual-Wavelength Orthogonal FMCW Laser Fuze in a Complex Aerosol Environment. IEEE Sens. J. 2024, 24, 11306–11315. [Google Scholar]
- Arfan, M.; Asif, M.; Althobaiti, S.; Althobaiti, A. Scattering analysis of structured light beam for rainy atmosphere. Opt. Quantum Electron. 2024, 56, 1610. [Google Scholar] [CrossRef]
- Ceolato, R.; Berg, M. Aerosol light extinction and backscattering: A review with a lidar perspective. J. Quant. Spectrosc. Radiat. Transf. 2021, 262, 107492. [Google Scholar] [CrossRef]
- Chen, H.; Liu, Y.; Zhu, X.; Wang, F.J. Simulation of the characteristics of backscattering signals for frequency modulated continuous wave laser fuze. Acta Armamentarii 2015, 36, 2247–2253. [Google Scholar]
- Song, C.; Cui, Y.; Liu, B. FMCW Laser fuze multiple scattering model and accurate fixed-distance algorithm in a smoke environment. Sensors 2020, 20, 2604. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Ma, C.; Qi, B.; Guo, P.; Yang, S.; Gao, L.; Huo, J. Study on backscattering characteristics of pulsed laser fuze in smoke. Infrared Laser Eng. 2020, 49, 38–44. [Google Scholar]
- Wang, H.; Zu, Y.; Tian, T.; Li, A. Characteristics of laser transmission in different types of aerosols. Acta Phys. Sin. 2013, 62, 324–333. [Google Scholar]
- Chen, P.; Zhao, J.; Du, X.; Zhu, C. Study on the influence of aerosol macroscopic characteristics on backscattering signals. In Proceedings of the 3rd International Conference on Photonics and Optical Engineering, Xi’an, China, 5–8 December 2018; Volume 10305, p. 110521B. [Google Scholar]
- Bao, J.; Zha, B.; Xu, C.; Zhang, H. Study of a laser echo in an inhomogeneous dust environment with a continuous field Monte Carlo radiative transfer model. Opt. Express 2021, 29, 17976–17996. [Google Scholar] [CrossRef]
- Xu, C.; Zha, B.; Zhang, R.; Xia, J.; Zheng, Z.; Li, S. Echo characteristics of pulsed lasers in non-uniform smoke environments. Opt. Express 2024, 32, 24222–24241. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, B.; Liang, Y.; Huang, Z. Virtual simulation of the effect of FMCW laser fuse detector’s component performance variability on target echo characteristics under smoke interference. Materials 2022, 15, 4268. [Google Scholar] [CrossRef]
- Liu, B.; Song, C.; Duan, Y. The characteristics simulation of FMCW laser backscattering signals. Opt. Rev. 2018, 25, 197–204. [Google Scholar] [CrossRef]
- Bahmeh, Z.; Zangeneh, H. Detection of a target hidden in dense cloud clutter using an echo pattern of pulsed laser radar systems. Laser Phys. 2023, 33, 086203. [Google Scholar] [CrossRef]
- Wang, F.; Chen, H.; Ma, C.; Xu, L. Construction of backscattering echo caused by cloud in laser fuze. Optik 2018, 171, 153–160. [Google Scholar] [CrossRef]
- Prahl, S.; Keijzer, M.; Jacques, S.; Weich, A. A Monte Carlo model of light propagation in tissue. In Dosimetry of Laser Radiation in Medicine and Biology; SPIE: St Bellingham, WA, USA, 2017; Volume 10305, pp. 1030509–1030510. [Google Scholar]
- Poole, L.; Venable, D.; Campbell, J. Semianalytic Monte Carlo radiative transfer model for oceanographic lidar systems. Appl. Opt. 1981, 20, 3653. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Wu, Z.; Cao, Y. Practical Six-parameter bidirectional reflectance distribution function model for rough surface. Acta Opt. Sin. 2012, 32, 313–318. [Google Scholar]
- Kong, W.; Wan, F.; Yu, L.; Wang, C.; Sun, H.; Wang, R.; Chen, W. Dynamic Detection of Decomposition Gases in Eco-Friendly C5F10O Gas-Insulated Power Equipment by Fiber-Enhanced Raman Spectroscopy. Anal. Chem. 2024, 96, 15313–15321. [Google Scholar] [CrossRef] [PubMed]






| Simulation Parameter | Value | Simulation Parameter | Value |
|---|---|---|---|
| Photon number N0 | Sampling time interval t (ns) | 0.1 | |
| (mrad) | 73 | (ns) | 5, 10, 20, 40, 60, 80, 100 |
| (mrad) | 19.6 | Smoke particle size range d (μm) | 0.01–50 |
| (mm) | 12.5 | ||
| (mm) | 40, 50, 60, 70, 80, 90, 100 | Smoke complex refractive index mr | 1.52 + 0.008 i |
| (nm) | 905 | ) | 300, 500, 700, 900 |
| (m) | 4, 6, 8, 10 | 0.2, 0.4, 0.6, 0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Zhang, R.; Zheng, Z.; Zha, B.; Cao, W.; Zhang, H. Analysis of Pulsed Laser Target Echo Characteristics in Non-Uniform Smoke Environments. Photonics 2025, 12, 362. https://doi.org/10.3390/photonics12040362
Xu C, Zhang R, Zheng Z, Zha B, Cao W, Zhang H. Analysis of Pulsed Laser Target Echo Characteristics in Non-Uniform Smoke Environments. Photonics. 2025; 12(4):362. https://doi.org/10.3390/photonics12040362
Chicago/Turabian StyleXu, Chenyoushi, Ruihua Zhang, Zhen Zheng, Bingting Zha, Weiping Cao, and He Zhang. 2025. "Analysis of Pulsed Laser Target Echo Characteristics in Non-Uniform Smoke Environments" Photonics 12, no. 4: 362. https://doi.org/10.3390/photonics12040362
APA StyleXu, C., Zhang, R., Zheng, Z., Zha, B., Cao, W., & Zhang, H. (2025). Analysis of Pulsed Laser Target Echo Characteristics in Non-Uniform Smoke Environments. Photonics, 12(4), 362. https://doi.org/10.3390/photonics12040362





