Novel Focusing Performances of High-Numerical-Aperture Micro-Fresnel Zone Plates with Selective Occlusion
Abstract
1. Introduction
2. Materials and Methods
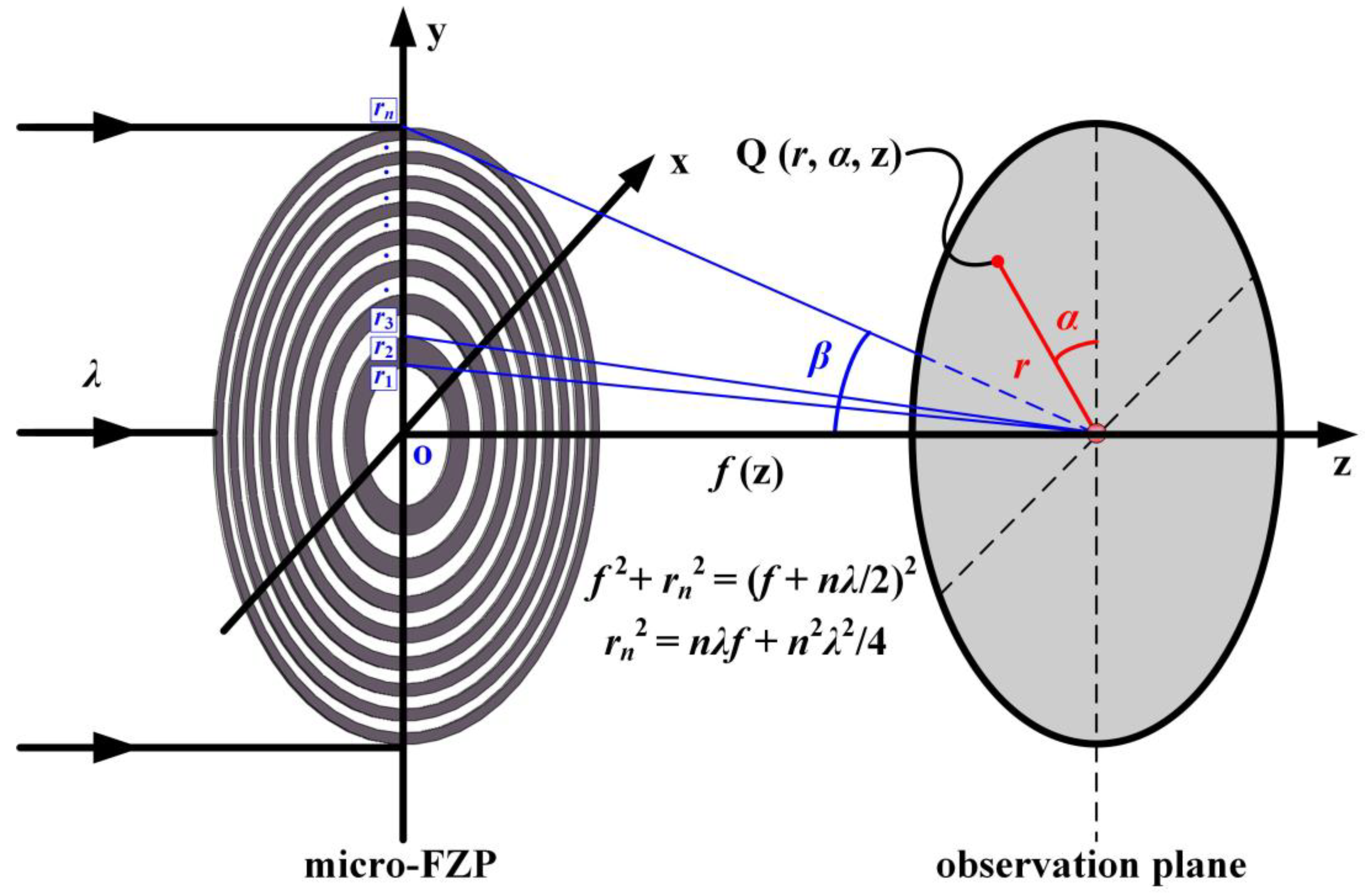
2.1. Micro-FZP
2.2. VAS Representation for Micro-FZPs
2.3. Rigorous Electromagnetic Validation of Micro-FZPs
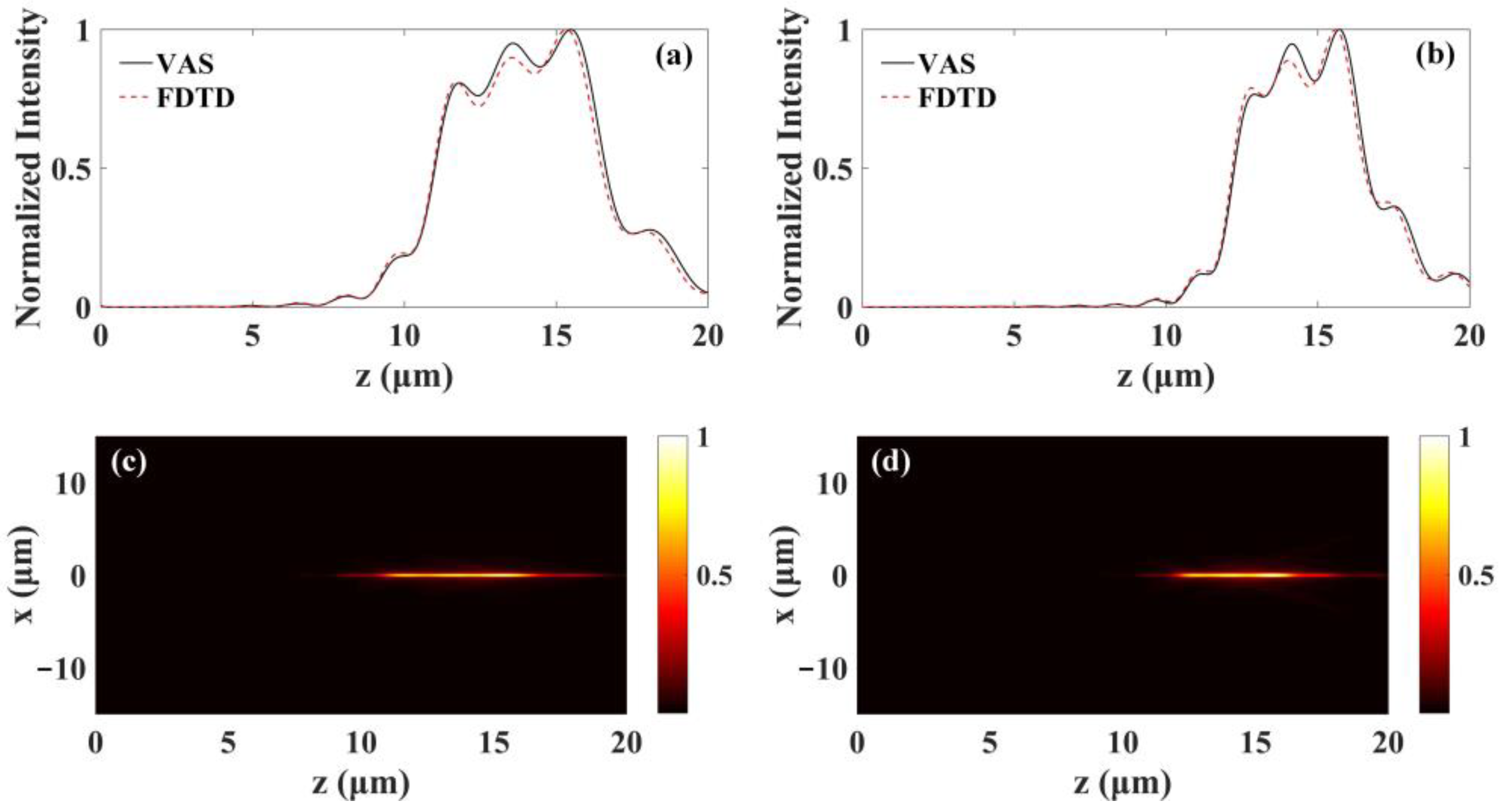
3. Results and Discussion
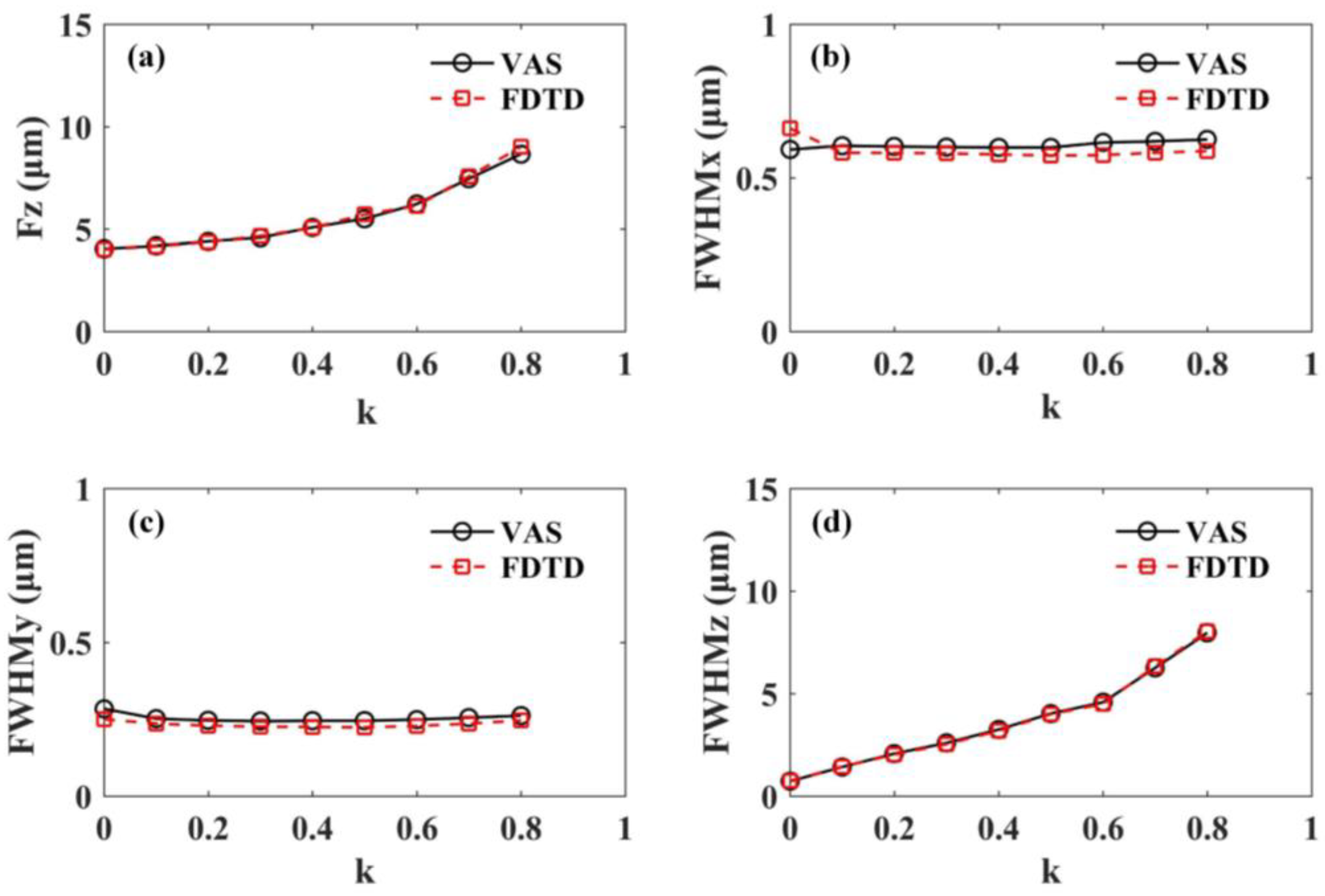
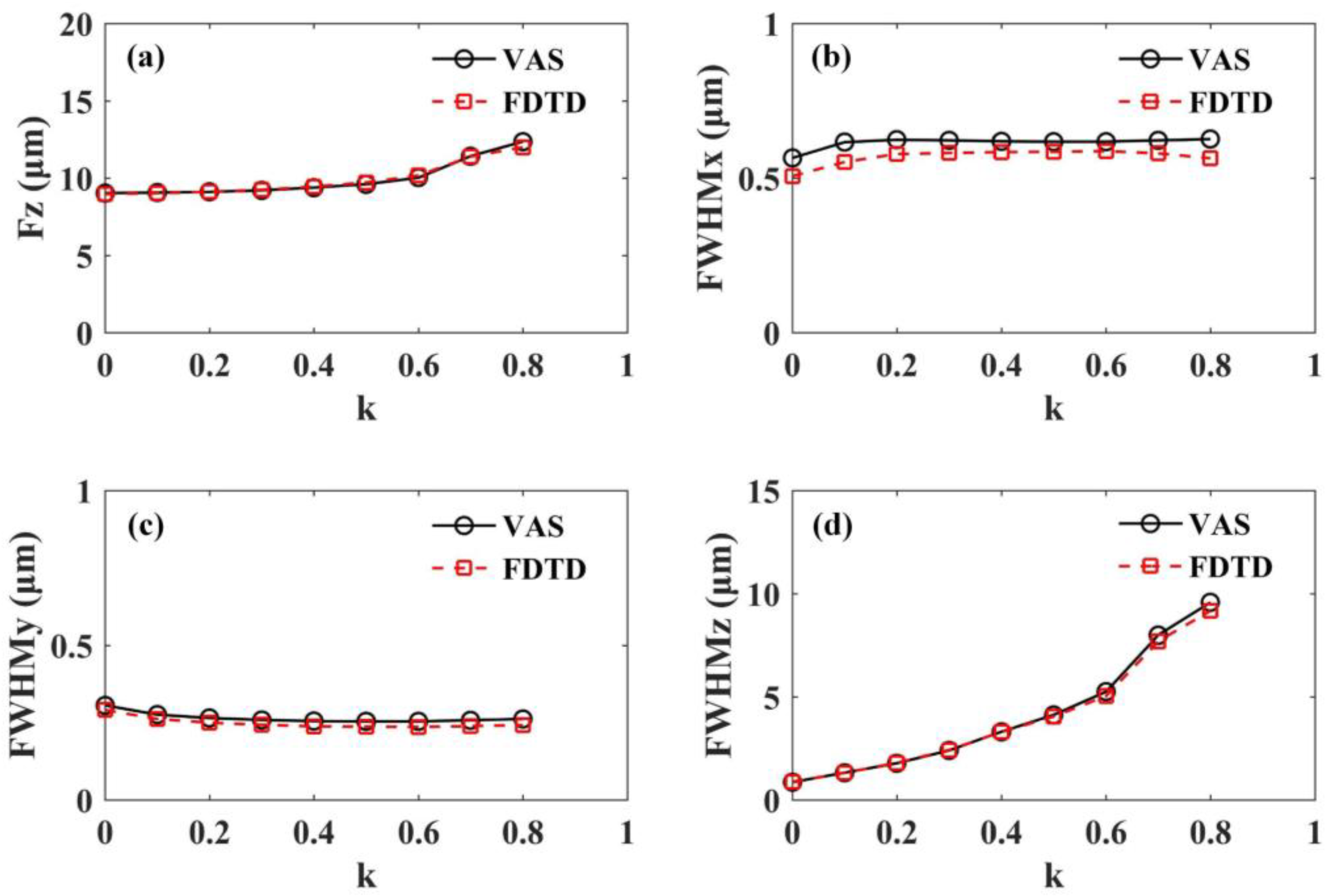
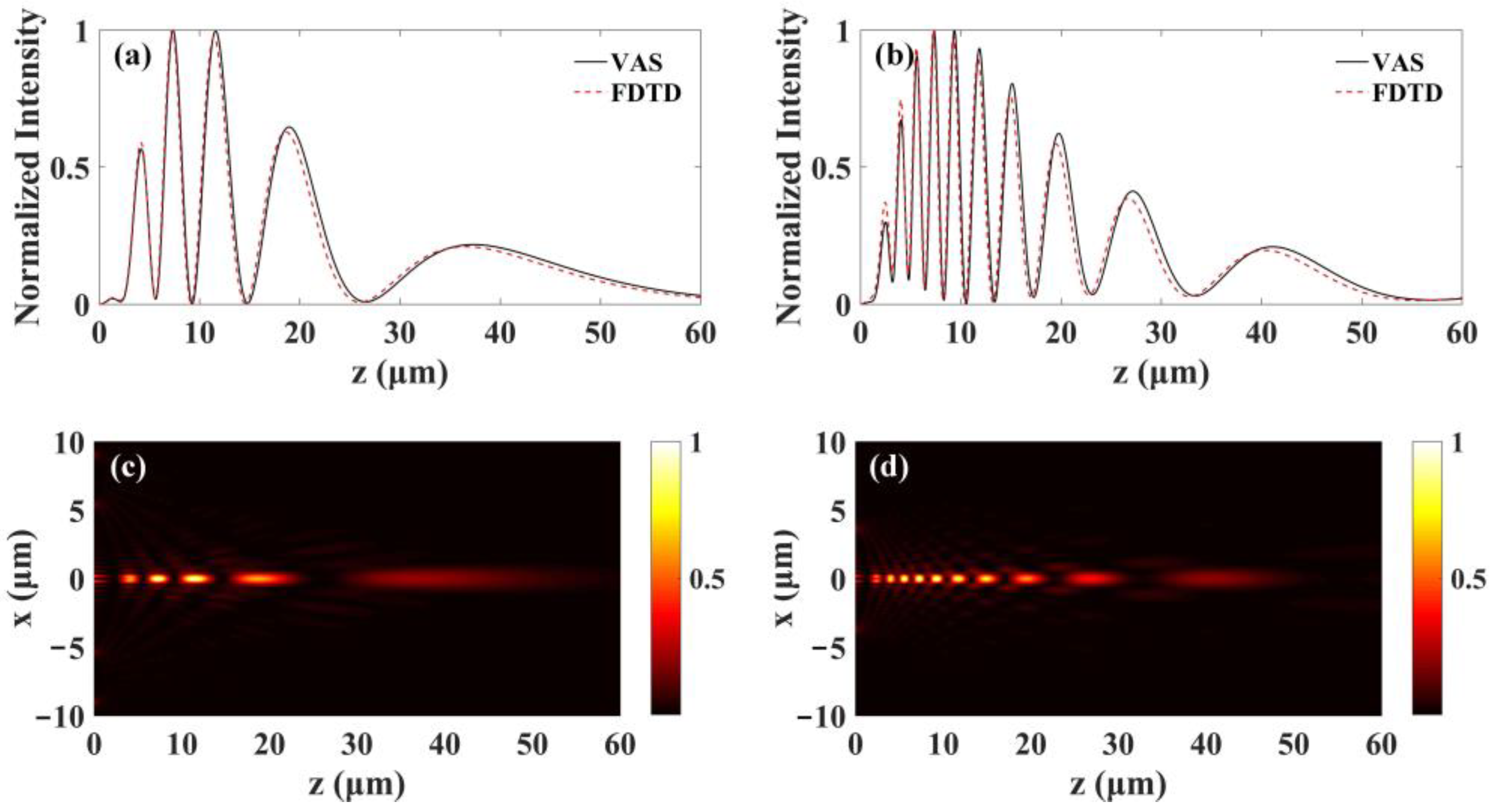
3.1. Central Occlusion
3.2. Intermittent Occlusion of Different Rings
3.3. Combination of Central Occlusion and Wavelength Shift
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Soret, J.L. Ueber die durch Kreisgitter erzeugten Diffractionsphänomene. Ann. Phys. Chem. 1875, 156, 99–113. [Google Scholar] [CrossRef]
- Rayleigh, L. Reprinted in Lord Rayleigh Scientific Papers; Cambridge University Press: Cambridge, UK, 1887; Volume 3, pp. 74–79. [Google Scholar]
- Wood, R.W. Phase-Reversal Zone Plate and Diffraction-Telescopes. Philos. Mag. Ser. 5 1898, 45, 511–523. [Google Scholar] [CrossRef]
- Wiltse, J.C. The Fresnel Zone-Plate Lens. In Proceedings of the 1985 Technical Symposium East, Arlington, VA, USA, 10–12 April 1985; Volume 544, pp. 41–47. [Google Scholar]
- Zhu, J.; Yang, Y.; Liao, S.; Xue, Q. Aperture-shared millimeter-wave/sub-6 GHz dual-band antenna hybridizing Fabry–Pérot cavity and Fresnel zone plate. IEEE Trans. Antenn. Propag. 2021, 69, 8170–8181. [Google Scholar] [CrossRef]
- Henderson, V.A.; Johnson, M.Y.H.; Kale, Y.B.; Griffin, P.F.; Riis, E.; Arnold, A.S. Optical characterisation of micro-fabricated Fresnel zone plates for atomic waveguides. Opt. Express 2020, 28, 9072–9081. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Wong, H. A Millimeter-Wave Fabry–Pérot Cavity Antenna Using Fresnel Zone Plate Integrated PRS. IEEE Trans. Antenn. Propag. 2020, 68, 564–568. [Google Scholar] [CrossRef]
- Menon, R.; Patel, A.; Gil, D.; Smith, H. Maskless lithography. Mater. Today 2005, 8, 26–33. [Google Scholar] [CrossRef]
- Judd, T.E.; Scott, R.G.; Sinuco, G.; Montgomery, T.; Martin, A.; Kruger, P.; Fromhold, T. Zone-plate focusing of Bose–Einstein condensates for atom optics and erasable high-speed lithography of quantum electronic components. New J. Phys. 2009, 12, 1558–1564. [Google Scholar] [CrossRef][Green Version]
- Soltau, J.; Meyer, P.; Hartmann, R.; Strüder, L.; Soltau, H.; Salditt, T. Full-field x-ray fluorescence imaging using a Fresnel zone plate coded aperture. Optica 2023, 10, 127–133. [Google Scholar] [CrossRef]
- Anton, S.R.; Shabairou, N.; Stanciu, S.G.; Stanciu, G.A.; Zalevsky, Z. Enhanced imaging with binary circular Dammann Fresnel zone plate. Opt. Express 2024, 32, 16248–16259. [Google Scholar] [CrossRef]
- Wakabayashi, D.; Suzuki, Y.; Shibazaki, Y.; Sugiyama, H.; Hirano, K.; Nishimura, R.; Hyodo, K.; Igarashi, N.; Funamori, N. X-ray zooming microscopy with two Fresnel zone plates. Rev. Sci. Instrum. 2022, 93, 033701. [Google Scholar] [CrossRef]
- Flenner, S.; Kubec, A.; David, C.; Storm, M.; Schaber, C.F.; Vollrath, F.; Müller, M.; Greving, I.; Hagemann, J. Hard X-ray nano-holotomography with a Fresnel zone plate. Opt. Express 2020, 28, 37514–37525. [Google Scholar] [CrossRef] [PubMed]
- Ishii, Y.; Yamamoto, K.; Yokoyama, Y.; Mizumaki, M.; Nakao, H.; Arima, T.; Yamasaki, Y. Soft- X-Ray Vortex Beam Detected by Inline Holography. Phys. Rev. Appl. 2020, 14, 064069. [Google Scholar] [CrossRef]
- Lider, V.V. Focusing diffraction optics for orbital telescopes. Opt. Spectrosc. 2023, 131, 1016–1042. [Google Scholar] [CrossRef]
- Britten, J.A.; Dixit, S.N.; DeBruyckere, M.; Steadfast, D. Large-aperture fast multilevel Fresnel zone lenses in glass and ultrathin polymer films for visible and near-infrared imaging applications. Appl. Opt. 2014, 53, 2312–2316. [Google Scholar] [CrossRef] [PubMed]
- Hawkes, P.W.; Spence, J.C.H. Springer Handbook of Microscopy; Springer: Berlin/Heidelberg, Germany, 2019; Volume 23. [Google Scholar]
- Kalosha, V.P.; Golub, I. Toward the subdiffraction focusing limit of optical superresolution. Opt. Lett. 2007, 32, 3540–3542. [Google Scholar] [CrossRef]
- Mote, R.G.; Yu, S.F.; Ng, B.K.; Wei, Z.; Lau, S.P. Near-field focusing properties of zone plates in visible regime—New insights. Opt. Express 2008, 16, 9554–9564. [Google Scholar] [CrossRef]
- Mote, R.G.; Yu, S.F.; Zhou, W.; Li, X.F. Subwavelength focusing behavior of high numerical-aperture phase Fresnel zone plates under various polarization states. Appl. Phys. Lett. 2009, 95, 191113. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, T.; Yang, S.; Li, G.; Li, S.; He, T. Axial intensity distribution of a micro-Fresnel zone plate at an arbitrary numerical aperture. Opt. Express 2021, 29, 12093–12109. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V. Concept of near-field millimeter-wave imaging system with a spatial resolution beyond the Abbe barrier. In Proceedings of the 2008 China-Japan Joint Microwave Conference, Shanghai, China, 10–12 September 2008; pp. 509–512. [Google Scholar]
- Zhang, Y.; An, H.; Zhang, D.; Cui, G.; Ruan, X. Diffraction theory of high numerical aperture subwavelength circular binary phase Fresnel zone plate. Opt. Express 2014, 22, 27425–27436. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, C.; Zhuang, Y. Effect of the shadowing in high-numerical-aperture binary phase Fresnel zone plates. Opt. Commun. 2014, 317, 88–92. [Google Scholar] [CrossRef]
- Liu, T.; Liu, Q.; Yang, S.; Jiang, Z.; Wang, T.; Zhang, G. Investigation of axial and transverse focal spot sizes of Fresnel zone plates. Appl. Opt. 2017, 56, 3725–3729. [Google Scholar] [CrossRef] [PubMed]
- Xue, S.; Liu, Q.; Liu, T.; Yang, S.; Su, P.; Liu, K.; Tian, T.; Wang, T. Electromagnetic exploration of focusing properties of high-numerical-aperture micro-Fresnel zone plates. Opt. Commun. 2018, 426, 41–45. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Nalimov, A.G.; Kotlyar, M.V.; O’Faolain, L.; Kozlova, E.S. Tight focusing of laser light using a chromium Fresnel zone plate. Opt. Express 2017, 25, 19662. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Liu, T.; Zhou, X.; Cao, P.; Wu, X.; Wang, J.; Liu, W.; Yao, X.; Wang, L. Experimental verification of the super-resolution focusing optical needle and imaging with a new type Fresnel zone plate. Opt. Commun. 2023, 546, 129742. [Google Scholar] [CrossRef]
- Liu, Q.; Deng, Y.; Xu, J.; Wang, J.; Liu, W.; Yao, X. Generation of a sub-wavelength optical needle by wavelength shifting and center masking of a Fresnel zone plate. Opt. Mater. Express 2024, 14, 356–366. [Google Scholar] [CrossRef]
- He, T.; Liu, T.; Liu, K.; Li, G.; Wang, J.; Tian, B.; Yang, S. Effect of manufacturing errors on focusing performance of large-scale super-oscillatory lens. Acta Opt. Sin. 2020, 40, 2005001. [Google Scholar]
- Yu, Y.; Li, W.; Li, H.; Li, M.; Yuan, W. An investigation of influencing factors on practical sub-diffraction-limit focusing of planar super-oscillation lenses. Nanomaterials 2018, 8, 185. [Google Scholar] [CrossRef]
- Attwood, D. Soft X-Rays and Extreme Ultraviolet Radiation: Principles and Applications; Cambridge University Press: Cambridge, UK, 2000; Chapter 9. [Google Scholar]
- Minin, I.V.; Minin, O.V. Control of focusing properties of diffraction elements. Sov. J. Quantum Electron. 1990, 20, 198–199. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V. Reference phase in diffractive lens antennas: A review. J. Infrared Millim. Terahertz Waves 2011, 32, 801–822. [Google Scholar] [CrossRef]
- Tarrazó-Serrano, D.; Castiñeira-Ibáñez, S.; Minin, O.V.; Candelas, P.; Rubio, C.; Minin, I.V. Design of acoustical Bessel-like beam formation by a pupil masked Soret zone plate lens. Sensors 2019, 19, 378. [Google Scholar] [CrossRef]
- Pfeiffer, F.; David, C.; van der Veen, J.F.; Bergemann, C. Nanometer focusing properties of Fresnel zone plates described by dynamical diffraction theory. Phys. Rev. B 2006, 73, 245331. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, T.; Yang, S.; Wang, T.; Wang, Y. Validation of vectorial theories for the focusing of high numerical aperture Fresnel zone plates. Opt. Commun. 2018, 429, 119–126. [Google Scholar] [CrossRef]
- Liu, T.; Tan, J.; Liu, J.; Wang, H. Vectorial design of superoscillatory lens. Opt. Express 2013, 21, 15090–15101. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Shen, T.; Yang, S.; Jiang, Z. Subwavelength focusing by binary multi-annular plates: Design theory and experiment. J. Opt. 2015, 17, 035610. [Google Scholar] [CrossRef]
- Liu, T.; Wang, T.; Yang, S.; Sun, L.; Jiang, Z. Rigorous electromagnetic test of super-oscillatory lens. Opt. Express 2015, 23, 32139–32148. [Google Scholar] [CrossRef]
- Liang, H.; Lin, Q.; Xie, X.; Sun, Q.; Wang, Y.; Zhou, L.; Liu, L.; Yu, X.; Zhou, J.; Krauss, T.F.; et al. Ultrahigh numerical aperture metalens at visible wavelengths. Nano Lett. 2018, 18, 4460–4466. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, X.; Cao, P.; Wu, X.; Liu, W.; Yao, X.; Wang, J.; Wang, L. Focusing performances of high numerical aperture Fresnel zone plates under different immersion media. AIP Adv. 2023, 13, 105305. [Google Scholar] [CrossRef]
- Liu, T.; Yang, S.; Jiang, Z. Electromagnetic exploration of far-field super-focusing nanostructured metasurfaces. Opt. Express 2016, 24, 16297–16308. [Google Scholar] [CrossRef]
- Dorn, R.; Quabis, S.; Leuchs, G. Sharper focus for a radially polarized light beam. Phys. Rev. Lett. 2003, 91, 233901. [Google Scholar] [CrossRef]
- Rogers, E.T.; Lindberg, J.; Roy, T.; Savo, S.; Chad, J.E.; Dennis, M.R.; Zheludev, N.I. A super-oscillatory lens optical microscope for subwavelength imaging. Nat. Mater. 2012, 11, 432–435. [Google Scholar] [CrossRef]
- Li, W.; Yu, Y.; Yuan, W. Flexible focusing patterns realization of centimeter-scale planar super-oscillatory lenses in parallel fabrication. Nanoscale 2019, 11, 311–320. [Google Scholar] [CrossRef] [PubMed]
- Tang, D.; Wang, C.; Zhao, Z.; Wang, Y.; Pu, M.; Li, X.; Gao, P.; Luo, X. Ultrabroadband superoscillatory lens composed by plasmonic metasurfaces for subdiffraction light focusing. Laser Photonics Rev. 2016, 9, 713–719. [Google Scholar] [CrossRef]
- Gan, Z.; Cao, Y.; Evans, R.A.; Gu, M. Three-dimensional deep sub-diffraction optical beam lithography with 9 nm feature size. Nat. Commun. 2013, 4, 2061. [Google Scholar] [CrossRef]
- Qin, F.; Huang, K.; Wu, J.; Teng, J.; Qiu, C.; Hong, M. A supercritical lens optical label-free microscopy: Sub-diffraction resolution and ultra-long working distance. Adv. Mater. 2017, 29, 1602721. [Google Scholar] [CrossRef] [PubMed]
- Gu, M.; Li, X.; Cao, Y. Optical storage arrays: A perspective for future big data storage. Light Sci. Appl. 2014, 3, e177. [Google Scholar] [CrossRef]

| micro-FZP | λ (nm) | η | N | f (μm) | NA |
|---|---|---|---|---|---|
| micro-FZP1 | 633 | 1.0 (air) | 40 | 4 | 0.971 |
| micro-FZP2 | 633 | 1.0 (air) | 50 | 9 | 0.932 |
| micro-FZP1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| r1–10 | 1.622 | 2.338 | 2.915 | 3.425 | 3.894 | 4.336 | 4.757 | 5.164 | 5.559 | 5.945 |
| r11–20 | 6.322 | 6.694 | 7.060 | 7.422 | 7.780 | 8.134 | 8.485 | 8.834 | 9.180 | 9.524 |
| r21–30 | 9.867 | 10.207 | 10.546 | 10.884 | 11.221 | 11.556 | 11.891 | 12.224 | 12.557 | 12.889 |
| r31–40 | 13.220 | 13.550 | 13.880 | 14.209 | 14.537 | 14.865 | 15.193 | 15.520 | 15.847 | 16.173 |
| micro-FZP2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| r1–10 | 2.408 | 3.434 | 4.242 | 4.939 | 5.567 | 6.147 | 6.692 | 7.210 | 7.706 | 8.185 |
| r11–20 | 8.648 | 9.099 | 9.539 | 9.970 | 10.392 | 10.807 | 11.216 | 11.619 | 12.017 | 12.410 |
| r21–30 | 12.799 | 13.184 | 13.566 | 13.944 | 14.319 | 14.691 | 15.061 | 15.429 | 15.794 | 16.158 |
| r31–40 | 16.519 | 16.878 | 17.236 | 17.593 | 17.947 | 18.301 | 18.653 | 19.004 | 19.353 | 19.702 |
| r41–50 | 20.049 | 20.396 | 20.741 | 21.086 | 21.429 | 21.772 | 22.114 | 22.456 | 22.796 | 23.136 |
| k | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | |
|---|---|---|---|---|---|---|---|---|---|---|
| FZ (μm) | VAS | 4.04 | 4.18 | 4.40 | 4.58 | 5.08 | 5.50 | 6.22 | 7.46 | 8.66 |
| FDTD | 4.01 | 4.16 | 4.37 | 4.66 | 5.05 | 5.71 | 6.13 | 7.57 | 9.01 | |
| FWHMx (μm) | VAS | 0.592 | 0.605 | 0.602 | 0.600 | 0.599 | 0.599 | 0.615 | 0.619 | 0.625 |
| FDTD | 0.661 | 0.582 | 0.581 | 0.580 | 0.576 | 0.573 | 0.574 | 0.582 | 0.587 | |
| FWHMy (μm) | VAS | 0.284 | 0.252 | 0.246 | 0.244 | 0.245 | 0.245 | 0.249 | 0.255 | 0.262 |
| FDTD | 0.250 | 0.236 | 0.229 | 0.226 | 0.225 | 0.224 | 0.228 | 0.236 | 0.246 | |
| FWHMz (μm) | VAS | 0.72 | 1.42 | 2.07 | 2.59 | 3.25 | 4.03 | 4.58 | 6.26 | 7.96 |
| FDTD | 0.74 | 1.43 | 2.03 | 2.53 | 3.19 | 4.00 | 4.50 | 6.34 | 8.04 | |
| k | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | |
|---|---|---|---|---|---|---|---|---|---|---|
| FZ (μm) | VAS | 9.02 | 9.06 | 9.10 | 9.20 | 9.38 | 9.60 | 10.02 | 11.42 | 12.36 |
| FDTD | 8.96 | 9.02 | 9.11 | 9.23 | 9.44 | 9.71 | 10.16 | 11.39 | 11.99 | |
| FWHMx (μm) | VAS | 0.565 | 0.616 | 0.624 | 0.622 | 0.619 | 0.618 | 0.618 | 0.622 | 0.626 |
| FDTD | 0.506 | 0.552 | 0.578 | 0.581 | 0.584 | 0.585 | 0.587 | 0.580 | 0.564 | |
| FWHMy (μm) | VAS | 0.306 | 0.276 | 0.265 | 0.259 | 0.255 | 0.254 | 0.254 | 0.258 | 0.262 |
| FDTD | 0.291 | 0.262 | 0.250 | 0.243 | 0.238 | 0.237 | 0.236 | 0.239 | 0.242 | |
| FWHMz (μm) | VAS | 0.86 | 1.32 | 1.78 | 2.40 | 3.31 | 4.13 | 5.25 | 7.99 | 9.57 |
| FDTD | 0.88 | 1.31 | 1.80 | 2.42 | 3.30 | 4.05 | 5.04 | 7.69 | 9.16 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Wu, Y.; Deng, Y.; Wang, J.; Liu, W.; Yao, X. Novel Focusing Performances of High-Numerical-Aperture Micro-Fresnel Zone Plates with Selective Occlusion. Photonics 2025, 12, 372. https://doi.org/10.3390/photonics12040372
Liu Q, Wu Y, Deng Y, Wang J, Liu W, Yao X. Novel Focusing Performances of High-Numerical-Aperture Micro-Fresnel Zone Plates with Selective Occlusion. Photonics. 2025; 12(4):372. https://doi.org/10.3390/photonics12040372
Chicago/Turabian StyleLiu, Qiang, Yunpeng Wu, Yuanhao Deng, Junli Wang, Wenshuai Liu, and Xiaomin Yao. 2025. "Novel Focusing Performances of High-Numerical-Aperture Micro-Fresnel Zone Plates with Selective Occlusion" Photonics 12, no. 4: 372. https://doi.org/10.3390/photonics12040372
APA StyleLiu, Q., Wu, Y., Deng, Y., Wang, J., Liu, W., & Yao, X. (2025). Novel Focusing Performances of High-Numerical-Aperture Micro-Fresnel Zone Plates with Selective Occlusion. Photonics, 12(4), 372. https://doi.org/10.3390/photonics12040372





