Dual-Band Topological Valley Cavity in Mid-Infrared Range
Abstract
1. Introduction
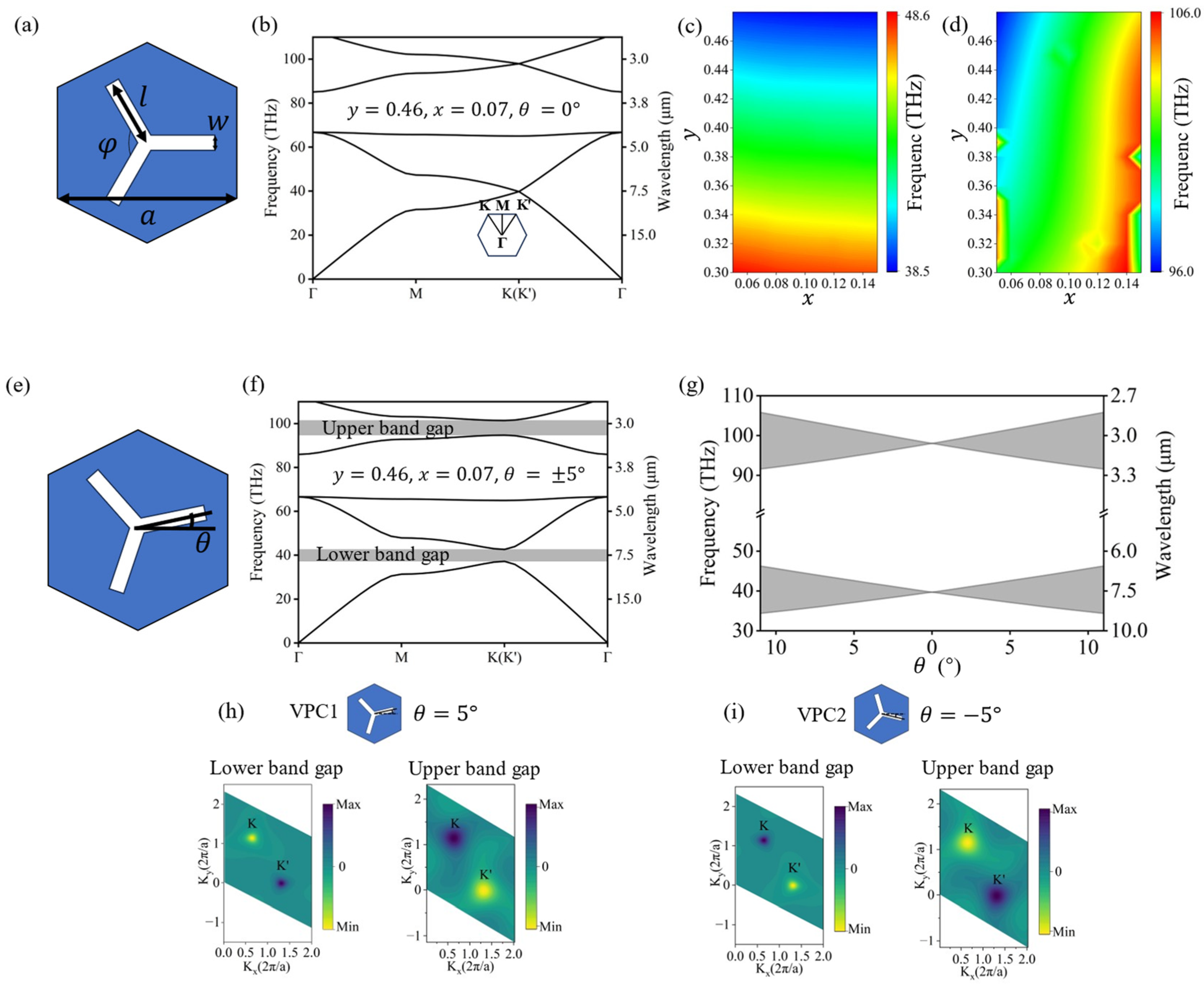
2. Design of Valley Photonic Crystals
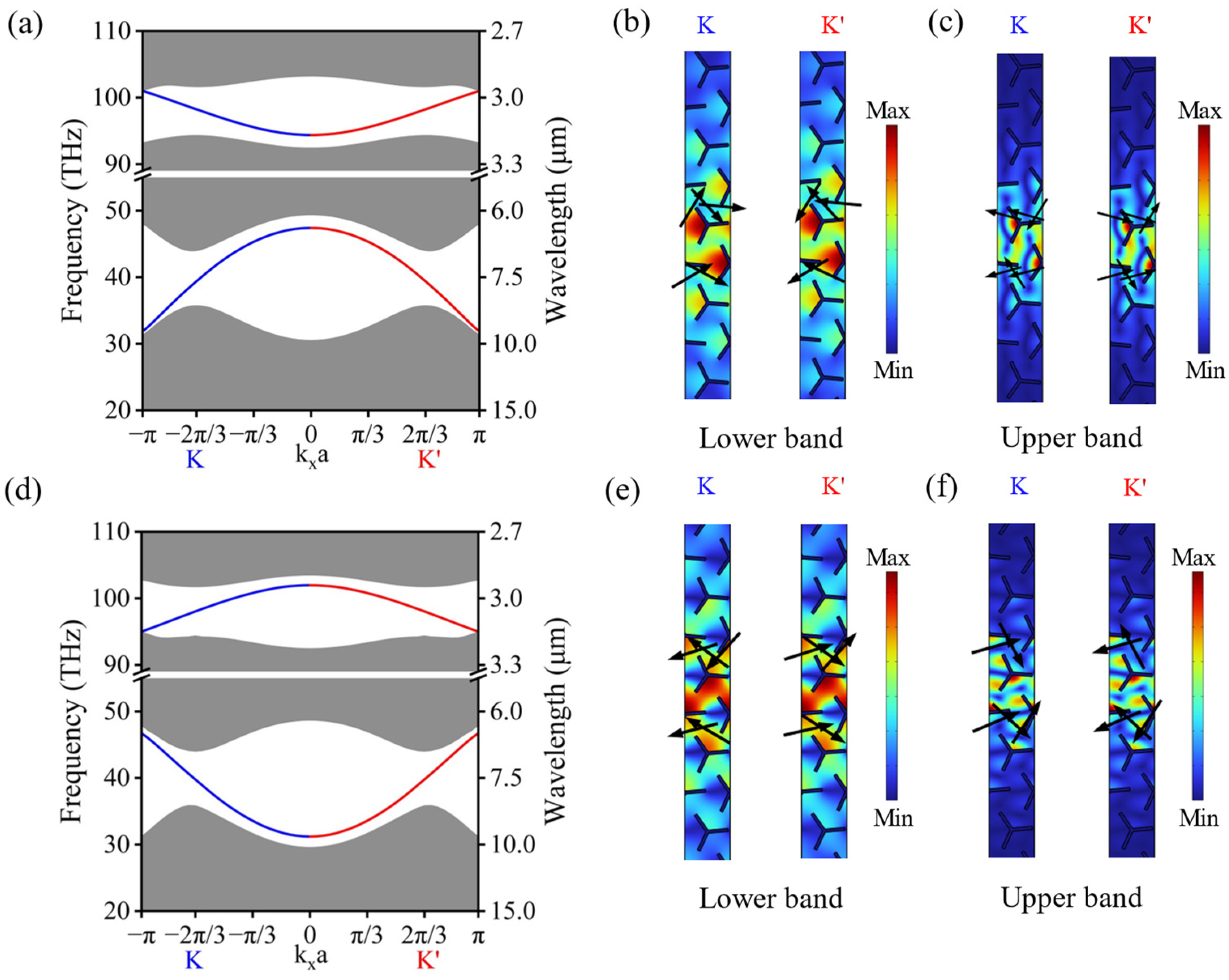
3. Valley Edge States Characteristics
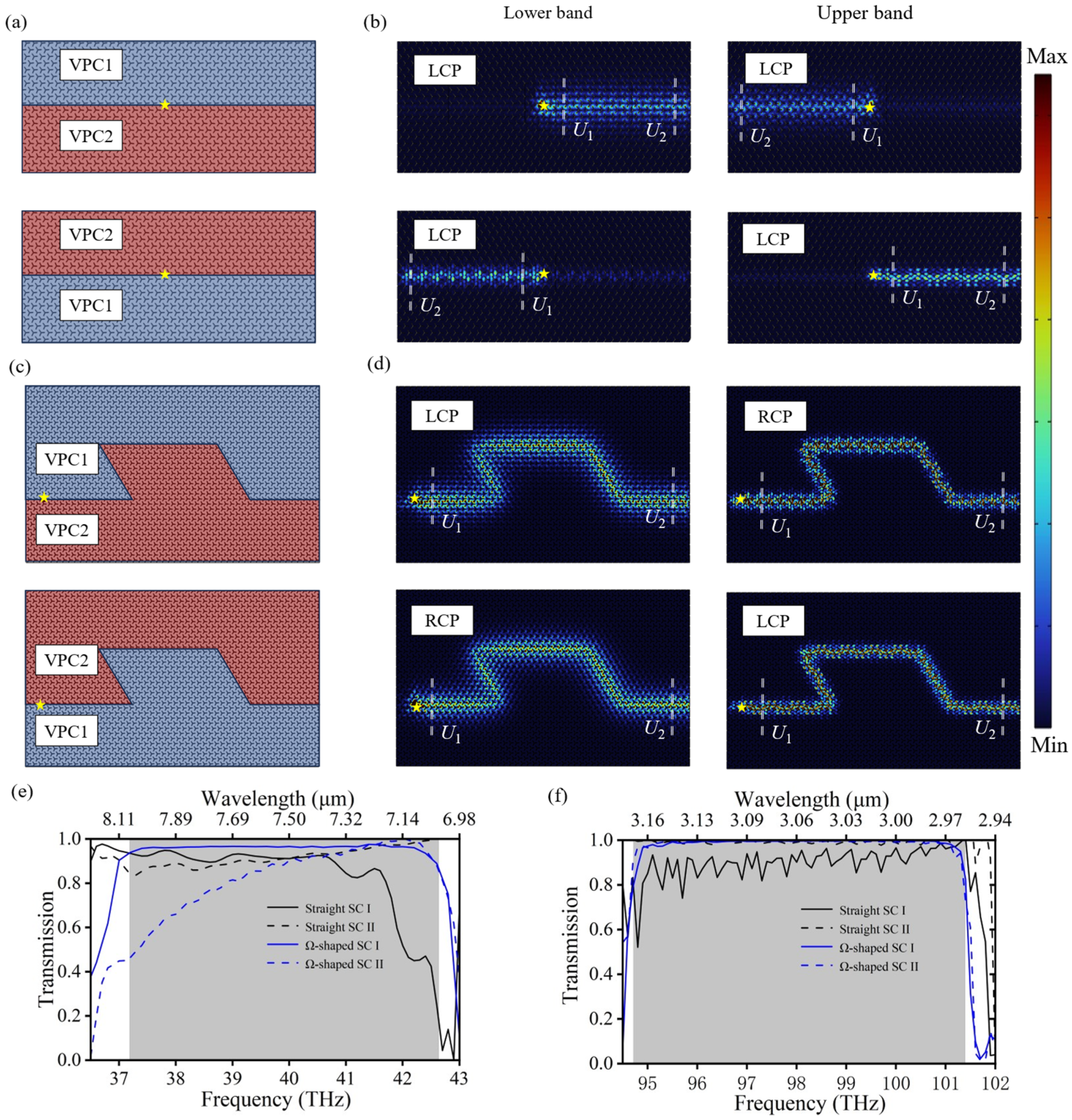
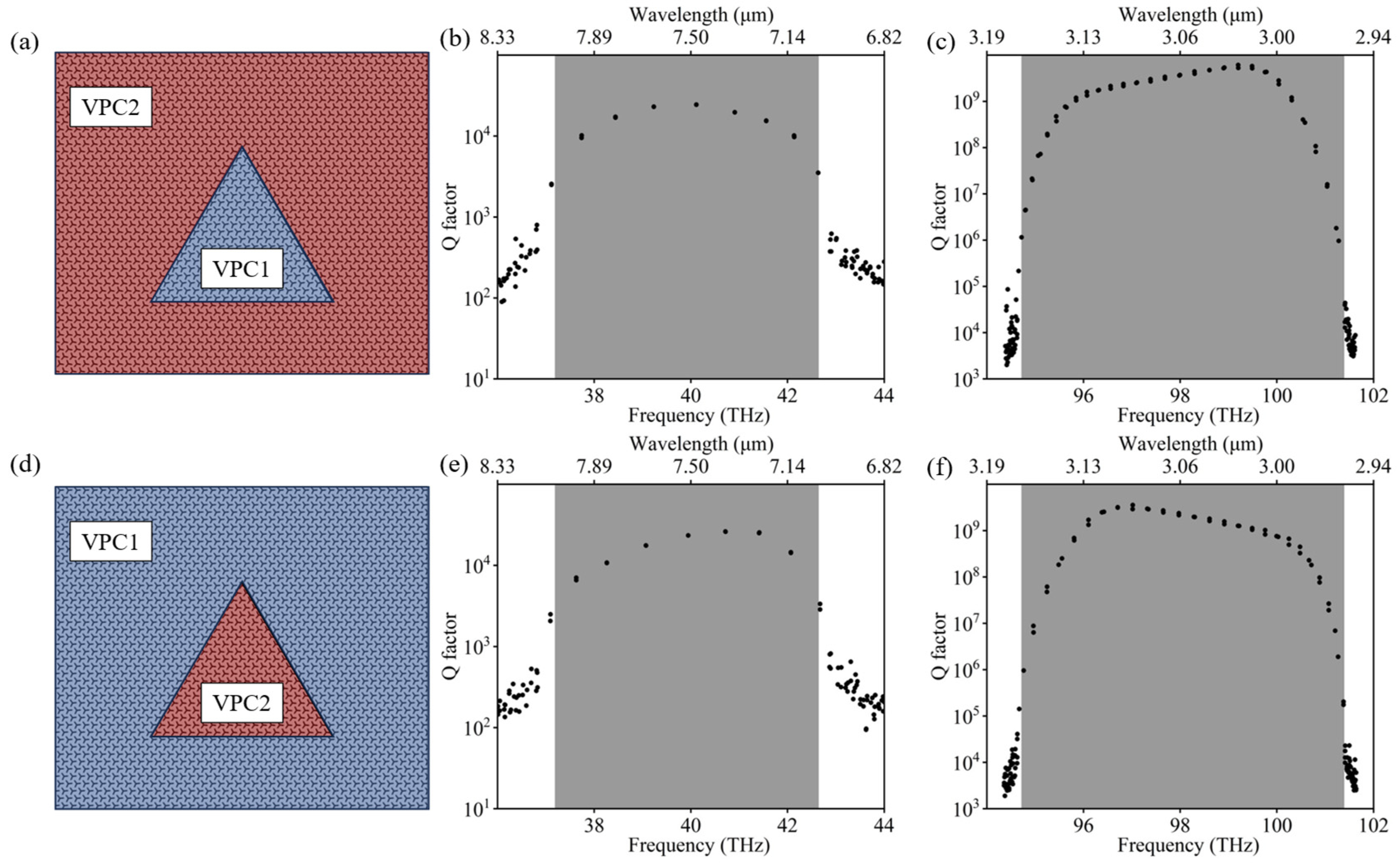
4. Valley Photonic Crystals Cavity Based on Valley Edge States
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, L.; Liu, Y.; Li, M.; Zhou, X.; Wang, S.; Zhao, Q.; Li, Z.; Tao, L.; Xiao, X.; Song, K.; et al. Dual-band large-area topological edge states and higher-order corner states in a valley Hall photonic crystal. Phys. Rev. B 2024, 110, 155415. [Google Scholar] [CrossRef]
- Guo, P.-Y.; Li, W.; Hu, J.; Wang, H.-X. Dual-band topological large-area waveguide transport in photonic heterostructures. Phys. Rev. B 2024, 110, 035115. [Google Scholar] [CrossRef]
- Lu, L.; Joannopoulos, J.D.; Soljačić, M. Topological photonics. Nat. Photonics 2014, 8, 821–829. [Google Scholar] [CrossRef]
- Khanikaev, A.B.; Shvets, G. Two-dimensional topological photonics. Nat. Photonics 2017, 11, 763–773. [Google Scholar] [CrossRef]
- Ozawa, T.; Price, H.M.; Amo, A.; Goldman, N.; Hafezi, M.; Lu, L.; Rechtsman, M.C.; Schuster, D.; Simon, J.; Zilberberg, O. Topological photonics. Rev. Mod. Phys. 2019, 91, 015006. [Google Scholar] [CrossRef]
- Dong, J.W.; Chen, X.D.; Zhu, H.; Wang, Y.; Zhang, X. Valley photonic crystals for control of spin and topology. Nat. Mater. 2017, 16, 298–302. [Google Scholar] [CrossRef]
- Yang, Y.; Yamagami, Y.; Yu, X.; Pitchappa, P.; Webber, J.; Zhang, B.; Fujita, M.; Nagatsuma, T.; Singh, R. Terahertz topological photonics for on-chip communication. Nat. Photonics 2020, 14, 446–451. [Google Scholar] [CrossRef]
- Zeng, Y.; Chattopadhyay, U.; Zhu, B.; Qiang, B.; Li, J.; Jin, Y.; Li, L.; Davies, A.G.; Linfield, E.H.; Zhang, B.; et al. Electrically pumped topological laser with valley edge modes. Nature 2020, 578, 246–250. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, L.; Zhang, D.; Gao, S. Topological cavity laser with valley edge states. Opt. Express 2022, 30, 4965–4977. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Yang, J.-K.; Hwang, Y.; Oh, S.S. Evolution of topological edge modes from honeycomb photonic crystals to triangular-lattice photonic crystals. Phys. Rev. Res. 2021, 3, L022025. [Google Scholar] [CrossRef]
- He, X.T.; Liang, E.T.; Yuan, J.J.; Qiu, H.Y.; Chen, X.D.; Zhao, F.L.; Dong, J.W. A silicon-on-insulator slab for topological valley transport. Nat. Commun. 2019, 10, 872. [Google Scholar] [CrossRef]
- Hafezi, M.; Demler, E.A.; Lukin, M.D.; Taylor, J.M. Robust optical delay lines with topological protection. Nat. Phys. 2011, 7, 907–912. [Google Scholar] [CrossRef]
- Peano, V.; Houde, M.; Marquardt, F.; Clerk, A.A. Topological Quantum Fluctuations and Traveling Wave Amplifiers. Phys. Rev. X 2016, 6, 041026. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Y.; Leykam, D.; Chong, Y.D. Optical isolation with nonlinear topological photonics. New J. Phys. 2017, 19, 095002. [Google Scholar] [CrossRef]
- Barik, S.; Karasahin, A.; Flower, C.; Cai, T.; Miyake, H.; DeGottardi, W.; Hafezi, M.; Waks, E. A topological quantum optics interface. Science 2018, 359, 666–668. [Google Scholar] [CrossRef]
- Zhong, H.; Kartashov, Y.V.; Szameit, A.; Li, Y.; Liu, C.; Zhang, Y. Theory of topological corner state laser in Kagome waveguide arrays. APL Photonics 2021, 6, 040802. [Google Scholar] [CrossRef]
- Gao, Y.-F.; He, Y.-H.; Maimaiti, A.; Jin, M.-C.; He, Y.; Qi, X.-F. Manipulation of coupling between topological edge state and corner state in photonic crystals. Opt. Laser Technol. 2022, 155, 108387. [Google Scholar] [CrossRef]
- Shi, A.; Yan, B.; Ge, R.; Xie, J.; Peng, Y.; Li, H.; Sha, W.E.I.; Liu, J. Coupled cavity-waveguide based on topological corner state and edge state. Opt. Lett. 2021, 46, 1089–1092. [Google Scholar] [CrossRef]
- Han, S.; Cui, J.; Chua, Y.; Zeng, Y.; Hu, L.; Dai, M.; Wang, F.; Sun, F.; Zhu, S.; Li, L.; et al. Electrically-pumped compact topological bulk lasers driven by band-inverted bound states in the continuum. Light Sci. Appl. 2023, 12, 145. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, L.; He, M.; Wang, Z.; Lin, X.; Gao, F.; Yang, Y.; Zhang, B.; Chen, H. Valley-Hall Photonic Topological Insulators with Dual-Band Kink States. Adv. Opt. Mater. 2019, 7, 1900036. [Google Scholar] [CrossRef]
- Chen, M.L.N.; Jiang, L.J.; Lan, Z.; Sha, W.E.I. Coexistence of pseudospin- and valley-Hall-like edge states in a photonic crystal with C3v symmetry. Phys. Rev. Res. 2020, 2, 043148. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.X.; Liang, L.; Zhu, W.; Fan, L.; Lin, Z.K.; Li, F.; Zhang, X.; Luan, P.G.; Poo, Y.; et al. Hybrid topological photonic crystals. Nat. Commun. 2023, 14, 4457. [Google Scholar] [CrossRef] [PubMed]
- Yan, B.; Peng, Y.; Xie, J.; Peng, Y.; Shi, A.; Li, H.; Gao, F.; Peng, P.; Jiang, J.; Liu, J.; et al. Multifrequency and Multimode Topological Waveguides in a Stampfli-Triangle Photonic Crystal with Large Valley Chern Numbers. Laser Photonic Rev. 2024, 18, 2300686. [Google Scholar] [CrossRef]
- He, X.-T.; Liu, J.-W.; Shi, F.-L.; Shen, K.; Chen, W.-J.; Chen, X.-D.; Dong, J.-W. Dual-polarization two-dimensional valley photonic crystals. Sci. China Phys. Mech. Astron. 2022, 65, 284212. [Google Scholar] [CrossRef]
- Lan, Z.; You, J.W.; Panoiu, N.C. Nonlinear one-way edge-mode interactions for frequency mixing in topological photonic crystals. Phys. Rev. B 2020, 101, 155422. [Google Scholar] [CrossRef]
- Lan, Z.; You, J.W.; Ren, Q.; Sha, W.E.I.; Panoiu, N.C. Second-harmonic generation via double topological valley-Hall kink modes in all-dielectric photonic crystals. Phys. Rev. A 2021, 103, L041502. [Google Scholar] [CrossRef]
- Xing, H.; Xu, G.; Lu, D.; Fan, J.; Xue, Z.; Gao, Z.; Cong, L. Terahertz topological photonic crystals with dual edge states for efficient routing. Opt. Lett. 2023, 48, 2805–2808. [Google Scholar] [CrossRef]
- Qi, Z.; Hu, G.; Deng, C.; Sun, H.; Sun, Y.; Li, Y.; Liu, B.; Bai, Y.; Chen, S.; Cui, Y. Electrical tunable topological valley photonic crystals for on-chip optical communications in the telecom band. Nanophotonics 2022, 11, 4273–4285. [Google Scholar] [CrossRef]
- Tang, S.; Xu, Y.; Ding, F.; Liu, F. Continuously tunable topological defects and topological edge states in dielectric photonic crystals. Phys. Rev. B 2023, 107, L041403. [Google Scholar] [CrossRef]
- Wang, Y.; You, J.W.; Panoiu, N.C. All-optical control of topological valley transport in graphene metasurfaces. Opt. Express 2023, 31, 10401–10410. [Google Scholar] [CrossRef] [PubMed]
- Dai, C.; Liu, T.; Wang, D.; Zhou, L. Multiplexing near- and far-field functionalities with high-efficiency bi-channel metasurfaces. PhotoniX 2024, 5, 11. [Google Scholar] [CrossRef]
- Li, M.; Liu, Y.; Du, L.; Li, P.; Dong, Y.; Tao, L.; Li, Z.; Guo, Y.; Song, K.; Zhao, X. Ultrabroadband valley transmission and corner states in valley photonic crystals with dendritic structure. Commun. Phys. 2024, 7, 214. [Google Scholar] [CrossRef]
- Zhang, J.; Si, Y.; Zhang, Y.; Wang, B.; Wang, X. Dual-Band High-Throughput and High-Contrast All-Optical Topology Logic Gates. Micromachines 2024, 15, 1492. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, B.; Wang, R.; Wang, X. Transport characteristics of topological edge states in dual-band valley photonic crystals. Acta Opt. Sin. 2023, 43, 0916001. [Google Scholar] [CrossRef]
- Cai, C.; Li, X.; He, G.; Lian, F.; Li, M.; Wang, Q.; Qin, Y. Inverse design of dual-band photonic topological insulator beam splitters for efficient light transmission. J. Phys. D Appl. Phys. 2023, 57, 135301. [Google Scholar] [CrossRef]
- Xu, K.; Xiao, Z.; Deng, X.; Xie, G.; Fang, M.; Huang, Z. Topology Optimization-Based Design of Topological Edge-State Wavelength Division Multiplexer. IEEE Photonics Technol. Lett. 2023, 35, 773–776. [Google Scholar] [CrossRef]
- Yi, F.; Liu, M.Q.; Wang, N.N.; Wang, B.X.; Zhao, C.Y. Near-field observation of mid-infrared edge modes in topological photonic crystals. Appl. Phys. Lett. 2023, 123, 081110. [Google Scholar] [CrossRef]
- Qiu, P.; Liang, R.; Qiu, W.; Chen, H.; Ren, J.; Lin, Z.; Wang, J.X.; Kan, Q.; Pan, J.Q. Topologically protected edge states in graphene plasmonic crystals. Opt. Express 2017, 25, 22587–22594. [Google Scholar] [CrossRef]
- Ebrahim-Zadeh, M.; Sorokina, I.T. Mid-Infrared Coherent Sources and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Hu, J.; Meyer, J.; Richardson, K.; Shah, L. Feature issue introduction: Mid-IR photonic materials. Opt. Mater. Express 2013, 3, 1571–1575. [Google Scholar] [CrossRef]
- Soref, R. Mid-infrared photonics in silicon and germanium. Nat. Photonics 2010, 4, 495–497. [Google Scholar] [CrossRef]
- Lu, C.; Han, Z.; Cai, Y.; Gao, Y.; Wen, Z. Exploring edge states in square–octagon moiré lattice. APL Photonics 2024, 9, 056109. [Google Scholar] [CrossRef]
- Guan, Z.; Chen, X.-D.; Mo, H.-C.; Liu, J.-W.; Shu, Q.-Y.; Cao, Y.; Chen, W.-J.; Dong, J.-W. Tunable topological boundary modes enabled by synthetic translation dimension. APL Photonics 2024, 9, 076116. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, L.; Chen, F.; Yan, Q.; Xi, R.; Chen, H.; Yang, Y. Photonic Topological Valley-Locked Waveguides. ACS Photonics 2021, 8, 1400–1406. [Google Scholar] [CrossRef]
- Cheng, Q.; Wang, S.; Lv, J.; Liu, N. Topological photonic crystal biosensor with valley edge modes based on a silicon-on-insulator slab. Opt. Express 2022, 30, 10792–10801. [Google Scholar] [CrossRef]
- Lu, J.; Qiu, C.; Ye, L.; Fan, X.; Ke, M.; Zhang, F.; Liu, Z. Observation of topological valley transport of sound in sonic crystals. Nat. Phys. 2016, 13, 369–374. [Google Scholar] [CrossRef]
- Jia, D.; Ge, Y.; Xue, H.; Yuan, S.-Q.; Sun, H.-X.; Yang, Y.; Liu, X.-J.; Zhang, B. Topological refraction in dual-band valley sonic crystals. Phys. Rev. B 2021, 103, 144309. [Google Scholar] [CrossRef]
- Rockstuhl, C.; Scharf, T. Amorphous Nanophotonics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, C.; Yu, J.; Chen, C.; Lai, Y.; Cheng, S.; Chen, Y.; Li, Y.; Liu, S.; Zhang, J.; Liu, F. Dual-Band Topological Valley Cavity in Mid-Infrared Range. Photonics 2025, 12, 420. https://doi.org/10.3390/photonics12050420
Kang C, Yu J, Chen C, Lai Y, Cheng S, Chen Y, Li Y, Liu S, Zhang J, Liu F. Dual-Band Topological Valley Cavity in Mid-Infrared Range. Photonics. 2025; 12(5):420. https://doi.org/10.3390/photonics12050420
Chicago/Turabian StyleKang, Chen, Jinling Yu, Can Chen, Yunfeng Lai, Shuying Cheng, Yonghai Chen, Yuan Li, Shuman Liu, Jinchuan Zhang, and Fengqi Liu. 2025. "Dual-Band Topological Valley Cavity in Mid-Infrared Range" Photonics 12, no. 5: 420. https://doi.org/10.3390/photonics12050420
APA StyleKang, C., Yu, J., Chen, C., Lai, Y., Cheng, S., Chen, Y., Li, Y., Liu, S., Zhang, J., & Liu, F. (2025). Dual-Band Topological Valley Cavity in Mid-Infrared Range. Photonics, 12(5), 420. https://doi.org/10.3390/photonics12050420




