Next Article in Journal
A Flexible Photonic Method for Angle-of-Arrival and Frequency Measurements
Previous Article in Journal
Feasibility and Safety of Endoscopic Balloon-Assisted Laser Treatment (EBLT) for Gastroesophageal Reflux Disease: Functional, Structural, and Gene Expression Analysis in Preclinical Model
Previous Article in Special Issue
Acceleration of Heavy Ions by Ultrafast High-Peak-Power Lasers: Advances, Challenges, and Perspectives
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Photonics
Volume 12
Issue 5
10.3390/photonics12050422
photonics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Molecular Alignment Under Strong Laser Pulses: Progress and Applications

by
Ming Wang
,
Enliang Zhang
,
Qingqing Liang
* and
Yi Liu
*
Shanghai Key Lab of Modern Optical System, University of Shanghai for Science and Technology, Shanghai 200093, China
*
Authors to whom correspondence should be addressed.
Photonics 2025, 12(5), 422; https://doi.org/10.3390/photonics12050422 (registering DOI)
Submission received: 31 March 2025 / Revised: 22 April 2025 / Accepted: 24 April 2025 / Published: 28 April 2025
(This article belongs to the Special Issue Advances in Ultrafast Laser Science and Applications)
Browse Figures
Versions Notes

Abstract

:
Molecular alignment under strong laser pulses is an important tool for manipulating quantum states and investigating ultrafast phenomena. This review summarizes two decades of advancement in laser-driven alignment techniques, such as cross-polarized double pulses, optical centrifuges, and elliptically truncated fields. Given the prominent emphasis on transformational applications in current alignment research, we outline its importance in cutting-edge applications under strong laser pulses, such as chiral discrimination, high-harmonic generation (HHG), photoelectron angular distributions (PADs) and ionization yields in photoionization, and Terahertz (THz) manipulation. These interdisciplinary developments provide fundamental insights into ultrafast molecular dynamics. They also establish frameworks for advanced light–matter interaction control.

1. Introduction

Since its initial discovery in CO molecules under intense laser fields by Normand et al. [1], molecular alignment—the process by which the primary axis of molecules becomes spatially ordered along a given direction without directional preference—has progressed from basic theoretical investigations to multidimensional control and interdisciplinary applications. It is vital to differentiate alignment, which includes spatial ordering of molecular axes, from orientation, which requires directional control (e.g., setting a molecule’s permanent dipole moment to point in a given direction). As the spatial arrangement of molecules plays a significant role in many light–matter interactions [2], molecular alignment serves as a potent tool in strong-field reaction dynamics.
The importance of molecular alignment manifests in two key aspects. First, alignment changes the spatial symmetry of molecular systems, transforming isotropic molecular ensembles into directionally dependent systems, thereby presenting an appropriate environment for researching stereoscopic effects in light–molecule interactions [2,3]. For instance, in photodissociation reactions, aligned molecules regulate the spatial distribution of fragment ions, which will expose quantum state dependent reaction pathways [4]. Second, molecular alignment serves as an intermediate control tool, permitting coherent manipulation of rotating quantum states through external fields, which subsequently influences nonlinear optical processes, such as HHG and THz radiation [5,6]. Recent improvements in femtosecond laser technology have achieved alignment control with sub-cycle temporal precision and sub-angstrom spatial resolution [2], offering new opportunities for molecular imaging and quantum information processing [4].
This review begins by revisiting the conceptual framework and classifications of molecular alignment, followed by a concise overview of research progress over the past two decades [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51]. We then emphasize applications of laser-induced molecular alignment in cutting-edge research domains, including chiral discrimination [52,53,54,55,56,57,58], HHG [59,60,61,62,63,64], PADs and ionization yields in photoionization [65,66,67,68,69,70,71], and THz manipulation [72,73,74,75,76,77,78,79,80]. By collating and critically assessing these advancements, this work aims to serve as a reference guide for researchers seeking to leverage molecular alignment techniques in their experimental and theoretical studies.

2. Strong-Field Molecular Alignment: Progress

2.1. Dynamics of Molecular Alignment Under Linearly Polarized Laser Pulse

To understand the mechanism of molecular alignment, we start with a fundamental scenario: a linear molecule with a linearly polarized laser beam. Under this circumstance, molecules can be efficiently described as rigid rotors (Figure 1).
For a rigid rotor molecule subjected to a laser field E (t), the total dipole moment in the ground state is stated as [6]: μ = μ0 + μind, where μ0 represents the permanent dipole moment, and μind signifies the dipole moment induced by the external field. Consequently, the interaction potential between the dipole moment and the laser field can be expressed as U = −μ·E. By solving the Schrödinger equation with this potential, we obtain the molecular wave function. However, individual molecules do not display alignment directly; instead, the ensemble-averaged alignment parameter 〈cos2θ〉 is employed to describe the alignment, with θ being the angle between the molecular axis and the laser polarization direction. This parameter is calculated by Boltzmann statistics [81].
In the situation of isotropic orientations, such as when no external field is present, 〈cos2θ〉 produces a value of 1/3. If the molecule axis aligns exactly with the laser polarization direction, 〈cos2θ〉 reaches a maximum of 1. Conversely, when the molecular axis is orthogonal to the laser field’s polarization direction, 〈cos2θ〉 will collapse to 0. The observed values of 〈cos2θ〉 usually fall within the range of 0 to 1, with 1/3 acting as the reference for isotropic distributions.
Alignment processes are classified based on the dynamical mechanisms of laser–molecule interaction [22,29]:
Adiabatic alignment: Achieved by a slowly varying field (τ ≫ Trot), where molecules will adiabatically follow the field, obtaining quasi static alignment dictated by the instantaneous field intensity. In this case, alignment disappears soon after the pulse terminates. This process hinges on continuous torque from the sustained field.
Nonadiabatic alignment: Generated using ultrashort pulses (τ ≪ Trot) or specially phase-modulated long pulses (e.g., abruptly truncated adiabatic pulses). Here, the laser induces rotating wave packets, which evolve freely post-pulse to achieve periodic field-free alignment via quantum interference of rotation states. Typical rotational periods for molecules like N2 and CO2 are around the picosecond range, necessitating femtosecond pulses for control [1,5]. Notably, even pulses with τ > Trot can achieve nonadiabatic alignment through abrupt turn-off profiles or spectral phase engineering, exemplified by V-shaped phase modulation [29].
A recent study on van der Waals clusters expanded alignment dynamics beyond single molecules to weakly bound complexes. Studies on He2 dimers exhibited ultrafast rotational wave packet control by anisotropic laser-dressed potentials [82], whereas Ar2 research by Wu et al. developed alignment revival dynamics governed by polarizability anisotropy [83]. Investigations of N2-Ar clusters found rotational dephasing sensitive to Ar atom geometry (in-plane vs. out-of-plane) and intermolecular vibrational coupling [84]. Work on noble gas dimers further described centrifugal distortion effects during high-J rotational excitation, enabling precise extraction of rotational constants [85]. These findings bridge isolated-molecule alignment to solvated environments through direct interrogation of intermolecular forces.
Building on this foundation, superfluid helium nanodroplets—a prototypical quantum solvated system—provide a platform to probe alignment under controlled dissipation. Impulsive alignment experiments demonstrated that molecular rotation in droplets was slowed by helium coupling, suppressing revival structures due to increased effective inertia (CH3I, [86]). Conversely, adiabatic alignment with rapid pulse truncation yielded field-free alignment of large molecules (e.g., dibromoterthiophene) lasting >10 ps [87], utilizing helium’s low-temperature damping to sustain spatial order. Rotational coherence spectroscopy measured changing rotational constants [88] and centrifugal distortion [89], proving gas-phase-like dynamics with adjusted parameters. Notably, small molecules (D2) aligned nearly freely in droplets [90], while larger systems (I2) exhibited helium-mediated slowing [91]. These advances have established helium droplets as a versatile tool for investigating alignment in dissipative environments and enabling ultrafast imaging of complex systems.

2.2. Advances in Techniques of Strong-Field Molecular Alignment

The rapid development of laser technology stimulates advances in techniques of molecular alignment. By manipulating the essential laser parameters, including pulse sequence, polarization, duration (fs to ps regimes), peak intensity (1012–1014 W/cm2), and spectral bandwidth, quantum-state-resolved control of molecular alignments with sub-angstrom spatial accuracy will be accomplished.

2.2.1. Pulse Sequence Techniques

At the very beginning, single linearly polarized femtosecond pulses were largely used in molecular alignment research, during which alignment degrees were determined via Coulomb explosion imaging [7,8] (e.g., 〈cos2θ〉 mapping through fragment velocity distributions) or weak-field birefringence detection [9,10]. The development of twin pulse techniques constituted a fundamental breakthrough in field-free alignment [11,12,13,14,15,16]. For example, Fleischer et al. produced chirality-dependent unidirectional orientation in HSOH molecules using two cross-polarized pulses to break cylindrical symmetry [11], whereas Corkum’s group achieved an alignment degree of 〈cos2θ〉 ≈ 0.68 for complicated compounds, like iodobenzene [14], by this technique. Subsequent innovations include Zhdanovich et al.’s ’chiral pulse train’ for enantiomer-selective control via incrementally rotated polarization [17], and Cryan et al.’s octet-pulse protocol, which pushed the alignment limit of N2 to 〈cos2θ〉 = 0.75 under ambient conditions [18].

2.2.2. Polarization Modulation Techniques

Beyond conventional pulse sequences, the development of polarization modulation techniques, particularly through elliptically polarized laser fields, has revolutionized molecular alignment by offering multidimensional control [19,20,21,22,23,24,25,26]. These techniques circumvent the planar confinement limitations of linearly polarized fields by decoupling orthogonal electric field components and coupling them to different molecular polarizability axes, allowing for full three-dimensional (3D) spatial locking and extending alignment capabilities to polyatomic systems. The technique leverages the anisotropic polarizability tensor to impose orientation-dependent potentials, in which the major and minor axes of the elliptically polarized field interact with the principal polarizability directions of asymmetric top molecules. Larsen et al., for example, demonstrated that elliptical polarization may limit all three molecular axes of 3,4-dibromothiophene at the same time, with the maximum polarizability axis aligning along the major polarization component and the intermediate axis along the minor component [19]. Subsequent research found that adjusting the ellipticity parameter and inter-pulse delays allows for fine control over both in-field and post-pulse alignment dynamics [20], with Liu et al. demonstrating that optimal field-free 3D alignment necessitates balancing rotational state populations via tailored pulse ellipticity [21]. The efficacy of this technique is demonstrated by Lee et al., who used Coulomb explosion imaging to achieve field-free 3D alignment in SO2 with 〈cos2θx〉 = 0.65 and 〈cos2θy〉 = 0.60 [23]. Underwood et al. then extended this to complex poly-atomics, like ethene, by breaking cylindrical symmetry with orthogonally polarized dual-pulse schemes [24]. These approaches have proven robust against thermal effects, with Lapert et al. demonstrating permanent planar alignment even at elevated rotating temperatures using tailored pulse sequences [22]. Recent improvements in helium nanodroplet settings have further improved alignment precision by maintaining adiabatic-like confinement through the low-temperature dissipation of the super-fluid [25].
Expanding polarization modulation techniques, Wu et al. [26] showed field-free 3D molecular orientation using cross-polarized two-color pulses: A Y-polarized fundamental wave aligns the major axis via polarizability anisotropy, whereas a Z-polarized second harmonic orients the minor axis through hyperpolarizability. Phase control (φ1) reverses the orientation direction, enabling all-optical 3D control without static fields—a critical leap toward chiral-resolved applications.

2.2.3. Pulse Shaping and Hybrid Methods

By precisely controlling rotational wave packets, pulse shaping techniques have made it possible to create customized optical fields for improved molecular alignment in addition to polarization modulation [27,28,29,30,31,32,33,34,35]. Important applications include single-cycle THz pulses, which use the dynamic Stark effect to align linear molecules, like OCS, without the need for a field, with alignment degrees greater than 〈cos2θ〉 = 0.5 in ambient settings [27,28]. As evidenced by a 50% improvement in CO alignment (〈cos2θ〉 = 0.67) via selective rotational state coupling, V-shaped spectral phase modulation has become a potent technique for alignment efficiency optimization [29,30]. Studies of extreme rotational dynamics and centrifugal distortion have been made possible by the successful acceleration of diatomic molecules, such as O2, to hyper-rotational states (J = 50 ℏ), using optical centrifuges that use chirped circularly polarized pulses [31,32].
Furthermore, hybrid schemes synergize distinct temporal and polarization properties of multiple fields, offering precise control over molecular axes for applications in ultrafast imaging and stereodynamics [33,34,35,36]. For instance, hybrid approaches incorporating electrostatic fields with elliptically polarized ns-to-fs laser pulses, as shown by Takei et al. [33], enable field-free orientation by adiabatically preparing rotational wave packets before rapid truncation. Similarly, Mullins et al. demonstrated strong 3D alignment of indole (C8H7N) with 〈cos2δ〉 = 0.89 using elliptically polarized, truncated fs pulses, exploiting the interplay between adiabatic shaping and impulsive kicks to enhance post-pulse alignment [34]. Complementary strategies, such as combining THz pulses with pre-alignment via two-color fs pulses, leverage quantum interference to amplify orientation [35,36]. By combining the rapid control of fs pulses with the resonant rotational excitation of THz fields, these methods overcome multi-axis alignment challenges.
The integration of pulse shaping techniques with rotational echo phenomena has emerged as a pivotal strategy for ultrafast molecular control. By leveraging tailored pulse sequences (e.g., time-delayed cross-polarized kicks), alignment echoes enable sub-picosecond tracking of collisional decoherence, challenging classical approximations in thermal relaxation [37]. Recent breakthroughs include k-alignment echoes produced by circularly polarized fields, which reveal polar-azimuthal coupling via 4π phase-space analysis [38], and multidimensional echo variants—fractional, spatially rotational, and imaginary echoes—visualized by Coulomb explosion imaging [39,40]. These methods have been successfully applied to high-density gases, quantifying collisional decay rates (τE ≈ 77 ps amagat) under extreme pressures [41], thereby bridging quantum-resolved dynamics with macroscopic molecular interactions.

2.2.4. Theoretical Advances

Theoretical discoveries have explained the fundamental physics of laser alignment. By studying initial rotational state populations [42], pulse duration effects [44], and angular momentum coupling [44], models quantify the interplay between molecule polarizability anisotropy and laser polarization matching. Integrated with experimental data, these frameworks decode control mechanisms in multi-color resonant fields [45], THz pulse trains [46,47,48], and biochromatic settings [49,50], while linking molecular structures (e.g., polarizability tensors [51] with alignment efficiency—achieving prediction accuracies within 5% errors.

3. Strong-Field Molecular Alignment: Applications

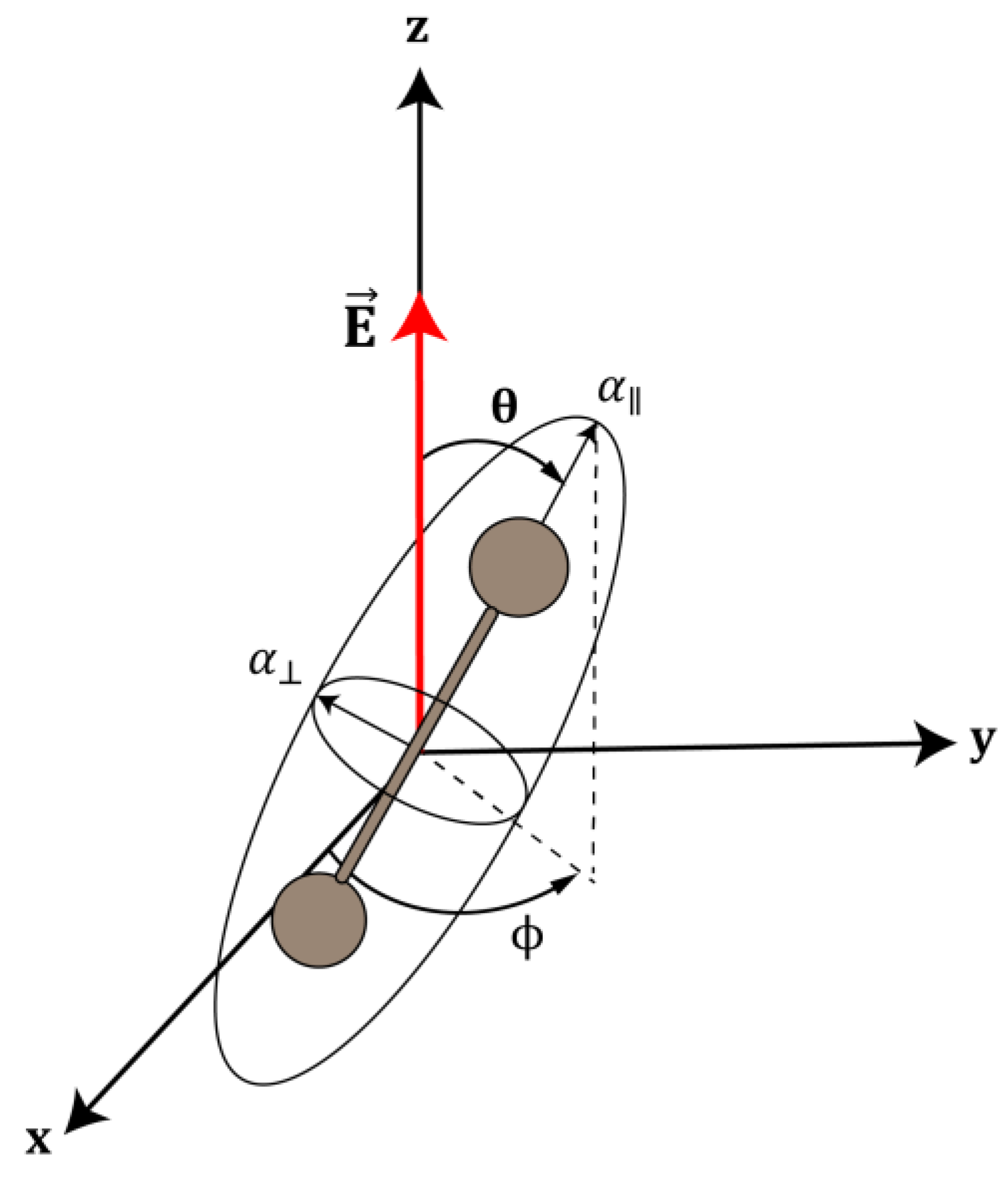
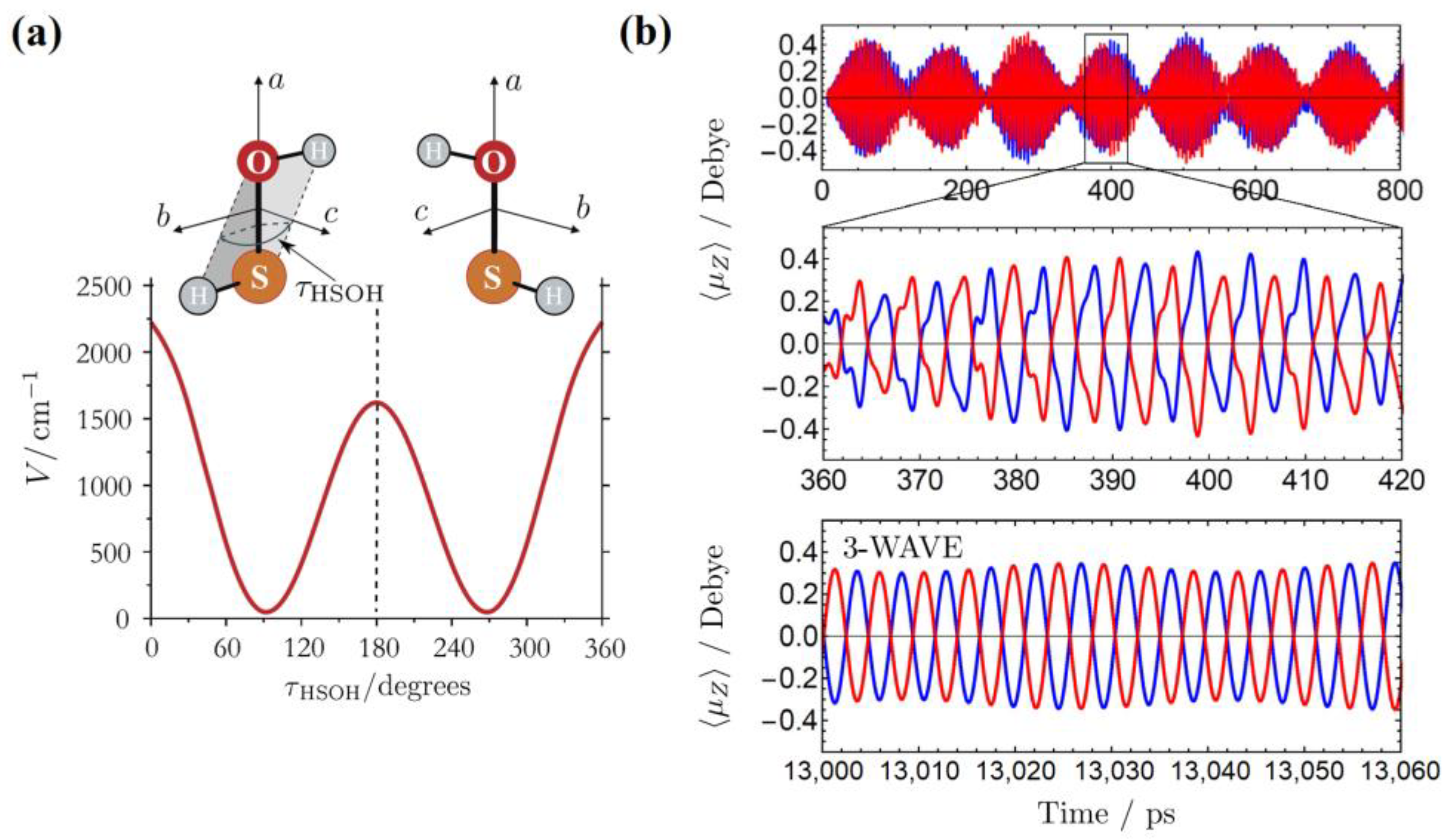
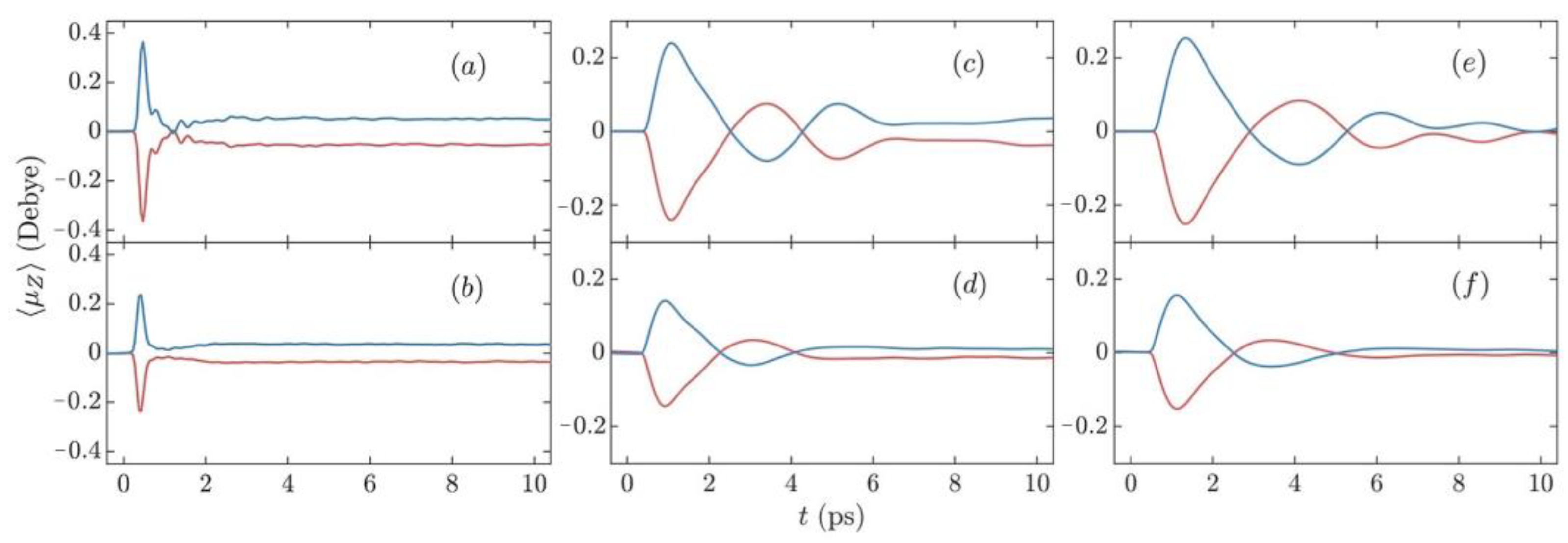
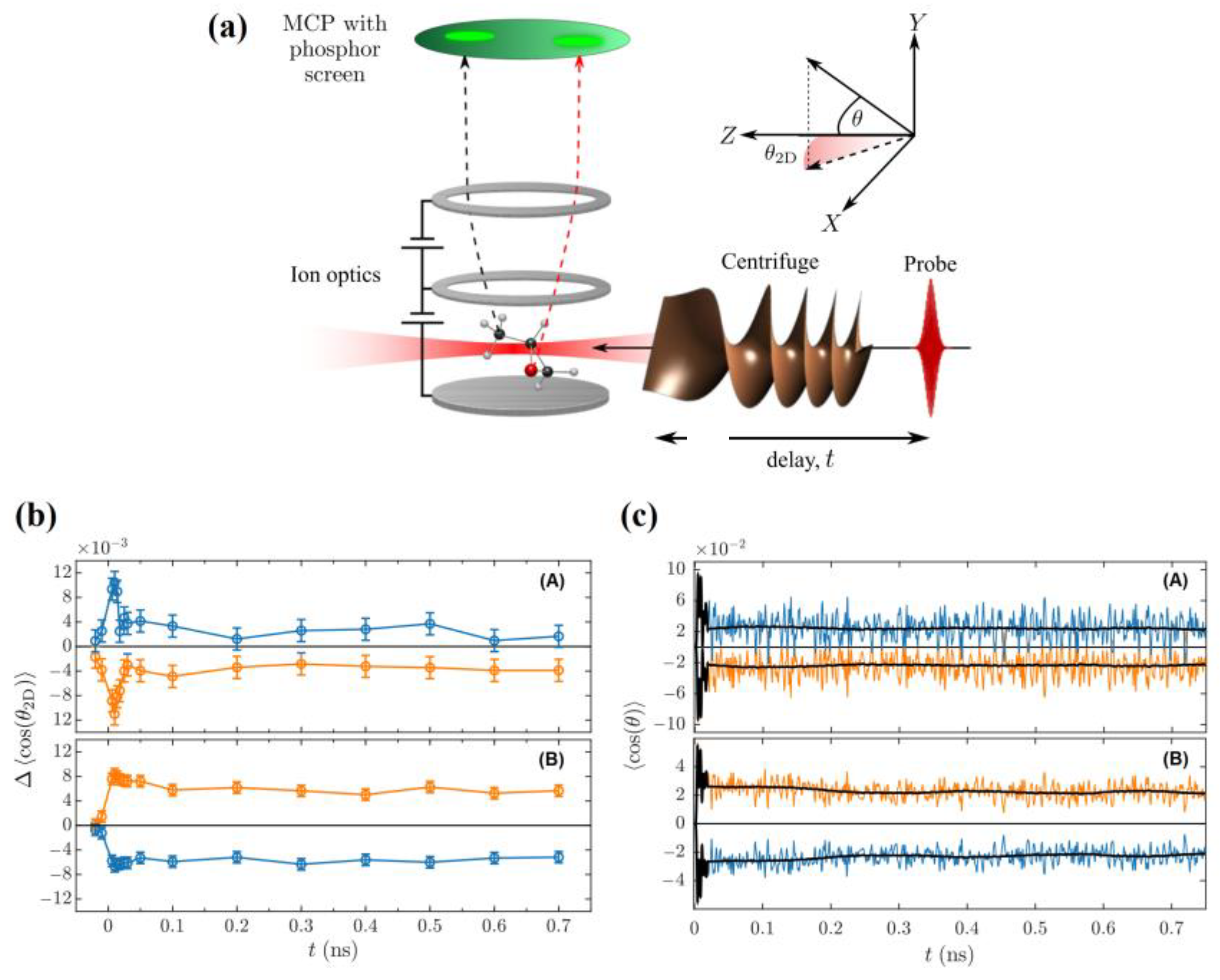
3.1. Enantioselective Orientation of Chiral Molecules

Since the thalidomide catastrophe in the 1960s [92], thorough enantiomeric purity control has become a cornerstone of pharmaceutical science. Unlike isotropic molecular ensembles, oriented chiral systems amplify stereochemical discrimination by transforming minor parity discrepancies into observable signals [52,53,54,55,56,57,58]. While standard linearly polarized lasers orient molecules via dipole torque (〈cos2θ〉 ∝ E2), enantiomer distinction necessitates chirality-sensitive field interactions [55]. Building upon Fleischer’s double-pulse framework [11], Yachmenev and Yurchenko demonstrated that cross-polarized double pulses cause chirality-dependent dynamics [52]. They utilized a first pulse aligning the primary axis (e.g., HSOH a-axis, Figure 2a), followed by a delayed second pulse at 45° that leverages enantiomeric differences in off-diagonal polarizability components (Δαac) to create π-phase-shifted dipole oscillations 〈μz〉, as seen in Figure 2b. Numerical calculations indicate perfect anti-phase dipole oscillations between HSOH enantiomers under double-pulse excitation. This phase contrast enables microwave three-wave mixing to identify enantiomeric excess below 10−7 via rotational transition interferometry [53].
Twisted polarization fields, demonstrated by optical centrifuges [54,55,56,57], signifies a paradigm change from phase modulation to angular momentum manipulation in chiral molecule orientation. Averbukh et al. provided theoretical foundations for regulating molecule rotation using twisted polarization fields [54]. They demonstrated that crossed linear-polarized laser pulses induced unidirectional torque along the most polarizable axis of asymmetric chiral molecules via off-diagonal polarizability components (e.g., αac). This classical mechanism predicted the transient orientation of enantiomers with opposite dipole oscillations, directly connecting molecular chirality to polarization-induced torque. Building on this theory, Averbukh et al. [55,56] later employed optical centrifuge with accelerated rotating polarization (β = 0.05 rad/ps2) to drive propylene oxide (PPO) molecules into unidirectional rotation about their principal b-axis, while inducing enantiomer-specific permanent orientation via off-diagonal polarizability components (e.g., αac), as shown in Figure 3c,d. The experimental findings reveal that this orientation remained over 700 ps under field-free conditions (Figure 4b,c), with opposing 〈cos2θ〉 values for (R)- and (S)-PPO enantiomers, directly connected to the sign reversal of αac. The directional preference of the molecular axis was substantiated by Coulomb explosion imaging of O+/C+ fragment velocity anisotropy, as depicted in Figure 4a, where velocity maps revealed enantiomer-dependent 〈sinθ2D〉 asymmetries [55,57]. Quantum mechanical simulations, as shown in Figure 4c, confirmed the rigid-rotor model, exhibiting quantitative agreement between the estimated 〈μZ〉 dynamics and the experimental results.
Dynamic nanoconfinement approaches have opened new possibilities in interfacial chiral analysis [58]. For example, self-assembly of ISODBA inside tunneling microscopy (STM)-fabricated nanocorrals indicated that anisotropic alignment of alkyl chains under spatial confinement violates chiral symmetry, encouraging preferential production of a single enantiomorph. This phenomenon emerges from synergistic effects between tip-induced directional perturbations and molecule–substrate electronic interaction, providing innovative techniques for surface chiral catalysis and separation. Optical centrifuges enable enantiomer-resolved bulk detection, while nanoconfinement facilitates interfacial chirality manipulation. These techniques bridge gas-phase spectroscopy and surface science, both critical for developing asymmetric synthesis and medication safety measures.

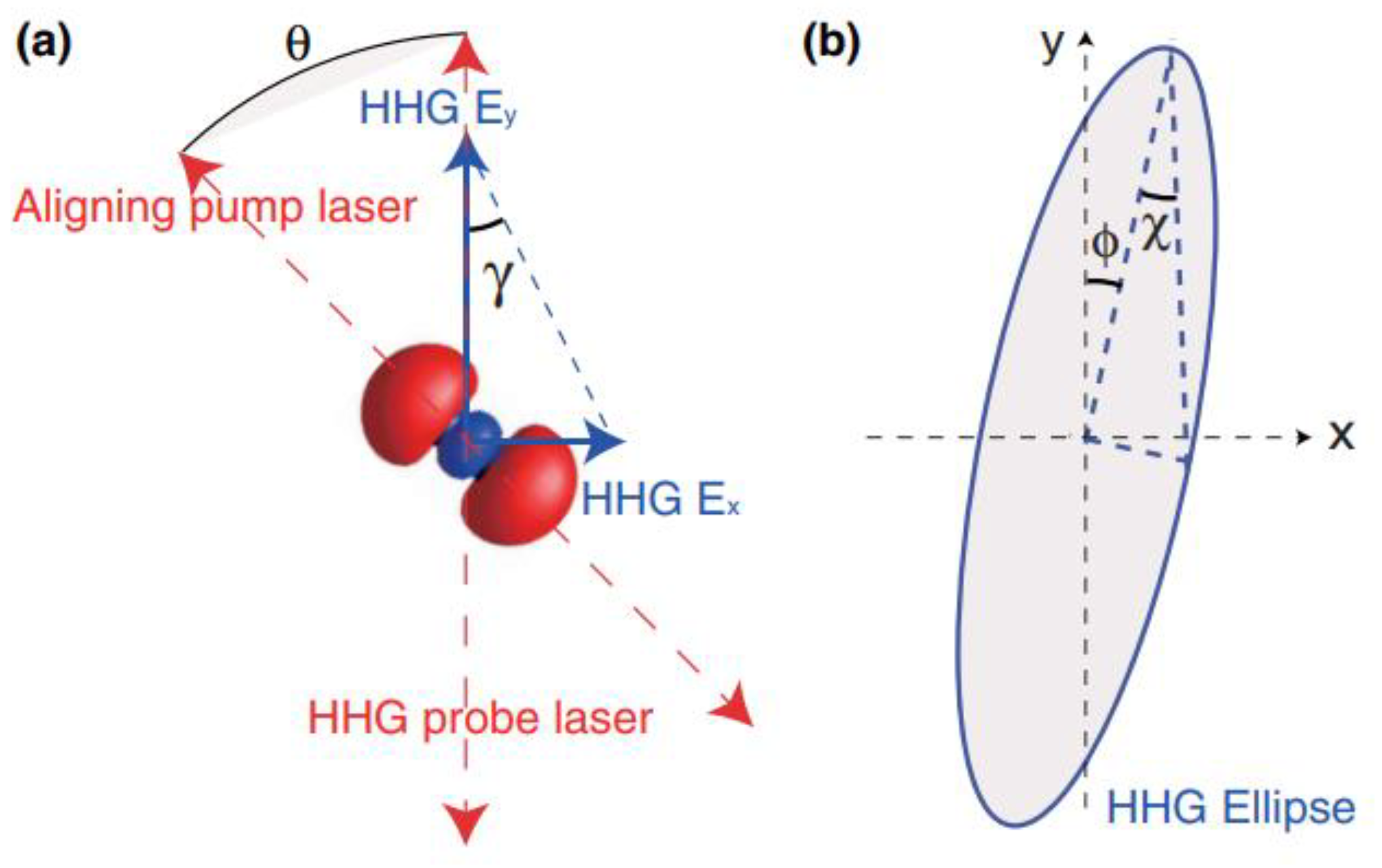
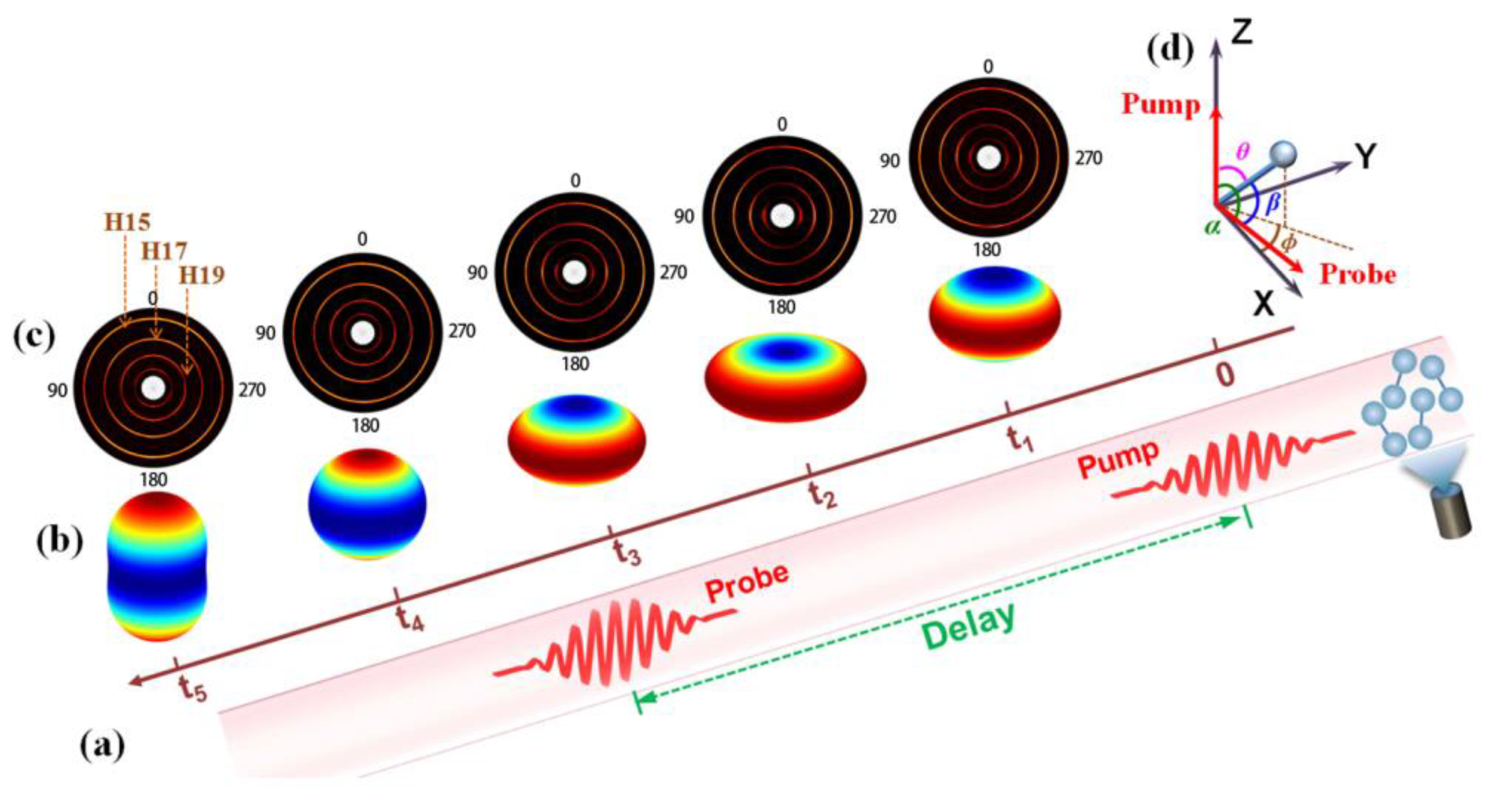
3.2. Alignment-Dependent HHG

In ultrafast dynamics of intense laser field–matter interactions, HHG serves as a unique instrument for studying molecular structure and electron mobility. Gas-phase HHG can be represented by the three-step model [93], whose basic mechanism incorporates laser-induced electron tunneling, acceleration, and recollision radiation. Critically, the chance of electron recollision considerably increases when the driving field is linearly polarized or exhibits low ellipticity. For anisotropic molecular systems, ionization efficiency and harmonic radiation intensity substantially depend on the angle between the molecular axis and the laser polarization direction [59]. Consequently, precise regulation of molecular alignment has become important for researching alignment-dependent HHG [60,61,62,63,64].
The work of Velotta et al., in 2001 [59], first accomplished spatial alignment of high-density gas-phase molecules (CS2, N2) and indicated considerable HHG modulation by molecular orientation. By coupling a 300 ps linearly polarized pump pulse with a 70 fs probe pulse, their experiments indicated that HHG intensity dramatically increased with enhanced molecular alignment. However, for CO2 molecules, vertical alignment sup-pressed harmonic emission, attributable to the anisotropic dipole phase φdip ∝ (Up − Ip) τs, where Up is the ponderomotive potential, Ip is the ionization potential, and τs the recollision time [59]. Subsequent investigations further demonstrated that short-pulse-induced realignment and phase-matching effects during propagation also influenced harmonic yield [64].
Molecular alignment not only regulates HHG strength but also governs the participation of various orbitals. For instance, McFarland et al. [60] observed that when the N2 molecular axis was perpendicular to the laser polarization, the contribution of the second-highest occupied molecular orbital (HOMO-1) dominated the harmonic cutoff zone. The essential aspects for this approach include (1) extending the harmonic cutoff to shorter wavelengths compared to isotropic ensembles; (2) maximal emission intensity at a 90° angle between the molecule axis and laser polarization; and (3) noticeable impacts near the cutoff area. This underscores the important significance of lower-orbital electron dynamics in aligned-molecule HHG and suggests paths for orbital-selective probing.
Molecular alignment also enhances the polarization properties of HHG beyond conventional limits. In 2009, Zhou et al. [61] experimentally established that linearly polarized laser-driven aligned N2 molecules emit elliptically polarized harmonics with ellipticity up to 0.35 (21st harmonic order). This arises from alignment-induced anisotropy in the recombination dipole moment. Deviations of the molecular axis from the laser polarization direction generate a phase difference (Δϕ) between the parallel and perpendicular dipole components, leading to elliptical polarization, as seen in Figure 5. Further theoretical work [62] demonstrated that the polarization states of harmonics from aligned N2, CO2, and O2 can be accurately predicted using the quantitative rescattering (QRS) model, with ellipticity dictated by Δϕ and alignment distributions.
Conversely, due to the inherent link between HHG and molecular alignment, HHG can be utilized as a sensitive probe to evaluate molecular alignment dynamics. In 2019, He et al. proposed a machine learning-based angle-resolved high-order-harmonic spectroscopy (HHS) technique to resolve the spatiotemporal evolution of molecular alignment [63]. By applying a simulated annealing (SA) approach to reverse femtosecond-resolved harmonic angular distributions, they effectively recreated the dynamics of rotational wave packets in N2. For example, at 4.2 ps (half revival, antialignment) and 8.45 ps (full revival, alignment), the wave packets exhibited disk-like and cigar-like distributions, respectively, accompanied by clockwise rotation, as indicated in Figure 6. Similarly, Jiang et al. [64] derived transient alignment distributions of CO2 from HHG spectra using a genetic approach. This approach minimized propagation effects and multi-orbital interference, obtaining 〈cos2θ〉 retrieval errors below 5%.
Thus, precise control and detection of molecular alignment provide multidimensional insights into HHG: (1) selective enhancement of specific orbital contributions via alignment tuning; (2) analysis of recombination dipole anisotropy through harmonic polarization states; and (3) real-time tracking of rotational wave packet dynamics via machine learning and ultrafast imaging. These discoveries not only deepen our understanding of strong-field molecular dynamics but also set the framework for attosecond spectroscopy and molecular orbital tomography.

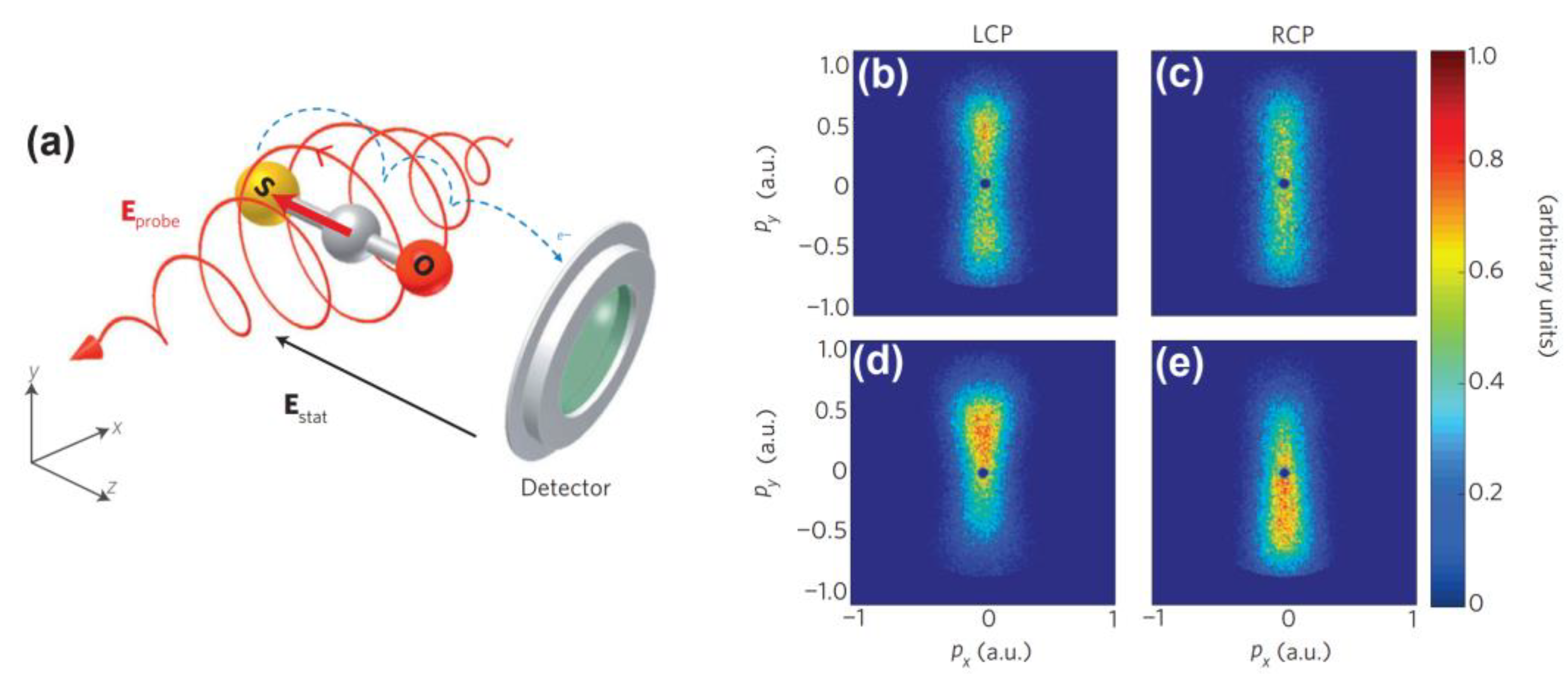
3.3. PADs and Ionization Efficiency via Molecular Alignment

Molecular alignment serves as a valuable technique for examining the anisotropy of PADs and ionization kinetics. When the molecule axis forms a certain angle with the laser polarization direction, ionization channels of differing symmetries (e.g., σ vs. π orbitals) are preferentially active, resulting in substantial directional dependency in ionization cross-sections [65,66,67]. This alignment-dependent variation in ionization efficiency directly governs the spatial patterns of photoelectron momentum distributions (e.g., six-lobe interference in H2+ or double-peak structures in CO2), offering a dynamic probe for resolving molecular orbital symmetry, internuclear distances, and electronic transition mechanisms [68,69].
For polar molecules, the interaction between their permanent dipole moment and a large static electric field (>50 kV/cm) creates “pendular states”, permitting brute-force orientation of molecular ensembles [65]. Li et al. selected pyridazine as a model system due to its strong permanent dipole moment (4 Debye) in the ground state and rotationally resolved ultraviolet absorption spectra, which permitted the simultaneous determination of the supersonic beam’s rotational temperature (2 K) [65]. Their experiments demonstrated a 40% enhancement in ionization efficiency when the resonant laser polarization was switched from parallel to perpendicular relative to the alignment field, confirming the alignment-dependent matching between the transition dipole moment (perpendicular to the molecular axis) and laser polarization. Furthermore, the association between molecular alignment and ionization cross-sections has been verified in polyatomic systems [67,68]. Transiently aligned N2 and CO2 displayed distinct anisotropy in single-photon ionization: N2 showed the greatest ionization when aligned perpendicular to the laser polarization (Figure 7c, left panel), and despite the different orbital symmetries (σg for N2 vs. πg for CO2), CO2 also displayed maximum ionization in the perpendicular alignment (Figure 7d, right panel). This shared perpendicular preference arises because the transition dipole orientations (perpendicular to the molecular axis) and the symmetry of high-energy continuum states dominate the ionization dynamics, overriding the initial orbital symmetry differences. Theoretical simulations suggest that molecular alignment modifies angular channel-specific cross-sections (e.g., Σ vs. Π transitions), thus defining the macroscopic PAD properties [67,69].
Moreover, time-resolved photoelectron imaging of pyridazine’s S1 state (π→3s transition) revealed rotational wave packet revivals (82 ps period), where angular modulations in PAD distinctly differentiated nodal features of the π* and 3s orbitals [70]. This highlights that PADs from aligned molecules under weak-field settings (~1014 W/cm2) operate as direct fingerprints of orbital symmetry. For strong-field ionization, Holmegaard et al. [66] offered two methods for molecular-frame PAD measurement: (i) post-ionization alignment using dissociative ionization, and (ii) pre-alignment employing coupled electrostatic and laser fields, followed by ionization. The latter technique, applied to three-dimensionally aligned benzonitrile, demonstrated decreased electron emission inside the molecular plane (Figure 8e), showing the spatial confinement effect of orbital nodes on PADs. Additionally, alignment-dependent control over circularly polarized photoionization asymmetry was revealed [66]. Pre-aligned OCS molecules displayed mirror-asymmetric electron momentum distributions under left/right circularly polarized pulses, with the asymmetry amplitude amplifying with improved alignment (Figure 8d,e). This effect comes from Stark shifts generated by interactions between the permanent dipole moment and the laser field, which modulate ionization thresholds and disrupt spatial symmetry. Such alignment-tunable chiral responses provide novel options for spin-polarized electron source design.
The regulating effect of molecular alignment extends to multiphoton ionization dynamics in excited states [71]. In resonance-enhanced multiphoton ionization (REMPI) of LiH, pre-alignment in the ground state boosts ionization probability, but excited-state alignment may decrease it due to orbital symmetry mismatch. Furthermore, asymmetry in momentum spectra caused by pre-alignment verifies the recording of molecular-frame information via angular interference effects. Recent research on H2+ under attosecond severe UV pulses [69] discovered alignment sensitivity dependents on inter-nuclear distance Rc: At equilibrium (Rc = 2 a.u.), a modest 4° misalignment tilts the six-lobe interference pattern; however, at Rc = 4 a.u., reduced disparity between the σ and π channel cross-sections diminishes alignment responsiveness. This underlines the multiscale interplay between molecular alignment and electrical structure, enhancing theoretical frameworks for attosecond molecular imaging.

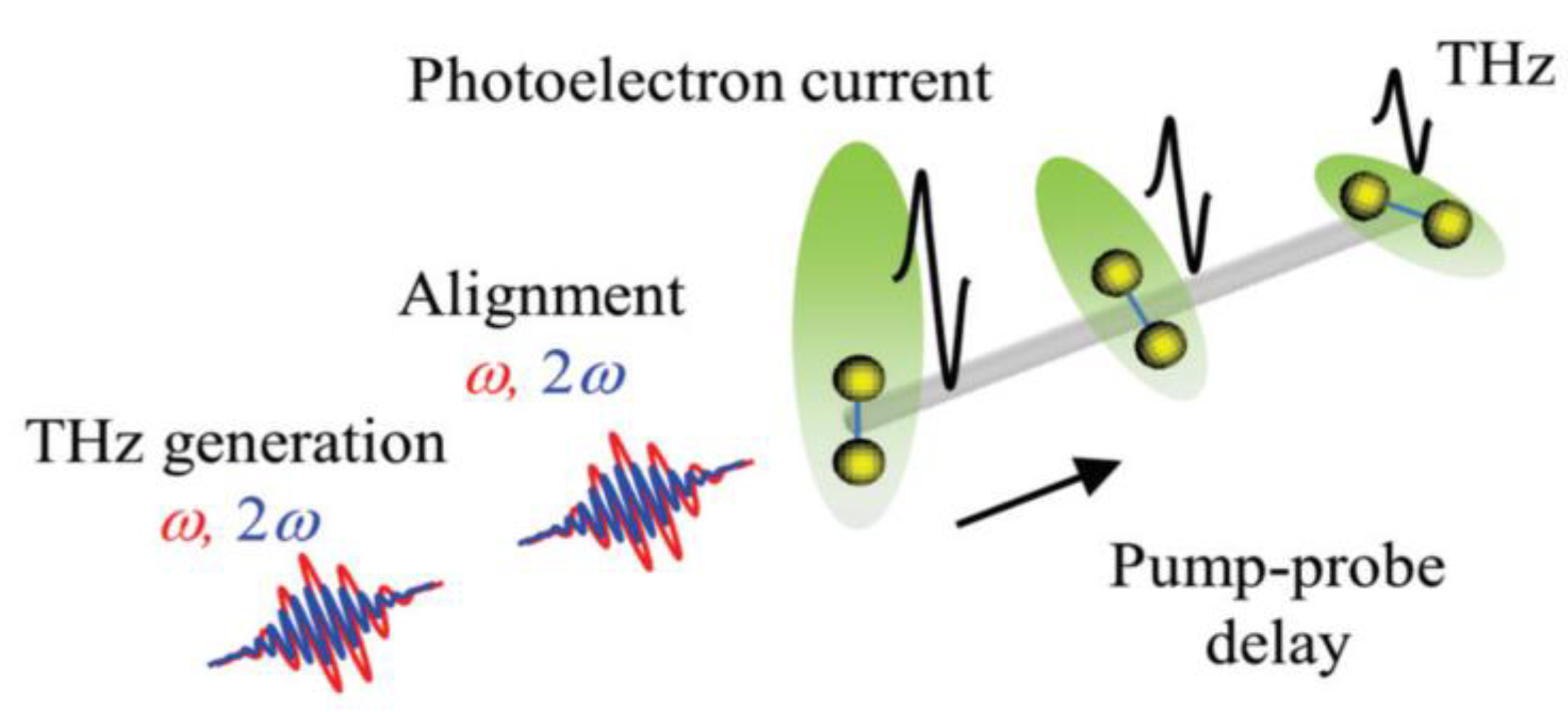
3.4. Alignment-Dependent THz Generation and Control

The THz band, positioned between microwave and infrared areas, exhibits unique resonance with molecular vibrational and rotational transitions, serving as a distinctive probe for exploring electromagnetic responses in complex media, nanostructures, and extreme field conditions. In recent years, laser-induced plasma filamentation for THz generation has attracted substantial attention due to its potential for remote radiation administration, particularly in non-destructive biomedical imaging applications. Molecular alignment technology, as a pivotal technique to regulate THz radiation [72,73,74,75,76,77,78], provides precise control of molecule–laser interactions [83,84], enabling unprecedented insights into THz-producing mechanisms and molecular structural information.
Orientation-dependent modulation of THz yields via ionization rate anisotropy has been experimentally confirmed in two-color laser-induced plasma generation schemes [72,73]. Kim et al. reported that nitrogen molecules oriented parallel to the two-color field polarization demonstrated 3–4 times larger ionization rates, greatly enhancing plasma currents and THz emission intensity [72]. As seen in Figure 9, their experimental approach featured a pump–probe configuration: a pre-aligning rotating Raman pump pulse caused temporary molecular orientation, followed by two-color ionization during field-free molecular revival phases (e.g., half-revival at ~4.1 ps). Through delay-dependent THz waveform observations coupled with plasma current modeling, they established quantitative connections between THz yields and molecular alignment distributions. This work revealed that molecular alignment not only governs ionization thresholds but also influences THz spatiotemporal properties through electron acceleration path modulation. Theoretical advancements by time-dependent Schrödinger equation (TDSE) simulations objectively examined the impact of appropriate THz phase delays and yields on two-color field characteristics (intensity, wavelength, and pulse duration), highlighting the dominance of tunneling ionization [73]. Below the ionization threshold (γ > 1, γ: Keldysh parameter), THz generation predominantly occurs via four-wave mixing, with optimal phase delays approaching 0 or π. In the tunneling domain (γ < 1), soft electron recollisions dominate THz emission, shifting optimal delays to ~0.6π. These models establish physical foundations for THz optimization via molecular alignment.
Polarization control of THz radiation extends beyond yield modulation via align-ment. Zeng’s group at East China Normal University [74,75] performed all-optical THz polarization manipulation in air utilizing two-color fields (800 nm + 400 nm) coordinated with molecular alignment revivals. This technique incorporates alignment-induced anisotropic refractive index changes, which synergistically influence two-color propagation through cross-phase modulation (XPM) and plasma defocusing effects. By temporally matching two-color pulses with molecular revival times (e.g., full revival of N2 at ~8.5 ps), they demonstrated THz polarization rotation, yielding linearly or elliptically polarized radiation. Of special relevance, Béjot et al. implemented a novel “transient wave-plate” effect (Figure 10) using argon plasma filament birefringence (from polarization-dependent nonlinear refractive indices), theoretically extending molecular alignment concepts to plasma systems [76]. This effect originates from the alignment-induced anisotropy of the third-order nonlinear susceptibility (χ(3)), which modulates the refractive index tensor in the plasma filament—a microscopic mechanism rigorously derived in Béjot et al.’s original work [76]. For a comprehensive theoretical analysis of alignment–plasma coupling, we refer readers to dedicated studies on ultrafast nonlinear optics.
Synergistic THz-HHG observations further confirmed alignment–THz relationships. Huang et al. [77] achieved synchronized detection of THz and HHG from aligned N2 molecules, revealing mutual orientation-dependent yields connected to the highest occupied molecular orbital (HOMO) symmetry. Their technology integrated electro-optic sampling with X-ray spectroscopy, enabling angle-resolved photoionization cross-section (PICS) retrieval through pump–probe angular scans. This technique bypassed classic ionization detection density restrictions by employing THz signals for ionization rate calibration, enabling novel pathways for molecular orbital imaging.
Theoretical improvements come from Wang’s team [78], who constructed a genetic algorithm-based inversion framework founded in the photocurrent model. By expanding molecular alignment distributions as polynomial functions and optimizing against angle-dependent THz yields, they effectively reconstructed alignment functions ρ(θ) for N2 and O2. This accomplishment underscores THz radiation’s sensitivity to orientation distributions, establishing it as a robust diagnostic tool for molecular alignment characterization.

4. Conclusions

In conclusion, we systematically traced the evolution of molecular alignment under strong laser pulses, confirming its critical role in decoding light–matter anisotropy. Molecular alignment breaks isotropic symmetry, enabling chiral detection with sensitivity beyond 10−7 and orbital-resolved high-harmonic imaging to map electronic structures. Equally transformational is its potential for quantum-state management, exemplified by 3D spatial locking of challenging asymmetric tops, like indole (〈cos2δ〉 > 0.89), which serves as a cornerstone for grasping ultrafast reaction dynamics. Looking forward, the confluence of machine learning-driven alignment retrieval and attosecond angular streaking offers atomic-resolution molecular movies. Future efforts should heat decoherence in poly-atomic systems and propose universal metrics for 3D alignment characterization. Emerging technologies, such as tailored pulse optimization and ultrafast X-ray free-electron lasers, may further unravel sub-femtosecond alignment dynamics. These advancements are expected to enhance precision metrology and quantum-controlled chemistry.

Author Contributions

Conceptualization, Y.L.; methodology, Y.L.; formal analysis, Y.L. and Q.L.; resources, Y.L. and Q.L.; funding acquisition, Y.L. and Q.L.; writing—original draft preparation, M.W. and E.Z.; writing—review and editing, Q.L. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (11904232, 12034013) and the Shanghai Science and Technology Commission (22ZR1444100).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Normand, D.; Lompre, L.; Cornaggia, C.; Physics, O. Laser-induced molecular alignment probed by a double-pulse experiment. J. Phys. B 1992, 25, L497. [Google Scholar] [CrossRef]
  2. Stapelfeldt, H.; Seideman, T. Colloquium: Aligning molecules with strong laser pulses. Rev. Mod. Phys. 2003, 75, 543–557. [Google Scholar] [CrossRef]
  3. Xu, N. One-Dimensional Molecular Alignment Induced by Femtosecond Laser Pulses. Ph.D. Thesis, Peking University, Beijing, China, 2008. [Google Scholar]
  4. Friedrich, B.; Herschbach, D. Alignment and trapping of molecules in intense laser fields. Phys. Rev. Lett. 1995, 74, 4623–4626. [Google Scholar] [CrossRef]
  5. Liu, F.C. Rotational State Selection and Alignment/Orientation of Molecules in External Fields. Ph.D. Thesis, Jilin University, Changchun, China, 2006. [Google Scholar]
  6. Spanner, M. Field-Free Alignment and Strong Field Control of Molecular Rotors. Ph.D. Thesis, University of Waterloo, Waterloo, ON, USA, 2004. [Google Scholar]
  7. Dooley, P.W.; Litvinyuk, I.V.; Lee, K.F.; Rayner, D.M.; Spanner, M.; Villeneuve, D.M.; Corkum, P.B. Direct imaging of rotational wave-packet dynamics of diatomic molecules. Phys. Rev. A 2003, 68, 023406. [Google Scholar] [CrossRef]
  8. De, S.; Znakovskaya, I.; Ray, D.; Anis, F.; Johnson, N.G.; Bocharova, I.A.; Magrakvelidze, M.; Esry, B.D.; Cocke, C.L.; Litvinyuk, I.V.; et al. Field-free orientation of CO molecules by femtosecond two-color laser fields. Phys. Rev. Lett. 2009, 103, 153002. [Google Scholar] [CrossRef] [PubMed]
  9. Renard, V.; Faucher, O.; Lavorel, B. Measurement of laser-induced alignment of molecules by cross defocusing. Opt. Lett. 2005, 30, 70–72. [Google Scholar] [CrossRef]
  10. Xu, N.; Wu, C.; Gao, Y.; Jiang, H.; Yang, H.; Gong, Q. Measurement of the field-free alignment of diatomic molecules. J. Phys. Chem. A 2008, 112, 612–617. [Google Scholar] [CrossRef]
  11. Fleischer, S.; Khodorkovsky, Y.; Prior, Y.; Sh Averbukh, I. Controlling the sense of molecular rotation. New J. Phys. 2009, 11, 105039. [Google Scholar] [CrossRef]
  12. Hoque, M.Z.; Lapert, M.; Hertz, E.; Billard, F.; Sugny, D.; Lavorel, B.; Faucher, O. Observation of laser-induced field-free permanent planar alignment of molecules. Phys. Rev. A 2011, 84, 013409. [Google Scholar] [CrossRef]
  13. Lin, K.; Song, Q.; Gong, X.; Ji, Q.; Pan, H.; Ding, J.; Zeng, H.; Wu, J. Visualizing molecular unidirectional rotation. Phys. Rev. A 2015, 92, 013410. [Google Scholar] [CrossRef]
  14. Lee, K.F.; Litvinyuk, I.V.; Dooley, P.W.; Spanner, M.; Villeneuve, D.M.; Corkum, P.B. Two-pulse alignment of molecules. J. Phys. B 2004, 37, L43–L48. [Google Scholar] [CrossRef]
  15. Bloomquist, C.; Zhdanovich, S.; Milner, A.A.; Milner, V. Directional spinning of molecules with sequences of femtosecond pulses. Phys. Rev. A 2012, 86, 063413. [Google Scholar] [CrossRef]
  16. Fleischer, S.; Averbukh, I.S.; Prior, Y. Selective control of molecular rotation. J. Phys. B 2008, 41, 074018. [Google Scholar] [CrossRef]
  17. Zhdanovich, S.; Milner, A.A.; Bloomquist, C.; Floss, J.; Averbukh, I.; Hepburn, J.W.; Milner, V. Control of molecular rotation with a chiral train of ultrashort pulses. Phys. Rev. Lett. 2011, 107, 243004. [Google Scholar] [CrossRef]
  18. Cryan, J.P.; Bucksbaum, P.H.; Coffee, R.N. Field-free alignment in repetitively kicked nitrogen gas. Phys. Rev. A 2009, 80, 063412. [Google Scholar] [CrossRef]
  19. Larsen, J.J.; Sakai, H.; Safvan, C.P.; Wendt-Larsen, I.; Stapelfeldt, H. Aligning molecules with intense nonresonant laser fields. J. Chem. Phys. 1999, 111, 7774–7781. [Google Scholar] [CrossRef]
  20. Larsen, J.J.; Hald, K.; Bjerre, N.; Stapelfeldt, H.; Seideman, T. Three dimensional alignment of molecules using elliptically polarized laser fields. Phys. Rev. Lett. 2000, 85, 2470–2473. [Google Scholar] [CrossRef]
  21. Jingsong Liu, J.L.; Qiyuan Cheng, Q.C.; Daguang Yue, D.Y.; Xucong Zhou, X.Z.; Qingtian Meng, Q.M. Dynamical analysis of the effect of elliptically polarized laser pulses on molecular alignment and orientation. Chin. Opt. Lett. 2018, 16, 103201. [Google Scholar] [CrossRef]
  22. Lapert, M.; Hertz, E.; Guérin, S.; Sugny, D. Field-free permanent molecular planar alignment. Phys. Rev. A 2009, 80, 051403. [Google Scholar] [CrossRef]
  23. Lee, K.F.; Villeneuve, D.M.; Corkum, P.B.; Stolow, A.; Underwood, J.G. Field-free three-dimensional alignment of polyatomic molecules. Phys. Rev. Lett. 2006, 97, 173001. [Google Scholar] [CrossRef]
  24. Underwood, J.G.; Sussman, B.J.; Stolow, A. Field-free three dimensional molecular axis alignment. Phys. Rev. Lett. 2005, 94, 143002. [Google Scholar] [CrossRef] [PubMed]
  25. Chatterley, A.S.; Shepperson, B.; Stapelfeldt, H. Three-Dimensional Molecular Alignment Inside Helium Nanodroplets. Phys. Rev. Lett. 2017, 119, 073202. [Google Scholar] [CrossRef]
  26. Lin, K.; Tutunnikov, I.; Qiang, J.; Ma, J.; Song, Q.; Ji, Q.; Zhang, W.; Li, H.; Sun, F.; Gong, X. All-optical field-free three-dimensional orientation of asymmetric-top molecules. Nat. Commun. 2018, 9, 5134. [Google Scholar] [CrossRef] [PubMed]
  27. Machholm, M.; Henriksen, N.E. Field-free orientation of molecules. Phys. Rev. Lett. 2001, 87, 193001. [Google Scholar] [CrossRef]
  28. Fleischer, S.; Zhou, Y.; Field, R.W.; Nelson, K.A. Molecular orientation and alignment by intense single-cycle THz pulses. Phys. Rev. Lett. 2011, 107, 163603. [Google Scholar] [CrossRef]
  29. Xu, S.; Yao, Y.; Lu, C.; Ding, J.; Jia, T.; Zhang, S.; Sun, Z. Manipulating field-free molecular alignment byV-shaped femtosecond laser pulses. Phys. Rev. A 2014, 89, 053420. [Google Scholar] [CrossRef]
  30. Huang, Y.; Xu, S.; Zhang, S. Selective excitation and control of the molecular orientation by a phase shaped laser pulse. RSC Adv. 2016, 6, 100295–100299. [Google Scholar] [CrossRef]
  31. Karczmarek, J.; Wright, J.; Corkum, P.; Ivanov, M. Optical Centrifuge for Molecules. Phys. Rev. Lett. 1999, 82, 3420–3423. [Google Scholar] [CrossRef]
  32. Milner, A.A.; Korobenko, A.; Milner, V. Field-free long-lived alignment of molecules with a two-dimensional optical centrifuge. Phys. Rev. A 2016, 93, 053408. [Google Scholar] [CrossRef]
  33. Takei, D.; Mun, J.H.; Minemoto, S.; Sakai, H. Laser-field-free three-dimensional molecular orientation. Phys. Rev. A 2016, 94, 013401. [Google Scholar] [CrossRef]
  34. Mullins, T.; Karamatskos, E.T.; Wiese, J.; Onvlee, J.; Rouzee, A.; Yachmenev, A.; Trippel, S.; Kupper, J. Picosecond pulse-shaping for strong three-dimensional field-free alignment of generic asymmetric-top molecules. Nat. Commun. 2022, 13, 1431. [Google Scholar] [CrossRef] [PubMed]
  35. Shu, C.-C.; Henriksen, N.E. Field-free molecular orientation induced by single-cycle THz pulses: The role of resonance and quantum interference. Phys. Rev. A 2013, 87, 013408. [Google Scholar] [CrossRef]
  36. Liu, Y.; Li, J.; Yu, J.; Cong, S.-L. Field-free molecular orientation by two-color shaped laser pulse together with time-delayed THz laser pulse. Laser Phys. Lett. 2013, 10, 076001. [Google Scholar] [CrossRef]
  37. Ma, J.; Zhang, H.; Lavorel, B.; Billard, F.; Hertz, E.; Wu, J.; Boulet, C.; Hartmann, J.-M.; Faucher, O. Observing Collisions beyond the Secular Approximation Limit. Nat. Commun. 2019, 10, 5780. [Google Scholar] [CrossRef] [PubMed]
  38. Lu, C.; Xu, L.; Zhou, L.; Shi, M.; Lu, P.; Lin, K.; Wu, J. Laser-Induced k-Alignment Echoes and 4pi Phase-Space Analysis. Phys. Rev. A 2024, 110, 33102. [Google Scholar] [CrossRef]
  39. Karras, G.; Hertz, E.; Billard, F.; Lavorel, B.; Hartmann, J.-M.; Faucher, O.; Gershnabel, E.; Prior, Y.; Averbukh, I.S. Orientation and Alignment Echoes. Phys. Rev. Lett. 2015, 114, 153601. [Google Scholar] [CrossRef]
  40. Lin, K.; Lu, P.; Ma, J.; Gong, X.; Song, Q.; Ji, Q.; Zhang, W.; Zeng, H.; Wu, J.; Karras, G.; et al. Echoes in Space and Time. Phys. Rev. X 2016, 6, 41056. [Google Scholar] [CrossRef]
  41. Zhang, H.; Lavorel, B.; Billard, F.; Hartmann, J.-M.; Hertz, E.; Faucher, O.; Ma, J.; Wu, J.; Gershnabel, E.; Prior, Y.; et al. Rotational Echoes as a Tool for Investigating Ultrafast Collisional Dynamics of Molecules. Phys. Rev. Lett. 2019, 122, 193401. [Google Scholar] [CrossRef]
  42. Li, S.-Y.; Guo, F.-M.; Wang, J.; Yang, Y.-J.; Jin, M.-X. Field-free orientation of diatomic molecule via the linearly polarized resonant pulses. Chin. Phys. B 2015, 24, 104205. [Google Scholar] [CrossRef]
  43. Tyagi, A.; Maan, A.; Ahlawat, D.S.; Prasad, V. Effect of aligning pulse train on the orientation and alignment of a molecule in presence of orienting pulse. Spectrochim. Acta A 2017, 173, 13–18. [Google Scholar] [CrossRef]
  44. Kitano, K.; Hasegawa, H.; Ohshima, Y. Ultrafast angular momentum orientation by linearly polarized laser fields. Phys. Rev. Lett. 2009, 103, 223002. [Google Scholar] [CrossRef] [PubMed]
  45. Zhang, J.-P.; Wang, S.; Henriksen, N.E. Optimal field-free orientation of molecules with resonant tailored multicolor fields. Phys. Rev. A 2023, 107, 033118. [Google Scholar] [CrossRef]
  46. Dang, H.-P.; Wang, S.; Zhan, W.-S.; Zai, J.-B.; Han, X. Field-free orientation dynamics of CO molecule by combining two-color shaped laser pulse with THz laser pulse train. Chem. Phys. 2015, 461, 81–88. [Google Scholar] [CrossRef]
  47. Kraus, P.M.; Baykusheva, D.; Worner, H.J. Two-pulse field-free orientation reveals anisotropy of molecular shape resonance. Phys. Rev. Lett. 2014, 113, 023001. [Google Scholar] [CrossRef]
  48. Egodapitiya, K.N.; Li, S.; Jones, R.R. Terahertz-induced field-free orientation of rotationally excited molecules. Phys. Rev. Lett. 2014, 112, 103002. [Google Scholar] [CrossRef] [PubMed]
  49. Trippel, S.; Mullins, T.; Muller, N.L.; Kienitz, J.S.; Gonzalez-Ferez, R.; Kupper, J. Two-state wave packet for strong field-free molecular orientation. Phys. Rev. Lett. 2015, 114, 103003. [Google Scholar] [CrossRef]
  50. Chi, F.; Yang, Y.; Guo, F. Controlling field-free molecular orientation with combined circularly and linearly polarized resonant pulses at low rotational temperatures. Chem. Phys. Lett. 2013, 556, 350–354. [Google Scholar] [CrossRef]
  51. Sonoda, K.; Iwasaki, A.; Yamanouchi, K.; Hasegawa, H. Field-free molecular orientation of nonadiabatically aligned OCS. Chem. Phys. Lett. 2018, 693, 114–120. [Google Scholar] [CrossRef]
  52. Yachmenev, A.; Yurchenko, S.N. Detecting Chirality in Molecules by Linearly Polarized Laser Fields. Phys. Rev. Lett. 2016, 117, 033001. [Google Scholar] [CrossRef]
  53. Patterson, D.; Doyle, J.M. Sensitive chiral analysis via microwave three-wave mixing. Phys. Rev. Lett. 2013, 111, 023008. [Google Scholar] [CrossRef]
  54. Gershnabel, E.; Averbukh, I.S. Orienting Asymmetric Molecules by Laser Fields with Twisted Polarization. Phys. Rev. Lett. 2018, 120, 083204. [Google Scholar] [CrossRef]
  55. Tutunnikov, I.; Gershnabel, E.; Gold, S.; Averbukh, I.S. Selective Orientation of Chiral Molecules by Laser Fields with Twisted Polarization. J. Phys. Chem. Lett. 2018, 9, 1105–1111. [Google Scholar] [CrossRef] [PubMed]
  56. Tutunnikov, I.; Floß, J.; Gershnabel, E.; Brumer, P.; Averbukh, I.S.; Milner, A.A.; Milner, V. Observation of persistent orientation of chiral molecules by a laser field with twisted polarization. Phys. Rev. A 2020, 101, 021403. [Google Scholar] [CrossRef]
  57. Milner, A.A.; Fordyce, J.A.M.; MacPhail-Bartley, I.; Wasserman, W.; Milner, V.; Tutunnikov, I.; Averbukh, I.S. Controlled Enantioselective Orientation of Chiral Molecules with an Optical Centrifuge. Phys. Rev. Lett. 2019, 122, 223201. [Google Scholar] [CrossRef] [PubMed]
  58. Tessari, Z.; Tahara, K.; De Feyter, S. Molecular Alignment and Chiral Bias under Dynamic Nanoconfinement Conditions: The Impact of Molecular Symmetry. J. Phys. Chem. C 2023, 127, 9248–9256. [Google Scholar] [CrossRef]
  59. Velotta, R.; Hay, N.; Mason, M.B.; Castillejo, M.; Marangos, J.P. High-Order Harmonic Generation in Aligned Molecules. Phys. Rev. Lett. 2001, 87, 183901. [Google Scholar] [CrossRef]
  60. McFarland, B.K.; Farrell, J.P.; Bucksbaum, P.H.; Guhr, M. High harmonic generation from multiple orbitals in N2. Science 2008, 322, 1232–1235. [Google Scholar] [CrossRef]
  61. Zhou, X.; Lock, R.; Wagner, N.; Li, W.; Kapteyn, H.C.; Murnane, M.M. Elliptically polarized high-order harmonic emission from molecules in linearly polarized laser fields. Phys. Rev. Lett. 2009, 102, 073902. [Google Scholar] [CrossRef]
  62. Le, A.-T.; Lucchese, R.R.; Lin, C.D. Polarization and ellipticity of high-order harmonics from aligned molecules generated by linearly polarized intense laser pulses. Phys. Rev. A 2010, 82, 023814. [Google Scholar] [CrossRef]
  63. He, Y.; He, L.; Lan, P.; Wang, B.; Li, L.; Zhu, X.; Cao, W.; Lu, P. Direct imaging of molecular rotation with high-order-harmonic generation. Phys. Rev. A 2019, 99, 053419. [Google Scholar] [CrossRef]
  64. Jiang, C.; Jiang, H.; Chen, Y.; Li, B.; Lin, C.; Jin, C. Genetic-algorithm retrieval of the molecular alignment distribution with high-order harmonics generated from transiently aligned CO2 molecules. Phys. Rev. A 2022, 105, 023111. [Google Scholar] [CrossRef]
  65. Li, H.; Franks, K.J.; Hanson, R.J.; Kong, W. Brute Force Orientation and Alignment of Pyridazine Probed by Resonantly Enhanced Multiphoton Ionization. J. Phys. Chem. A 1998, 102, 8084–8090. [Google Scholar] [CrossRef]
  66. Holmegaard, L.; Hansen, J.L.; Kalhøj, L.; Louise Kragh, S.; Stapelfeldt, H.; Filsinger, F.; Küpper, J.; Meijer, G.; Dimitrovski, D.; Abu-samha, M.; et al. Photoelectron angular distributions from strong-field ionization of oriented molecules. Nat. Phys. 2010, 6, 428–432. [Google Scholar] [CrossRef]
  67. Jin, C.; Le, A.-T.; Zhao, S.-F.; Lucchese, R.; Lin, C.J.P.R.A. Theoretical study of photoelectron angular distributions in single-photon ionization of aligned N2 and CO2. Phys. Rev. A 2010, 81, 033421. [Google Scholar] [CrossRef]
  68. Thomann, I.; Lock, R.; Sharma, V.; Gagnon, E.; Pratt, S.T.; Kapteyn, H.C.; Murnane, M.M.; Li, W. Direct measurement of the angular dependence of the single-photon ionization of aligned N2 and CO2. J. Phys. Chem. A 2008, 112, 9382–9386. [Google Scholar] [CrossRef]
  69. Liu, X.; Gao, S.; Wang, N.; Zhu, F.; Jiao, L.; Liu, A. Alignment sensitivity of molecular-frame photoelectron momentum and angular distribution of H2+by XUV attosecond pulses. Commun. Theor. Phys. 2023, 75, 035503. [Google Scholar] [CrossRef]
  70. Tsubouchi, M.; Whitaker, B.J.; Wang, L.; Kohguchi, H.; Suzuki, T. Photoelectron imaging on time-dependent molecular alignment created by a femtosecond laser pulse. Phys. Rev. Lett. 2001, 86, 4500–4503. [Google Scholar] [CrossRef]
  71. Zhou, M.; Guo, M.Q.; Yu, J.; Chai, S.; Cong, S.L. The influence of molecular alignment and orientation in the ground state and excited state on the resonance-enhanced multi-photon ionization dynamics. Spectrochim. Acta A 2021, 262, 120154. [Google Scholar] [CrossRef]
  72. You, Y.; Oh, T.; Fallahkhair, A.; Kim, K. Alignment-dependent terahertz radiation in two-color photoionization of molecules. Phys. Rev. A 2013, 87, 035401. [Google Scholar] [CrossRef]
  73. Chen, W.; Huang, Y.; Meng, C.; Liu, J.; Zhou, Z.; Zhang, D.; Yuan, J.; Zhao, Z. Theoretical study of terahertz generation from atoms and aligned molecules driven by two-color laser fields. Phys. Rev. A 2015, 92, 033410. [Google Scholar] [CrossRef]
  74. Wu, J.; Tong, Y.; Li, M.; Pan, H.; Zeng, H. THz generation by a two-color pulse in prealigned molecules. Phys. Rev. A 2010, 82, 053416. [Google Scholar] [CrossRef]
  75. Li, M.; Pan, H.; Tong, Y.; Chen, C.; Shi, Y.; Wu, J.; Zeng, H. All-optical ultrafast polarization switching of terahertz radiation by impulsive molecular alignment. Opt. Lett. 2011, 36, 3633–3635. [Google Scholar] [CrossRef]
  76. Béjot, P.; Petit, Y.; Bonacina, L.; Kasparian, J.; Moret, M.; Wolf, J.-P. Ultrafast gaseous “half-wave plate”. Opt. Express 2008, 16, 7564–7570. [Google Scholar] [CrossRef] [PubMed]
  77. Huang, Y.; Meng, C.; Wang, X.; Lu, Z.; Zhang, D.; Chen, W.; Zhao, J.; Yuan, J.; Zhao, Z. Joint Measurements of Terahertz Wave Generation and High-Harmonic Generation from Aligned Nitrogen Molecules Reveal Angle-Resolved Molecular Structures. Phys. Rev. Lett. 2015, 115, 123002. [Google Scholar] [CrossRef]
  78. Li, Y.-N.; Du, J.-X.; Zhang, L.; Jiao, Z.-H.; Zhao, S.-F.; Wang, G.-L. Retrieval of the molecular alignment distribution from THz generation. Phys. Rev. A 2023, 108, 063103. [Google Scholar] [CrossRef]
  79. Xu, L.; Tutunnikov, I.; Prior, Y.; Averbukh, I.S. Enhanced persistent orientation of asymmetric-top molecules induced by cross-polarized terahertz pulses. Phys. Rev. Res. 2024, 6, 013201. [Google Scholar] [CrossRef]
  80. Rohrbach, D.; Beéry, L.; Mousavi, S.J.; Frey, H.M.; Kang, B.J.; Zyaee, E.; Feurer, T. THz-induced gas alignment in dispersionless field enhancing waveguides. Opt. Express 2025, 33, 3315–3324. [Google Scholar] [CrossRef]
  81. Cercignani, C. The Boltzmann Equation; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
  82. Kunitski, M.; Guan, Q.; Maschkiwitz, H.; Hahnenbruch, J.; Eckart, S.; Zeller, S.; Kalinin, A.; Schöffler, M.; Schmidt, L.P.H.; Jahnke, T.; et al. Ultrafast Manipulation of the Weakly Bound Helium Dimer. Nat. Phys. 2021, 17, 174–178. [Google Scholar] [CrossRef]
  83. Wu, J.; Vredenborg, A.; Ulrich, B.; Schmidt, L.P.H.; Meckel, M.; Voss, S.; Sann, H.; Kim, H.; Jahnke, T.; Dörner, R. Nonadiabatic Alignment of van Der Waals--Force-Bound Argon Dimers by Femtosecond Laser Pulses. Phys. Rev. A 2011, 83, 61403. [Google Scholar] [CrossRef]
  84. Lu, C.; Xu, L.; Zhou, L.; Shi, M.; Lu, P.; Li, W.; Dörner, R.; Lin, K.; Wu, J. Intermolecular Interactions Probed by Rotational Dynamics in Gas-Phase Clusters. Nat. Commun. 2024, 15, 4360. [Google Scholar] [CrossRef]
  85. Von Veltheim, A.; Borchers, B.; Steinmeyer, G.; Rottke, H. Imaging the Impulsive Alignment of Noble-Gas Dimers via Coulomb Explosion. Phys. Rev. A 2014, 89, 23432. [Google Scholar] [CrossRef]
  86. Pentlehner, D.; Nielsen, J.H.; Slenczka, A.; Mølmer, K.; Stapelfeldt, H. Impulsive Laser Induced Alignment of Molecules Dissolved in Helium Nanodroplets. Phys. Rev. Lett. 2013, 110, 93002. [Google Scholar] [CrossRef]
  87. Chatterley, A.S.; Schouder, C.; Christiansen, L.; Shepperson, B.; Rasmussen, M.H.; Stapelfeldt, H. Long-Lasting Field-Free Alignment of Large Molecules inside Helium Nanodroplets. Nat. Commun. 2019, 10, 133. [Google Scholar] [CrossRef]
  88. Chatterley, A.S.; Christiansen, L.; Schouder, C.A.; Jørgensen, A.V.; Shepperson, B.; Cherepanov, I.N.; Bighin, G.; Zillich, R.E.; Lemeshko, M.; Stapelfeldt, H. Rotational Coherence Spectroscopy of Molecules in Helium Nanodroplets: Reconciling the Time and the Frequency Domains. Phys. Rev. Lett. 2020, 125, 13001. [Google Scholar] [CrossRef] [PubMed]
  89. Cherepanov, I.N.; Bighin, G.; Schouder, C.A.; Chatterley, A.S.; Albrechtsen, S.H.; Muñoz, A.V.; Christiansen, L.; Stapelfeldt, H.; Lemeshko, M. Excited Rotational States of Molecules in a Superfluid. Phys. Rev. A 2021, 104, L061303. [Google Scholar] [CrossRef]
  90. Qiang, J.; Zhou, L.; Lu, P.; Lin, K.; Ma, Y.; Pan, S.; Lu, C.; Jiang, W.; Sun, F.; Zhang, W.; et al. Femtosecond Rotational Dynamics of D2 Molecules in Superfluid Helium Nanodroplets. Phys. Rev. Lett. 2022, 128, 243201. [Google Scholar] [CrossRef] [PubMed]
  91. Shepperson, B.; Søndergaard, A.A.; Christiansen, L.; Kaczmarczyk, J.; Zillich, R.E.; Lemeshko, M.; Stapelfeldt, H. Laser-Induced Rotation of Iodine Molecules in Helium Nanodroplets: Revivals and Breaking Free. Phys. Rev. Lett. 2017, 118, 203203. [Google Scholar] [CrossRef] [PubMed]
  92. Zhang, W.; Zhang, S.; Guo, D.; Zhao, L.; Yu, L.; Zhang, H.; He, Y.J. Great concern for chiral pharmaceuticals from the thalidomide tragedy. Univ. Chem. 2019, 34, 1–12. [Google Scholar] [CrossRef]
  93. Corkum, P.B. Plasma perspective on strong-field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef]
Photonics 12 00422 g001
Figure 1. Spatial coordinates of a linear molecule. The orientation angle θ between the molecule axis and the laser electric field E determines the alignment degree. α∥ and α⊥ denote the polarizability components parallel and perpendicular to the molecule axis. ϕ is the azimuth angle.
Figure 1. Spatial coordinates of a linear molecule. The orientation angle θ between the molecule axis and the laser electric field E determines the alignment degree. α∥ and α⊥ denote the polarizability components parallel and perpendicular to the molecule axis. ϕ is the azimuth angle.
Photonics 12 00422 g001
Photonics 12 00422 g002
Figure 2. (a) Torsional PES of HSOH along τHSOH with enantiomer abc frames. (b) Time evolution of (μZ) for enantiomers ψL (blue) and ψR (red) under double-pulse excitation (6 ps delay, 45° polarization). Bottom: Three-wave simulation using three-level transition system [52].
Figure 2. (a) Torsional PES of HSOH along τHSOH with enantiomer abc frames. (b) Time evolution of (μZ) for enantiomers ψL (blue) and ψR (red) under double-pulse excitation (6 ps delay, 45° polarization). Bottom: Three-wave simulation using three-level transition system [52].
Photonics 12 00422 g002
Photonics 12 00422 g003
Figure 3. Enantiomer-specific 〈μz〉 vs. time under double-pulse excitation: (a,b) HSOH at (a) 0 K (t = 0.32 ps) and (b) 50 K (t = 0.27 ps). (c,d) PPO at (c) 0 K (t = 0.45 ps) and (d) 50 K (t = 0.38 ps). (e,f) Ethyl oxirane molecule (EtOx) at (e) 0 K (t = 0.60 ps) and (f) 50 K (t = 0.50 ps). (Blue/red: enantiomer pairs) [55].
Figure 3. Enantiomer-specific 〈μz〉 vs. time under double-pulse excitation: (a,b) HSOH at (a) 0 K (t = 0.32 ps) and (b) 50 K (t = 0.27 ps). (c,d) PPO at (c) 0 K (t = 0.45 ps) and (d) 50 K (t = 0.38 ps). (e,f) Ethyl oxirane molecule (EtOx) at (e) 0 K (t = 0.60 ps) and (f) 50 K (t = 0.50 ps). (Blue/red: enantiomer pairs) [55].
Photonics 12 00422 g003
Photonics 12 00422 g004
Figure 4. (a) Schematic illustration of experimental geometry for the optical centrifuge spinning cold PPO in He jet. Coulomb explosion imaging via VMI spectrometer records fragment distributions (θ/θ2D defined in inset). (b) Experimental 2D orientation factor Δ〈cosθ2D〉 vs. delay t for (A) O+ (B) C+ fragments: (R)-PPO (orange), (S)-PPO (blue) with color inversion between panels. (c) QM-calculated 〈cosθ〉 (3D orientation factor): (A) O+ (B) C+ velocities. Black curves: 100 ps sliding average. I0 = 5 × 1012 W/cm2, below the ionization threshold to avoid plasma effects [56].
Figure 4. (a) Schematic illustration of experimental geometry for the optical centrifuge spinning cold PPO in He jet. Coulomb explosion imaging via VMI spectrometer records fragment distributions (θ/θ2D defined in inset). (b) Experimental 2D orientation factor Δ〈cosθ2D〉 vs. delay t for (A) O+ (B) C+ fragments: (R)-PPO (orange), (S)-PPO (blue) with color inversion between panels. (c) QM-calculated 〈cosθ〉 (3D orientation factor): (A) O+ (B) C+ velocities. Black curves: 100 ps sliding average. I0 = 5 × 1012 W/cm2, below the ionization threshold to avoid plasma effects [56].
Photonics 12 00422 g004
Photonics 12 00422 g005
Figure 5. (Color online). HHG from aligned N2. (a) Parallel (‖) and perpendicular (⊥) components with γ = arctan(|Ex/Ey|). (b) HHG ellipse orientation ϕ: major axis vs. y-axis, and ellipticity angle χ = arctan(ε). [61].
Figure 5. (Color online). HHG from aligned N2. (a) Parallel (‖) and perpendicular (⊥) components with γ = arctan(|Ex/Ey|). (b) HHG ellipse orientation ϕ: major axis vs. y-axis, and ellipticity angle χ = arctan(ε). [61].
Photonics 12 00422 g005
Photonics 12 00422 g006
Figure 6. (a) Pump–probe experimental scheme: z-polarized pump induces rotational wave packets (RWPs), and time-delayed probe generates HHG. Angle-resolved harmonics measured via xz-plane polarization scanning (see d). (b) Simulated 3D RWPs at specified delays. (c) Angle-resolved harmonic spectra corresponding to (b). (d) Experimental geometry [63].
Figure 6. (a) Pump–probe experimental scheme: z-polarized pump induces rotational wave packets (RWPs), and time-delayed probe generates HHG. Angle-resolved harmonics measured via xz-plane polarization scanning (see d). (b) Simulated 3D RWPs at specified delays. (c) Angle-resolved harmonic spectra corresponding to (b). (d) Experimental geometry [63].
Photonics 12 00422 g006
Photonics 12 00422 g007
Figure 7. Left: N2: (a) alignment 〈cos2θ〉 vs. delay near 1st half-revival; (b) 43-eV ionization yield from transiently aligned N2 (theory: line, exp: squares); (c) angular dependence of the ionization rate: single-photon (43-eV) ionization (solid) vs. multiphoton ionization by an IR laser (2 × 1014 W/cm2, dashed). Right: CO2: (a) alignment dynamics; (b) 43-eV ionization yield; (c) X/A/B- ionic states of CO2+ cross-sections vs. θ; (d) 43-eV vs. IR (1.1 × 1014 W/cm2) angular dependence of the ionization rate [67].
Figure 7. Left: N2: (a) alignment 〈cos2θ〉 vs. delay near 1st half-revival; (b) 43-eV ionization yield from transiently aligned N2 (theory: line, exp: squares); (c) angular dependence of the ionization rate: single-photon (43-eV) ionization (solid) vs. multiphoton ionization by an IR laser (2 × 1014 W/cm2, dashed). Right: CO2: (a) alignment dynamics; (b) 43-eV ionization yield; (c) X/A/B- ionic states of CO2+ cross-sections vs. θ; (d) 43-eV vs. IR (1.1 × 1014 W/cm2) angular dependence of the ionization rate [67].
Photonics 12 00422 g007
Photonics 12 00422 g008
Figure 8. Experimental photoelectron images from OCS. (a) Experimental setup: OCS orientation in Estat (red arrow = permanent dipole). The LCP probe pulse ionizes the molecule and imparts an upward momentum to the freed electron, resulting in recording on the upper part of the detector. (b) Two-dimensional electron momentum: LCP probe on random OCS (polarization ⊥ detector). (c) As (b) with RCP probe. (d,e) Aligned OCS under LCP/RCP (alignment pulse polarization ⊥ detector). [66].
Figure 8. Experimental photoelectron images from OCS. (a) Experimental setup: OCS orientation in Estat (red arrow = permanent dipole). The LCP probe pulse ionizes the molecule and imparts an upward momentum to the freed electron, resulting in recording on the upper part of the detector. (b) Two-dimensional electron momentum: LCP probe on random OCS (polarization ⊥ detector). (c) As (b) with RCP probe. (d,e) Aligned OCS under LCP/RCP (alignment pulse polarization ⊥ detector). [66].
Photonics 12 00422 g008
Photonics 12 00422 g009
Figure 9. Schematic of alignment-dependent photoionization of nitrogen molecules in a pump–probe setup. The pump pulse (800 nm, 100 fs, 1 × 1014 W/cm2) induces rotational wave packets, while the two-color probe pulse (800 nm + 400 nm, 50 fs, 5 × 1013 W/cm2) generates THz radiation [72].
Figure 9. Schematic of alignment-dependent photoionization of nitrogen molecules in a pump–probe setup. The pump pulse (800 nm, 100 fs, 1 × 1014 W/cm2) induces rotational wave packets, while the two-color probe pulse (800 nm + 400 nm, 50 fs, 5 × 1013 W/cm2) generates THz radiation [72].
Photonics 12 00422 g009
Photonics 12 00422 g010
Figure 10. Filament-induced birefringence (λ/2-plate equivalence) in 3-bar Ar. (a,b) Transmitted intensity polar plots (half-pattern shown): (a) filament polarization: 0°; (b) probe polarization rotation: −55°→57° (Δ112°) via co-propagation. (c) Experimental probe rotation (dots) matches ideal λ/2-plate behavior (line) [76].
Figure 10. Filament-induced birefringence (λ/2-plate equivalence) in 3-bar Ar. (a,b) Transmitted intensity polar plots (half-pattern shown): (a) filament polarization: 0°; (b) probe polarization rotation: −55°→57° (Δ112°) via co-propagation. (c) Experimental probe rotation (dots) matches ideal λ/2-plate behavior (line) [76].
Photonics 12 00422 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wang, M.; Zhang, E.; Liang, Q.; Liu, Y. Molecular Alignment Under Strong Laser Pulses: Progress and Applications. Photonics 2025, 12, 422. https://doi.org/10.3390/photonics12050422

AMA Style

Wang M, Zhang E, Liang Q, Liu Y. Molecular Alignment Under Strong Laser Pulses: Progress and Applications. Photonics. 2025; 12(5):422. https://doi.org/10.3390/photonics12050422

Chicago/Turabian Style

Wang, Ming, Enliang Zhang, Qingqing Liang, and Yi Liu. 2025. "Molecular Alignment Under Strong Laser Pulses: Progress and Applications" Photonics 12, no. 5: 422. https://doi.org/10.3390/photonics12050422

APA Style

Wang, M., Zhang, E., Liang, Q., & Liu, Y. (2025). Molecular Alignment Under Strong Laser Pulses: Progress and Applications. Photonics, 12(5), 422. https://doi.org/10.3390/photonics12050422

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop