Numerical Study on the Soliton Mode-Locking of the Er3+-Doped Fluoride Fiber Laser at ~3 μm with Nonlinear Polarization Rotation
Abstract
:1. Introduction
2. Numerical Model
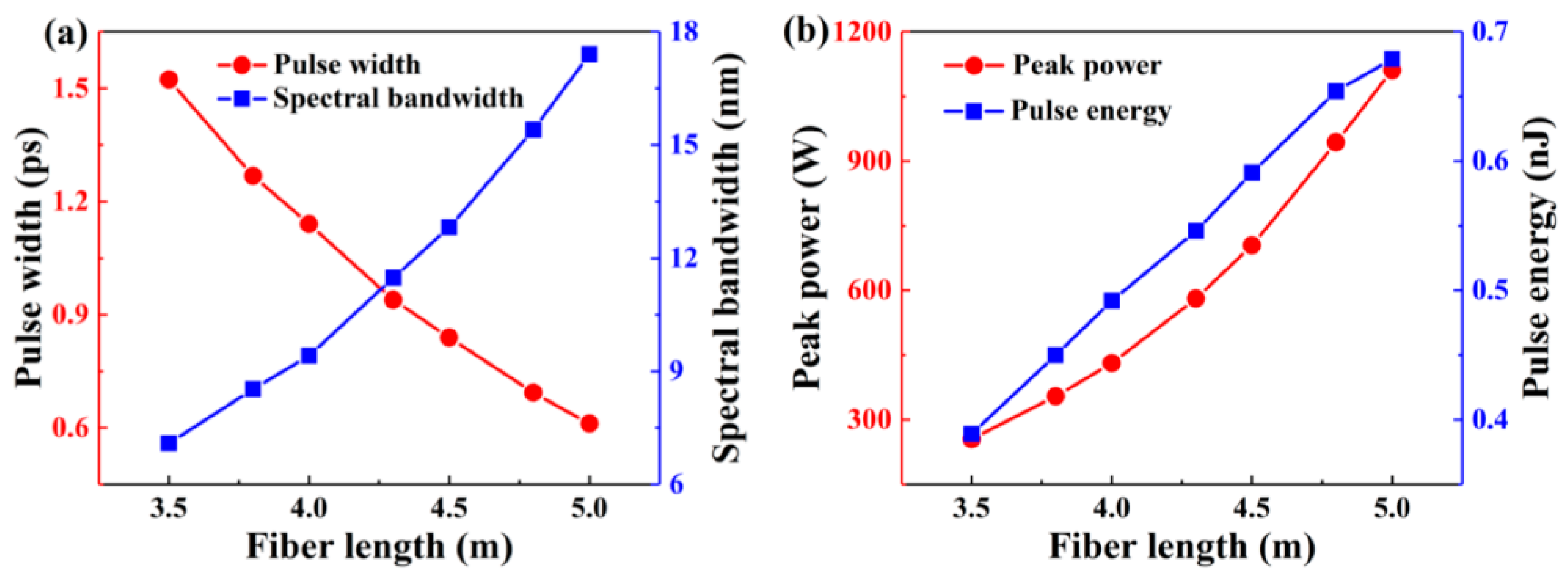
3. Numerical Simulation Results and Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jackson, S.D. Towards high-power mid-infrared emission from a fibre laser. Nat. Photon. 2012, 6, 423–431. [Google Scholar] [CrossRef]
- Zhu, X.; Peyghambarian, N. High-power ZBLAN glass fiber lasers: Review and prospect. Adv. Opto Electron. 2010, 2010, 501956. [Google Scholar] [CrossRef]
- Shen, Y.; Huang, K.; Luan, K.; Zhu, Y.; Yu, L. 26 mJ total output from a gain-switched single-mode Er3+-doped Zblan fiber laser operating at 2.8 μm. J. Russ. Laser Res. 2017, 38, 84–90. [Google Scholar] [CrossRef]
- Wise, F.W.; Chong, A.; Renninger, W.H. High-energy femtosecond fiber lasers based on pulse propagation at normal dispersion. Laser Photon. Rev. 2008, 2, 58–73. [Google Scholar] [CrossRef]
- Gao, C.X.; Wang, Z.Q.; Luo, H.; Zhan, L. High energy all-fiber Tm-doped femtosecond soliton laser mode-locked by nonlinear polarization rotation. J. Lightw. Technol. 2017, 35, 2988–2993. [Google Scholar] [CrossRef]
- Tang, P.H.; Qin, Z.P.; Liu, J.; Zhao, C.J.; Xie, G.Q.; Wen, S.C.; Qian, L.J. Watt-level passively mode-locked Er3+-doped ZBLAN fiber laser at 2.8 μm. Opt. Lett. 2015, 40, 4855–4858. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.L.; Wang, Y.S.; Chen, H.W.; Luan, K.P.; Tao, M.M.; Si, J.H. Wavelength-tunable passively mode-locked mid-infrared Er3+-doped ZBLAN fiber laser. Sci. Rep. 2017, 7, 14913. [Google Scholar] [CrossRef] [PubMed]
- Hu, T.; Hudson, D.D.; Jackson, S.D. Stable, self-starting, passively mode-locked fiber ring laser of the 3 μm class. Opt. Lett. 2014, 39, 2133–2136. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.W.; Zhu, X.S.; Wang, F.Q.; Xu, S.; Li, Y.; Guo, X.L.; Balakrishnan, K.; Norwood, R.A.; Peyghambarian, N. Graphene mode-locked fiber laser at 2.8 μm. IEEE Photon. Technol. Lett. 2016, 28, 7–10. [Google Scholar] [CrossRef]
- Zhao, C.J.; Zhang, H.; Qi, X.; Chen, Y.; Wang, Z.T.; Wen, S.C.; Tang, D.Y. Ultra-short pulse generation by a topological insulator based saturable absorber. Appl. Phys. Lett. 2012, 101, 201106. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, M.; Tang, P.H.; Chen, S.Q.; Du, J.; Jiang, G.B.; Li, Y.; Zhao, C.J.; Zhang, H.; Wen, S.C. The formation of various multi-soliton patterns and noise-like pulse in a fiber laser passively mode-locked by a topological insulator based saturable absorber. Laser Phys. Lett. 2014, 11, 055101. [Google Scholar] [CrossRef]
- Woodward, R.I.; Howe, R.C.T.; Hu, G.; Torrisi, F.; Zhang, M.; Hasan, T.; Kelleher, J.R. Few-layer MoS2 saturable absorbers for short-pulse laser technology: Current status and future perspectives. Photon. Res. 2015, 3, A30–A42. [Google Scholar] [CrossRef]
- Sotor, J.; Sobon, G.; Macherzynski, W.; Paletko, P.; Abramski, K.M. Black phosphorus saturable absorber for ultrashort pulse generation. Appl. Phys. Lett. 2015, 107, 051108. [Google Scholar] [CrossRef] [Green Version]
- Li, J.F.; Luo, H.Y.; Zhai, B.; Lu, R.G.; Guo, Z.N.; Zhang, H.; Liu, Y. Black phosphorus: A two-dimension saturable absorption material for mid-infrared Q-switched and mode-locked fiber lasers. Sci. Rep. 2016, 6, 30361. [Google Scholar] [CrossRef] [PubMed]
- Qin, Z.P.; Xie, G.Q.; Zhao, C.J.; Wen, S.C.; Yuan, P.; Qian, L.J. Mid-infrared mode-locked pulse generation with multilayer black phosphorus as saturable absorber. Opt. Lett. 2016, 41, 56–59. [Google Scholar] [CrossRef] [PubMed]
- Ge, Y.Q.; Zhu, Z.F.; Xu, Y.H.; Chen, Y.X.; Chen, S.; Liang, Z.M.; Song, Y.F.; Zou, Y.S.; Zeng, H.B.; Xu, S.X.; et al. Broadband nonlinear photoresponse of 2D TiS2 for ultrashort pulse generation and all-optical thresholding devices. Adv. Opt. Mater. 2018, 6, 1701166. [Google Scholar] [CrossRef]
- Lyu, Y.; Li, J.F.; Hu, Y.X.; Wang, Y.Z.; Wei, C.; Liu, Y. Theoretical comparison of NPR and hybrid mode-locked soliton thulium-doped fiber lasers. IEEE Photon. J. 2017, 9, 1–11. [Google Scholar] [CrossRef]
- Zhao, L.M.; Tang, D.Y.; Wu, X.; Zhang, H. Dissipative soliton generation in Yb-fiber laser with an invisible intracavity bandpass filter. Opt. Lett. 2010, 35, 2756–2758. [Google Scholar] [CrossRef] [PubMed]
- Nikodem, M.P.; Budnicki, A.; Tomczyk, G.; Abramski, K.M. Investigation of passively mode-locked erbium doped fiber ring laser due to nonlinear polarization rotation. Opto-Electron. Rev. 2008, 16, 194–198. [Google Scholar] [CrossRef] [Green Version]
- Hu, T.; Jackson, S.D.; Hudson, D.D. Ultrafast pulses from a mid-infrared fiber laser. Opt. Lett. 2015, 40, 4226–4228. [Google Scholar] [CrossRef] [PubMed]
- Duval, S.; Bernier, M.; Fortin, V.; Genest, J.; Piché, M.; Vallée, R. Femtosecond fiber lasers reach the mid-infrared. Optica 2015, 2, 623–625. [Google Scholar] [CrossRef]
- Antipov, S.; Hudson, D.D.; Fuerbach, A.; Jackson, S.D. High-power mid-infrared femtosecond fiber laser in the water vapor transmission window. Optica 2016, 3, 1373–1376. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics, 3rd ed.; Academic Press: San Diego, CA, USA, 2001; pp. 51–55. [Google Scholar]
- Man, W.S.; Tam, H.Y.; Demokan, M.S.; Wai, P.K.A.; Tang, D.Y. Mechanism of intrinsic wavelength tuning and sideband asymmetry in a passively mode-locked soliton fiber ring laser. J. Opt. Soc. Am. B 2000, 17, 28–33. [Google Scholar] [CrossRef]
- Zhao, B.; Tang, D.Y.; Zhao, L.M.; Shum, P.; Tam, H.Y. Pulse-train nonuniformity in a fiber soliton ring laser mode-locked by using the nonlinear polarization rotation technique. Phys. Rev. A 2004, 69, 043808. [Google Scholar] [CrossRef] [Green Version]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Yan, W.; Liang, S.; Tan, C.; Tang, P. Numerical Study on the Soliton Mode-Locking of the Er3+-Doped Fluoride Fiber Laser at ~3 μm with Nonlinear Polarization Rotation. Photonics 2019, 6, 25. https://doi.org/10.3390/photonics6010025
Zhang F, Yan W, Liang S, Tan C, Tang P. Numerical Study on the Soliton Mode-Locking of the Er3+-Doped Fluoride Fiber Laser at ~3 μm with Nonlinear Polarization Rotation. Photonics. 2019; 6(1):25. https://doi.org/10.3390/photonics6010025
Chicago/Turabian StyleZhang, Feijuan, Wenyan Yan, Shengnan Liang, Chao Tan, and Pinghua Tang. 2019. "Numerical Study on the Soliton Mode-Locking of the Er3+-Doped Fluoride Fiber Laser at ~3 μm with Nonlinear Polarization Rotation" Photonics 6, no. 1: 25. https://doi.org/10.3390/photonics6010025
APA StyleZhang, F., Yan, W., Liang, S., Tan, C., & Tang, P. (2019). Numerical Study on the Soliton Mode-Locking of the Er3+-Doped Fluoride Fiber Laser at ~3 μm with Nonlinear Polarization Rotation. Photonics, 6(1), 25. https://doi.org/10.3390/photonics6010025




