Numerical Analysis of Nonlocal Optical Response of Metallic Nanoshells
Abstract
:1. Introduction
2. Quantum Hydrodynamic Theory
3. Geometry of the Problem
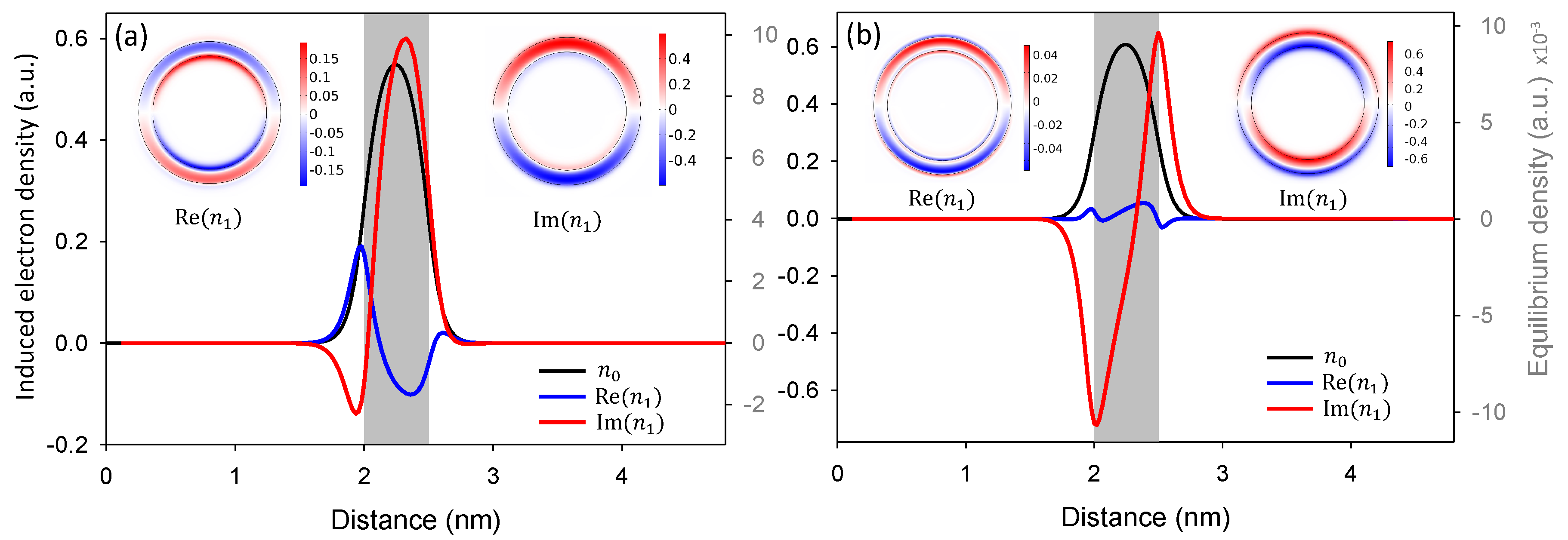
4. Numerical Results and Discussion
4.1. Na Nanoshell
4.2. Au Nanoshell
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LRA | Local response approximation |
| TFHT | Thomas–Fermi hydrodynamic theory |
| QHT | Quantum hydrodynamic theory |
| LEM | Lower energy mode |
| HEM | Higher energy mode |
References
- Kreibig, U.; Vollmer, M. Optical Properties of Metal Clusters; Springer: Heidelberg, Germany, 1995. [Google Scholar]
- Kelly, K.L.; Coronado, E.; Zhao, L.L.; Schatz, G.C. The optical properties of metal nanoparticles: The influence of size, shape and dielectric environment. J. Phys. Chem. B 2003, 107, 668–677. [Google Scholar] [CrossRef]
- Yu, Y.-Y.; Chang, S.-S.; Lee, C.-L.; Wang, C.R.C. Gold nanorods: Electrochemical synthesis and optical properties. J. Phys. Chem. B 1997, 101, 6661–6664. [Google Scholar] [CrossRef]
- Jin, R.; Cao, Y.; Mirkin, C.A.; Kelly, K.L.; Schatz, G.C.; Zheng, J.G. Photoinduced conversion of silver nanospheres to nanoprisms. Science 2001, 294, 1901–1903. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Xia, Y. Shape-controlled synthesis of gold and silver nanoparticles. Science 2002, 298, 2176–2179. [Google Scholar] [CrossRef]
- Raza, S.; Toscano, G.; Jauho, A.P.; Wubs, M.; Mortensen, N.A. Unusual resonances in nanoplasmonic structures due to nonlocal response. Phys. Rev. B 2011, 84, 121412. [Google Scholar] [CrossRef]
- Raza, S.; Bozhevolnyi, S.I.; Wubs, M.; Mortensen, N.A. Nonlocal optical response in metallic nanostructures. J. Phys. Condens. Matter 2015, 27, 183204. [Google Scholar] [CrossRef] [Green Version]
- Toscano, G.; Raza, S.; Jauho, A.P.; Mortensen, N.A.; Wubs, M. Modified field enhancement and extinction by plasmonic nanowire dimers due to nonlocal response. Opt. Express 2012, 20, 4176–4188. [Google Scholar] [CrossRef] [PubMed]
- Ciracì, C.; Hill, R.T.; Mock, J.J.; Urzhumov, Y.; Fernández-Domínguez, A.I.; Maier, S.A.; Pendry, J.B.; Chilkoti, A.; Smith, D.R. Probing the ultimate limits of plasmonic enhancement. Science 2012, 337, 1072–1074. [Google Scholar] [CrossRef]
- Ciracì, C.; Urzhumov, Y.A.; Smith, D.R. Effects of classical nonlocality on the optical response of three-dimensional plasmonic nanodimers. J. Opt. Soc. Am. B 2013, 30, 2731–2736. [Google Scholar] [CrossRef]
- Zhu, W.; Esteban, R.; Borisov, A.G.; Baumberg, J.J.; Nordlander, P.; Lezec, H.J.; Aizpurua, J.; Crozier, K.B. Quantum mechanical effects in plasmonic structures with subnanometre gaps. Nat. Commun. 2016, 7, 11495. [Google Scholar] [CrossRef] [Green Version]
- Savage, K.J.; Hawkeye, M.M.; Esteban, R.; Borisov, A.G.; Aizpurua, J.; Baumberg, J.J. Revealing the quantum regime in tunneling plasmonics. Nature 2012, 491, 574–577. [Google Scholar] [CrossRef] [PubMed]
- Scholl, J.A.; García-Etxarri, A.; Koh, A.L.; Dionne, J.A. Observation of quantum tunneling between two plasmonic nanoparticles. Nano Lett. 2013, 13, 564–569. [Google Scholar] [CrossRef]
- Ullrich, C.A. Time-Dependent Density Functional Theory: Concepts and Applications; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Lermé, J.; Palpant, B.; Cottancin, E.; Pellarin, M.; Prével, B.; Vialle, J.L.; Broyer, M. Quantum extension of mie’s theory in the dipolar approximation. Phys. Rev. B 1999, 60, 16151–16156. [Google Scholar] [CrossRef]
- Esteban, R.; Borisov, A.G.; Nordlander, P.; Aizpurua, J. Bridging quantum and classical plasmonics with a quantum-corrected model. Nat. Commun. 2012, 3, 825. [Google Scholar] [CrossRef] [Green Version]
- Luo, Y.; Fernández-Domínguez, A.I.; Wiener, A.; Maier, S.A.; Bendry, J.B. Surface plasmons and nonlocality: A simple model. Rev. Mod. Phys. 2013, 111, 093901. [Google Scholar] [CrossRef]
- Yan, W.; Wubs, M.; Mortensen, N.A. Projected dipole model for quantum plasmonics. Phys. Rev. Lett. 2015, 115, 137403. [Google Scholar] [CrossRef] [PubMed]
- Zapata, M.; Beltrán, A.S.C.; Borisov, A.G.; Aizupura, J. Quantum effects in the optical response of extended plasmonic gaps: Validation of the quantum corrected model in core-shell nanomatryushkas. Opt. Express 2015, 23, 8134–8149. [Google Scholar] [CrossRef]
- Toscano, G.; Straubel, J.; Kwiatkowski, A.; Rockstuhl, C.; Evers, F.; Xu, H.; Mortensen, N.A.; Wubs, M. Resonance shifts and spill-out effects in self-consistent hydrodynamic nanoplasmonics. Nat. Commun. 2015, 6, 7132. [Google Scholar] [CrossRef] [Green Version]
- Ciracì, C.; Sala, F.D. Quantum hydrodynamic theory for plasmonics: Impact of the electron density tail. Phys. Rev. B 2016, 93, 205405. [Google Scholar] [CrossRef]
- Ciracì, C. Current-dependent potential for nonlocal absorption in quantum hydrodynamic theory. Phys. Rev. B 2017, 95, 245434. [Google Scholar] [CrossRef] [Green Version]
- Khalid, M.; Sala, F.D.; Ciracì, C. Optical properties of plasmonic core-shell nanomatryoshkas: A quantum hydrodynamic analysis. Opt. Express 2018, 26, 17322–17334. [Google Scholar] [CrossRef]
- Oldenburg, S.J.; Averitt, R.D.; Westcott, S.L.; Halas, N.J. Nanoengineering of optical resonances. Chem. Phys. Lett. 1998, 288, 243–247. [Google Scholar] [CrossRef]
- Oldenburg, S.J.; Jackson, J.B.; Westcott, S.L.; Halas, N.J. Infrared extinction properties of gold nanoshells. Appl. Phys. Lett. 1999, 75, 2897–2899. [Google Scholar] [CrossRef]
- Aizpurua, J.; Hanarp, P.; Sutherland, D.S.; Kall, M.; Bryant, G.W.; de Abajo, F.J.G. Optical properties of gold nanorings. Phys. Rev. Lett. 2003, 90, 57401. [Google Scholar] [CrossRef]
- Averitt, R.D.; Sarkar, D.; Halas, N.J. Plasmon resonance shifts of Au-coated Au2S nanoshells: Insight into multicomponent nanoparticle growth. Phys. Rev. Lett. 1997, 78, 4217–4220. [Google Scholar] [CrossRef]
- Prodan, E.; Nordlander, P.; Halas, N.J. Effects of dielectric screening on the optical properties of metallic nanoshells. Chem. Phys. Lett. 2003, 368, 94–101. [Google Scholar] [CrossRef]
- Prodan, E.; Radloff, C.; Halas, N.J.; Nordlander, P. A hybridization model for the plasmon response of complex nanostructures. Science 2003, 302, 419–422. [Google Scholar] [CrossRef]
- Prodan, E.; Nordlander, P. Plasmon hybridization in spherical nanoparticles. J. Chem. Phys. 2004, 120, 5444–5454. [Google Scholar] [CrossRef]
- Baer, R.; Neuhauser, D.; Weiss, S. Enhanced absorption induced by a metallic nanoshell. Nano Lett. 2004, 4, 85–88. [Google Scholar] [CrossRef]
- West, J.L.; Halas, N.J. Engineered nanomaterials for biophotonics application: Improving sensing, imaging, and therapeutics. Annu. Rev. Biomed. Eng. 2003, 5, 285–292. [Google Scholar] [CrossRef]
- Khlebtsov, B.N.; Khlebtsov, N.G. Biosensing potential of silica/gold nanoshells: Sensitivity of plasmon resonance to the local dielectric environment. J. Quant. Spectr. Radiat. Trans. 2007, 106, 154–169. [Google Scholar] [CrossRef]
- Oldenburg, S.J.; Westcott, S.L.; Averitt, R.D.; Halas, N.J. Surface enhanced Raman scattering in the near infrared using metal nanoshell substrates. J. Chem. Phys. 1999, 111, 4729–4735. [Google Scholar] [CrossRef]
- Hao, E.; Li, S.; Bailey, S.L.; Zou, S.; Schatz, G.C.; Hupp, J.T. Optical properties of metal nanoshells. J. Phys. Chem. B 2004, 108, 1224–1229. [Google Scholar] [CrossRef]
- Goude, Z.E.; Leung, P.T. Surface enhanced Raman scattering from metallic nanoshells with nonlocal dielectric response. Solid State Commun. 2007, 143, 416–420. [Google Scholar] [CrossRef]
- Hirsch, L.R.; Stafford, R.J.; Bankson, J.A.; Sershen, S.R.; Rivera, B.; Price, R.E.; Hazle, J.D.; Halas, N.J.; West, J.L. Nanoshell-mediated near-infrared thermal therapy of tumors under magnetic resonance guidance. Proc. Natl. Acad. Sci. USA 2003, 100, 13549–13555. [Google Scholar] [CrossRef]
- Khlebtsov, B.; Zharov, V.; Melnikov, A.; Tuchin, V.; Khlebtsov, N. Optical amplification of photothermal therapy with gold nanoparticles and nanoclusters. Nanotechnology 2006, 17, 5167–5179. [Google Scholar] [CrossRef]
- Harris, N.; Ford, M.J.; Cortie, M.B. Optimization of plasmonic heating by gold nanospheres and nanoshells. J. Phys. Chem. B 2006, 110, 10701–10707. [Google Scholar] [CrossRef]
- Comsol Multiphysics. Available online: http://www.comsol.com (accessed on 7 April 2019).
- Ciracì, C.; Urzhumov, Y.A.; Smith, D.R. Far-field analysis of axially symmetric three-dimensional directional cloaks. Opt. Express 2013, 21, 9397–9406. [Google Scholar] [CrossRef]
- Prodan, E.; Lee, A.; Nordlander, P. The effect of a dielectric core and embedding medium on the polarizability of metallic nanoshells. Chem. Phys. Lett. 2002, 360, 325–332. [Google Scholar] [CrossRef]
- Ekardt, W. Size-dependent photoabsorption and photoemission of small metal particles. Phys. Rev. B 1985, 31, 6360–6370. [Google Scholar] [CrossRef]
- Brack, M. The physics of simple metal clusters: Self-consistent jellium model and semiclassical approaches. Rev. Mod. Phys. 1993, 65, 677–732. [Google Scholar] [CrossRef]
- Prodan, E.; Nordlander, P. Structural tunability of the plasmon resonances in metallic nanoshells. Nano Lett. 2003, 3, 543–547. [Google Scholar] [CrossRef]
- Shayesteh, S.F.; Saie, M. The effect of surface plasmon resonance on optical response in dielectric (core)-metal (shell) nanoparticles. Pramana-J. Phys. 2015, 85, 1245–1255. [Google Scholar] [CrossRef]
- Zuloaga, J.; Prodan, E.; Nordlander, P. Quantum description of the plasmon resonances of a nanoparticle dimer. Nano Lett. 2009, 9, 887–891. [Google Scholar] [CrossRef]
- Teperik, T.V.; Nordlander, P.; Aizpurua, J.; Borisov, A.G. Robust Subnanometric plasmon ruler by rescaling of the nonlocal optical response. Phys. Rev. Lett. 2013, 110, 263901. [Google Scholar] [CrossRef] [PubMed]
- Rojas, R.; Claro, F.; Fuchs, R. Nonlocal response of a small coated sphere. Phys. Rev. B 1988, 37, 6799–6807. [Google Scholar] [CrossRef]
- David, C.; de Abajo, J.G. Spatial nonlocality in the optical response of metal nanoparticles. J. Phys. Chem. C 2011, 115, 19470–19475. [Google Scholar] [CrossRef]
- Huang, Y.; Goa, L. Superscattering of light from core-shell nonlocal plasmonic nanoparticles. J. Phys. Chem. C 2014, 118, 30170–30178. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, J.J.; Goa, L. Antibonding and bonding lasing modes with low gain threshold in nonlocal metallic nanoshell. Opt. Express 2015, 23, 8818–8828. [Google Scholar] [CrossRef]
- Tserkezis, C.; Gantzounis, G.; Stefanou, N. Collective plasmonic modes in ordered assemblies of metallic nanoshells. J. Phys. Condens. Matter 2008, 20, 075232. [Google Scholar] [CrossRef]
- Tserkezis, C.; Stefanou, N.; Wubs, M.; Mortensen, N.A. Molecular fluorescence enhancement in plasmonic environments: Exploring the role of nonlocal effects. Nanoscale 2016, 8, 17532–17541. [Google Scholar] [CrossRef] [PubMed]







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalid, M.; Ciracì, C. Numerical Analysis of Nonlocal Optical Response of Metallic Nanoshells. Photonics 2019, 6, 39. https://doi.org/10.3390/photonics6020039
Khalid M, Ciracì C. Numerical Analysis of Nonlocal Optical Response of Metallic Nanoshells. Photonics. 2019; 6(2):39. https://doi.org/10.3390/photonics6020039
Chicago/Turabian StyleKhalid, Muhammad, and Cristian Ciracì. 2019. "Numerical Analysis of Nonlocal Optical Response of Metallic Nanoshells" Photonics 6, no. 2: 39. https://doi.org/10.3390/photonics6020039
APA StyleKhalid, M., & Ciracì, C. (2019). Numerical Analysis of Nonlocal Optical Response of Metallic Nanoshells. Photonics, 6(2), 39. https://doi.org/10.3390/photonics6020039




