Synchronization of Mutually Delay-Coupled Quantum Cascade Lasers with Distinct Pump Strengths
Abstract
:1. Introduction
2. Dimensionless Equations
3. Compound Laser Modes
3.1. Equal Pumps
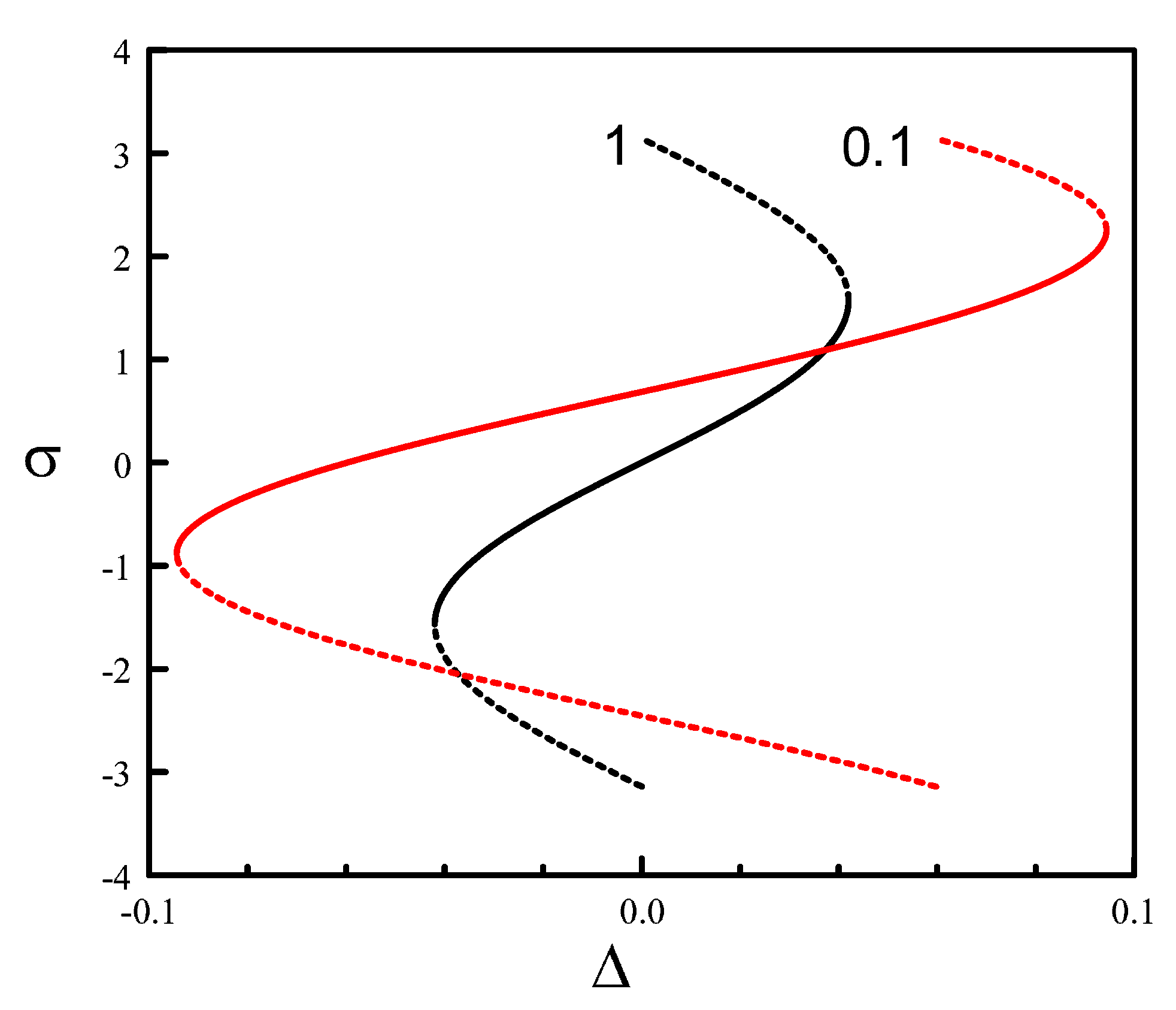
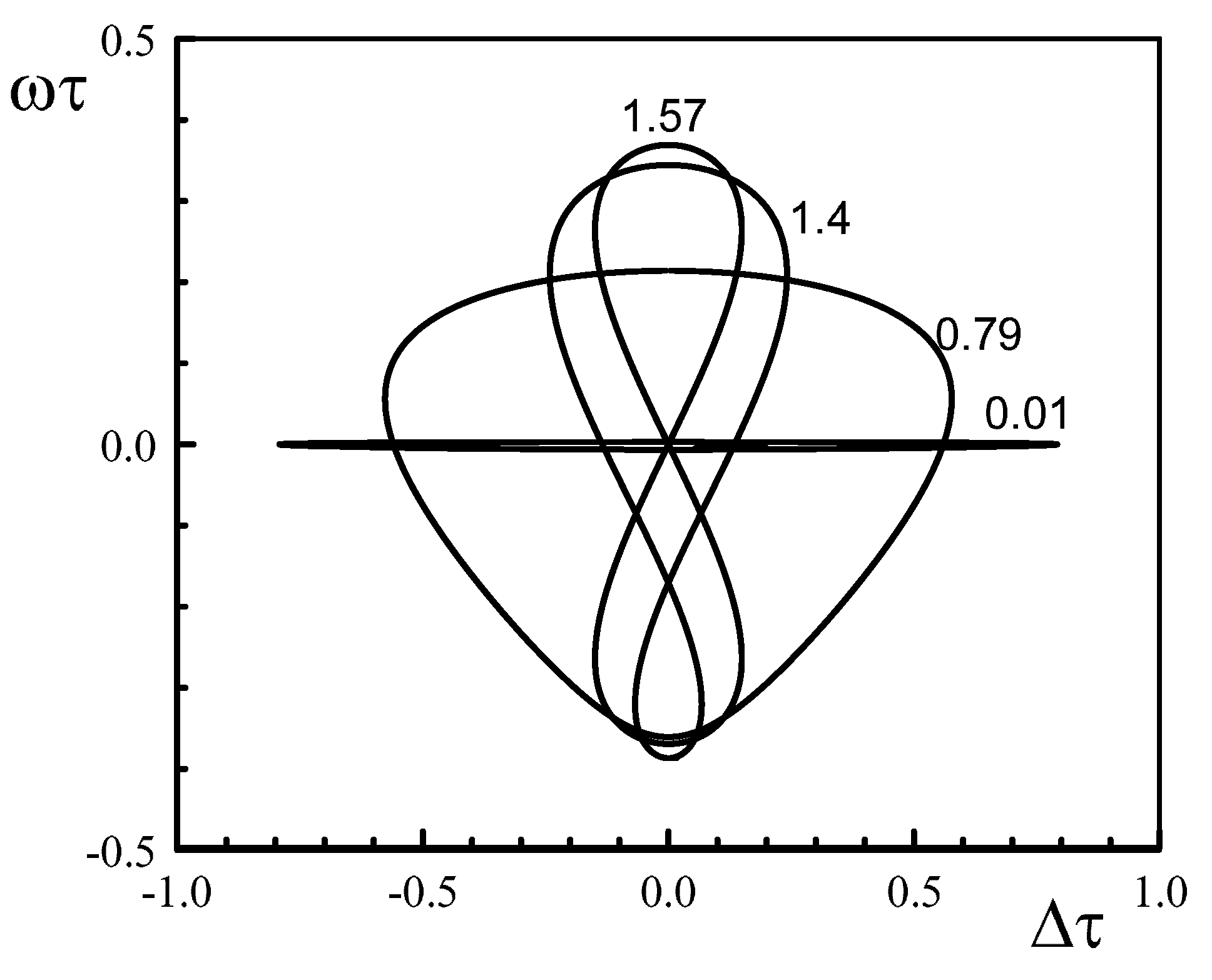
3.2. Unequal Pumps
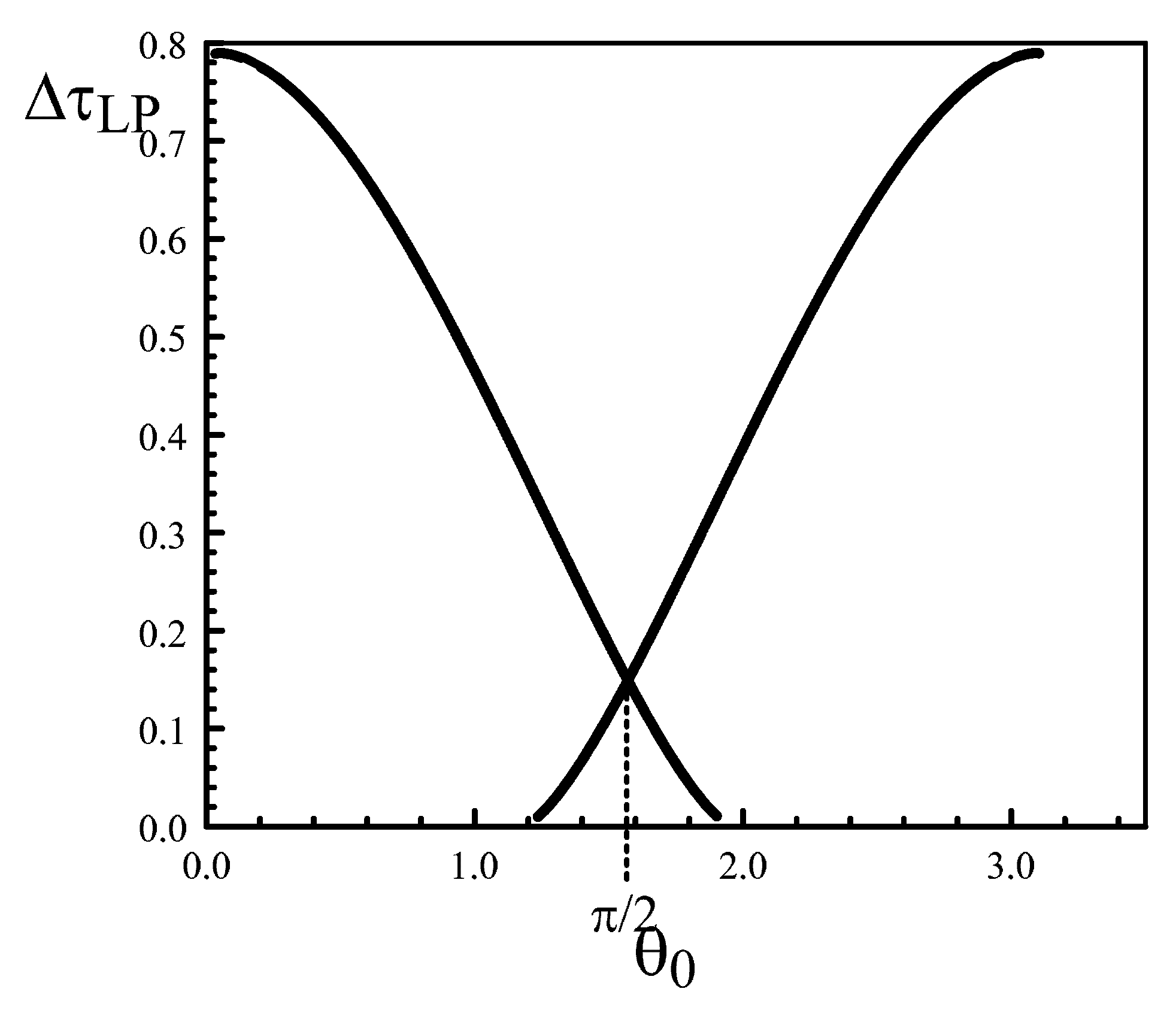
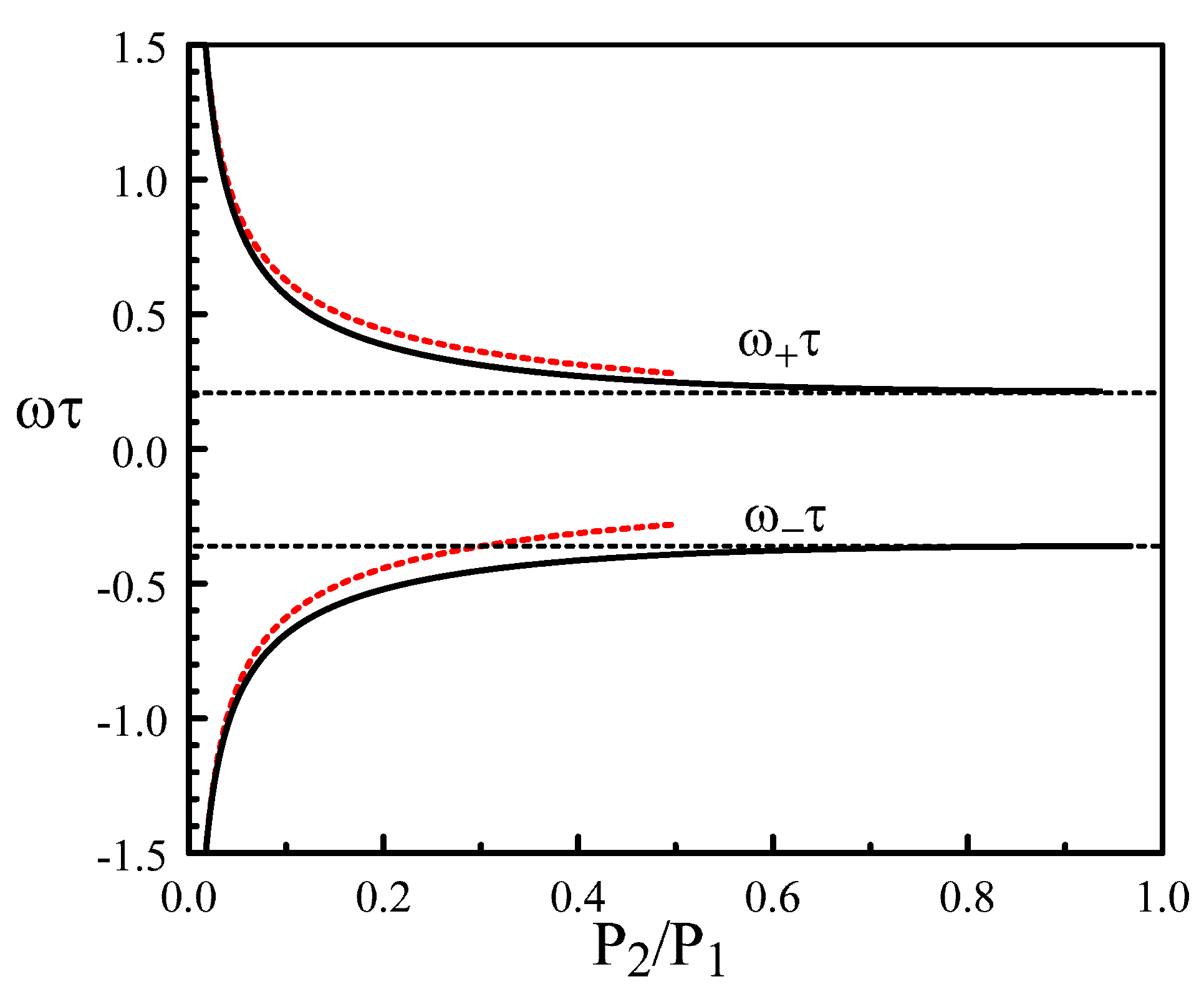
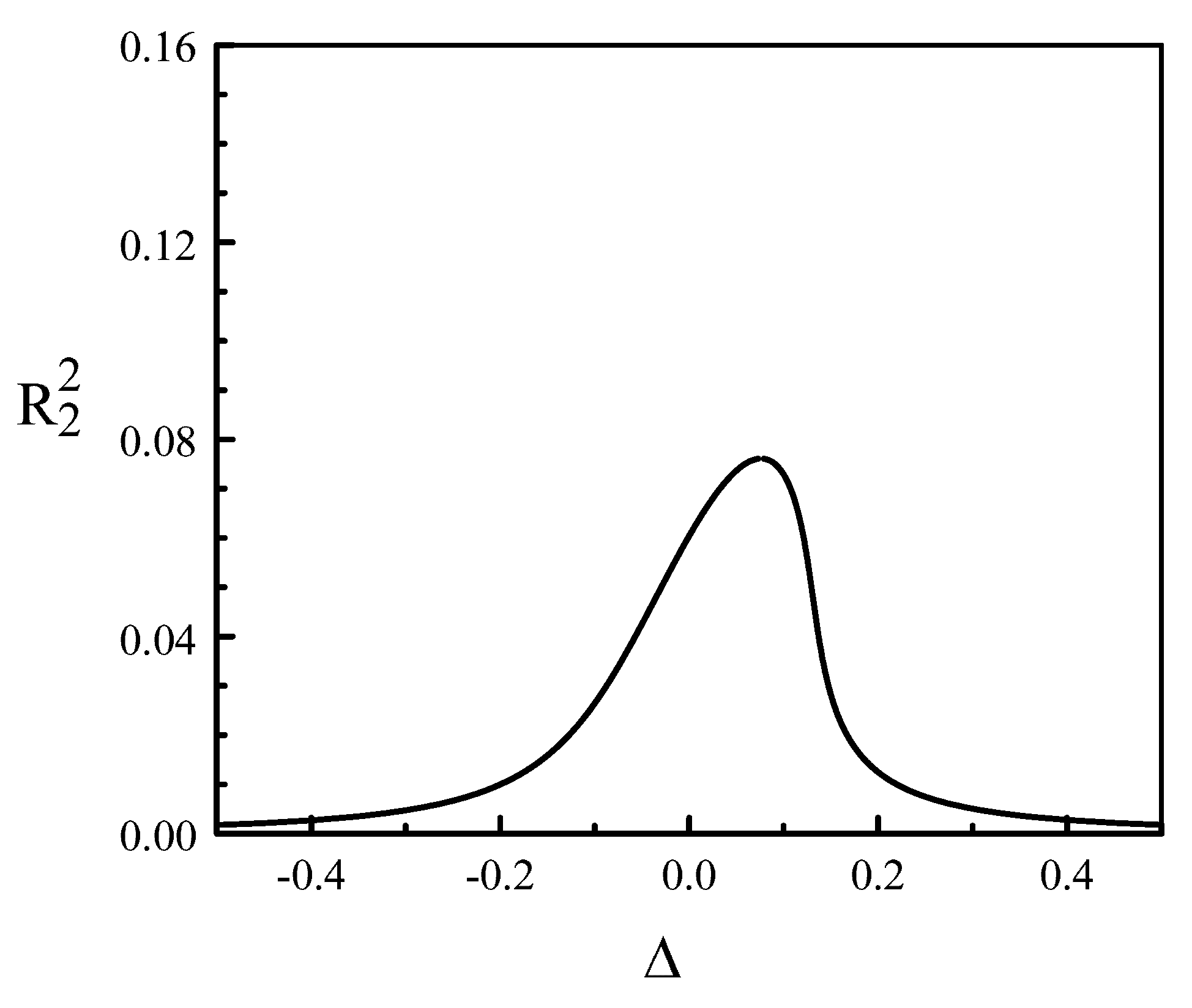
4. The Limit of Small Ratios of the Two Pumps
5. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Yao, Y.; Hoffman, A.J.; Gmachl, C.F. Mid-infrared quantum cascade lasers. Nat. Photonics 2012, 6, 432–439. [Google Scholar] [CrossRef]
- Razeghi, M.; Lu, Q.; Bandyopadhyay, N.; Zhou, W.; Heydari, D.; Bai, Y.; Slivken, S. Quantum cascade lasers: From tool to product. Opt. Express 2015, 23, 8462–8475. [Google Scholar] [CrossRef] [PubMed]
- Isensee, K.; Kröger-Lui, N.; Petrich, W. Biomedical applications of mid-infrared quantum cascade lasers—A review. Analyst 2018, 143, 5888–5911. [Google Scholar] [CrossRef] [PubMed]
- Kosterev, A.; Wysocki, G.; Bakhirkin, Y.; So, S.; Lewicki, R.; Fraser, M.; Tittel, F.; Curl, R.F. Application of quantum cascade lasers to trace gas analysis. Appl. Phys. B 2008, 90, 165–176. [Google Scholar] [CrossRef]
- Rakic, A.D.; Taimre, T.; Bertling, K.; Lim, Y.L.; Dean, P.; Valavanis, A.; Indjin, D. Sensing and imaging using laser feedback interferometry with quantum cascade lasers. Appl. Phys. Rev. 2019, 6, 021320. [Google Scholar] [CrossRef] [Green Version]
- Herdt, A.; Mohr, T.; Lenstra, D.; Elsäßer, W. Injection dynamics of mutually delay-coupled non-identical quantum cascade lasers. In Proceedings of the International Symposium on Physics and Applications of Laser Dynamics 2017 (IS-PALD 2017), Paris, France, 15–17 November 2017. [Google Scholar]
- Bogris, A.; Herdt, A.; Syvridis, D.; Elsäßer, W. Mid-Infrared Gas Sensor Based on Mutually Injection Locked Quantum Cascade Lasers. IEEE J. Sel. Top. Quant. 2017, 23, 1500107. [Google Scholar] [CrossRef]
- Herdt, A.; Weidmann, M.; Mohr, T.; Lenstra, D.; Elsäßer, W. Theory of delay-coupled nonidentical quantum cascade lasers. In Proceedings of the Semiconductor Lasers and Laser Dynamics VIII. International Society for Optics and Photonics, Strasburg, Francja, 22–26 April 2018; p. 106820H. [Google Scholar]
- Krall, M.; Martl, M.; Bachmann, D.; Deutsch, C.; Andrews, A.M.; Schrenk, W.; Strasser, G.; Unterrainer, K. Coupled cavity terahertz quantum cascade lasers with integrated emission monitoring. Opt. Express 2015, 23, 3581–3588. [Google Scholar] [CrossRef]
- Han, H.; Shore, K.A. Analysis of high-frequency oscillations in mutually-coupled nano-lasers. Opt. Express 2018, 26, 10013–10022. [Google Scholar] [CrossRef]
- Dubois, F.M.; Seifikar, M.; Perrott, A.H.; Peters, F.H. Modeling mutually coupled non-identical semiconductor lasers on photonic integrated circuits. Appl. Opt. 2018, 57, E154–E162. [Google Scholar] [CrossRef]
- Seifikar, M.; Amann, A.; Peters, F.H. Dynamics of two identical mutually delay-coupled semiconductor lasers in photonic integrated circuits. Appl. Opt. 2018, 57, E37–E44. [Google Scholar] [CrossRef]
- Kreinberg, S.; Porte, X.; Schicke, D.; Lingnau, B.; Schneider, C.N.; Höfling, S.H.; Kanter, I.; Lüdge, K.L.; Reitzenstein, S. Mutual coupling and synchronization of optically coupled quantum-dot micropillar lasers at ultra-low light levels. Nat. Commun. 2019, 10, 1539. [Google Scholar] [CrossRef] [PubMed]
- Jungling, T.; Porte, X.; Oliver, N.; Soriano, M.C.; Fischer, I. A unifying analysis of chaos synchronization and consistency in delay-coupled semiconductor lasers. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1501609. [Google Scholar] [CrossRef]
- Wünsche, H.-J.; Bauer, S.; Kreissl, J.; Ushakov, O.; Korneyev, N.; Henneberger, F.; Wille, E.; Erzgräber, H.; Peil, M.; Elsäßer, W.; et al. Synchronization of delay-coupled oscillators: A study on semiconductor lasers. Phys. Rev. Lett. 2005, 94, 163901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wille, E.; Peil, M.; Fischer, I.; Elsäßer, W. Dynamical scenarios of mutually delay-coupled semiconductor lasers in the short coupling regime. In Semiconductor Lasers and Laser Dynamics; International Society for Optics and Photonics: Bellingham, WA, USA, 2004; pp. 41–50. [Google Scholar]
- Erzgräber, H.; Lenstra, D.; Krauskopf, B.; Fischer, I. Dynamical properties of mutually delayed coupled semiconductor lasers. In Semiconductor Lasers and Laser Dynamics; International Society for Optics and Photonics: Bellingham, WA, USA, 2004; pp. 352–361. [Google Scholar]
- Erzgräber, H.Y.; Krauskopf, B.; Lenstra, D. Mode structure of delay coupled semiconductor lasers: Influence of the pump current. J. Opt. B 2005, 7, 361–371. [Google Scholar] [CrossRef] [Green Version]
- Erzgräber, H.; Krauskopf, B.; Lenstra, D. Compound Laser Modes of Mutually Delay-Coupled Lasers. SIAM J. Appl. Dyn. Syst. 2006, 5, 30–65. [Google Scholar] [CrossRef]
- Erzgräber, H.; Wille, E.; Krauskopf, B.; Fischer, I. Amplitude-phase dynamics near the locking region of two delay-coupled semiconductor lasers. Nonlinearity 2009, 22, 585–600. [Google Scholar] [CrossRef]
- Soriano, M.C.; Garcia-Ojalvo, J.; Mirasso, C.R.; Fischer, I. Complex Photonics: Dynamics and applications of delay-coupled semiconductor lasers. Rev. Mod. Phys. 2013, 85, 421–470. [Google Scholar] [CrossRef] [Green Version]
- Yanchuk, S.; Schneider, K.R.; Recke, L. Dynamics of two mutually coupled semiconductor lasers: Instantaneous coupling limit. Phys. Rev. E 2004, 69, 056221. [Google Scholar] [CrossRef]
- Kominis, Y.; Choquette, K.D.; Bountis, A.; Kovanis, K. Exceptional Points in Two Dissimilar Coupled Diode Lasers. Appl. Phys. Lett. 2018, 113, 081103. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; Thompson, B.J.; Dave, H.; Fryslie, S.T.M.; Choquette, K.D. Non-Hermiticity and Exceptional Points in Coherently Coupled Vertical Cavity Laser Diode Arrays. Appl. Phys. Lett. 2019, 114, 0661103. [Google Scholar] [CrossRef]
- Miri, M.A.; Alù, A. Exceptional points in optics and photonics. Science 2019, 363, eaar7709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, W.; Özdemir, S.K.; Zhao, G.; Wiersig, J.; Yang, L. Exceptional points enhance sensing in an optical microcavity. Nature 2017, 548, 192–196. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Fryslie, S.T.M.; Thompson, B.J.; Carney, P.S.; Choquette, K.D. Parity-time symmetry in coherently coupled vertical cavity laser arrays. Optica 2017, 4, 323–329. [Google Scholar] [CrossRef] [Green Version]
- Friart, G.; Van der Sande, G.; Verschaffelt, G.; Erneux, T. Analytical stability boundaries for quantum cascade lasers subject to optical feedback. Phys. Rev. E 2016, 93, 052201. [Google Scholar] [CrossRef]
- Jumpertz, L.; Schires, K.; Carras, M.; Sciamanna, M.; Grillot, F. Chaotic light at mid-infrared wavelength. Light Sci. Appl. 2016, 5, e16088. [Google Scholar] [CrossRef] [Green Version]
- Clerkin, E.; O’Brien, S.; Amann, A. Multistabilities and symmetry-broken one-color and two-color states in closely coupled single-mode lasers. Phys. Rev. E 2014, 89, 032919. [Google Scholar] [CrossRef] [Green Version]
- Lenstra, D. Self-consistent rate-equation theory of coupling in mutually injected semiconductor lasers. In Physics and Simulation of Optoelectronic Devices XXV; International Society for Optics and Photonics: Bellingham, WA, USA, 2017; p. 100980K. [Google Scholar]
- Erneux, T.; Kovanis, V.; Gavrielides, A. Nonlinear dynamics of an injected quantum cascade laser. Phys. Rev. E 2013, 88, 032907. [Google Scholar] [CrossRef] [Green Version]
- Gensty, T.; Elsäßer, W.; Mann, C. Intensity noise properties of quantum cascade lasers. Opt. Express 2005, 13, 2032–2039. [Google Scholar] [CrossRef] [Green Version]
- Gensty, T.; Elsäßer, W. Semiclassical model for the relative intensity noise of intersubband quantum cascade lasers. Opt. Commun. 2005, 6256, 171–183. [Google Scholar] [CrossRef]
- Vicente, R.; Mulet, J.; Sciamanna, M.; Mirasso, C.R. Simple interpretation of the dynamics of mutually coupled semiconductor lasers with detuning. Proc. SPIE 2004, 5349, 307–318. [Google Scholar]
- Schuster, H.G.; Wagner, P. Mutual entrainment of two limit-cycles oscillators with time delayed coupling. Prog. Theor. Phys. 1989, 81, 939–945. [Google Scholar] [CrossRef] [Green Version]
- Niebur, E.; Schuster, H.G.; Kammen, D. Collective frequencies and metastability in networks of limit-cycle oscillators with time delay. Phys. Rev. Lett. 1991, 67, 2753. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adams, M.J.; Li, N.; Cemlyn, B.B.; Susanto, H.; Henning, I.D. Effects of detuning, gain-guiding, and index antiguiding on the dynamics of two laterally coupled semiconductor lasers. Phys. Rev. A 2017, 95, 053869. [Google Scholar] [CrossRef] [Green Version]
- Kominis, Y.; Kovanis, V.; Bountis, T. Controllable asymmetric phase-locked states of the fundamental active photonic dimer. Phys. Rev. A 2017, 96, 043836. [Google Scholar] [CrossRef] [Green Version]
- Kominis, Y.; Kovanis, V.; Bountis, T. Spectral signatures of exceptional points and bifurcations in the fundamental active photonic dimer. Phys. Rev. A 2017, 96, 053837. [Google Scholar] [CrossRef] [Green Version]
- Winful, H.G.; Wang, S.S. Stability of phase locking in coupled semiconductor laser arrays. Appl. Phys. Lett. 1988, 53, 1894–1896. [Google Scholar] [CrossRef] [Green Version]
- Mayol, C.; Toral, R.; Mirasso, C.R.; Natiello, M.A. Class-A lasers with injected signal: Bifurcation set and Lyapunov–potential function. Phys. Rev. A 2002, 66, 013808. [Google Scholar] [CrossRef] [Green Version]
- Kelleher, B.; Hegarty, S.P.; Huyet, G. Optically injected lasers: The transition from class B to class A lasers. Phys. Rev. E 2012, 86, 066206. [Google Scholar] [CrossRef]
- Tredicce, J.R.; Arecchi, F.T.; Lippi, G.L.; Puccioni, G.P. Instabilities in lasers with an injected signal. J. Opt. Soc. Am. B 1985, 2, 173–183. [Google Scholar] [CrossRef] [Green Version]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erneux, T.; Lenstra, D. Synchronization of Mutually Delay-Coupled Quantum Cascade Lasers with Distinct Pump Strengths. Photonics 2019, 6, 125. https://doi.org/10.3390/photonics6040125
Erneux T, Lenstra D. Synchronization of Mutually Delay-Coupled Quantum Cascade Lasers with Distinct Pump Strengths. Photonics. 2019; 6(4):125. https://doi.org/10.3390/photonics6040125
Chicago/Turabian StyleErneux, Thomas, and Daan Lenstra. 2019. "Synchronization of Mutually Delay-Coupled Quantum Cascade Lasers with Distinct Pump Strengths" Photonics 6, no. 4: 125. https://doi.org/10.3390/photonics6040125
APA StyleErneux, T., & Lenstra, D. (2019). Synchronization of Mutually Delay-Coupled Quantum Cascade Lasers with Distinct Pump Strengths. Photonics, 6(4), 125. https://doi.org/10.3390/photonics6040125





