Liquid-Filled Highly Asymmetric Photonic Crystal Fiber Sagnac Interferometer Temperature Sensor
Abstract
1. Introduction
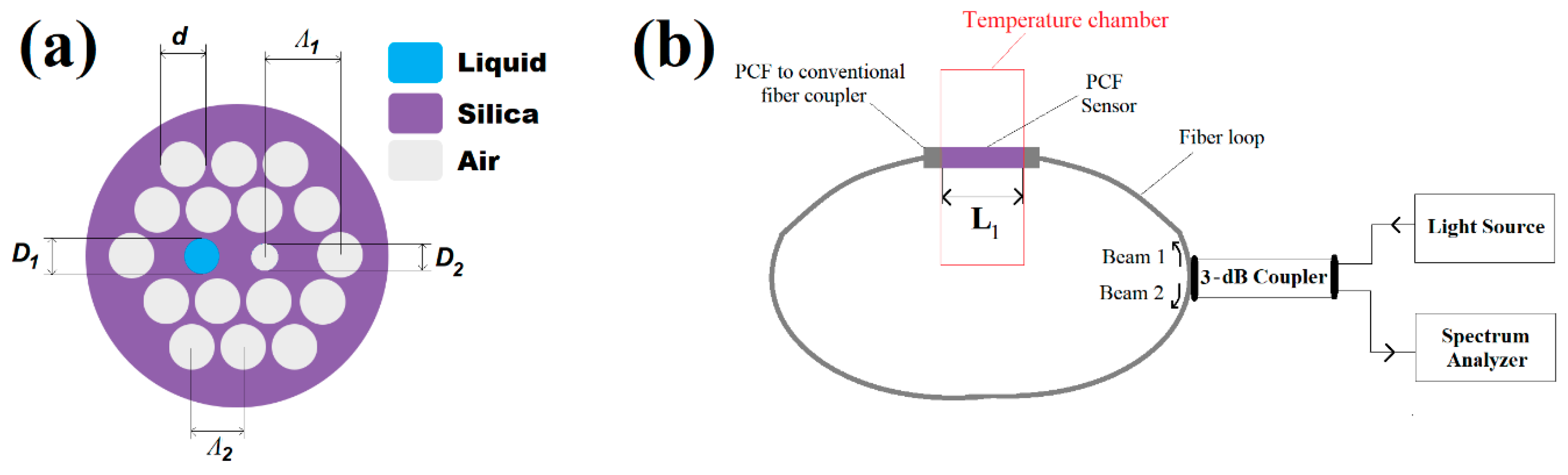
2. Sensor Design
2.1. Materials and Methods
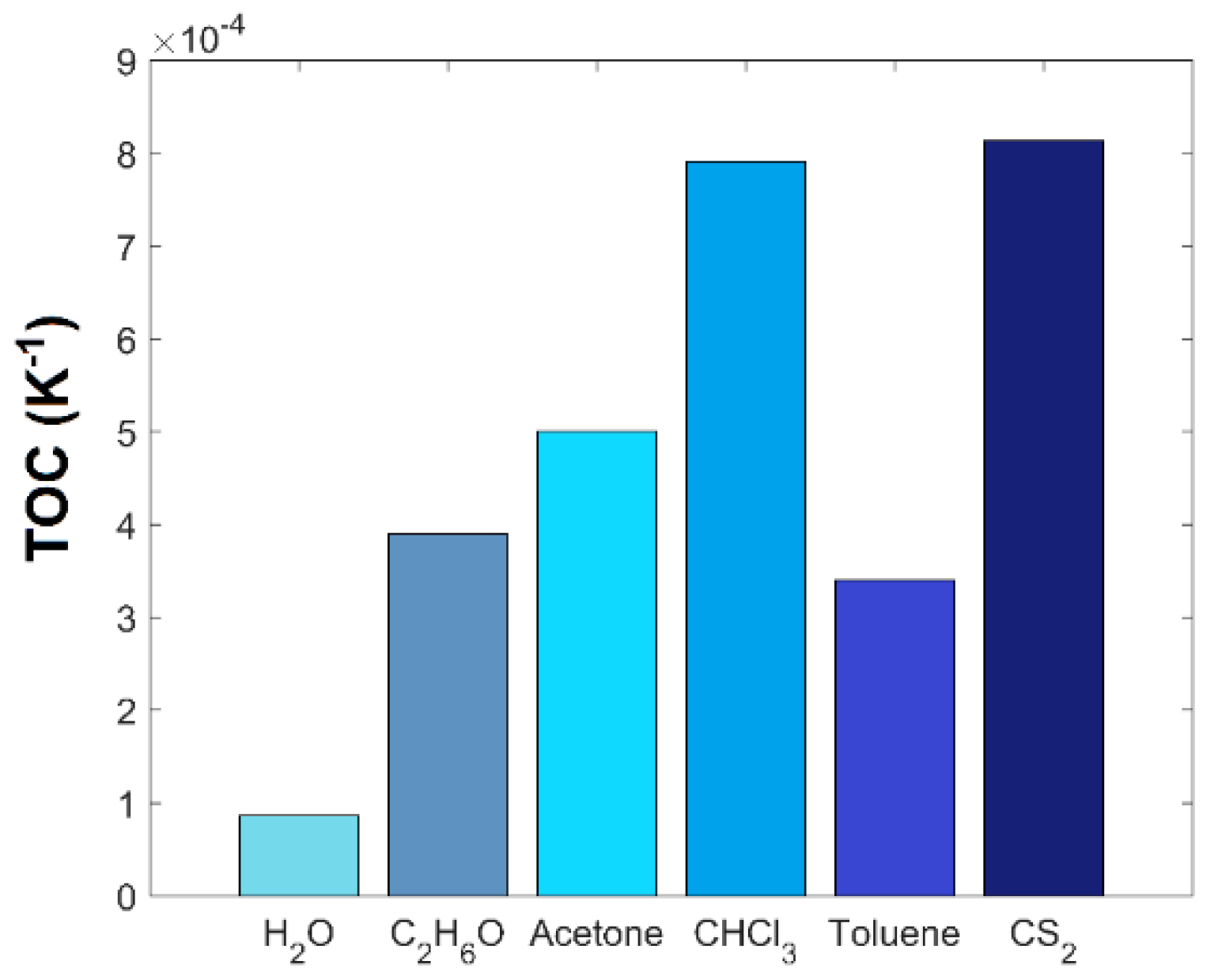
2.2. Optical Materials
2.3. Birefringence and Sagnac Interferometry
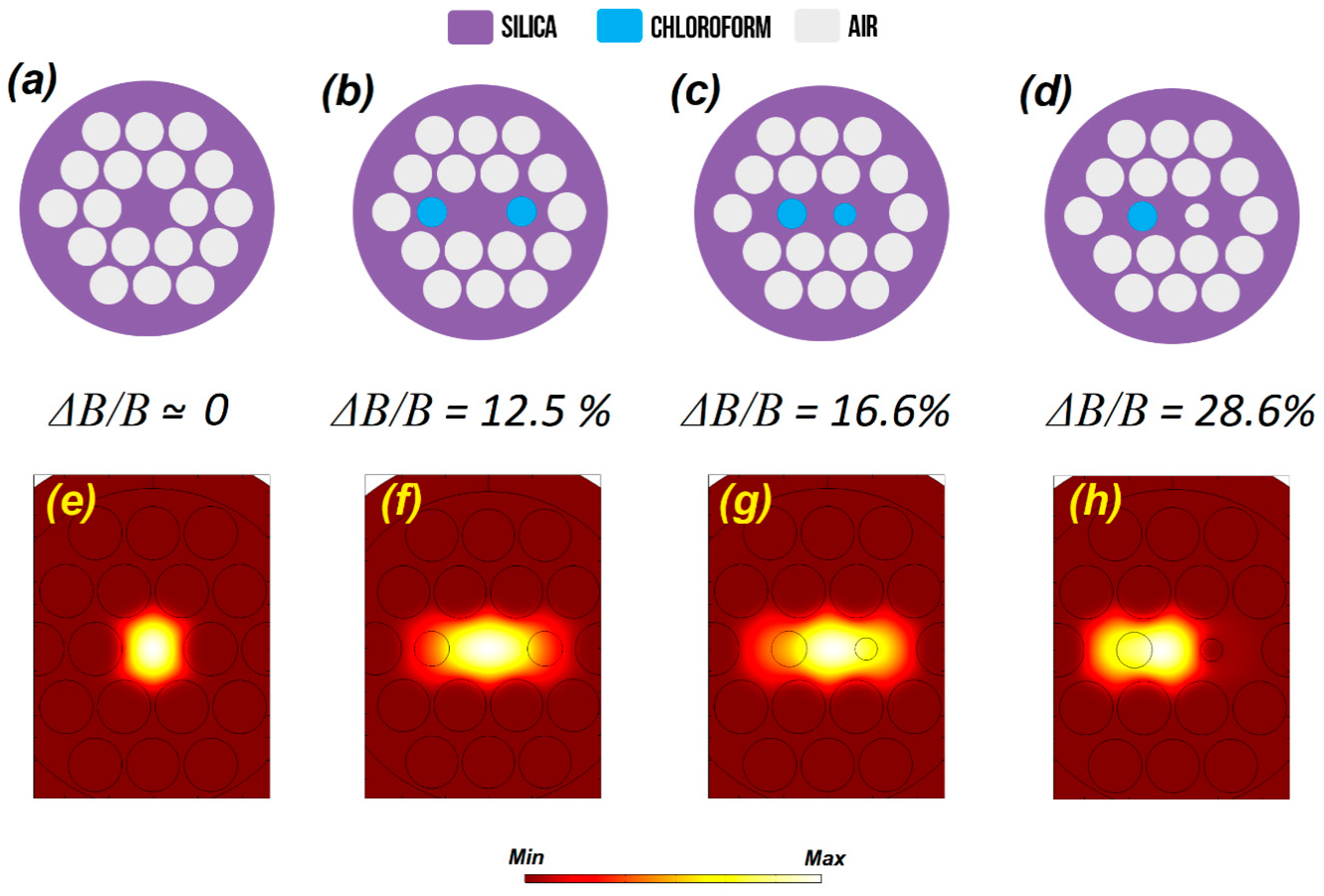
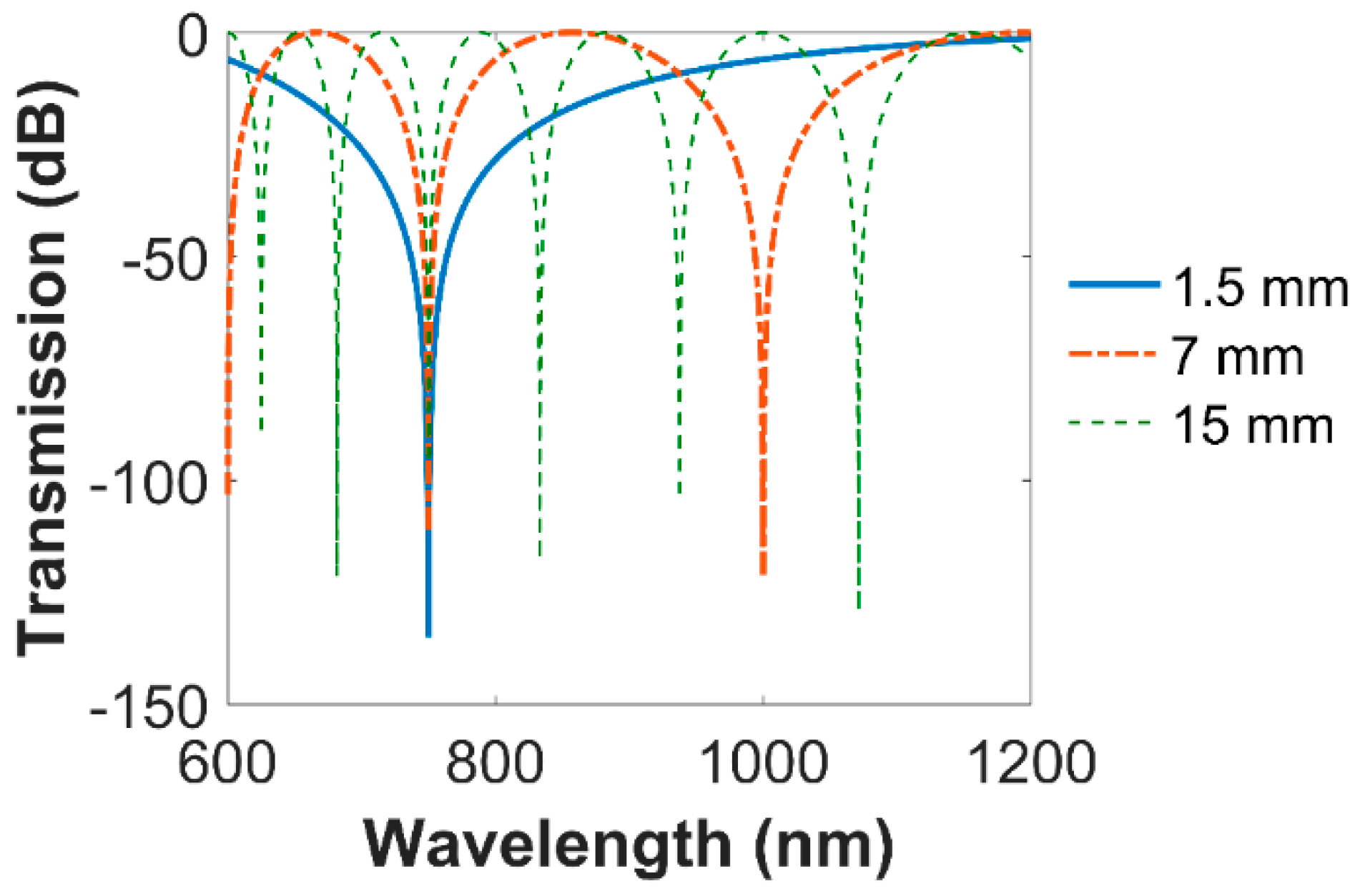
3. Design of the Sensor and Birefringence Sensitivity
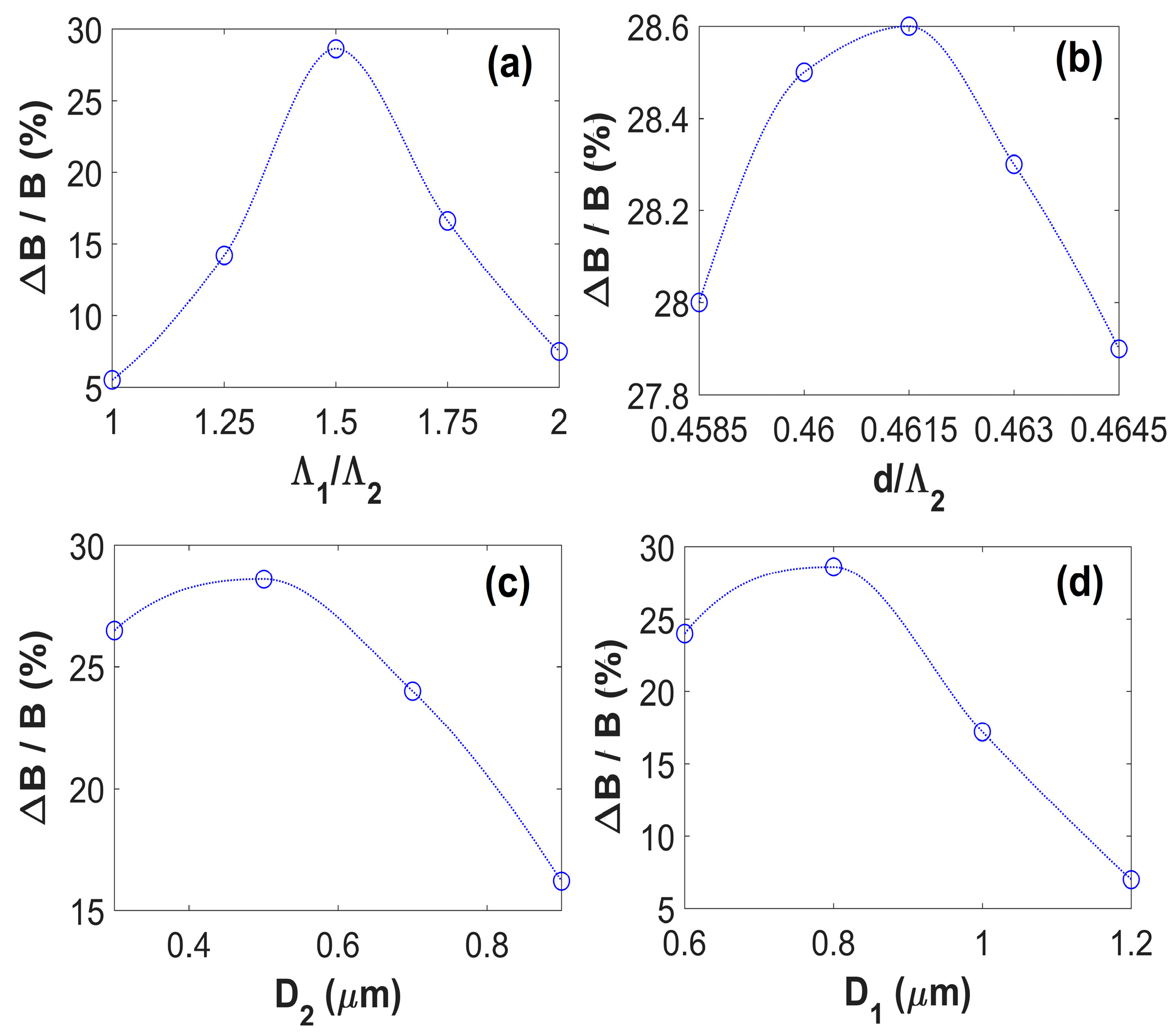
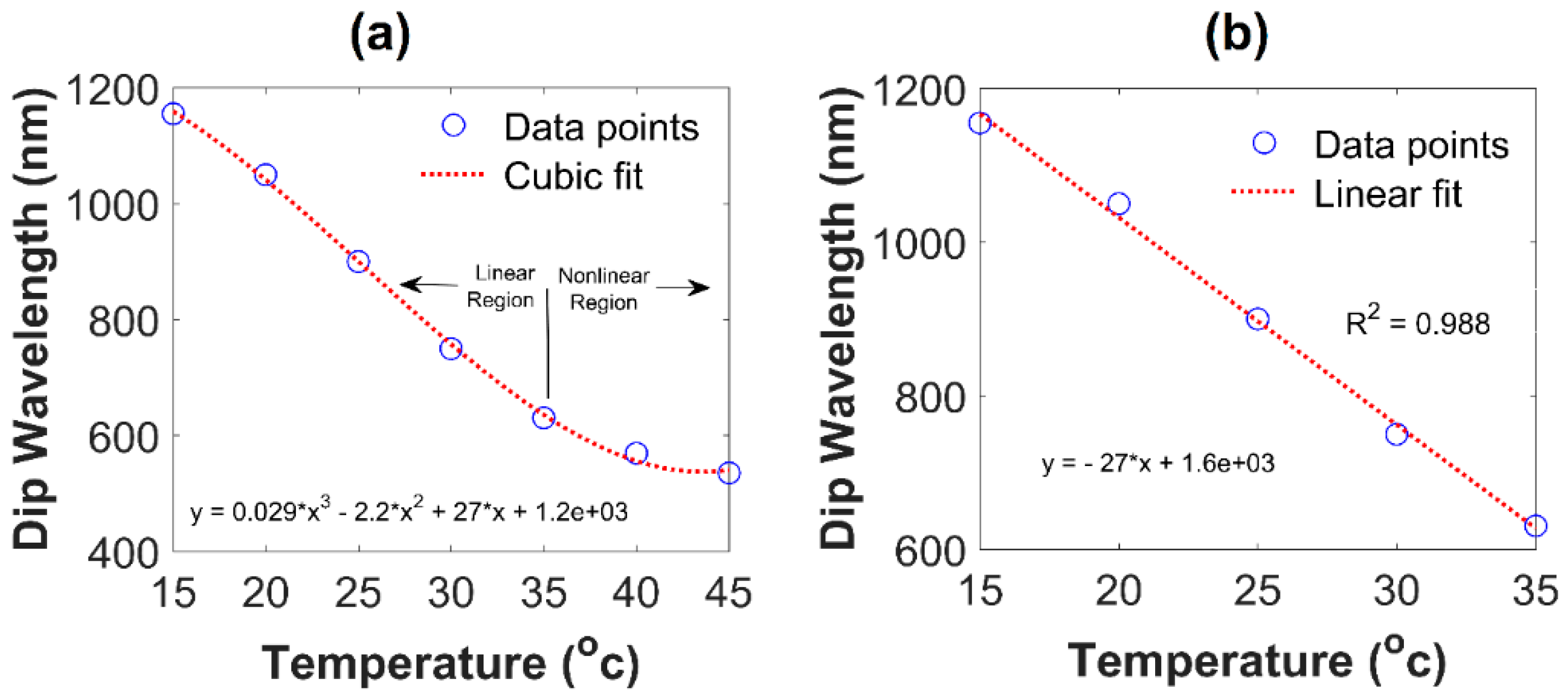
4. Performance Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bowden, C.M.; Zheltikov, A.M. Nonlinear optics of photonic crystals introduction. J. Opt. Soc. Am. B 2002, 19, 2046–2048. [Google Scholar] [CrossRef]
- Pathak, A.K.; Singh, V.K. A wide range and highly sensitive optical fiber pH sensor using polyacrylamide hydrogel. Opt. Fiber Technol. 2017, 39, 43–48. [Google Scholar] [CrossRef]
- Wadsworth, W.; Knight, J.; Birks, T. State-of-the-art photonic crystal fiber. Opt. Photonics News 2012, 23, 24–31. [Google Scholar] [CrossRef][Green Version]
- Monfared, Y.E.; Liang, C.; Khosravi, R.; Kacerovska, B.; Yang, S. Selectively toluene-filled photonic crystal fiber Sagnac interferometer for temperature sensing applications. Results Phys. 2019, 13, 102297. [Google Scholar] [CrossRef]
- Ahmadian, A.; Monfared, Y.E. Chalcogenide-tellurite composite photonic crystal fiber: Extreme non-linearity meets large birefringence. Appl. Sci. 2019, 9, 4445. [Google Scholar] [CrossRef]
- Cui, Y.; Shum, P.; Hu, D.; Wang, G.; Humbert, G.; Dinh, X. Temperature sensor by using selectively filled photonic crystal fiber Sagnac interferometer. IEEE Photonics J. 2012, 4, 1801–1808. [Google Scholar] [CrossRef]
- Qian, W.; Zhao, C.; He, S.; Dong, X.; Zhang, S.; Zhang, Z.; Jin, S.; Guo, J.; Wei, H. High-sensitivity temperature sensor based on an alcohol-filled photonic crystal fiber loop mirror. Opt. Lett. 2011, 36, 1548–1550. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, M.; Hao, C.; Zhao, Z.; Yao, J. Temperature sensing using photonic crystal fiber filled with silver nanowires and liquid. IEEE Photonics J. 2014, 6, 1–7. [Google Scholar] [CrossRef]
- Han, T.; Liu, Y.; Wang, Z.; Guo, J.; Wu, Z.; Wang, S.; Li, Z.; Zhou, W. Unique characteristics of a selective-filling photonic crystal fiber Sagnac interferometer and its application as high sensitivity sensor. Opt. Express 2013, 21, 122–128. [Google Scholar] [CrossRef]
- Vera, E.; Cordeiro, C.; Torres, P. Highly sensitive temperature sensor using a Sagnac loop interferometer based on a side-hole photonic crystal fiber filled with metal. Appl. Opt. 2017, 56, 156–162. [Google Scholar] [CrossRef]
- Sasaki, M.; Ando, T.; Nogawa, S.; Hane, K. Direct photolithography on optical fiber end. Jpn. J. Appl. Phys. 2002, 41, 4350–4355. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, Y.; Yariv, A. Fabrication of function microstructured optical fibers through a selective-filling technique. Appl. Phys. Lett. 2005, 85, 5182–5184. [Google Scholar] [CrossRef]
- Liu, J.; Cheng, T.; Yeo, Y.; Wang, Y.; Xue, L.; Xu, Z.; Wang, D. Light beam coupling between standard single mode fibers and highly nonlinear photonic crystal fibers based on the fused biconical tapering technique. Opt. Express 2009, 17, 3115–3123. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Manuel, R.; May-Arrioja, D.A.; Acevedo-Mijangos, J.; Domínguez-Cruz, R.F.; López-Cortés, D.; Torres-Cisneros, M. Ultra-high sensitivity temperature sensor using a fiber loop mirror based on a water-filled asymmetric two-hole fiber. IEEE Sens. 2020. [Google Scholar] [CrossRef]
- Pilla, V.; Munin, E.; Gesualdi, M.R.R. Measurement of the thermo-optic coefficient in liquids by laser-induced conical diffraction and thermal lens technique. J. Opt. A Pure Appl. Opt. 2009, 11, 105201. [Google Scholar] [CrossRef]
- Kim, Y.H.; Park, S.J.; Jeon, S.; Ju, S.; Park, C.; Han, W.; Lee, B. Thermo-optic coefficient measurement of liquids based on simultaneous temperature and refractive index sensing capability of a two-mode fiber interferometric probe. Opt. Express 2012, 20, 23744–23754. [Google Scholar] [CrossRef]
- Monfared, Y.E.; Ponomarenko, S.A. Extremely nonlinear carbon-disulfide-filled photonic crystal fiber with controllable dispersion. Opt. Mater. 2019, 88, 406–411. [Google Scholar] [CrossRef]
- Monfared, Y.E.; Hajati, M.; Liang, C.; Yang, S.; Qasymeh, M. Quasi-D-shaped fiber optic plasmonic biosensor for high-index analyte detection. IEEE Sens. 2019. [Google Scholar] [CrossRef]
- Malitson, I.H. Interspecimen comparison of the refractive index of fused silica. J. Opt. Soc. Am. 1965, 55, 1205–1208. [Google Scholar] [CrossRef]
- Ayyanar, N.; Vasanth, R.; Rajab, J.; Vigneswaran, D.; Lakshmi, B.; Sumathia, M.; Porseziand, K. Highly efficient compact temperature sensor using liquid infiltrated asymmetric dual elliptical core photonic crystal fiber. Opt. Mater. 2017, 64, 482–574. [Google Scholar] [CrossRef]
- Monfared, Y.E. Refractive index sensor based on surface plasmon resonance excitation in a d-shaped photonic crystal fiber coated by titanium nitride. Plasmonics 2020, 15, 535–542. [Google Scholar] [CrossRef]
- Rifat, A.A.; Mahdiraji, G.A.; Sua, Y.M.; Ahmed, R.; Shee, Y.G.; Adikan, F.R.M. Highly sensitive multi-core flat fiber surface plasmon resonance refractive index sensor. Opt. Express 2016, 24, 2485–2495. [Google Scholar] [CrossRef] [PubMed]
- Vázquez, C.; Tapetado, A.; Pinzón, P.J.; Montero, D.S.; López-Cardona1, J.D.; Contreras, P.; Zubia, J. Temperature sensing using optical fibers in harsh environments. In Proceedings of the 19th International Conference on Transparent Optical Networks (ICTON), Girona, Spain, 2–6 July 2017; pp. 1–4. [Google Scholar]
- Zhang, M.; Ma, X.; Wang, L.; Lai, S.; Zhou, H.; Zhao, H.; Liao, Y. photonic sensors review progress of optical fiber sensors and its application in harsh environment. Photonic Sens. 2011, 1, 84–89. [Google Scholar] [CrossRef][Green Version]



| Ref [6] | Ref [7] | Ref [4] | This Work | |
|---|---|---|---|---|
| Infiltration Liquid | Water | Alcohol | Toluene | Chloroform |
| Maximum Birefringence | 1.999 × 10−4 | 3.5 × 10−4 | 8.68 × 10−5 | 7.7 × 10−4 |
| Average Sensitivity (nm/°C) | 2.58 | 6.6 | 11 | 17.53 |
| Temperature Range (°C) | 25–42 | 8–34 | 20–30 | 15–35 |
| Resolution (°C) | 4 × 10−3 | - | - | 5.7 × 10−4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monfared, Y.E.; Ahmadian, A.; Dhasarathan, V.; Liang, C. Liquid-Filled Highly Asymmetric Photonic Crystal Fiber Sagnac Interferometer Temperature Sensor. Photonics 2020, 7, 33. https://doi.org/10.3390/photonics7020033
Monfared YE, Ahmadian A, Dhasarathan V, Liang C. Liquid-Filled Highly Asymmetric Photonic Crystal Fiber Sagnac Interferometer Temperature Sensor. Photonics. 2020; 7(2):33. https://doi.org/10.3390/photonics7020033
Chicago/Turabian StyleMonfared, Yashar E., Amir Ahmadian, Vigneswaran Dhasarathan, and Chunhao Liang. 2020. "Liquid-Filled Highly Asymmetric Photonic Crystal Fiber Sagnac Interferometer Temperature Sensor" Photonics 7, no. 2: 33. https://doi.org/10.3390/photonics7020033
APA StyleMonfared, Y. E., Ahmadian, A., Dhasarathan, V., & Liang, C. (2020). Liquid-Filled Highly Asymmetric Photonic Crystal Fiber Sagnac Interferometer Temperature Sensor. Photonics, 7(2), 33. https://doi.org/10.3390/photonics7020033







