Microstructured Fibers Based on Tellurite Glass for Nonlinear Conversion of Mid-IR Ultrashort Optical Pulses
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental
2.2. Numerical
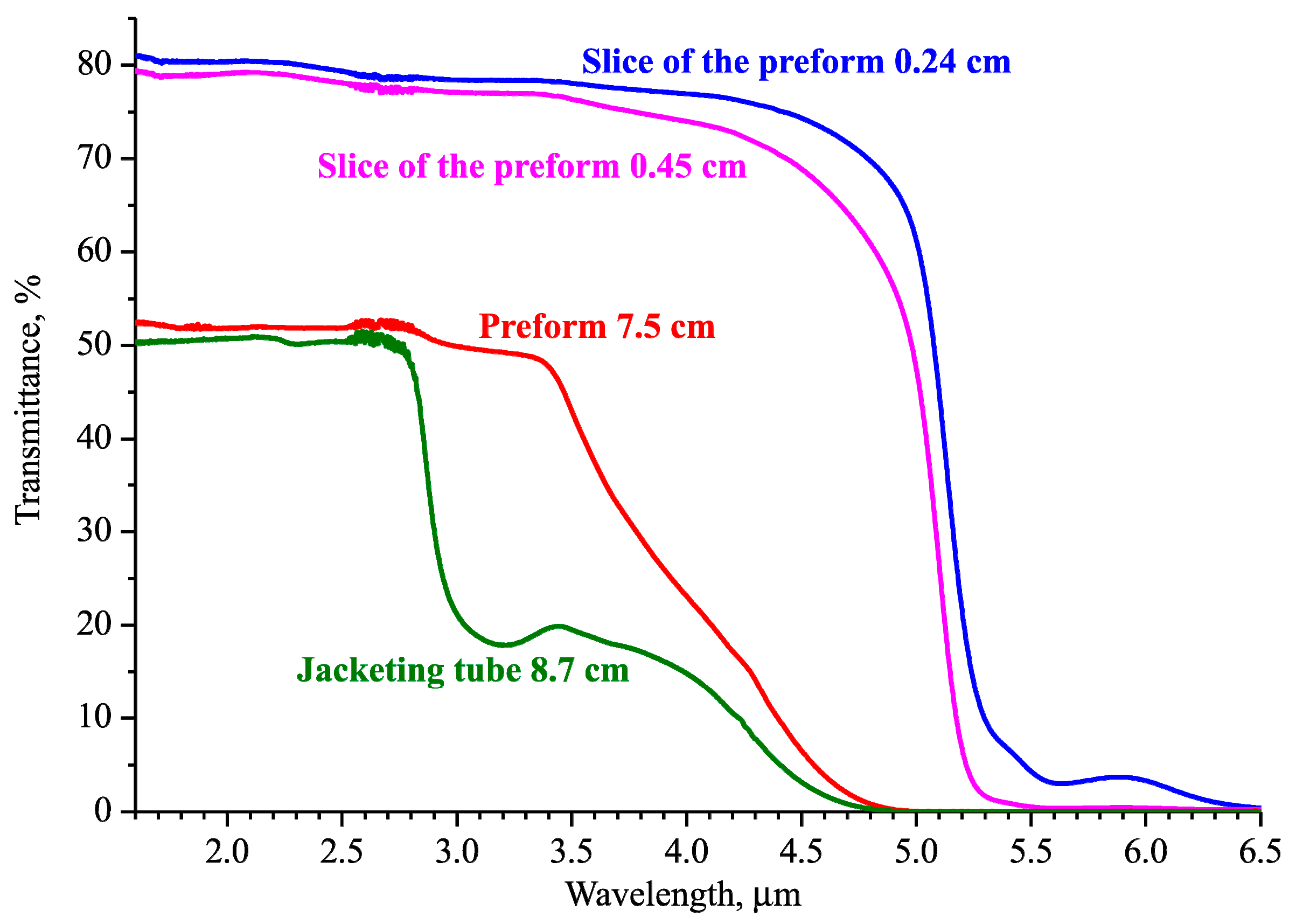
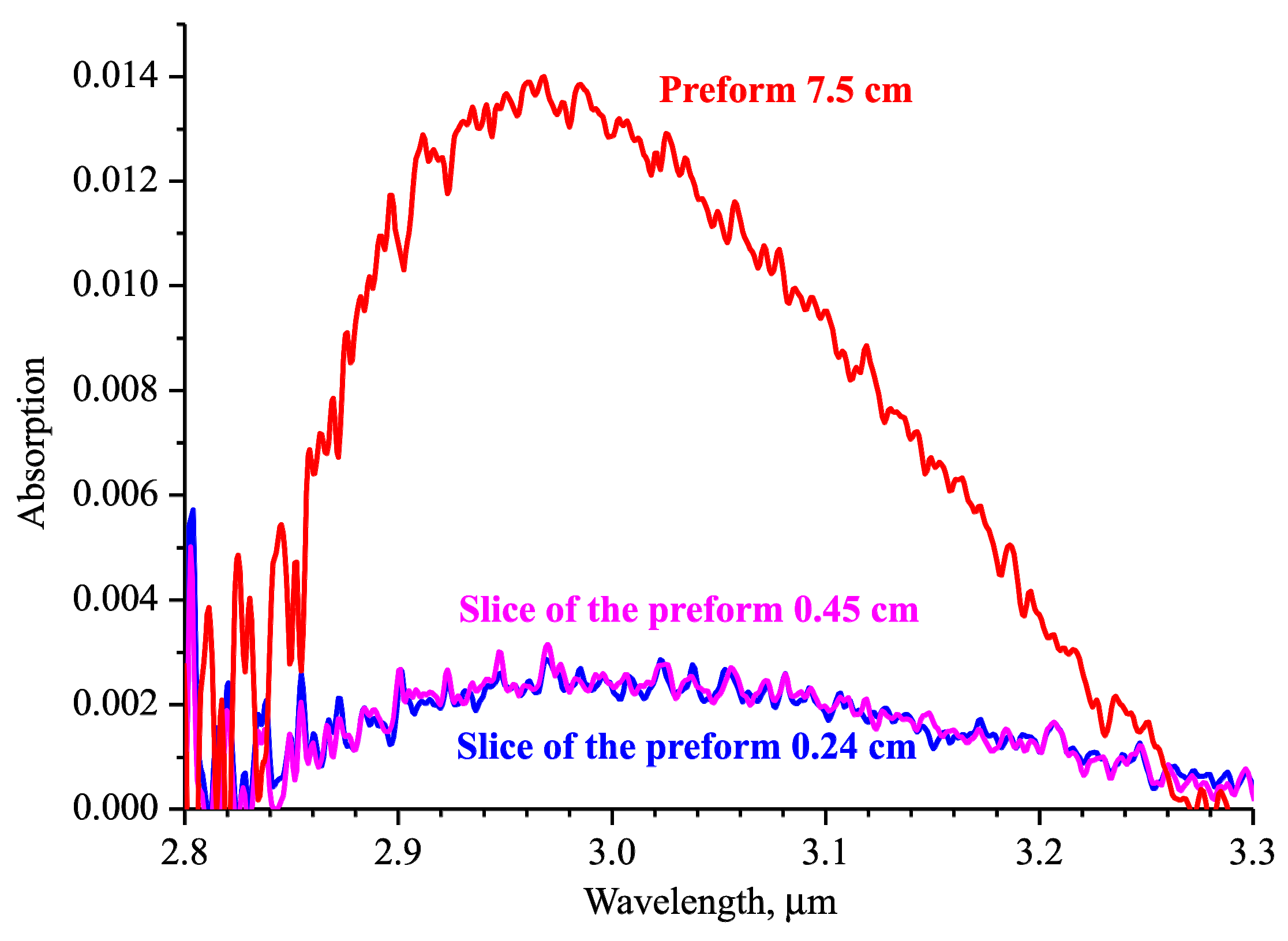
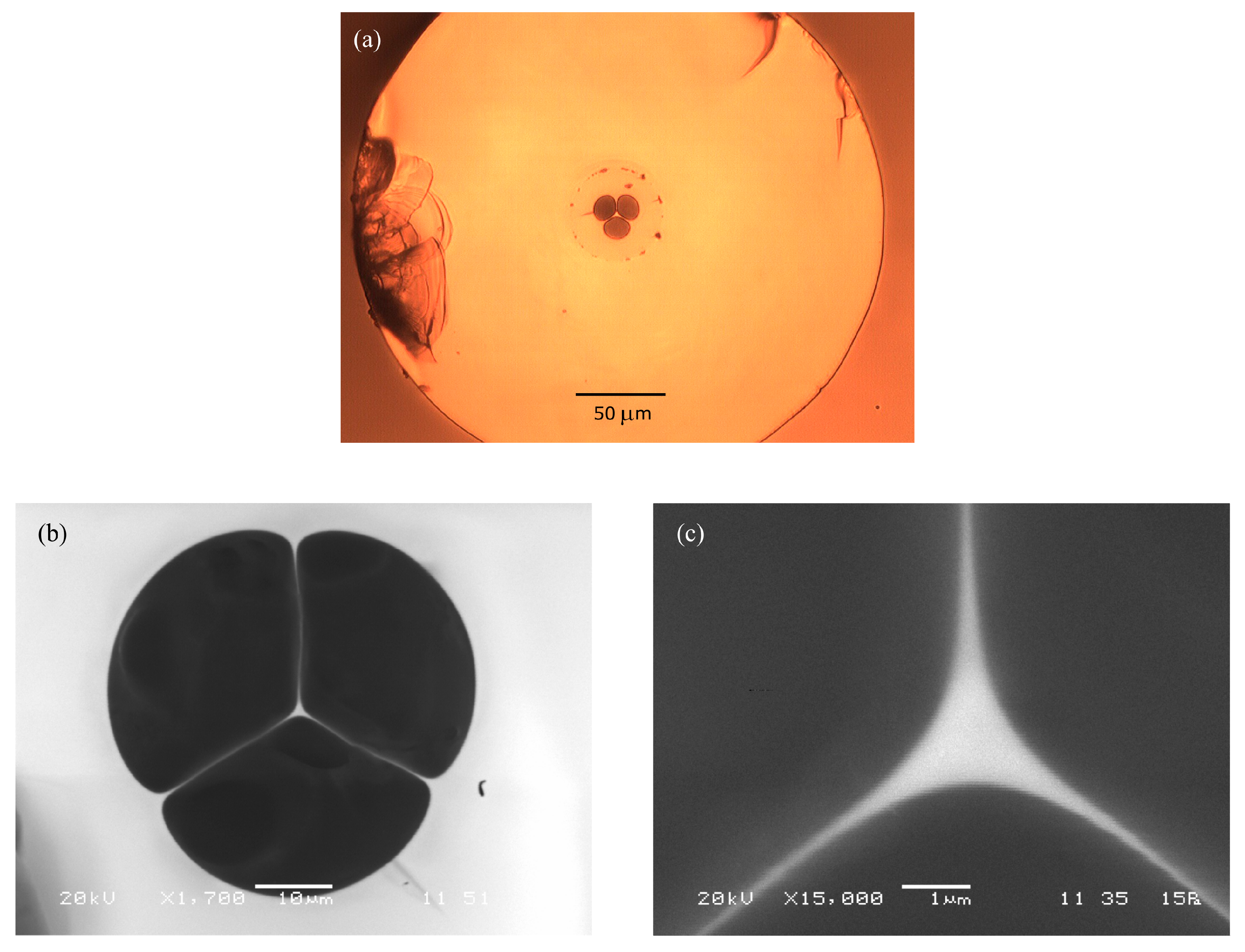
3. Experimental Results
4. Numerical Results
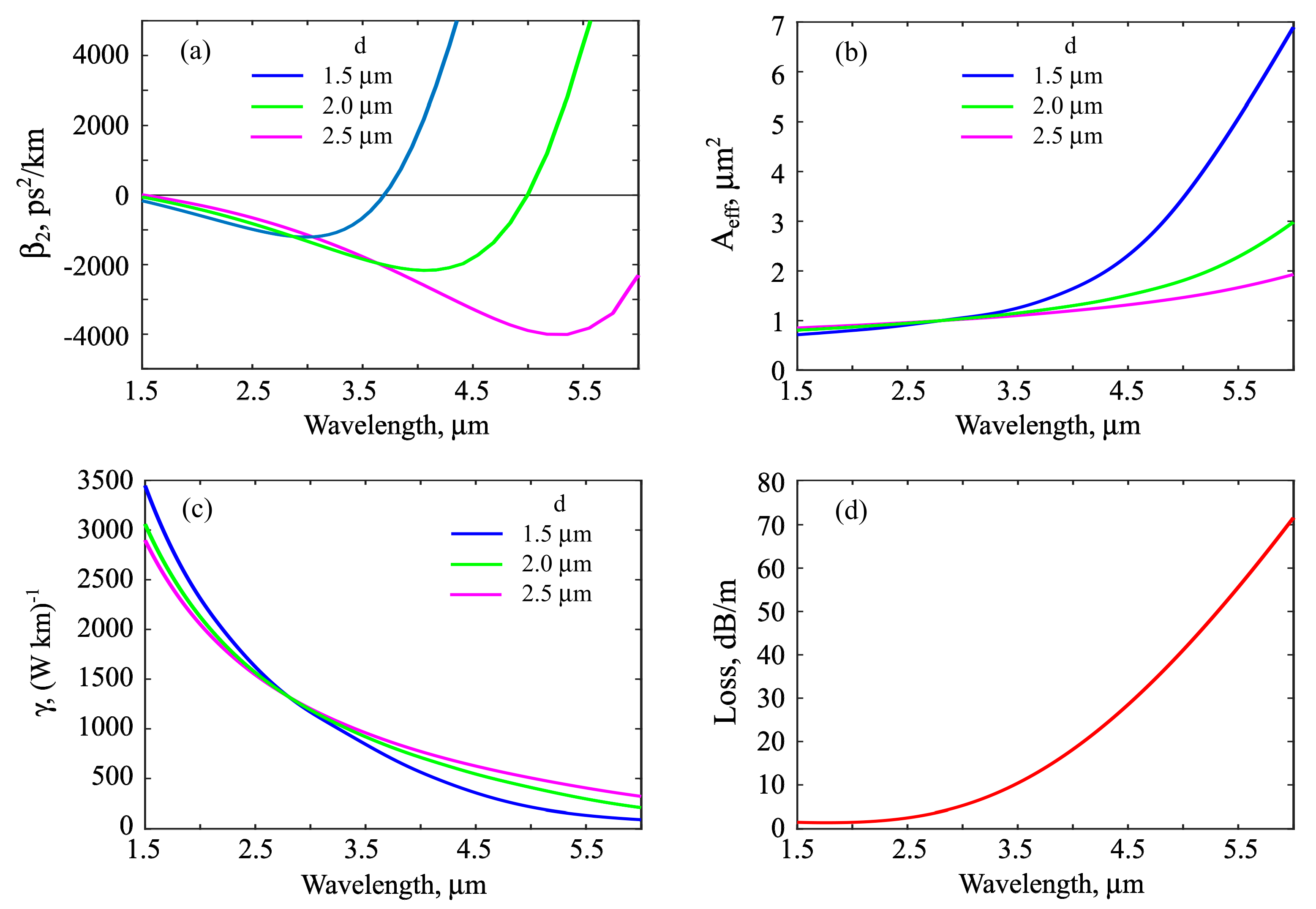
4.1. Dispersion and Nonlinearity of MS Fibers
4.2. SSFS in MS Fibers
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tao, G.; Ebendorff-Heidepriem, H.; Stolyarov, A.M.; Danto, S.; Badding, J.V.; Fink, Y.; Ballato, J.; Abouraddy, A.F. Infrared fibers. Adv. Opt. Photonics 2015, 7, 379–458. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Z.F.; Tam, H.Y.; Tao, X. Multifunctional smart optical fibers: Materials, fabrication, and sensing applications. Photonics 2019, 6, 48. [Google Scholar] [CrossRef] [Green Version]
- Bufetov, I.A.; Kosolapov, A.F.; Pryamikov, A.D.; Gladyshev, A.V.; Kolyadin, A.N.; Krylov, A.A.; Yatsenko, Y.P.; Biriukov, A.S. Revolver hollow core optical fibers. Fibers 2018, 6, 39. [Google Scholar] [CrossRef] [Green Version]
- Falconi, M.C.; Laneve, D.; Prudenzano, F. Advances in mid-IR fiber lasers: Tellurite, fluoride and chalcogenide. Fibers 2017, 5, 23. [Google Scholar] [CrossRef] [Green Version]
- Dai, S.; Wang, Y.; Peng, X.; Zhang, P.; Wang, X.; Xu, Y. A review of mid-infrared supercontinuum generation in chalcogenide glass fibers. Appl. Sci. 2018, 8, 707. [Google Scholar] [CrossRef] [Green Version]
- Petersen, C.R.; Møller, U.; Kubat, I.; Zhou, B.; Dupont, S.; Ramsay, J.; Benson, T.; Sujecki, S.; Abdel-Moneim, N.; Tang, Z.; et al. Mid-infrared supercontinuum covering the 1.4–13.3 μm molecular fingerprint region using ultra-high NA chalcogenide step-index fibre. Nat. Photonics 2014, 8, 830. [Google Scholar] [CrossRef]
- Saini, T.S.; Hoa, N.P.T.; Tuan, T.H.; Luo, X.; Suzuki, T.; Ohishi, Y. Tapered tellurite step-index optical fiber for coherent near-to-mid-IR supercontinuum generation: experiment and modeling. Appl. Opt. 2019, 58, 415–421. [Google Scholar] [CrossRef] [PubMed]
- Martinez, R.A.; Plant, G.; Guo, K.; Janiszewski, B.; Freeman, M.J.; Maynard, R.L.; Islam, M.N.; Terry, F.L.; Alvarez, O.; Chenard, F.; et al. Mid-infrared supercontinuum generation from 1.6 to >11 μm using concatenated step-index fluoride and chalcogenide fibers. Opt. Lett. 2018, 43, 296–299. [Google Scholar] [CrossRef] [PubMed]
- Duval, S.; Gauthier, J.C.; Robichaud, L.R.; Paradis, P.; Olivier, M.; Fortin, V.; Bernier, M.; Piché, M.; Vallée, R. Watt-level fiber-based femtosecond laser source tunable from 2.8 to 3.6 μm. Opt. Lett. 2016, 41, 5294–5297. [Google Scholar] [CrossRef]
- Tang, Y.; Wright, L.G.; Charan, K.; Wang, T.; Xu, C.; Wise, F.W. Generation of intense 100 fs solitons tunable from 2 to 4.3 μm in fluoride fiber. Optica 2016, 3, 948–951. [Google Scholar] [CrossRef]
- Cheng, T.; Kanou, Y.; Asano, K.; Deng, D.; Liao, M.; Matsumoto, M.; Misumi, T.; Suzuki, T.; Ohishi, Y. Soliton self-frequency shift and dispersive wave in a hybrid four-hole AsSe2-As2S5 microstructured optical fiber. Appl. Phys. Lett. 2014, 104, 121911. [Google Scholar] [CrossRef]
- Bi, W.; Li, X.; Xing, Z.; Zhou, Q.; Fang, Y.; Gao, W.; Xiong, L.; Hu, L.; Liao, M. Wavelength conversion through soliton self-frequency shift in tellurite microstructured fiber with picosecond pump pulse. J. Appl. Phys. 2016, 119, 043102. [Google Scholar] [CrossRef]
- Koptev, M.Y.; Anashkina, E.A.; Andrianov, A.V.; Dorofeev, V.V.; Kosolapov, A.F.; Muravyev, S.V.; Kim, A.V. Widely tunable mid-infrared fiber laser source based on soliton self-frequency shift in microstructured tellurite fiber. Opt. Lett. 2015, 40, 4094–4097. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Cheng, T.; Deng, D.; Sega, D.; Liu, L.; Xue, X.; Suzuki, T.; Ohishi, Y. Tunable soliton generation in a birefringent tellurite microstructured optical fiber. IEEE Photonics Technol. Lett. 2015, 27, 1547–1549. [Google Scholar] [CrossRef]
- Domachuk, P.; Wolchover, N.A.; Cronin-Golomb, M.; Wang, A.; George, A.K.; Cordeiro, C.M.B.; Knight, J.C.; Omenetto, F.G. Over 4000 nm bandwidth of mid-IR supercontinuum generation in sub-centimeter segments of highly nonlinear tellurite PCFs. Opt. Express 2008, 16, 7161–7168. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thapa, R.; Rhonehouse, D.; Nguyen, D.; Wiersma, K.; Smith, C.; Zong, J.; Chavez-Pirson, A. Mid-IR supercontinuum generation in ultra-low loss, dispersion-zero shifted tellurite glass fiber with extended coverage beyond 4.5 μm. In Technologies for Optical Countermeasures X; And High-Power Lasers 2013: Technology and Systems; International Society for Optics and Photonics: Bellingham, WA, USA, 2013; Volume 8898, p. 889808. [Google Scholar] [CrossRef]
- Kedenburg, S.; Strutynski, C.; Kibler, B.; Froidevaux, P.; Désévédavy, F.; Gadret, G.; Jules, J.-C.; Steinle, T.; Mörz, F.; Steinmann, A.; et al. High repetition rate mid-infrared supercontinuum generation from 1.3 to 5.3 μm in robust step-index tellurite fibers. JOSA B 2017, 34, 601–607. [Google Scholar] [CrossRef]
- Mirov, S.B.; Moskalev, I.S.; Vasilyev, S.; Smolski, V.; Fedorov, V.V.; Martyshkin, D.; Peppers, J.; Mirov, M.; Dergachev, A.; Gapontsev, V. Frontiers of mid-IR lasers based on transition metal doped chalcogenides. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1601829. [Google Scholar] [CrossRef]
- Duval, S.; Bernier, M.; Fortin, V.; Genest, J.; Piché, M.; Vallée, R. Femtosecond fiber lasers reach the mid-infrared. Optica 2015, 2, 623–626. [Google Scholar] [CrossRef]
- Gu, H.; Qin, Z.; Xie, G.; Hai, T.; Yuan, P.; Ma, J.; Qian, L. Generation of 131 fs mode-locked pulses from 2.8 μm Er:ZBLAN fiber laser. Chin. Opt. Lett. 2020, 18, 031402. [Google Scholar] [CrossRef]
- Antipov, S.; Hudson, D.D.; Fuerbach, A.; Jackson, S.D. High-power mid-infrared femtosecond fiber laser in the water vapor transmission window. Optica 2016, 3, 1373–1376. [Google Scholar] [CrossRef] [Green Version]
- Anashkina, E.A.; Koptev, M.Y.; Andrianov, A.V.; Dorofeev, V.V.; Singh, S.; Leuchs, G.; Kim, A.V. Reconstruction of optical pulse intensity and phase based on SPM spectra measurements in microstructured tellurite fiber in telecommunication range. J. Lightwave Technol. 2019, 37, 4375–4381. [Google Scholar] [CrossRef]
- Pakarzadeh, H.; Forghani, S.E.; Amiri, I.S. Propagation of telecommunication pulses in photonics nanowires: A comparative physics study. Results Phys. 2019, 13, 102342. [Google Scholar] [CrossRef]
- Cheng, T.; Zhang, F.; Tanaka, S.; Li, S.; Yan, X.; Zhang, X.; Suzuki, T.; Ohishi, Y. Ultrafast all-optical signal modulation induced by optical Kerr effect in a tellurite photonic bandgap fiber. Photonics 2019, 6, 113. [Google Scholar] [CrossRef] [Green Version]
- Dianov, E.M. Fibre optics: Forty years later. Quantum Electron. 2010, 40, 1. [Google Scholar] [CrossRef]
- Senkans, U.; Braunfelds, J.; Lyashuk, I.; Porins, J.; Spolitis, S.; Bobrovs, V. Research on FBG-Based Sensor Networks and Their Coexistence with Fiber Optical Transmission Systems. J. Sens. 2019, 2019, 6459387. [Google Scholar] [CrossRef] [Green Version]
- Anashkina, E.A.; Dorofeev, V.V.; Koltashev, V.V.; Kim, A.V. Development of Er3+-doped high-purity tellurite glass fibers for gain-switched laser operation at 2.7 μm. Opt. Mater. Express 2017, 7, 4337–4351. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Dorofeev, V.V.; Muravyev, S.V.; Motorin, S.E.; Andrianov, A.V.; Sorokin, A.A.; Koptev, M.Y.; Singh, S.; Kim, A.V. Possibilities of laser amplification and measurement of the field structure of ultrashort pulses in the range of 2.7–3 μm in tellurite glass fibres doped with erbium ions. Quantum Electron. 2018, 48, 1118–1127. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Andrianov, A.V.; Dorofeev, V.V.; Kim, A.V. Toward a mid-infrared femtosecond laser system with suspended-core tungstate-tellurite glass fibers. Appl. Opt. 2016, 55, 4522–4530. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics, 6th ed.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Foster, M.A.; Moll, K.D.; Gaeta, A.L. Optimal waveguide dimensions for nonlinear interactions. Opt. Express 2004, 12, 2880–2887. [Google Scholar] [CrossRef] [Green Version]
- Laegsgaard, J. Mode profile dispersion in the generalized nonlinear Schrödinger equation. Opt. Express 2007, 15, 16110–16123. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Shiryaev, V.S.; Koptev, M.Y.; Stepanov, B.S.; Muravyev, S.V. Development of As-Se tapered suspended-core fibers for ultra-broadband mid-IR wavelength conversion. J. Non Cryst. Solids 2018, 480, 43–50. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Shiryaev, V.S.; Snopatin, G.E.; Muraviev, S.V.; Kim, A.V. On the possibility of mid-IR supercontinuum generation in As-Se-Te/As-S core/clad fibers with all-fiber femtosecond pump source. J. Non Cryst. Solids 2018, 480, 38–42. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.; Qin, G.; Liao, M.; Suzuki, T.; Ohishi, Y. Transient Raman response effects on the soliton self-frequency shift in tellurite microstructured optical fiber. JOSA B 2011, 28, 1831–1836. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Sorokin, A.A.; Marisova, M.P.; Andrianov, A.V. Development and numerical simulation of tellurite glass microresonators for optical frequency comb generation. J. Non Cryst. Solids 2019, 522, 119567. [Google Scholar] [CrossRef]
- Liao, M.; Gao, W.; Duan, Z.; Yan, X.; Suzuki, T.; Ohishi, Y. Directly draw highly nonlinear tellurite microstructured fiber with diameter varying sharply in a short fiber length. Opt. Express 2012, 20, 1141–1150. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Zhou, N.; Li, Q.; Jia, Z.; Wang, F.; Qin, W.; Zhang, D.; Qin, G. Design of all-solid W-type index fluorotellurite fibers with near-zero-flattened chromatic dispersion for optical frequency comb generation. Appl. Opt. 2019, 58, 8852–8857. [Google Scholar] [CrossRef] [PubMed]



| C1 | C2 | C3 | C4, μm2 | C5, μm2 |
|---|---|---|---|---|
| 2.4909866 | 1.9515037 | 3.0212592 | 0.056740339 | 225 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anashkina, E.A.; Dorofeev, V.V.; Skobelev, S.A.; Balakin, A.A.; Motorin, S.E.; Kosolapov, A.F.; Andrianov, A.V. Microstructured Fibers Based on Tellurite Glass for Nonlinear Conversion of Mid-IR Ultrashort Optical Pulses. Photonics 2020, 7, 51. https://doi.org/10.3390/photonics7030051
Anashkina EA, Dorofeev VV, Skobelev SA, Balakin AA, Motorin SE, Kosolapov AF, Andrianov AV. Microstructured Fibers Based on Tellurite Glass for Nonlinear Conversion of Mid-IR Ultrashort Optical Pulses. Photonics. 2020; 7(3):51. https://doi.org/10.3390/photonics7030051
Chicago/Turabian StyleAnashkina, Elena A., Vitaly V. Dorofeev, Sergey A. Skobelev, Alexey A. Balakin, Sergei E. Motorin, Alexey F. Kosolapov, and Alexey V. Andrianov. 2020. "Microstructured Fibers Based on Tellurite Glass for Nonlinear Conversion of Mid-IR Ultrashort Optical Pulses" Photonics 7, no. 3: 51. https://doi.org/10.3390/photonics7030051
APA StyleAnashkina, E. A., Dorofeev, V. V., Skobelev, S. A., Balakin, A. A., Motorin, S. E., Kosolapov, A. F., & Andrianov, A. V. (2020). Microstructured Fibers Based on Tellurite Glass for Nonlinear Conversion of Mid-IR Ultrashort Optical Pulses. Photonics, 7(3), 51. https://doi.org/10.3390/photonics7030051







