A Programmable Mode-Locked Fiber Laser Using Phase-Only Pulse Shaping and the Genetic Algorithm
Abstract
:1. Introduction
2. Principle of Operation
2.1. Basic Laser Cavity
2.2. Phase-Only Pulse Shaper
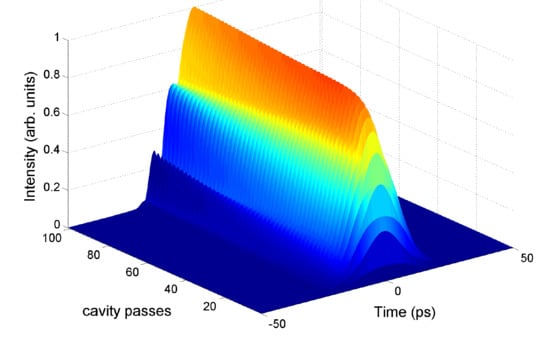
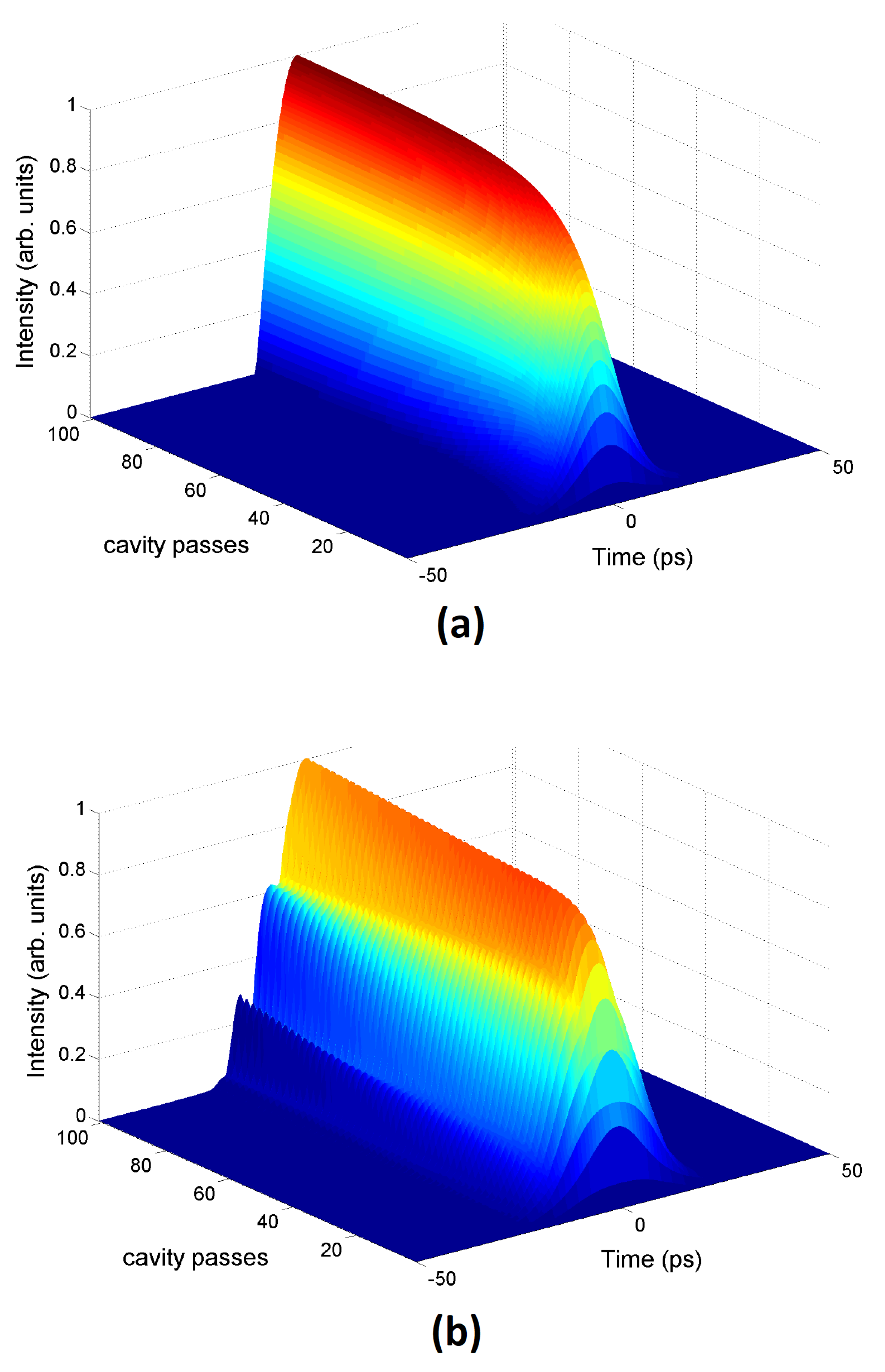
3. Simulation Results
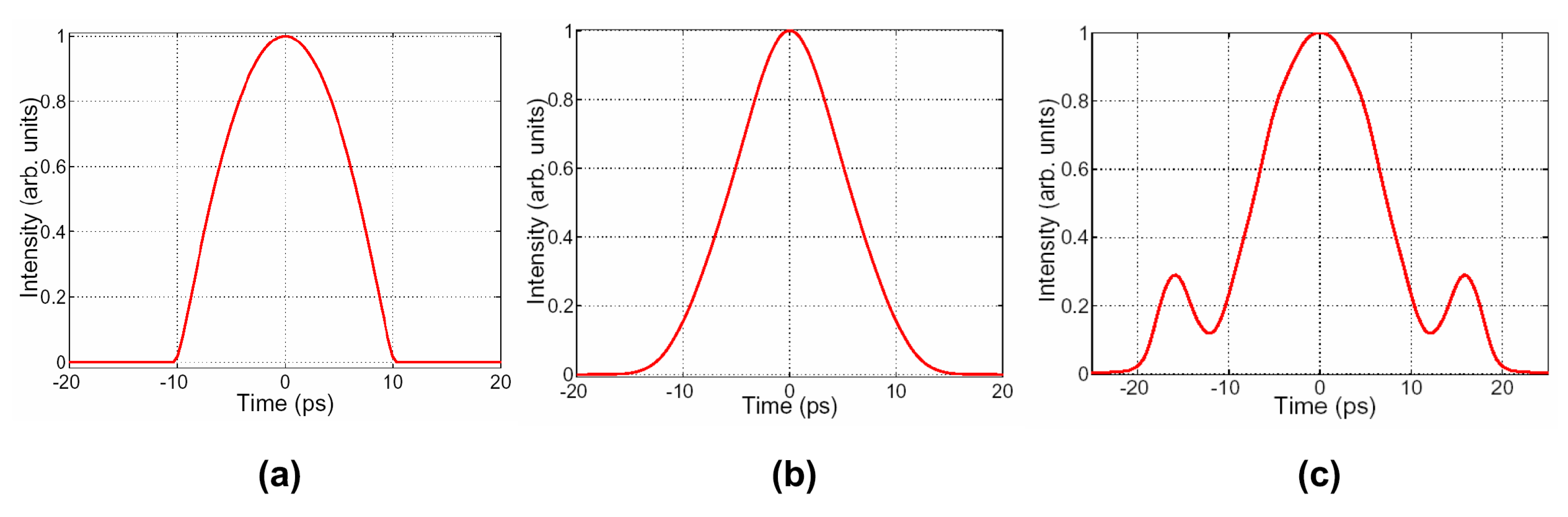
3.1. Test Codewords
3.2. Optimization Methods
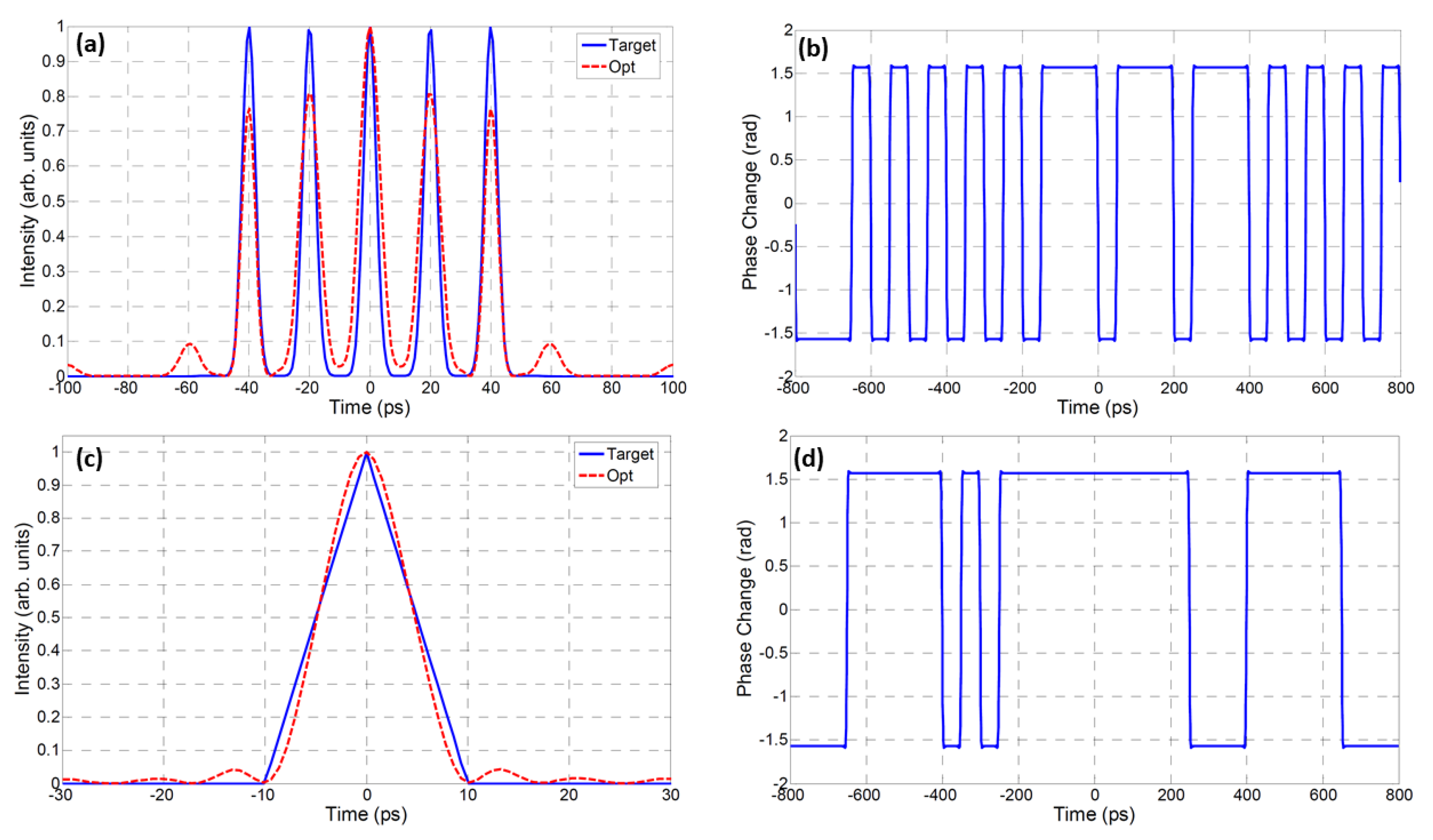
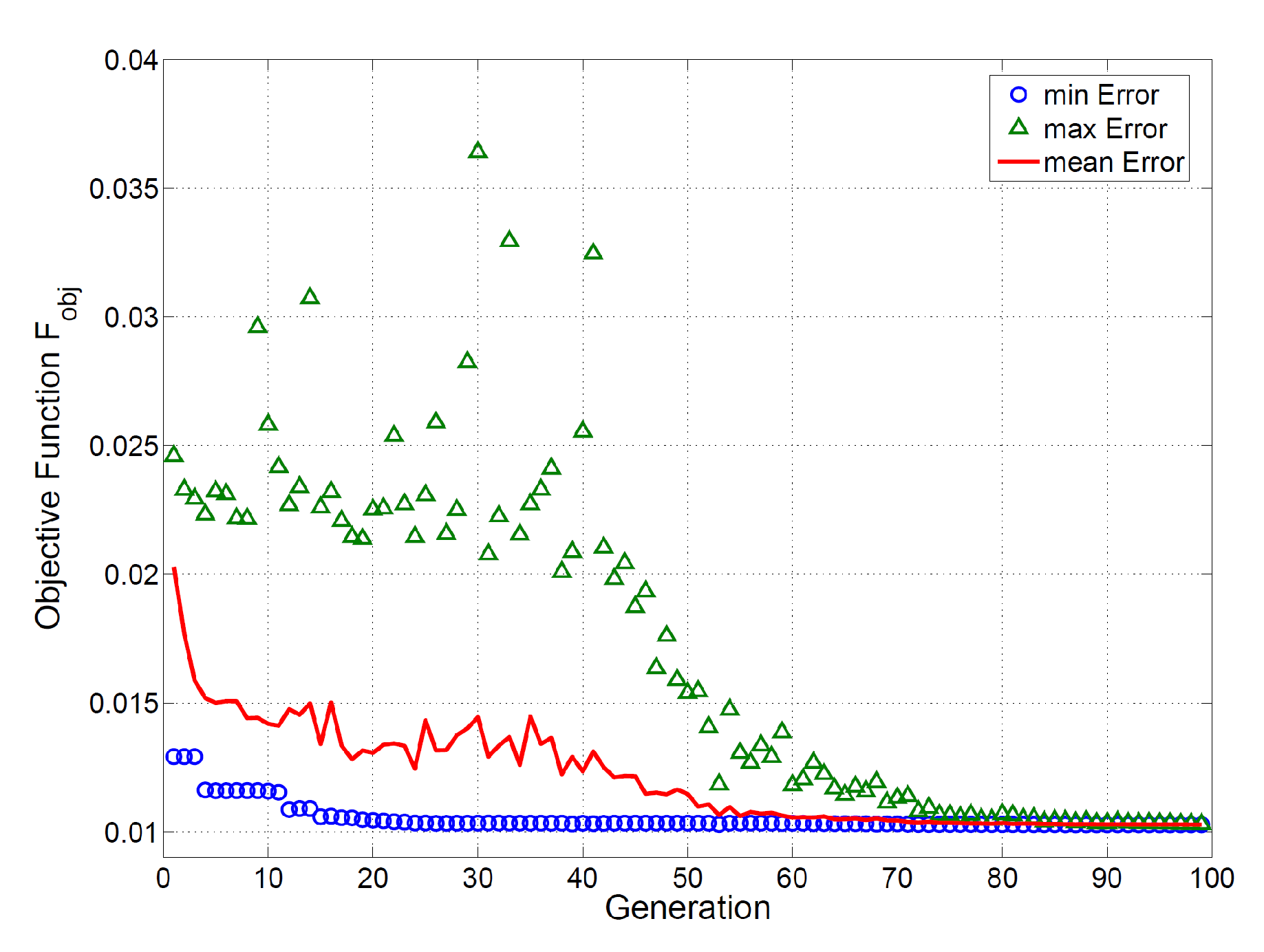
3.3. Genetic Algorithm Method
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, C.-H.; Benedick, A.J.; Fendel, P.; Glenday, A.G.; Kärtner, F.X.; Phillips, D.F.; Sasselov, D.; Szentgyorgyi, A.; Walsworth, R.L. A laser frequency comb that enables radial velocity measurements with a precision of 1 cm s-1. Nature 2008, 452, 610–612. [Google Scholar] [CrossRef] [Green Version]
- Hergenroder, R.; Samek, O.; Hommes, V. Femtosecond laser ablation elemental mass spectrometry. Mass Spectrom. Rev. 2006, 25, 551–572. [Google Scholar] [CrossRef] [PubMed]
- Schimmel, G.; Produit, T.; Mongin, D.; Kasparian, J.; Wolf, J.-P. Free space laser telecommunication through fog. Optica 2018, 5, 1338–1341. [Google Scholar] [CrossRef]
- Karar, A.S. Super Gaussian pulse generation in a passively mode-locked fiber laser. Optik 2019, 194, 163072. [Google Scholar] [CrossRef]
- Liu, W.; Fan, J.; Xie, C.; Song, Y.; Gu, C.; Chai, L.; Wang, C.; Hu, M. Programmable controlled mode-locked fiber laser using a digital micromirror device. Opt. Lett. 2017, 42, 1923–1926. [Google Scholar] [CrossRef] [PubMed]
- Prawiharjo, J.; Daga, N.K.; Geng, R.; Price, J.H.V.; Hanna, D.C.; Richardson, D.J.; Shepherd, D.P. High fidelity femtosecond pulses from an ultrafast fiber laser system via adaptive amplitude and phase pre-shaping. Opt. Express 2008, 16, 15074–15089. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ivanenko, A.; Kobtsev, S.; Nyushkov, B.; Serebrennikov, K.; Lutsenko, D. Mode-locked fibre laser with e-controlled cavity length in ultra-wide range. Proc. SPIE Nanophotonics Micro/Nano Opt. V 2019, 11193, 111931B. [Google Scholar]
- Nyushkov, B.N.; Kobtsev, S.M.; Ivanenko, A.V.; Smirnov, S.V. Programmable optical waveform generation in a mode-locked gain-modulated SOA-fiber laser. Opt. Soc. Am. B 2019, 36, 3133–3138. [Google Scholar] [CrossRef]
- Sutter, D.H.; Steinmeyer, G.; Gallmann, L.; Matuschek, N.; Morier-Genoud, F.; Keller, U.; Scheuer, V.; Angelow, G.; Tschudi, T. Semiconductor saturable-absorber mirror assisted Kerr lens mode-locked Ti:sapphire laser producing pulses in the two-cycle regime. Opt. Lett. 1999, 24, 631–633. [Google Scholar] [CrossRef]
- Weiner, A.M.; Oudin, S.; Leaird, D.E.; Reitze, D.H. Shaping of femtosecond pulses using phase-only filters designed by simulated annealing. J. Opt. Soc. Am. A 1993, 10, 1112–1120. [Google Scholar] [CrossRef]
- Weiner, A.M. Femtosecond pulse shaping using spatial light modulators. Rev. Sci. Instrum. 2000, 71, 1929–1960. [Google Scholar] [CrossRef]
- Jiang, Z.; Seo, D.S.; Leaird, D.E.; Weiner, M.A. Spectral line-by-line pulse shaping. Opt. Lett. 2005, 30, 1557–1559. [Google Scholar] [CrossRef] [PubMed]
- Willits, J.T.; Weiner, A.M.; Cundiff, S.T. Theory of rapid-update line-byline pulse shaping. Opt. Express 2008, 16, 315–327. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Huang, C.B.; Leaird, D.E.; Weiner, A.M. Optical arbitrary waveform processing of more than 100 spectral comb lines. Nature Photon. 2007, 1, 463–467. [Google Scholar] [CrossRef]
- Petropoulos, P.; Ibsen, M.; Ellis, A.; Richardson, D. Rectangular pulse generation based on pulse reshaping using a superstructured fiber Bragg grating. J. Light. Technol. 2001, 19, 746–752. [Google Scholar] [CrossRef] [Green Version]
- Park, Y.; Kulishov, M.; Slavk, R.; Azaña, J. Picosecond and sub-picosecond flat-top pulse generation using uniform long-period fiber gratings. Opt. Express 2006, 14, 12670–12678. [Google Scholar] [CrossRef]
- Karar, A.S.; Smy, T.; Steele, A.L. Nonlinear Dynamics of a Passively Mode-Locked Fiber Laser Containing a Long-Period Fiber Grating. IEEE J. Quantum Electron. 2008, 44, 254–261. [Google Scholar] [CrossRef]
- Slavik, R.; Oxenlowe, L.K.; Galili, M.; Mulvad, H.C.H.; Park, Y.; Azaña, J.; Jeppesen, P. Demultiplexing of 320-Gb/s OTDM data using ultrashort flat-top pulses. IEEE Photon. Technol. Lett. 2007, 19, 1855–1857. [Google Scholar] [CrossRef]
- Azaña, J.; Berger, N.; Levit, B.; Fischer, B. Reconfigurable generation of high repetition-rate optical pulse sequences based on time-domain phase-only filtering. Opt. Lett. 2005, 30, 3228–3230. [Google Scholar] [CrossRef]
- Saperstein, R.E.; Alic, N.; Panasenko, D.; Rokitski, R.; Fainman, Y. Time domain waveform processing by chromatic dispersion for temporal shaping of optical pulses. J. Opt. Soc. Am. B 2005, 22, 2427–2436. [Google Scholar] [CrossRef]
- Wang, X.; Wada, N. Spectral phase encoding of ultra-short optical pulse in time domain for OCDMA application. Opt. Express 2007, 15, 7319–7326. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kolner, B.H. Space-time duality and the theory of temporal imaging. IEEE J. Quantum Electron. 1994, 30, 1951–1963. [Google Scholar] [CrossRef]
- Thomas, S.; Malacarne, A.; Poti, L.; Bogoni, A.; Azaña, J. Programmable all-fibre optical pulse shaper based on time-domain binary phase-only linear filtering. In Proceedings of the 34th European Conference on Optical Communications (ECOC), Brussels, Belgium, 21–25 September 2008. [Google Scholar]
- Schreiber, T.; Ortaç¸, B.; Limpert, J.; Tünnermann, A. On the study of pulse evolution in ultra-short pulse mode-locked fiber lasers by numerical simulations. Opt. Express 2007, 15, 8252–8262. [Google Scholar] [CrossRef] [PubMed]
- Ilday, F.Ö.; Buckley, J.R.; Clark, W.G.; Wise, F.W. Self-similar evolution of parabolic pulses in a laser. Phys. Rev. Lett. 2004, 92, 213902. [Google Scholar] [CrossRef] [Green Version]
- Haus, H.A. Mode-locking of lasers. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 1173–1185. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics; Academic Press: New York, NY, USA, 2001. [Google Scholar]
- Duling, I.N., III. Subpicosecond all-fiber erbium laser. Electron. Lett. 1991, 27, 544–545. [Google Scholar] [CrossRef]
- Chang, Q.; Jia, E.; Suny, W. Difference schemes for solving the generalized nonlinear Schrödinger equation. J. Comp. Phys. 1999, 148, 397–415. [Google Scholar] [CrossRef]
- Wang, Z.; Hagerstrom, A.; Anderson, J.Q.; Tong, W.; Wu, M.; Carr, L.D.; Eykholt, R.; Kalinikos, B.A. Chaotic spin-wave solitons in magnetic film feedback rings. Phys. Rev. Lett. 2011, 107, 114102. [Google Scholar] [CrossRef] [Green Version]
- Hacker, M.; Stobrawa, G.; Feurer, T. Iterative Fourier transform algorithm for phase-only pulse shaping. Opt. Express 2001, 9, 191–199. [Google Scholar] [CrossRef]
- Rundquist, A.; Efimov, A.; Reitze, D.H. Pulse shaping with the Gerchberg-Saxton algorithm. J. Opt. Soc. Am. B 2002, 19, 2468–2478. [Google Scholar] [CrossRef]
- Zeidler, D.; Frey, S.; Kompa, K.-L.; Motzkus, M. Evolutionary algorithms and their application to optimal control studies. Phys. Rev. A 2001, 64, 023420. [Google Scholar] [CrossRef] [Green Version]
- Goldberg, D.E. Genetic Algorithm in Search, Optimization and Machine Learning; Addison-Wesley: Reading, MA, USA, 1997. [Google Scholar]
- Schwefel, H.P. Evolution and Optimum Seeking; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Latkin, A.I.; Boscolo, S.; Turitsyn, S.K. Passive nonlinear pulse shaping in normally dispersive fiber. In Proceedings of the OFC/NFOEC 2008-2008 Conference on Optical Fiber Communication/National Fiber Optic Engineers Conference, San Diego, CA, USA, 24–28 February 2008. [Google Scholar]


| Parameter | Symbol | Value |
|---|---|---|
| Group velocity dispersion | 15.3 /mm | |
| Nonlinear parameter | 0.0018 | |
| FWHM of reference pulse | 200 fs | |
| Wavelength of operation | 1550 nm | |
| Nonlinear refractive index | 2.6 × 10 | |
| Effective cross-sectional area | 60 | |
| Dispersion length | ||
| Pulse peak power | ||
| Fibre attenuation |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karar, A.S.; Ghandour, R.; Mahariq, I.; Alboon, S.A.; Maaz, I.; Neji, B.; Barakat, J.M.H. A Programmable Mode-Locked Fiber Laser Using Phase-Only Pulse Shaping and the Genetic Algorithm. Photonics 2020, 7, 69. https://doi.org/10.3390/photonics7030069
Karar AS, Ghandour R, Mahariq I, Alboon SA, Maaz I, Neji B, Barakat JMH. A Programmable Mode-Locked Fiber Laser Using Phase-Only Pulse Shaping and the Genetic Algorithm. Photonics. 2020; 7(3):69. https://doi.org/10.3390/photonics7030069
Chicago/Turabian StyleKarar, Abdullah S., Raymond Ghandour, Ibrahim Mahariq, Shadi A. Alboon, Issam Maaz, Bilel Neji, and Julien Moussa H. Barakat. 2020. "A Programmable Mode-Locked Fiber Laser Using Phase-Only Pulse Shaping and the Genetic Algorithm" Photonics 7, no. 3: 69. https://doi.org/10.3390/photonics7030069
APA StyleKarar, A. S., Ghandour, R., Mahariq, I., Alboon, S. A., Maaz, I., Neji, B., & Barakat, J. M. H. (2020). A Programmable Mode-Locked Fiber Laser Using Phase-Only Pulse Shaping and the Genetic Algorithm. Photonics, 7(3), 69. https://doi.org/10.3390/photonics7030069