Microsphere-Based Optical Frequency Comb Generator for 200 GHz Spaced WDM Data Transmission System
Abstract
1. Introduction
2. Methods
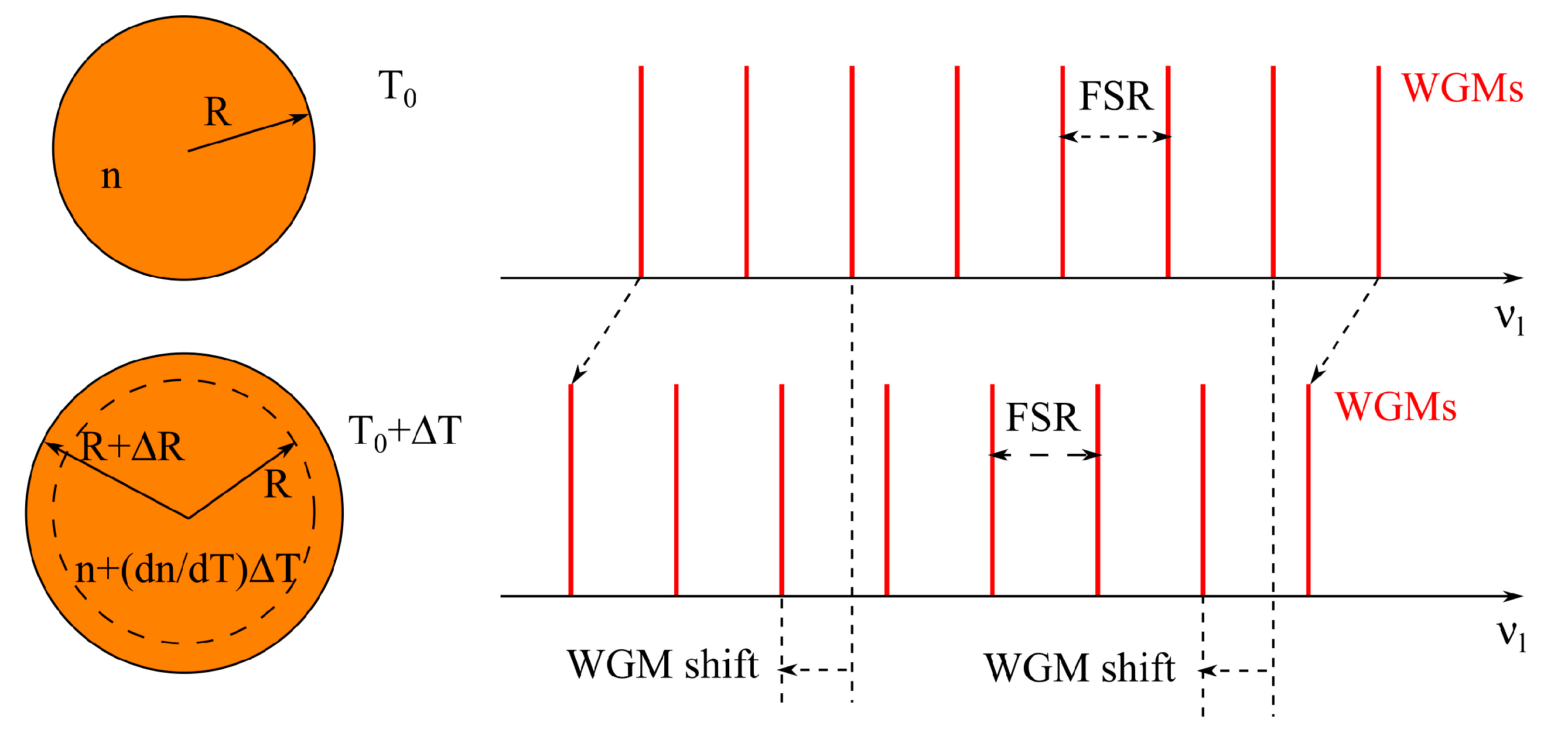
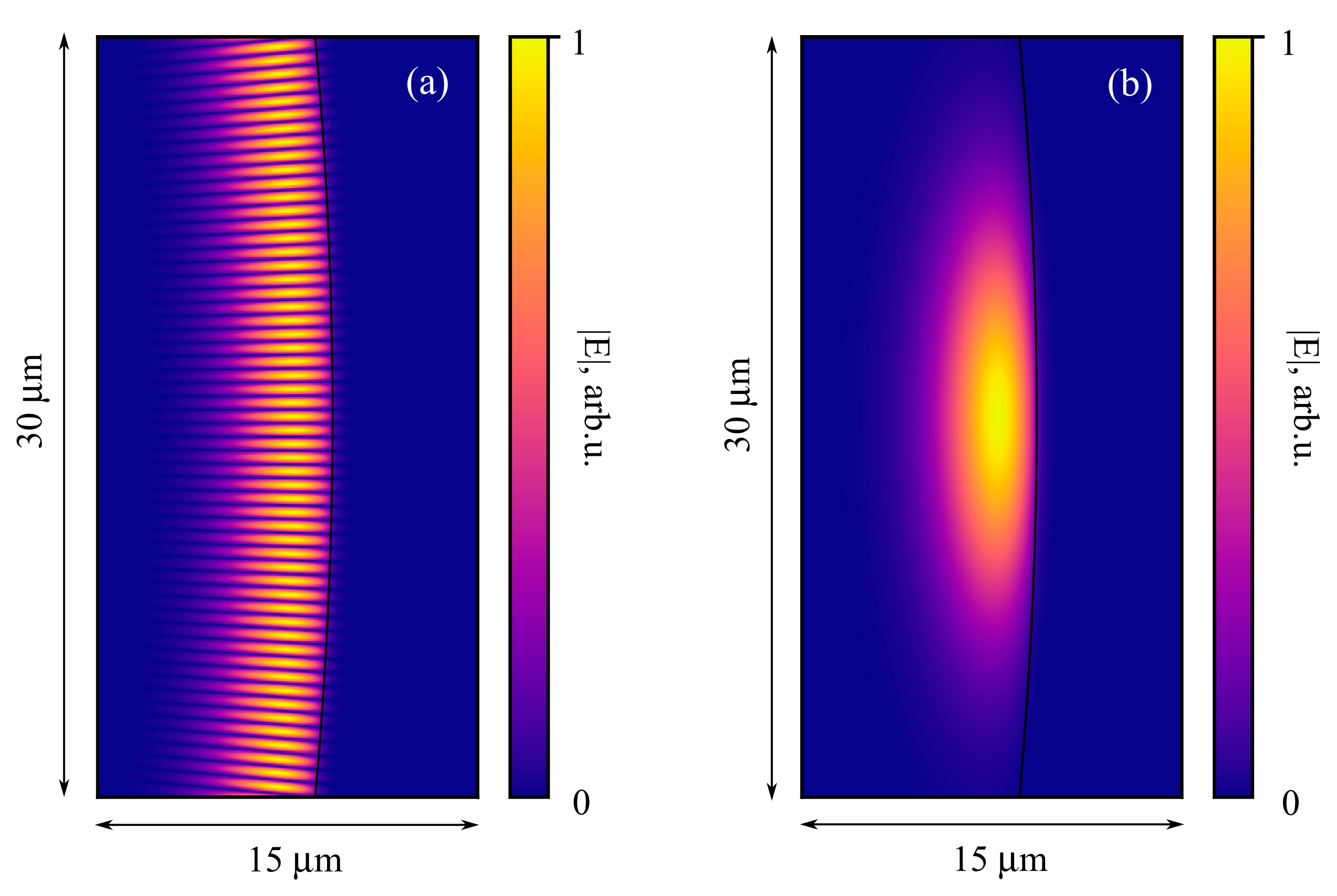
2.1. Calculation of Microresonator Characteristics
2.2. Simulation of OFC Generation
2.3. Simulation of Silica Microsphere OFC Generator-Based 4-Channel 200 GHz Spaced IM/DD WDM-PON Transmission System
3. Results
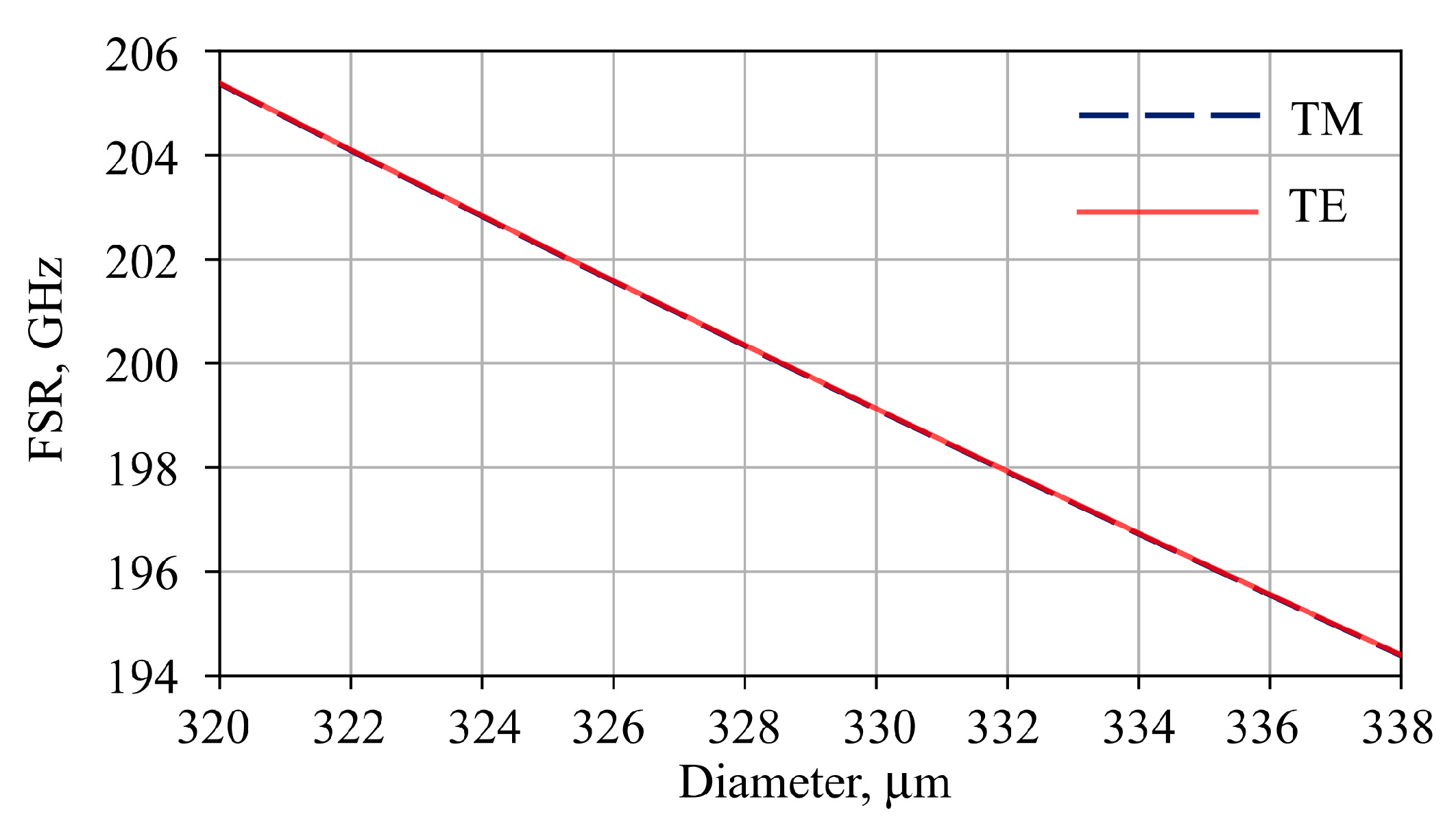
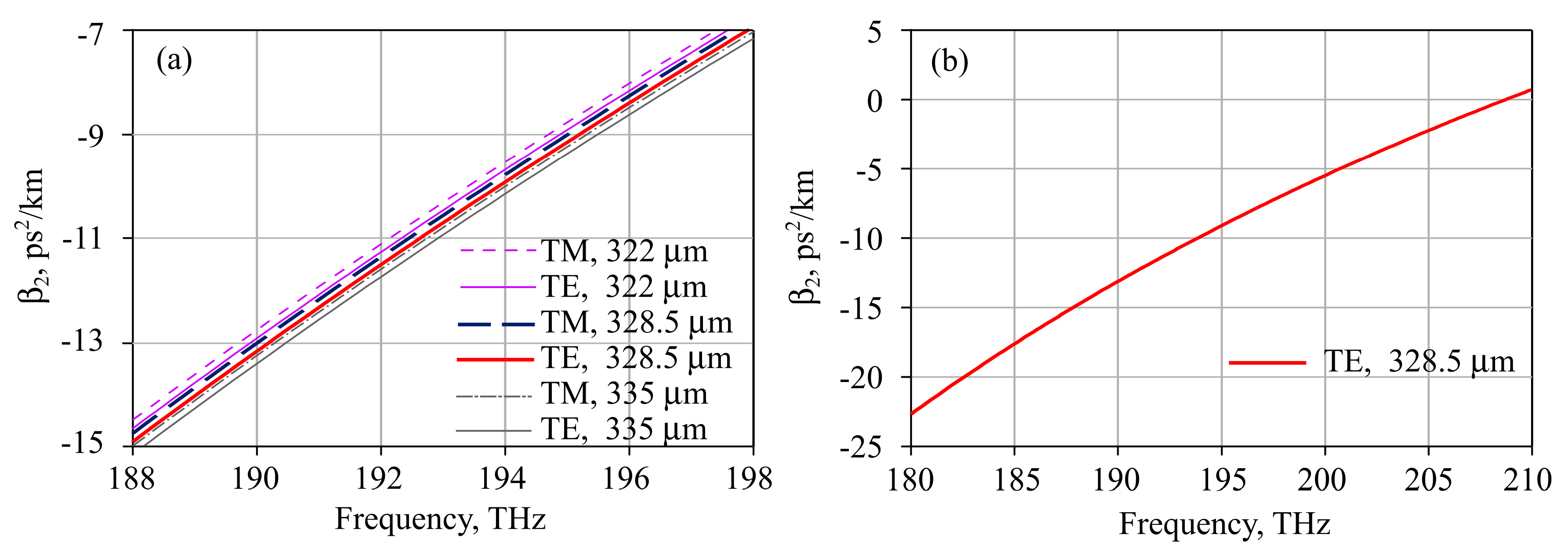
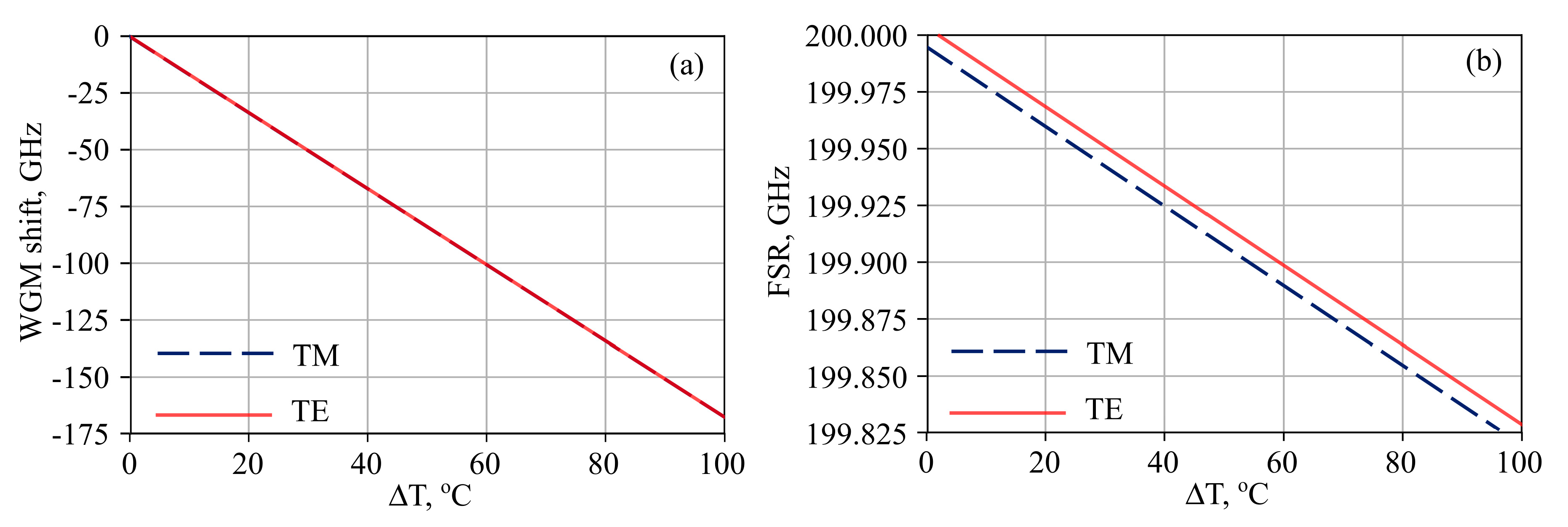
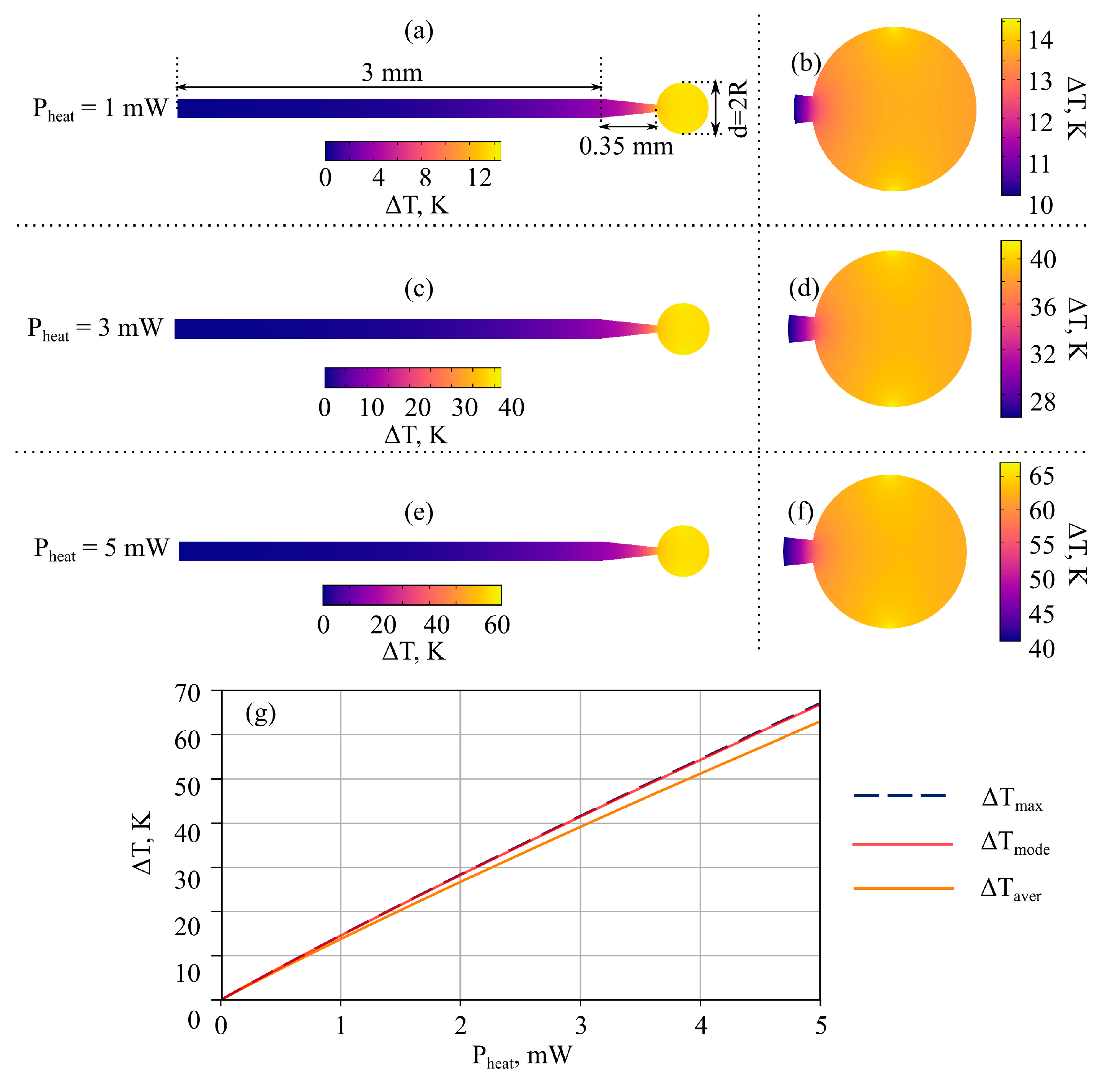
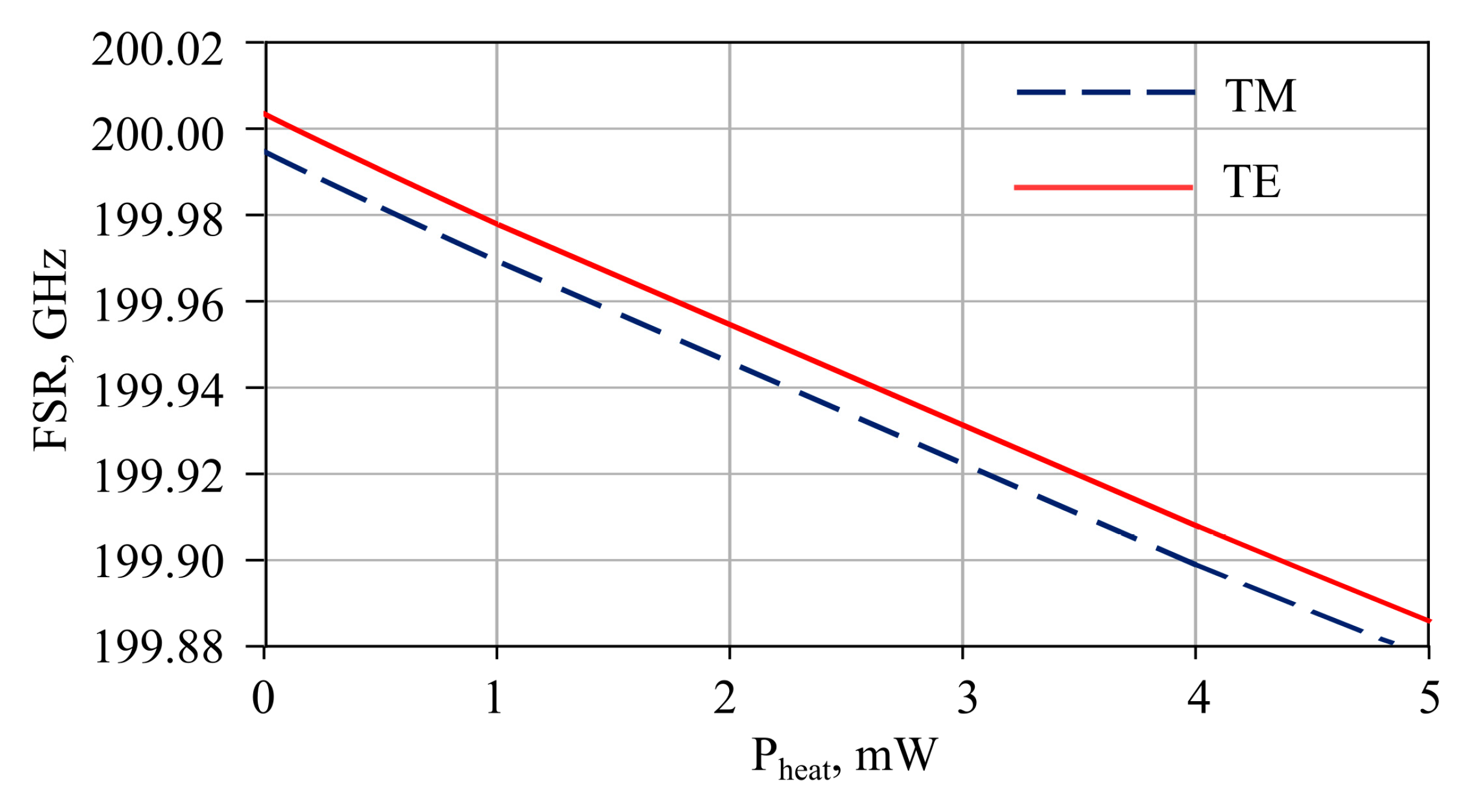
3.1. Microresonator Characteristics
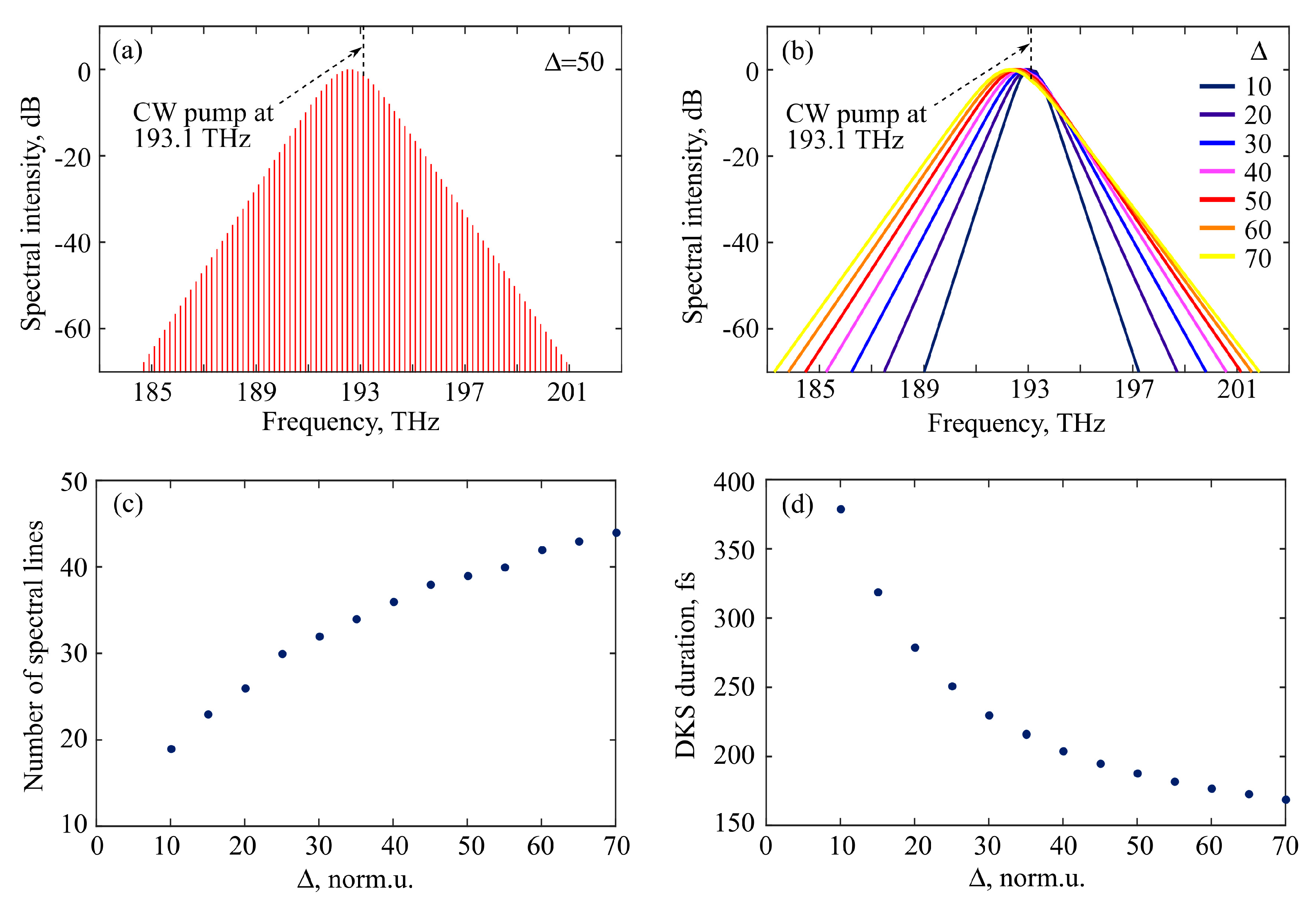
3.2. OFC Generation in DKS Regime
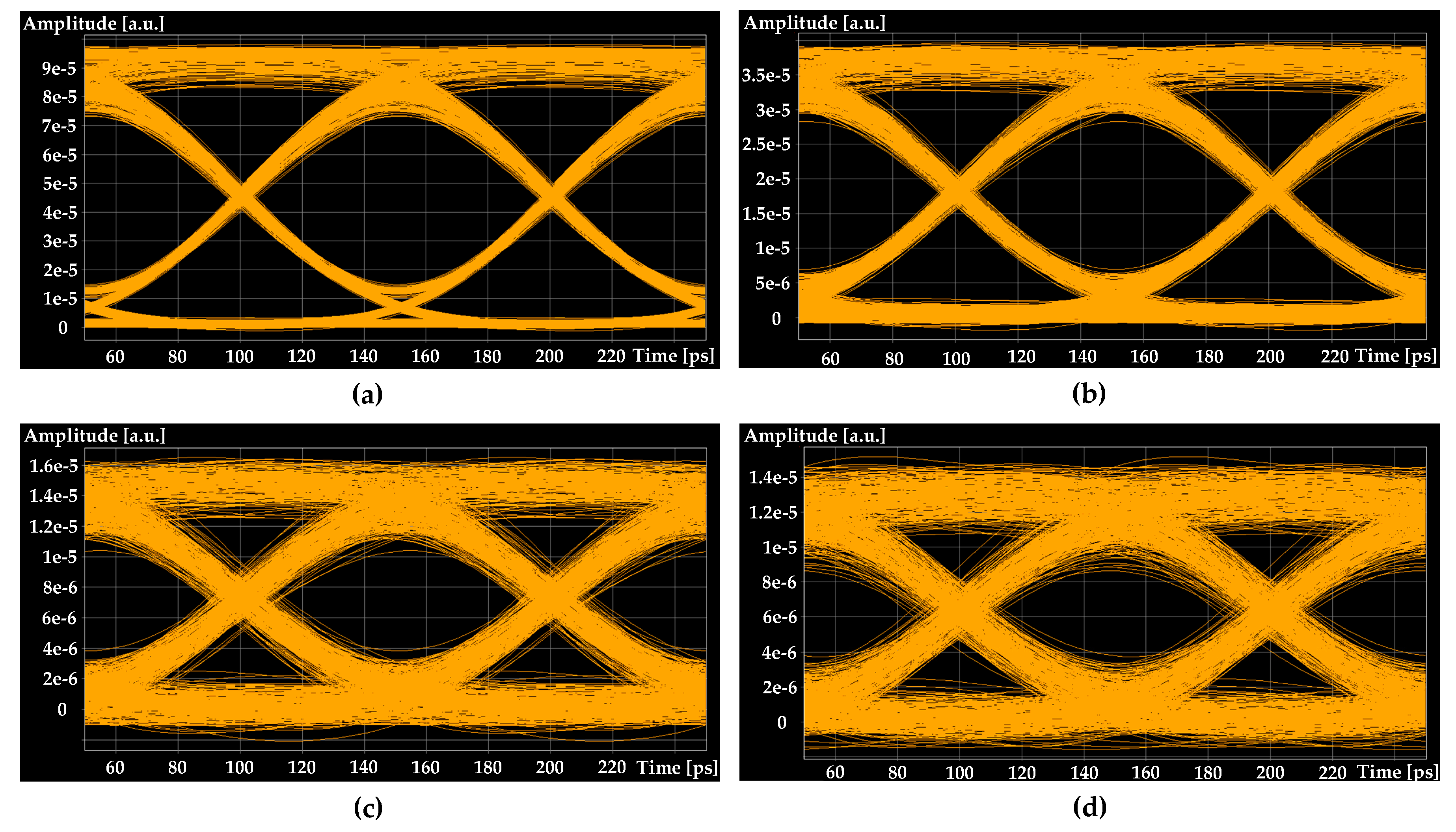
3.3. Architecture and Simulation of 4-Channel 200 GHz Spaced IM/DD WDM-PON Transmission System
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| OFC | optical frequency comb |
| WGM | whispering gallery mode |
| WDM | wavelength-division multiplexing |
| PON | passive optical network |
| FSR | free spectral range |
| TM | transverse magnetic |
| TE | transverse electric |
| CW | continuous wave |
| DKS | dissipative Kerr soliton |
| FWHM | full width at half maximum |
| BER | bit error rate |
| NRZ | non-return-to-zero |
| OOK | on-off keying |
| IM/DD | intensity modulation direct detection |
| NG-PON2 | Next-generation PON |
| ASE | amplified spontaneous emission |
| ASI | amplified spontaneous emission light source |
| AWG | arrayed-waveguide-grating |
| LPF | low-pass filter |
| MZM | Mach–Zehnder modulator |
| OBPF | optical band-pass filter |
| WGMR | whispering gallery mode resonator |
| MUX | multiplexed |
| de-MUX | demultiplexer |
| PIN | photodiode |
| SMF | single-mode fiber |
| B2B | back-to-back |
| WR | wavelength-routed |
| QoT | quality of transmission |
| ITU-T | International Telecommunication Union–telecommunication standardization sector |
| OCNR | optical carrier-to-noise power ratio |
| CO | central office |
References
- Pasquazi, A.; Peccianti, M.; Razzari, L.; Moss, D.J.; Coen, S.; Erkintalo, M.; Chembo, Y.K.; Hansson, T.; Wabnitz, S.; Del’Haye, P.; et al. Micro-combs: A novel generation of optical sources. Phys. Rep. 2018, 729, 1–81. [Google Scholar] [CrossRef]
- Strekalov, D.V.; Marquardt, C.; Matsko, A.B.; Schwefel, H.G.; Leuchs, G. Nonlinear and quantum optics with whispering gallery resonators. J. Opt. 2016, 18, 123002. [Google Scholar] [CrossRef]
- Suh, M.G.; Yang, Q.F.; Yang, K.Y.; Yi, X.; Vahala, K.J. Microresonator soliton dual-comb spectroscopy. Science 2016, 354, 600–603. [Google Scholar] [CrossRef]
- Yu, M.; Okawachi, Y.; Griffith, A.G.; Picqué, N.; Lipson, M.; Gaeta, A.L. Silicon-chip-based mid-infrared dual-comb spectroscopy. Nat. Commun. 2018, 9, 1869. [Google Scholar] [CrossRef]
- Xue, X.; Xuan, Y.; Kim, H.J.; Wang, J.; Leaird, D.E.; Qi, M.; Weiner, A.M. Programmable single-bandpass photonic RF filter based on Kerr comb from a microring. J. Lightw. Technol. 2014, 4, 3557–3565. [Google Scholar] [CrossRef]
- Suh, M.G.; Yi, X.; Lai, Y.H.; Leifer, S.; Grudinin, I.S.; Vasisht, G.; Martin, E.C.; Fitzgerald, M.P.; Doppmann, G.; Wang, J.; et al. Searching for exoplanets using a microresonator astrocomb. Nat. Photonics 2019, 13, 25–30. [Google Scholar] [CrossRef]
- Kues, M.; Reimer, C.; Lukens, J.M.; Munro, W.J.; Weiner, A.M.; Moss, D.J.; Morandotti, R. Quantum optical microcombs. Nat. Photonics 2019, 13, 170–179. [Google Scholar] [CrossRef]
- Engin, E.; Bonneau, D.; Natarajan, C.M.; Clark, A.S.; Tanner, M.G.; Hadfield, R.H.; Dorenbos, S.N.; Zwiller, V.; Ohira, K.; Suzuki, N.; et al. Photon pair generation in a silicon micro-ring resonator with reverse bias enhancement. Opt. Express 2013, 21, 27826–27834. [Google Scholar] [CrossRef]
- Monteiro, F.; Martin, A.; Sanguinetti, B.; Zbinden, H.; Thew, R.T. Narrowband photon pair source for quantum networks. Opt. Express 2014, 22, 4371–4378. [Google Scholar] [CrossRef]
- Kumar, R.; Ong, J.R.; Recchio, J.; Srinivasan, K.; Mookherjea, S. Spectrally multiplexed and tunable wavelength photon pairs at 1.55 μm from a silicon coupled-resonator optical waveguide. Opt. Lett. 2013, 38, 2969–2971. [Google Scholar] [CrossRef]
- Raussendorf, R.; Briegel, H.J. A one-way quantum computer. Phys. Rev. Lett. 2001, 86, 5188–5191. [Google Scholar] [CrossRef]
- Walther, P.; Resch, K.J.; Rudolph, T.; Schenck, E.; Weinfurter, H.; Vedral, V.; Aspelmeyer, M.; Zeilinger, A. Experimental one-way quantum computing. Nature 2005, 434, 169–176. [Google Scholar] [CrossRef] [PubMed]
- Company, V.T.; Scroder, J.; Fulop, A.; Mazur, M.; Lundberg, L.; Helhason, O.B.; Karlsson, M.; Andrekson, P.A. Laser Frequency Combs for Coherent Optical Communications. J. Lightw. Technol. 2019, 37, 1663–1670. [Google Scholar] [CrossRef]
- Pfeifle, J.; Weimann, C.; Bach, F.; Riemensberger, J.; Hartinger, K.; Hillerkuss, D.; Jordan, M.; Holtzwarth, B.; Kippenberg, T.J.; Leuthold, J.; et al. Microresonator-Based Optical Frequency Combs for High-Bitrate WDM Data Transmission. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 4–8 March 2012. [Google Scholar] [CrossRef]
- Pfeifle, J.; Brasch, V.; Lauermann, M.; Yu, Y.; Wegner, D.; Herr, T.; Hartinger, K.; Schindler, P.; Li, J.; Hillerkuss, D.; et al. Coherent terabit communications with microresonator Kerr frequency combs. Nat. Photonics 2014, 8, 375–380. [Google Scholar] [CrossRef] [PubMed]
- Pfeifle, J.; Coillet, A.; Henriet, R.; Saleh, K.; Schindler, P.; Weimann, C.; Freude, W.; Balakireva, I.V.; Larger, L.; Koos, C.; et al. Optimally Coherent Kerr Combs Generated with Crystalline Whispering Gallery Mode Resonators for Ultrahigh Capacity Fiber Communications. Phys. Rev. Lett. 2015, 114, 093902. [Google Scholar] [CrossRef]
- Marin-Palomo, P.; Kemal, J.N.; Karpov, M.; Kordts, A.; Pfeifle, J.; Pfeiffer, M.H.P.; Trocha, P.; Wolf, S.; Brasch, V.; Anderson, M.H.; et al. Microresonator-based solitons for massively parallel coherent optical communications. Nature 2017, 546, 274–279. [Google Scholar] [CrossRef]
- Pfeifle., J.; Yu, Y.; Schindler, P.C.; Brasch, V.; Weimann, C.; Hartinger, K.; Holzwarth, R.; Freude, W.; Kippenberg, T.J.; Koos, C. Transmission of a 1.44 Tbit/s data stream using a feedback-stabilized SiN Kerr Frequency Comb Source. In Proceedings of the Optical Fiber Communication Conference, San Francisco, CA, USA, 9–13 March 2014. [Google Scholar] [CrossRef]
- Pfeifle, J.; Kordts, A.; Marin, P.; Karpov, M.; Pfeiffer, M.; Brasch, V.; Rosenberger, R.; Kemal, J.; Wolf, S.; Freude, W.; et al. Full C and L-Band Transmission at 20 Tbit/s Using Cavity-Soliton Kerr Frequency Comb Source. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 10–15 May 2015. [Google Scholar] [CrossRef]
- Fülöp, A.; Mazur, M.; Lorences-Riesgo, A.; Helgason, Ó.B.; Wang, P.H.; Xuan, Y.; Leaird, D.E.; Qi, M.; Andrekson, P.A.; Weiner, A.M.; et al. High-order coherent communications using mode-locked dark-pulse Kerr combs from microresonators. Nat. Commun. 2018, 9, 1598. [Google Scholar] [CrossRef]
- Addanki, S.; Yupapin, P.; Amiri, I.S. Enhanced NRZ multi-carriers modulation technologies for microresonators in THz technology applications. Results Phys. 2019, 12, 178–189. [Google Scholar] [CrossRef]
- Hu, H.; Da Ros, F.; Pu, M.; Ye, F.; Ingerslev, K.; Da Silva, E.P.; Nooruzzaman, M.; Semenova, E.; Guan, P.; Zibar, D.; et al. Single-source chip-based frequency comb enabling extreme parallel data transmission. Nat. Photonics 2018, 12, 469–473. [Google Scholar] [CrossRef]
- Peichang, L.; Changjing, B.; Almaiman, A.; Kordts, A.; Karpov, M.; Pfeiffer, M.H.P.; Lin, Z.; Alishahi, F.; Yinwen, C.; Kaiheng, Z.; et al. Demonstration of Multiple Kerr-frequency-Comb Generation Using Different Lines From Another Kerr Comb Located Up to 50 km Away. J. Lightw. Technol. 2019, 37, 579–584. [Google Scholar] [CrossRef]
- Kovach, A.; Chen, D.; He, J.; Choi, H.; Dogan, A.H.; Ghasemkhani, M.; Taheri, H.; Armani, A.M. Emerging material systems for integrated optical Kerr frequency combs. Adv. Opt. Photonics 2020, 12, 135–222. [Google Scholar] [CrossRef]
- Gorodetsky, M.L.; Savchenkov, A.A.; Ilchenko, V.S. Ultimate Q of optical microsphere resonators. Opt. Lett. 1996, 21, 453–455. [Google Scholar] [CrossRef] [PubMed]
- Spillane, S.M.; Kippenberg, T.J.; Vahala, K.J. Ultralow-threshold Raman laser using a spherical dielectric microcavity. Nature 2002, 415, 621–623. [Google Scholar] [CrossRef] [PubMed]
- Webb, K.E.; Erkintalo, M.; Coen, S.; Murdoch, S.G. Experimental observation of coherent cavity soliton frequency combs in silica microspheres. Opt. Lett. 2016, 41, 4613–4616. [Google Scholar] [CrossRef]
- Andrianov, A.V.; Anashkina, E.A. Single-mode silica microsphere Raman laser tunable in the U-band and beyond. Results Phys. 2020, 17, 103084. [Google Scholar] [CrossRef]
- ITU-T G.694.1 Recommendation. Spectral Grids for WDM Applications: DWDM Frequency Grid. Available online: https://www.itu.int/itu-t/recommendations/rec.aspx?rec=11482&lang=en (accessed on 10 September 2020).
- Fujii, S.; Tanabe, T. Dispersion engineering and measurement of whispering gallery mode microresonator for Kerr frequency comb generation. Nanophotonics 2020, 9, 1087–1104. [Google Scholar] [CrossRef]
- Godey, C.; Balakireva, I.V.; Coillet, A.; Chembo, Y.K. Stability analysis of the spatiotemporal Lugiato-Lefever model for Kerr optical frequency combs in the anomalous and normal dispersion regimes. Phys. Rev. A 2014, 89, 063814. [Google Scholar] [CrossRef]
- Carmon, T.; Yang, L.; Vahala, K.J. Dynamical thermal behavior and thermal self-stability of microcavities. Opt. Express 2004, 12, 4742–4750. [Google Scholar] [CrossRef]
- Herr, T.; Brasch, V.; Jost, J.D.; Wang, C.Y.; Kondratiev, N.M.; Gorodetsky, M.L.; Kippenberg, T.J. Temporal solitons in optical microresonators. Nat. Photonics 2014, 8, 145–152. [Google Scholar] [CrossRef]
- Oraevsky, A.N. Whispering-gallery waves. Quantum Electron. 2020, 32, 377–400. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics, 6th ed.; Elsevier: London, UK, 2019. [Google Scholar]
- Powell, M.J.D. A hybrid method for nonlinear equations. In Numerical Methods for Nonlinear Equations; Rabinowitz, P., Ed.; Gordon and Breach: London, UK, 1970. [Google Scholar]
- Andrianov, A.V.; Marisova, M.P.; Dorofeev, V.V.; Anashkina, E.A. Thermal shift of whispering gallery modes in tellurite glass microspheres. Results Phys. 2020, 17, 103128. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Sorokin, A.A.; Marisova, M.P.; Andrianov, A.V. Development and numerical simulation of spherical microresonators based on SiO2–GeO2 germanosilicate glasses for generation of optical frequency combs. Quantum Electron. 2019, 49, 371–376. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Marisova, M.P.; Sorokin, A.A.; Andrianov, A.V. Numerical simulation of mid-infrared optical frequency comb generation in chalcogenide As2S3 microbubble resonators. Photonics 2019, 6, 55. [Google Scholar] [CrossRef]
- ITU-T Recommendation G.989.2. Digital Sections and Digital Line System—Optical Linesystems for Local and Access Networks—40-Gigabit-Capable Passive Optical Networks 2 (NG-PON2): Physical Media Dependent (PMD) Layer Specification; ITU-T: Geneva, Switzerland, 2019; pp. 1–122. [Google Scholar]
- Coen, S.; Erkintalo, M. Universal scaling laws of Kerr frequency combs. Opt. Lett. 2013, 38, 1790–1792. [Google Scholar] [CrossRef]
- Shen, B.; Chang, L.; Liu, J.; Wang, H.; Yang, Q.F.; Xiang, C.; Wang, R.N.; He, J.; Liu, T.; Xie, W.; et al. Integrated turnkey soliton microcombs. Nature 2020, 582, 365–369. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Anderson, M.; Coen, S.; Murdoch, S.G.; Erkintalo, M. Stimulated Raman scattering imposes fundamental limits to the duration and bandwidth of temporal cavity solitons. Phys. Rev. Lett. 2018, 120, 053902. [Google Scholar] [CrossRef]
- Milián, C.; Gorbach, A.V.; Taki, M.; Yulin, A.V.; Skryabin, D.V. Solitons and frequency combs in silica microring resonators: Interplay of the Raman and higher-order dispersion effects. Phys. Rev. A 2015, 92, 033851. [Google Scholar] [CrossRef]
- IXblue Photonics. MX-LN Series 1550 nm Band Intensity Modulators; Technical Specification; iXblue Photonics: Paris, France, 2019; pp. 1–6. [Google Scholar]
- Amonics. 10G Receiver Module; Technical Specification; Amonics Ltd.: Hong Kong, China, 2008; pp. 1–2. [Google Scholar]
- Lobanov, V.E.; Lihachev, G.V.; Pavlov, N.G.; Cherenkov, A.V.; Kippenberg, T.J.; Gorodetsky, M.L. Harmonization of chaos into a soliton in Kerr frequency combs. Opt. Express 2016, 24, 27382–27394. [Google Scholar] [CrossRef]
- Suchkov, S.V.; Sumetsky, M.; Sukhorukov, A.A. Frequency comb generation in SNAP bottle resonators. Opt. Lett. 2017, 42, 2149–2152. [Google Scholar] [CrossRef]
- Oreshnikov, I.; Skryabin, D.V. Multiple nonlinear resonances and frequency combs in bottle microresonators. Opt. Express 2017, 25, 10306–10311. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anashkina, E.A.; Marisova, M.P.; Andrianov, A.V.; Akhmedzhanov, R.A.; Murnieks, R.; Tokman, M.D.; Skladova, L.; Oladyshkin, I.V.; Salgals, T.; Lyashuk, I.; et al. Microsphere-Based Optical Frequency Comb Generator for 200 GHz Spaced WDM Data Transmission System. Photonics 2020, 7, 72. https://doi.org/10.3390/photonics7030072
Anashkina EA, Marisova MP, Andrianov AV, Akhmedzhanov RA, Murnieks R, Tokman MD, Skladova L, Oladyshkin IV, Salgals T, Lyashuk I, et al. Microsphere-Based Optical Frequency Comb Generator for 200 GHz Spaced WDM Data Transmission System. Photonics. 2020; 7(3):72. https://doi.org/10.3390/photonics7030072
Chicago/Turabian StyleAnashkina, Elena A., Maria P. Marisova, Alexey V. Andrianov, Rinat A. Akhmedzhanov, Rihards Murnieks, Mikhail D. Tokman, Laura Skladova, Ivan V. Oladyshkin, Toms Salgals, Ilya Lyashuk, and et al. 2020. "Microsphere-Based Optical Frequency Comb Generator for 200 GHz Spaced WDM Data Transmission System" Photonics 7, no. 3: 72. https://doi.org/10.3390/photonics7030072
APA StyleAnashkina, E. A., Marisova, M. P., Andrianov, A. V., Akhmedzhanov, R. A., Murnieks, R., Tokman, M. D., Skladova, L., Oladyshkin, I. V., Salgals, T., Lyashuk, I., Sorokin, A., Spolitis, S., Leuchs, G., & Bobrovs, V. (2020). Microsphere-Based Optical Frequency Comb Generator for 200 GHz Spaced WDM Data Transmission System. Photonics, 7(3), 72. https://doi.org/10.3390/photonics7030072








