Machine Learning Techniques in Radio-over-Fiber Systems and Networks
Abstract
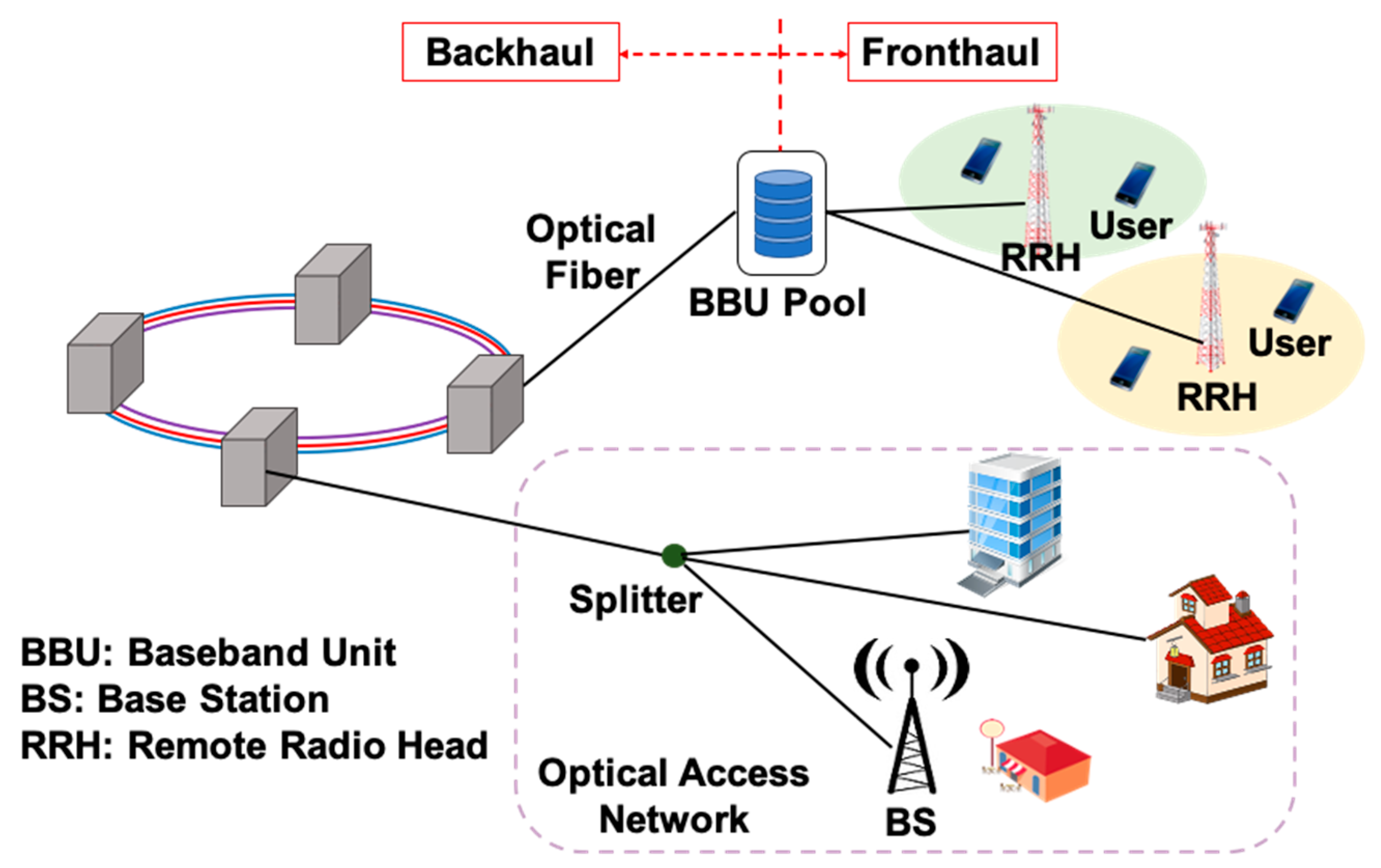
:1. Introduction
2. Impairments in RoF Systems
2.1. Fiber Chromatic Dispersion—Fading
2.2. Nonlinearity
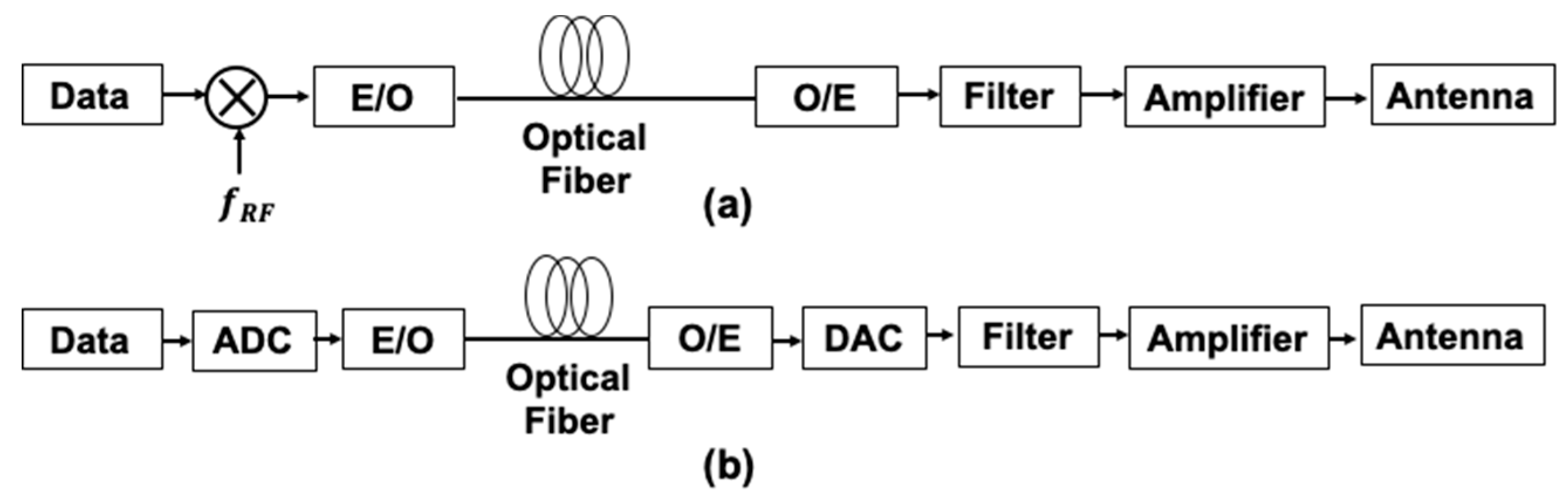
2.3. Impairment Compensataion Techniques—Digital Signal Processing and DRoF
3. ML-Based Signal Processing in RoF Systems
3.1. ML Techniques in Optical Communication Systems
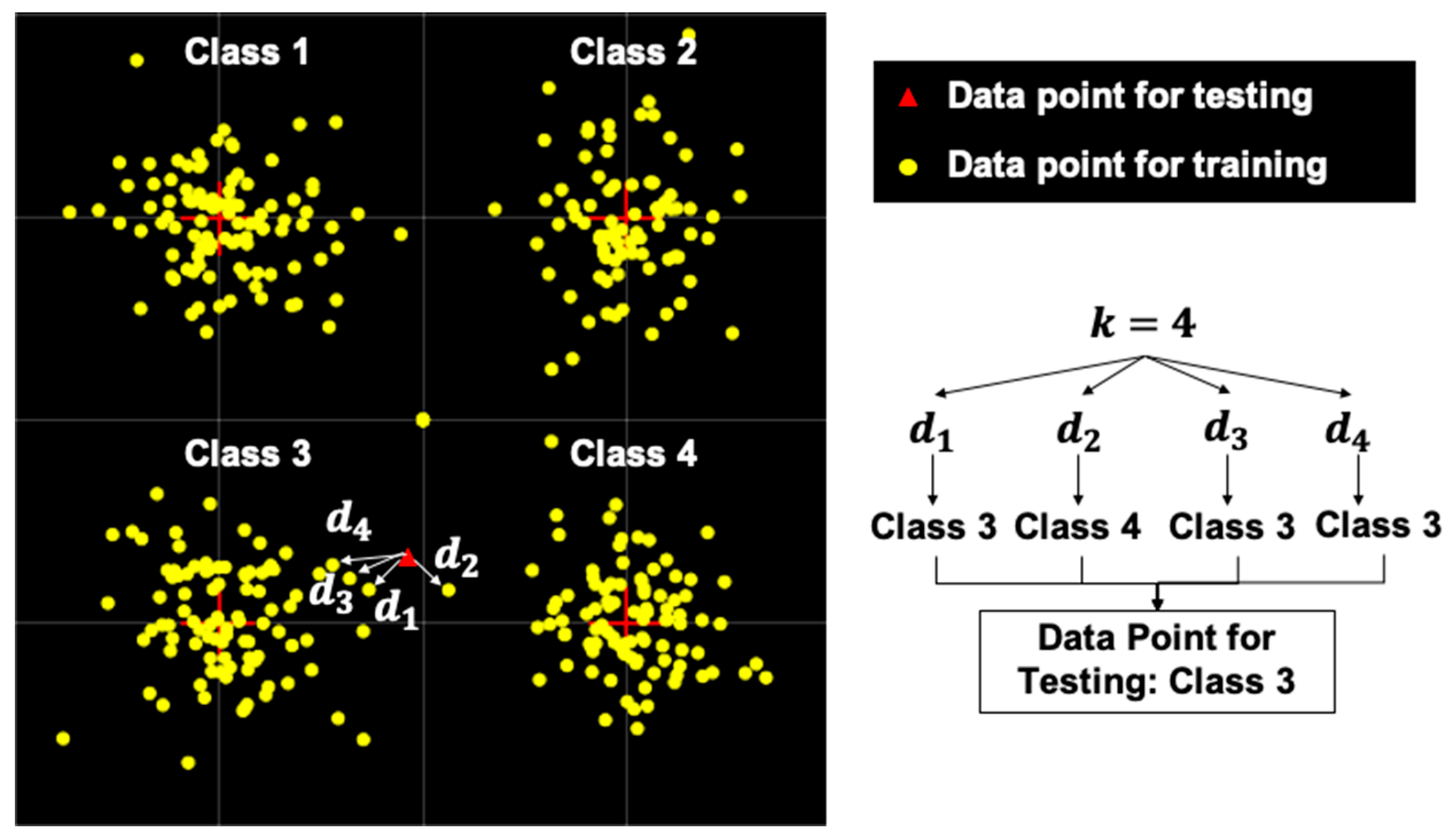
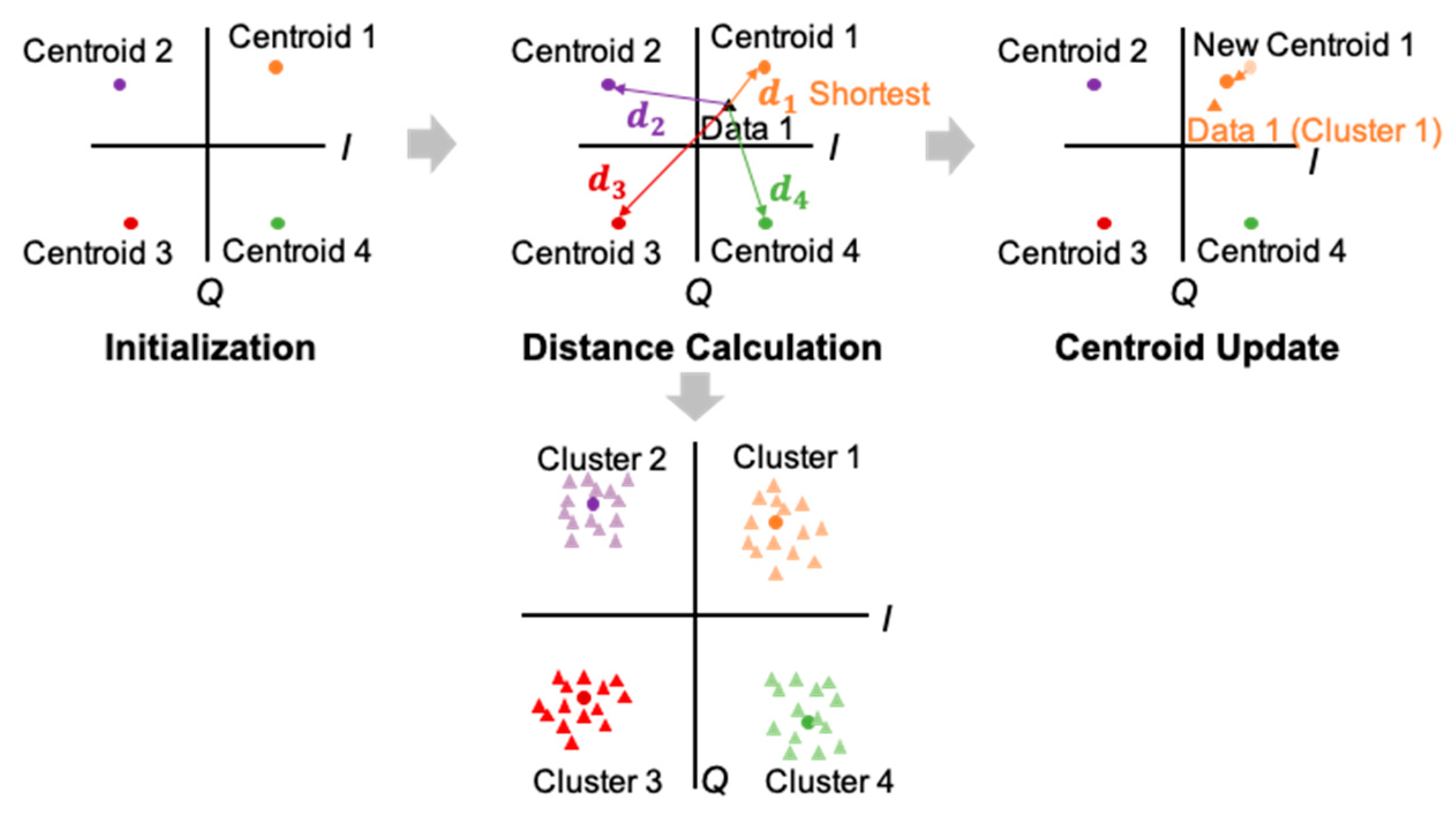
3.2. Non-Neural Network-Based Signal Processing Techniques in RoF Systems
| ML Algorithm | RoF System Configuration | Simulation or Experiment | Performance Improvement | Note |
|---|---|---|---|---|
| KNN/SVM [70] | 75 GHz RF (baseband over fiber), 80 km fiber, 16 QAM-DMT, 10 GBaud/s | Simulation | 0.6 dB over maximum likelihood detection (similar for KNN/SVM) | >2 k training data for KNN, >1.5 k training data for SVM |
| SVM [72] | 56.2 GHz RF (OCS modulation), 15 km fiber, 0.4 GBaud/s, 16-QAM, 64-QAM, 16-APSK and 32-APSK | Experiment | Compared with k-means: 1.2 dB for 16-QAM, 1.3 dB for 64-QPAM, 1.8 dB for 16-APSK, 1.3 dB for 32-APSK | Lower complexity compared with k-means |
| SVM [73] | 2 GHz and 2.5 GHz RF, 16-QAM | Experiment | 1.5 dB over system without SVM | 500 symbols for training |
| k-means [75] | 6 GHz RF, 78.8 km fiber, Gb/s, QPSK | Experiment | N. A. | N. A. |
| FCM-GK [76] | 6 GHz RF, 78.8 km fiber, 250 GBaud/s, 16-QAM and 4 + 12 PSK | Experiment | 3.1 dB for 16-QAM, 1.4 dB for 4 + 12 PSK (OSNR) | Compared with k-means: 1 dB for 16-QAM, 1.4 dB for 4 + 12 PSK (OSNR) |
3.3. Neural Network-Based ML Signal Processing Techniques in RoF Systems
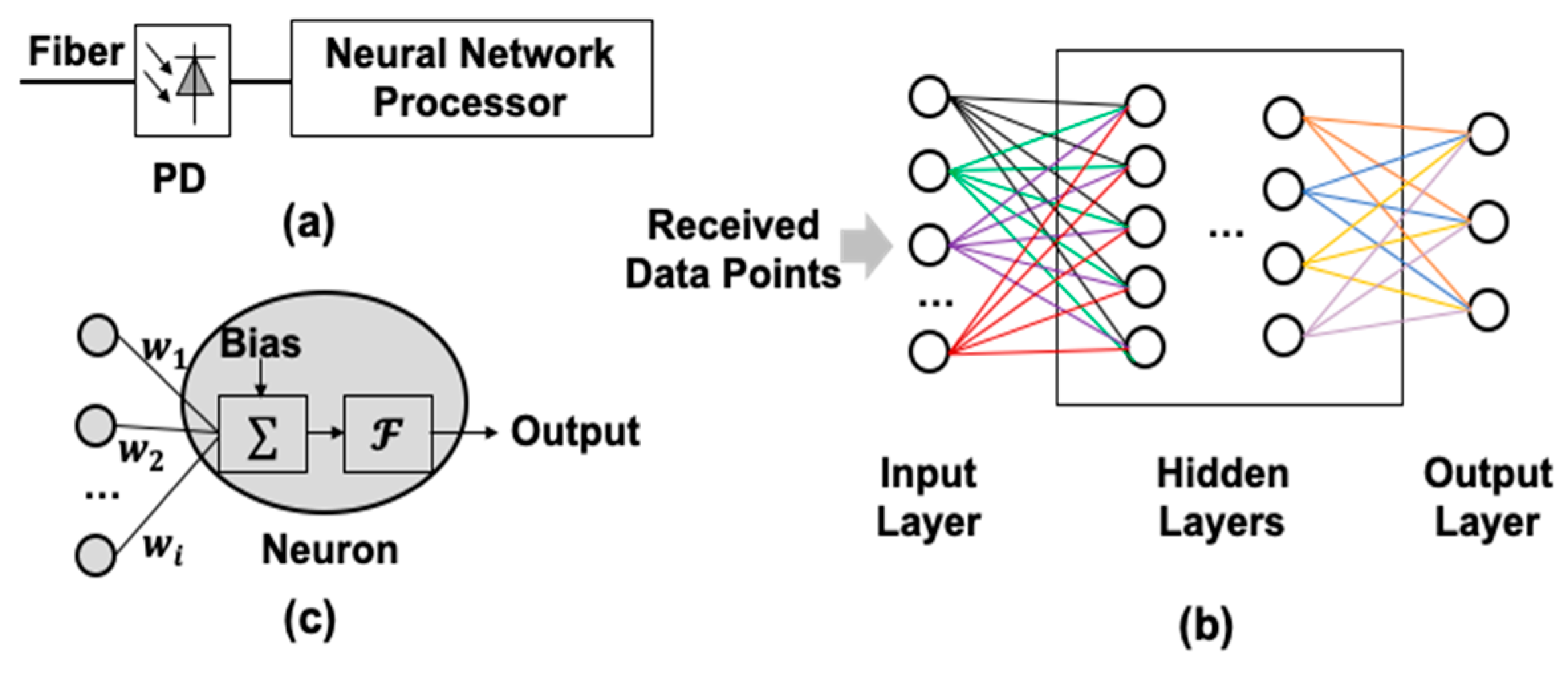
3.3.1. Introduction of Neural Network-Based Signal Processing
3.3.2. Summary of Neural Network-Based Signal Processing in RoF Systems
3.3.3. Neural Network Equalizers in RoF Systems
3.3.4. Neural Network Decoders in RoF Systems
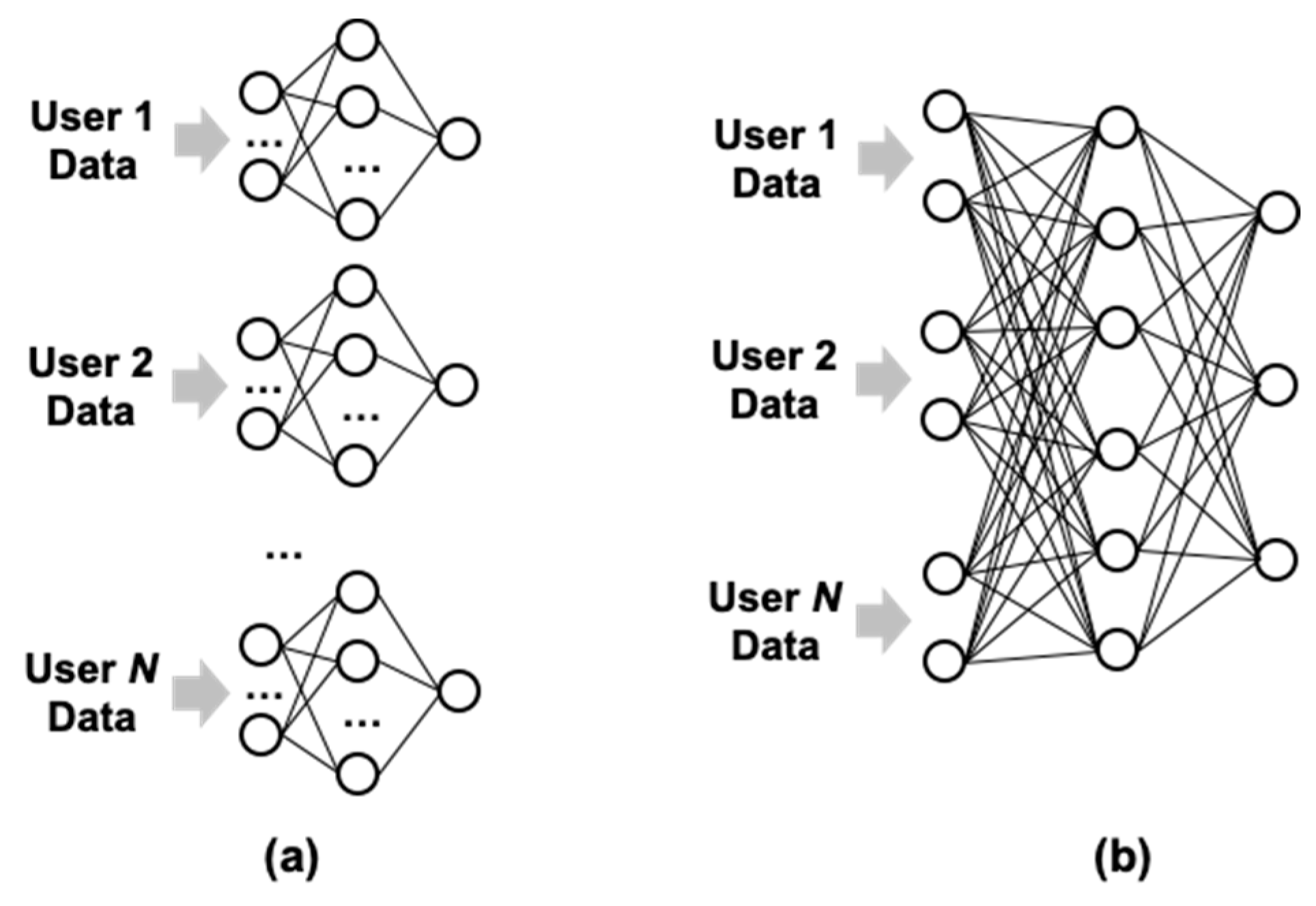
3.3.5. Other Physical Layer Signal Processing Applications of Neural Networks in RoF Systems
4. Open Questions and Possible Future Directions: ML-Based Signal Processing in RoF Systems
5. ML Models for RoF Network Management and Resource Allocation
5.1. Supervised Learning in RoF Network Management and Resource Allocation
| Category of Learning | ML Algorithm | Objective/Target | Note |
|---|---|---|---|
| Supervised Learning | FCNN [104,105] | Modulation format recognition | Signal amplitude histogram [104], FCNN as autoencoder [105] |
| FCNN [106,107] | Backhaul network resource allocation | Capturing nonlinearity in data traffic for accurate traffic prediction | |
| KNN [108] | DBA and reducing uplink latency | Forecasting the traffic for allocating bandwidth | |
| SVM [110] | C-RAN fronthaul DBA | Traffic classification for useless data shifting | |
| FCNN [111] | C-RAN fronthaul DBA | TDM-PON based C-RAN | |
| LSTM RNN [112,113] | C-RAN fronthaul DBA | 30 min traffic prediction in advance [112], combined with edge computing [113] | |
| CapsNet [114] | C-RAN fronthaul DBA | Better traffic classification accuracy with CapsNet than FCNN or RNN | |
| DHNN [115] | Network fault detection and positioning | Rapid locating of multiple network failures | |
| Reinforcement Learning | Q-learning algorithm [116] | High precision time synchronization | <100 ns synchronization accuracy achieved |
| Q-learning algorithm [117] | Dynamic RF channel selection | Reward criteria: Minimizing SINR | |
| Q-learning algorithm [118] | Optimize the placement of DU and CU | Reward criteria: Capacity and latency | |
| Q-learning algorithm [119] | Optimize BBU placement and routing in C-RAN | Reward criteria: Bandwidth and latency | |
| SARSA learning algorithm [120] | Real-time interference avoidance | Reward criteria: Log-value of BER difference between different states | |
| Q-learning algorithm [121] | Minimize power consumption | Reward criteria: Network power consumption and transition power consumption | |
| AC learning algorithm [122] | Maximize the users’ satisfaction in QoS | Reward criteria: Average data rate, head-of-line packet delay and average packet loss | |
| Q-learning algorithm [123] | Routing policy to maximize profit of infrastructure provider | Reward criteria: Revenue generated by a connectivity service | |
| Q-learning algorithm [124] | Slice admission strategy to maximize profit of infrastructure provider | Reward criteria: Loss induced by the slice request and the maximum potential revenue of a slice request |
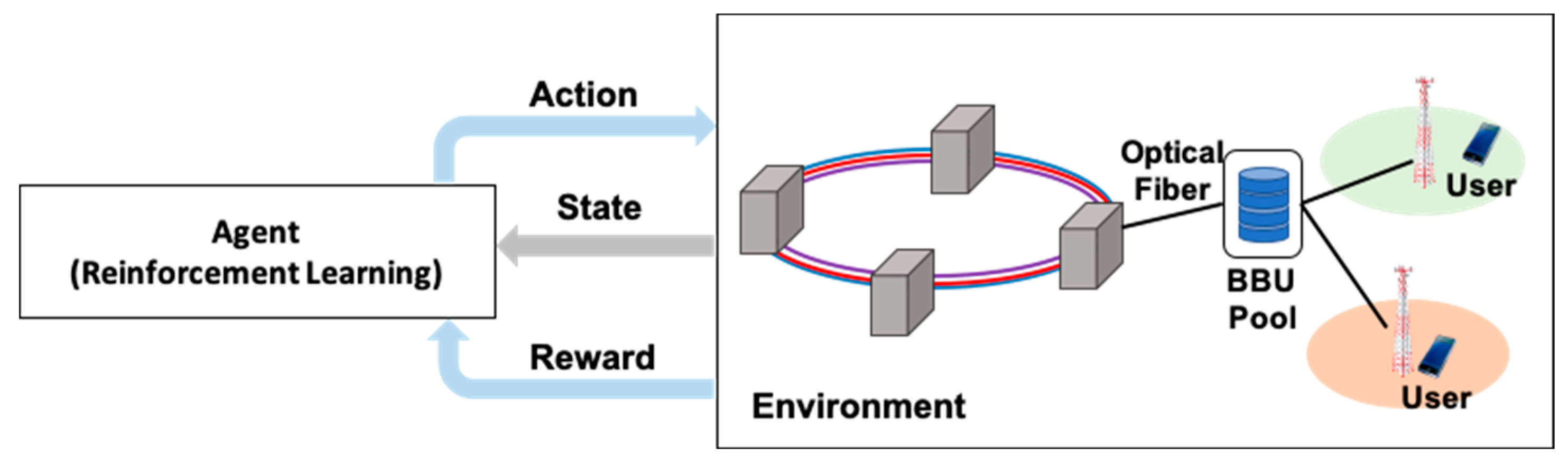
5.2. Reinforcement Learning in RoF Network Management and Resource Allocation
5.3. Open Questions and Possible Future Directions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, P.; Xiao, Y.; Xiao, M.; Li, S. 6G wireless communications: Vision and potential techniques. IEEE Netw. 2019, 33, 70–75. [Google Scholar] [CrossRef]
- David, K.; Berndt, H. 6G vision and requirements: Is there any need for beyond 5G? IEEE Veh. Technol. Mag. 2018, 13, 72–80. [Google Scholar] [CrossRef]
- Bjornson, E.; Perre, L.V.D.; Buzzi, S.; Larsson, E.G. Massive MIMO in sub-6GHz and mmWave: Physical, practical, and use-case differences. IEEE Wirel. Commun. 2019, 26, 100–108. [Google Scholar] [CrossRef] [Green Version]
- Elayan, H.; Amin, O.; Shubair, R.M.; Alouini, M.-S. Terahertz communication: The opportunities of wireless technology beyond 5G. In Proceedings of the International Conference on Advanced Communication Technologies and Networking, Marrakech, Morocco, 2–4 April 2018; pp. 1–5. [Google Scholar]
- Rappaport, T.S.; Xing, Y.; Kanhere, O.; Ju, S.; Madanayake, A.; Mandal, S.; Alkhateeb, A.; Trichopoulos, G.C. Wireless communications and applications above 100 GHz: Opportunities and challenges for 6G and beyond. IEEE Access 2019, 7, 78729–78757. [Google Scholar] [CrossRef]
- Wake, D.; Nkansah, A.; Gomes, N.J. Radio over fiber link design for next generation wireless systems. J. Lightw. Technol. 2010, 28, 2456–2464. [Google Scholar] [CrossRef] [Green Version]
- Novak, D.; Waterhouse, R.B.; Nirmalathas, A.; Lim, C.; Gamage, P.; Clark, T.R.; Dennis, M.L.; Nanzer, J.A. Radio-over-fiber technologies for emerging wireless systems. IEEE J. Quantum Electron. 2016, 52, 0600311. [Google Scholar] [CrossRef]
- Stohr, A.; Mitchell, J.E.; Leiba, Y. Transparent wireless access to optical WDM networks using a novel coherent radio-over-fiber (CRoF) approach. In Proceedings of the International Conference on Transparent Optical Networks, Graz, Austria, 6–10 July 2014; p. We.D4.3. [Google Scholar]
- Zhu, M.; Zhang, L.; Wang, J.; Cheng, L.; Liu, C.; Chang, G.-K. Radio-over-fiber access architecture for integrated broadband wireless services. J. Lightw. Technol. 2013, 31, 3614–3620. [Google Scholar] [CrossRef]
- Tian, Y.; Lee, K.-L.; Lim, C.; Nirmalathas, A. 60 GHz analog radio-over-fiber fronthaul investigations. J. Lightw. Technol. 2017, 35, 4304–4320. [Google Scholar] [CrossRef]
- Dat, P.T.; Kanno, A.; Inagaki, K.; Kawanishi, T. High-capacity wireless backhaul network using seamless convergence of radio-over-fiber and 90-GHz millimeter-wave. J. Lightw. Technol. 2014, 32, 3910–3923. [Google Scholar] [CrossRef]
- Musumeci, F.; Rottondi, C.; Nag, A.; Macaluso, I.; Zibar, D.; Ruffini, M.; Tornatore, M. An overview on application of machine learning techniques in optical networks. IEEE Commun. Surv. Tutor. 2019, 21, 1383–1408. [Google Scholar] [CrossRef] [Green Version]
- Khan, F.N.; Fan, Q.; Lu, C.; Lau, A.P.T. An optical communication’s perspective on machine learning and its applications. J. Lightw. Technol. 2019, 37, 493–516. [Google Scholar] [CrossRef]
- Hadi, M.U. Machine learning methods for optical communications. Trends Comput. Sci. Inf. Technol. 2020, 5, 55–57. [Google Scholar]
- Gliese, U.; Norskov, S.; Nielsen, T.N. Chromatic dispersion in fiber-optic microwave and millimeter-wave links. IEEE Trans. Microw. Theory Techn. 1996, 44, 1716–1724. [Google Scholar] [CrossRef]
- Lim, C.; Lee, K.-L.; Nirmalathas, A.; Novak, D.; Waterhouse, R. Impact of chromatic dispersion on 60 GHz radio-over-fiber transmission. In Proceedings of the Annual Meeting of the IEEE Lasers and Electro-Optics Society, Acapulco, Mexico, 9–13 November 2008; pp. 89–90. [Google Scholar]
- Smith, G.; Novak, D.; Ahmed, Z. Technique for optical SSB generation to overcome dispersion penalties in fibre-radio systems. Electron. Lett. 1997, 33, 74–75. [Google Scholar] [CrossRef]
- Weiß, M.; Huchard, M.; Stohr, A.; Charbonnier, B.; Fedderwitz, S.; Jager, D.S. 60-GHz photonic millimeter-wave link for short-to-medium range wireless transmission up to 12.5 Gb/s. J. Lightw. Technol. 2008, 26, 2424–2429. [Google Scholar] [CrossRef]
- Lim, C.; Nirmalathas, A.; Lee, K.-L.; Novak, D.; Waterhouse, R. Intermodulation distortion improvement for fiber-radio applications incorporating OSSB+C modulation in an optical integrated-access environment. J. Lightw. Technol. 2007, 25, 1602–1612. [Google Scholar] [CrossRef]
- Jia, Z.; Yu, J.; Chang, G.-K. A full-duplex radio-over-fiber system based on optical carrier suppression and reuse. IEEE Photon. Technol. Lett. 2006, 18, 1726–1728. [Google Scholar]
- Li, X.; Yu, J.; Zhang, J.; Xiao, J.; Zhang, Z.; Xu, Y.; Chen, L. QAM vector signal generation by optical carrier suppression and precoding techniques. IEEE Photon. Technol. Lett. 2015, 27, 1977–1980. [Google Scholar] [CrossRef]
- Lim, C.; Attygalle, M.; Nirmalathas, A.; Novak, D.; Waterhouse, R. Analysis of optical carrier-to-sideband ratio for improving transmission performance in fiber-radio links. IEEE Trans. Microw. Theory Techn. 2006, 54, 2181–2187. [Google Scholar] [CrossRef]
- James, J.; Pengbo, S.; Nkansah, A.; Xing, L.; Gomes, N.J. Nonlinearity and noise effects in multi-level signal millimeter-wave over fiber transmission using single and dual wavelength modulation. IEEE Tran. Microw. Theory Tech. 2010, 58, 3189–3198. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Zhang, X. Impact of nonlinear distortion in radio over fiber systems with single-sideband and tandem single-sideband subcarrier modulations. J. Lightw. Technol. 2006, 24, 2076–2090. [Google Scholar]
- Wang, J.; Liu, C.; Zhu, M.; Yi, A.; Cheng, L.; Chang, G.-K. Investigation of data-dependent channel cross-modulation in multiband radio-over-fiber systems. J. Lightw. Technol. 2014, 32, 1861–1871. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, R.; Shen, D.; Liu, T. Linearization technologies for broadband radio-over-fiber transmission systems. Photonics 2014, 1, 455–472. [Google Scholar] [CrossRef]
- Ismail, T.; Liu, C.-P.; Mitchell, J.E.; Seeds, A.J. High-dynamic-range wireless-over-fiber link using feedforward linearization. J. Lightw. Technol. 2007, 25, 3274–3282. [Google Scholar] [CrossRef]
- Park, S.-H.; Choi, Y.-W. Significant suppression of the third intermodulation distortion in transmission system with optical feedforward linearized transmitter. IEEE Photon. Technol. Lett. 2005, 17, 1280–1282. [Google Scholar] [CrossRef]
- Korotky, S.K.; Ridder, R.M. Dual parallel modulation schemes for low-distortion analog optical transmission. IEEE J. Sel. Areas Commun. 1990, 8, 1377–1381. [Google Scholar] [CrossRef]
- Haas, B.M.; Murphy, T.E. A simple, linearized, phase-modulated analog optical transmission system. IEEE Photon. Technol. Lett. 2007, 19, 729–731. [Google Scholar] [CrossRef]
- Masella, B.; Hraimel, B.; Zhang, X. Enhanced spurious-free dynamic range using mixed polarization in optical single sideband Mach-Zehnder modulator. J. Lightw. Technol. 2009, 27, 3034–3041. [Google Scholar] [CrossRef]
- Hraimei, B.; Zhang, X.; Jiang, W.; Wu, K.; Liu, T.; Xu, T.; Nie, Q.; Xu, K. Experimental demonstration of mixed-polarization to linearize electro-absorption modulators in radio-over-fiber links. IEEE Photon. Technol. Lett. 2011, 23, 230–232. [Google Scholar] [CrossRef]
- Lee, G.W.; Han, S.K. Linear dual electro absorption modulator for analog optical transmission. Microw. Opt. Technol. Lett. 1999, 22, 369–373. [Google Scholar] [CrossRef]
- Shen, Y.; Hraimei, B.; Zhang, X.; Cowan, G.E.R.; Wu, K.; Liu, T. A novel analog broadband RF predistortion circuit to linearize electro-absorption modulators in multiband OFDM radio-over-fiber systems. IEEE Tran. Microw. Theory Tech. 2010, 58, 3327–3335. [Google Scholar] [CrossRef]
- Lee, S.-H.; Kang, J.-M.; Choi, I.-H.; Han, S.-K. Linearization of DFB laser diode by external light-injected cross-gain modulation for radio-over-fiber link. IEEE Photon. Technol. Lett. 2006, 18, 1545–1547. [Google Scholar]
- Jeon, D.-H.; Jung, H.-D.; Han, S.-K. Mitigation of dispersion-induced effects using SOA in analog optical transmission. IEEE Photon. Technol. Lett. 2002, 14, 1166–1168. [Google Scholar] [CrossRef]
- Hraimel, B.; Zhang, X. Low-cost broadband predistortion-linearized single-drive x-cut Mach-Zehnder modulator for radio-over-fiber systems. IEEE Photon. Technol. Lett. 2012, 24, 1571–1573. [Google Scholar] [CrossRef]
- Roselli, L.; Borgioni, V.; Zepparelli, F.; Ambrosi, F.; Comez, M.; Faccin, P.; Casini, A. Analog laser predistortion for multiservice radio-over-fiber systems. J. Lightw. Technol. 2003, 21, 1211–1223. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Saha, S.; Zhu, R.; Liu, T.; Shen, D. Analog pre-distortion circuit for radio over fiber transmission. IEEE Photon. Technol. Lett. 2016, 28, 2541–2544. [Google Scholar] [CrossRef]
- Kitayama, K. Ultimate performance of optical DSB signal-based millimeter-wave fiber-radio system: Effect of laser phase noise. J. Lightw. Technol. 1999, 17, 1774–1781. [Google Scholar] [CrossRef]
- Li, L.; Zhang, G.; Zheng, X.; Li, S.; Zhang, H.; Zhou, B. Phase noise suppression for single-sideband, modulation radio-over-fiber systems adopting optical spectrum processing. IEEE Photon. Technol. Lett. 2013, 25, 1024–1026. [Google Scholar] [CrossRef]
- Kuri, T.; Sakamoto, T.; Kawanishi, T. An effect of detuning frequency in DSP-assisted offset-frequency-spaced two-tone optical coherent detection for radio-over-fiber signal. In Proceedings of the IEEE Photonics Conference, San Diego, CA, USA, 12–16 October 2014; pp. 75–76. [Google Scholar]
- Lin, C.-T.; Wei, C.-C.; Chao, M.-I. Phase noise suppression of optical OFDM signals in 60-GHz RoF transmission system. Opt. Express 2011, 19, 10423–10428. [Google Scholar] [CrossRef]
- Noweir, M.; Zhou, Q.; Kwan, A.; Valivarthi, R.; Helaoui, M.; Tittel, W.; Channouchi, F.M. Digitally linearized radio-over fiber transmitter architecture for cloud radio access network’s downlink. IEEE Tran. Microw. Theory Tech. 2018, 66, 3564–3574. [Google Scholar] [CrossRef]
- Cui, Y.; Dai, Y.; Yin, F.; Lv, Q.; Li, J.; Xu, K.; Lin, J. Enhanced spurious-free dynamic range in intensity-modulated analog photonic link using digital postprocessing. IEEE Photon. J. 2014, 6, 7900608. [Google Scholar] [CrossRef] [Green Version]
- Kim, B.G.; Bae, S.H.; Kim, H.; Chung, Y.C. DSP-based CSO cancellation technique for RoF transmission system implemented by using directly modulated laser. Opt. Express 2017, 25, 12152–12160. [Google Scholar] [CrossRef]
- Hadi, M.U.; Nanni, J.; Polleux, J.-L.; Traverso, P.A.; Tartarini, G. Direct digital predistortion technique for the compensation of laser chirp and fiber dispertion in long haul radio over fiber links. Opt. Quantum Electron. 2019, 51, 205. [Google Scholar] [CrossRef]
- Hadi, M.U.; Traverso, P.A.; Tartarini, G.; Venard, O.; Polleux, J.-L. Digital predistortion for linearlity improvement of VCSEL-SSMF-based radio-over-fiber links. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 155–157. [Google Scholar] [CrossRef]
- Hadi, M.U.; Nanni, J.; Venard, O.; Baudoin, G.; Polleux, J.-L.; Tartarini, G. Practically feasible closed-loop digital predistortion for VCSEL-MMF-based radio-over-fiber links. Radioengineering 2020, 29, 37–43. [Google Scholar] [CrossRef]
- Vieira, L.C.; Gomes, N.J. Eperimental demonstration of digital predistortion for orthogonal frequency-division multiplexing-radio over fiber links near laser resonance. IET Optoelectron. 2015, 9, 310–316. [Google Scholar] [CrossRef] [Green Version]
- Hadi, M.U.; Kantana, C.; Traverso, P.A.; Tartarini, G.; Venard, O.; Baudoin, G.; Polleux, J.-L. Assessment of digital predistortion methods for DFB-SSMF radio-over-fiber links linearization. Microw. Opt. Technol. Lett. 2020, 62, 540–546. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, T.; Shen, D. Investigation of broadband digital predistortion for broadband radio over fiber transmission systems. Opt. Commun. 2016, 381, 346–351. [Google Scholar] [CrossRef]
- Gamage, P.A.; Nirmalathas, A.; Lim, C.; Novak, D.; Waterhouse, R. Design and analysis of digitized RF-over-fiber links. J. Lightw. Technol. 2009, 27, 2052–2061. [Google Scholar] [CrossRef]
- Zhang, L.; Pang, X.; Ozolins, O.; Udalcovs, A.; Popov, S.; Xiao, S.; Hu, W.; Chen, J. Spectrally efficient digitized radio-over-fiber system with k-means clustering-based multidimensional quantization. Opt. Lett. 2018, 43, 1546–1549. [Google Scholar] [CrossRef]
- Shiina, R.; Fujiwara, T.; Taniguchi, T.; Ikeda, S. DRoF-based optical video re-transmission of commercial RF broadcast signals. J. Opt. Commun. Netw. 2019, 11, 559–567. [Google Scholar] [CrossRef]
- Mathe, D.M.; Neto, B.; Oliveira, R.S.; Teixeira, A.L.J.; Costa, J.C.W.A. Adaptive signal compression in intermediate frequency band for DRoF mobile fronthaul. IEEE Photon. Technol. Lett. 2019, 31, 579–582. [Google Scholar] [CrossRef]
- Li, H.; Verplaetse, M.; Verbist, J.; Kerrebrouck, J.V.; Breyne, L.; Wu, C.-Y.; Bogaert, L.; Moeneclaey, B.; Yin, X.; Bauwelinck, J.; et al. Real-time 100 GS/s sigma-delta modulator for all-digital radio-over-fiber transmission. J. Lightw. Technol. 2020, 38, 386–393. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Udalcovs, A.; Lin, R.; Ozolins, O.; Pang, X.; Gan, L.; Schatz, R.; Tang, M.; Fu, S.; Liu, D.; et al. Towards terabit digital radio over fiber systems: Architectures and key technologies. IEEE Commun. Mag. 2019, 57, 131–137. [Google Scholar] [CrossRef] [Green Version]
- Hadi, M.U.; Jung, H.; Traverso, P.A.; Tartarini, G. Experimental evaluation of real-time sigma-delta radio over fiber system for fronthaul applications. Int. J. Microw. Wirel. Technol. 2020, 1–10. [Google Scholar] [CrossRef]
- Sezgin, I.C.; Dahlgren, M.; Eriksson, T.; Coldrey, M.; Larsson, C.; Gustavsson, J.; Fager, C. A low-complexity distributed-MIMO testbed based on high-speed sigma-delta-over-fiber. IEEE Trans. Microw. Theory Techn. 2019, 67, 2861–2872. [Google Scholar] [CrossRef]
- Breyne, L.; Torfs, G.; Yin, X.; Demeester, P.; Bauwelinck, J. Comparison between analog radio-over-fiber and sigma delta modulated radio-over-fiber. IEEE Photon. Technol. Lett. 2017, 29, 1808–1811. [Google Scholar] [CrossRef] [Green Version]
- Boada, R.; Borkowski, R.; Monroy, I.T. Clustering algorithms for Stokes space modulation format recognition. Opt. Express 2015, 23, 15521–15531. [Google Scholar] [CrossRef] [Green Version]
- Kiran, Y.V.; Venkatesh, T.; Murthy, C.S.R. A reinforcement learning framework for path selection and wavelength selection in optical burst switched networks. IEEE J. Sel. Area Comm. 2007, 25, 18–26. [Google Scholar] [CrossRef]
- Chen, X.; Proietti, R.; Yoo, S.J.B. Building autonomic elastic optical networks with deep reinforcement learning. IEEE Commun. Mag. 2019, 25, 18–26. [Google Scholar] [CrossRef]
- Luo, X.; Shi, C.; Wang, L.; Chen, X.; Li, Y.; Yang, T. Leveraging double-agent-based deep reinforcement learning to global optimization of elastic optical networks with enhanced survivability. Opt. Express 2019, 27, 7896–7911. [Google Scholar] [CrossRef]
- He, J.; Lee, J.; Song, T.; Li, H.; Kandeepan, S.; Wang, K. Recurrent neural network (RNN) for delay-tolerant repetition-coded (RC) indoor optical wireless communication systems. Opt. Lett. 2019, 44, 3745–3748. [Google Scholar] [CrossRef]
- Yi, L.; Liao, T.; Huang, L.; Xue, L.; Li, P.; Hu, W. Machine learning for 100 Gb/s/λ passive optical network. J. Lightw. Technol. 2019, 37, 1621–1630. [Google Scholar] [CrossRef]
- Chi, N.; Zhao, Y.; Shi, M.; Zou, P.; Lu, X. Guassian kernel-aided deep neural network equalizer utilized in underwater PAM8 visible light communication system. Opt. Express 2018, 26, 26700–26712. [Google Scholar] [CrossRef]
- He, J.; Lee, J.; Song, T.; Li, H.; Kandeepan, S.; Wang, K. Delay-tolerant indoor optical wireless communication systems based on attention-augmented recurrent neural network. J. Lightw. Technol. 2020, 38, 4632–4640. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, M.; Fu, M.; Cai, Z.; Li, Z.; Han, H.; Cui, Y.; Luo, B. Nonlinearity mitigation using a machine learning detector based on k-nearest neighbors. IEEE Photon. Technol. Lett. 2016, 28, 2102–2105. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, Y.; Yu, J. Nonlinearity mitigation of RoF signal using machine learning based classifier. In Proceedings of the Asia Communications and Photonics Conference, Guangzhou, China, 10–13 November 2017; p. Su2A.28. [Google Scholar]
- Cui, Y.; Zhang, M.; Wang, D.; Liu, S.; Li, Z.; Chang, G.K. Bit-based support vector machine nonlinear detector for millimeter-wave radio-over-fiber mobile fronthaul systems. Opt. Express 2017, 25, 26186–26197. [Google Scholar] [CrossRef]
- Li, D.; Yu, S.; Jiang, T.; Han, Y.; Gu, W. An M-ary SVM-based detection for 16-QAM RoF system with data-dependent cross modulation distortion. In Proceedings of the Asia Communications and Photonics Conference, Hong Kong, 19–23 November 2015; p. ASu3J.4. [Google Scholar]
- Sebald, D.J.; Bucklew, J.A. Support vector machine and the multiple hypothesis test problem. IEEE Trans. Signal Process. 2001, 49, 2865–2872. [Google Scholar] [CrossRef]
- Gonzalez, N.G.; Zibar, D.; Caballero, A.; Monroy, I.T. Experimental 2.5-Gb/s QPSK WDM phase-modulated radio-over-fiber link with digital demodulation by a K-means algorithm. IEEE Photon. Technol. Lett. 2010, 22, 335–337. [Google Scholar] [CrossRef]
- Fernandez, E.A.; Torres, J.J.G.; Soto, A.M.C.; Gonzalez, N.G. Radio-over-fiber signal demodulation in the presence of non-Gaussian distortions based on subregion constellation processing. Opt. Fiber Technol. 2019, 53, 102062. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- He, J.; Qi, J.; Ramamohanarao, K. A joint context-aware embedding for trip recommendations. In Proceedings of the IEEE International Conference on Data Engineering, Macao, China, 8–11 April 2019; pp. 292–303. [Google Scholar]
- Otter, D.W.; Medina, J.R.; Kalita, J.K. A survey of the usages of deep learning for natural language processing. IEEE Trans. Neural Netw. Learn. Syst. 2020. accepted. [Google Scholar]
- Liu, S.; Wang, X.; Zhang, W.; Shen, G.; Tian, H. An adaptive activated ANN equalizer applied in millimeter-wave RoF transmission system. IEEE Photon. Technol. Lett. 2017, 29, 1935–1938. [Google Scholar] [CrossRef]
- Tao, L.; Chen, L.; Liu, Q. Nonlinearity mitigation with neural networks in vector mm-wave system. Opt. Commun. 2019, 430, 219–222. [Google Scholar] [CrossRef]
- Liu, S.; Xu, M.; Wang, J.; Lu, F.; Zhang, W.; Tian, H.; Chang, G.K. A multilevel artificial neural network nonlinear equalizer for millimeter-wave mobile fronthaul systems. J. Lightw. Technol. 2017, 35, 4406–4417. [Google Scholar] [CrossRef]
- Liu, S.; Alfadhli, Y.M.; Shen, S.; Tian, H.; Chang, G.K. Mitigation of multi-user access impairments in 5G A-RoF-based mobile-fronthaul utilizing machine learning for an artificial neural network nonlinear equalizer. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 11–15 March 2018; p. W4B.3. [Google Scholar]
- Liu, S.; Alfadhli, Y.M.; Shen, S.; Xu, M.; Tian, H.; Chang, G.K. A novel ANN equalizer to mitigate nonlinear interference in analog-RoF mobile fronthaul. IEEE Photon. Technol. Lett. 2018, 30, 1675–1678. [Google Scholar] [CrossRef]
- Liu, E.; Yu, Z.; Yin, C.; Xu, K. Nonlinear distortions compensation based on artificial neural networks in wideband and multi-carrier systems. IEEE J. Quantum Electron. 2019, 55, 800305. [Google Scholar] [CrossRef]
- Liu, J.; Zou, X.; Bai, W. Performance enhancement of UFMC based radio over fiber system using ANN equalizer. In Proceedings of the Asia Communications and Photonics Conference, Hangzhou, China, 26–29 October 2018; p. M4A.331. [Google Scholar]
- Safari, L.; Baghersalimi, G.; Karami, A.; Kiani, A. On the equalization of an OFDM-based radio-over-fiber system using neural networks. Radioengineering 2017, 26, 162–169. [Google Scholar] [CrossRef]
- Zhou, Q.; Lu, F.; Xu, M.; Peng, P.-C.; Liu, S.; Shen, S.; Zhang, R.; Yao, S.; Finkelstein, J.; Chang, G.-K. Enhanced multi-level signal recovery in mobile fronthaul network using DNN decoder. IEEE Photon. Technol. Lett. 2018, 30, 1511–1514. [Google Scholar] [CrossRef]
- Ying, H.; Zhu, M.; Zhang, J.; Yi, X.; Lin, Y.; Zhou, H.; Qiu, K. Artificial neural network for nonlinear distortion mitigation in optical SSB NPAM-4 direct-detection system. In Proceedings of the International Conference on Optical Communications and Networks, Wuzhen, China, 7–10 August 2017; pp. 1–3. [Google Scholar]
- Zhou, Q.; Zhang, R.; Chen, Y.-W.; Shen, S.; Su, S.-J.; Finkelstein, J.; Chang, G.-K. Combining efficient probabilistic shaping and deep neural network to mitigate capacity crunch in 5G fronthaul. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 8–12 March 2020; p. T4D.1. [Google Scholar]
- Liao, M.; Tseng, J.-S.; Yan, J.-H.; Chen, H.-R.; Liou, S.-H.; Feng, K.-M. Neural network based NOMA demultiplexing with high flexibility and low latency for 5G radio-over-fiber system. In Proceedings of the Asia Communications and Photonics Conference, Chengdu, China, 2–5 November 2019; p. T4B.3. [Google Scholar]
- Liu, S.; Peng, P.-C.; Hsu, C.-W.; He, J.; Tian, H.; Chang, G.-K. An artificial neural network MIMO demultiplexer for small-cell mm-wave RoF coordinated multi-point transmission system. In Proceedings of the European Conference on Optical Communication, Rome, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar]
- Lee, J.; He, J.; Wang, Y.; Fang, C.; Wang, K. Experimental demonstration of millimeter-wave radio-over-fiber system with convolutional neural network and binary convolutional neural network (BCNN). arXiv 2020, arXiv:2001.02018. [Google Scholar]
- Lee, J.; He, J.; Wang, K. Neural networks and FPGA hardware accelerators for millimeter-wave radio-over-fiber systems. In Proceedings of the International Conference on Transparent Optical Networks, Bari, Italy, 19–23 July 2020; p. Mo.D1.5. [Google Scholar]
- Awoye, A.; Leeson, M.S.; Green, R.J. Neural network based adaptive predistortion for radio over fiber links. In Proceedings of the International Conference on Transparent Optical Networks, Coventry, UK, 2–5 July 2012; p. We.C3.4. [Google Scholar]
- Eriksson, T.A.; Bulow, H.; Leven, A. Applying neural networks in optical communication systems: Possible pitfalls. IEEE Photon. Technol. Lett. 2017, 29, 2091–2094. [Google Scholar] [CrossRef] [Green Version]
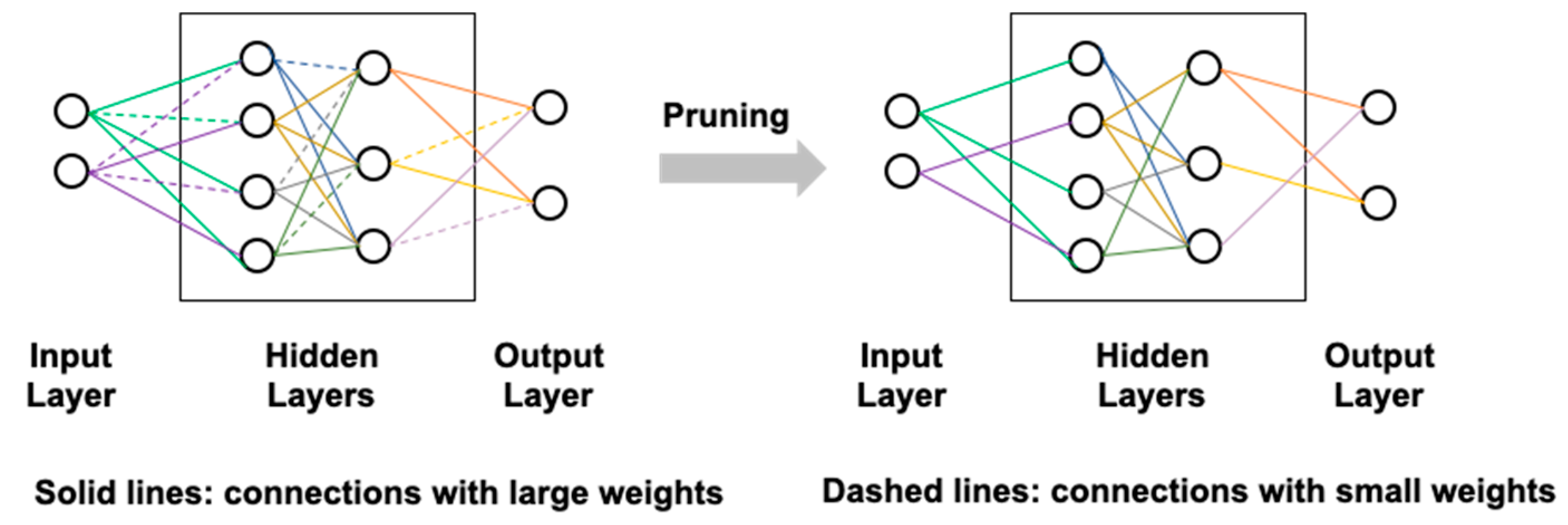
- Wan, Z.; Li, J.; Shu, L.; Luo, M.; Li, X.; Fu, S.; Xu, K. Nonlinear equalization based on pruned artificial neural networks for 112-Gb/s SSB-PAM4 transmission over 80-km SSMF. Opt. Express 2018, 26, 10631–10642. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, L.; Zhu, M.; Hu, S.; Xu, B.; Qiu, K. Fast remodelling for nonlinear distortion mitigation based on transfer learning. Opt. Lett. 2019, 44, 4243–4246. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- An, S.; Zhu, Q.; Li, J.; Ling, Y.; Su, Y. 112-Gb/s SSB 16-QAM signal transmission over 120-km SMF with direct detection using a MIMO-ANN nonlinear equalizer. Opt. Express 2019, 27, 12794–12805. [Google Scholar] [CrossRef]
- Ye, J.; Guo, Y.; Li, P.; Yan, L.; Pan, W.; Zou, X. 2-D quantization scheme utilizing SOFM neural network clustering for a DRoF system. Opt. Lett. 2018, 43, 4663–4666. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Y.; Zhi, T.; Chen, T. A survey of neural network accelerators. Front. Comput. Sci. 2017, 11, 746–761. [Google Scholar] [CrossRef]
- Lee, J.; He, J.; Wang, K. FPGA-based neural network accelerators for millimeter-wave radio-over-fiber systems. Opt. Express 2020, 28, 13384–13400. [Google Scholar] [CrossRef] [PubMed]
- Guesmi, L.; Menif, M. Modulation formats recognition technique using artificial network networks for radio over fiber systems. In Proceedings of the International Conference on Transparent Optical Networks, Budapest, Hungary, 5–9 July 2015; p. Tu.P.6. [Google Scholar]
- Alharbi, M.; Alhuseini, A.; Ragheb, A.; Altamimi, M.; Alshawi, T.; Alshebeili, S. Authomatic modulation classification: Investigation for millimeter wave over fiber channels. IEEE Photon. Technol. Lett. 2019, 31, 1092–1095. [Google Scholar] [CrossRef]
- Loumiotis, I.; Adamopoulou, E.; Demestichas, K.; Kosmides, P.; Theologou, M. Artificial neural networks for traffic prediction in 4G networks. In Proceedings of the International Wireless Internet Conference, Lisbon, Portugal, 13–14 November 2014; pp. 141–146. [Google Scholar]
- Loumiotis, I.; Stamatiadi, T.; Adamopoulou, E.; Demestichas, K.; Sykas, E. Dynamic backhaul resource allocation in wireless networks using artificial neural network. Electron. Lett. 2013, 49, 539–541. [Google Scholar] [CrossRef]
- Ruan, L.; Dias, M.P.I.; Wong, E. Enhancing latency performance through intelligence bandwidth allocation decisions: A survey and comparative study of machine learning techniques. J. Opt. Commun. Netw. 2020, 12, B20–B32. [Google Scholar] [CrossRef]
- Sarigiannidis, P.; Pliatsios, D.; Zygiridis, T.; Kantartzis, N. DAMA: A data mining forecasting DBA scheme for XG-PONs. In Proceedings of the International Conference on Modern Circuits and Systems Technologies, Thessaloniki, Greece, 12–14 May 2016; pp. 1–4. [Google Scholar]
- Wu, Y.; Tornatore, M.; Zhao, Y.; Mukherjee, B. Traffic classification and sifting to improve TDM-EPON fronthaul upstream efficiency. J. Opt. Commun. Netw. 2018, 10, C15–C26. [Google Scholar] [CrossRef]
- Mikaeil, A.M.; Hu, W.; Hussain, S.B. A low-latency traffic estimation based TDM-PON mobile front-haul for small cell cloud-RAN employing feed-forward artificial neural network. In Proceedings of the International Conference on Transparent Optical Networks, Bucharest, Romania, 1–5 July 2018; p. We.B2.5. [Google Scholar]
- Mo, W.; Gutterman, C.L.; Li, Y.; Zussman, G.; Kilper, D.C. Deep neural network based dynamic resource reallocation of BBU pools in 5G C-RAN ROADM network. In Proceedings of the Optical Fiber Communications Conference, San Diego, CA, USA, 11–15 March 2018; p. Th1B.4. [Google Scholar]
- Chien, W.-C.; Lai, C.-F.; Chao, H.-C. Dynamic resource prediction and allocation in C-RAN with edge artificial intelligence. IEEE. Trans. Ind. Electron. 2019, 15, 4306–4314. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, H.; Yu, A.; Yao, Q.; Bao, B.; Zhang, J. Capsule networks-based traffic prediction for resources deployment in B5G fronthaul network. In Proceedings of the International Wireless Communications and Mobile Computing, Limassol, Cyprus, 15–19 June 2020; pp. 1213–1215. [Google Scholar]
- Yang, H.; Wang, B.; Yao, Q.; Yu, A.; Zhang, J. Efficient hybrid multi-faults location based on Hopefield neural network in 5G coexisting radio and optical wireless networks. IEEE. Trans. Cogn. Commun. Netw. 2019, 5, 1218–1228. [Google Scholar] [CrossRef]
- Yu, A.; Yu, B.; Yang, H.; Yao, Q.; Zhang, J.; Cheriet, M. Deep reinforcement learning based time syncrhonization routing optimization for C-RoFN in beyond 5G. In Proceedings of the International Wireless Communications and Mobile Computing, Limassol, Cyprus, 15–19 June 2020; pp. 865–867. [Google Scholar]
- Li, Y.; Ji, H.; Li, X.; Leung, V.C.M. Dynamic channel selection with reinforcement learning for cognitive WLAN over fiber. Int. J. Commun. Syst. 2012, 25, 1077–1090. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, J.; Gao, Z.; Ji, Y. Service-oriented DU-CU placement using reinforcement learning in 5G/B5G converged wireless-optical networks. In Proceedings of the Optical Fiber Communications Conference, San Diego, CA, USA, 8–12 March 2020; p. T4D.5. [Google Scholar]
- Gao, Z.; Zhang, J.; Yan, S.; Xiao, Y.; Simeonidou, D.; Ji, Y. Deep reinforcement learning for BBU placement and routing in C-RAN. In Proceedings of the Optical Fiber Communications Conference, San Diego, CA, USA, 3–7 March 2019; p. W2A.22. [Google Scholar]
- Zhou, Q.; Chen, Y.-W.; Shen, S.; Kong, Y.; Xu, M.; Zhang, J.; Chang, G.-K. Proactive real-time interference avoidance in a 5G millimeter-wave over fiber mobile fronthaul using SARSA reinforcement learning. Opt. Lett. 2019, 44, 4347–4350. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, Y.; Tang, J.; Wang, J.; Gursoy, M.C. A deep reinforcement learning based framework for power-efficient resource allocation in cloud RANs. In Proceedings of the IEEE International Conference on Communications, Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Comsa, I.-S.; Domenico, A.D.; Ktenas, D. QoS-driven scheduling in 5G radio access networks—A reinforcement learning approach. In Proceedings of the IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–7. [Google Scholar]
- Natalino, C.; Raza, M.R.; Ohlen, P.; Batista, P.; Santos, M.; Wosinska, L.; Monti, P. Machine-learning-based routing of QoS-constrained connectivity services in optical transport networks. In Proceedings of the Advanced Photonics Congress, Zurich, Switzerland, 2–5 July 2018; p. NeW3F.5. [Google Scholar]
- Raza, M.R.; Natalino, C.; Ohlen, P.; Wosinska, L.; Monti, P. Reinforcement learning for slicing in a 5G flexible RAN. J. Lightw. Technol. 2019, 37, 5161–5169. [Google Scholar] [CrossRef] [Green Version]
- Nirmalathas, A.; Song, T.; Edirisinghe, S.; Tian, L.; Lim, C.; Wong, E.; Wang, K.; Ranaweera, C.; Alameh, K. Gigabit/s optical wireless access and indoor networks. In Proceedings of the Optical Fiber Communications Conference, San Diego, CA, USA, 8–12 March 2020; p. M2H.5. [Google Scholar]
- Dong, A.; Amin, O.; Shihada, B.; Alouini, M.-S. What should 66 be? Nat. Electron. 2020, 3, 20–29. [Google Scholar] [CrossRef] [Green Version]





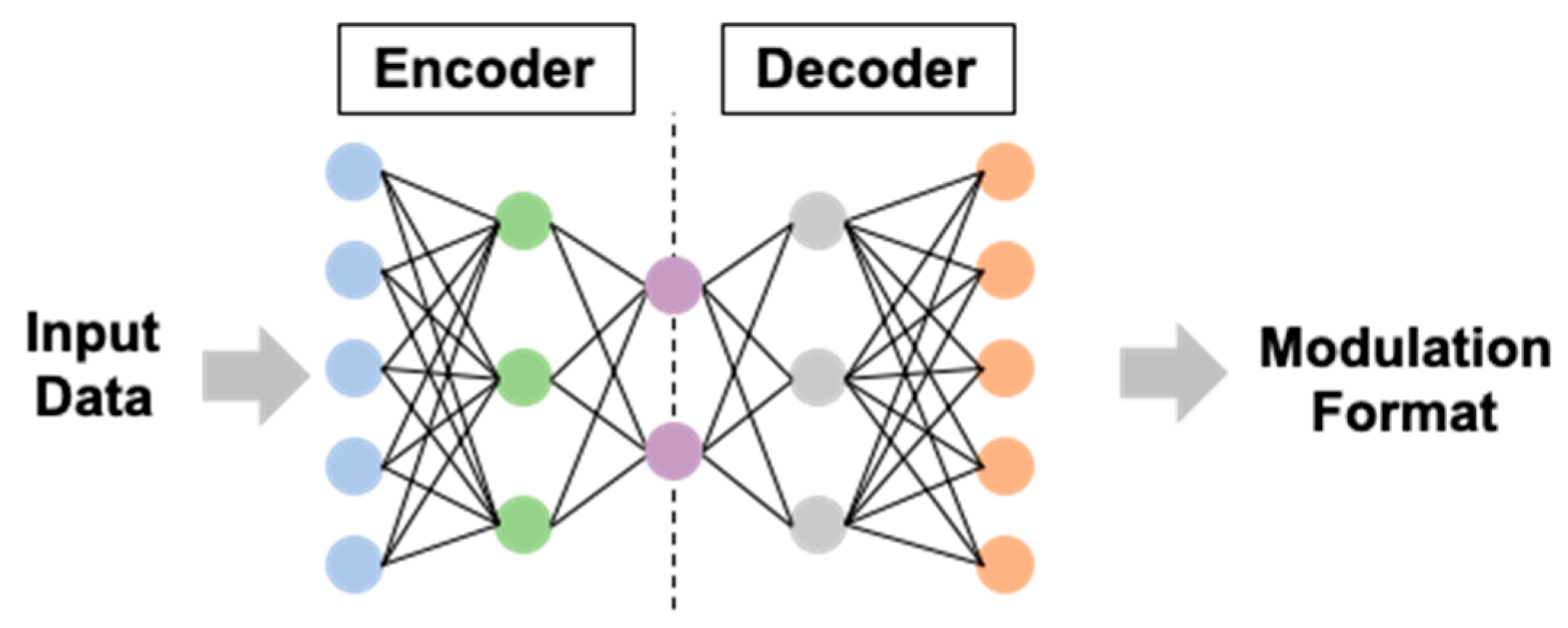
| Type of Neural Network | RoF System Configuration | Simulation or Experiment | Performance Improvement | Note |
|---|---|---|---|---|
| FCNN [80] | 60 GHz RF (DSB), 10 km fiber and 1.2 m wireless, BPSK, 5 Gbps | Experiment | 2 dB and 0.7 dB over Volterra equalizer for B2B and 10 km fiber | Adaptive activation function (reduce training iterations from 4000 to 2000) |
| FCNN [82] | 60 GHz RF (baseband over fiber), 15 km fiber, 0.4 GBaud/s, 16-QAM or 64-QAM | Experiment | Nonlinearity and phase rotations suppressed | Complex-value multi-level activation function |
| FCNN [83,84] | 60 GHz RF uplink, 0.8 m wireless and 15 km fiber (400 MHz IF over fiber), 266.7 Mbps | Experiment | Larger improvement with the joint equalization FCNN | 10,000 symbols for training |
| FCNN [85] | 5 GHz and 20 GHz RF signals | Experiment | 22.18 dB and 29.76 dB suppression for IMD3 and XMD | Good generalization against the interfere RF power |
| FCNN [86] | 10 GHz RF, 16 QAM UFMC at 20 Gbps (simulation), 4 QAM UFMC at 8 Gpbs (experiment) | Simulation + Experiment | EVM reduced by >50% compared with ZF (simulation) | 1% symbol used for training |
| FCNN [87] | 1800 with IM/DD (baseband over fiber), PAM8 | Experiment | 1.6 dB better receiver sensitivity than Volterra nonlinear equalizer | 64,000 data points for training. Equalizer + decoder |
| FCNN [88] | 20 km fiber (baseband over fiber), 80 Gbps, PS-PAM8 | Experiment | 3.2 dB better receiver sensitivity than LMS equalizer | 2 hidden layers, each with 1024 neurons. 60% data for training |
| FCNN [91] | 28 GHz RF uplink, 25 km fiber (4 GHz IF over fiber), 3 GHz signal, 4 QAM-OFDM | Experiment | NOMA demultiplexing latency reduced | Demultiplexing only (ZF equalization) |
| FCNN [92] | 56 GHz RF (OCS), about 10 km fiber, 2.344 Gbps, 16-QAM-OFDM | Experiment | Improved tolerance of channel synchronization | Demultiplexing only (frequency domain equalization) |
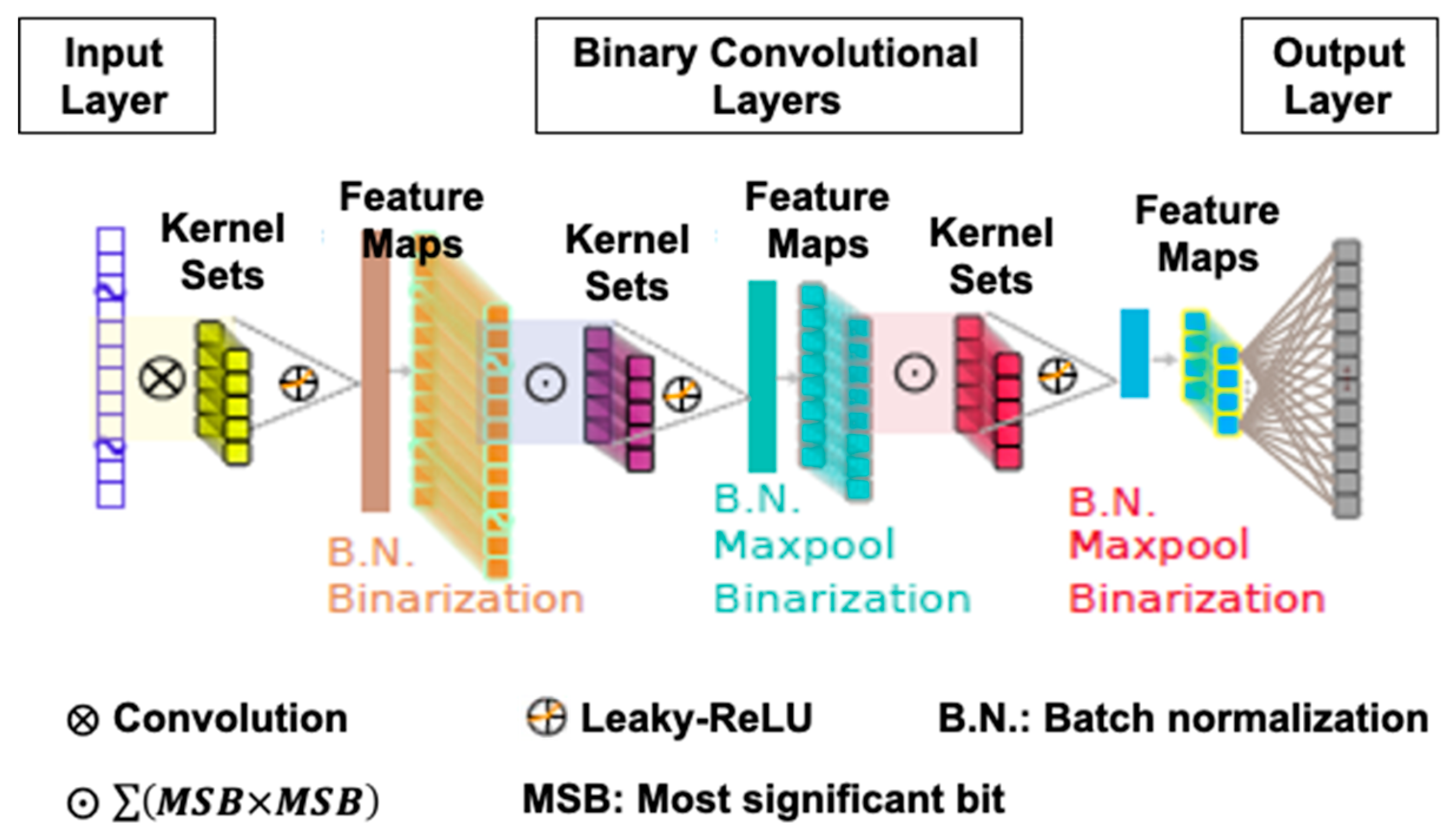
| CNN [93,94] | 60 GHz RF (OCS), up to 20 km fiber, 5 Gbps, PAM | Experiment | Similar BER with FCNN, 50% less training iterations and 30% smaller training dataset | 2 convolutional layers with 8 and 16 feature sets and kernel size |
| BCNN [93,94] | Same as above | Experiment | Slightly worse BER than FCNN or CNN, lower computation cost than CNN | 3 binary convolutional layers with 48, 64 and 72 feature sets and kernel size |
| Reference | Number of Hidden Layers | Number of Nodes in Layers | Activation Function | Type of Output Layer |
|---|---|---|---|---|
| [80] | 1 | Input: 12, Hidden: 16, Output: 1 | Modified Sigmoid function with variable coefficient | Fully-connected |
| [82] | 1 | Input: 10, Hidden: 10, Output: 1 | Modified Sigmoid function with multilevel | Fully-connected |
| [83,84] | 1 | Multi-users, Input: 20, Hidden: 24, Output: 4 | Modified Sigmoid function with multilevel | Fully-connected |
| [85] | 4 | N.A. | Sigmoid function | Fully-connected |
| [86] | 1 | Input: N.A., Hidden: 8–64, Output: N.A. | N.A. | Fully-connected |
| [87] | 1 | Input: 20, Hidden: 65, Output: 1 | Sigmoid function | Fully-connected |
| [88] | 2 | Input: 128, Hidden 1: 1024, Hidden 2: 2014, Output: 8 | Selu function | Fully-connected (softmax) |
| [89] | 1 | Input: 14, Hidden: 40, Output: 4 | Sigmoid function | Fully-connected (softmax) |
| [90] | 2 | Input: 160, Hidden 1: 1024, Hidden 2: 2014, Output: 8 | Selu function | Fully-connected (softmax) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Lee, J.; Kandeepan, S.; Wang, K. Machine Learning Techniques in Radio-over-Fiber Systems and Networks. Photonics 2020, 7, 105. https://doi.org/10.3390/photonics7040105
He J, Lee J, Kandeepan S, Wang K. Machine Learning Techniques in Radio-over-Fiber Systems and Networks. Photonics. 2020; 7(4):105. https://doi.org/10.3390/photonics7040105
Chicago/Turabian StyleHe, Jiayuan, Jeonghun Lee, Sithamparanathan Kandeepan, and Ke Wang. 2020. "Machine Learning Techniques in Radio-over-Fiber Systems and Networks" Photonics 7, no. 4: 105. https://doi.org/10.3390/photonics7040105
APA StyleHe, J., Lee, J., Kandeepan, S., & Wang, K. (2020). Machine Learning Techniques in Radio-over-Fiber Systems and Networks. Photonics, 7(4), 105. https://doi.org/10.3390/photonics7040105






