1. Introduction
When humans began traveling into space in the 1960s, one major, immediately recognized concern was the severe attenuation of radio communications caused by the plasma formed around the reentry vehicle. In particular, it was determined that when a vehicle moves at very high velocities within the atmosphere, the air in front of the vehicle becomes highly compressed and a shock wave is formed. This gas compression creates a significant amount of heat [
1]. With enough heat, the gases in the air within the shock wave will ionize and, thus, an electron plasma is created.
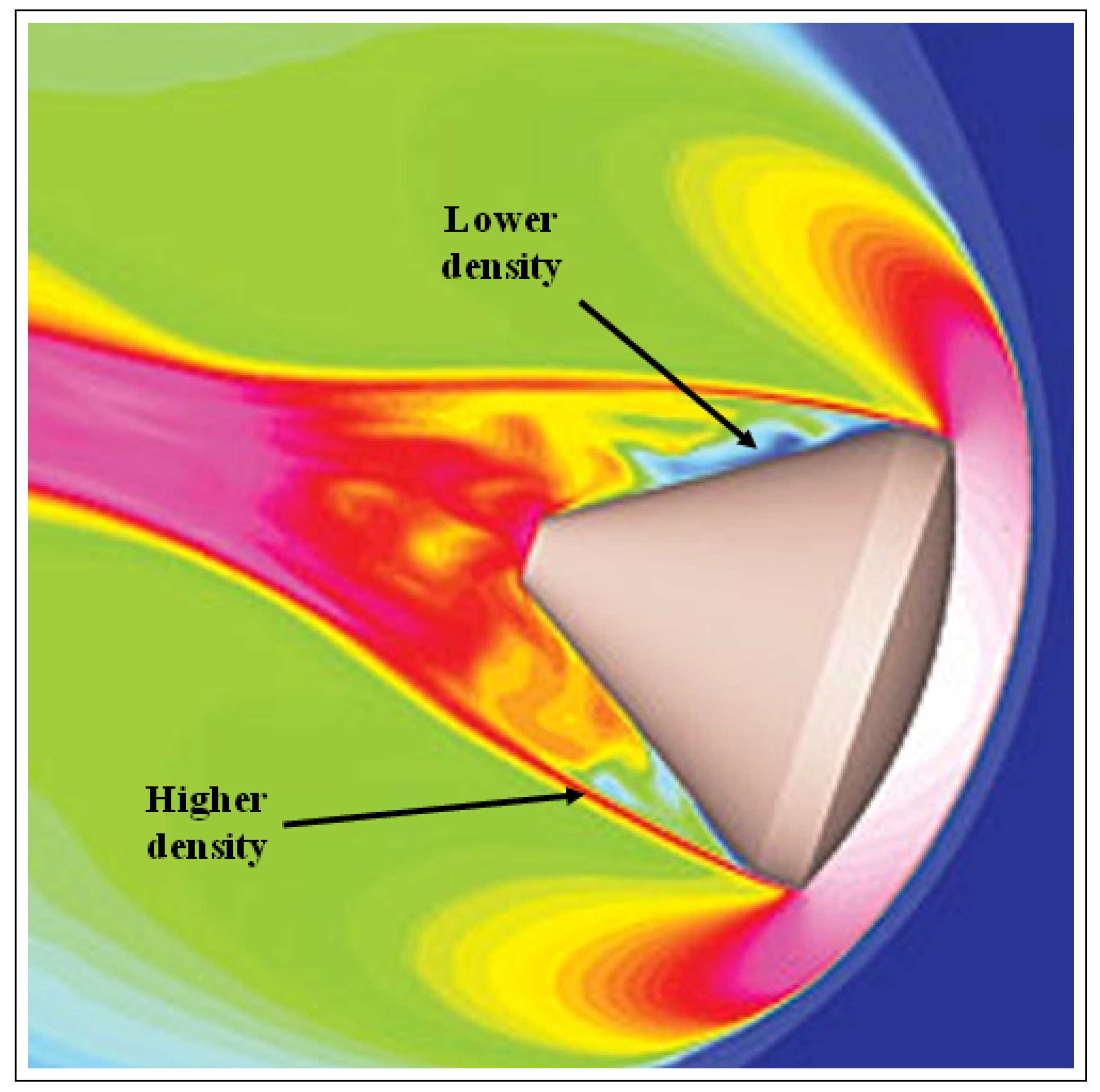
The presence of a plasma layer causes attenuation of the electromagnetic signals propagating through it. These signals are associated with a variety of radio frequency (RF) systems such as voice communications, telemetry, and global positioning system (GPS) data. The attenuation increases as the thickness and density of the plasma surrounding the reentry vehicle increases. An illustration of the plasma sheath surrounding a reentry vehicle is given in
Figure 1. Regions of lower and higher plasma density near the vehicle are indicated. The associated effects can become so severe that complete loss of voice communications and even GPS acquisition can occur.
This RF blackout can last anywhere from 90 s to 10 min depending on the trajectory and velocity of the reentry vehicle [
3]. It has had severe consequences, for example, in the unmanned Genesis mission to collect samples of solar winds. During reentry of the capsule, a sensor failure caused a parachute to not deploy. If mission control had been in contact with it, a backup parachute could have been deployed to avoid the capsule from crashing into the Utah desert [
4]. Similarly, hypersonic flight has been pursued with both manned and un-manned vehicles since 1961, e.g., with the X-15 hypersonic airplane which flew at Mach 6.7 using only rockets [
5]. As with the space vehicle reentry scenario, sustained hypersonic flight also faces the potential loss of communications, telemetry and GPS signals. Renewed interest in the RF blackout issue has arisen from the resurgence in interest into hypersonic delivery systems. Consequently, a reasonable solution to the RF blackout problem would greatly increase the chance of mission success for both space missions and hypersonic vehicular technologies.
Many approaches to ameliorate the RF blackout problem have been tried with varying degrees of success [
3]. Specifically, remote antenna assemblies [
6], which use antennas placed on sharp slender probes ahead of the plasma sheath of a blunt-nosed vehicle; magnetic windows [
7], which require generation of powerful magnetic fields; and the addition of quenchants to reduce the electron density [
8] or change chemical reaction rates [
9]. Implementing one or a combination of solutions may be the most appropriate path forward, depending on the application. System designers will need to evaluate all approaches as research continues to develop and explore new options. The focus in this paper is on a purely electromagnetics-based approach.
An artificial medium, the bed of nails or wire medium [
10], was created to study this plasma-related communications problem during the early stages of the Mercury-Gemini-Apollo space program in the 1960s. As will be described in
Section 2, the electron plasma acts as an epsilon-negative (ENG) medium for frequencies below its plasma frequency. It will be modeled as a Drude medium, and its electromagnetic attenuation and reflection mechanisms will be explained with it. This wire medium was popularized in the early stages of the birth of metamaterials [
11], and is now often recognized from the first reports of negative index [
12] and negative refraction [
13]. A matching mu-negative metasurface based on split-ring resonator (SRR) elements will be introduced in
Section 3. It is related to the SRR-based bulk metamaterial designed for artificial magnetic conductor (AMC) applications [
14]. As discussed in [
15,
16], an appropriate pairing of a MNG metamaterial layer with an ENG one leads to an effective medium through which electromagnetic waves will propagate. The developed MNG metasurfaces are loaded with varactors to enable an adjustable resonance frequency that can be matched to an ENG (plasma) medium with a specific permittivity value. It will be demonstrated that these SRR-based metasurfaces can be tuned to maximize the field transmission through the resulting MNG-ENG plasma layered medium. Finally, the propagation of signals through the MNG-ENG plasma effective medium will be modeled with the fields radiated by both dipole and Huygens dipole antennas in
Section 4. It will be demonstrated that the transmitted signal strength and cardioid-shaped pattern associated with the Huygens dipole antenna is an efficacious solution to the RF blackout problem. This metamterial-inspired answer to a long-standing practical issue associated with reentry and hypersonic vehicles will be summarized in
Section 5.
3. Drude Model
The Lorentz model of the polarization field,
, in a dielectric represents its response to the presence of an electromagnetic field in it. It is a second order differential equation that is synonymous with the damped simple harmonic oscillator model of a spring or the model of a RLC circuit. It is given by Equation (
3) [
16,
18].
where
is the damping rate,
is the resonance frequency, and
is the exciting electric field. Because of the difference in mass of an electron and a nucleus, this model of the wave–matter interaction principally describes the motion of the electrons. The resonance frequency is associated primarily with the restoring (attractive) force of the nucleus; the damping rate is associated with all of the interactions between an atom’s constituents.
The Lorentz model reduces to the Drude model when the restoring force is negligible in comparison to the driving force of the electromagnetic field. Therefore, the Drude model is applicable in cases where the material has a large amount of free electrons, such as metal or plasma. Assuming the engineering time convention
, the time harmonic form of the Drude model describes the relative permittivity of a plasma as [
16]
where the damping rate
takes the role of the plasma collision frequency and represents the losses. It is clear that in the case of a lossless Drude medium, Equation (
4) tells us that
when
. Thus, a low loss plasma essentially acts as an ENG medium when an electromagnetic field is propagating in it when the source frequency
is smaller than the plasma frequency
. Consequently, the plasma acts as an ENG medium depending on its density through
and
, and the field interacting with it.
Assuming the electron density is known, the plasma and collision frequencies can be calculated. The real part of the relative permittivity versus frequency can then be computed from Equation (
4). The result is the plot given in
Figure 3 with the electron density and the source frequency as the two independent axes. The real part of the permittivity is negative at low frequencies when the electron density is small. As the electron density increases, the negative region of the real permittivity extends into higher frequencies.
5. Antenna Performance in the Presence of the 2-Layer MNG-ENG Structure
The unit cell (i.e., the planar, periodic, transversely infinite) simulations demonstrated the proof of concept that a MNG-based metasurface can be designed to enable a passband in the presence of an electron plasma (i.e., an ENG medium). As an antenna on a reentry or hypersonic vehicle is ideally positioned within rather than on the structure for aerodynamic and structural integrity purposes, the MNG metasurface would be integrated as a window in the surface of the vehicle with the application antenna being located behind it relative to the exterior. Thus, simulations of the response of an antenna radiating in free space from the MNG side of the MNG-ENG structure were performed. The results demonstrate that the antenna–MNG metastructure can be designed to achieve application-significant transmission through the ENG-based plasma, e.g., for communications purposes.
5.1. Dipole Performance
Simulations with an idealized electrically small dipole antenna first illustrate this concept. The standard dipole antenna pattern is well known [
30]. The peak gain is 1.76 dBi.
Figure 12 shows the simulation model in the presence of the two-layer metastructure. A finite-sized MNG-based metasurface that consists of nine SRR unit cells is introduced on the antenna side of the ENG (plasma) layer. The thicknesses of the Duroid substrate and the plasma region were again fixed at 1.0 mm. The dipole antenna is centered along the y-axis at the origin and has the total length 11.8 mm. The dipole was implemented using 0.6 mm diameter cylinders with a 2.0 mm gap between them driven by a 50
discrete port. The finite-sized SRR material is located 10.0 mm away (
at 5.1 GHz, slightly beyond the reactive near field of the dipole,
). This offset distance from the metasurface is sufficient for this short dipole to effectively illuminate a significant portion of it directly, exciting its steady state MNG response. Note that the ENG material is located on the free space side opposite to that of the antenna as it would be for the reentry scenario. Also note that the linearly polarized dipole antenna is oriented along the x-axis. Consequently, its broadside electric field is also oriented along the x-axis, which is the optimal configuration, i.e., the electric field is oriented across the gaps of the two split rings in each SRR element to maximize the response of the metasurface.
The ENG region’s relative permittivity was set at
and its relative permeability was set at
. The unit cell design of the MNG metasurface was the same as the infinite periodic case; it was matched to the ENG region to obtain the passband at 5.1 GHz shown in
Figure 7 by specifying the capacitance value to be 1.0 pF. Because the metasurface is now finite in size, the actual transmission values are not identical to the infinite periodic case. Any reflection or absorption effects associated with this fact will now be exposed with comparisons of the far-field performance characteristics of the antenna in free space and in the presence of the layered MNG-ENG metastructure.
The far-field directivities of the dipole in its E- and H-planes are presented in the
Figure 13. Its frequency, 5.1 GHz, is matched to the passband of the MNG-ENG structure. Moreover, the size of the dipole is small relative to the overall size of the metasurface as is its distance from it. Consequently, there is very little leakage of the radiated field diffracted around it. The dipole was artificially matched to its idealized source to yield its best performance. The maximum directivity in the “exterior” (“interior”) free space region shown in the E-plane in
Figure 13a is 4.07 dBi (4.45 dBi) in the broadside +z (-z) direction. The higher than free-space broadside directivity in the
plane is an immediate consequence of the significant narrowing of the field pattern brought about by the inherent enhanced response of the metastructure to the x-directed electric field. On the other hand, the expected omnidirectional directivity pattern in the H-plane in
Figure 13b only shows a bit of distortion along the y-directions. This distortion is the direct result of the magnetic fields of the finite-sized dipole, which are no longer parallel to the metasurface but rather, are obliquely incident on it. Thus, they impact the performance of the SRR elements, which in fact have a bi-anisotropic response. Nonetheless, the results demonstrate that the effective DNG metastructure does provide an passband window for signals radiated by the dipole antenna. Nevertheless, the dipole itself, being a bidirectional radiator, directs slightly more than half of its radiated power into the source region. In particular, the realized gain in the broadside, +z-direction is 2.48 dBi and is 2.85 dBi in the -z-direction.
5.2. Huygens Design Performance
Ultimately, a unidirectional antenna is highly desired for any “sub-exterior surface” antenna system. The electrically small Huygens dipole antennas developed in [
31,
32,
33,
34] are advantageous in this regard. The linearly-polarized Huygens antenna is made up of three major components: a capacitively loaded loop (CLL), an Egyptian axe dipole (EAD), and a smaller dipole that excites these near-field resonant parasitic (NFRP) elements by coupling energy into them. In free space they are electrically small systems that radiate a broad beamwidth, unidirectional cardioid pattern with basically a 3 dB peak directivity enhancement over that of an equivalent sized dipole antenna. The Huygens design in [
31] was modified to have the same operating frequency as that of the dipole case, 5.1 GHz. The modified design is shown in
Figure 14, and the design parameters are shown in
Table 1.
Its performance was verified first in free space. The CST simulation results are shown in
Figure 15. The cardioid nature of the patterns is immediately recognized. The peak directivity, 4.15 dBi, at 5.1 GHz is in the broadside +z direction; the corresponding front-to-back ratio (FTBR) is 10.9 dB. The corresponding peak realized gain value is 3.58 dBi. The associated minimum FTBR is 10.9 dB. The radiation efficiency is 88.6%.
The same MNG-ENG metastructure used in the dipole case was then introduced. As the Huygens antenna is also linearly polarized, it was also oriented with its electric NFRP element oriented along the x-axis as shown in
Figure 14a to maximize the response of the MNG metasurface. Moreover, as with the dipole antenna, it was located 10 mm from the front surface of the MNG layer.
The corresponding realized gain patterns in the two principal planes,
= 0
and
= 90
, at 5.1 GHz of the Huygens dipole antenna in the presence of the MNG-ENG layered metastructure with
= −2.0 in the plasma layer and the capacitor = 1.0 pF to attain the MNG layer with
, are shown in
Figure 16a. The peak directivity, 5.87 dBi, at 5.1 GHz remains in the broadside +z direction; the corresponding FTBR is 4.7 dB. The associated peak realized gain in the +z-direction is 3.40 dBi, and the radiation efficiency is 92.9%.
Note that the cardioid nature of the patterns is distorted from their free space shape but its resemblance is still recognizable. The MNG-ENG structure has unbalanced the relative electric and magnetic dipole responses of the free-space Huygens design. Nevertheless, the results clearly demonstrate that significant field levels are radiated into the exterior, free space region. In fact, these results compare favorably with the free space ones. They clearly demonstrate that the combination of the metastructure and a Huygens dipole antenna could potentially be successful in mitigating the plasma blackout problem.
Moreover, note that there was an unexpected directivity improvement in the +z-direction along with some narrowing in the patterns in both the and planes. It is associated with the fact that the MNG-ENG pair in this case is a conjugate match. In particular, the MNG-ENG metastructure is nearly transparent at every incident angle. However, due to the anisotropic nature of the SRRs in the realistic MNG layer, its response does vary away from the broadside direction. It was found that this effect actually causes the MNG-ENG metastructure to act as a lens, directing more power into the broadside direction with a corresponding narrowing of the realized gain patterns.
Another consequence of the lensing effect is that the beamwidth in the
= 90
plane can be adjusted at the cost of realized gain by varying the distance between the metastructure and the Huygens dipole antenna. The results of a parameter study of the pattern quality as the distance between the antenna and the metastructure was varied are summarized in
Table 2. The general effects are clearly seen in the comparison between the 5.5 mm spacing results shown in
Figure 16b and the 10.0 mm spacing results in
Figure 16a.
Moving the antenna away from the metastructure narrows the −3 dB beamwidth while increasing the realized gain in the +z direction and generally reducing the associated FTBR value. On the other hand, moving the antenna closer to the metastructure generally broadens the beamwidth while decreasing the realized gain and increasing the FTBR. While the lensing effect is more severe and particularly noticeable in the
plane, where the SRRs have their strongest response, the beamwidth remains relatively constant between 50
to 60
despite the dramatic visual narrowing of the pattern. It is found that if the antenna is moved too close to the metastructure, the beamwidth in the
= 90
plane becomes much larger than 180
and the FTBR decreases as the overall pattern tends to become essentially fan-like. The 5.5 mm and 7.0 mm spacing choices yield both acceptable realized gain and FTBR values. Comparing the realized gain patterns in
Figure 16, the differences in the peak directivity and FTBR features are now understood.
6. Parameter Studies
With these very positive directivity results in hand, the thickness of the plasma and its impact on the magnitude of the field radiated past it into free space became yet another interesting issue. Returning to the TMM code, variations of the plasma thickness and incident angle were investigated to understand how the attenuation changes as the incident angle does. The results are shown in
Figure 17.
As the plasma thickness increases, the attenuation increases quickly for large off-axis angles. The effect causes the beam to narrow as the plasma thickness increases. This narrowing outcome supports the desire to have a more directive antenna for the application. The previous results for the antenna-MNG layer distance of separation then suggest that this off-axis angle effect might be somewhat counteracted by moving the antenna farther away to increase the resulting directivity and narrowing the beam further. On the other hand, depending on where the receiving antenna is relative to the location of the antenna system in the reentry vehicle, one might want to move the antenna closer to the MNG interface to enhance the probability of receiving the transmitted signal knowing that this separation distance will widen the beamwidth even though an increased attenuation penalty would occur. A system engineering design analysis as to whether or not the position of the antenna should be movable to take advantage of this physics may be advantageous.
As demonstrated in [
15], a conjugate match requires that
or equivalently with
for the Region 3 and 4 material properties that we have assumed. Consequently, with the Region 3 permittivity set to
, this means that if
is varied linearly with the plasma thickness as
, the conjugate match should be maintained. As the SRR design is frequency tunable, the actual value of
could be increased simply by moving its resonance point closer to the operating frequency.
To investigate if there would be any advantage to adjusting its value in anticipation of a particular thickness, the TMM code was used to calculate the attenuation experienced by the fields with the MNG-layer permeability adjusted for the thickness of the plasma. The results obtained by setting
1.0 mm and
are shown in
Figure 18 for
again varying from 1.0 to 20.0 mm for three different values of
. While they appear to show some slight advantage at further distances, the results actually indicate that the initial level of the field in the plasma region is negatively affected by not matching the plasma next to the vehicle. There is no means to recoup the signal level once it has entered into the plasma region. This result confirms that the best strategy is to match the MNG layer to the permittivity of the ENG layer as it begins.
As discussed in many recent reentry plasma studies [
23,
24], the plasma density of the plasma layer is not constant as the distance from the reentry vehicle increases, i.e., the permittivity of the plasma has a profile. As noted above, it depends on many factors such as the actual vehicle shape, its angle of attack entering the atmosphere, and its speed. To understand the impact of the profile on the transmitted signal, the four region problem was considered with the simple profile for Region 3 shown in
Figure 19a. The permittivity has
−2.0 in the 1.0 mm thick layer at the reentry vehicle’s surface and assumes a plasma density in the sheath that reaches its maximum at 30.0 mm away from it and then reaches free space at a distance of 50.0 mm. The calculated transmission coefficient with
−2.0 is shown in
Figure 19b.
The main takeaway from this result is that the attenuation level reaches a maximum value that is just slightly less than −40 dB for this profile and then begins to decrease to zero at the outer boundary of the plasma. As noted above, the signal would thus experience a decrease of around that maximum value. While it seems to be a large decrease, even larger attenuation levels are encountered in existing practical systems. For example, the up and down links for satellite communications to and from the earth experience path losses from 100–200 dB each way depending on the signal frequencies, weather, and satellite altitudes [
35,
36]. These large propagation losses explain why large reflector antennas with extremely high directivities are required to counteract them in such communication scenarios. Again, the analysis indicates that a proper matching of the permeability of a single MNG layer to the permittivity of the plasma next to the reentry vehicle leads to a potential, practical engineering solution.
Nevertheless, instead of restricting oneself to a single MNG layer that may require a rather large negative permeability value to counteract a high plasma density region next to the vehicle, one could consider replacing the single layer with a multilayer structure that alternates artificially realized ENG and MNG layers [
15] until the initial layer of the plasma region is reached to obtain an effective
value to match the anticipated plasma thickness or negative permittivity value, and therefore its associated larger
value. In this sense, the plasma layer is always instantiated as the last layer, with the rest of the layers being optimized to provide the conjugate match and the consequent DNG metastructure. This multilayer approach requires the thickness of each layer,
, for
, to be less than about 1/8th of the wavelength in each layer, i.e.,
, where
is the index of refraction in the m-th layer. By changing
, the multilayer structure can be designed to act as a bandpass filter with the thickness
determining the center frequency of the filter. This response is well-known; it is what is encountered in one-dimensional periodic structures [
37,
38] such as Bragg mirrors [
39,
40].
The S-parameters of a representative 10-layer structure of alternating
and
layers for 2 different layer and plasma thicknesses,
mm
, and
mm
, where
mm is the wavelength in each layer at 5.1 GHz, are shown in
Figure 20a,b, respectively. The band pass response at the desired operating frequency is clearly obtained in the 5.23 mm case. Note that if the dielectric thickness,
, was increased much beyond a fifth of the source wavelength, then the dramatic evanescent wave decay shown with the previous two layer cases takes over. Even though its response may become quite narrow in bandwidth because the plasma layer may be thick, by designing the resulting Bragg filter to have its maximum transmission at the desired operating frequency, i.e., to have it tuned to the resonance frequency of the Huygens dipole antenna and completely encompass its narrow bandwidth, a relatively strong signal—even a Morse code signal at a specific frequency—could be inserted into the plasma region with a significant chance of reaching the free space region with strong enough signal strength to establish even rudimentary communications during reentry. Similarly, the narrow bandwidth signal emitted by a GPS satellite could reach a well-placed receiving antenna in the vehicle.
7. Conclusions
The design of a metasurface and a Huygens dipole antenna to facilitate the transmission of signals through a reentry plasma was examined. A 1.0 mm thick SRR-based MNG metasurface was developed whose properties are tunable. It was combined with the plasma layer to form a two-layer MNG-ENG metastructure that produced a passband with very high transmission levels. The DNG properties of this metastructure overcame the deleterious evanescent field behavior when only the ENG plasma layer is present. It was demonstrated with both electrically small dipole and Huygens dipole antennas that significant power could be radiated into the the plasma region with an appropriately configured MNG-ENG metastructure. The MNG-ENG structure was specifically designed to be a conjugate match for the base case with a 1.0 mm thick plasma with next to the reentry vehicle, i.e., the MNG layer was designed to have at the C-band operating frequency, 5.1 GHz. The peak realized gain with the Huygens dipole antenna was up to 2.01 dBi higher than the simple dipole reference case.
Further adaptability of the MNG-ENG metastructure was demonstrated on the basis of the anisotropic nature of the SRRs to facilitate a narrowing of the beamwidth of the radiated fields along the direction orthogonal to the linear polarization direction of the antennas while essentially maintaining a consistent beamwidth, but narrower overall pattern in the parallel direction. Moving the Huygens dipole antenna closer to the metastructure creates a broader beam at the expense of some broadside peak realized gain and vice versa. This feature to narrow or widen the beamwidth could help the applicability of the reported approach. It also could allow the pattern of a single system to transition dynamically between a wide and narrow beamwidth if the position of the antenna was allowed to change physically relative to the metastructure.
Several different properties of the complex media system were explored to understand the level of attenuation a radiated signal would face under different plasma conditions. Both constant and profiled plasma permittivity issues were investigated. The results indicated that the best approach was to conjugately match the MNG layer to the properties of the plasma layer next to the reentry vehicle. While the resulting attenuation corresponding to a plausible plasma profile associated with a reentry scenario was considerable, the maximum level nevertheless was not perceived to be insurmountable in practice.
This work has identified a path to potentially overcome the blackout problem faced by reentry spacecraft and hypersonic aerial vehicles. While the tunable two layer MNG-ENG metastructure was proven to be effective for the assumed plasma thickness, extending the range and properties of the metastructure, such as with the multilayer Bragg filter design to conjugately match the plasma permittivity and thickness, is currently under investigation. The simple varactor-based tunability of the MNG metasurface illustrates that it could be readily matched to the various plasma regions that might be faced during reentry. Moreover, it was demonstrated that the Huygens dipole antenna design could be modified to adapt to the projected plasma conditions and resulting MNG-ENG structure. Thus, the developed approach could significantly extend the communication window of the aerial vehicle with its mission control center by crucial seconds or minutes depending on the trajectory and speed of the aerial vehicle as it propagates through the atmosphere.